Capitolo 38 Un’applicazione concreta

Consideriamo un altro esempio che ci consentirà di approfondire la nostra conoscenza dei modelli LGM. L’esempio che discuteremo utilizza un campione di dati artificiali chiamato Demo.growth in cui si ipotizza che un determinato punteggio venga misurato su quattro punti temporali. I dati sono i seguenti:

data(Demo.growth)
glimpse(Demo.growth)
#> Rows: 400
#> Columns: 10
#> $ t1 <dbl> 1.7256454, -1.9841595, 0.3195183, 0.7769485, 0.4489440, -1.7469951,…
#> $ t2 <dbl> 2.1424005, -4.4006027, -1.2691171, 3.5313707, -0.7727747, -0.996340…
#> $ t3 <dbl> 2.77317167, -6.01655626, 1.56001603, 3.13821140, -1.50351504, -0.82…
#> $ t4 <dbl> 2.51595586, -7.02961801, 2.86852958, 5.36374139, 0.07846742, 0.5669…
#> $ x1 <dbl> -1.1641026, -1.7454025, 0.9202112, 2.3595236, -1.0887077, -0.513516…
#> $ x2 <dbl> 0.17422932, -1.57686022, -0.14181802, 0.70796813, -1.00999772, -0.1…
#> $ c1 <dbl> -0.02767765, -2.03196724, 0.05237496, 0.01911429, 0.65243274, -0.04…
#> $ c2 <dbl> 0.55492337, 0.12533477, -1.25774075, 0.64738300, 0.73091476, -0.416…
#> $ c3 <dbl> 0.254478433, -1.564232274, -1.803390895, -0.432379510, -0.753781573…
#> $ c4 <dbl> -1.00639541, 1.22926875, -0.32725761, -1.03239779, -0.02745598, 0.5…

La variabile dipendente è rappresentata dalle quattro colonne chiamate t1, t2, t3 e t4 che corrispondono alla serie temporale con quattro misurazioni per ciascun soggetto.

Trasformiamo i dati in formato long:

demo_growth_long <- Demo.growth %>%
  dplyr::select(t1, t2, t3, t4) %>%
  pivot_longer(
    cols = starts_with("t"),
    names_to = "t",
    values_to = "y"
  ) %>%
  as.data.frame()
demo_growth_long$time <- rep(0:3, 400)
demo_growth_long$id <- rep(1:400, each = 4)

Esaminiamo un campione casuale di 9 soggetti. È presente una notevole variazione da soggetto a soggetto:

id_sel <- sample(1:400, 9)
d <- demo_growth_long[demo_growth_long$id %in% id_sel, ]
d %>%
  ggplot(aes(x = time, y = y)) +
  geom_line() +
  facet_wrap(~id)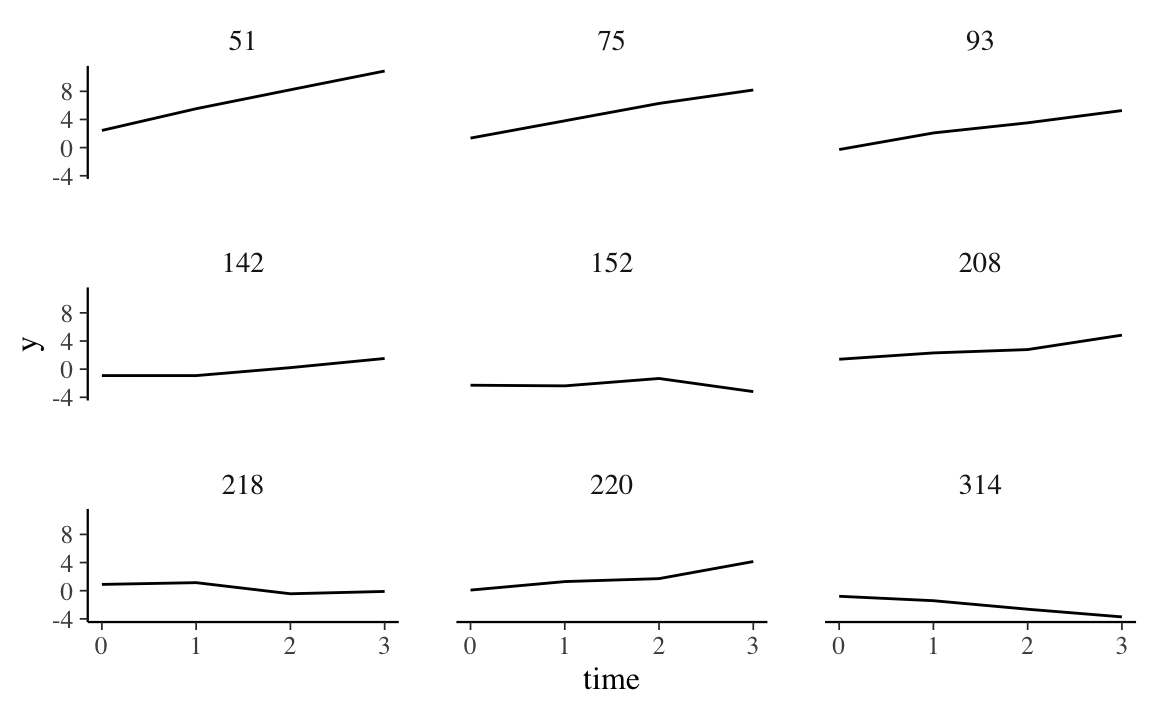

Notiamo che una funzione lineare è appropriata per rendere conto della variazione temporale della variabile risposta:

d %>%
  ggplot(aes(x = time, y = y)) +
  geom_point() +
  stat_smooth(method = "lm", se = FALSE) +
  facet_wrap(~id)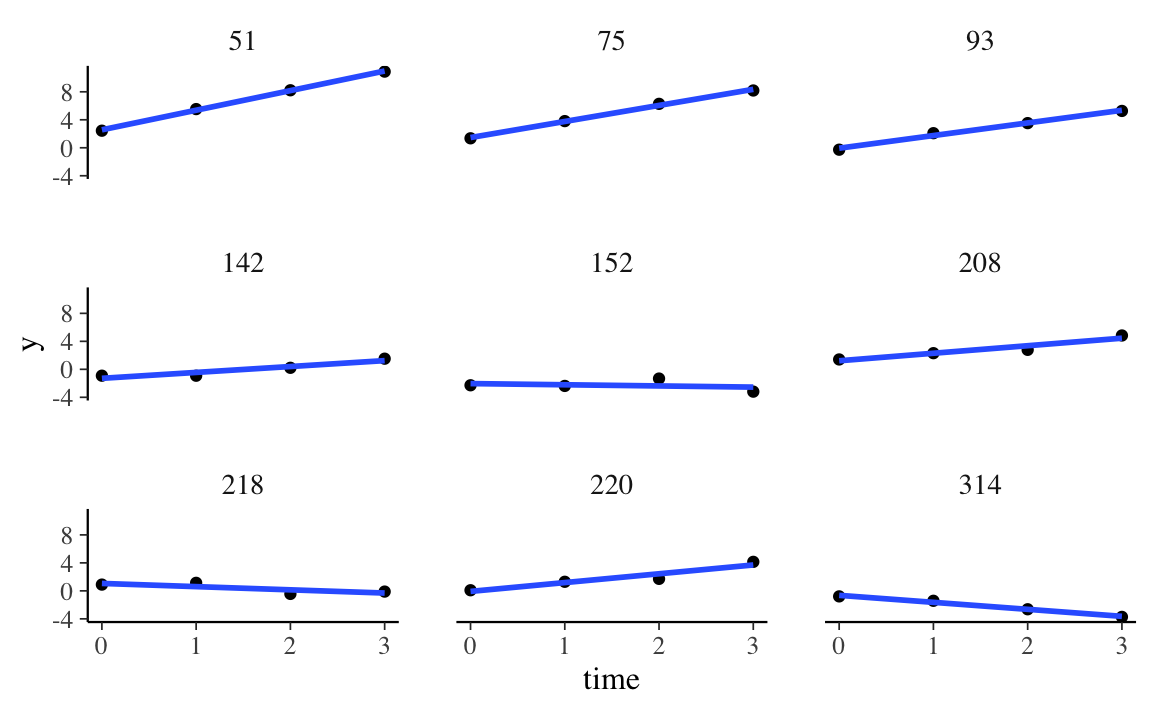

Complessivamente, i dati suggeriscono un andamento crescente della variabile risposta in funzione del tempo:

demo_growth_long %>%
  ggplot(aes(time, y, group = id)) +
  geom_line(alpha = 0.1) + # add individual line with transparency
  stat_summary( # add average line
    aes(group = 1),
    fun = mean,
    geom = "line",
    size = 1.5,
    color = "black"
  ) +
  labs(x = "Time", y = "y")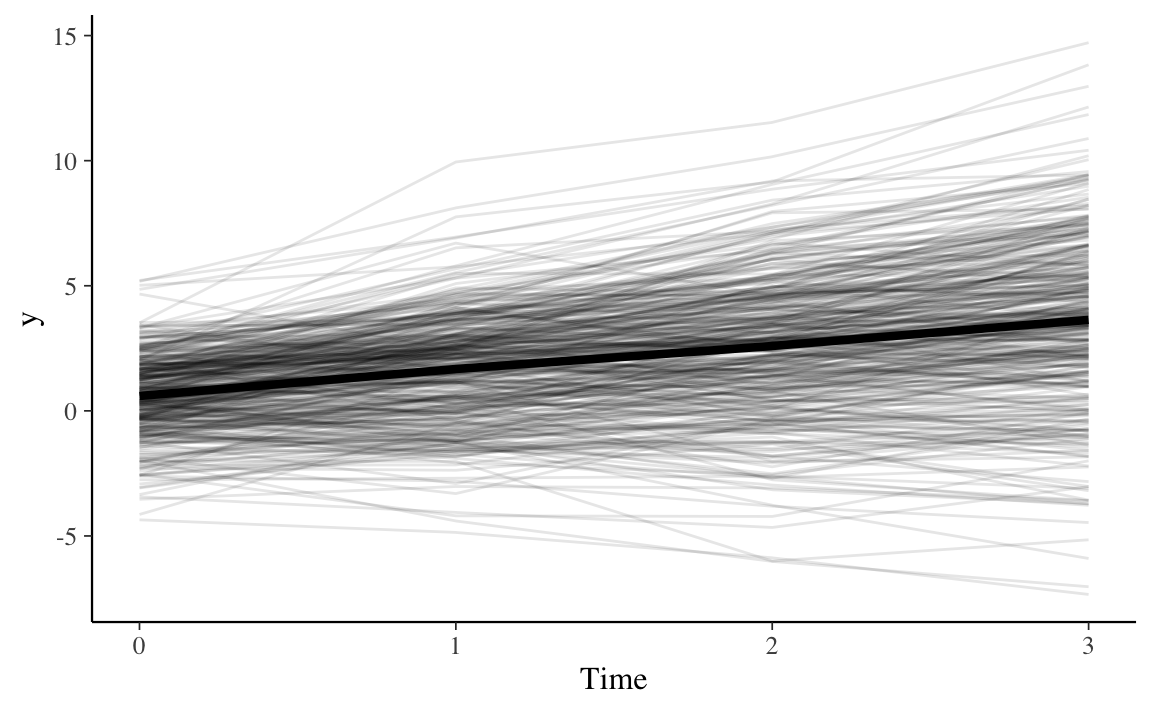

Abbiamo visto come un modello lineare di crescita latente corrisponde ad un modello fattoriale con due variabili latenti: un fattore (\(\eta_0\)) che specifica il “punteggio vero” delle intercette individuali e un fattore (\(\eta_1\)) che speficita il “punteggio vero” delle pendenze delle rette di regressione per i singoli individui. Nella sintassi lavaan il modello LGM diventa:

model <- "
 i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
 s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4
"

Si noti che, per il fattore \(\eta_0\) (che rappresenta le intercette), i valori delle saturazioni fattoriali sono fissate a 1 – questo è il motivo per cui \(\alpha_0\) e \(\zeta_{00}\) compaiono da soli nell’equazione precedente: in maniera esplicita sono \(1 \cdot \alpha_0\) e \(1 \cdot \zeta_{00}\).

Le saturazioni per il fattore \(\eta_1\) (che specifica le pendenze delle funzioni lineari) sono fissate ai valori che descrivono la variazione temporale: qui i valori \(\lambda_j\) da 0 a 3.

Il modello include anche la correlazione tra \(\eta_0\) e \(\eta_1\), rappresentata dalla doppia freccia \(\zeta_{01}\). Se \(\zeta_{01} > 0\), questo significa che, con il passare del tempo, i partecipanti tendono a diventare sempre più diversi tra loro; un’interpretazione opposta si ha se \(\zeta_{01}< 0\).

Adattiamo il modello ai dati:

fit <- growth(model, data = Demo.growth)
summary(fit)
#> lavaan 0.6.15 ended normally after 29 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                         9
#> 
#>   Number of observations                           400
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                                 8.069
#>   Degrees of freedom                                 5
#>   P-value (Chi-square)                           0.152
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>   i =~                                                
#>     t1                1.000                           
#>     t2                1.000                           
#>     t3                1.000                           
#>     t4                1.000                           
#>   s =~                                                
#>     t1                0.000                           
#>     t2                1.000                           
#>     t3                2.000                           
#>     t4                3.000                           
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>   i ~~                                                
#>     s                 0.618    0.071    8.686    0.000
#> 
#> Intercepts:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>    .t1                0.000                           
#>    .t2                0.000                           
#>    .t3                0.000                           
#>    .t4                0.000                           
#>     i                 0.615    0.077    8.007    0.000
#>     s                 1.006    0.042   24.076    0.000
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>    .t1                0.595    0.086    6.944    0.000
#>    .t2                0.676    0.061   11.061    0.000
#>    .t3                0.635    0.072    8.761    0.000
#>    .t4                0.508    0.124    4.090    0.000
#>     i                 1.932    0.173   11.194    0.000
#>     s                 0.587    0.052   11.336    0.000

Esaminiamo il path diagram.

semPaths(
  fit,
  layout = "tree",
  intercepts = FALSE,
  posCol = c("black"),
  edge.label.cex = 0.00001,
  sizeMan = 7,
  what = "path",
  optimizeLatRes = TRUE,
  residuals = TRUE,
  style = "lisrel"
)

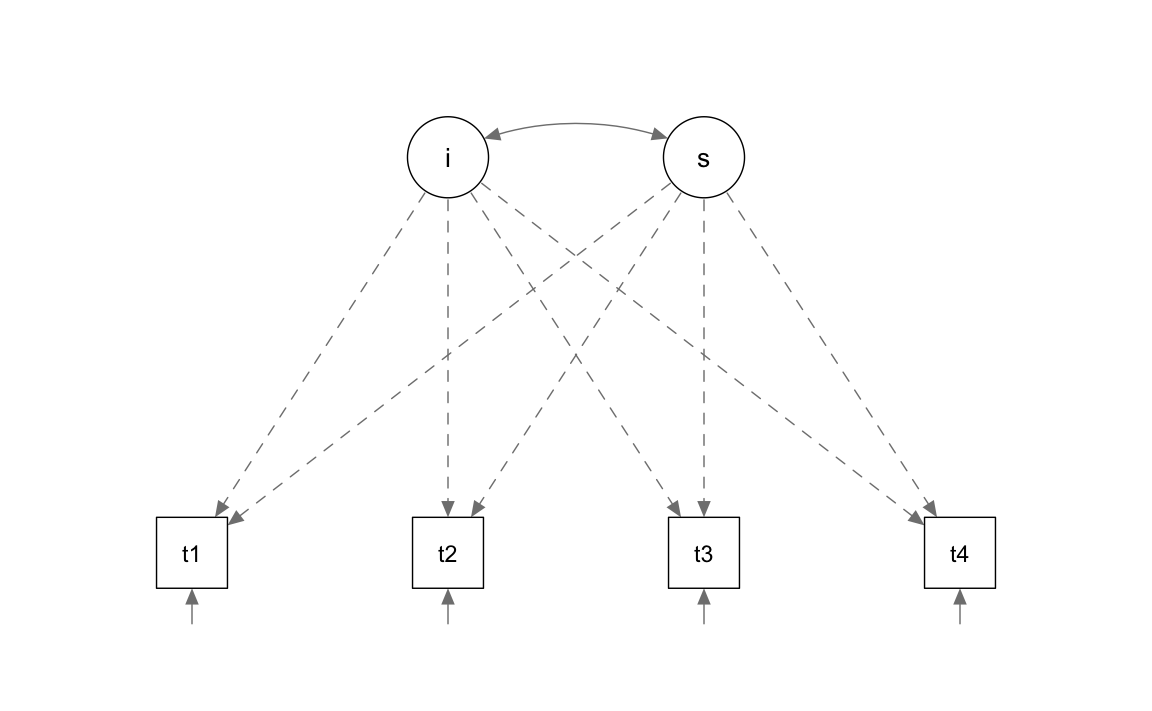
Ci sono 6 tipi di parametri di interesse:

kable(coef(fit), booktabs = TRUE, format = "markdown")

	x
t1~~t1	0.5952890
t2~~t2	0.6760337
t3~~t3	0.6348906
t4~~t4	0.5076449
i~~i	1.9319804
s~~s	0.5869142
i~~s	0.6178630
i~1	0.6146957
s~1	1.0062943

l’intercetta \(i\) = 0.615 è il valore atteso della variabile risposta al momento \(t_0\);
la pendenza \(s\) = 1.006 è il tasso di cambiamento medio della variabile risposta nel tempo. Ad ogni successivo momento temporale, il valore medio della variabile risposta aumenta in media di 1.006 punti;
varianza \(i\) = 1.932 misura la variazione tra i soggetti al momento \(t_0\) (ci dice quanto sono diverse le intercette delle rette di regressione tra i soggetti);
varianza \(s\) = 0.587 misura la variazione del tasso di crescita tra i soggetti (ci dice quanto sono diverse le pendenze delle rette di regressione tra i soggetti);
varianze t1, …, t4: i valori da 0.595 a 0.508 descrivono la variazione tra i soggetti in ciascun momento del tempo;
la covarianza tra i e s = 0.618 ci dice che i valori della variabile risposta diventano via via più diversi nel tempo tra i rispondenti (un valore negativo avrebbe l’interpretazione opposta).

Le stime dell’intercetta e della pendenza della funzione di crescita per ciascun partecipante si ottengono nel modo seguente:

rand_eff <- as.data.frame(lavPredict(fit))
head(rand_eff)
#>            i           s
#> 1  1.2275557  0.60278312
#> 2 -2.6795847 -1.38498215
#> 3 -0.2955058  0.88828376
#> 4  1.1576419  1.34051395
#> 5 -0.4355522  0.03193498
#> 6 -1.3121802  0.50258530

Istogrammi delle stime individuali dell’intercetta e della pendenza della curva di crescita si ottengono nel modo seguente:

gi <- rand_eff %>%
  ggplot(aes(x = i)) +
  geom_histogram()
gh <- rand_eff %>%
  ggplot(aes(x = s)) +
  geom_histogram()
gi + gh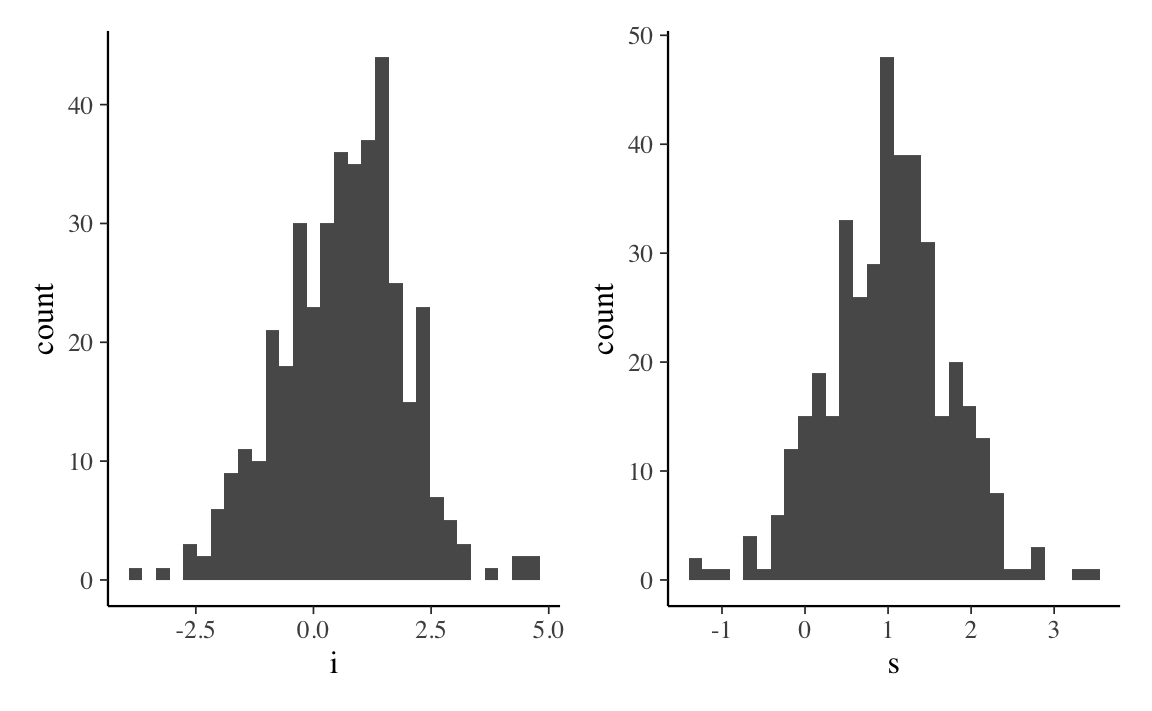

38.0.1 Visualizzare il cambiamento

È utile visualizzare i punteggi previsti dal modello. A tal fine, useremo qui la funzione predict() per creare un nuovo oggetto \(\mathsf{R}\) che contiene i punteggi previsti a livello individuale per l’intercetta e la pendenza.

pred_lgm <- predict(fit)
head(pred_lgm)
#>               i           s
#> [1,]  1.2275557  0.60278312
#> [2,] -2.6795847 -1.38498215
#> [3,] -0.2955058  0.88828376
#> [4,]  1.1576419  1.34051395
#> [5,] -0.4355522  0.03193498
#> [6,] -1.3121802  0.50258530

Questi sono i valori previsti dal modello per ciascun partecipante. Se calcoliamo la media di queste variabili otteniamo gli stessi risultati che sono stati riportati sopra:

# average of the intercepts (first column)
mean(pred_lgm[, 1])
#> [1] 0.6146957
# average of the slope (second column)
mean(pred_lgm[, 2])
#> [1] 1.006294

Il cambiamento nel tempo previsto dal modello per il soggetto \(j\)-esimo è

\[ y_j = \eta_0 + \lambda_j \eta_1. \]

Il cambiamento previsto per tutti i soggetti può essere visualizzato nel modo seguente:

# create long data for each individual
pred_lgm_long <- map(
  0:3, # loop over time
  function(x) pred_lgm[, 1] + x * pred_lgm[, 2]
) %>%
  reduce(cbind) %>% # bring together the wave predictions
  as.data.frame() %>% # make data frame
  setNames(str_c("time", 0:3)) %>% # give names to variables
  mutate(id = row_number()) %>% # make unique id
  gather(-id, key = time, value = pred) # make long format
# make graph
pred_lgm_long %>%
  ggplot(aes(time, pred, group = id)) + # what variables to plot?
  geom_line(alpha = 0.1) + # add a transparent line for each person
  stat_summary( # add average line
    aes(group = 1),
    fun = mean,
    geom = "line",
    size = 1.5,
    color = "black"
  ) +
  labs(y = "y", x = "time")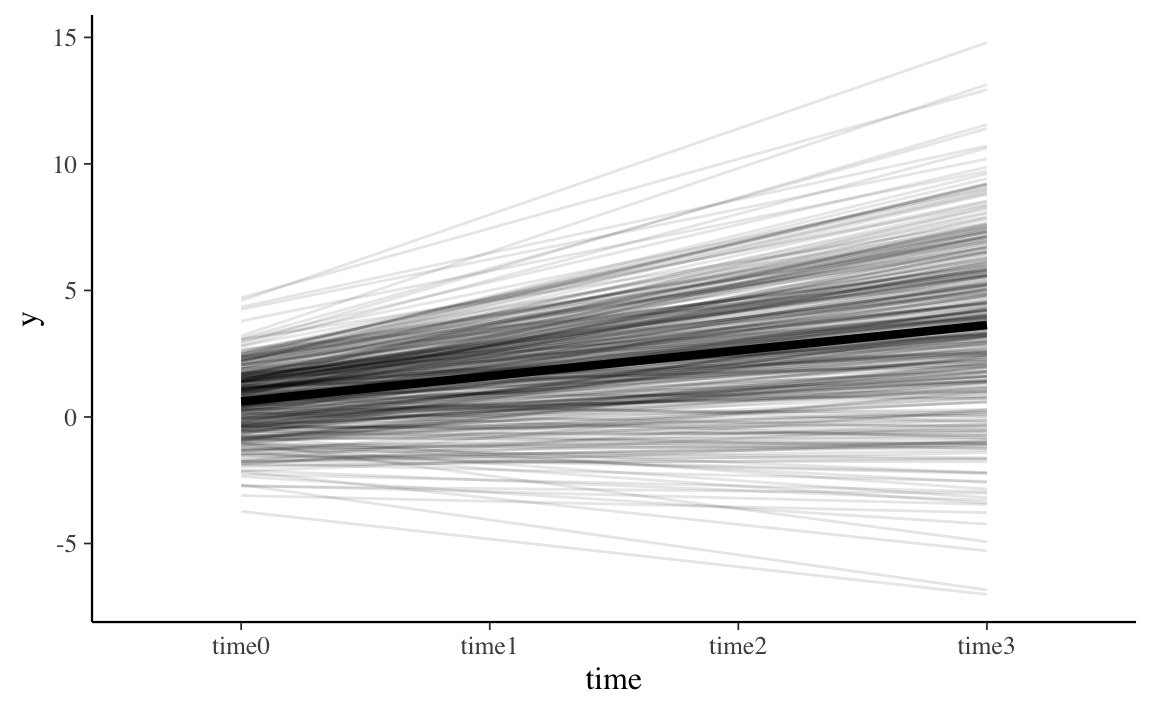

La linea nera più spessa rappresenta l’intercetta media e la pendenza media della curva di crescita del modello LGM. Ogni individuo ha una sua specifica intercetta e uno specifico tasso di cambiamento e questa diversità è catturata nelle componenti di varianza del modello.

38.0.2 Dati ordinali vs. intervalli temporali

La specificazione s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4 assume che il tempo sia misurato per intervalli costanti. Questa sintassi può essere usata anche quando il tempo è misurato su una scala a livello ordinale, ovvero quando supponiamo diverse rilevazioni temporali e ci chiediamo cosa succede passando da una alla successiva, senza specificare precisamente qual è la distanza temporale tra le varie rilevazioni. In alternativa è possibile specificare in termini assoluti il tempo trascorso tra le diverse rilevazioni temporali – questo è possibile solo se tali distanze temporali sono costanti tra i vari soggetti. Ad esempio, se passano 2, 3 e 9 mesi dalla prima rilevazione, avremo il seguente modello.

model_a <- "
 i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
 s =~ 0*t1 + 2*t2 + 6*t3 + 9*t4
"

La scelta di utilizzare il tempo su scala ordinale rispetto a quello assoluto non cambia il numero di parametri del modello o i gradi di libertà. Tuttavia la media dei punteggi fattoriali che rappresentano l’intercetta e la pendenza può cambiare e l’interpretazione di questi termini cambierà di conseguenza.

fit_a <- growth(model_a, data = Demo.growth)
kable(coef(fit_a), booktabs = TRUE, format = "markdown")

	x
t1~~t1	0.75840584
t2~~t2	0.80990552
t3~~t3	0.63209463
t4~~t4	0.49864811
i~~i	2.04046924
s~~s	0.05802979
i~~s	0.23300623
i~1	0.76120704
s~1	0.31906615

Mentre in precedenza l’interpretazione era che la media della variabile risposta aumenta in media 1.006 punti passando da una rilevazione temporale alla successiva, nel caso della presente specificazione temporale in mesi possiamo dire che media della variabile risposta aumenta in media 0.319 punti dopo l’incremento temporale di un mese.

38.0.3 Verifica di ipotesi

È anche possibile utilizzare le funzionalità di lavaan per verificare specifiche ipotesi di interesse relative ai dati longitudinali. Ad esempio, una possibile domanda riguarda l’uguaglianza degli errori nel tempo. Tale domanda può essere affrontata introducendo dei vincoli nella specificazione del modello LGM (come abbiamo anche visto in precedenza) e, successivamente, confrontando la bontà dell’adattamento del modello vincolato e del modello generale.

Il modello vincolato è

model_eqerr <- "
 i =~ 1*t1 + 1*t2 + 1*t3 + 1*t4
 s =~ 0*t1 + 1*t2 + 2*t3 + 3*t4
 t1 ~~ a*t1
 t2 ~~ a*t2
 t3 ~~ a*t3
 t4 ~~ a*t4
"

Adattiamo il modello vincolato:

fit_eqerr <- growth(model_eqerr, data = Demo.growth)

Confrontiamo il modello vincolato con il modello libero:

anova(fit, fit_eqerr)
#> 
#> Chi-Squared Difference Test
#> 
#>           Df    AIC    BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
#> fit        5 5528.1 5564.0 8.0687                                    
#> fit_eqerr  8 5523.7 5547.7 9.6779     1.6091     0       3     0.6573

Il test del rapporto di verosimiglianza (likelihood ratio) eseguito dalla funzione anova() produce un \(p\)-valore di 0.6573. Ciò significa che, per i dati esaminati, non emerge una decremento nella bontà dell’adattamento degna di nota se passiamo dal modello libero al modello vincolato. Per questi dati, dunque, sembra ragionevole assumere l’equaglianza della varianza degli errori nel tempo.