32.4 Modello di crescita lineare
Nella discussione dei modelli di crescita, dopo il modello di assenza di crescita, si esamina sempre il modello di crescita lineare a causa della sua semplicità. Inoltre, i modelli di crescita lineare sono spesso un punto di partenza quando si cerca di comprendere il cambiamento all’interno della persona.
Implementiamo dunque un modello di crescita latente lineare.
lg_math_lavaan_model <- "
# latent variable definitions
#intercept (note intercept is a reserved term)
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
#linear slope
eta_2 =~ 0*math2
eta_2 =~ 1*math3
eta_2 =~ 2*math4
eta_2 =~ 3*math5
eta_2 =~ 4*math6
eta_2 =~ 5*math7
eta_2 =~ 6*math8
# factor variances
eta_1 ~~ eta_1
eta_2 ~~ eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ start(35)*1
eta_2 ~ start(4)*1
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
" # end of model definitionAdattiamo il modello ai dati.
lg_math_lavaan_fit <- sem(lg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml"
)Esaminiamo il risultato ottenuto.
summary(lg_math_lavaan_fit, fit.measures = TRUE)
#> lavaan 0.6.15 ended normally after 27 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 12
#> Number of equality constraints 6
#>
#> Used Total
#> Number of observations 932 933
#> Number of missing patterns 60
#>
#> Model Test User Model:
#>
#> Test statistic 204.484
#> Degrees of freedom 29
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 862.334
#> Degrees of freedom 21
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.791
#> Tucker-Lewis Index (TLI) 0.849
#>
#> Robust Comparative Fit Index (CFI) 0.896
#> Robust Tucker-Lewis Index (TLI) 0.925
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -7968.693
#> Loglikelihood unrestricted model (H1) -7866.451
#>
#> Akaike (AIC) 15949.386
#> Bayesian (BIC) 15978.410
#> Sample-size adjusted Bayesian (SABIC) 15959.354
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.081
#> 90 Percent confidence interval - lower 0.070
#> 90 Percent confidence interval - upper 0.091
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.550
#>
#> Robust RMSEA 0.134
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.233
#> P-value H_0: Robust RMSEA <= 0.050 0.136
#> P-value H_0: Robust RMSEA >= 0.080 0.792
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.121
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 =~
#> math2 1.000
#> math3 1.000
#> math4 1.000
#> math5 1.000
#> math6 1.000
#> math7 1.000
#> math8 1.000
#> eta_2 =~
#> math2 0.000
#> math3 1.000
#> math4 2.000
#> math5 3.000
#> math6 4.000
#> math7 5.000
#> math8 6.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 ~~
#> eta_2 -0.181 1.150 -0.158 0.875
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 35.267 0.355 99.229 0.000
#> eta_2 4.339 0.088 49.136 0.000
#> .math2 0.000
#> .math3 0.000
#> .math4 0.000
#> .math5 0.000
#> .math6 0.000
#> .math7 0.000
#> .math8 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 64.562 5.659 11.408 0.000
#> eta_2 0.733 0.327 2.238 0.025
#> .math2 (thet) 36.230 1.867 19.410 0.000
#> .math3 (thet) 36.230 1.867 19.410 0.000
#> .math4 (thet) 36.230 1.867 19.410 0.000
#> .math5 (thet) 36.230 1.867 19.410 0.000
#> .math6 (thet) 36.230 1.867 19.410 0.000
#> .math7 (thet) 36.230 1.867 19.410 0.000
#> .math8 (thet) 36.230 1.867 19.410 0.000Generiamo un diagramma di percorso.
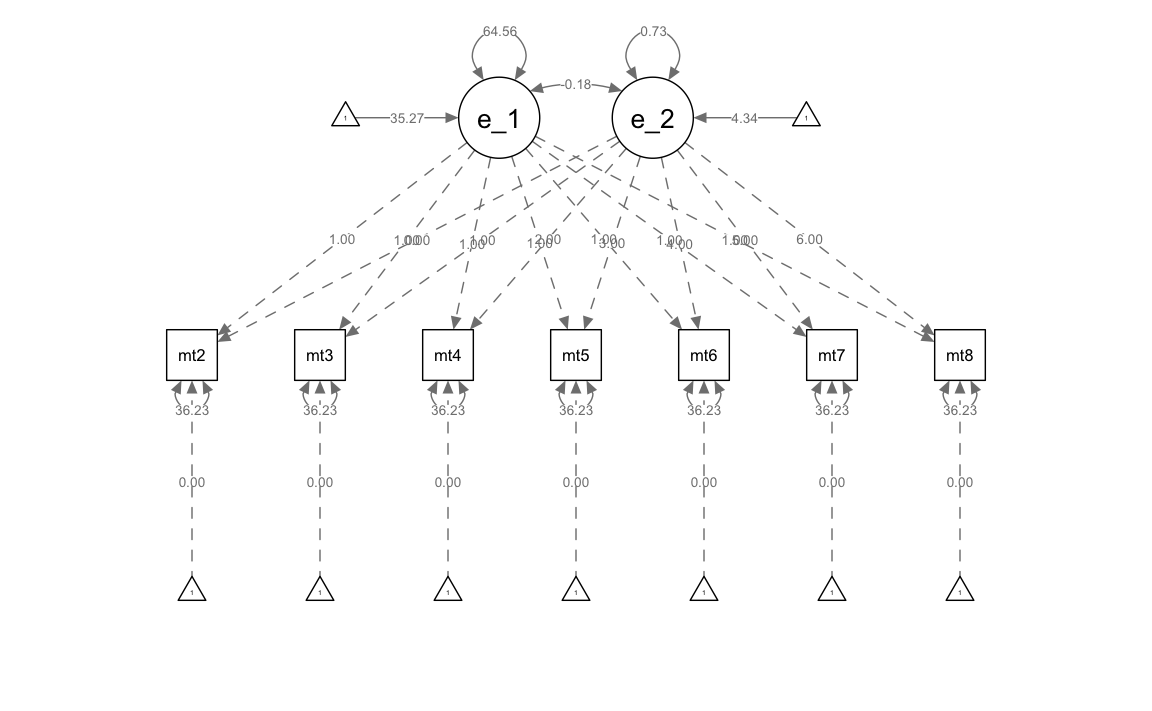
Esaminiamo le traiettorie di crescita.
nlsy_math_predicted <- as.data.frame(cbind(nlsy_math_wide$id, lavPredict(lg_math_lavaan_fit)))
# naming columns
names(nlsy_math_predicted) <- c("id", "eta_1", "eta_2")
head(nlsy_math_predicted)
#> id eta_1 eta_2
#> 1 201 36.94675 4.534084
#> 2 303 26.03589 4.050780
#> 3 2702 49.70187 4.594148
#> 4 4303 41.04200 4.548063
#> 5 5002 37.01241 4.496745
#> 6 5005 37.68809 4.324197# calculating implied manifest scores
nlsy_math_predicted$math2 <- 1 * nlsy_math_predicted$eta_1 + 0 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math3 <- 1 * nlsy_math_predicted$eta_1 + 1 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math4 <- 1 * nlsy_math_predicted$eta_1 + 2 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math5 <- 1 * nlsy_math_predicted$eta_1 + 3 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math6 <- 1 * nlsy_math_predicted$eta_1 + 4 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math7 <- 1 * nlsy_math_predicted$eta_1 + 5 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math8 <- 1 * nlsy_math_predicted$eta_1 + 6 * nlsy_math_predicted$eta_2
# reshaping wide to long
nlsy_math_predicted_long <- reshape(
data = nlsy_math_predicted,
timevar = c("grade"),
idvar = "id",
varying = c(
"math2", "math3", "math4",
"math5", "math6", "math7", "math8"
),
direction = "long", sep = ""
)
# sorting for easy viewing
# order by id and time
nlsy_math_predicted_long <- nlsy_math_predicted_long[order(nlsy_math_predicted_long$id, nlsy_math_predicted_long$grade), ]
# intraindividual change trajetories
ggplot(
data = nlsy_math_predicted_long[which(nlsy_math_predicted_long$id < 80000), ], # data set
aes(x = grade, y = math, group = id)
) + # setting variables
# geom_point(size=.5) + #adding points to plot
geom_line() + # adding lines to plot
theme_bw() + # changing style/background
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "Predicted PIAT Mathematics"
)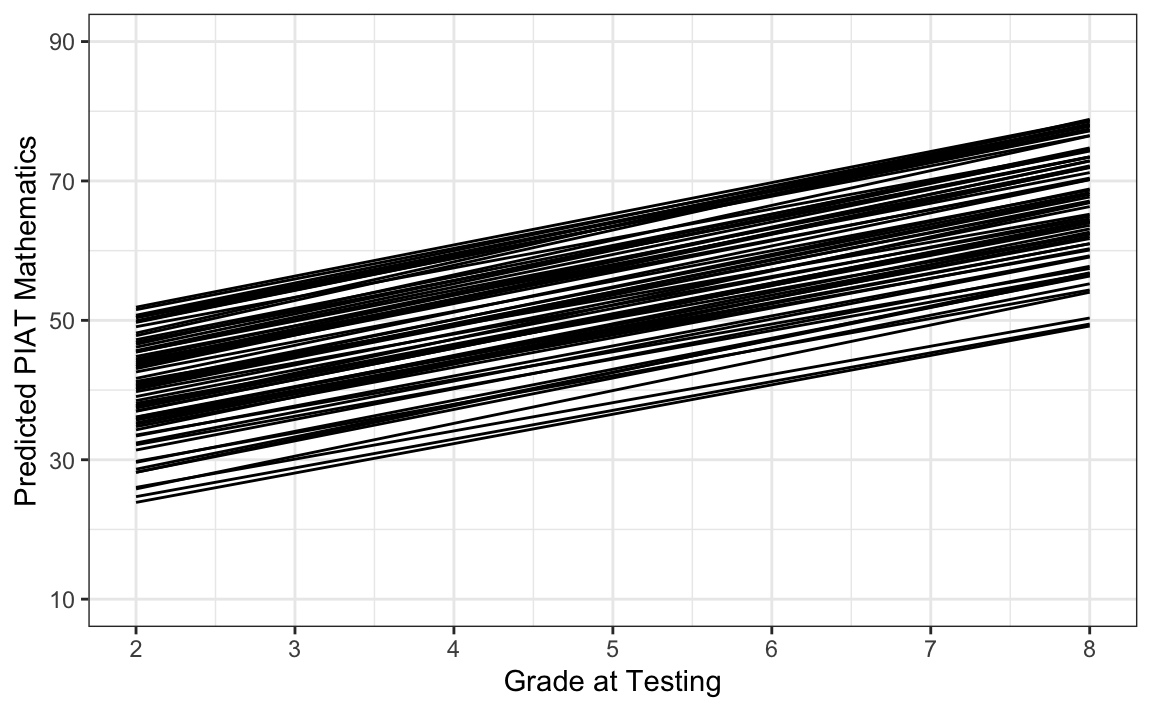
Dal grafico si può notare che questo modello rappresenta la traiettoria di ogni bambino come una linea retta, con alcune differenze interindividuali nella velocità del cambiamento intraindividuale. Questo tutorial ha dunque illustrato come impostare e adattare modelli di crescita lineare nel framework di modellizzazione SEM utilizzando il pacchetto lavaan in R, nonché come calcolare e rappresentare graficamente le traiettorie di crescita previste dal modello.