Capitolo 34 Covariate indipendenti dal tempo
Partendo dai modelli di crescita lineare descritti nei capitoli precedenti, ci chiediamo se le differenze individuali nelle traiettorie di cambiamento siano associate ad altre variabili. Questo capitolo introduce modelli che esaminano se la variabilità nell’intercetta e nella pendenza del modello di crescita lineare può essere spiegata da covariate invarianti nel tempo. Queste sono variabili a livello di persona che non cambiano nel tempo, come il genere, le condizioni sperimentali e lo stato socio-economico. Nel contesto dei modelli a crescita latente, tali variabili vengono considerate come variabili indipendenti in un modello di regressione multipla in cui l’intercetta e la pendenza del modello di crescita lineare sono le variabili dipendenti. Le covariate invarianti nel tempo possono essere continue, ordinali o categoriche.
Studiando come le differenze individuali nell’intercetta e nella pendenza sono correlate ad altre variabili a livello della persona, possiamo comprendere le possibili ragioni per cui gli individui cambiano in modi diversi. Tuttavia, i risultati di questi modelli non forniscono ulteriori inferenze sulla causalità rispetto ai tipici modelli di regressione. Gli utenti dovrebbero essere cauti quando discutono tali effetti e tenere presente se la covariata invariante nel tempo è stata assegnata in maniera casuale nel contesto di un protocollo sperimentale, oppure se i dati provengono da ricerche osservazionali.
Per questo esempio considereremo i dati di prestazione matematica dal data set NLSY-CYA Long Data (si veda Grimm, Ram, and Estabrook 2016). Iniziamo a leggere i dati.
# set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_long_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_long <- dat
# Add names the columns of the data set
names(nlsy_math_long) <- c(
"id", "female", "lb_wght",
"anti_k1", "math", "grade",
"occ", "age", "men",
"spring", "anti"
)
# view the first few observations in the data set
head(nlsy_math_long, 10)
#> id female lb_wght anti_k1 math grade occ age men spring anti
#> 1 201 1 0 0 38 3 2 111 0 1 0
#> 2 201 1 0 0 55 5 3 135 1 1 0
#> 3 303 1 0 1 26 2 2 121 0 1 2
#> 4 303 1 0 1 33 5 3 145 0 1 2
#> 5 2702 0 0 0 56 2 2 100 NA 1 0
#> 6 2702 0 0 0 58 4 3 125 NA 1 2
#> 7 2702 0 0 0 80 8 4 173 NA 1 2
#> 8 4303 1 0 0 41 3 2 115 0 0 1
#> 9 4303 1 0 0 58 4 3 135 0 1 2
#> 10 5002 0 0 4 46 4 2 117 NA 1 4# intraindividual change trajetories
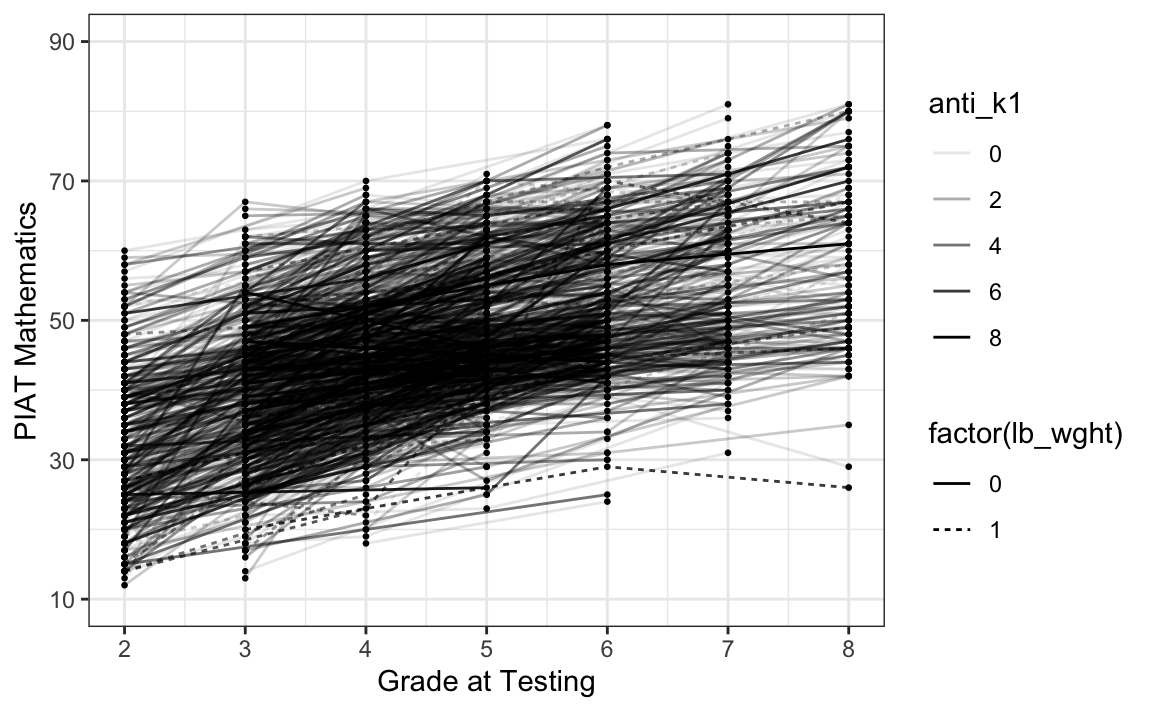
ggplot(
data = nlsy_math_long, # data set
aes(x = grade, y = math, group = id)
) + # setting variables
geom_point(size = .5) + # adding points to plot
geom_line(aes(linetype = factor(lb_wght), alpha = anti_k1)) + # adding lines to plot
theme_bw() + # changing style/background
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "PIAT Mathematics"
)
Per semplicità, leggiamo gli stessi dati in formato wide da un file.
# set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_wide_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_wide <- dat
# Give the variable names
names(nlsy_math_wide) <- c(
"id", "female", "lb_wght", "anti_k1",
"math2", "math3", "math4", "math5", "math6", "math7", "math8",
"age2", "age3", "age4", "age5", "age6", "age7", "age8",
"men2", "men3", "men4", "men5", "men6", "men7", "men8",
"spring2", "spring3", "spring4", "spring5", "spring6", "spring7", "spring8",
"anti2", "anti3", "anti4", "anti5", "anti6", "anti7", "anti8"
)
# view the first few observations (and columns) in the data set
head(nlsy_math_wide[, 1:11], 10)
#> id female lb_wght anti_k1 math2 math3 math4 math5 math6 math7 math8
#> 1 201 1 0 0 NA 38 NA 55 NA NA NA
#> 2 303 1 0 1 26 NA NA 33 NA NA NA
#> 3 2702 0 0 0 56 NA 58 NA NA NA 80
#> 4 4303 1 0 0 NA 41 58 NA NA NA NA
#> 5 5002 0 0 4 NA NA 46 NA 54 NA 66
#> 6 5005 1 0 0 35 NA 50 NA 60 NA 59
#> 7 5701 0 0 2 NA 62 61 NA NA NA NA
#> 8 6102 0 0 0 NA NA 55 67 NA 81 NA
#> 9 6801 1 0 0 NA 54 NA 62 NA 66 NA
#> 10 6802 0 0 0 NA 55 NA 66 NA 68 NASpecifichiamo il modello SEM.
# writing out linear growth model with tic in full SEM way
lg_math_tic_lavaan_model <- "
#latent variable definitions
#intercept
eta1 =~ 1*math2+
1*math3+
1*math4+
1*math5+
1*math6+
1*math7+
1*math8
#linear slope
eta2 =~ 0*math2+
1*math3+
2*math4+
3*math5+
4*math6+
5*math7+
6*math8
#factor variances
eta1 ~~ eta1
eta2 ~~ eta2
#factor covariance
eta1 ~~ eta2
#manifest variances (set equal by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
#latent means (freely estimated)
eta1 ~ 1
eta2 ~ 1
#manifest means (fixed to zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
#Time invariant covaraite
#regression of time-invariant covariate on intercept and slope factors
eta1~lb_wght+anti_k1
eta2~lb_wght+anti_k1
#variance of TIV covariates
lb_wght ~~ lb_wght
anti_k1 ~~ anti_k1
#covariance of TIV covaraites
lb_wght ~~ anti_k1
#means of TIV covariates (freely estimated)
lb_wght ~ 1
anti_k1 ~ 1
" # end of model definitionAdattiamo il modello ai dati.
lg_math_tic_lavaan_fit <- sem(lg_math_tic_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml"
)Esaminiamo la soluzione ottenuta.
summary(lg_math_tic_lavaan_fit, fit.measures = TRUE)
#> lavaan 0.6.15 ended normally after 117 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 21
#> Number of equality constraints 6
#>
#> Number of observations 933
#> Number of missing patterns 61
#>
#> Model Test User Model:
#>
#> Test statistic 220.221
#> Degrees of freedom 39
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 892.616
#> Degrees of freedom 36
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.788
#> Tucker-Lewis Index (TLI) 0.805
#>
#> Robust Comparative Fit Index (CFI) 0.920
#> Robust Tucker-Lewis Index (TLI) 0.926
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -9785.085
#> Loglikelihood unrestricted model (H1) -9674.975
#>
#> Akaike (AIC) 19600.171
#> Bayesian (BIC) 19672.747
#> Sample-size adjusted Bayesian (SABIC) 19625.108
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.071
#> 90 Percent confidence interval - lower 0.062
#> 90 Percent confidence interval - upper 0.080
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.046
#>
#> Robust RMSEA 0.100
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.183
#> P-value H_0: Robust RMSEA <= 0.050 0.218
#> P-value H_0: Robust RMSEA >= 0.080 0.654
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.097
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> eta1 =~
#> math2 1.000
#> math3 1.000
#> math4 1.000
#> math5 1.000
#> math6 1.000
#> math7 1.000
#> math8 1.000
#> eta2 =~
#> math2 0.000
#> math3 1.000
#> math4 2.000
#> math5 3.000
#> math6 4.000
#> math7 5.000
#> math8 6.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> eta1 ~
#> lb_wght -2.716 1.294 -2.099 0.036
#> anti_k1 -0.551 0.232 -2.369 0.018
#> eta2 ~
#> lb_wght 0.625 0.333 1.873 0.061
#> anti_k1 -0.019 0.059 -0.327 0.743
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 ~~
#> .eta2 -0.078 1.145 -0.068 0.945
#> lb_wght ~~
#> anti_k1 0.007 0.014 0.548 0.584
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 36.290 0.497 73.052 0.000
#> .eta2 4.315 0.122 35.420 0.000
#> .math2 0.000
#> .math3 0.000
#> .math4 0.000
#> .math5 0.000
#> .math6 0.000
#> .math7 0.000
#> .math8 0.000
#> lb_wght 0.080 0.009 9.031 0.000
#> anti_k1 1.454 0.050 29.216 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 63.064 5.609 11.242 0.000
#> .eta2 0.713 0.326 2.185 0.029
#> .math2 (thet) 36.257 1.868 19.406 0.000
#> .math3 (thet) 36.257 1.868 19.406 0.000
#> .math4 (thet) 36.257 1.868 19.406 0.000
#> .math5 (thet) 36.257 1.868 19.406 0.000
#> .math6 (thet) 36.257 1.868 19.406 0.000
#> .math7 (thet) 36.257 1.868 19.406 0.000
#> .math8 (thet) 36.257 1.868 19.406 0.000
#> lb_wght 0.074 0.003 21.599 0.000
#> anti_k1 2.312 0.107 21.599 0.000Creiamo un diagramma di percorso.
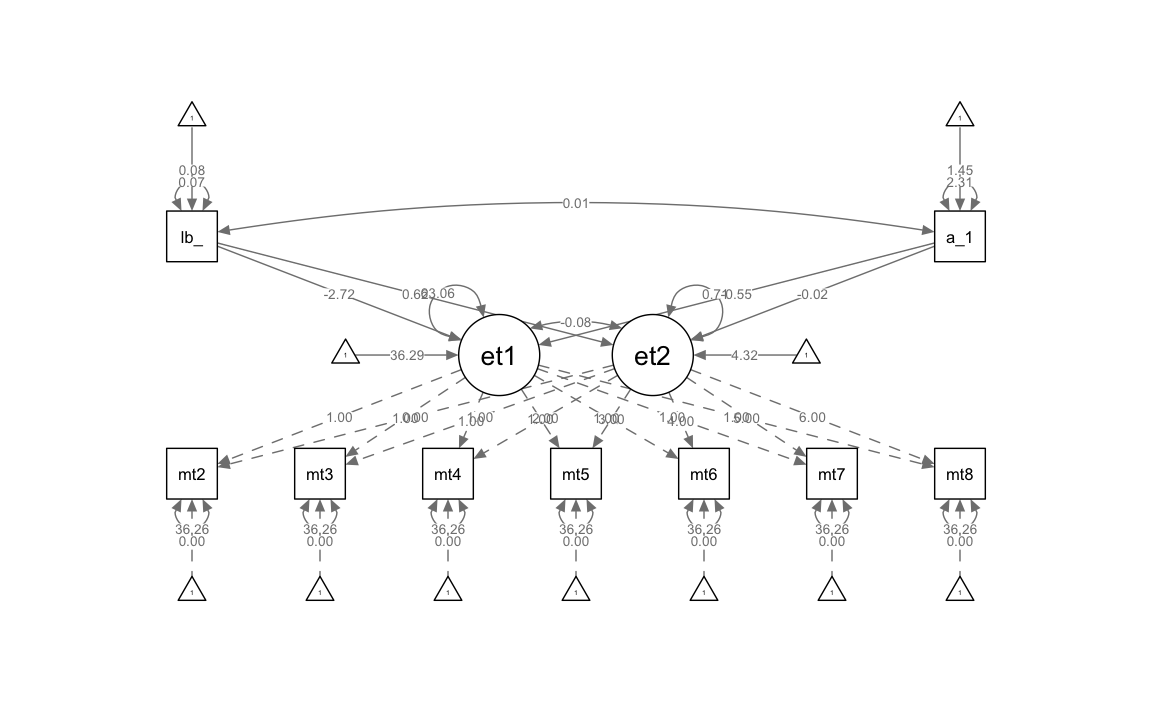
34.0.1 Valutare il contributo delle covariate
Per valutare se le covariate considerate forniscono un contributo sostanziale al modello confronteremo il modello precedente con un modello vincolato in cui l’effetto delle covariate viene fissato come uguale a zero.
# writing out linear growth model with tic in full SEM way
lg_math_ticZERO_lavaan_model <- "
#latent variable definitions
#intercept
eta1 =~ 1*math2+
1*math3+
1*math4+
1*math5+
1*math6+
1*math7+
1*math8
#linear slope
eta2 =~ 0*math2+
1*math3+
2*math4+
3*math5+
4*math6+
5*math7+
6*math8
#factor variances
eta1 ~~ eta1
eta2 ~~ eta2
#factor covariance
eta1 ~~ eta2
#manifest variances (set equal by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
#latent means (freely estimated)
eta1 ~ 1
eta2 ~ 1
#manifest means (fixed to zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
#Time invariant covaraite
#regression of time-invariant covariate on intercept and slope factors
#FIXED to 0
eta1~0*lb_wght+0*anti_k1
eta2~0*lb_wght+0*anti_k1
#variance of TIV covariates
lb_wght ~~ lb_wght
anti_k1 ~~ anti_k1
#covariance of TIV covaraites
lb_wght ~~ anti_k1
#means of TIV covariates (freely estimated)
lb_wght ~ 1
anti_k1 ~ 1
" # end of model definitionAdattiamo il modello ai dati.
lg_math_ticZERO_lavaan_fit <- sem(lg_math_ticZERO_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml"
)Esaminiamo il risultato ottenuto.
summary(lg_math_ticZERO_lavaan_fit, fit.measures = TRUE)
#> lavaan 0.6.15 ended normally after 102 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 17
#> Number of equality constraints 6
#>
#> Number of observations 933
#> Number of missing patterns 61
#>
#> Model Test User Model:
#>
#> Test statistic 234.467
#> Degrees of freedom 43
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 892.616
#> Degrees of freedom 36
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.776
#> Tucker-Lewis Index (TLI) 0.813
#>
#> Robust Comparative Fit Index (CFI) 0.917
#> Robust Tucker-Lewis Index (TLI) 0.931
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -9792.208
#> Loglikelihood unrestricted model (H1) -9674.975
#>
#> Akaike (AIC) 19606.416
#> Bayesian (BIC) 19659.638
#> Sample-size adjusted Bayesian (SABIC) 19624.703
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.069
#> 90 Percent confidence interval - lower 0.061
#> 90 Percent confidence interval - upper 0.078
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.020
#>
#> Robust RMSEA 0.097
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.173
#> P-value H_0: Robust RMSEA <= 0.050 0.208
#> P-value H_0: Robust RMSEA >= 0.080 0.646
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.103
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> eta1 =~
#> math2 1.000
#> math3 1.000
#> math4 1.000
#> math5 1.000
#> math6 1.000
#> math7 1.000
#> math8 1.000
#> eta2 =~
#> math2 0.000
#> math3 1.000
#> math4 2.000
#> math5 3.000
#> math6 4.000
#> math7 5.000
#> math8 6.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> eta1 ~
#> lb_wght 0.000
#> anti_k1 0.000
#> eta2 ~
#> lb_wght 0.000
#> anti_k1 0.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 ~~
#> .eta2 -0.181 1.150 -0.158 0.875
#> lb_wght ~~
#> anti_k1 0.007 0.014 0.548 0.584
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 35.267 0.355 99.229 0.000
#> .eta2 4.339 0.088 49.136 0.000
#> .math2 0.000
#> .math3 0.000
#> .math4 0.000
#> .math5 0.000
#> .math6 0.000
#> .math7 0.000
#> .math8 0.000
#> lb_wght 0.080 0.009 9.031 0.000
#> anti_k1 1.454 0.050 29.216 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .eta1 64.562 5.659 11.408 0.000
#> .eta2 0.733 0.327 2.238 0.025
#> .math2 (thet) 36.230 1.867 19.410 0.000
#> .math3 (thet) 36.230 1.867 19.410 0.000
#> .math4 (thet) 36.230 1.867 19.410 0.000
#> .math5 (thet) 36.230 1.867 19.410 0.000
#> .math6 (thet) 36.230 1.867 19.410 0.000
#> .math7 (thet) 36.230 1.867 19.410 0.000
#> .math8 (thet) 36.230 1.867 19.410 0.000
#> lb_wght 0.074 0.003 21.599 0.000
#> anti_k1 2.312 0.107 21.599 0.000Generiamo il diagramma di percorso.
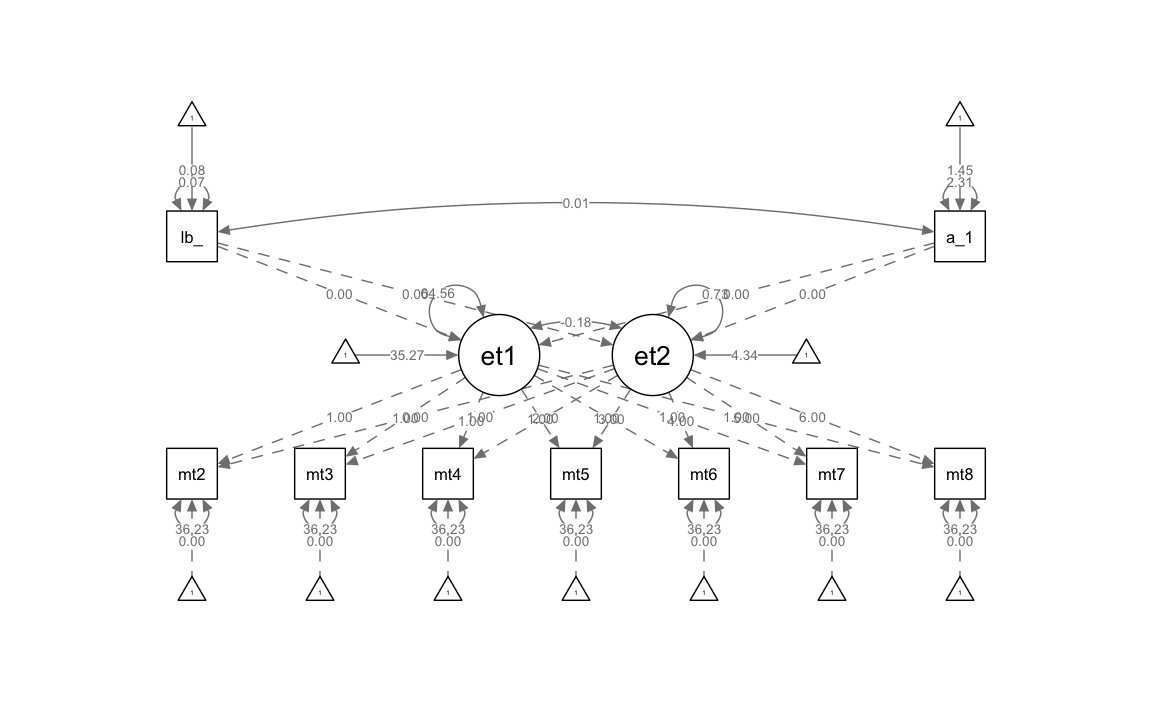
Eseguiamo il confronto tra i due modelli mediante il test del rapporto tra verosimiglianze.
anova(lg_math_tic_lavaan_fit, lg_math_ticZERO_lavaan_fit)
#>
#> Chi-Squared Difference Test
#>
#> Df AIC BIC Chisq Chisq diff RMSEA Df diff
#> lg_math_tic_lavaan_fit 39 19600 19673 220.22
#> lg_math_ticZERO_lavaan_fit 43 19606 19660 234.47 14.245 0.052395 4
#> Pr(>Chisq)
#> lg_math_tic_lavaan_fit
#> lg_math_ticZERO_lavaan_fit 0.006552 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Il valore-p associato alla statistica chi-quadrato relativa alla differenza tra i due modelli è piccolo. Questo significa che i vincoli aggiuntivi hanno impattato in maniera sostanziale la bontà di adattamento del modello ai dati. Da ciò concludiamo che le covariate forniscono un contributo utile al modello.