17.1 Punteggi fattoriali

Fino ad ora abbiamo considerato le strategie di costruzione del modello basate sulla stima e sull’interpretazione delle saturazioni fattoriali e delle comunalità. Questo è il primo passo nella costruzione del modello fattoriale. È però possibile compiere un passo ulteriore, ovvero quello della stima dei punteggi fattoriali (factor scores) i quali risultano utili sia per interpretare i risultati dell’analisi fattoriale che per fare diagnostica. I punteggi fattoriali forniscono le previsioni dei livelli dei fattori latenti per ogni rispondente. Esistono vari metodi di stima dei punteggi fattoriali. Tra questi troviamo il metodo di Thomson basato sulla regressione e il metodo di Bartlett basato sulla massima verosimiglianza. Entrambi questi metodi sono implementati nel software .

17.1.1 Stima dei punteggi fattoriali

Si definiscono punteggi fattoriali i valori assunti dai fattori comuni (inosservabili) in corrispondenza delle osservazioni campionarie. Il metodo di Thomson stima i punteggi fattoriali in base all’approccio della regressione multipla, ovvero, impiegando la matrice delle correlazioni tra le variabili e la matrice di struttura (ovvero, la matrice delle correlazioni delle variabili con i fattori). Per ottenere le stime dei punteggi fattoriali con il metodo di Thomson è necessario specificare nella funzione factanal() l’opzione scores = "regression".

17.1.2 Dimostrazione di Thurstone

Prima di descrivere il metodo della regressione, esaminiamo la dimostrazione che Thurstone (1947) ha fornito per illustrare il significato dei punteggi fattoriali (si veda Loehlin, 1987). L’idea è quella di esaminare la stima dei punteggi fattoriali in una situazione in cui i tali punteggi sono conosciuti, in maniera tale da potere controllare il risultato dell’analisi.

Si consideri un insieme di 1000 scatole di cui conosciamo le dimensioni \(x, y, z\):

set.seed(123)
n <- 1e3
x <- rnorm(n, 100, 1.5)
y <- rnorm(n, 200, 1.5)
z <- rnorm(n, 300, 1.5)

Il problema è quello di stimare le dimensioni delle scatole disponendo soltanto di una serie di misure indirette, corrotte dal rumore di misura. Thurstone (1947) utilizzò le seguenti trasformazioni delle dimensioni delle scatole (si veda Jennrich, 2007).

s <- 40
y1 <- rnorm(n, mean(x), s)
y2 <- rnorm(n, mean(y), s)
y3 <- rnorm(n, mean(z), s)
y4 <- x * y + rnorm(n, 0, s)
y5 <- x * z + rnorm(n, 0, s)
y6 <- y * z + rnorm(n, 0, s)
y7 <- x^2 * y + rnorm(n, 0, s)
y8 <- x * y^2 + rnorm(n, 0, s)
y9 <- x^2 * z + rnorm(n, 0, s)
y10 <- x * z^2 + rnorm(n, 0, s)
y11 <- y^2 * z + rnorm(n, 0, s)
y12 <- y * z^2 + rnorm(n, 0, s)
y13 <- y^2 * z + rnorm(n, 0, s)
y14 <- y * z^2 + rnorm(n, 0, s)
y15 <- x / y + rnorm(n, 0, s)
y16 <- y / x + rnorm(n, 0, s)
y17 <- x / z + rnorm(n, 0, s)
y18 <- z / x + rnorm(n, 0, s)
y19 <- y / z + rnorm(n, 0, s)
y20 <- z / y + rnorm(n, 0, s)
y21 <- 2 * x + 2 * y + rnorm(n, 0, s)
y22 <- 2 * x + 2 * z + rnorm(n, 0, s)
y23 <- 2 * y + 2 * z + rnorm(n, 0, s)

Eseguiamo l’analisi fattoriale con una soluzione a tre fattori sui dati così creati.

Y <- cbind(
  y1, y2, y3, y4, y5, y6, y7, y8, y9,
  y10, y11, y12, y13, y14, y15, y16,
  y17, y18, y19, y20, y21, y22, y23
)

fa <- factanal(
  Y,
  factors = 3,
  scores = "regression",
  lower = 0.01
)

L’opzione scores = "regression" richiede il calcolo dei punteggi fattoriali con il metodo della regressione. Nel caso di una rotazione Varimax (default della funzione factanal()), i punteggi fattoriali risultano ovviamente incorrelati:

cor(
  cbind(fa$scores[, 1], fa$scores[, 2], fa$scores[, 3])
) %>%
  round(3)
#>        [,1]  [,2]   [,3]
#> [1,]  1.000 0.002 -0.001
#> [2,]  0.002 1.000  0.005
#> [3,] -0.001 0.005  1.000

Generiamo ora i diagrammi di dispersione che mettono in relazione le dimensioni originarie delle scatole (\(x, y, z\)) con i punteggi fattoriali sui tre fattori. Se l’analisi ha successo, ci aspettiamo un’alta correlazione tra i punteggi fattoriali di ogni fattore e una sola delle dimensioni delle scatole \(x\), \(y\), \(z\).

p1 <- tibble(x, fs1 = fa$scores[, 1]) %>%
  ggplot(aes(x, fs1)) +
  geom_point(alpha = 0.2)
p2 <- tibble(y, fs1 = fa$scores[, 1]) %>%
  ggplot(aes(y, fs1)) +
  geom_point(alpha = 0.2)
p3 <- tibble(z, fs1 = fa$scores[, 1]) %>%
  ggplot(aes(z, fs1)) +
  geom_point(alpha = 0.2)

p4 <- tibble(x, fs2 = fa$scores[, 2]) %>%
  ggplot(aes(x, fs2)) +
  geom_point(alpha = 0.2)
p5 <- tibble(y, fs2 = fa$scores[, 2]) %>%
  ggplot(aes(y, fs2)) +
  geom_point(alpha = 0.2)
p6 <- tibble(z, fs2 = fa$scores[, 2]) %>%
  ggplot(aes(z, fs2)) +
  geom_point(alpha = 0.2)

p7 <- tibble(x, fs3 = fa$scores[, 3]) %>%
  ggplot(aes(x, fs3)) +
  geom_point(alpha = 0.2)
p8 <- tibble(y, fs3 = fa$scores[, 3]) %>%
  ggplot(aes(y, fs3)) +
  geom_point(alpha = 0.2)
p9 <- tibble(z, fs3 = fa$scores[, 3]) %>%
  ggplot(aes(z, fs3)) +
  geom_point(alpha = 0.2)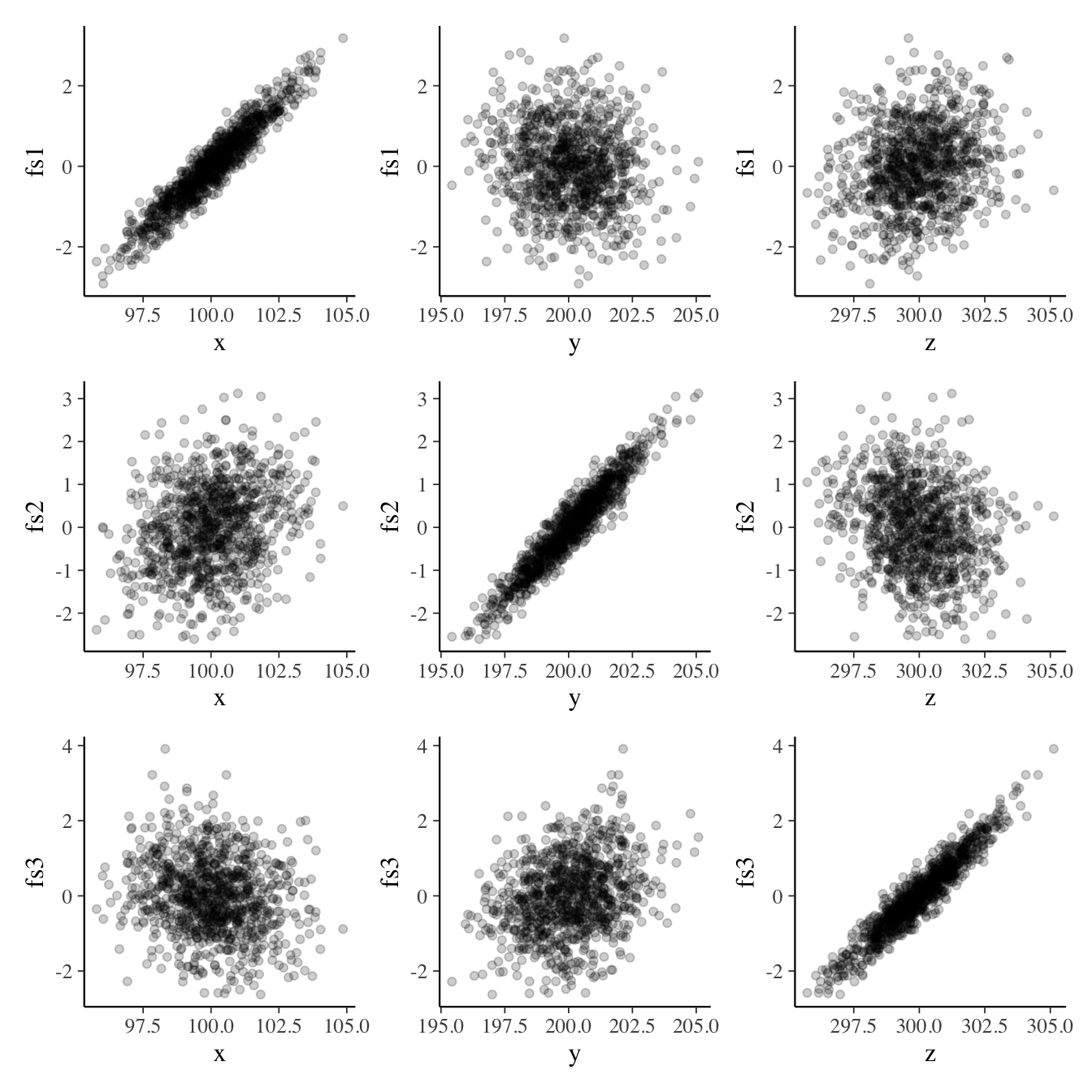

(p1 | p2 | p3) /
  (p4 | p5 | p6) /
  (p7 | p8 | p9)

I risultati riportati nella figura confermano le aspettative.

Il metodo della regressione pone il problema della stima dei punteggi fattoriali nei termini di una ideale regressione di ogni fattore rispetto a tutte le variabili osservate. Per il fattore \(j\)-esimo, si può scrivere la seguente equazione:

\[ \begin{aligned} F_j =& \beta_{1j}y_1 + \dots + \beta_{pm}y_p + \varepsilon_j \end{aligned} \]

dove \(F_j\) sono i punteggi fattoriali e \(y\) sono le variabili osservate standardizzate \((Y-\bar{Y})/s\). In forma matriciale, il modello diventa

\[ \textbf{F} = \textbf{y} \textbf{B} + \boldsymbol{\varepsilon} \]

I coefficienti parziali di regressione B sono ignoti. Tuttavia, possono essere calcolati utilizzando i metodi della regressione lineare. Nel modello di regressione, infatti, i coefficienti dei minimi quadrati possono essere calcolati utilizzando due matrici di correlazioni: la matrice \(\textbf{R}_{xx}\) (le correlazioni tra le variabili \(X\)) e la matrice \(\textbf{R}_{xy}\) (le correlazioni tra le variabili \(X\) e la variabile \(Y\):

\[ \hat{\textbf{B}} = \textbf{R}_{xx}^{-1}\textbf{R}_{xy} \]

Nel caso dell’analisi fattoriale, \(\textbf{R}_{xx}\) corrisponde alla matrice delle correlazioni tra le variabili osservate e \(\textbf{R}_{xy}\) corrisponde alla matrice di struttura (la matrice delle correlazioni tra le variabili osservate e i fattori). Se i fattori sono ortogonali, la matrice di struttura coincide con la matrice dei pesi fattoriali \(\hat{\boldsymbol{\Lambda}}\).

I coefficienti B dell’equazione precedente possono dunque essere trovati nel modo seguente:

\[\begin{equation} \hat{\textbf{B}} = \textbf{R}_{yy}^{-1}\textbf{R}_{xf}= \textbf{R}^{-1}\hat{\boldsymbol{\Lambda}} \end{equation}\]

Una volta stimati i coefficienti \(\hat{\textbf{B}}\), i punteggi fattoriali si calcolano allo stesso modo dei punteggi teorici del modello di regressione:

\[\begin{equation} \hat{\textbf{F}} = \textbf{y} \hat{\textbf{B}} = \textbf{y} \textbf{R}^{-1}\hat{\boldsymbol{\Lambda}}, \end{equation}\]

dove \(\textbf{y}\) è la matrice delle variabili osservate standardizzate \((Y-\bar{Y})/s\).

Esercizio 17.1 Si utilizzino i dati dass21.txt che corrispondono alla somministrazione del test DASS-21 a 334 partecipanti. Lo schema di codifica si può trovare seguendo questo link. Ci si focalizzi sulla sottoscala Stress del DASS-21. Si trovino i punteggi fattoriali usando la funzione factanal() e si replichi il risultato seguendo la procedura delineata sopra.