31.1 Preliminari
I modelli di crescita sono tipicamente applicati a dati ottenuti da studi in cui sono state ottenute diverse misure ripetute da più individui. Tradizionalmente, gli studi longitudinali erano progettati in modo tale che il numero di valutazioni ripetute fosse relativamente basso (cioè <8) e il numero di individui fosse relativamente elevato (cioè >200). Tuttavia, i progressi sia nelle considerazioni teoriche del cambiamento (ad esempio, la non linearità) sia nella tecnologia per la raccolta dei dati (ad esempio, sondaggi basati sul web, smartphone) hanno notevolmente ampliato le possibilità di raccolta e analisi dei dati longitudinali: Grimm, Ram, and Estabrook (2016) discutono applicazioni di modelli di crescita a dati longitudinali ottenuti fino a 50.000 persone e fino a 1.000 valutazioni ripetute.
Questa complessità richiede che il ricercatore sia ben versato in (1) la manipolazione delle strutture dei dati longitudinali (ad esempio, il ridimensionamento dei dati dal formato wide al formato long), (2) la rappresentazione grafica dei dati longitudinali e (3) lo screening dei dati longitudinali.
31.1.1 Strutture dei dati
I dati longitudinali tipicamente si presentano in due forme: long e wide. Nel formato long, la descrizione del tempo è sulle righe; nel formato wide le variabili relative ad ogni occasione temporale sono organizzate in colonne.
È possibile trasformere i dati dal formato long in formato wide e viceversa usando le funzioni R pivot_wider() e pivot_longer(). La sintassi è spiegata nella pagina web tidyr.
31.1.2 Visualizzazione di dati longitudinali
Come in qualsiasi analisi statistica, è importante esaminare attentamente i dati. Ciò include la produzione di sia riepiloghi quantitativi che visualizzazioni. Per fare un esempio di visualizzazione di dati longitudinali, esaminiamo il cambiamento nel rendimento in matematica dei bambini durante la scuola elementare e media utilizzando il set di dati NLSY-CYA (i dati sono presentati nel capitolo 3 del libro di Grimm, Ram, and Estabrook 2016).
Iniziamo a leggere i dati.
# set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_long_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_long <- dat
# Add names the columns of the data set
names(nlsy_math_long) <- c(
"id", "female", "lb_wght",
"anti_k1", "math", "grade",
"occ", "age", "men",
"spring", "anti"
)
# view the first few observations in the data set
head(nlsy_math_long)
#> id female lb_wght anti_k1 math grade occ age men spring anti
#> 1 201 1 0 0 38 3 2 111 0 1 0
#> 2 201 1 0 0 55 5 3 135 1 1 0
#> 3 303 1 0 1 26 2 2 121 0 1 2
#> 4 303 1 0 1 33 5 3 145 0 1 2
#> 5 2702 0 0 0 56 2 2 100 NA 1 0
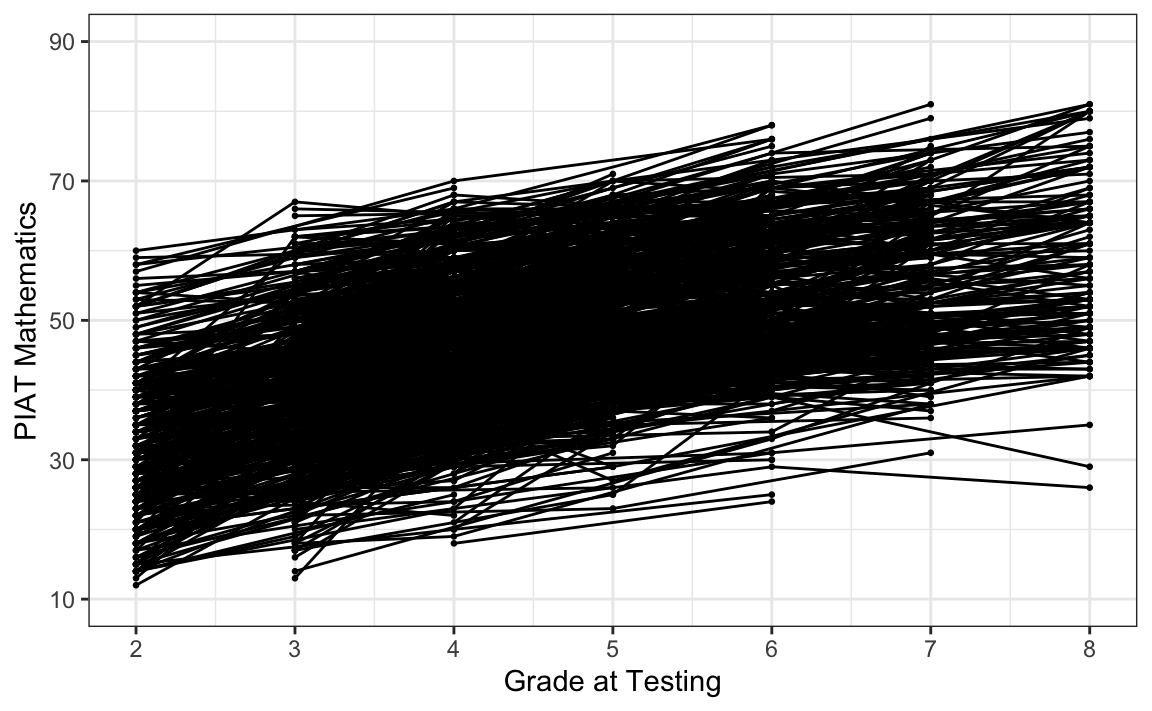
#> 6 2702 0 0 0 58 4 3 125 NA 1 2Le traiettorie di cambiamento intra-individuale possono essere prodotte nel modo seguente.
nlsy_math_long |> # data set
ggplot(aes(x = grade, y = math, group = id)) + # setting variables
geom_point(size = .5) + # adding points to plot
geom_line() + # adding lines to plot
theme_bw() + # changing style/background
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "PIAT Mathematics"
)
31.1.3 Data screening
Prima di adattare i modelli di crescita, è importante esaminare i dati e ottenere informazioni di base sulle variabili da utilizzare nell’analisi. La selezione preliminare dovrebbe includere l’esame della distribuzione dei punteggi per ogni variabile. Come al solito, le principali statistiche descrittive univariate includono la media, la mediana, la varianza (deviazione standard), l’asimmetria, la curtosi, il minimo, il massimo, l’intervallo e il numero di osservazioni per ogni variabile in base alla metrica del tempo scelta. Le statistiche descrittive bivariate includono correlazioni/covarianze e tabelle di frequenza bivariate per variabili nominali o ordinali. Tutte queste statistiche possono essere esaminate per individuare schemi e relazioni non lineari, così come potenziali valori anomali e codici errati.
I dati longitudinali sono speciali perché sono ordinati, il che può essere indicizzato lungo una o più metriche del tempo (variabili come occasione di misurazione, età, data, tempo dall’evento, numero di esposizioni, ecc.). Ad esempio, è immediatamente informativo esaminare come la media, la varianza e il numero di casi disponibili cambiano attraverso le misure ripetute (ad esempio wght5, wght6, wght7). Si noti che la selezione della metrica del tempo influenza notevolmente come i risultati di qualsiasi modello di crescita specifico possono essere interpretati. Pertanto, nella fase di selezione dei dati è importante considerare come varie proprietà dei dati longitudinali differiscano quando i dati sono organizzati in relazione a diverse metriche del tempo.
Per i dati dell’esempio, le statistiche descrittive possono essere ottenute nel modo seguente.
describe(nlsy_math_long)
#> vars n mean sd median trimmed mad min max
#> id 1 2221 528449.15 327303.70 497403 515466.90 384144.63 201 1256601
#> female 2 2221 0.49 0.50 0 0.49 0.00 0 1
#> lb_wght 3 2221 0.08 0.27 0 0.00 0.00 0 1
#> anti_k1 4 2221 1.42 1.50 1 1.19 1.48 0 8
#> math 5 2221 46.12 12.80 46 46.22 11.86 12 81
#> grade 6 2221 4.51 1.77 4 4.44 1.48 2 8
#> occ 7 2221 2.84 0.79 3 2.77 1.48 2 5
#> age 8 2221 126.90 22.06 126 126.28 25.20 82 175
#> men 9 1074 0.19 0.40 0 0.12 0.00 0 1
#> spring 10 2221 0.65 0.48 1 0.69 0.00 0 1
#> anti 11 2170 1.58 1.54 1 1.38 1.48 0 8
#> range skew kurtosis se
#> id 1256400 0.30 -0.90 6945.07
#> female 1 0.03 -2.00 0.01
#> lb_wght 1 3.10 7.63 0.01
#> anti_k1 8 1.14 1.14 0.03
#> math 69 -0.03 -0.18 0.27
#> grade 6 0.26 -0.92 0.04
#> occ 3 0.55 -0.48 0.02
#> age 93 0.19 -0.91 0.47
#> men 1 1.54 0.37 0.01
#> spring 1 -0.63 -1.61 0.01
#> anti 8 0.98 0.64 0.03Esaminiamo le statistiche descrittive bivariate.
cor(nlsy_math_long, use = "pairwise.complete.obs") |>
round(2)
#> id female lb_wght anti_k1 math grade occ age men spring anti
#> id 1.00 -0.01 -0.01 -0.02 -0.22 -0.01 0.01 -0.01 -0.02 -0.11 0.01
#> female -0.01 1.00 0.06 -0.09 -0.05 0.00 -0.02 -0.04 0.02 0.04 -0.07
#> lb_wght -0.01 0.06 1.00 0.03 -0.03 -0.02 -0.03 0.01 0.04 0.03 0.02
#> anti_k1 -0.02 -0.09 0.03 1.00 -0.08 -0.03 -0.04 -0.01 0.01 -0.01 0.52
#> math -0.22 -0.05 -0.03 -0.08 1.00 0.59 0.53 0.58 0.30 0.29 -0.05
#> grade -0.01 0.00 -0.02 -0.03 0.59 1.00 0.87 0.95 0.62 0.12 0.04
#> occ 0.01 -0.02 -0.03 -0.04 0.53 0.87 1.00 0.86 0.57 0.17 0.04
#> age -0.01 -0.04 0.01 -0.01 0.58 0.95 0.86 1.00 0.64 0.21 0.06
#> men -0.02 0.02 0.04 0.01 0.30 0.62 0.57 0.64 1.00 0.16 0.13
#> spring -0.11 0.04 0.03 -0.01 0.29 0.12 0.17 0.21 0.16 1.00 -0.01
#> anti 0.01 -0.07 0.02 0.52 -0.05 0.04 0.04 0.06 0.13 -0.01 1.0031.1.4 Attendibilità
Come in tutte le analisi, i ricercatori dovrebbero esaminare l’affidabilità dei loro strumenti di misurazione.
31.1.5 Invarianza di misurazione
Quando si lavora con dati di misure ripetute, la comparabilità dei punteggi tra le occasioni di misurazione richiede un certo livello di invarianza di misurazione. Lo strumento di misurazione misura lo stesso costrutto nella stessa metrica in ogni occasione? Formalmente, l’invarianza di misurazione garantisce che i punteggi siano confrontabili sia tra le persone che tra le occasioni di misurazione. Ad esempio, l’invarianza di misurazione tra le misure ripetute del peso degli individui è facilitata dall’uso dello stesso dispositivo di misurazione (bilancia) ogni anno, a condizione che la bilancia sia tarata nello stesso modo ogni anno. Se la bilancia è tarata in modo diverso in occasioni diverse o se vengono utilizzate unità di misura diverse, i punteggi risultanti non possono essere confrontati quantitativamente: lo strumento di misurazione è non invariante. Quando si lavora con dispositivi fisici, l’invarianza di misurazione viene testata e garantita attraverso la taratura. Quando si lavora con scale psicologiche, l’invarianza di misurazione viene o assunta (il che non ideale) o testata utilizzando modelli di misurazione formali.