9.7 Attendibilità e modello di regressione lineare
In parole semplici, la CTT (Teoria Classica dei Test) si basa sul modello di regressione lineare, dove i punteggi osservati sono considerati come variabile dipendente e i punteggi veri come variabile indipendente. Il coefficiente di attendibilità \(\rho_{XT}^2\) rappresenta la proporzione di varianza nella variabile dipendente spiegata dalla variabile indipendente in un modello di regressione lineare con una pendenza unitaria e un’intercetta di zero. In altre parole, il coefficiente di attendibilità è equivalente al coefficiente di determinazione del modello di regressione.
9.7.1 Simulazione
Per dare un contenuto concreto alle affermazioni precedenti, consideriamo la seguente simulazione svolta in \(\textsf{R}\). In tale simulazione il punteggio vero \(T\) e l’errore \(E\) sono creati in modo tale da soddisfare i vincoli della CTT: \(T\) e \(E\) sono variabili casuali gaussiane tra loro incorrelate. Nella simulazione generiamo 100 coppie di valori \(X\) e \(T\) con i seguenti parametri: \(T \sim \mathcal{N}(\mu_T = 12, \sigma^2_T = 6)\), \(E \sim \mathcal{N}(\mu_E = 0, \sigma^2_T = 3)\):
set.seed(123)
library("MASS")
n <- 100
Sigma <- matrix(c(6, 0, 0, 3), byrow = TRUE, ncol = 2)
Sigma
#> [,1] [,2]
#> [1,] 6 0
#> [2,] 0 3
mu <- c(12, 0)
mu
#> [1] 12 0
Y <- mvrnorm(n, mu, Sigma, empirical = TRUE)
T <- Y[, 1]
E <- Y[, 2]Le istruzioni precedenti (empirical = TRUE) creano un campione di valori nei quali le medie e la matrice di covarianze assumono esattamente i valori richiesti. Possiamo dunque immaginare tale insieme di dati come la “popolazione”.
Secondo la CTT, il punteggio osservato è \(X = T + E\). Simuliamo dunque il punteggio osservato \(X\) come:
Le prime 6 osservazioni così ottenute sono:
head(cbind(T, E, X))
#> T E X
#> [1,] 11.148054 -1.5708292 9.577225
#> [2,] 13.137936 -0.3334731 12.804463
#> [3,] 10.391355 2.5457324 12.937087
#> [4,] 11.452152 -0.1955005 11.256652
#> [5,] 9.978233 -0.4919698 9.486263
#> [6,] 10.729882 2.9609180 13.690800Un diagramma di dispersione è fornito nella figura seguente:
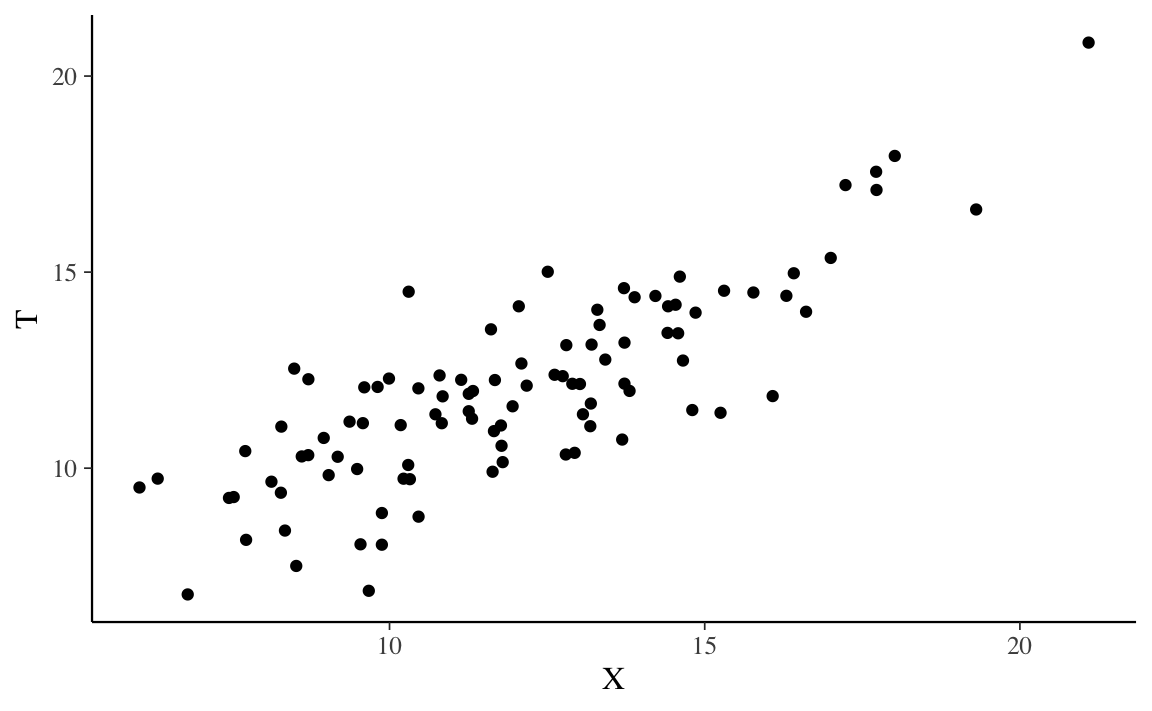
FIGURA 9.1: Simulazione della relazione tra punteggio osservato e punteggio vero per 100 individui in base alle assunzioni della CTT.
Secondo la CTT, il valore atteso di \(T\) è uguale al valore atteso di \(X\). Verifichiamo questa assunzione nei nostri dati:
L’errore deve avere media zero, varianza \(\sigma_E^2\) e deve essere incorrelato con \(T\):
Ricordiamo che la radice quadrata della varianza degli errori è l’errore standard della misurazione, \(\sigma_E\). La quantità \(\sqrt{\sigma_E^2}\) fornisce una misura della dispersione del punteggio osservato attorno al valore vero, nella condizione ipotetica di ripetute somministrazioni del test:
Dato che \(T\) e \(E\) sono incorrelati, ne segue che la varianza del punteggio osservato \(X\) è uguale alla somma della varianza del punteggio vero \(T\) e della varianza degli errori \(E\):
La varianza del punteggio vero \(T\) è uguale alla covarianza tra il punteggio vero \(T\) e il punteggio osservato \(X\):
La correlazione tra punteggio osservato e punteggio vero è uguale al rapporto tra la deviazione standard del punteggio vero e la deviazione standard del punteggio osservato:
Per la CTT, l’attendibilità è uguale al quadrato del coefficiente di correlazione tra il punteggio vero \(T\) e il punteggio osservato \(X\), ovvero:
La motivazione di questa simulazione è quella di mettere in relazione il coefficiente di attendibilità, calcolato con la formula della CTT (come abbiamo fatto sopra), con il modello di regressione lineare. Analizziamo dunque i dati della simulazione mediante il seguente modello di regressione lineare:
\[ X = a + b T + E. \]
Usando \(\textsf{R}\) otteniamo:
fm <- lm(X ~ T)
summary(fm)
#>
#> Call:
#> lm(formula = X ~ T)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1967 -1.1013 0.0524 1.1551 4.2393
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.527e-15 8.746e-01 0 1
#> T 1.000e+00 7.143e-02 14 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.741 on 98 degrees of freedom
#> Multiple R-squared: 0.6667, Adjusted R-squared: 0.6633
#> F-statistic: 196 on 1 and 98 DF, p-value: < 2.2e-16Si noti che la retta di regressione ha intercetta 0 e pendenza 1. Questo è coerente con l’assunzione \(\mathbb{E}(X) = \mathbb{E}(T)\). Ma il risultato più importante di questa simulazione è che il coefficiente di determinazione (\(R^2\) = 0.67) del modello di regressione \(X = 0 + 1 \times T + E\) è identico al coefficiente di attendibilità calcolato con la formula \(\rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}\):
Ciò ci consente di interpretare il coefficiente di attendibilità nel modo seguente: l’attendibilità di un test non è altro che la quota di varianza del punteggio osservato \(X\) che viene spiegata dalla regressione di \(X\) sul punteggio vero \(T\) in un modello di regressione lineare dove \(\alpha\) = 0 e \(\beta\) = 1.