12.1 Attendibilità
Nell’esempio seguente, utilizziamo il set di dati SAPA per dimostrare come calcolare varie stime di coerenza interna in R. Ricordiamo che il data.frame SAPA (Synthetic Aperture Personality Assessment) è costituito da 1525 risposte a 16 item per la valutazione della personalità. Gli item misurano il ragionamento di base, la manipolazione di serie alfanumeriche, il ragionamento con matrici e la capacità di rotazione mentale.
Carichiamo i dati.
Esaminiamo i dati mancanti.
num_miss(SAPA)
#> num_miss perc_miss
#> reason.4 2 0.13
#> reason.16 1 0.07
#> reason.17 2 0.13
#> reason.19 2 0.13
#> letter.7 1 0.07
#> letter.33 2 0.13
#> letter.34 2 0.13
#> letter.58 0 0.00
#> matrix.45 2 0.13
#> matrix.46 1 0.07
#> matrix.47 2 0.13
#> matrix.55 1 0.07
#> rotate.3 2 0.13
#> rotate.4 2 0.13
#> rotate.6 2 0.13
#> rotate.8 1 0.07Una semplice misura di coerenza interna è la affidabilità split-half. Una stima dell’affidabilità split-half può essere ottenuta dividendo un test in due parti equivalenti, calcolando i punteggi totali delle due parti e correlandoli. Ci sono molti modi per creare la suddivisione (ad esempio, selezionando gli item pari e quelli dispari, oppure in modo casuale, ecc.). Di seguito calcoliamo l’affidabilità split-half selezionando gli item pari e quelli dispari.
In questo secondo caso, l’affidabilità split-half è calcolata selezionando due sottoinsiemi casuali di item della stessa numerosità.
È noto che la stima dell’affidabilità split-half è distorta verso il basso (R. J. Cohen, Swerdlik e Sturman, 2013). La correzione Spearman-Brown può essere applicata per superare questo problema. Per fare ciò, basta passare l’argomento sb = TRUE alla funzione split_half().
Dopo aver applicato la correzione di Spearman-Brown, l’affidabilità split-half è ora stimata a 0.862, che è un po’ più alta.
Data la nostra attuale stima di affidabilità, possiamo anche determinare la lunghezza di un test per ottenere l’affidabilità desiderata. Possiamo farlo usando la funzione test_length() in hemp. Supponendo di volere un’affidabilità di 0.95, possiamo determinare di quanti item dovrebbe essere costituito il test. Nella chiamata a test_length(), specifichiamo r_type = "split" in modo che l’affidabilità attuale venga calcolata utilizzando l’affidabilità split-half con la correzione di Spearman-Brown.
Se vogliamo un test con un’affidabilità di 0.95, dato che il nostro test attuale ha un’affidabilità di 0.862 basata su 16 item, avremmo bisogno di un test che consiste di almeno 49 item.
La misura più comune della consistenza interna è il coefficiente alfa (Cronbach, 1951). Il coefficiente alfa rappresenta la media di tutte le possibili correlazioni split-half. Può essere calcolato utilizzando la funzione coef_alpha() in hemp.
Anche se le stime puntuali di affidabilità possono essere utili, è generalmente utile calcolare un intervallo di confidenza. Quando la dimensione del campione è piccola, le ipotesi dei modelli statistici non sono soddisfatte o la distribuzione campionaria di un parametro è sconosciuta, allora il bootstrap può essere utilizzato per costruire una distribuzione campionaria empirica, che possiamo quindi utilizzare per creare intervalli di confidenza (Efron & Tibshirani, 1986 ).
La nostra motivazione per l’introduzione del bootstrapping è che consente la creazione di intervalli di confidenza e incertezza indipendentemente dal parametro stimato. Pertanto, mentre illustriamo l’uso del bootstrap per il coefficiente alfa, questo può essere facilmente applicato per l’affidabilità split-half di cui sopra, la validità o le statistiche dell’analisi degli item presentati più avanti e in molti altri contesti.
Per eseguire il bootstrap per il coefficiente alfa, possiamo usare, ad esempio, il pacchetto boot (Canty & Ripley, 2017).
Dobbiamo creare una funzione da passare alla funzione boot, che chiamiamo alpha_fun(). Questa funzione accetta due argomenti: un set di dati, chiamato data, e una matrice di indici, chiamata row Questi argomenti vengono quindi passati alla funzione coef_alpha. Ciò consentirà alla funzione boot di eseguire un campionamento con rimpiazzo delle righe di data e creare una distribuzione empirica per il coefficiente alfa.
alpha_boot <- boot(SAPA, alpha_fun, R = 1e3)
alpha_boot
#>
#> ORDINARY NONPARAMETRIC BOOTSTRAP
#>
#>
#> Call:
#> boot(data = SAPA, statistic = alpha_fun, R = 1000)
#>
#>
#> Bootstrap Statistics :
#> original bias std. error
#> t1* 0.841 -0.00026 0.005432487La figura seguente mostra un istogramma e un Q-Q plot della distribuzione empirica per il coefficiente alfa basato sui 1000 campioni.
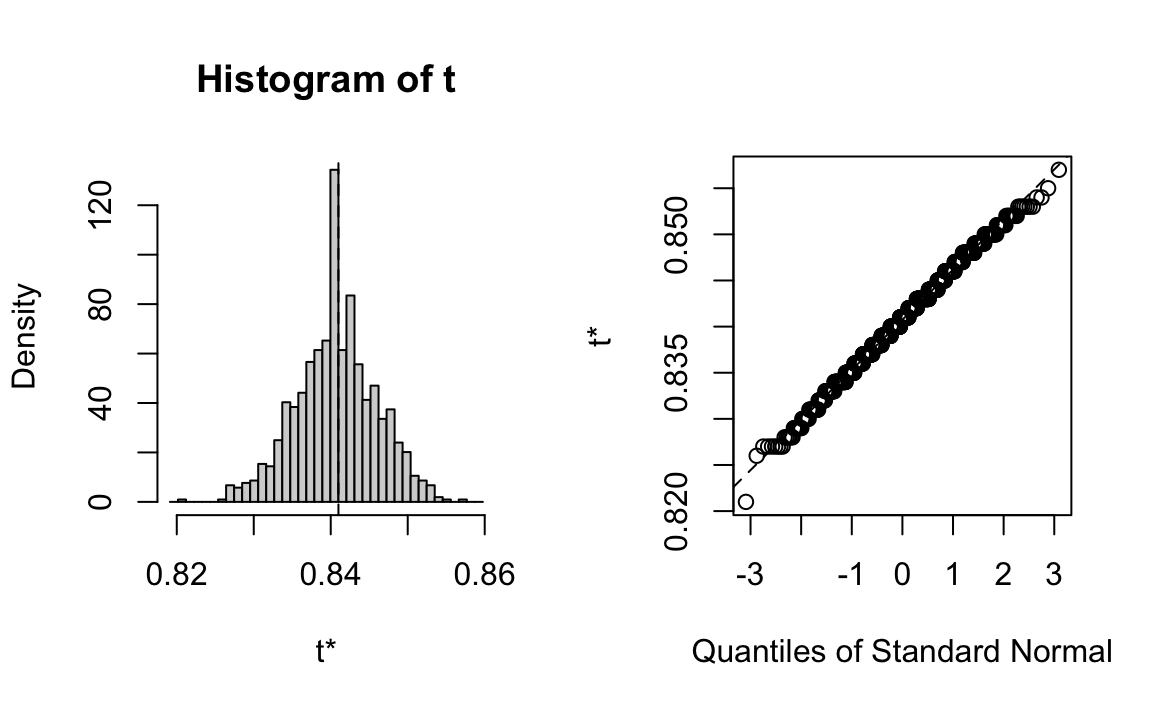
Utilizziamo la funzione boot.ci() per calcolare gli intervalli di confidenza al 95% utilizzando gli intervalli norm, basic e perc. In breve, gli intervalli basic e perc fanno meno assunzioni rispetto agli intervalli norm (ovvero, nessuna assunzione di normalità asintotica). Se la distribuzione empirica si discosta dalla normalità, allora gli intervalli basic e perc sono una scelta migliore.
boot.ci(alpha_boot, type = c("norm", "basic", "perc"))
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 1000 bootstrap replicates
#>
#> CALL :
#> boot.ci(boot.out = alpha_boot, type = c("norm", "basic", "perc"))
#>
#> Intervals :
#> Level Normal Basic Percentile
#> 95% ( 0.8306, 0.8519 ) ( 0.8310, 0.8520 ) ( 0.8300, 0.8510 )
#> Calculations and Intervals on Original ScaleSi può concludere che per la maggior parte degli scopi l’attendibilità sembra essere sufficientemente alta da non richiedere l’onere aggiuntivo per i rispondenti di aumentare la lunghezza dello strumento.