18.2 Path analysis e regressione multipla

Vi è una stretta relazione tra path analysis e regressione multipla, tanto che la regressione può essere considerata un caso particolare di path analysis. Per semplicità, si supponga che le variabili siano state standardizzate, anche se la stessa analisi può essere condotta per variabili grezze. Il path diagram mostra la relazione tra tutte le variabili, comprendendo anche i fattori di disturbo, e fornisce dunque la rappresentazione grafica di un sistema di equazioni simultanee. Nel caso di due regressori, il modello di regressione multipla può essere rappresentato tramite il path diagram riportato nella Figura 18.2.

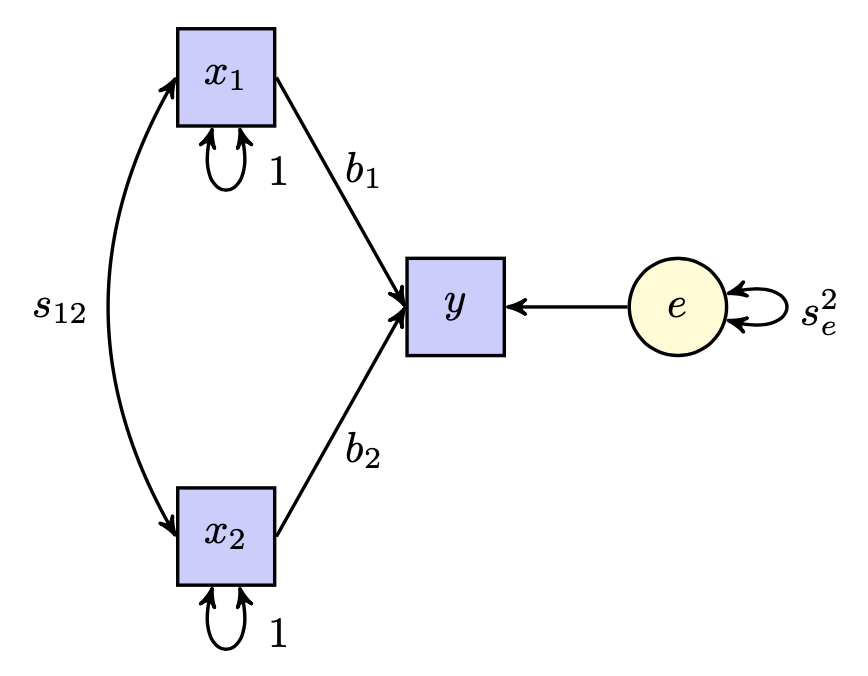
FIGURA 18.2: Path diagram per il modello di regressione multipla con due regressori.

I coefficienti di percorso associati alle frecce orientate esprimono la portata del nesso causale e corrispondono ai pesi beta (ovvero ai coefficienti parziali di regressione standardizzati). Le frecce non orientate esprimono la portata della pura associazione tra variabili e dunque corrispondono alle correlazioni.

Nel caso di due variabili esogene \(x_1\) e \(x_2\), il modello di regressione diventa

\[ y = b_{1} x_1 + b_{2} x_2 + 1 \cdot e, \]

dove \(y\) è la variabile endogena ed \(e\) è il fattore di disturbo. Tale modello di regressione può essere rappresentato graficamente come indicato nella figura precedente.

Nella figura, le frecce dritte indicano un’influenza causale dalla variabile da cui parte la freccia a quella a cui la freccia arriva. A tali frecce dritte sono associati i coefficienti di percorso \(b_1\) e \(b_2\) (ovvero i pesi beta). Il coefficiente 1 rappresenta l’effetto del fattore di disturbo \(e\) sulla variabile endogena \(y\), implicito nelle equazioni e reso esplicito nella figura.

Si noti che si hanno tante equazioni quante sono le variabili endogene. Nel caso presente, c’è un’unica equazione in quanto vi è una sola variabile endogena (ovvero la \(y\), le cui cause sono interne al path diagram). All’interno di ciascuna equazione, inoltre, ci saranno tanti termini quante sono le frecce dritte che puntano verso la variabile endogena. Nell’esempio, ci sono tre termini, uno per ciascun freccia dritta.