38.2 Crescita non lineare
Ripetiamo la procedura di analisi descritta sopra introducendo un cambiamento relativo alla descrizione del cambiamento: verrà considerato un modello nel quale la crescita non è lineare.
Nelle analisi seguenti useremo i seguenti indici di bontà di adattamento.
selected_fit_stats <-
c(
"chisq.scaled",
"df.scaled", ## must be >0 to test G.O.F.
"pvalue.scaled", ## ideally n.s.
"cfi.scaled", ## ideally ≥ 0.95
"rmsea.scaled", ## ideally ≤ 0.05
"rmsea.pvalue.scaled", ## ideally n.s.
"srmr" ## ideally < 0.08
)Supponiamo che la popolazione possa essere descritta dal seguente modello.
growth_mod <-
"
## intercept & slope growth terms for X
iX =~ 1*x1 + 1*x2 + 1*x3 + 1*x4
sX =~ 0*x1 + 1*x2 + 2*x3 + 3*x4
## intercept, slope, & quadratic terms for Y
iY =~ 1*y1 + 1*y2 + 1*y3 + 1*y4
sY =~ 0*y1 + 1*y2 + 2*y3 + 3*y4
qY =~ 0*y1 + 1*y2 + 4*y3 + 9*y4
## set variances
y4 ~~ 2*y4
x4 ~~ 1*x4
## set latent means/intercepts
iX ~ 2*1
sX ~ 1*1
sY ~ -1*1
qY ~ -1.5*1
sY ~ 2*predictor
outcome ~ 2*iX + 3*sY
"È possibile usare la funzione simulateData() di lavaan per simulare un campione di dati estratto da una popolazione definita come abbiamo fatto sopra. La simulazione include due variabili misurate in quattro punti temporali.
sim_growth_dat <- lavaan::simulateData(
model = growth_mod,
model.type = "growth",
seed = 82020,
orthogonal = FALSE,
auto.cov.y = TRUE,
auto.var = TRUE
)Le variabili sono chiamate x1, x2, x3, x4, per la misurazione di x ai tempi 1, 2, 3, 4. Lo stesso per la y.
head(sim_growth_dat)
#> x1 x2 x3 x4 y1 y2 y3
#> 1 1.033229 2.746064 4.9423623 8.41058044 3.36324415 -1.196550 -11.103494
#> 2 3.192802 3.057675 0.7965786 0.84592869 -1.60039704 -5.970381 -10.399366
#> 3 3.758457 4.712351 5.6308218 4.76577291 2.58001675 -3.272134 -11.312994
#> 4 2.700514 4.921257 6.7116263 10.13354061 0.03886676 0.510869 -5.937016
#> 5 1.259807 1.526301 1.6663799 -0.09959486 0.53939838 -4.274106 -12.968362
#> 6 2.547125 5.426192 4.9463195 8.48790397 2.18069542 1.590009 -2.253218
#> y4 outcome predictor
#> 1 -31.509255 2.161186 -0.4893276
#> 2 -19.908088 5.089750 0.5199749
#> 3 -26.681111 3.173129 -0.5938816
#> 4 -7.836099 1.035215 -0.7813707
#> 5 -22.595311 -4.352557 -0.7067630
#> 6 -8.892786 3.277985 -1.2978592Aggiungo qui un codice identificativo per ciascun partecipante.
Nei dati simulati, la variabile x cambia linearmente nel tempo e la variabile y cambia seguendo un andamento quadratico. Esaminiamo i dati con un grafico.
x_plot <-
pivot_longer(sim_growth_dat,
cols = x1:x4,
names_to = "x",
names_prefix = "x"
)
individual_x_trajectories <-
ggplot(
x_plot,
aes(
x = as.numeric(x),
y = value,
group = participant_n,
color = participant_n
)
) +
geom_line(alpha = 0.2) +
labs(
title = "Observed Trajectories of x",
x = "Timepoint",
y = "x"
) +
xlim(1, 4) +
theme(legend.position = "none")
individual_x_trajectories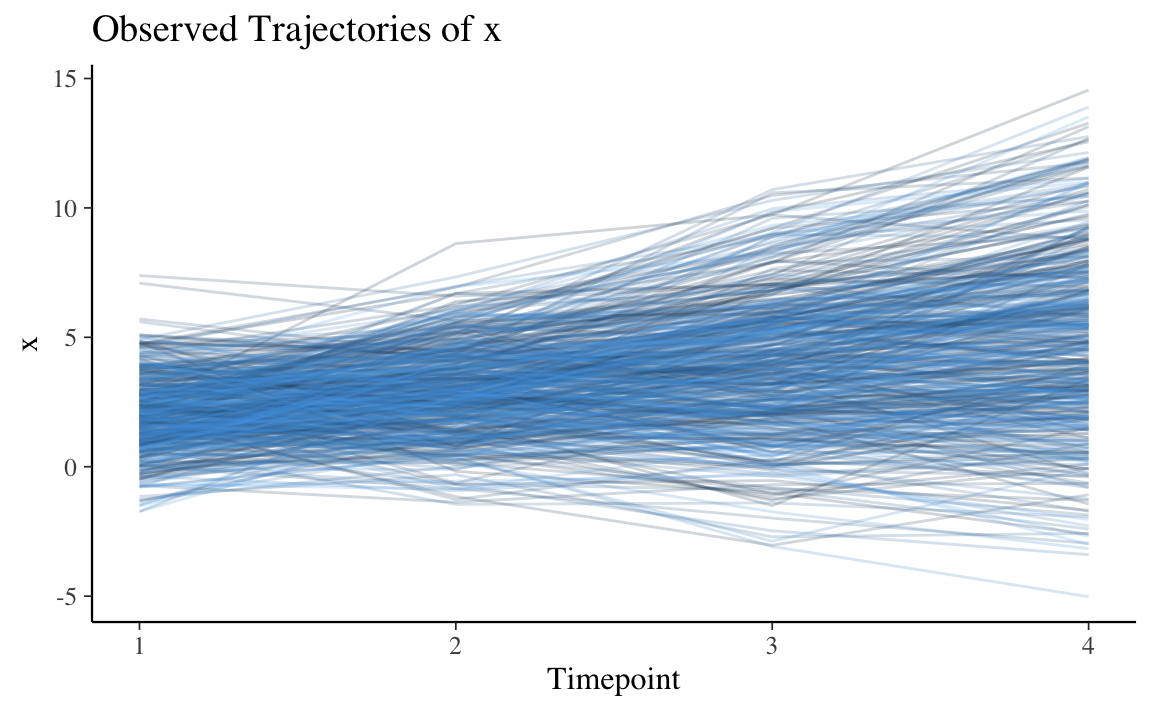
Su può vedere che la variabile x segue una crescita lineare, ma un modello quadratico molto “debole” potrebbe adattarsi meglio ai dati, quindi sarà necessario controllare se in effetti questo è vero.
Esaminiamo ora la variabile y.
y_plot <-
pivot_longer(sim_growth_dat,
cols = y1:y4,
names_to = "y",
names_prefix = "y"
)
individual_y_trajectories <-
ggplot(
y_plot,
aes(
x = as.numeric(y),
y = value,
group = participant_n,
color = participant_n
)
) +
geom_line(alpha = 0.2) +
labs(
title = "Observed trajectories of y",
x = "Timepoint",
y = "y"
) +
xlim(1, 4) +
theme(legend.position = "none")
individual_y_trajectories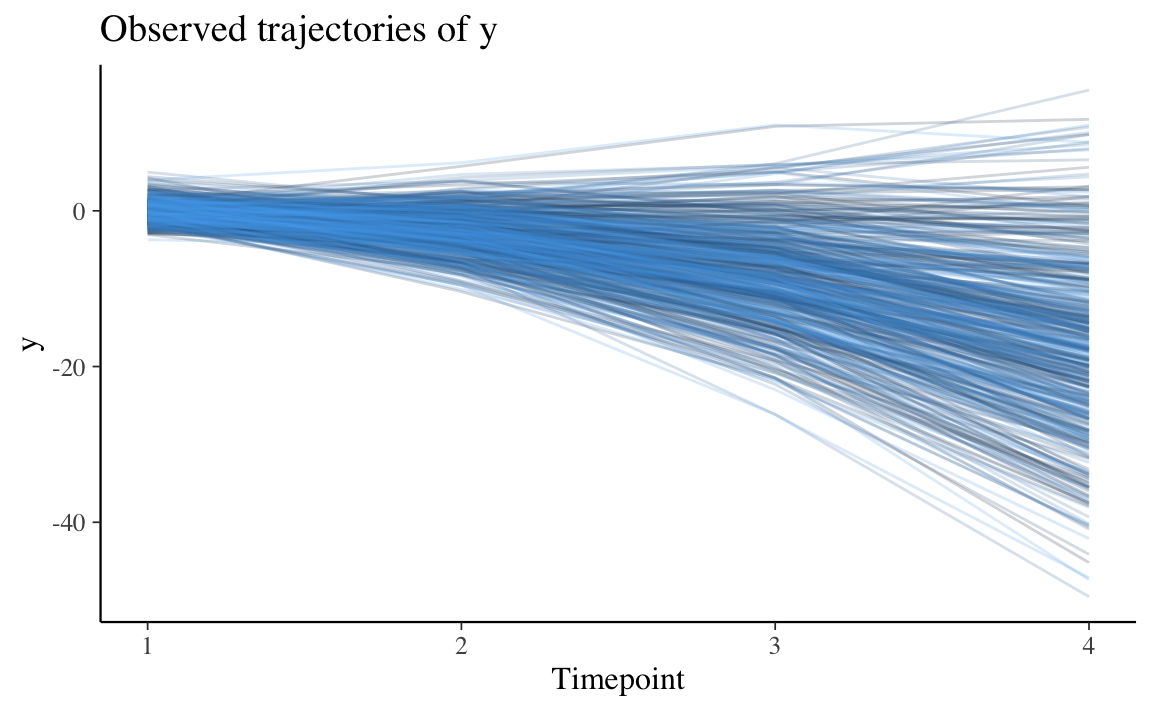
È chiaro che la y diminuisce in media con il tempo, ma c’è anche molta variabilità in ciò che accade nei singoli casi. Per questi dati, sia un modello lineare sia un modello quadratico sembrano appropriati per descrivere il cambiamento nei dati, anche se un modello quadratico sembra più appropriato.