B.2 Matrici

Una matrice costituisce un insieme rettangolare di scalari ordinati per riga e colonna. Può anche essere vista come la raccolta di \(m\) vettori colonna di dimensione \(n\) o come la raccolta di \(n\) vettori riga di dimensione \(m\). Per esempio:

\[ \boldsymbol{A} = \left[ \begin{array}{c c c} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{array} \right] \]

In \(\mathsf{R}\) abbiamo

M <- matrix(
  c(1, 2, 3, 4, 5, 6),
  ncol = 3,
  byrow = TRUE
)
M
#>      [,1] [,2] [,3]
#> [1,]    1    2    3
#> [2,]    4    5    6

B.2.1 Dimensioni della matrice

I numeri interi \(m\) ed \(n\) si dicono dimensioni della matrice, ovvero \(\boldsymbol{A}\) si dice matrice di dimensioni \(m \times n\) o di ordine \(m \times n\). Nel caso presente, la matrice \(\boldsymbol{A}\) ha dimensioni \(2 \times 3\).

dim(M)
#> [1] 2 3

B.2.2 Matrice trasposta

Si definisce matrice trasposta di \(\boldsymbol{A}\), e si denota con \(\boldsymbol{A}'\) oppure \(\boldsymbol{A}'\), la matrice \(\boldsymbol{B} = \boldsymbol{A}'\) di ordine \(n \times m\) cui elementi sono:

\[ b_{ij} = a_{ji}, \quad i = 1 \dots m, j = 1 \dots n \]

Per esempio,

\[ \left[ \begin{array}{c c} -2 & 5\\ 3 & 1\\ 7 & -6 \end{array} \right]'= \left[ \begin{array}{c c c} -2 & 3 & 7\\ 5 & 1 & -6 \end{array} \right] \]

B.2.3 Matrice simmetrica

Se accade che \(\boldsymbol{A} = \boldsymbol{A}'\) allora la matrice è detta simmetrica.

\[ \boldsymbol{A} = \left[ \begin{array}{c c c} 7 & 1 & 2\\ 1 & 8 & 3\\ 2 & 3 & 9 \end{array} \right] \]

• \((\boldsymbol{A} + \boldsymbol{B})' = (\boldsymbol{A})' + (\boldsymbol{B})'\)

• \((\boldsymbol{A} - \boldsymbol{B})' = (\boldsymbol{A})' - (\boldsymbol{B})'\)

• \((\boldsymbol{a} + \boldsymbol{b})' = (\boldsymbol{a})' + (\boldsymbol{b})'\)

• \((\boldsymbol{a} - \boldsymbol{b})' = (\boldsymbol{a})' - (\boldsymbol{b})'\)

B.2.4 Matrice quadrata o rettangolare

Se \(m = n\) allora la matrice \(\boldsymbol{A}\) si dice quadrata di dimensione \(n\) o di ordine \(n\) altrimenti si dice rettangolare. Le righe di \(\boldsymbol{A}\) sono \([a_{11}\ a_{12}\ a_{13}]\) e \([a_{21}\ a_{22}\ a_{23}]\). Le colonne di \(\boldsymbol{A}\) sono \(\left[\begin{array}{c} a_{11} \\ a_{21} \end{array} \right]\), \(\left[ \begin{array}{c} a_{12} \\ a_{22} \end{array} \right]\) e \(\left[ \begin{array}{c} a_{13} \\ a_{23} \end{array} \right]\).

B.2.5 Diagonale principale

Se \(i\) e \(j\) sono numeri interi con \(1 \leq i \leq m\) e \(1 \leq j \leq n\) allora l’elemento della matrice \(\boldsymbol{A}\) di dimensione \(m \times n\) che si trova in posizione (\(i, j\)) viene indicato con \(a_{ij}\). Gli elementi \(a_{ij}\) di una matrice quadrata \(\boldsymbol{A}\) di ordine \(n\) tali che \(i = j\) sono detti elementi principali o diagonali e formano la cosiddetta diagonale principale di \(\boldsymbol{A}\).

\[ \boldsymbol{A} = \left[ \begin{array}{c c c} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array} \right] \]

B.2.6 Matrice diagonale

Se gli elementi \(a_{ij}\) di una matrice quadrata \(\boldsymbol{A}\) sono tali che \(a_{ij} =0\) e \(a_{ii} \neq 0\), allora la matrice \(\boldsymbol{A}\) viene detta matrice diagonale.

\[ \boldsymbol{A} = \left[ \begin{array}{c c c} a_{11} & 0 & 0\\ 0 & a_{22} & 0\\ 0 & 0 & a_{33} \end{array} \right] \]

B.2.7 Matrice identità

Si definisce matrice identità di ordine \(n\) la matrice quadrata diagonale \(\boldsymbol{I}_n\) avente tutti gli elementi principali uguali a \(1\):

\[ \boldsymbol{I}_3 = \left[ \begin{array}{c c c} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right] \]

La matrice identità ha la stessa funzione del numero “1” nel sistema dei numeri reali.

B.2.8 Matrici diagonali e triangolari

Gli elementi di una matrice che si trovano al di sopra della diagonale principale sono detti sopradiagonali, mentre quelli che si trovano al di sotto della stessa diagonale principale sono detti sottodiagonali. Se una matrice ha tutti gli elementi sopradiagonali e sottodiagonali uguali a zero viene detta matrice diagonale. Se invece ha solo gli elementi sopradiagonali nulli allora viene detta triangolare inferiore. Se ha gli elementi sottodiagonali nulli allora è detta triangolare superiore.

B.2.9 Somma e sottrazione

La somma e la sottrazione di due matrici sono operazioni definite elemento per elemento. Per sommare due matrici sommiamo gli elementi corrispondenti. Per sottrarre due matrici sottraiamo gli elementi corrispondenti. Si noti che queste operazioni hanno senso solo se le due matrici hanno le stesse dimensioni (altrimenti queste operazioni non sono definite). Per esempio,

\[ \left[ \begin{array}{c c} -2 & 5\\ 3 & 1\\ 7 & -6 \end{array} \right]+ \left[ \begin{array}{c c} 3 & -2\\ 4 & 5\\ 10 & -3 \end{array} \right]= \left[ \begin{array}{c c} 1 & 3\\ 7 & 6\\ 17 & -9 \end{array} \right] \]

A <- matrix(
  c(-2, 5, 3, 1, 7, -6),
  nrow = 3, byrow = TRUE
)
A
#>      [,1] [,2]
#> [1,]   -2    5
#> [2,]    3    1
#> [3,]    7   -6

B <- matrix(
  c(3, -2, 4, 5, 10, -3),
  nrow = 3, byrow = TRUE
)
B
#>      [,1] [,2]
#> [1,]    3   -2
#> [2,]    4    5
#> [3,]   10   -3

A + B
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    7    6
#> [3,]   17   -9

\[ \left[ \begin{array}{c c} -2 & 5\\ 3 & 1\\ 7 & -6 \end{array} \right]- \left[ \begin{array}{c c} 3 & -2\\ 4 & 5\\ 10 & -3 \end{array} \right]= \left[ \begin{array}{c c} -5 & 7\\ -1 & -4\\ -3 & -3 \end{array} \right] \]

A - B
#>      [,1] [,2]
#> [1,]   -5    7
#> [2,]   -1   -4
#> [3,]   -3   -3

B.2.10 Moltiplicazione di scalari e matrici

L’effetto della moltiplicazione di una matrice \(\boldsymbol{A}\) di qualsiasi dimensione per un numero reale b (scalare) è quello di moltiplicare ciascun elemento in \(\boldsymbol{A}\) per b. Questo è equivalente a sommare \(\boldsymbol{A}\) a se stessa b volte. Per esempio,

\[ 3 \left[ \begin{array}{c c} -2 & 5\\ 3 & 1\\ 7 & -6 \end{array} \right]= \left[ \begin{array}{c c} -6 & 15\\ 9 & 3\\ 21 & -18 \end{array} \right] \]

3 * A
#>      [,1] [,2]
#> [1,]   -6   15
#> [2,]    9    3
#> [3,]   21  -18

B.2.11 Proprietà della somma e differenza

È facile verificare che la somma e la differenza cosı̀ definite godono delle proprietà commutativa e associativa. Siano \(k\) uno scalare e \(A\) e \(B\) due matrici aventi le stesse dimensioni. Allora

• \(\boldsymbol{A}+ \boldsymbol{B} = \boldsymbol{B} + \boldsymbol{A}\)(Proprietà commutativa)
• \(\boldsymbol{A} + (\boldsymbol{B} + \boldsymbol{C}) = (\boldsymbol{A} + \boldsymbol{B}) + \boldsymbol{C}\) (Proprietà associativa)
• \(k(l\boldsymbol{A}) = (kl)\boldsymbol{A}\)
• \(k(\boldsymbol{A} + \boldsymbol{B}) = k\boldsymbol{A} + k\boldsymbol{B}\)(Proprietà distributiva)
• \((k+l)\boldsymbol{A} = k\boldsymbol{A} + l\boldsymbol{A}\)
• \(1\boldsymbol{A} = \boldsymbol{A}\)

B.2.12 Prodotto di matrici

La moltiplicazione di matrici non è un’operazione intuitiva come la somma e la differenza, ma fornisce uno strumento potente per eseguire una lunga serie di calcoli in un modo molto semplice. L’ordine è importante: il numero delle colonne della prima matrice deve essere uguale al numero di righe della seconda matrice. Quando ciò accade le matrici si dicono conformabili, altrimenti si dicono non conformabili.

Sia \(\boldsymbol{A}\) una matrice \(m \times p\) e \(\boldsymbol{B}\) una matrice \(p \times n\). Il prodotto tra le due matrici \(\boldsymbol{C} = \boldsymbol{AB}\) è la matrice di ordine \(m \times n\) il cui elemento generico è

\[ c_{ij} = \sum_{k=1}^{p} a_{ik}a_{kj}, \quad i = 1 \dots m, j = 1 \dots n \]

Pertanto, il prodotto si effettua riga per colonna. È facile verificare che il prodotto tra matrici gode della proprietà associativa ma in generale non di quella commutativa. Vale invece la seguente proprietà:

\[ (\boldsymbol{AB})' = \boldsymbol{B}'\boldsymbol{A}' \]

Ad esempio, siano \(\boldsymbol{A}\) e \(\boldsymbol{B}\) le seguenti matrici

\[ \left[ \begin{array}{c c c} -2 & 1 & 1\\ 1 & 1 & 4\\ 2 & -3 & 2 \end{array} \right] \quad \text{e} \quad \left[ \begin{array}{c c c} 3 & -2 &1\\ 4 & 5 & 0\\ 1 & -3 & 1 \end{array} \right] \]

Calcoliamo la matrice \(\boldsymbol{C} = \boldsymbol{AB}\). L’elemento \(c_{ij}\) è uguale alla somma dei prodotti degli elementi della i-esima riga di \(\boldsymbol{A}\) per la j-esima colonna di \(\boldsymbol{B}\).

\(c_{11} = (-2) \cdot 3 + 1 \cdot 4 + 1 \cdot 1 = -1\)

\(c_{12} = (-2) \cdot (-2) + 1 \cdot 5 + 1 \cdot (-3) = 6\)

\(c_{13} = (-2) \cdot 3 + 1 \cdot 0 + 1 \cdot 1 = -1\)

\(c_{21} = 1 \cdot 3 + 1 \cdot 4 + 4 \cdot 1 = 11\)

\(c_{22} = 1 \cdot (-2) + 1 \cdot 5 + 4 \cdot (-3) = -9\)

\(c_{23} = 1 \cdot 3 + 1 \cdot 0 + 4 \cdot 1 = 5\)

\(c_{31} = 2 \cdot 3 +(-3) \cdot 4 + 2 \cdot 1 = -4\)

\(c_{32} = 2 \cdot (-2) +(-3) \cdot 5 + 2 \cdot (-3) = -25\)

\(c_{33} = 2 \cdot 1 + (-3) \cdot 0 + 2 \cdot 1 = 4\)

In definitiva

\[ \boldsymbol{C} = \left[ \begin{array}{c c c} -1 & 6 & -1\\ 11 & -9 & 5\\ -4 & -25 & 4 \end{array} \right] \]

A <- matrix(
  c(-2, 1, 1, 1, 1, 4, 2, -3, 2),
  nrow = 3,
  byrow = TRUE
)
A
#>      [,1] [,2] [,3]
#> [1,]   -2    1    1
#> [2,]    1    1    4
#> [3,]    2   -3    2

B <- matrix(
  c(3, -2, 1, 4, 5, 0, 1, -3, 1),
  nrow = 3,
  byrow = TRUE
)
B
#>      [,1] [,2] [,3]
#> [1,]    3   -2    1
#> [2,]    4    5    0
#> [3,]    1   -3    1

A %*% B
#>      [,1] [,2] [,3]
#> [1,]   -1    6   -1
#> [2,]   11   -9    5
#> [3,]   -4  -25    4

Calcolando il prodotto \(\boldsymbol{D} = \boldsymbol{BA}\) si trova invece:

\[ \boldsymbol{D} = \left[ \begin{array}{c c c} -6 & -2 & -3\\ -3 & 9 & 24\\ -3 & -5 & -9 \end{array} \right] \]

da cui risulta evidente che \(\boldsymbol{AB} \neq \boldsymbol{BA}\).

B %*% A
#>      [,1] [,2] [,3]
#> [1,]   -6   -2   -3
#> [2,]   -3    9   24
#> [3,]   -3   -5   -9

B.2.13 Proprietà del prodotto di matrici

• \(\boldsymbol{A}(\boldsymbol{B} + \boldsymbol{C}) = \boldsymbol{AB} + \boldsymbol{AC}\)
• \((\boldsymbol{A} + \boldsymbol{B})\boldsymbol{C} = \boldsymbol{AC} + \boldsymbol{BC}\)
• Per qualunque matrice \(\boldsymbol{A}\), \(\boldsymbol{A}'\boldsymbol{A}\) sarà una matrice quadrata.
• \((\boldsymbol{AB})' = \boldsymbol{B}'\boldsymbol{A}'\)

B.2.14 Casi particolari

La matrice identità è l’elemento neutro per il prodotto, cioè se \(\boldsymbol{I}\) è una matrice \(n \times n\) si ha

\[ \boldsymbol{A} \boldsymbol{I}_n = \boldsymbol{I}_n \boldsymbol{A} = \boldsymbol{A}. \]

Per esempio,

\[ \boldsymbol{IA} = \left(% \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}% \right) \left(% \begin{array}{ccc} 2 & 3 & -1 \\ 1 & 4 & 7 \\ \end{array}% \right)= \left(% \begin{array}{ccc} 2 & 3 & -1 \\ 1 & 4 & 7 \\ \end{array}% \right) \]

In R la matrice identità si crea nel modo seguente.

diag(2)
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1

Dunque

A <- matrix(
  c(2, 3, -1, 1, 4, 7),
  nrow = 2, byrow = TRUE
)
A
#>      [,1] [,2] [,3]
#> [1,]    2    3   -1
#> [2,]    1    4    7

diag(2) %*% A
#>      [,1] [,2] [,3]
#> [1,]    2    3   -1
#> [2,]    1    4    7

A %*% diag(3)
#>      [,1] [,2] [,3]
#> [1,]    2    3   -1
#> [2,]    1    4    7

Un secondo caso particolare si verifica quando una matrice è costituita da un’unica colonna o un’unica riga. Se la matrice \(\boldsymbol{A}\) si riduce ad una sola colonna (o una sola riga) e viene detta vettore colonna (o riga) ad \(m\) elementi o componenti. Un vettore colonna è una matrice \(n \times 1\); un vettore riga è una matrice \(1 \times m\). Se \(\boldsymbol{a}\) è un vettore colonna di \(m\) elementi allora \(\boldsymbol{a}'\) è un vettore riga sempre di \(m\) elementi.

Per le operazioni tra vettori valgono le stesse regole viste per le matrici, cioè la somma e la differenza sono possibili tra vettori dello stesso tipo e con lo stesso numero di componenti. La moltiplicazione è possibile tra una matrice e un vettore di dimensioni appropriate, e tra due vettori di dimensioni appropriate. In questo secondo caso, distinguiamo tra prodotto interno e prodotto esterno.

B.2.15 Operazioni tra vettori

Il prodotto interno (o scalare) di un vettore \(\boldsymbol{a}'\) \(1 \times n\) che premoltiplica un vettore \(\boldsymbol{b}\) \(n \times 1\) produce uno scalare:

\[ \boldsymbol{a}'\boldsymbol{b} = \sum_{i=1}^{n}a_i b_i \]

Dati due vettori \(\boldsymbol{a}\), \(\boldsymbol{b}\) di ordini \(n \times 1\) e \(m \times 1\), il prodotto esterno \(\boldsymbol{C} = \boldsymbol{ab}'\) è una matrice \(n \times m\) di elementi \(c_{ij} = a_i b_j\).

B.2.16 Prodotto interno

Siano \(\boldsymbol{a}\) e \(\boldsymbol{b}\) i seguenti vettori:

\[ \left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right] \quad e \quad \left[ \begin{array}{c} -1 \\ -2 \\ 4 \end{array} \right] \]

Il prodotto interno è:

\[ \boldsymbol{a}'\boldsymbol{b}= 1 \cdot (-1) + 2 \cdot (-2) + 3 \cdot 4 = 7 \]

Osserviamo che tale operazione gode della proprietà commutativa, poichè \(\boldsymbol{b}'\boldsymbol{a}=7\).

a <- matrix(
  c(1, 2, 3),
  nrow = 3,
  byrow = TRUE
)
a
#>      [,1]
#> [1,]    1
#> [2,]    2
#> [3,]    3

b <- matrix(
  c(-1, -2, 4),
  nrow = 3,
  byrow = TRUE
)
b
#>      [,1]
#> [1,]   -1
#> [2,]   -2
#> [3,]    4

t(a) %*% b
#>      [,1]
#> [1,]    7

B.2.17 Prodotto esterno

Il prodotto esterno è la matrice

\[ \boldsymbol{C} = \boldsymbol{a}\boldsymbol{b}'= \left[ \begin{array}{c c c} -1 & -2 & 4\\ -2 & -4 & 8\\ -3 & -6 & 12 \end{array} \right] \]

a %*% t(b)
#>      [,1] [,2] [,3]
#> [1,]   -1   -2    4
#> [2,]   -2   -4    8
#> [3,]   -3   -6   12

Tale prodotto non gode della proprietà commutativa, infatti:

\[ \boldsymbol{D} = \boldsymbol{b}\boldsymbol{a}'= \left[ \begin{array}{c c c} -1 & -2 & -3\\ -2 & -4 & -6\\ 4 & 8 & 12 \end{array} \right] \]

b %*% t(a)
#>      [,1] [,2] [,3]
#> [1,]   -1   -2   -3
#> [2,]   -2   -4   -6
#> [3,]    4    8   12

B.2.18 Traccia di una matrice

Si definisce traccia di una matrice quadrata \(\boldsymbol{A}\) \(n \times n\), e si denota con \(tr(\boldsymbol{A})\) la somma degli elementi sulla diagonale principale di \(\boldsymbol{A}\):

\[ tr(\boldsymbol{A}) = \sum_{i=1}^{n} a_{ii} \]

La traccia gode delle seguenti proprietà:

\[ \begin{aligned} &tr(\rho \boldsymbol{A}) = \rho tr( \boldsymbol{A}) \notag \\ &tr(\boldsymbol{A} + \boldsymbol{B}) = tr( \boldsymbol{A})+tr( \boldsymbol{B}) \notag \\ &tr(\boldsymbol{A}') = tr( \boldsymbol{A}) \notag \\ &tr(\boldsymbol{AB}) = tr( \boldsymbol{BA}) \notag\end{aligned} \]

Per esempio, sia

\[ \boldsymbol{A} = \left[ \begin{array}{c c c} 7 & 1 & 2\\ 1 & 8 & 3\\ 2 & 3 & 9 \end{array} \right] \]

allora

\[ tr(\boldsymbol{A}) = 7 + 8 + 9 = 24. \]

A <- matrix(
  c(7, 1, 2, 1, 8, 3, 2, 3, 9),
  nrow = 3,
  byrow = TRUE
)
A
#>      [,1] [,2] [,3]
#> [1,]    7    1    2
#> [2,]    1    8    3
#> [3,]    2    3    9

sum(diag(A))
#> [1] 24

B.2.18.0.1 Dipendenza lineare

Si consideri la matrice

\[ \boldsymbol{A}= \left(% \begin{array}{ccc} 1 & 1 & 1 \\ 3 & 1 & 5 \\ 2 & 3 & 1 \\ \end{array}% \right) \]

Siano \(\boldsymbol{c}_1\), \(\boldsymbol{c}_2\), \(\boldsymbol{c}_3\) le colonne di \(\boldsymbol{A}\). Si noti che

\[ 2\boldsymbol{c}_1 + -\boldsymbol{c}_2 + - \boldsymbol{c}_3 = \boldsymbol{0} \]

dove \(\boldsymbol{0}\) è un vettore (\(3 \times 1\)) di zeri.

Dato che le 3 colonne di \(\boldsymbol{A}\) possono essere combinate linearmente in modo da produrre un vettore \(\boldsymbol{0}\) vi è chiaramente una qualche forma di relazione, o dipendenza, tra le informazioni nelle colonne. Detto in un altro modo, sembra esserci una qualche duplicazione delle informazione nelle colonne. In generale, si dice che \(k\) colonne \(\boldsymbol{c}_1, \boldsymbol{c}_2, \dots \boldsymbol{c}_k\) di una matrice sono linearmente dipendenti se esiste un insieme di valori scalari \(\lambda_1, \dots, \lambda_k\) tale per cui

\[ \lambda_1 \boldsymbol{c}_1 + \dots + \lambda_k \boldsymbol{c}_k=\boldsymbol{0} \]

e almeno uno dei valori \(\lambda_i\) non è uguale a 0.

La dipendenza lineare implica che ciascun vettore colonna è una combinazione degli altri. Per esempio

\[ \boldsymbol{c}_k= -(\lambda_1 \boldsymbol{c}_1 + \dots + \lambda_{k-1} \boldsymbol{c}_{k-1})/\lambda_k \]

Questo implica che tutta “l’informazione” della matrice è contenuta in un sottoinsieme delle colonne – se \(k-1\) colonne sono conosciute, l’ultima resta determinata. È in questo senso che abbiamo detto che l’informazione della matrice veniva “duplicata”.

Se l’unico insieme di valori scalari \(\lambda_i\) che soddisfa l’equazione

\[ \lambda_1 \boldsymbol{c}_1 + \dots + \lambda_k \boldsymbol{c}_k=\boldsymbol{0} \]

è un vettore di zeri, allora questo significa che non vi è alcuna relazione tra le colonne della matrice. Le colonne si dicono linearmente indipendenti, nel senso che non contengono alcuna “duplicazione” di informazione.

B.2.19 Rango di una matrice

Il rango della matrice è il massimo numero di vettori colonna linearmente indipendenti che possono essere selezionati dalla matrice. In maniera equivalente, il rango di una matrice può essere definito come il massimo numero di vettori riga linermente indipendenti. Il rango minimo di una matrice è 1, il che significa che vi è una colonna tale per cui le altre colonne sono dei multipli di questa. Per l’esempio precedente, il rango della matrice \(\boldsymbol{A}\) è 2.

Se la matrice è quadrata, \(\boldsymbol{A}_{n \times n}\), ed è costituita da vettori tutti indipendenti tra di loro, allora il suo rango è \(n\). Se, invece, la matrice è rettangolare, \(\boldsymbol{A}_{m \times n}\), allora il suo rango può essere al massimo il più piccolo tra i due valori m ed n, cioè:

\[ r(\boldsymbol{A}_{m \times n}) \leq min(m,n) \]

B.2.20 Matrice inversa

L’inversa di una matrice quadrata è l’analogo del reciproco per gli scalari. Se \(b\) è uno scalare e \(b=0\), allora il reciproco di \(b\), \(1/b\) non esiste – non è definito. Allo stesso modo, vi sono delle matrici che “si comportano come lo 0” e per le quali l’inversa non è definita. Tali matrici si dicono singolari.

Sia \(\boldsymbol{A}\) una matrice quadrata di dimensione \(n\). Si definisce matrice inversa la matrice, denotata con \(\boldsymbol{A}^{-1}\), che premoltiplicata o postmoltiplicata per \(\boldsymbol{A}\) fornisce la matrice identità:

\[ \boldsymbol{A}\boldsymbol{A}^{-1}=\boldsymbol{A}^{-1}\boldsymbol{A}=\boldsymbol{I} \]

La condizione per l’esistenza e l’unicità di \(\boldsymbol{A}^{-1}\) è che le colonne di \(\boldsymbol{A}\) siano linearmente indipendenti.

Nel caso di una matrice diagonale la determinazione della matrice inversa risulta immediata: \(\boldsymbol{D}^{-1}= diag(1/d_1, \dots, 1/d_n)\). Nel caso di una matrice non diagonale, la matrice inversa si trova usando il computer dove complicate formule per matrici di qualunque dimensione sono implementate in vari software. Solo per matrici di piccole dimensioni sono disponibili semplici espressioni analitiche per il calcolo della matrice inversa.

Per esempio, sia

\[ \boldsymbol{A} = \left[ \begin{array}{c c} 3 & 4 \\ 2 & 6 \end{array} \right] \]

allora

\[ \boldsymbol{A}^{-1} = \left[ \begin{array}{c c} .6 & -.4 \\ -.2 & .3 \end{array} \right] \]

e

\[ \boldsymbol{A}\boldsymbol{A}^{-1} =\left[ \begin{array}{c c} 3 & 4 \\ 2 & 6 \end{array} \right] \left[ \begin{array}{c c} .6 & -.4 \\ -.2 & .3 \end{array} \right] = \left[ \begin{array}{c c} 1 & 0 \\ 0 & 1 \end{array} \right] \]

A <- matrix(
  c(3, 4, 2, 6),
  nrow = 2,
  byrow = TRUE
)
A
#>      [,1] [,2]
#> [1,]    3    4
#> [2,]    2    6

solve(A)
#>      [,1] [,2]
#> [1,]  0.6 -0.4
#> [2,] -0.2  0.3

A %*% solve(A)
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1

solve(A) %*% A
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1

Se \(\boldsymbol{A}\) e \(\boldsymbol{B}\) sono due matrici non singolari aventi le stesse dimensioni, allora l’inversa del loro prodotto è uguale al prodotto delle loro inverse nella sequenza opposta:

\[ (\boldsymbol{AB})^{-1}=\boldsymbol{B}^{-1}\boldsymbol{A}^{-1} \]

B <- matrix(
  c(1, 2, 9, 7),
  nrow = 2,
  byrow = TRUE
)
B
#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    9    7

solve(A %*% B)
#>            [,1]       [,2]
#> [1,] -0.4181818  0.3090909
#> [2,]  0.5090909 -0.3545455

solve(B) %*% solve(A)
#>            [,1]       [,2]
#> [1,] -0.4181818  0.3090909
#> [2,]  0.5090909 -0.3545455

L’inversa della trasposta di una matrice non singolare è uguale alla trasposta dell’inversa:

\[ (\boldsymbol{A}')^{-1}=(\boldsymbol{A}^{-1})' \]

solve(t(A))
#>      [,1] [,2]
#> [1,]  0.6 -0.2
#> [2,] -0.4  0.3

t(solve(A))
#>      [,1] [,2]
#> [1,]  0.6 -0.2
#> [2,] -0.4  0.3

B.2.21 Determinante di una matrice

Sia \(\boldsymbol{A}\) una matrice quadrata. Il determinante di \(\boldsymbol{A}\) è uno scalare, \(|\boldsymbol{A}|\), il cui valore assoluto misura il volume del parallelepipedo delimitato dalle colonne di \(\boldsymbol{A}\). Nel caso della matrice identità il volume è pari a 1, per cui \(|\boldsymbol{I}| =1\). Per una matrice diagonale \(\boldsymbol{D} = diag(d_1, \dots, d_n)\) si ha

\[ |\boldsymbol{D}| = d_1 \cdot d_2, \dots, d_n = \prod_{i=1}^{n}d_i \]

Per una matrice \(2 \times 2\)

\[ \boldsymbol{A} = \left[ \begin{array}{c c} a_{11}& a_{12} \\ a_{21} & a_{22} \end{array} \right] \]

il determinante di \(\boldsymbol{A}\) vale:

\[ |\boldsymbol{A}| = a_{11}a_{22}-a_{12}a_{21} \]

Per esempio:

\[ \boldsymbol{A} = \left[ \begin{array}{c c} 1 & -2 \\ 3 & 9 \end{array} \right] \quad |\boldsymbol{A}| = 1\cdot 9 - (-2) \cdot 3 = 15 \]

Il determinante è definito anche per matrici di dimensioni superiori anche se, in quel caso, i calcoli sono molto più complessi (una volta ancora, si usi il computer!).

A <- matrix(
  c(1, -2, 3, 9),
  nrow = 2,
  byrow = TRUE
)
A
#>      [,1] [,2]
#> [1,]    1   -2
#> [2,]    3    9

det(A)
#> [1] 15

B.2.22 Determinante e inversa

Vi è una relazione tra il determinante e l’inversa di una matrice. Se la matrice \(\boldsymbol{A}\) ha dimensioni \(2 \times 2\) l’inversa di \(\boldsymbol{A}\) si trova nel modo seguente

\[ \boldsymbol{A}^{-1} = \frac{1}{|\boldsymbol{A}|} \left[ \begin{array}{c c} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{array} \right] \]

Anche per le matrici di dimensioni maggiori la matrice inversa è definita nei termini del determinante, ma le formule di calcolo sono molto più complesse.

Per esempio, sia

\[ \boldsymbol{A} = \left[ \begin{array}{c c} 3 & 4 \\ 2 & 6 \end{array} \right] \]

allora

\[ \boldsymbol{A}^{-1} = \frac{1}{10} \left[ \begin{array}{c c} 6 & -4 \\ -2 & 3 \end{array} \right]= \left[ \begin{array}{c c} .6 & -.4 \\ -.2 & .3 \end{array} \right] \]

In precedenza abbiamo detto che, in alcuni casi, una matrice “si comporta come lo 0.” Il determinante di una matrice è ci dice quando una matrice “si comporta come lo 0.” \(|\boldsymbol{A}| = 0\), infatti, se una riga (o una colonna) è una combinazione lineare di due (o più) righe (o colonne) di \(\boldsymbol{A}\).

Per esempio, nel caso di una matrice (\(2 \times 2\))

\[ \boldsymbol{A} = \left( \begin{array}{c c} a_{11}& a_{12} \\ a_{21} & a_{22} \end{array} \right) \]

supponiamo che

\[ \left(% \begin{array}{c} a_{11} \\ a_{21} \\ \end{array}% \right)=2 \left(% \begin{array}{c} a_{12} \\ a_{22} \\ \end{array}% \right)\]

Allora

\[ \boldsymbol{A} = \left( \begin{array}{c c} 2a_{12}& a_{12} \\ 2a_{22} & a_{22} \end{array} \right) \]

e

\[ |\boldsymbol{A}| = 2a_{12}a_{22}-2a_{12}a_{22}=0 \]

In conclusione, se il determinante è uguale a zero, allora la matrice inversa non esiste. Nel caso di una matrice (\(2 \times 2\)), infatti, la formula dell’inversa richiede la divisione per \(a_{11}a_{22}-a_{12}a_{21}\) che, nel caso di una matrice singolare, è uguale a zero.

A <- matrix(
  c(2, 4, 3, 6),
  nrow = 2,
  byrow = TRUE
)
A
#>      [,1] [,2]
#> [1,]    2    4
#> [2,]    3    6

det(A)
#> [1] 0

# solve(A)

B.2.23 Proprietà del determinante

• \(|\boldsymbol{A}'| = |\boldsymbol{A}|\).
• Se \(\boldsymbol{A}\) contiene una colonna o una riga i cui elementi sono tutti 0, allora \(|\boldsymbol{A}|=0\).
• Se \(\boldsymbol{A}\) contiene due colonne (o righe) identiche, allora \(|\boldsymbol{A}|=0\).
• \(|\boldsymbol{A}| = 0\) se una riga (o una colonna) è combinazione lineare di due (o più) righe (o colonne) di \(\boldsymbol{A}\).
• \(|\boldsymbol{A}| = 1/|\boldsymbol{A}^{-1}|\).
• \(|\boldsymbol{I}| = 1\).
• \(|\boldsymbol{A} \boldsymbol{B}| = |\boldsymbol{A}| |\boldsymbol{B}|\).

Per una matrice quadrata \(\boldsymbol{A}\), le seguenti affermazioni sono equivalenti: \(\boldsymbol{A}\) è non singolare, \(|\boldsymbol{A}|\neq 0\), \(\boldsymbol{A}^{-1}\) esiste.

B.2.24 Radici e vettori latenti

Dal determinante di una matrice si possono ricavare le radici latenti o autovalori (denotati da \(\lambda_i\)) e i vettori latenti o autovettori della matrice. Alle nozioni di autovalore e autovettore verrà qui fornita un’interpretazione geometrica.

Simuliamo di dati di due variabili associate tra loro:

library("car")
set.seed(123456)
npoints <- 20
x <- as.numeric(scale(rnorm(npoints, 0, 1)))
y <- as.numeric(scale(3 * x + rnorm(npoints, 0, 2)))
mean(x)
#> [1] 1.076511e-17
mean(y)
#> [1] -1.872959e-17
cor(x, y)
#> [1] 0.8291033

Disegnamo il diagramma di dispersione con un ellisse che contiene la nube di punti:

Y <- cbind(x, y)
car::dataEllipse(
  Y[, 1], Y[, 2],
  levels = 0.95,
  lty = 2,
  ylim = c(-3, 3),
  xlim = c(-3, 3)
)

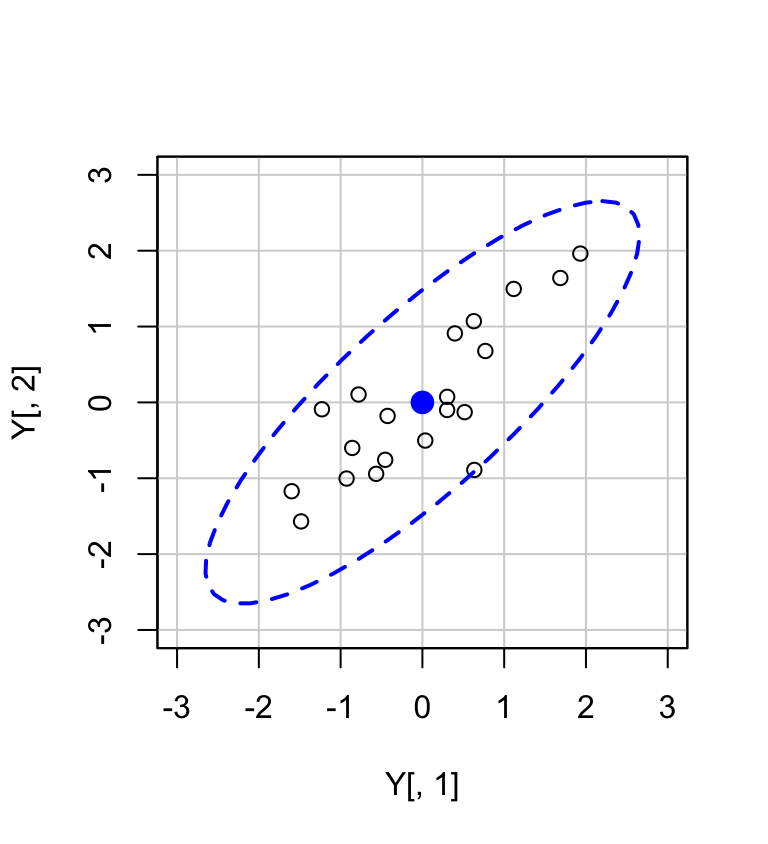
Se racchiudiamo le osservazioni (\(v_1, v_2\)) con un’ellisse, allora la lunghezza dei semiassi maggiori e minori dell’ellisse sarà proporzionale a \(\sqrt{\lambda_1}\) e \(\sqrt{\lambda_2}\). L’asse maggiore è la linea passante per il punto (\(\bar{v_1}, \bar{v_2}\)) nella direzione determinata dal primo autovettore \(\boldsymbol{a}_1'\) con pendenza uguale a \(a_{12}/a_{11}\). L’asse minore è la linea passante per il punto (\(\bar{v_1}, \bar{v_2}\)) nella direzione determinata dal secondo autovettore \(\boldsymbol{a}_2\).

Calcoliamo ora gli autovettori e gli autovalori:

s <- cov(Y)
ee <- eigen(s)

Disegniamo gli assi dell’ellisse:

car::dataEllipse(
  Y[, 1], Y[, 2],
  levels = 0.95,
  lty = 2,
  ylim = c(-3, 3),
  xlim = c(-3, 3)
)
k <- 2.65
arrows(
  0, 0,
  k * sqrt(ee$values[1]) * ee$vectors[1],
  k * sqrt(ee$values[1]) * ee$vectors[2],
  code = 2,
  col = "red",
  lwd = 2
)
arrows(
  0, 0,
  k * sqrt(ee$values[2]) * ee$vectors[1],
  k * sqrt(ee$values[2]) * -ee$vectors[2],
  code = 2,
  col = "red",
  lwd = 2
)

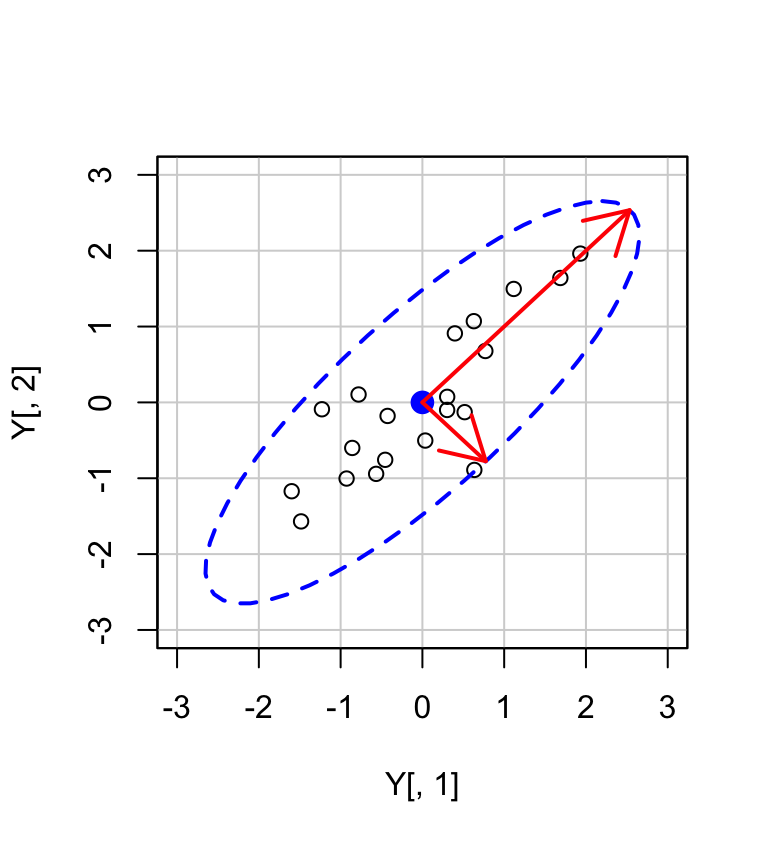
Tale analisi si può estendere a qualunque numero di variabili. Per esempio, nel caso di tre variabili, possiamo pensare di disegnare un ellisoide attorno ad una nube di punti nello spazio tridimensionale. Anche in questo caso, gli autovalori e gli associati autovettori corrisponderanno agli assi dell’elissoide.

B.2.25 Scomposizione spettrale di una matrice

Data una matrice quadrata e simmetrica di dimensione \(n\), \(\boldsymbol{A}\), esistono una matrice diagonale \(\boldsymbol{\Lambda}\) e una matrice ortogonale \(\boldsymbol{V}\) tali che

\[\boldsymbol{A} =\boldsymbol{V} \boldsymbol{\Lambda} \boldsymbol{V}',\] dove

• \(\boldsymbol{\Lambda}\) è una matrice diagonale i cui elementi sono gli autovalori di \(\boldsymbol{A}\): \(\boldsymbol{\Lambda} = diag(\lambda_1, \lambda_2, \dots, \lambda_n)\);
• \(\boldsymbol{V}\) è una matrice ortogonale le cui colonne \((v_1, v_2, \dots, v_p)\) sono gli autovettori di \(\boldsymbol{A}\) associati ai rispettivi autovalori.

In maniera equivalente

\[\boldsymbol{A} \boldsymbol{V} = \boldsymbol{\Lambda} \boldsymbol{V}'.\]

Premoltiplicando entrambi i membri per \(\boldsymbol{V}'\) si ottiene

\[\boldsymbol{V}'\boldsymbol{A} \boldsymbol{V} = \boldsymbol{\Lambda},\]

da cui l’affermazione che la matrice degli autovettori diagonalizza \(\boldsymbol{A}\).

Per esempio,

sigma <- matrix(
  data = c(1, 0.5, 0.5, 1.25),
  nrow = 2,
  ncol = 2
)
sigma
#>      [,1] [,2]
#> [1,]  1.0 0.50
#> [2,]  0.5 1.25

out <- eigen(sigma)
out
#> eigen() decomposition
#> $values
#> [1] 1.6403882 0.6096118
#> 
#> $vectors
#>           [,1]       [,2]
#> [1,] 0.6154122 -0.7882054
#> [2,] 0.7882054  0.6154122

Lambda <- diag(out$values)
Lambda
#>          [,1]      [,2]
#> [1,] 1.640388 0.0000000
#> [2,] 0.000000 0.6096118

U <- out$vectors
U
#>           [,1]       [,2]
#> [1,] 0.6154122 -0.7882054
#> [2,] 0.7882054  0.6154122

U %*% Lambda %*% t(U)
#>      [,1] [,2]
#> [1,]  1.0 0.50
#> [2,]  0.5 1.25

B.2.26 Autovalori e determinante

Il determinante di una matrice è il prodotto degli autovalori:

\[\begin{aligned} |\boldsymbol{A}| &= \prod_{i=1}^{p} \lambda_i. \notag \end{aligned}\]

La traccia di una matrice è uguale alla somma degli autovalori:

\[\begin{aligned} tr(\boldsymbol{A}) &= \sum_{i=1}^{p} \lambda_i. \notag \end{aligned}\]

sigma <- matrix(data = c(1, 0.5, 0.5, 2), nrow = 2, ncol = 2)
sigma
#>      [,1] [,2]
#> [1,]  1.0  0.5
#> [2,]  0.5  2.0

out <- eigen(sigma)
out
#> eigen() decomposition
#> $values
#> [1] 2.2071068 0.7928932
#> 
#> $vectors
#>           [,1]       [,2]
#> [1,] 0.3826834 -0.9238795
#> [2,] 0.9238795  0.3826834

La traccia di una matrice è uguale alla somma degli autovalori:

sum(out$values)
#> [1] 3

Il determinante di una matrice è il prodotto degli autovalori:

det(sigma)
#> [1] 1.75
out$values[1] * out$values[2]
#> [1] 1.75

Gli autovalori di \(\boldsymbol{A}^{-1}\) sono i reciproci degli autovalori di \(\boldsymbol{A}\); gli autovettori sono coincidenti.

Allen, Mary J, and Wendy M Yen. 2001. Introduction to Measurement Theory. Waveland Press.

Barrett, Paul. 2007. “Structural Equation Modelling: Adjudging Model Fit.” Personality and Individual Differences 42 (5): 815–24.

Beaujean, A Alexander. 2014. Latent Variable Modeling Using r: A Step-by-Step Guide. Routledge.

Brown, Timothy A. 2015. Confirmatory Factor Analysis for Applied Research. Guilford publications.

Charter, Richard A. 1996. “Revisiting the Standard Errors of Measurement, Estimate, and Prediction and Their Application to Test Scores.” Perceptual and Motor Skills 82 (3): 1139–44.

Charter, Richard A, and Leonard S Feldt. 2001. “Confidence Intervals for True Scores: Is There a Correct Approach?” Journal of Psychoeducational Assessment 19 (4): 350–64.

Cronbach, Lee J. 1951. “Coefficient Alpha and the Internal Structure of Tests.” Psychometrika 16 (3): 297–334.

Cumming, Geoff. 2014. “The New Statistics: Why and How.” Psychological Science 25 (1): 7–29.

Desjardins, Christopher D, and Okan Bulut. 2018. Handbook of Educational Measurement and Psychometrics Using r. CRC Press.

Dudek, Frank J. 1979. “The Continuing Misinterpretation of the Standard Error of Measurement.” Psychological Bulletin 86 (2): 335--337.

Goodman, Steven N, Daniele Fanelli, and John PA Ioannidis. 2016. “What Does Research Reproducibility Mean?” Science Translational Medicine 8 (341): 341ps12–12.

Grimm, Kevin J, Nilam Ram, and Ryne Estabrook. 2016. Growth Modeling: Structural Equation and Multilevel Modeling Approaches. Guilford Publications.

Grolemund, Garrett. 2014. Hands-on Programming with R: Write Your Own Functions and Simulations. O’Reilly Media, Inc.

Gulliksen, Harold. 1961. “Measurement of Learning and Mental Abilities.” Princeton University.

Hu, Li-tze, and Peter M Bentler. 1998. “Fit Indices in Covariance Structure Modeling: Sensitivity to Underparameterized Model Misspecification.” Psychological Methods 3 (4): 424--453.

Ioannidis, John PA. 2005. “Why Most Published Research Findings Are False.” PLoS Medicine 2 (8): e124.

Jöreskog, Karl G. 1969. “A General Approach to Confirmatory Maximum Likelihood Factor Analysis.” Psychometrika 34 (2): 183–202.

———. 1978. “Structural Analysis of Covariance and Correlation Matrices.” Psychometrika 43 (4): 443–77.

Kan, Kees-Jan, Han LJ van der Maas, and Stephen Z Levine. 2019. “Extending Psychometric Network Analysis: Empirical Evidence Against g in Favor of Mutualism?” Intelligence 73: 52–62.

Kline, Paul. 2013. Handbook of Psychological Testing. Routledge.

Kuder, G Frederic, and Marion W Richardson. 1937. “The Theory of the Estimation of Test Reliability.” Psychometrika 2 (3): 151–60.

Lewis, Charles. 1986. “Test Theory and Psychometrika: The Past Twenty-Five Years.” Psychometrika 51 (1): 11–22.

Lord, Frederic M, and Melvin R Novick. 1968. Statistical Theories of Mental Test Scores. Addison-Wesley.

Mauro, Robert. 1990. “Understanding LOVE (left out variables error): A method for estimating the effects of omitted variables.” Psychological Bulletin 108 (2): 314–29.

McDonald, Roderick P. 2013. Test Theory: A Unified Treatment. Psychology Press.

McNamara, Amelia, and Nicholas J Horton. 2018. “Wrangling Categorical Data in r.” The American Statistician 72 (1): 97–104.

Meredith, William. 1993. “Measurement Invariance, Factor Analysis and Factorial Invariance.” Psychometrika 58 (4): 525–43.

Nunnally, Jum C. 1994. Psychometric Theory. McGraw-Hill.

Open Science Collaboration and others. 2015. “Estimating the Reproducibility of Psychological Science.” Science 349 (6251): aac4716.

R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Samejima, Fumiko. 1983. “Constant Information Model on the Dichotomous Response Level.” In New Horizons in Testing, 287–308. Elsevier.

Savage, Van M, Andrew P Allen, James H Brown, James F Gillooly, Alexander B Herman, William H Woodruff, and Geoffrey B West. 2007. “Scaling of Number, Size, and Metabolic Rate of Cells with Body Size in Mammals.” Proceedings of the National Academy of Sciences 104 (11): 4718–23.

Savage, Van M, and Geoffrey B West. 2007. “A Quantitative, Theoretical Framework for Understanding Mammalian Sleep.” Proceedings of the National Academy of Sciences 104 (3): 1051–56.

Spearman, C. 1904. “General Intelligence Objectively Determined and Measured.” American Journal of Psychology 15: 201–93.

Svetina, Dubravka, Leslie Rutkowski, and David Rutkowski. 2020. “Multiple-Group Invariance with Categorical Outcomes Using Updated Guidelines: An Illustration Using m Plus and the Lavaan/Semtools Packages.” Structural Equation Modeling: A Multidisciplinary Journal 27 (1): 111–30.

Thurstone, Louis Leon. 1947. “Multiple-Factor Analysis; a Development and Expansion of the Vectors of Mind.”

Wechsler, David. 2008. “Wechsler Adult Intelligence Scale–Fourth Edition (WAIS–IV).” San Antonio, TX: NCS Pearson 22 (498): 816–27.

Wilkinson, Leland. 2012. “The Grammar of Graphics.” In Handbook of Computational Statistics, 375–414. Springer.

Wu, Hao, and Ryne Estabrook. 2016. “Identification of Confirmatory Factor Analysis Models of Different Levels of Invariance for Ordered Categorical Outcomes.” Psychometrika 81 (4): 1014–45.

Xia, Yan, and Yanyun Yang. 2019. “RMSEA, CFI, and TLI in Structural Equation Modeling with Ordered Categorical Data: The Story They Tell Depends on the Estimation Methods.” Behavior Research Methods 51 (1): 409–28.