14.4 Introduzione a lavaan | Appunti di Costruzione e validazione di strumenti di misura dell’efficacia dell’intervento psicologico in neuropsicologia

14.4 Introduzione a `lavaan`

14.4.1 Sintassi del modello

Al cuore del pacchetto lavaan si trova la “sintassi del modello”. La sintassi del modello è una descrizione del modello da stimare. In questa sezione, spieghiamo brevemente gli elementi della sintassi del modello lavaan.

Nell’ambiente R, una formula di regressione ha la seguente forma:

y ~ x1 + x2 + x3 + x4

In questa formula, la tilde (“~”) è l’operatore di regressione. Sul lato sinistro dell’operatore, abbiamo la variabile dipendente (y), e sul lato destro abbiamo le variabili indipendenti, separate dall’operatore “+” . In lavaan, un modello tipico è semplicemente un insieme (o sistema) di formule di regressione, in cui alcune variabili (che iniziano con una ‘f’ qui sotto) possono essere latenti. Ad esempio:

y ~ f1 + f2 + x1 + x2
f1 ~ f2 + f3
f2 ~ f3 + x1 + x2

Se abbiamo variabili latenti in una qualsiasi delle formule di regressione, dobbiamo “definirle” elencando i loro indicatori (manifesti o latenti). Lo facciamo utilizzando l’operatore speciale “=~”, che può essere letto come “è misurato da”. Ad esempio, per definire le tre variabili latenti f1, f2 e f3, possiamo usare qualcosa del genere:

f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9 + y10

Inoltre, le varianze e le covarianze sono specificate utilizzando un operatore “doppia tilde”, ad esempio:

y1 ~~ y1 # varianza
y1 ~~ y2 # covarianza
f1 ~~ f2 # covarianza

E infine, le intercette per le variabili osservate e latenti sono semplici formule di regressione con solo una intercetta (esplicitamente indicato dal numero “1”) come unico predittore:

y1 ~ 1
f1 ~ 1

Utilizzando questi quattro tipi di formule, è possibile descrivere una vasta gamma di modelli di variabili latenti. L’attuale insieme di tipi di formula è riassunto nella tabella sottostante.

tipo di formula	operatore	mnemonic
definizione variabile latente	=~	è misurato da
regressione	~	viene regredito su
(co)varianza (residuale)	~~	è correlato con
intercetta	~ 1	intercetta

Una sintassi completa del modello lavaan è semplicemente una combinazione di questi tipi di formule, racchiusi tra virgolette singole. Ad esempio:

my_model <- ' 
  # regressions
  y1 + y2 ~ f1 + f2 + x1 + x2
  f1 ~ f2 + f3
  f2 ~ f3 + x1 + x2

  # latent variable definitions 
  f1 =~ y1 + y2 + y3 
  f2 =~ y4 + y5 + y6 
  f3 =~ y7 + y8 + y9
  
  # variances and covariances 
  y1 ~~ y1 
  y1 ~~ y2 
  f1 ~~ f2

  # intercepts 
  y1 ~ 1 
  f1 ~ 1
'

Per adattare il modello ai dati usiamo la seguente sintassi.

fit <- cfa(model = my_model, data = my_data)

14.4.2 Un esempio concreto

Analizziamo nuovamente i dati di Spearman che abbiamo esaminato in precedenza usando lavaan. La matrice completa dei dati di Spearman è messa a disposizione da Kan, Maas, and Levine (2019). Iniziamo a caricare i pacchetti necessari:

library("lavaan")
library("semPlot")
library("knitr")
library("kableExtra")
library("tidyr")
library("corrplot")

Specifichiamo il nome delle variabili manifeste

varnames <- c(
  "Classics", "French", "English", "Math", "Pitch", "Music"
)

e il loro numero

ny <- length(varnames)

Creiamo la matrice di correlazione:

spearman_cor_mat <- matrix(
  c(
    1.00, .83, .78, .70, .66, .63,
    .83, 1.00, .67, .67, .65, .57,
    .78, .67, 1.00, .64, .54, .51,
    .70, .67, .64, 1.00, .45, .51,
    .66, .65, .54, .45, 1.00, .40,
    .63, .57, .51, .51, .40, 1.00
  ),
  ny, ny,
  byrow = TRUE,
  dimnames = list(varnames, varnames)
)

Specifichiamo l’ampiezza campionaria:

n <- 33

Definiamo il modello unifattoriale in lavaan. L’operatore =~ si può leggere dicendo che la variabile latente a sinistra dell’operatore viene identificata dalle variabili manifeste elencate a destra dell’operatore e separate dal segno +. Per il caso presente, il modello dei due fattori di Spearman può essere specificato come segue.

spearman_mod <- "
  g =~ Classics + French + English + Math + Pitch + Music
"

Adattiamo il modello ai dati con la funzione cfa():

fit1 <- lavaan::cfa(
  spearman_mod,
  sample.cov = spearman_cor_mat,
  sample.nobs = n,
  std.lv = TRUE
)

La funzione cfa() è una funzione dedicata per adattare modelli di analisi fattoriale confermativa. Il primo argomento è il modello specificato dall’utente. Il secondo argomento è il dataset che contiene le variabili osservate. L’argomento std.lv = TRUE specifica che imponiamo una varianza pari a 1 a tutte le variabili latenti comuni (nel caso presente, solo una). Ciò consente di stimare le saturazioni fattoriali.

Una volta adattato il modello, la funzione summary() ci consente di esaminare la soluzione ottenuta:

summary(
  fit1,
  fit.measures = TRUE,
  standardized = TRUE
)
#> lavaan 0.6.15 ended normally after 23 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        12
#> 
#>   Number of observations                            33
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                                 2.913
#>   Degrees of freedom                                 9
#>   P-value (Chi-square)                           0.968
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                               133.625
#>   Degrees of freedom                                15
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    1.000
#>   Tucker-Lewis Index (TLI)                       1.086
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)               -212.547
#>   Loglikelihood unrestricted model (H1)       -211.091
#>                                                       
#>   Akaike (AIC)                                 449.094
#>   Bayesian (BIC)                               467.052
#>   Sample-size adjusted Bayesian (SABIC)        429.622
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.000
#>   90 Percent confidence interval - lower         0.000
#>   90 Percent confidence interval - upper         0.000
#>   P-value H_0: RMSEA <= 0.050                    0.976
#>   P-value H_0: RMSEA >= 0.080                    0.016
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.025
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   g =~                                                                  
#>     Classics          0.942    0.129    7.314    0.000    0.942    0.956
#>     French            0.857    0.137    6.239    0.000    0.857    0.871
#>     English           0.795    0.143    5.545    0.000    0.795    0.807
#>     Math              0.732    0.149    4.923    0.000    0.732    0.743
#>     Pitch             0.678    0.153    4.438    0.000    0.678    0.689
#>     Music             0.643    0.155    4.142    0.000    0.643    0.653
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .Classics          0.083    0.051    1.629    0.103    0.083    0.086
#>    .French            0.234    0.072    3.244    0.001    0.234    0.242
#>    .English           0.338    0.094    3.610    0.000    0.338    0.349
#>    .Math              0.434    0.115    3.773    0.000    0.434    0.447
#>    .Pitch             0.510    0.132    3.855    0.000    0.510    0.526
#>    .Music             0.556    0.143    3.893    0.000    0.556    0.573
#>     g                 1.000                               1.000    1.000

L’output consiste in tre parti. Le prime nove righe sono chiamate intestazione. L’intestazione contiene le seguenti informazioni:

il numero di versione di lavaan
se l’ottimizzazione è terminata normalmente o meno e quante iterazioni sono state necessarie
lo stimatore utilizzato (qui: ML, per la massima verosimiglianza)
l’ottimizzatore utilizzato per trovare i valori dei parametri di adattamento migliori per questo stimatore (qui: NLMINB)
il numero di parametri del modello (qui: 12)
il numero di osservazioni che sono state effettivamente utilizzate nell’analisi (qui: 33)
una sezione chiamata “Model Test User Model”: che fornisce una statistica di test, i gradi di libertà e un valore p per il modello specificato dall’utente.

La sezione successiva contiene ulteriori misure di adattamento e viene mostrata solo se si utilizza l’argomento opzionale fit.measures = TRUE. Inizia con la riga Model Test Baseline Model: e termina con il valore per l’SRMR. L’ultima sezione contiene le stime dei parametri. Inizia con informazioni (tecniche) sul metodo utilizzato per calcolare gli errori standard. Quindi, vengono elencati tutti i parametri liberi (e fissati) inclusi nel modello. Di solito, prima vengono mostrate le variabili latenti, seguite dalle covarianze e dalle varianze (residui). La prima colonna (Stima) contiene il valore del parametro (stimato o fisso) per ogni parametro del modello; la seconda colonna (Std.err) contiene l’errore standard per ogni parametro stimato; la terza colonna (Z-value) contiene la statistica di Wald (che viene semplicemente ottenuta dividendo il valore del parametro per il suo errore standard), e l’ultima colonna (P(>|z|)) contiene il valore p per testare l’ipotesi nulla che il valore del parametro sia uguale a zero nella popolazione.

Si noti che nella sezione Varianze: c’è un punto prima dei nomi delle variabili osservate. Ciò perché sono variabili dipendenti (o endogene) (predette dalle variabili latenti) e quindi il valore della varianza stampato in output è una stima della varianza residua: la varianza rimanente che non è spiegata dal/i predittore/i. Al contrario, non c’è un punto prima dei nomi delle variabili latenti, perché in questo modello sono variabili esogene. I valori delle varianze qui sono le varianze totali stimate delle variabili latenti.

È possibile semplificare l’output dalla funzione summary() in maniera tale da stampare solo la tabella completa delle stime dei parametri e degli errori standard. Qui usiamo coef(fit1).

kable(round(coef(fit1), 2), booktabs = TRUE, format = "markdown")

	x
g=~Classics	0.94
g=~French	0.86
g=~English	0.79
g=~Math	0.73
g=~Pitch	0.68
g=~Music	0.64
Classics~~Classics	0.08
French~~French	0.23
English~~English	0.34
Math~~Math	0.43
Pitch~~Pitch	0.51
Music~~Music	0.56

Senza usare kable, l’output diventa il seguente.

parameterEstimates(fit1, standardized = TRUE)
#>         lhs op      rhs   est    se     z pvalue ci.lower ci.upper std.lv
#> 1         g =~ Classics 0.942 0.129 7.314  0.000    0.689    1.194  0.942
#> 2         g =~   French 0.857 0.137 6.239  0.000    0.588    1.127  0.857
#> 3         g =~  English 0.795 0.143 5.545  0.000    0.514    1.076  0.795
#> 4         g =~     Math 0.732 0.149 4.923  0.000    0.441    1.024  0.732
#> 5         g =~    Pitch 0.678 0.153 4.438  0.000    0.379    0.978  0.678
#> 6         g =~    Music 0.643 0.155 4.142  0.000    0.339    0.948  0.643
#> 7  Classics ~~ Classics 0.083 0.051 1.629  0.103   -0.017    0.183  0.083
#> 8    French ~~   French 0.234 0.072 3.244  0.001    0.093    0.376  0.234
#> 9   English ~~  English 0.338 0.094 3.610  0.000    0.154    0.522  0.338
#> 10     Math ~~     Math 0.434 0.115 3.773  0.000    0.208    0.659  0.434
#> 11    Pitch ~~    Pitch 0.510 0.132 3.855  0.000    0.251    0.769  0.510
#> 12    Music ~~    Music 0.556 0.143 3.893  0.000    0.276    0.836  0.556
#> 13        g ~~        g 1.000 0.000    NA     NA    1.000    1.000  1.000
#>    std.all std.nox
#> 1    0.956   0.956
#> 2    0.871   0.871
#> 3    0.807   0.807
#> 4    0.743   0.743
#> 5    0.689   0.689
#> 6    0.653   0.653
#> 7    0.086   0.086
#> 8    0.242   0.242
#> 9    0.349   0.349
#> 10   0.447   0.447
#> 11   0.526   0.526
#> 12   0.573   0.573
#> 13   1.000   1.000

Usando invece kable con opportuni parametri, otteniamo:

parameterEstimates(fit1, standardized = TRUE) %>%
  dplyr::filter(op == "=~") %>%
  dplyr::select(
    "Latent Factor" = lhs,
    Indicator = rhs,
    B = est,
    SE = se,
    Z = z,
    "p-value" = pvalue,
    Beta = std.all
  ) %>%
  knitr::kable(
    digits = 3, booktabs = TRUE, format = "markdown",
    caption = "Factor Loadings"
  )

TABELLA 14.1: Factor Loadings
Latent Factor	Indicator	B	SE	Z	Beta
g	Classics	0.942	0.129	7.314	0.956
g	French	0.857	0.137	6.239	0.871
g	English	0.795	0.143	5.545	0.807
g	Math	0.732	0.149	4.923	0.743
g	Pitch	0.678	0.153	4.438	0.689
g	Music	0.643	0.155	4.142	0.653

Esaminiamo la matrice delle correlazioni residue:

cor_table <- residuals(fit1, type = "cor")$cov
knitr::kable(
  cor_table,
  digits = 3,
  format = "markdown",
  booktabs = TRUE
)

	Classics	French	English	Math	Pitch	Music
Classics	0.000	-0.003	0.008	-0.011	0.001	0.005
French	-0.003	0.000	-0.033	0.023	0.050	0.001
English	0.008	-0.033	0.000	0.040	-0.016	-0.017
Math	-0.011	0.023	0.040	0.000	-0.062	0.024
Pitch	0.001	0.050	-0.016	-0.062	0.000	-0.050
Music	0.005	0.001	-0.017	0.024	-0.050	0.000

Creiamo un qq-plot dei residui:

res1 <- residuals(fit1, type = "cor")$cov
res1[upper.tri(res1, diag = TRUE)] <- NA
v1 <- as.vector(res1)
v2 <- v1[!is.na(v1)]

tibble(v2) %>%
  ggplot(aes(sample = v2)) +
  stat_qq() +
  stat_qq_line()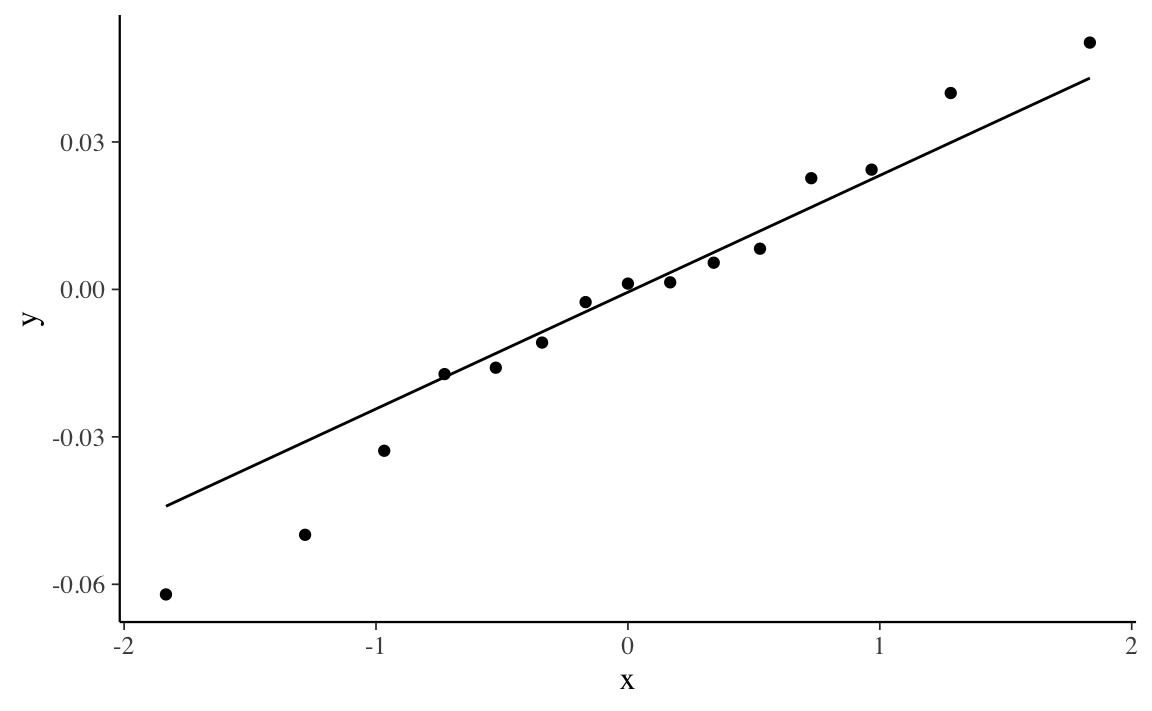

14.4.3 Diagrammi di percorso

Il pacchetto semPlot consente di disegnare diagrammi di percorso per vari modelli SEM. La funzione semPaths prende in input un oggetto creato da lavaan e disegna il diagramma, con diverse opzioni disponibili. Il diagramma prodotto controlla le dimensioni dei caratteri/etichette, la visualizzazione dei residui e il colore dei percorsi/coefficienti. Sono disponibili queste e molte altre opzioni di controllo.

semPaths(
  fit1,
  "std",
  posCol = c("black"),
  edge.label.cex = 1.2,
  sizeMan = 7
)

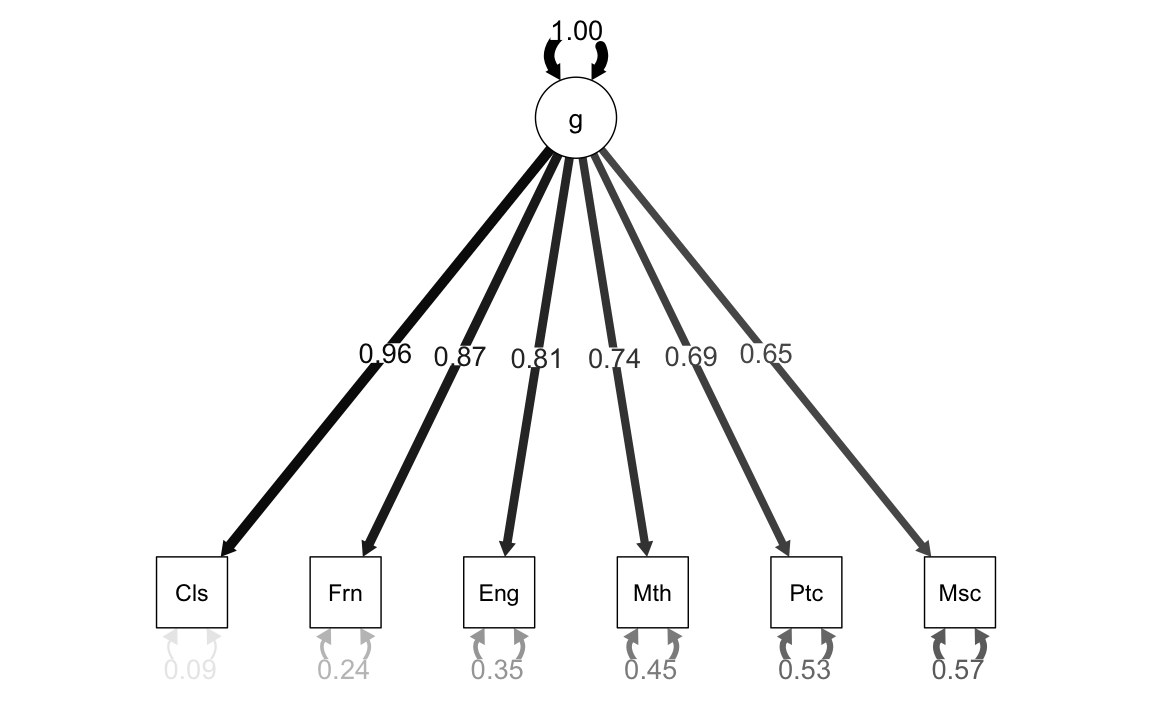
Il calcolo delle saturazioni fattoriali con il metodo del centroide aveva prodotto il seguente risultato:

classici (Cls): 0.97
inglese (Eng): 0.84
matematica (Mth): 0.73
pitch discrimination (Ptc): 0.65

Si noti la somiglianza con i valori ottenuti mediante il metodo di massima verosimiglianza riportati nella figura.

14.4.4 Analisi fattoriale esplorativa

Quando abbiamo un’unica variabile latente, l’analisi fattoriale confermativa si riduce al caso dell’analisi fattoriale esplorativa. Esaminiamo qui sotto la sintassi per l’analisi fattoriale esplorativa in lavaan.

Specifichiamo il modello.

efa_model <- '
    efa("efa")*g =~ Classics + French + English + Math + Pitch + Music
'

Adattiamo il modello ai dati.

fit2 <- lavaan::cfa(
  efa_model,
  sample.cov = spearman_cor_mat,
  sample.nobs = n,
  std.lv = TRUE
)

Esaminiamo la soluzione ottenuta.

summary(fit2, standardized = TRUE)
#> lavaan 0.6.15 ended normally after 3 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        12
#> 
#>   Rotation method                       GEOMIN OBLIQUE
#>   Geomin epsilon                                 0.001
#>   Rotation algorithm (rstarts)                GPA (30)
#>   Standardized metric                             TRUE
#>   Row weights                                     None
#> 
#>   Number of observations                            33
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                                 2.913
#>   Degrees of freedom                                 9
#>   P-value (Chi-square)                           0.968
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   g =~ efa                                                              
#>     Classics          0.942    0.129    7.314    0.000    0.942    0.956
#>     French            0.857    0.137    6.239    0.000    0.857    0.871
#>     English           0.795    0.143    5.545    0.000    0.795    0.807
#>     Math              0.732    0.149    4.923    0.000    0.732    0.743
#>     Pitch             0.678    0.153    4.438    0.000    0.678    0.689
#>     Music             0.643    0.155    4.142    0.000    0.643    0.653
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .Classics          0.083    0.051    1.629    0.103    0.083    0.086
#>    .French            0.234    0.072    3.244    0.001    0.234    0.242
#>    .English           0.338    0.094    3.610    0.000    0.338    0.349
#>    .Math              0.434    0.115    3.773    0.000    0.434    0.447
#>    .Pitch             0.510    0.132    3.855    0.000    0.510    0.526
#>    .Music             0.556    0.143    3.893    0.000    0.556    0.573
#>     g                 1.000                               1.000    1.000

References

Kan, Kees-Jan, Han LJ van der Maas, and Stephen Z Levine. 2019. “Extending Psychometric Network Analysis: Empirical Evidence Against g in Favor of Mutualism?” Intelligence 73: 52–62.