26.4 Analisi degli item
L’analisi degli item svolge un ruolo importante nello sviluppo e nella revisione dei test psicometrici. L’analisi degli item esamina le risposte fornite ai singoli item del questionario allo scopo di valutare la qualità degli item e del questionario nel suo complesso. Sotto al rubrica di analisi degli item possiamo raggruppare le procedure che possono essere utilizzate per descrivere la difficoltà degli item, le relazioni tra coppie di item, il punteggio totale del test, le relazioni tra gli item e il punteggio totale del test. Tali analisi statistiche vengono usate per la selezione degli item al fine di costruire un questionario omogeneo, attendibile e dotato di validità predittiva.
La selezione degli item di un test, però, non può essere svolta in maniera automatica usando soltanto criteri statistici quali quelli elencati sopra. La selezione degli item, invece, deve anche tenere includere considerazioni di ordine teorico basate sulla centralità degli item rispetto alla definizione del costrutto e considerazioni relative agli scopi della misurazione e al modo in cui l’item è stato formulato e costruito. Se alcuni aspetti di un costrutto non vengono rappresentanti da item che soddisfano i criteri statistici descritti sopra, o se c’è un numero insufficiente di item per produrre uno strumento attendibile, allora alcuni item dovranno essere riscritti. Nella riformulazione degli item, risultano utili le intuizioni che si sono guadagnate dalle analisi statistiche degli item che si sono dovuti scartare.
26.4.1 Difficoltà degli item
Una statistica comune da calcolare durante l’analisi degli item è la proporzione di esaminandi che rispondono correttamente ad ogni item. Questa è nota come difficoltà dell’item, p. La proporzione \(p_j\) di partecipanti che rispondono correttamente all’item \(j\)-esimo, o proporzione di partecipanti che si dichiarano in accordo con l’affermazione espressa dall’item, se il test non è di prestazione, fornisce una stima del livello di difficoltà \(\pi_j\) dell’item.
In realtà, \(p_j\) dovrebbe essere chiamato “facilità dell’item” in quanto assume il suo valore maggiore (ovvero \(1\)) quando tutti i rispondenti rispondono correttamente all’item e il suo valore minimo (ovvero \(0\)) quando le risposte sono tutte sbagliate. Questo valore non va confuso con la difficoltà dell’item nella teoria della risposta agli item o con il valore-\(p\) dei test di ipotesi frequentisti.
I valori \(p_j\) giocano un ruolo importante nelle procedure di selezione degli item. La difficoltà degli item deve essere interpretata in riferimento alla probabilità di indovinare la risposta corretta. Si suppone, infatti, che i rispondenti tirino ad indovinare quando non conoscono la risposta alla domanda di un questionario. Nel caso di item dicotomici, per esempio, ci possiamo aspettare un valore \(p_j\) pari a \(0.50\) sulla base del caso soltanto; nel caso di item a risposta multipla con quattro opzioni di scelta, invece, \(p_j\) assume un valore pari a \(0.25\) quando i rispondenti tirano ad indovinare.
Se il test è composto per la maggior parte da item “facili”, allora il test non sarà in grado di discriminare tra rispondenti con diversi livelli di abilità, in quanto quasi tutti i rispondenti saranno in grado di fornire una risposta corretta alla maggioranza degli item. Lo stesso si può dire per un test composto da item “difficili”. Se il test è composto unicamente da item di difficoltà media, non potrà differenziare i rispondenti che hanno un grado di abilità media da quelli con abilità superiori alla media, dato che non ci sono item “difficili”, e neppure da quelli con abilità inferiori alla media, dato che non ci sono item “facili”.
In generale, dunque, è buona pratica costruire test composti da item che coprano tutti i livelli di difficoltà. La scelta che viene usualmente fatta è quella di una dispersione moderata e simmetrica del livello di difficoltà attorno ad un valore leggermente superiore al valore che sta a metà tra il livello del caso (\(1.0\) diviso per il numero di alternative) e il punteggio pieno (\(1.0\)).
Per item che presentano cinque alternative di risposta, ad esempio, il livello del caso è pari a \(1.0 / 5 = 0.20\). Il livello ottimale di difficoltà è uguale a
\[ 0.20 + (1.0 - 0.20) / 2 = 0.60. \]
Per item dicotomici, il livello del caso è \(1.0 / 2 = 0.50\) e il livello ottimale di difficoltà è uguale a
\[ 0.50 + (1.00 - 0.50) / 2 = 0.75. \]
In generale, item con livelli di difficoltà superiore a \(0.90\) o inferiore a \(0.20\) dovrebbero essere utilizzati con cautela.
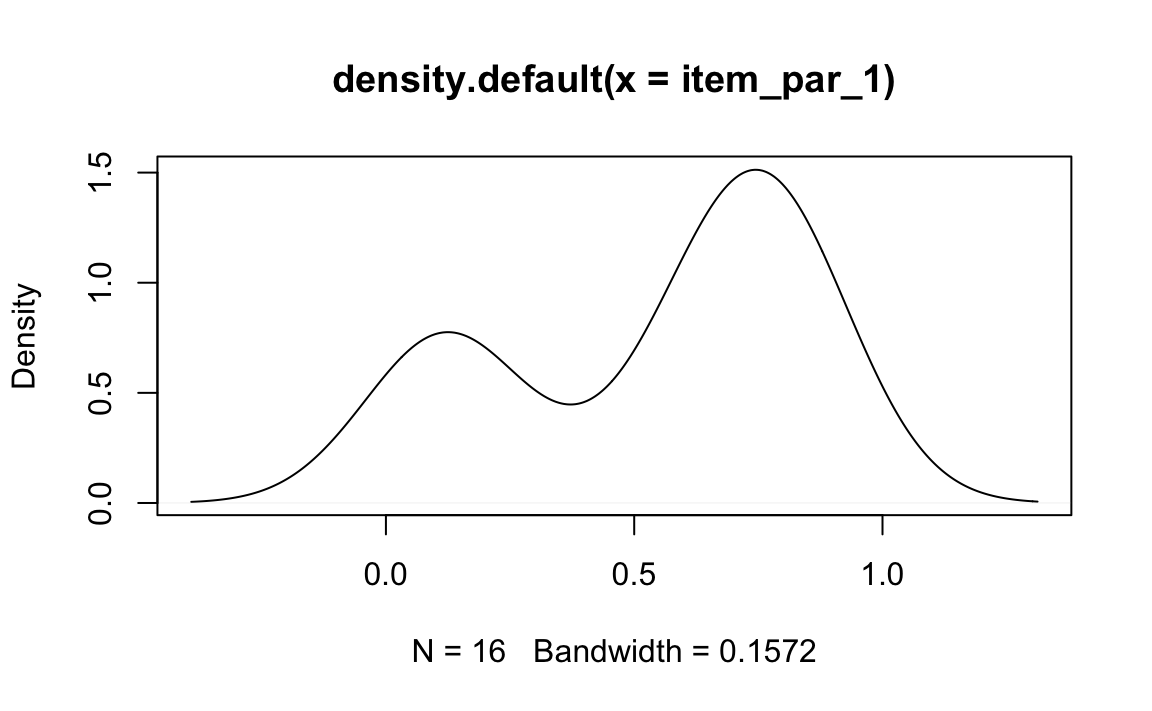
Esempio 26.6 Riporto qui sotto le proporzioni di risposte corrette (usando la correzione per il guessing) di 192 studenti di Psicometria nel primo parziale dell’AA 2021/2022. Il test aveva 16 item con 5 alternative di risposta ciascuno. Dunque la difficoltà media ottimale è pari a 0.6.
item_par_1 <- c(
0.54255319, 0.76063830, 0.64361702, 0.65957447, 0.67021277, 0.12234043,
0.14361702, 0.18085106, 0.76063830, 0.82978723, 0.81914894, 0.84042553,
0.07978723, 0.07978723, 0.76063830, 0.79255319
)Nel compito, la difficoltà media è risultata essere un po’ inferiore.
La distribuzione dei livelli di difficoltà degli item suggerisce che forse alcuni item “difficili” si sarebbero potuti sostituire con item di difficoltà media.
Un altro esempio riguarda il data set SAPA del pacchetto hemp. Per questi dati possiamo utilizzare la funzione colMeans per calcolare la difficoltà degli item. Poiché abbiamo dei partecipanti che hanno risposte mancanti su alcuni item, dobbiamo passare l’argomento na.rm = TRUE per ignorare i dati mancanti. In caso contrario, la funzione colMeans restituirebbe NA per gli item che hanno almeno un valore mancante. Per rendere più leggibili i valori di difficoltà degli item, arrotondiamo a tre decimali utilizzando la funzione round.
item_diff <- colMeans(SAPA, na.rm = TRUE)
round(item_diff, 3)
#> reason.4 reason.16 reason.17 reason.19 letter.7 letter.33 letter.34 letter.58
#> 0.640 0.698 0.697 0.615 0.600 0.571 0.613 0.444
#> matrix.45 matrix.46 matrix.47 matrix.55 rotate.3 rotate.4 rotate.6 rotate.8
#> 0.526 0.550 0.614 0.374 0.194 0.213 0.299 0.185L’output mostra che gli item reason.16 e reason.17 ottengono i livelli di difficoltà più alti, mentre rotate.8 ha il livello di difficoltà più basso. Circa il 70% degli studenti è stato in grado di rispondere correttamente a reason.16 e reason.17, mentre solo il 19% ha risposto correttamente a rotate.8.
26.4.2 Correzione per guessing
Alle volte i valori \(p_j\) sono calcolati introducendo una correzione per le risposte fornite casualmente dai soggetti (guessing). Si consideri un test a scelta multipla composto da item aventi ciascuno \(C\) alternative di risposta ed una sola risposta corretta. Si supponga che un rispondente risponda correttamente a \(R\) item e risponda in maniera sbagliata a \(W\) item.
La correzione per guessing si ottiene applicando una formula basata sul seguente ragionamento. Se assumiamo che un rispondente si limita a tirare ad indovinare allora, ogni \(C\) risposte, ci aspettiamo 1 risposta giusta e \(C-1\) risposte sbagliate. Per calcolare il punteggio totale del test in modo da eliminare il numero di risposte corrette ottenute tirando ad indovinare è necessario sottrarre 1 punto per ogni \(C-1\) item a cui è stata fornita una risposta corretta. Questo ragionamento conduce alla seguente formula:
\[\begin{equation} FS = R - \frac{W}{C - 1}, \tag{26.3} \end{equation}\]
con \(R\) = # risposte corrette, \(W\) = # risposte sbagliate, \(C\) = # alternative di risposta. Per esempio, se \(C=5\), allora è necessario sottrarre un punto ogni 4, il che è proprio quello che fa la (26.3).
La (26.3) produce un punteggio totale corretto per il guessing identico a quello che si otterrebbe assegnando 1 punto a ciascuna risposta corretta e assegnando \(- \frac{1}{C-1}\) punti alle risposte sbagliate; le risposte non date non vengono considerate.
La correzione per guessing rappresenta il tentativo di scomporre il numero totale di risposte corrette in due componenti: le risposte corrette dovute alle conoscenze del soggetto, le risposte che risultano corrette come effetto del caso. La stessa formula può anche essere utilizzata per calcolare la difficoltà degli item corretta per il guessing (come è stato fatto nell’esempio del parziale di Psicometria).
26.4.3 Discriminatività
La discriminatività è una misura di quanto ogni item è in grado di distinguere i soggetti con elevati livelli nel costrutto da quelli con un livello basso. L’indice di discriminatività \(D\) per i test di prestazione massima si trova nel modo seguente. Dopo avere calcolato il punteggio totale al test, si dividono i soggetti in due gruppi: soggetti con basso punteggio e soggetti con alto punteggio. Una volta definiti i due gruppi, l’indice di discriminatività \(D\) sarà dato da:
\[D = P(\text{alto}) - P(\text{basso}),\]
dove \(P(\text{alto}\) è la proporzione di soggetti che ha risposto correttamente all’item nel gruppo con punteggi alti e \(P(\text{basso}\) è la proporzione di soggetti che ha risposto correttamente all’item nel gruppo con punteggi bassi. Il valore di \(D\) può variare da -1 a +1. Nella tabella seguente sono fornite le linee guida per l’interpretazione di questo indice (Ebel, 1965).
| Valore di \(D\) | Commento |
|---|---|
| \(D \geq 0.40\) | Ottima, nessuna revisione |
| \(0.30 \leq D < 0.40\) | Buona, revisioni minime |
| \(0.20 \leq D < 0.30\) | Sufficiente, revisioni parziali |
| \(D < 0.20\) | Insufficiente, riformulazione o eliminazione |
La discriminatività degli item di tipo Likert viene valutata con la medesima procedura degli item dei testi di prestazione massima, anche se cambiano le procedure statistiche da utilizzare. Si può dividere la distribuzione dei punteggi totali (o punteggi medi) in quartili e confrontare il punteggio medio o mediano del quartile superiore con quello del quartile inferiore, oppure, se il test è orientato al criterio e lo scopo è selezionare gli item che discriminano meglio due gruppi precostituiti di soggetto, eseguire i medesimi confronti tra il gruppo target (ad esempio, pazienti) e quello “di controllo” (per esempio, popolazione generale).
È consigliabile valutare la dimensione dell’effetto, ad esempio attraverso l’indice \(d\) di Cohen. La dimensione dell’effetto dovrebbe essere almeno moderata (\(d > |0.50|\)).
Esempio 26.7 Per il primo parziale di Psicometria AA 2021/2022, l’indice \(d\) di Cohen calcolato sulla proporzione di risposte corrette per il gruppo di studenti con i punteggi più bassi (primo quartile) e il gruppo di studenti con i punteggi più alti (ultimo quartile) è stato di 4.76, 95% CI [4.0, 5.51]. L’indice complessivo di discriminatività sembra dunque adeguato. Sarebbe però necessario calcolare questo indice item per item.
26.4.4 Potere discriminante dell’item e analisi fattoriale
Un’altra statistica ampiamente utilizzata nell’analisi degli item è il potere discriminante degli item, che si riferisce alla capacità dell’item nel distinguere gli esaminandi con una alta abilità da quelli con una bassa abilità. Sebbene esistano molti modi per calcolare la discriminazione degli item, la forma più comune è la correlazione punto-biseriale tra le risposte degli esaminandi all’item e il loro punteggio totale nel test. Valori grandi e positivi indicano una forte relazione tra il rispondere correttamente all’item e avere un punteggio alto nel test, mentre valori vicini allo zero indicano nessuna relazione e valori negativi indicano che il rispondere correttamente all’item è associato a un punteggio complessivo del test più basso. Valori vicini allo zero o negativi suggeriscono che l’item potrebbe non funzionare correttamente. Alcune delle ragioni per ottenere una discriminazione degli item bassa o negativa potrebbero essere l’utilizzo di una chiave di risposta errata per l’item o l’assenza di risposte corrette. Indipendentemente dalla causa, gli item con correlazioni punto-biseriale basse o negative devono essere modificati, se il test/strumento è in fase di revisione, o rimossi dal test e dal punteggio.
Per calcolare il potere discriminante dell’item per i dati SAPA, prima calcoliamo il punteggio totale del test utilizzando la funzione rowSums insieme all’opzione na.rm = TRUE e lo salviamo come total_score. Successivamente, correlaziamo gli item in SAPA con il punteggio totale del test utilizzando la funzione cor. Specificamente, usiamo l’argomento use = "pairwise.complete.obs" nella funzione cor a causa della presenza di risposte mancanti. Infine, salviamo la matrice di correlazione come item_discr e la stampiamo.
total_score <- rowSums(SAPA, na.rm = TRUE)
item_discr <- cor(SAPA, total_score, use = "pairwise.complete.obs")
round(item_discr, 2)
#> [,1]
#> reason.4 0.59
#> reason.16 0.53
#> reason.17 0.59
#> reason.19 0.56
#> letter.7 0.58
#> letter.33 0.56
#> letter.34 0.59
#> letter.58 0.58
#> matrix.45 0.51
#> matrix.46 0.51
#> matrix.47 0.55
#> matrix.55 0.45
#> rotate.3 0.51
#> rotate.4 0.56
#> rotate.6 0.55
#> rotate.8 0.48I risultati mostrano che tutti gli item del test SAPA sono moderatamente e positivamente correlati con il punteggio totale del test. Questo indica che tutti gli item funzionano correttamente e non fornisce informazioni salienti su quali item rimuovere o modificare.
Un altro modo per calcolare il potere discriminante degli item consiste nel dividere i candidati in due gruppi (ad esempio, 1 = alto rendimento e 0 = basso rendimento) in base ai loro punteggi totali nel test e correlare questa variabile di raggruppamento con le risposte agli item. Questo è noto come indice di discriminazione degli item. Un’opzione per creare gruppi di alto e basso rendimento è selezionare il 25% più alto e il 25% più basso dei candidati in base ai loro punteggi totali nel test. Va notato che la decisione di utilizzare il 25% è arbitraria. Potremmo utilizzare un altro valore (ad esempio, il 10% o il 20%) per definire i gruppi di alto e basso rendimento. Dopo aver definito il punto di cut-off per i gruppi, calcoliamo la proporzione di candidati che hanno risposto correttamente all’elemento nei gruppi di alto e basso rendimento.
Nell’esempio seguente, calcoliamo l’indice di discriminazione dell’elemento reason.4 nel set di dati SAPA utilizzando la funzione idi del pacchetto hemp. Per specificare i gruppi di alto e basso rendimento, utilizziamo il valore perc_cut = .25 nella funzione idi.
Abbiamo scoperto che l’81% dei candidati nel gruppo di alto rendimento ha risposto correttamente all’item reason.4, mentre solo il 19% dei candidati nel gruppo di basso rendimento ha risposto correttamente. Questo suggerisce che l’item era più facile per i candidati di alto rendimento e più difficile per quelli di basso rendimento. Pertanto, possiamo dire che questo particolare item risulta utile per differenziare i due gruppi, ma non necessariamente all’interno di ciascun gruppo.
Secondo McDondald (1999), la nozione di potere discriminante dell’item può essere trattata in maniera più precisa nell’ambito del modello monofattoriale. Se l’insieme di item a disposizione non è eccessivamente grande (200 o meno), infatti, è possibile procedere alla selezione degli item migliori tramite l’analisi fattoriale – ovvero, scegliendo gli item con le saturazioni maggiori.
Esempio 26.8 Per il primo parziale di Psicometria AA 2021/2022 si ottiene la seguente soluzione fattoriale a due fattori. Questa soluzione sembra suggerire che gli item 1 e 5 forse andrebbero sostituiti, mentre gli altri item sembrano adeguati.
faT1 <- fa(r=cormat, nfactors=2, n.obs=192, rotate="oblimin")
faT1$loadings
Loadings:
MR1 MR2
i1 0.132
i2 0.270 0.107
i3 0.489
i4 0.343 0.365
i5 0.130 0.105
i6 0.565 -0.497
i7 0.527
i8 0.792
i9 0.363
i10 0.467 0.250
i11 0.459 0.190
i12 0.111 0.497
i13 0.401
i14 0.511 0.173
i15 0.206 0.252
i16 0.247 0.36526.4.5 Punteggio sull’item e punteggio totale
Il grado di associazione tra il punteggio sull’item e il punteggio totale viene considerato dalla teoria classica dei test come un indice che descrive il potere discriminante dell’item. Se il test fornisce una misura attendibile di un unico attributo, e se un item è fortemente associato al punteggio del test, allora l’item sarà in grado di distinguere tra rispondenti che ottengono un punteggio basso nel test e rispondenti che ottengono un punteggio alto nel test.
Nel caso di una forte associazione positiva tra il punteggio sull’item e il punteggio totale, la probabilità di risposta corretta sull’item è alta per rispondenti che ottengono un punteggio totale alto, e bassa per i rispondenti che ottengono un punteggio totale basso. Nel caso di una debole associazione tra il punteggio sull’item e il punteggio totale, invece, la probabilità di risposta corretta all’item non è predittiva del punteggio totale. Gli item con un basso potere discriminante dovrebbero dunque essere rimossi dal reattivo.
È necessario distinguere i casi in cui gli item sono dicotomici dal caso di item continui. Nel caso di item dicotomici e di un test unidimensionale, il potere discriminante viene calcolato mediante la correlazione biseriale o punto-biseriale.
26.4.6 Relazioni tra coppie di item
Le relazioni tra coppie di item sono importanti sia per la costruzione sia per la validazione dei test psicometrici. La teoria classica dei test definisce l’attendibilità di un test (o di un item) come il rapporto tra la varianza del punteggio vero e la varianza del punteggio osservato. Il coefficiente di attendibilità può però essere calcolato anche trovando la correlazione tra due forme parallele di un test (o tra due item). Inoltre, è possibile interpretare la correlazione tra due forme parallele di un test (o tra due item) come il quadrato del coefficiente di correlazione tra i punteggi osservati e i punteggi veri di un test (o di un item).
Molti indici sono disponibili per misurare il grado di associazione tra item. Per item quantitativi, possiamo usare la correlazione di Pearson o la covarianza. Per item qualitativi politomici ordinali, usiamo la correlazione policorica. Per item ordinali dicotomici, usiamo la correlazione tetracorica. Per item dicotomici usiamo, ad esempio, l’indice \(\phi\).
26.4.7 Ridondanza
Nel processo di raffinamento del test occorre anche tenere conto degli item ridondanti, ossia degli item che sono troppo associati tra loro. La ridondanza può essere valutata con indici statistici quali la correlazione: se due o più item hanno tra loro una correlazione maggiore di \(|0.70|\) viene mantenuto nell’item pool solo uno di essi, dato che gli altri item forniscono la stessa informazione.
26.4.8 Massimizzazione della varianza del punteggio totale
Uno dei criteri che possono essere utilizzati per la selezionare degli item che andranno a costituire la versione finale di un test è la massimizzazione della varianza del punteggio totale. Più in particolare, si vuole massimizzare il rapporto tra la varianza del punteggio totale e la somma delle varianze dei punteggi dei \(p\) item. Dato che il coefficiente \(\alpha\) di Cronbach ha la seguente forma:
\[\alpha = \frac{p}{p-1}\left[1- \frac{\sum \sigma^2_{Y_i}}{\sigma^2_T} \right],\]
la scelta di massimizzare il rapporto definito in precedenza avrà anche la conseguenza di massimizzare \(\alpha\).
McDonald (2013) fa notare che una procedura di selezione degli item basata sul principio della massimizzazione di \(\alpha\) ha però dei limiti. In primo luogo, tale procedura è appropriata solo quando l’insieme di item è troppo grande per selezionare gli item in base all’esame delle saturazioni fattoriali ottenute applicando il modello mono-fattoriale. In secondo luogo, McDonald (2013) nota che la procedura di selezione basata sulla massimizzazione di \(\alpha\) è adeguata solo nel caso di una struttura mono-fattoriale. La selezione degli item basata sulla massimizzazione di \(\alpha\) deve dunque essere accompagnata da considerazione relative al contenuto e alla struttura del costrutto.
26.4.9 Indice di affidabilità dell’item
Oltre agli indici di difficoltà e discriminazione degli elementi, un’altra statistica utile per l’analisi degli elementi è l’indice di affidabilità dell’elemento. L’indice di affidabilità dell’elemento (IRI) è definito come:
\[ IRI = S_i \cdot r_{i,tt}, \]
dove \(S_i\) è la deviazione standard dell’item \(i\) e \(r_{i,tt}\) è la correlazione tra l’item \(i\) e il punteggio totale del test. L’IRI può teoricamente variare tra -0.5 e 0.5, con valori grandi e positivi indicativi di alta affidabilità.
Di seguito calcoliamo l’IRI per tutti gli item nel set di dati SAPA. Possiamo farlo utilizzando la funzione iri in hemp.
iri(SAPA)
#> [,1]
#> reason.4 0.2820989
#> reason.16 0.2451971
#> reason.17 0.2692675
#> reason.19 0.2717135
#> letter.7 0.2865325
#> letter.33 0.2757209
#> letter.34 0.2897118
#> letter.58 0.2863221
#> matrix.45 0.2544930
#> matrix.46 0.2562540
#> matrix.47 0.2668171
#> matrix.55 0.2161230
#> rotate.3 0.2016459
#> rotate.4 0.2276081
#> rotate.6 0.2539219
#> rotate.8 0.1867207I risultati restituiti dalla funzione iri mostrano che l’IRI varia da circa 0.19 a 0.29 per il set di dati SAPA. Tutti questi sono valori ragionevoli per l’IRI (ovvero nessuno è negativo o vicino allo zero).
26.4.10 Indice di validità dell’item
Quando invece del punteggio totale del test viene utilizzato un criterio esterno, questo indice è noto come indice di validità dell’item (IVI). L’IVI può variare anche tra -0.5 e 0.5, con valori elevati (in valore assoluto) che indicano una validità maggiore. Valori negativi elevati indicano una maggiore validità quando ci si aspetta che gli elementi siano correlati in modo negativo con il criterio.
Nell’esempio seguente, utilizziamo la funzione ivi in hemp con “reason.17” come criterio esterno e “reason.4” come elemento di interesse e troviamo che l’IVI è 0.19.
26.4.11 Distrattori
Un altro aspetto importante degli elementi che deve essere analizzato sono le opzioni di risposta. Nel contesto dei test a scelta multipla, le opzioni di risposta alternative (cioè sbagliate) vengono definite “distrattori”. I distrattori svolgono un ruolo importante in un elemento a scelta multipla. Per garantire elementi a scelta multipla di alta qualità, è cruciale includere distrattori plausibili e ben funzionanti che siano più probabili di attirare i candidati con conoscenze parziali. I distrattori non plausibili potrebbero dover essere riscritti o sostituiti con un distrattore migliore. La qualità dei distrattori viene tipicamente valutata attraverso l’analisi dei distrattori. L’analisi dei distrattori viene spesso condotta osservando la proporzione di candidati che scelgono un distrattore particolare.
Per illustrare l’analisi dei distrattori, utilizziamo gli item del data set multiplechoice in hemp. Si tratta di un ipotetico test a scelta multipla composto da 27 item somministrati a 496 candidati. Le quattro opzioni di risposta sono codificate come 1, 2, 3 e 4 nel data set. Utilizziamo la funzione distract in hemp per calcolare la proporzione di candidati che selezionano ciascun distrattore.
distractors <- distract(multiplechoice)
head(distractors)
#> 1 2 3 4
#> item1 0.044 0.058 0.052 0.845
#> item2 0.109 0.069 0.792 0.030
#> item3 0.188 0.562 0.058 0.192
#> item4 0.034 0.125 0.742 0.099
#> item5 0.351 0.254 0.042 0.353
#> item6 0.081 0.198 0.558 0.163Nella tabella sopra, vediamo che molti item avevano distrattori selezionati circa il 5% delle volte o meno. Questi distrattori potrebbero essere candidati per una revisione in quanto sono stati approvati ad un livello così basso da suggerire che la maggior parte degli esaminandi non li ha considerati come opzioni plausibili. Per l’item 1, i distrattori funzionavano tutti più o meno allo stesso modo (ovvero circa il 5% delle volte ogniuno è stato approvato), suggerendo che funzionavano tutti bene rispetto l’uno all’altro, ma che l’item era troppo facile (la risposta corretta era l’opzione 4, selezionata dall’84.5% degli esaminandi). Al contrario, l’item 5 era un item più difficile, con la risposta corretta che ancora una volta era l’opzione 4. Le opzioni 1 e 2 erano molto probabilmente fraintendimenti, mentre l’opzione 3 potrebbe essere rivista o potenzialmente eliminata da questo item a causa del basso tasso di approvazione (solo il 4.2%). Dato l’approvazione molto alta dell’opzione 1 (35.1%), è molto probabile che anche questa opzione fosse corretta. Per ottenere una visione più completa del funzionamento dell’item, sarebbe consigliabile calcolare l’indice di discriminazione specifico per quell’item. Questo ci permetterebbe di ottenere ulteriori informazioni sulla capacità dell’item di distinguere tra candidati di alto e basso livello.