25.4 Matrice dei pesi fattoriali e matrice di struttura
Nella rotazione ortogonale i fattori sono incorrelati. Si consideri la situazione presentata nella figura 25.1, con due variabili latenti incorrelate (\(\xi_1\) e \(\xi_2\)) e quattro variabili manifeste (\(y_1\), \(y_2\), \(y_3\), \(y_4\)). Siano \(\lambda_{11}\), \(\lambda_{12}\), \(\lambda_{13}\) e \(\lambda_{14}\) le saturazioni fattoriali delle variabili nel primo fattore; siano \(\lambda_{21}\), \(\lambda_{22}\), \(\lambda_{23}\) e \(\lambda_{24}\) le saturazioni fattoriali delle variabili nel secondo fattore.
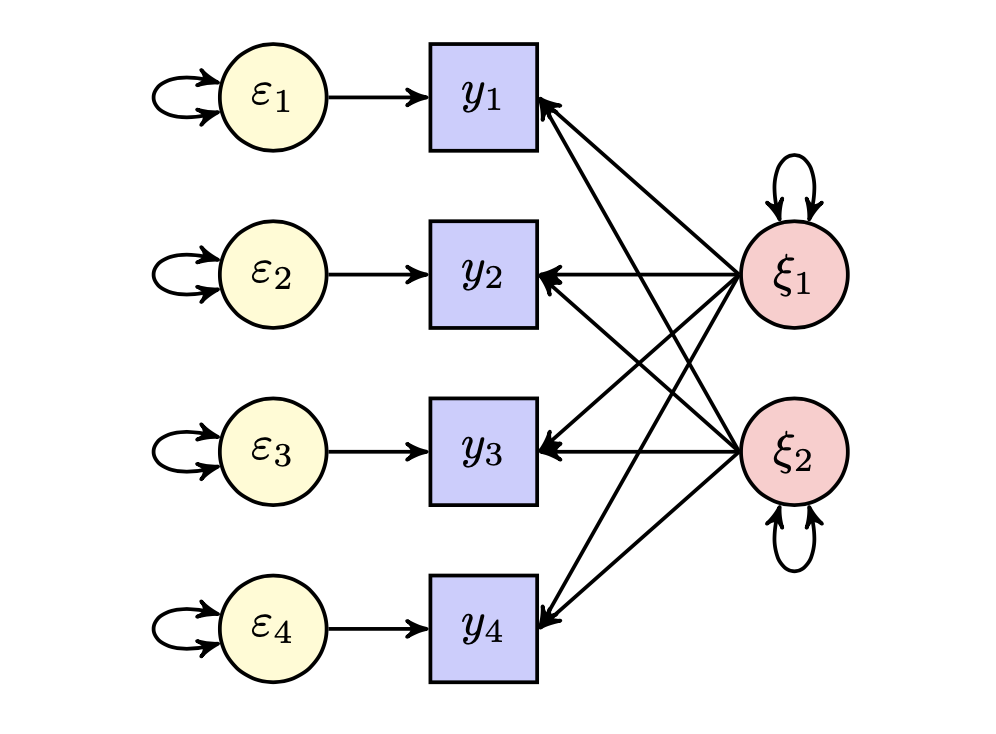
FIGURA 25.1: Modello fattoriale con due fattori comuni ortogonali.
In un diagramma di percorso, la correlazione tra due variabili contenute è uguale alla somma dei valori numerici di tutti i percorsi legittimi che collegano le variabili. Se i fattori comuni sono incorrelati (come nella figura 25.1, allora in un path diagram c’è un unico percorso legittimo che collega ciascuna variabile manifesta a ciascun fattore comune in base alle regole di Wright. Le correlazioni tra variabili manifeste e fattori comuni sono dunque uguali alle saturazioni fattoriali. Nel caso di fattori comuni sono incorrelati, dunque, la matrice delle saturazioni fattoriali descrive le correlazioni fra variabili e fattori. Si ricordi che le saturazioni fattoriali possono essere interpretate in maniera equivalente ai pesi beta del modello di regressione multipla, ovvero come la stima del contributo specifico di ciascun fattore comune nella determinazione della varianza spiegata degli item (Tabachnick & Fidell, 2001).
Nel caso della rotazione obliqua, invece, la soluzione fattoriale ruotata produce un insieme di fattori comuni fra loro correlati. Di conseguenza, la matrice delle saturazioni fattoriali non descrive le correlazioni fra variabili e fattori. Infatti, in un path diagram ci sono almeno due percorsi legittimi che collegano ciascuna variabile manifesta a ciascun fattore comune in base alle regole di Wright. Nel caso di una rotazione obliqua è quindi necessario specificare tre diverse matrici:
- la matrice delle saturazioni fattoriali, \(\hat{\boldsymbol{\Lambda}}\), detta matrice pattern (factor pattern matrix, o “configurazione,” o “matrice dei modelli”);
- la matrice delle correlazioni tra variabili manifeste e fattori, detta matrice di struttura (factor structure matrix);
- la matrice che esprime le correlazioni tra i fattori, \(\hat{\boldsymbol{\Phi}}\), detta matrice di intercorrelazione fattoriale.
In questo caso, la matrice pattern rappresenta l’analogo dei coefficienti parziali di regressione della variabile sul fattore, al netto degli altri fattori. Nel caso della rotazione obliqua, è la matrice che viene usata per determinare in che grado è stata raggiunta la “struttura semplice”.
Esaminiamo in dettaglio la soluzione fattoriale che viene prodotta da una rotazione obliqua. In tali circostanze, gli assi che rappresentano i fattori non sono ortogonali (ovvero, i fattori sono correlati) e, in un diagramma di percorso, le variabili manifeste sono collegate ai fattori attraverso due tipi distinti di percorsi. Tali percorsi rappresentano l’effetto “diretto” e “indiretto” dei fattori sulle variabili. Nel caso di una rotazione obliqua, come abbiamo detto sopra, le saturazioni fattoriali non coincidono con le correlazioni tra variabili e fattori. Si consideri la figura 25.2. Nel caso di una rotazione obliqua, la correlazione tra i due fattori comuni viene rappresentata mediante la freccia non direzionata \(\phi_{12}\) che collega \(\xi_1\) e \(\xi_2\). Nel diagramma di percorso della figura 25.2 ci sono due percorsi legittimi che, in base alle regole di Wright, consentono di collegare ciascuna variabile manifesta ad un fattore comune. Ad esempio, nel caso della variabile \(y_1\) e il fattore \(\xi_1\), i percorsi sono: la freccia causale \(\lambda_{11}\) che rappresenta l’effetto diretto di \(\xi_1\) su \(y_1\) e il percorso composto che rappresenta l’effetto indiretto di \(\xi_1\) su \(y_1\). Il valore numerico di tale percorso composto è uguale al prodotto \(\lambda_{21}\phi_{12}\). Nei termini dell’analisi dei percorsi, dunque, la correlazione tra \(\xi_1\) e \(y_1\) è uguale alla somma dei valori numerici dei percorsi legittimi che collegano \(y_1\) a \(\xi_1\), ovvero \(\lambda_{11} + \lambda_{21} \phi_{12}\).
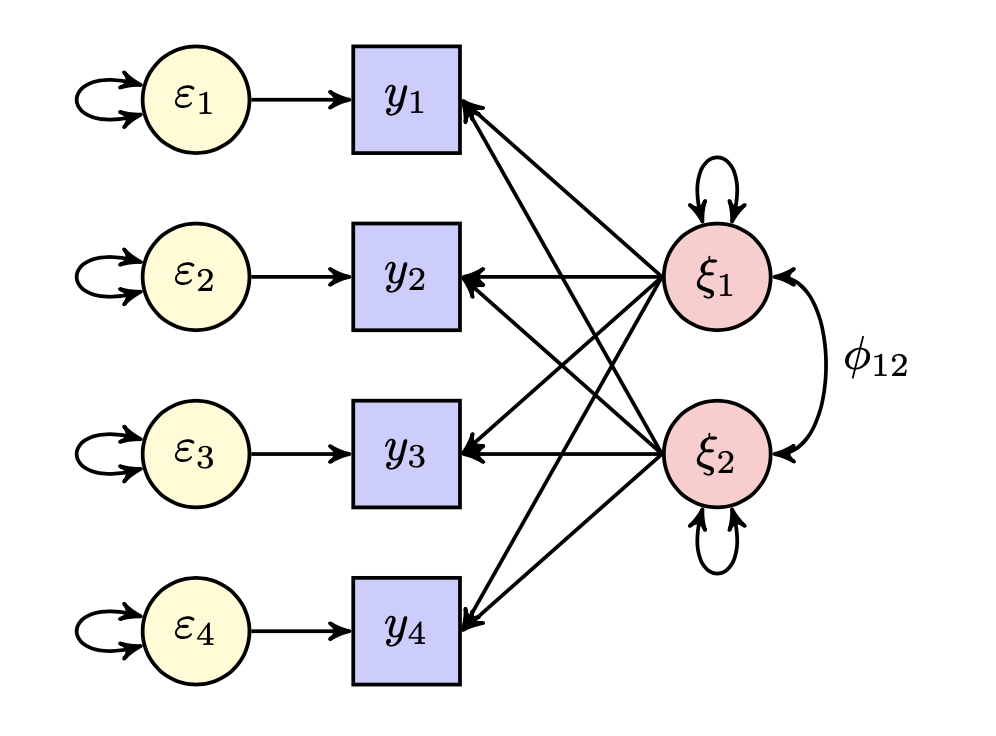
FIGURA 25.2: Modello fattoriale con due fattori comuni dopo una rotazione obliqua.
Per illustrare la rotazione obliqua, utilizziamo i dati discussi da Rencher (2002). Si consideri la matrice di correlazione presentata qui sotto.
R <- matrix(
c(
1.00, 0.735, 0.711, 0.704,
0.735, 1.00, 0.693, 0.709,
0.711, 0.693, 1.00, 0.839,
0.704, 0.709, 0.839, 1.00
),
ncol = 4,
byrow = TRUE
)
R
#> [,1] [,2] [,3] [,4]
#> [1,] 1.000 0.735 0.711 0.704
#> [2,] 0.735 1.000 0.693 0.709
#> [3,] 0.711 0.693 1.000 0.839
#> [4,] 0.704 0.709 0.839 1.000Iniziamo calcolando la soluzione a due fattori mediante il metodo delle componenti principali e una rotazione Varimax (ovvero, ortogonale). Otteniamo le seguenti saturazioni fattoriali.
f1_pc <- principal(R, 2, rotate = "varimax")
f1_pc
#> Principal Components Analysis
#> Call: principal(r = R, nfactors = 2, rotate = "varimax")
#> Standardized loadings (pattern matrix) based upon correlation matrix
#> RC1 RC2 h2 u2 com
#> 1 0.50 0.78 0.86 0.140 1.7
#> 2 0.47 0.81 0.88 0.124 1.6
#> 3 0.90 0.33 0.92 0.078 1.3
#> 4 0.89 0.35 0.92 0.083 1.3
#>
#> RC1 RC2
#> SS loadings 2.08 1.50
#> Proportion Var 0.52 0.37
#> Cumulative Var 0.52 0.89
#> Proportion Explained 0.58 0.42
#> Cumulative Proportion 0.58 1.00
#>
#> Mean item complexity = 1.5
#> Test of the hypothesis that 2 components are sufficient.
#>
#> The root mean square of the residuals (RMSR) is 0.06
#>
#> Fit based upon off diagonal values = 0.99Si noti che i due fattori non sono molto distinti. Consideriamo dunque la soluzione prodotta da una rotazione obliqua. Usiamo qui l’algoritmo Oblimin.
La matrice \(\hat{\boldsymbol{\Lambda}}\) delle saturazioni fattoriali si ricava come indicato di seguito.
cbind(pr_oblimin$load[, 1], pr_oblimin$load[, 2])
#> [,1] [,2]
#> [1,] 0.03206780 0.90186261
#> [2,] -0.02543116 0.95556536
#> [3,] 0.96858605 -0.01096737
#> [4,] 0.94726778 0.01327683La matrice \(\hat{\boldsymbol{\Phi}}\) di inter-correlazione fattoriale è la seguente.
La matrice di struttura, che riporta le correlazioni tra indicatori e fattori comuni, si ottiene pre-moltiplicando la matrice \(\boldsymbol{\Lambda}\) delle saturazioni fattoriali alla matrice \(\boldsymbol{\Phi}\) di inter-correlazione fattoriale.
\[ \text{matrice di struttura} = \boldsymbol{\Lambda}\boldsymbol{\Phi}. \]
Per esempio, la correlazione tra la prima variabile manifesta e il primo fattore si ottiene nel modo seguente.
L’intera matrice di struttura si può trovare eseguendo la moltiplicazione \(\boldsymbol{\Lambda}\boldsymbol{\Phi}\).