38.6 Parallel Process Model
Esaminiamo ora un modello che include sia i termini lineari che quadratici (quando richiesti) delle variabili x e y.
full_model <-
"
# intercept & slope growth terms for X
iX =~ 1*x1 + 1*x2 + 1*x3 + 1*x4
sX =~ 0*x1 + 1*x2 + 2*x3 + 3*x4
# intercept, slope, & quadratic terms for Y
iY =~ 1*y1 + 1*y2 + 1*y3 + 1*y4
sY =~ 0*y1 + 1*y2 + 2*y3 + 3*y4
qY =~ 0*y1 + 1*y2 + 4*y3 + 9*y4
# regress growth terms on predictor
qY + iY + sX + iX ~ predictor
sY ~ a1*predictor
# regress outcome on growth terms
outcome ~ iX + sX + iY + b1*sY + qY
# testing indirect effect
# predictor --> sY --> outcome
predictor_sY_outcome := a1*b1
"Adattiamo il modello ai dati.
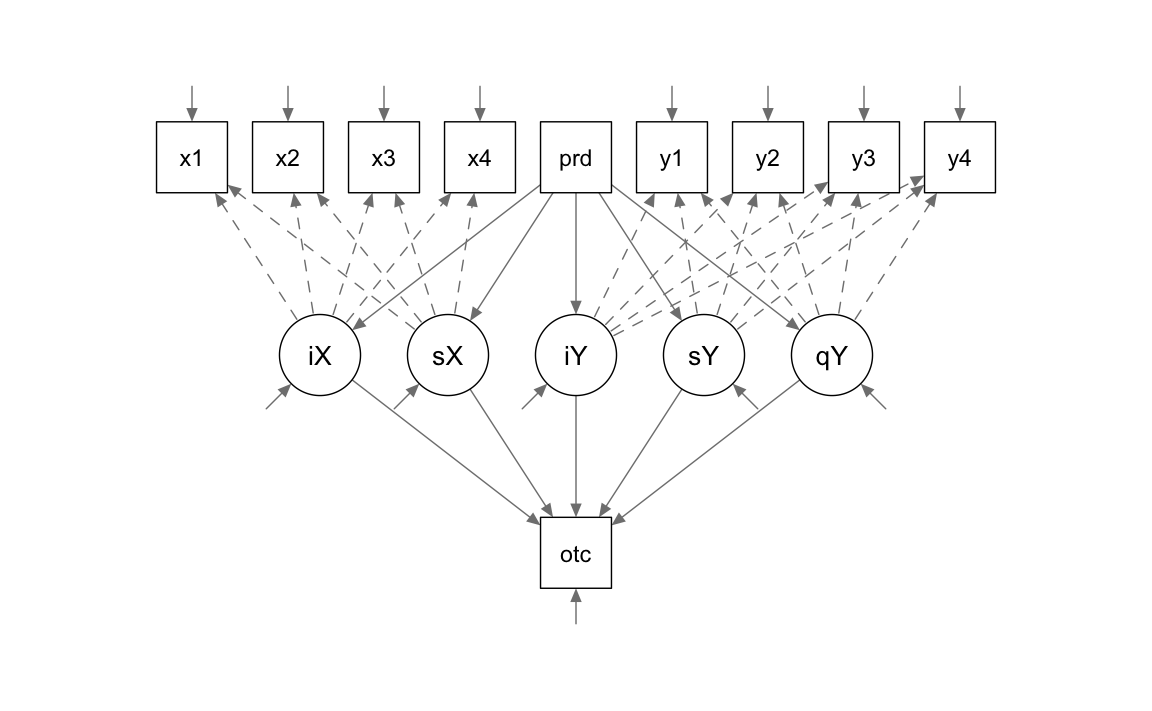
Esaminiamo il path diagram.
semPaths(
full_fit,
layout = "tree",
intercepts = FALSE,
posCol = c("black"),
edge.label.cex = 0.00001,
sizeMan = 7,
what = "path",
optimizeLatRes = TRUE,
residuals = TRUE,
style = "lisrel"
)
Valutiamo l’adattamento.
full_fit_stats <-
fitmeasures(
full_fit,
selected_fit_stats
)
round(full_fit_stats, 2)
#> chisq.scaled df.scaled pvalue.scaled cfi.scaled
#> 28.23 34.00 0.75 1.00
#> rmsea.scaled rmsea.pvalue.scaled srmr
#> 0.00 1.00 0.03Si ottiene un ottimo adattamento del modello ai dati (il che non è sorprendente, in quanto i dati sono stati simulati in base a tale modello).