15.8 Un esempio concreto

Applichiamo ora il risultato precedente ad un caso concreto. Consideriamo i dati utilizzati nella validazione italiana del Cognitive Style Questionnaire - Short Form (CSQ-SF, Meins et al. 2012). Il CSQ-SF viene utilizzato per misurare la vulnerabilità all’ansia e alla depressione. È costituito da cinque sottoscale: Internality, Globality, Stability, Negative consequences e Self-worth.

Leggiamo i dati in $\textsf{R}$:

csq <- rio::import(here::here("data", "csq540.csv"))

Il numero di partecipanti è

n <- nrow(csq)
n
#> [1] 540

Le statistiche descrittive si ottengono con la seguente istruzione:

psych::describe(csq, type = 2)
#>   vars   n  mean    sd median trimmed   mad min max range  skew kurtosis   se
#> I    1 540 47.76  5.78     48   47.87  4.45  21  64    43 -0.31     1.07 0.25
#> G    2 540 45.00 11.94     42   44.55 11.86  16  78    62  0.34    -0.70 0.51
#> S    3 540 44.60 12.18     42   44.24 13.34  16  77    61  0.27    -0.77 0.52
#> N    4 540 22.01  6.92     21   21.86  7.41   8  39    31  0.21    -0.74 0.30
#> W    5 540 44.05 13.10     43   43.66 13.34  16  79    63  0.31    -0.53 0.56

Esaminiamo la matrice di correlazione:

psych::pairs.panels(csq)

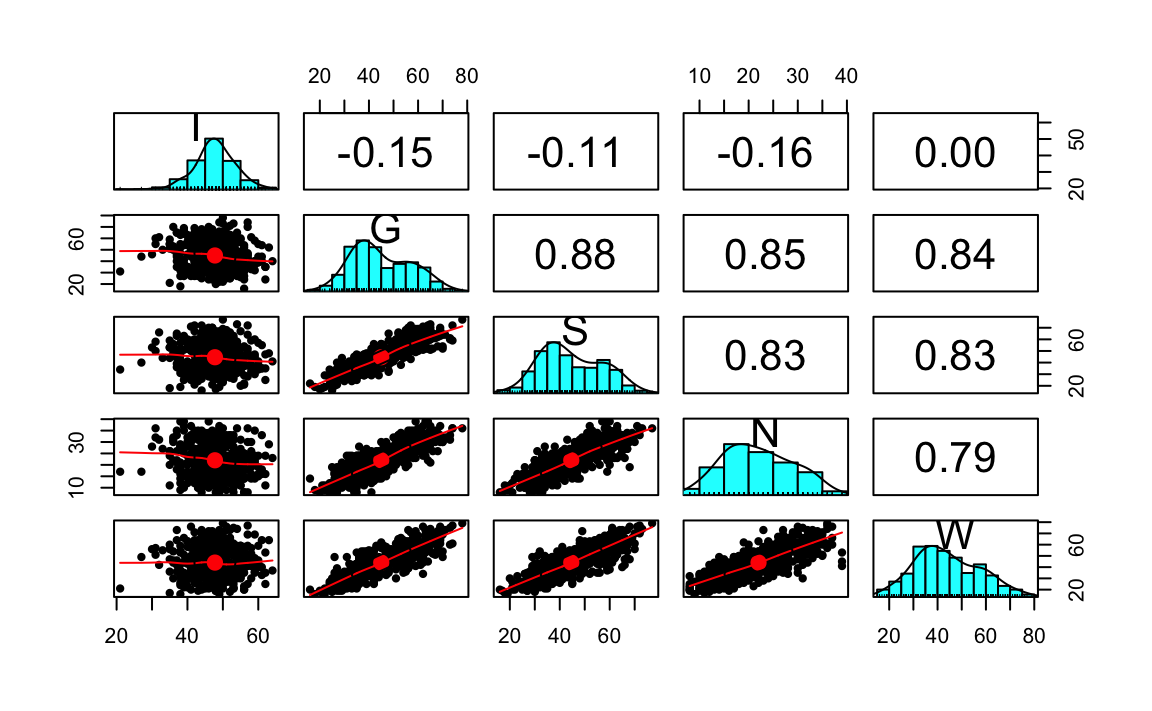
La sottoscala di Internality è problematica, come messo anche in evidenza dall’autore del test. La consideriamo comunque in questa analisi statistica.

Specifichiamo il modello unifattoriale nella sintassi di lavaan:

mod_csq <- "
   F =~ NA*I + G + S + N + W
   F ~~ 1*F
"

Adattiamo il modello ai dati:

fit <- lavaan:::cfa(
  mod_csq,
  data = csq
)

Esaminiamo i risultati:

summary(
  fit,
  standardized = TRUE,
  fit.measures = TRUE
)
#> lavaan 0.6.15 ended normally after 26 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        10
#> 
#>   Number of observations                           540
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                                46.716
#>   Degrees of freedom                                 5
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              2361.816
#>   Degrees of freedom                                10
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.982
#>   Tucker-Lewis Index (TLI)                       0.965
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)              -8741.781
#>   Loglikelihood unrestricted model (H1)      -8718.423
#>                                                       
#>   Akaike (AIC)                               17503.562
#>   Bayesian (BIC)                             17546.478
#>   Sample-size adjusted Bayesian (SABIC)      17514.734
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.124
#>   90 Percent confidence interval - lower         0.093
#>   90 Percent confidence interval - upper         0.158
#>   P-value H_0: RMSEA <= 0.050                    0.000
#>   P-value H_0: RMSEA >= 0.080                    0.989
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.033
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   F =~                                                                  
#>     I                 0.725    0.253    2.867    0.004    0.725    0.126
#>     G               -11.322    0.384  -29.481    0.000  -11.322   -0.949
#>     S               -11.342    0.398  -28.513    0.000  -11.342   -0.932
#>     N                -6.163    0.233  -26.398    0.000   -6.163   -0.891
#>     W               -11.598    0.444  -26.137    0.000  -11.598   -0.886
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>     F                 1.000                               1.000    1.000
#>    .I                32.840    2.000   16.420    0.000   32.840    0.984
#>    .G                14.038    1.473    9.532    0.000   14.038    0.099
#>    .S                19.508    1.718   11.353    0.000   19.508    0.132
#>    .N                 9.847    0.725   13.573    0.000    9.847    0.206
#>    .W                36.892    2.685   13.737    0.000   36.892    0.215

Esaminiamo solo le stime dei parametri del modello:

parameterEstimates(fit)
#>    lhs op rhs     est    se       z pvalue ci.lower ci.upper
#> 1    F =~   I   0.725 0.253   2.867  0.004    0.229    1.220
#> 2    F =~   G -11.322 0.384 -29.481  0.000  -12.075  -10.569
#> 3    F =~   S -11.342 0.398 -28.513  0.000  -12.122  -10.563
#> 4    F =~   N  -6.163 0.233 -26.398  0.000   -6.621   -5.705
#> 5    F =~   W -11.598 0.444 -26.137  0.000  -12.467  -10.728
#> 6    F ~~   F   1.000 0.000      NA     NA    1.000    1.000
#> 7    I ~~   I  32.840 2.000  16.420  0.000   28.920   36.759
#> 8    G ~~   G  14.038 1.473   9.532  0.000   11.151   16.924
#> 9    S ~~   S  19.508 1.718  11.353  0.000   16.140   22.876
#> 10   N ~~   N   9.847 0.725  13.573  0.000    8.425   11.269
#> 11   W ~~   W  36.892 2.685  13.737  0.000   31.628   42.155

Recuperiamo le specificità:

psi <- parameterEstimates(fit)$est[7:11]
psi
#> [1] 32.839665 14.037578 19.508119  9.846927 36.891617

Stimiamo l’errore standard della misurazione con la (15.1):

sqrt(sum(psi))
#> [1] 10.63597

Applichiamo ora la formula della TCT:

\[ \sigma_E = \sigma_X \sqrt{1 -\rho_{XX^\prime}}. \]

Per trovare $\sigma$ calcoliamo prima il punteggio totale:

tot_score <- rowSums(csq)

La deviazione standard di tot_score ci fornisce una stima di $\sigma_X$:

sigma <- sd(tot_score)
sigma
#> [1] 41.26414

Per applicare la formula della TCT abbiamo bisogno dell’attendibilità. La stimiamo usando la funzione reliability del pacchetto semTools dall’oggetto creato da lavaan:::cfa():

rel <- semTools::reliability(fit)
rel
#>                F
#> alpha  0.8506572
#> omega  0.9330313
#> omega2 0.9330313
#> omega3 0.9273385
#> avevar 0.7916575

Utilizzando $\Omega$ otteniamo:

sigma * sqrt(1 - rel[2])
#> [1] 10.67846

Si noti come il risultato sia molto simile a quello trovato con la formula della TCT.

15.8.1 Correlazioni osservate e riprodotte

Le correlazioni riprodotte dal modello si ottengono nel modo seguente dall’oggetto fit.

cor_mat <- lavInspect(fit, "cor.ov")
cor_mat
#>        I      G      S      N      W
#> I  1.000                            
#> G -0.119  1.000                     
#> S -0.117  0.885  1.000              
#> N -0.112  0.846  0.830  1.000       
#> W -0.111  0.841  0.825  0.789  1.000

Abbiamo visto come il modello unifattoriale predice che la correlazione tra due variabili manifeste sia il prodotto delle rispettive correlazioni fattoriali. Estraiamo le saturazioni fattoriali.

l <- inspect(fit, what = "std")$lambda
l
#>        F
#> I  0.126
#> G -0.949
#> S -0.932
#> N -0.891
#> W -0.886

Per esempio, se consideriamo I e G, la correlazione predetta dal modello fattoriale tra queste due sottoscale è data dal prodotto delle rispettive saturazioni fattoriali.

l[1] * l[2]
#> [1] -0.1191512

La matrice di correlazioni riprodotte riportata sopra mostra il risultato di questo prodotto per ciascuna coppia di variabili manifeste.

l %*% t(l) |> round(3)
#>        I      G      S      N      W
#> I  0.016 -0.119 -0.117 -0.112 -0.111
#> G -0.119  0.901  0.885  0.846  0.841
#> S -0.117  0.885  0.868  0.830  0.825
#> N -0.112  0.846  0.830  0.794  0.789
#> W -0.111  0.841  0.825  0.789  0.785

15.8.2 Scomposizione della varianza

Consideriamo la variabile manifesta W. Calcoliamo la varianza.

var(csq$W)
#> [1] 171.714

La varianza riprodotta di questa variabile, secondo il modello fattoriale, dovrebbe esere uguale alla somma di due componenti: la varianza predetta dall’effetto causale del fattore latente e la varianza residua. La varianza predetta dall’effetto causale del fattore latente è uguale alla saturazione elevata al quadrato:

(-11.598)^2
#> [1] 134.5136

Calcolo ora la proporzione di varianza residua normalizzando rispetto alla varianza osservata (non a quella riprodotta dal modello):

1 - (-11.598)^2 / var(csq$W)
#> [1] 0.2166416

Il valore così ottenuto è molto simile al valore della varianza residua di W.

Ripeto i calcoli per la variabile G

1 - (-11.322)^2 / var(csq$G)
#> [1] 0.1003729

e per la variabile I

1 - (0.725)^2 / var(csq$I)
#> [1] 0.9842755

In tutti i casi, i valori ottenuti sono molto simili alle varianze residue ipotizzate dal modello unifattoriale.

15.8.3 Correlazione tra variabili manifeste e fattore comune

Un modo per verificare il fatto che, nel modello unifattoriale, la saturazione fattoriale della $i$-esima variabile manifesta è uguale alla correlazione tra i punteggi osservati sulla i$-esima variabile manifesta e il fattore latente è quella di calcolare le correlazioni tra le variabili manifeste e i punteggi fattoriali. I punteggi fattoriali rappresentano una stima del punteggio “vero”, ovvero del punteggio che ciascun rispondente otterrebbe in assenza di errori di misurazione. Vedremo in seguito come si possono stimare i punteggi fattoriali. Per ora ci limitiamo a calcolarli usando lavaan.

head(lavPredict(fit))
#>               F
#> [1,]  0.2693790
#> [2,] -0.9110820
#> [3,]  0.1871406
#> [4,] -0.3315541
#> [5,]  0.8306627
#> [6,]  1.1534515

Abbiamo un punteggio diverso per ciascuno dei 540 individui che appartengono al campione di dati esaminato.

dim(lavPredict(fit))
#> [1] 540   1

Calcoliamo ora le correlazioni tra i valori osservati su ciascuna delle cinque scale del CSQ e le stime dei punteggi veri.

c(
  cor(csq$I, lavPredict(fit)),
  cor(csq$G, lavPredict(fit)),
  cor(csq$S, lavPredict(fit)),
  cor(csq$N, lavPredict(fit)),
  cor(csq$W, lavPredict(fit))
) |>
  round(3)
#> [1]  0.128 -0.970 -0.952 -0.910 -0.905

Si noti che i valori ottenui sono molto simili ai valori delle saturazioni fattoriali. La piccola differenza tra le correlazioni ottenute e i valori delle saturazioni fattoriali dipende dal fatto che abbiamo stimato i punteggi fattoriali.

inspect(fit, what = "std")$lambda
#>        F
#> I  0.126
#> G -0.949
#> S -0.932
#> N -0.891
#> W -0.886