16.2 Modello fattoriale: Fattori obliqui
Anche nel caso di fattori comuni correlati è possibile esprimere nei termini dei parametri del modello la covarianza teorica tra una variabile manifesta \(Y_i\) e uno dei fattori comuni, la covarianza teorica tra due variabili manifeste, e la comunalità di ciascuna variabile manifesta. Dato però che i fattori comuni risultano correlati, l’espressione fattoriale di tali quantità è più complessa che nel caso di fattori comuni ortogonali.
16.2.1 Covarianza teorica tra variabili e fattori
In base al modello multifattoriale con \(m\) fattori comuni la variabile \(Y_i\) è
\[ Y_i = \lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i. \tag{16.2} \]
Poniamoci il problema di trovare la covarianza teorica tra la variabile manifesta \(Y_i\) e il fattore comune \(\xi_j\). Come in precedenza, il problema si riduce a quello di trovare \(\mathbb{E}(Y_i \xi_j)\). Ne segue che
\[ \begin{equation} \begin{aligned} \mbox{Cov}(Y_i, \xi_j) &= \mathbb{E}(Y_i \xi_j)\notag\\ &=\mathbb{E}\left[(\lambda_{i1} \xi_1 + \dots + \lambda_{ij} \xi_j + \dots + \lambda_{im} \xi_m + \delta_i)\xi_j \right]\notag\\ &= \lambda_{i1}\underbrace{\mathbb{E}(\xi_1\xi_j)}_{\neq 0} + \dots + \lambda_{ij}\underbrace{\mathbb{E}(\xi_j^2)}_{=1} + \dots \notag\\ & \quad + \lambda_{im}\underbrace{\mathbb{E}(\xi_m\xi_j)}_{\neq 0} + \underbrace{\mathbb{E}(\delta_i \xi_j)}_{=0}\notag\\ &= \lambda_{ij} + \lambda_{i1} \mbox{Cov}(\xi_1, \xi_j) + \dots + \lambda_{im} \mbox{Cov}(\xi_m, \xi_j). \end{aligned} \end{equation} \]
Ad esempio, nel caso di tre fattori comuni \(\xi_1, \xi_2, \xi_3\), la covarianza tra \(Y_1\) e \(\xi_{1}\) diventa
\[ \lambda_{11} + \lambda_{12}\mbox{Cov}(\xi_1, \xi_2) + \lambda_{13}\mbox{Cov}(\xi_1, \xi_3). \]
16.2.2 Espressione fattoriale della varianza
Poniamoci ora il problema di trovare la varianza teorica della variabile manifesta \(Y_i\). In base al modello fattoriale, la variabile \(Y_i\) è specificata come nella (16.2). La varianza di \(Y_i\) è \(\mathbb{V}(Y_i) = \mathbb{E}(Y_i^2) -[\mathbb{E}(Y_i)]^2\). Però, avendo espresso \(Y_i\) nei termini della differenza dalla sua media, l’espressione della varianza si riduce a \(\mathbb{V}(Y_i) = \mathbb{E}(Y_i^2)\). Dobbiamo dunque sviluppare l’espressione
\[ \mathbb{E}(Y_i^2) = \mathbb{E}[(\lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i)^2]. \]
In conclusione, la varianza teorica di \(Y_i\) è uguale a
\[\begin{equation} \begin{split} \mathbb{V}(Y_i) &= \lambda_{i1}^2 + \lambda_{i2}^2 + \dots + \lambda_{im}^2 + \\ &\quad 2 \lambda_{i1} \lambda_{i2} \mbox{Cov}(\xi_1, \xi_2) + \dots + 2 \lambda_{i,m-1} \lambda_{im} \mbox{Cov}(\xi_{m-1}, \xi_m) + \\ &\quad \psi_{ii}.\notag \end{split} \end{equation}\]
Ad esempio, nel caso di tre fattori comuni, \(\xi_1, \xi_2, \xi_3\), la varianza di \(Y_1\) è
\[\begin{equation} \begin{split} \mathbb{V}(Y_1) = &\lambda_{11}^2 + \lambda_{12}^2 + \lambda_{13}^2 +\\ &\quad 2 \lambda_{11} \lambda_{12} \mbox{Cov}(\xi_1, \xi_2) + \\ &\quad 2 \lambda_{11} \lambda_{13} \mbox{Cov}(\xi_1, \xi_3) + \\ &\quad 2 \lambda_{12} \lambda_{13} \mbox{Cov}(\xi_2, \xi_3) + \\ &\quad \psi_{11}. \notag \end{split} \end{equation}\]
16.2.3 Covarianza teorica tra due variabili
Consideriamo ora il caso più semplice di due soli fattori comuni correlati e calcoliamo la covarianza tra \(Y_1\) e \(Y_2\):
\[\begin{equation} \begin{aligned} \mathbb{E}(Y_1 Y_2) =\mathbb{E}[(&\lambda_{11}\xi_1 + \lambda_{12}\xi_2+\delta_1) (\lambda_{21}\xi_1 + \lambda_{22}\xi_2+\delta_2)]\notag\\ =\mathbb{E}( &\lambda_{11}\lambda_{21}\xi_1^2 + \lambda_{11}\lambda_{22}\xi_1\xi_2 + \lambda_{11}\xi_1\delta_2 +\notag\\ +&\lambda_{12}\lambda_{21}\xi_1\xi_2 + \lambda_{12}\lambda_{22}\xi_2^2 + \lambda_{12}\xi_2\delta_2 +\notag\\ +&\lambda_{21}\xi_1\delta_1 + \lambda_{22}\xi_2\delta_1 + \delta_1\delta_2).\notag \end{aligned} \end{equation}\]
Distribuendo l’operatore di valore atteso, dato che \(\mathbb{E}(\xi^2)=1\) e \(\mathbb{E}(\xi \delta)=0\), otteniamo
\[ \mbox{Cov}(Y_1, Y_2) = \lambda_{11} \lambda_{21} + \lambda_{12} \lambda_{22} + \lambda_{12} \lambda_{21}\mbox{Cov}(\xi_1, \xi_2) +\lambda_{11} \lambda_{22}\mbox{Cov}(\xi_1, \xi_2). \]
In termini matriciali si scrive
\[ \boldsymbol{\Sigma} =\boldsymbol{\Lambda} \boldsymbol{\Phi} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\Psi}, \]
dove \(\boldsymbol{\Phi}\) è la matrice di ordine \(m \times m\) di varianze e covarianze tra i fattori comuni e \(\boldsymbol{\Psi}\) è una matrice diagonale di ordine \(p\) con le unicità delle variabili.
Esercizio 16.3 Consideriamo nuovamente i dati esaminati negli esercizi precedenti, ma questa volta il modello consente una correlazione tra i due fattori comuni:
fit2_cfa <- lavaan::cfa(
cfa_mod,
sample.cov = psychot_cor_mat,
sample.nobs = n,
orthogonal = FALSE,
std.lv = TRUE
)Visualizziamo il modello nel modo seguente:
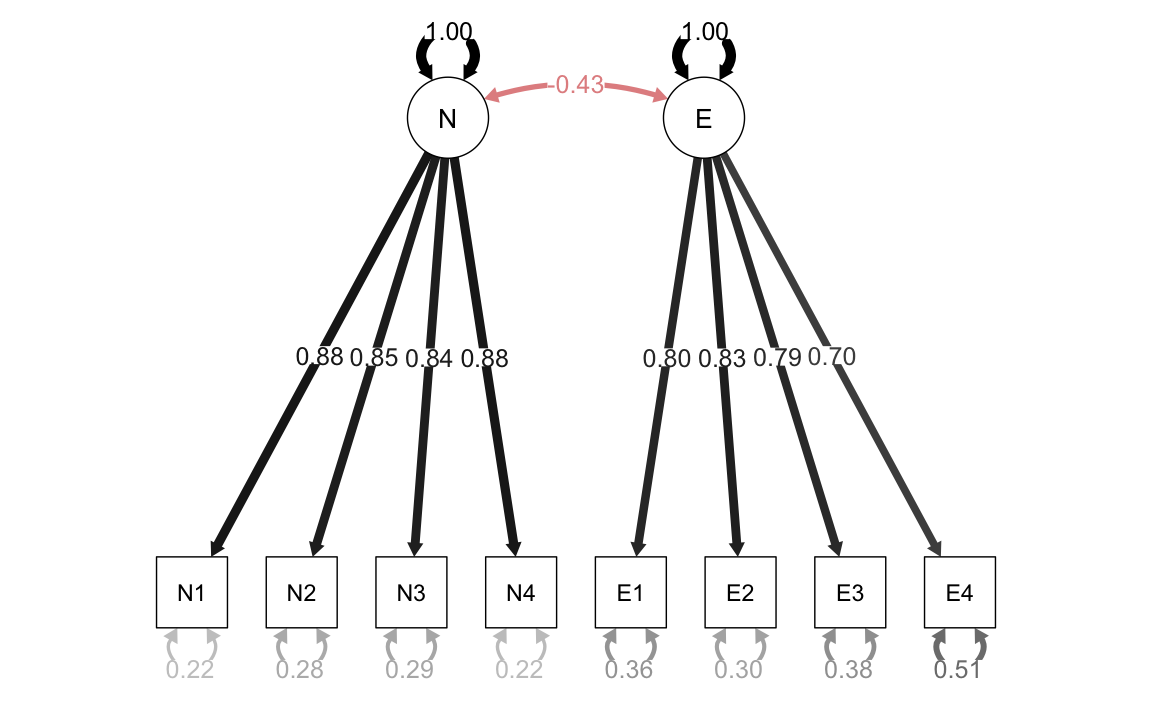
Esaminiamo le saturazioni fattoriali:
parameterEstimates(fit2_cfa, standardized = TRUE) %>%
dplyr::filter(op == "=~") %>%
dplyr::select(
"Latent Factor" = lhs,
Indicator = rhs,
B = est,
SE = se,
Z = z,
"p-value" = pvalue,
Beta = std.all
) %>%
knitr::kable(
digits = 3, booktabs = TRUE, format = "markdown",
caption = "Factor Loadings"
)| Latent Factor | Indicator | B | SE | Z | p-value | Beta |
|---|---|---|---|---|---|---|
| N | N1 | 0.883 | 0.051 | 17.472 | 0 | 0.885 |
| N | N2 | 0.847 | 0.052 | 16.337 | 0 | 0.849 |
| N | N3 | 0.842 | 0.052 | 16.190 | 0 | 0.844 |
| N | N4 | 0.880 | 0.051 | 17.381 | 0 | 0.882 |
| E | E1 | 0.800 | 0.055 | 14.465 | 0 | 0.802 |
| E | E2 | 0.832 | 0.054 | 15.294 | 0 | 0.834 |
| E | E3 | 0.788 | 0.056 | 14.150 | 0 | 0.789 |
| E | E4 | 0.698 | 0.058 | 11.974 | 0 | 0.699 |
Le saturazioni sono simili a quelle che abbiamo trovato in precedenza, In questo caso, però, la matrice delle correlazioni residue è adeguata:
cor_table <- residuals(fit2_cfa, type = "cor")$cov
knitr::kable(
cor_table,
digits = 3,
format = "markdown",
booktabs = TRUE
)| N1 | N2 | N3 | N4 | E1 | E2 | E3 | E4 | |
|---|---|---|---|---|---|---|---|---|
| N1 | 0.000 | 0.016 | -0.015 | -0.002 | -0.042 | 0.005 | 0.008 | -0.013 |
| N2 | 0.016 | 0.000 | -0.007 | -0.010 | -0.006 | 0.028 | 0.002 | 0.004 |
| N3 | -0.015 | -0.007 | 0.000 | 0.018 | -0.062 | 0.006 | -0.007 | -0.035 |
| N4 | -0.002 | -0.010 | 0.018 | 0.000 | -0.010 | 0.053 | 0.007 | 0.023 |
| E1 | -0.042 | -0.006 | -0.062 | -0.010 | 0.000 | 0.006 | 0.001 | -0.027 |
| E2 | 0.005 | 0.028 | 0.006 | 0.053 | 0.006 | 0.000 | -0.007 | 0.010 |
| E3 | 0.008 | 0.002 | -0.007 | 0.007 | 0.001 | -0.007 | 0.000 | 0.014 |
| E4 | -0.013 | 0.004 | -0.035 | 0.023 | -0.027 | 0.010 | 0.014 | 0.000 |
Esercizio 16.4 Esaminiamo più da vicino la matrice di correlazioni riprodotta dal modello, nel caso di fattori obliqui. Le saturazioni fattoriali sono:
lambda <- inspect(fit2_cfa, what = "std")$lambda
lambda
#> N E
#> N1 0.885 0.000
#> N2 0.849 0.000
#> N3 0.844 0.000
#> N4 0.882 0.000
#> E1 0.000 0.802
#> E2 0.000 0.834
#> E3 0.000 0.789
#> E4 0.000 0.699La matrice di intercorrelazoni fattoriali è
Le varianze residue sono:
Psi <- inspect(fit2_cfa, what = "std")$theta
Psi
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 0.217
#> N2 0.000 0.280
#> N3 0.000 0.000 0.288
#> N4 0.000 0.000 0.000 0.222
#> E1 0.000 0.000 0.000 0.000 0.357
#> E2 0.000 0.000 0.000 0.000 0.000 0.305
#> E3 0.000 0.000 0.000 0.000 0.000 0.000 0.377
#> E4 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.511Mediante i parametri del modello la matrice di correlazione si riproduce nel modo seguente:
\[ \boldsymbol{\Sigma} =\boldsymbol{\Lambda} \boldsymbol{\Phi} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\Psi}. \]
In \(\textsf{R}\) scriviamo:
R_hat <- lambda %*% Phi %*% t(lambda) + Psi
R_hat %>%
round(3)
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 1.000
#> N2 0.751 1.000
#> N3 0.746 0.716 1.000
#> N4 0.780 0.748 0.744 1.000
#> E1 -0.309 -0.296 -0.294 -0.308 1.000
#> E2 -0.321 -0.308 -0.306 -0.320 0.669 1.000
#> E3 -0.304 -0.291 -0.290 -0.303 0.633 0.658 1.000
#> E4 -0.269 -0.258 -0.257 -0.268 0.561 0.583 0.552 1.000Le correlazioni residue sono:
(psychot_cor_mat - R_hat) %>%
round(3)
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 0.000
#> N2 0.016 0.000
#> N3 -0.015 -0.007 0.000
#> N4 -0.002 -0.010 0.018 0.000
#> E1 -0.042 -0.006 -0.062 -0.010 0.000
#> E2 0.005 0.028 0.006 0.053 0.006 0.000
#> E3 0.008 0.002 -0.007 0.007 0.001 -0.007 0.000
#> E4 -0.013 0.004 -0.035 0.023 -0.027 0.010 0.014 0.000Questo risultato riproduce ciò che abbiamo trovato estraendo la matrice di correlazioni residue dall’oggetto creato dal lavaan::cfa mediante l’istruzione residuals(fit2_cfa, type = "cor")$cov.
Per fare un esempio relativo alla correlazione tra due indicatori, calcoliamo la correlazione predetta dal modello tra le variabili \(Y_1\) e \(Y_2\):
lambda[1, 1] * lambda[2, 1] + lambda[1, 2] * lambda[2, 2] +
lambda[1, 1] * lambda[2, 2] * Phi[1, 2] +
lambda[1, 2] * lambda[2, 1] * Phi[1, 2]
#> [1] 0.7507823Questo valore si avvicina al valore contenuto dell’elemento (1, 2) della matrice di correlazioni osservate:
Usando le funzonalità di lavaan la matrice di correlazione predetta si ottiene con:
fitted(fit2_cfa)$cov
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 0.996
#> N2 0.748 0.996
#> N3 0.743 0.713 0.996
#> N4 0.777 0.745 0.741 0.996
#> E1 -0.307 -0.295 -0.293 -0.306 0.996
#> E2 -0.320 -0.306 -0.305 -0.319 0.666 0.996
#> E3 -0.303 -0.290 -0.289 -0.302 0.630 0.656 0.996
#> E4 -0.268 -0.257 -0.255 -0.267 0.558 0.580 0.550 0.996La matrice dei residui è
resid(fit2_cfa)$cov
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 0.000
#> N2 0.016 0.000
#> N3 -0.015 -0.007 0.000
#> N4 -0.002 -0.010 0.018 0.000
#> E1 -0.042 -0.006 -0.062 -0.010 0.000
#> E2 0.005 0.028 0.006 0.053 0.006 0.000
#> E3 0.008 0.002 -0.007 0.007 0.001 -0.007 0.000
#> E4 -0.013 0.004 -0.035 0.023 -0.026 0.010 0.014 0.000La matrice dei residui standardizzati è
resid(fit2_cfa, type = "standardized")$cov
#> N1 N2 N3 N4 E1 E2 E3 E4
#> N1 0.000
#> N2 1.674 0.000
#> N3 -1.769 -0.569 0.000
#> N4 -0.350 -1.152 1.746 0.000
#> E1 -1.214 -0.161 -1.646 -0.294 0.000
#> E2 0.154 0.794 0.168 1.626 0.637 0.000
#> E3 0.219 0.062 -0.191 0.193 0.075 -0.693 0.000
#> E4 -0.314 0.092 -0.824 0.552 -1.481 0.624 0.690 0.000I valori precedenti possono essere considerati come punti z, dove i valori con un valore assoluto maggiore di 2 possono essere ritenuti problematici. Tuttavia, è importante considerare che in questo modo si stanno eseguendo molteplici confronti, pertanto, si dovrebbe considerare l’opportunità di applicare una qualche forma di correzione per i confronti multipli.