35.1 Invarianza tra gruppi
Definiamo il modello di crescita latente per i due gruppi.
# writing out linear growth model in full SEM way
mg_math_lavaan_model <- "
# latent variable definitions
#intercept (note intercept is a reserved term)
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
#linear slope
eta_2 =~ 0*math2
eta_2 =~ 1*math3
eta_2 =~ 2*math4
eta_2 =~ 3*math5
eta_2 =~ 4*math6
eta_2 =~ 5*math7
eta_2 =~ 6*math8
# factor variances
eta_1 ~~ eta_1
eta_2 ~~ eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ start(35)*1
eta_2 ~ start(4)*1
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
" # end of model definitionAdattiamo il modello ai dati specificando la separazione delle osservazioni in due gruppi e introducendo i vincoli di eguaglianza tra gruppi sulle saturazioni fattoriali, le medie, le varianze, le covarianze, e i residui. In questo modello, sostanzialmente, non c’è alcune differenza tra gruppi.
mg_math_lavaan_fitM1 <- sem(mg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml",
group = "lb_wght", # to separate groups
group.equal = c(
"loadings", # for constraints
"means",
"lv.variances",
"lv.covariances",
"residuals"
)
)Esaminiamo il risultato
summary(mg_math_lavaan_fitM1, fit.measures = TRUE)
#> lavaan 0.6.15 ended normally after 24 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 24
#> Number of equality constraints 18
#>
#> Number of observations per group: Used Total
#> 0 857 858
#> 1 75 75
#> Number of missing patterns per group:
#> 0 60
#> 1 25
#>
#> Model Test User Model:
#>
#> Test statistic 249.111
#> Degrees of freedom 64
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> 0 191.954
#> 1 57.156
#>
#> Model Test Baseline Model:
#>
#> Test statistic 887.887
#> Degrees of freedom 42
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.781
#> Tucker-Lewis Index (TLI) 0.856
#>
#> Robust Comparative Fit Index (CFI) 1.000
#> Robust Tucker-Lewis Index (TLI) 0.346
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -7968.693
#> Loglikelihood unrestricted model (H1) -7844.138
#>
#> Akaike (AIC) 15949.386
#> Bayesian (BIC) 15978.410
#> Sample-size adjusted Bayesian (SABIC) 15959.354
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.079
#> 90 Percent confidence interval - lower 0.069
#> 90 Percent confidence interval - upper 0.089
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.436
#>
#> Robust RMSEA 0.000
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.000
#> P-value H_0: Robust RMSEA <= 0.050 1.000
#> P-value H_0: Robust RMSEA >= 0.080 0.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.128
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#>
#> Group 1 [0]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 =~
#> math2 1.000
#> math3 1.000
#> math4 1.000
#> math5 1.000
#> math6 1.000
#> math7 1.000
#> math8 1.000
#> eta_2 =~
#> math2 0.000
#> math3 1.000
#> math4 2.000
#> math5 3.000
#> math6 4.000
#> math7 5.000
#> math8 6.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 ~~
#> eta_2 (.17.) -0.181 1.150 -0.158 0.875
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 (.18.) 35.267 0.355 99.229 0.000
#> eta_2 (.19.) 4.339 0.088 49.136 0.000
#> .math2 0.000
#> .math3 0.000
#> .math4 0.000
#> .math5 0.000
#> .math6 0.000
#> .math7 0.000
#> .math8 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 (.15.) 64.562 5.659 11.408 0.000
#> eta_2 (.16.) 0.733 0.327 2.238 0.025
#> .math2 (thet) 36.230 1.867 19.410 0.000
#> .math3 (thet) 36.230 1.867 19.410 0.000
#> .math4 (thet) 36.230 1.867 19.410 0.000
#> .math5 (thet) 36.230 1.867 19.410 0.000
#> .math6 (thet) 36.230 1.867 19.410 0.000
#> .math7 (thet) 36.230 1.867 19.410 0.000
#> .math8 (thet) 36.230 1.867 19.410 0.000
#>
#>
#> Group 2 [1]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 =~
#> math2 1.000
#> math3 1.000
#> math4 1.000
#> math5 1.000
#> math6 1.000
#> math7 1.000
#> math8 1.000
#> eta_2 =~
#> math2 0.000
#> math3 1.000
#> math4 2.000
#> math5 3.000
#> math6 4.000
#> math7 5.000
#> math8 6.000
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 ~~
#> eta_2 (.17.) -0.181 1.150 -0.158 0.875
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 (.18.) 35.267 0.355 99.229 0.000
#> eta_2 (.19.) 4.339 0.088 49.136 0.000
#> .math2 0.000
#> .math3 0.000
#> .math4 0.000
#> .math5 0.000
#> .math6 0.000
#> .math7 0.000
#> .math8 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> eta_1 (.15.) 64.562 5.659 11.408 0.000
#> eta_2 (.16.) 0.733 0.327 2.238 0.025
#> .math2 (thet) 36.230 1.867 19.410 0.000
#> .math3 (thet) 36.230 1.867 19.410 0.000
#> .math4 (thet) 36.230 1.867 19.410 0.000
#> .math5 (thet) 36.230 1.867 19.410 0.000
#> .math6 (thet) 36.230 1.867 19.410 0.000
#> .math7 (thet) 36.230 1.867 19.410 0.000
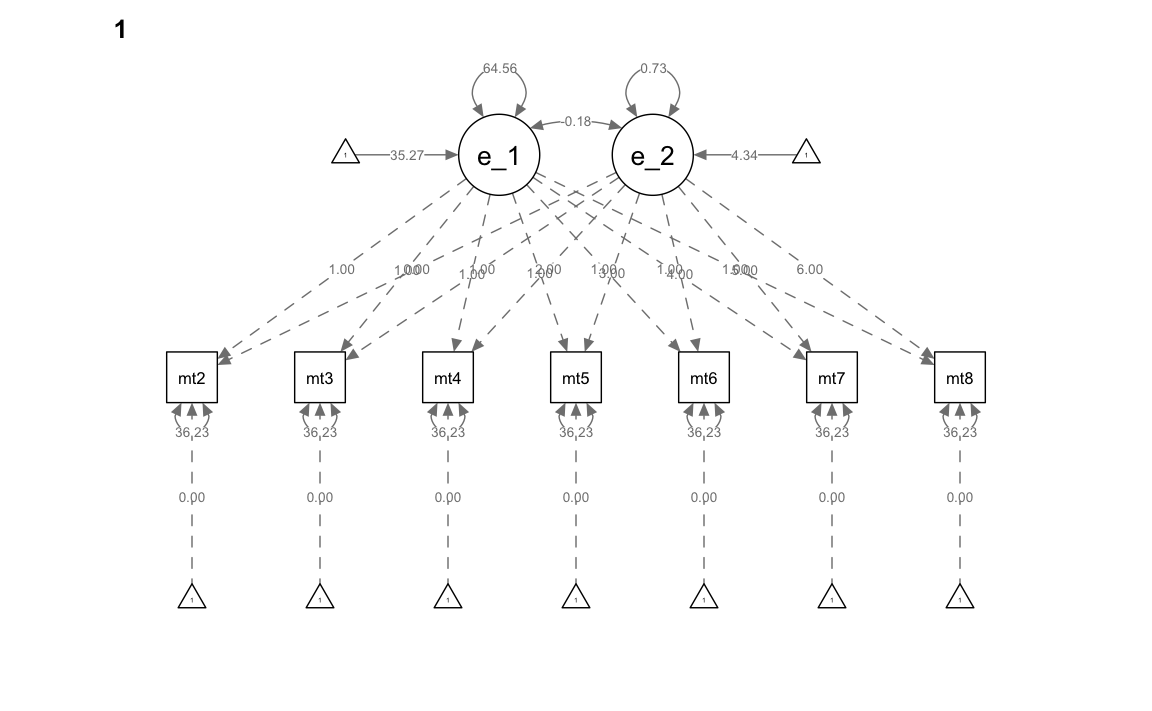
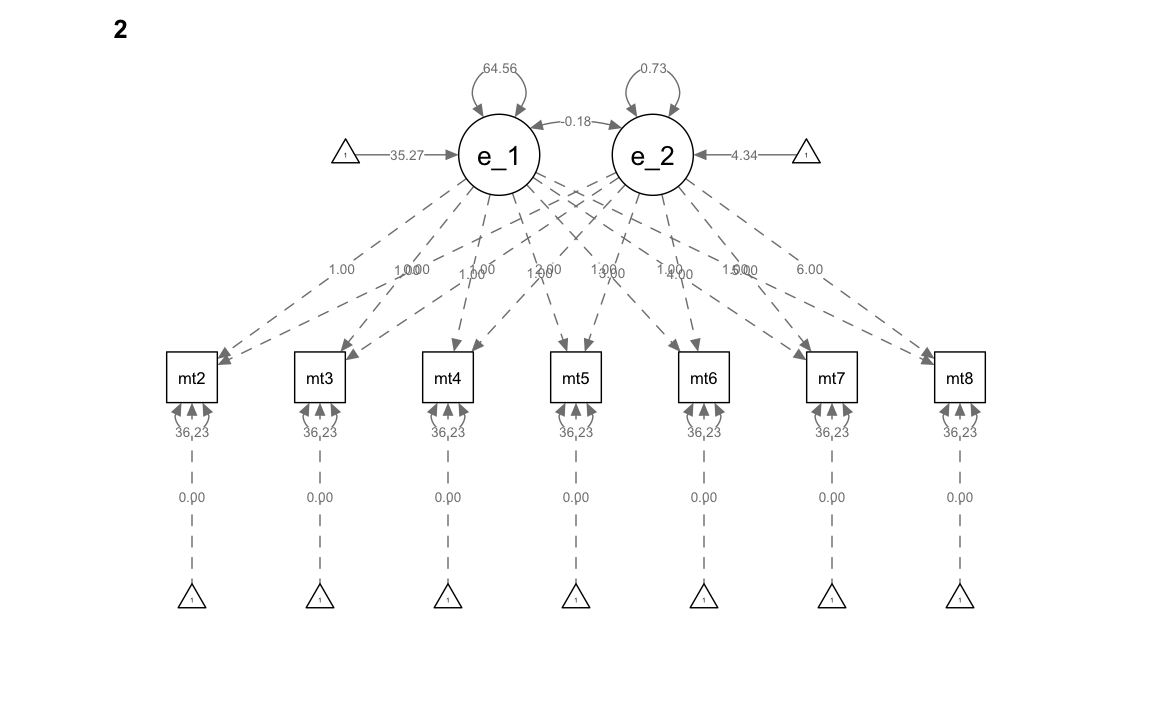
#> .math8 (thet) 36.230 1.867 19.410 0.000Creiamo il diagramma di percorso.