8.2 Regressione multipla

Nella regressione multipla vengono utilizzati \(k > 1\) predittori:

\[ y_i = \alpha + \sum_{j=1}^k \beta_j x_i + \varepsilon_i. \]

L’interpretazione geometrica è simile a quella del modello bivariato. Nel caso di due predittori, il valore atteso della \(y\) può essere rappresentato da un piano; nel caso di \(k > 2\) predittori, da un iper-piano. Nel caso di \(k=2\), tale piano è posto in uno spazio di dimensioni \(x_1\), \(x_2\) (che possiamo immaginare definire un piano orizzontale) e \(y\) (ortogonale a tale piano). La superficie piana che rappresenta \(\mathbb{E}(y)\) è inclinata in maniera tale che l’angolo tra il piano e l’asse \(x_1\) corrisponde a \(\beta_1\) e l’angolo tra il piano e l’asse \(x_2\) corrisponde a \(\beta_2\).

8.2.1 Significato dei coefficienti parziali di regressione

Ai coefficienti parziali del modello di regressione multipla possiamo assegnare la seguente interpretazione:

Il coefficiente parziale di regressione \(\beta_j\) rappresenta l’incremento atteso della \(y\) se \(x_j\) viene incrementata di un’unità, tenendo costante il valore delle altre variabili indipendenti.

Un modo per interpretare la locuzione “al netto dell’effetto delle altre variabili indipendenti” è quello di esaminare la relazione tra la \(y\) parzializzata e la \(x_j\) parzializzata. In questo contesto, parzializzare significa decomporre una variabile di due componenti: una componente che è linearmente predicibile da una o più altre variabili e una componente che è linearmente incorrelata con tali varibili “terze”.

Se eseguiamo questa “depurazione” dell’effetto delle variabili “terze” sia sulla \(y\) sia su \(x_j\), possiamo poi esaminare la relazione bivariata che intercorre tra la componente della \(y\) linearmente indipendente dalle variabili “terze” e la componente della \(x_j\) linearmente indipendente dalle variabili “terze”. Il coefficiente di regressione bivariato così ottenuto sarà identico al coefficiente parziale di regressione nel modello di regressione multipla. Questa procedura ci consente di assegnare un’interpretazione “intuitiva” al coefficiente parziale di regressione \(\beta_j\).

Esaminiamo un caso concreto.

d <- rio::import(
  here::here("data", "kidiq.dta")
)
glimpse(d)
#> Rows: 434
#> Columns: 5
#> $ kid_score <dbl> 65, 98, 85, 83, 115, 98, 69, 106, 102, 95, 91, 58, 84, 78, 1…
#> $ mom_hs    <dbl> 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, …
#> $ mom_iq    <dbl> 121.11753, 89.36188, 115.44316, 99.44964, 92.74571, 107.9018…
#> $ mom_work  <dbl> 4, 4, 4, 3, 4, 1, 4, 3, 1, 1, 1, 4, 4, 4, 2, 1, 3, 3, 4, 3, …
#> $ mom_age   <dbl> 27, 25, 27, 25, 27, 18, 20, 23, 24, 19, 23, 24, 27, 26, 24, …
fm <- lm(
  kid_score ~ mom_iq + mom_work + mom_age + mom_hs,
  data = d
)
fm$coef
#> (Intercept)      mom_iq    mom_work     mom_age      mom_hs 
#>  20.8226117   0.5620814   0.1337287   0.2198599   5.5611781

Eseguiamo la parzializzazione di \(y\) in funzione delle variabili mom_work, mom_age e mom_hs:

fm_y <- lm(kid_score ~ mom_work + mom_age + mom_hs, data = d)

Lo stesso per mom_iq:

fm_x <- lm(mom_iq ~ mom_work + mom_age + mom_hs, data = d)

Esaminiamo ora la regressione bivariata tra le componenti parzializzate della \(y\) e di \(x_j\):

mod <- lm(fm_y$residuals ~ fm_x$residuals)
mod$coef
#>    (Intercept) fm_x$residuals 
#>  -1.651851e-15   5.620814e-01

Si vede come il coefficiente di regressione bivariato risulta identico al corrispondente coefficiente parziale di regressione.

8.2.2 Relazioni causali

Un altro modo per interpretare i coefficienti parziali di regressione è nell’ambito dei quelli che vengono chiamati i path diagrams. I diagrammi di percorso, che tratteremo in seguito e qui solo anticipiamo, descrivono le relazioni “causali” tra variabili: le variabili a monte del diagramma di percorso rappresentano le “cause” esogene e le variabili a valle indicano gli effetti, ovvero le variabili endogene. I coefficienti di percorso vengono rappresentati graficamente come frecce orientate e corrispondono all’effetto diretto sulla variabile verso cui punta la freccia della variabile a monte della freccia. In tale rappresentazione grafica, i coefficienti di percorso non sono altro che i coefficienti parziali di regressione del modello di regressione multipla. In questo contesto, indicano l’effetto diretto atteso sulla variabile endogena in conseguenza dell’incremento di un’unità della variabile esogena, lasciano immutate tutte le altre relazioni strutturali del modello.

Usiamo la funzione sem() del pacchetto lavaan per definire il modello rappresentato nel successivo diagramma di percorso:

model <- "
  kid_score ~ mom_hs + mom_iq + mom_work + mom_age
"

Adattiamo il modello ai dati

fit <- sem(model, data = d)

Il diagramma di percorso si ottiene con le seguenti istruzioni:

semPaths(
  fit, "est",
  posCol = c("black"),
  edge.label.cex = 0.9,
  sizeMan = 7,
  what = "path"
)

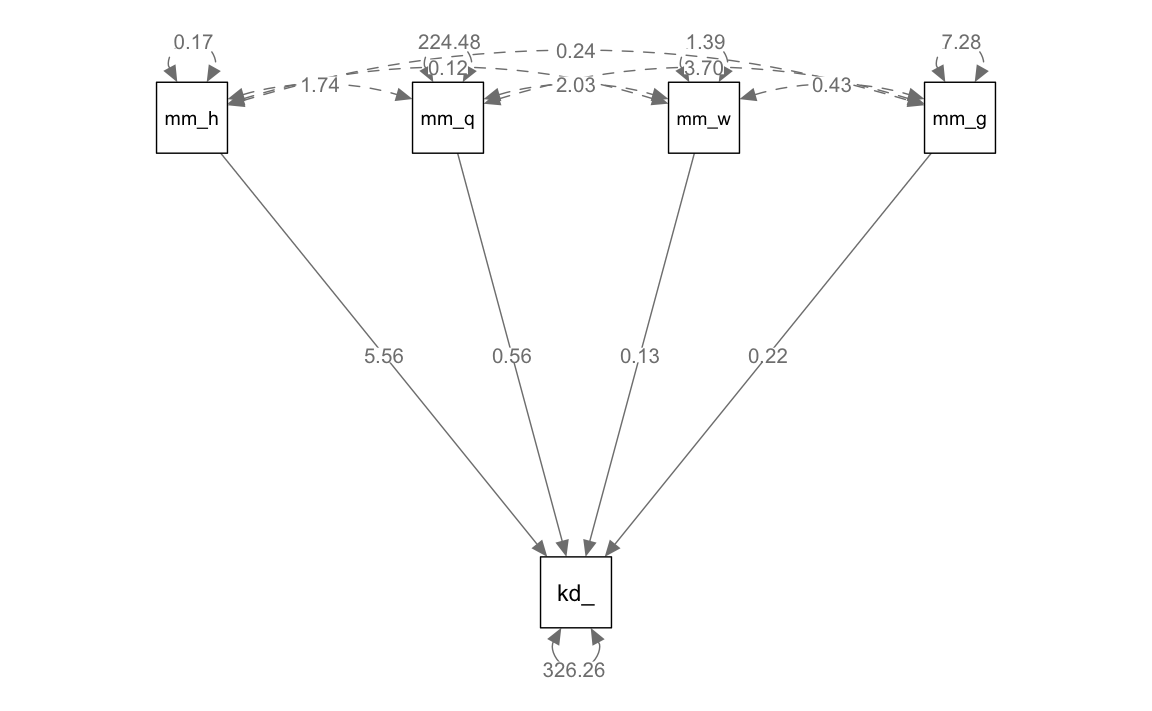
Come indicato nel diagramma, l’effetto diretto di mom_iq su kid_score è identico al corrispondente coefficiente parziale di regressione.

Il problema di capire se sia appropriato utilizzare un modello di regressione per descrivere le relazioni causali tra le variabili è affrontato nel prossimo paragrafo in riferimento all’errore di specificazione.

8.2.3 Errore di specificazione

Spiritosamente chiamato “heartbreak of L.O.V.E.” [Left-Out Variable Error; Mauro (1990)], l’errore di specificazione è una caratteristica fondamentale dei modelli di regressione che deve sempre essere tenuta a mente quando interpretiamo i risultati di questa tecnica di analisi statistica.

L’errore di specificazione si verifica quando escludiamo dal modello di regressione una variabile che ha due caratteristiche:

  • è associata con altre variabili inserite nel modello,
  • ha un effetto diretto sulla \(y\).

Come conseguenza dell’errore di specificazione, l’intensità e il segno dei coefficienti parziali di regressione risultano sistematicamente distorti.

Consideriamo un esempio con dati simulati nei quali immaginiamo che la prestazione sia positivamente associata alla motivazione e negativamente associata all’ansia. Immaginiamo inoltre che vi sia una correlazione positiva tra ansia a motivazione. Ci chiediamo cosa succede al coefficiente parziale della variabile “motivazione” se la variabile “ansia” viene esclusa dal modello di regressione.

set.seed(123)
n <- 400
anxiety <- rnorm(n, 10, 1.5)
motivation <- 4.0 * anxiety + rnorm(n, 0, 3.5)
cor(anxiety, motivation)
#> [1] 0.8617706

Creo la variabile performance come una combinazione lineare di motivazione e ansia nella quale la motivazione ha un effetto piccolo, ma positivo, sulla prestazione, e l’ansia ha un grande effetto negativo sulla prestazione:

performance <- 0.5 * motivation - 5.0 * anxiety + rnorm(n, 0, 3)

Salvo i dati in un DataFrame:

sim_dat2 <- tibble(performance, motivation, anxiety)

Eseguo l’analisi di regressione specificando in maniera corretta il modello, ovvero usando come predittori sia l’ansia che la depressione:

fm1 <- lm(performance ~ motivation + anxiety, sim_dat2)

Le stime dei coefficienti parziali di regressione recuperano correttamente l’intensità e il segno dei coefficienti utilizzati nel modello generatore dei dati:

coef(fm1)
#> (Intercept)  motivation     anxiety 
#>   1.3711965   0.4953886  -5.1052176

Eseguo ora l’analisi di regressione ignorando il predittore anxiety che ha le due caratteristiche di essere associato a motivation e di avere un effetto diretto sulla prestazione:

fm2 <- lm(performance ~ motivation, sim_dat2)
summary(fm2)
#> 
#> Call:
#> lm(formula = performance ~ motivation, data = sim_dat2)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -13.501  -3.409   0.005   3.311  12.616 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -12.39720    1.44591  -8.574 2.24e-16 ***
#> motivation   -0.43717    0.03553 -12.305  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 4.866 on 398 degrees of freedom
#> Multiple R-squared:  0.2756, Adjusted R-squared:  0.2738 
#> F-statistic: 151.4 on 1 and 398 DF,  p-value: < 2.2e-16

Si noti che, al di là della “significatività statistica” (si vedano le considerazioni fornite nel paragrafo sulla stepwise regression), il risultato prodotto dal modello di regressione è totalmente sbagliato: come conseguenza dell’errore di specificazione, il segno del coefficiente parziale di regressione della variabile “motivazione” è negativo, anche se nel modello generatore dei dati tale coefficiente aveva il segno opposto.

Quindi, se interpretiamo il coefficiente parziale ottenuto in termini casuali, siamo portati a concludere che la motivazione fa diminuire la prestazione. Ma in realtà è vero l’opposto.

È facile vedere perché si verifica l’errore di specificazione. Supponiamo che il vero modello sia

\[ y = \alpha + \beta_1 X_1 + \beta_2 X_2 + \varepsilon \]

il quale verrebbe stimato da

\[ y = a + b_1 X_1 + b_2 X_2 + e. \]

Supponiamo però che il ricercatore creda invece che

\[ y = \alpha^\prime + \beta_1^\prime X_1 + \varepsilon^\prime \]

e quindi stimi

\[ y = a^\prime + b_1^\prime X_1 + e^\prime \]

omettendo \(X_2\) dal modello.

Per capire che relazione intercorre tra \(b_1^\prime\) e \(b_1\), iniziamo a scrivere la formula per \(b_1^\prime\):

\[\begin{equation} b_1^\prime = \frac{\mbox{Cov}(X_1, Y)}{\mbox{Var}(X_1)}. \end{equation}\]

Sviluppando, otteniamo

\[\begin{equation} \begin{aligned} b_1^\prime &= \frac{\mbox{Cov}(X_1, a + b_1 X_1 + b_2 X_2 + e)}{\mbox{Var}(X_1)}\notag\\ &= \frac{\mbox{Cov}(X_1, a)+b_1 \mbox{Cov}(X_1, X_1) + b_2 \mbox{Cov}(X_1, X_2) + \mbox{Cov}(X_1, e)}{\mbox{Var}(X_1)}\notag\\ &= \frac{0 + b_1 \mbox{Var}(X_1) + b_2 \mbox{Cov}(X_1, X_2) + 0}{\mbox{Var}(X_1)}\notag\\ &= b_1 + b_2 \frac{\mbox{Cov}(X_1, X_2)}{\mbox{Var}(X_1)}. \end{aligned} \end{equation}\]

Quindi, se erroneamente omettiamo \(X_2\) dal modello, abbiamo che

\[\begin{equation} \mathbb{E}(b_1^\prime) = \beta_1 + \beta_2 \frac{\sigma_{12}}{\sigma_1^2}. \tag{8.1} \end{equation}\]

Verifichiamo tale conclusione per i dati dell’esempio che stiamo discutendo. Nel caso presente, \(X_1\) è motivation e \(X_2\) è anxiety. Applicando la (8.1) otteniamo lo stesso valore per il coefficiente di regressione associato a motivation che era stato ottenuto adattando ai dati il modello performance ~ motivation:

fm1$coef[2] + fm1$coef[3] *
  cov(sim_dat2$motivation, sim_dat2$anxiety) /
  var(sim_dat2$motivation)
#> motivation 
#> -0.4371675

Possiamo dunque concludere che \(b_1^\prime\) è uno stimatore distorto di \(\beta_1\). Si noti che questa distorsione non scompare all’aumentare della numerosità campionaria, il che (in termini statistici) significa che un tale stimatore è inconsistente. Quello che succede in pratica è che alla variabile \(X_1\) vengono attribuiti gli effetti delle variabili che sono state omesse dal modello. Si noti che una tale distorsione sistematica di \(b_1^\prime\) può essere evitata solo se si verificano due condizioni:

  • \(\beta_2 = 0\). Questo è ovvio, dato che, se \(\beta_2 = 0\), ciò significa che il modello non è specificato in modo errato, cioè \(X_2\) non appartiene al modello perché non ha un effetto diretto sulla \(Y\).
  • \(\sigma_{12} = 0\). Cioè, se \(X_1\) e \(X_2\) sono incorrelate, allora l’omissione di una delle due variabili non comporta stime distorte dell’effetto dell’altra.

8.2.4 Soppressione

Le conseguenze dell’errore di specificazione sono chiamate “soppressione” (suppression). In generale, si ha soppressione quando (1) il valore assoluto del peso beta di un predittore è maggiore di quello della sua correlazione bivariata con il criterio o (2) i due hanno segni opposti.

  • L’esempio descritto sopra è un caso di soppressione negativa, dove il predittore ha correlazioni bivariate positive con il criterio, ma si riceve un peso beta negativo nell’analisi di regressione multipla.
  • Un secondo tipo di soppressione è la soppressione classica, in cui un predittore non è correlato al criterio ma riceve un peso beta diverso da zero.
  • C’è anche la soppressione reciproca che può verificarsi quando due variabili sono correlate positivamente con il criterio ma negativamente tra loro.

8.2.5 Stepwise regression

Un’implicazione della soppressione è che i predittori non dovrebbero essere selezionati in base ai valori delle correlazioni bivariate con il criterio. Queste associazioni, dette di ordine zero, non controllano gli effetti degli altri predittori, quindi i loro valori possono essere fuorvianti rispetto ai coefficienti di regressione parziale per le stesse variabili. Per lo stesso motivo, il fatto che le correlazioni bivariate con il criterio siano statisticamente significative o meno è irrilevante per quanto riguarda la selezione dei predittori. Sebbene le procedure informatiche di regressione rendano facile i processi di selezione dei predittori in base a tali criteri, tali procedure sono da evitare. Il rischio è che anche piccole, ma non rilevate, non-linearità o effetti indiretti tra i predittori possano seriamente distocere i coefficienti di regressione parziale. È meglio selezionare giudiziosamente il minor numero di predittori sulla base di ragioni teoriche o dei risultati di ricerche precedenti. In altri termini, le procedure di stepwise regression non dovrebbero mai essere usate.

Una volta che sono stati selezionati, i predittori possono essere inseriti nell’equazione di regressione in due modi diversi:

  • tutti i predittori possono essere inseriti nel modello contemporaneamente;
  • i predittori possono essere inseriti nel modello sequenzialmente, mediante una serie di passaggi.

L’ordine di ingresso può essere determinato in base a standard: teorici (razionali) o empirici (statistici). Lo standard razionale corrisponde alla regressione gerarchica, in cui si comunica al computer un ordine fisso per inserire i predittori. Ad esempio, a volte le variabili demografiche vengono inserite nel primo passaggio, quindi nel secondo passaggio viene inserita una variabile psicologica di interesse. Questo ordine non solo controlla le variabili demografiche ma permette anche di valutare il potere predittivo della variabile psicologica, al di là di quello delle semplici variabili demografiche. Quest’ultimo può essere stimato come l’aumento della correlazione multipla al quadrato, o \(\Delta R^2\), da quella della fase 1 con solo predittori demografici a quella della fase 2 con tutti i predittori nell’equazione di regressione.

Un esempio di standard statistico è la regressione stepwise, in cui il computer seleziona l’inserimento dei predittori in base esclusivamente alla significatività statistica; cioè, viene chiesto: quale predittore, se inserito nell’equazione, avrebbe il valore_\(p\) più piccolo per il test del suo coefficiente di regressione parziale? Dopo la selezione, i predittori in una fase successiva possono essere rimossi dall’equazione di regressione in base ai loro valori-\(p\) (ad esempio, se \(p \geq\) .05). Il processo stepwise si interrompe quando, aggiungendo più predittori, \(\Delta R^2\) non migliora. Varianti della regressione stepwise includono forward inclusion, in cui i predittori selezionati non vengono successivamente rimossi dal modello, e backward elimination, che inizia con tutti i predittori nel modello per poi rimuoverne alcuni in passi successivi. Per le ragioni descritte nel paragrafo sull’errore di specificazione, i metodi basati sulle procedure di stepwise regression non dovrebbero mai essere usati. Infatti, i problemi relativi a tale procedura sono così gravi che varie riviste non accettano studi che fanno uso di una tale tecnica statistica. I risultati ottenuti con tali metodi, infatti, sono quasi certamente non replicabili in campioni diversi.

Una considerazione finale riguarda l’idea di rimuovere i predittori “non significativi” dal modello di regressione. Questa è una cattiva idea. Il ricercatore non deve sentirsi in dovere di trascurare quei predittore che non risultano “statisticamente significativi”. In campioni piccoli, la potenza dei test di significatività è bassa e la rimozione di un predittore non significativo può alterare sostanzialmente la soluzione. Se c’è una buona ragione per includere un predittore, allora è meglio lasciarlo nel modello, fino a prova contraria. In termini generali, qualsiasi considerazione basata sulla “significatività statistia” è fuorviante.

References

Mauro, Robert. 1990. “Understanding LOVE (left out variables error): A method for estimating the effects of omitted variables.” Psychological Bulletin 108 (2): 314–29.