here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(ggdag, patchwork)25 Le insidie dei punteggi di cambiamento: comprendere gli effetti causali negli studi longitudinali
Introduzione
La misurazione del cambiamento costituisce un obiettivo metodologico fondamentale nella ricerca psicologica longitudinale. Quando valutiamo l’efficacia di un intervento terapeutico, di un programma di prevenzione o di qualsiasi altro trattamento psicologico, la domanda che ci poniamo è apparentemente semplice: quanto è cambiato il paziente? Questa domanda, nella sua immediatezza intuitiva, ci porta spesso a creare quello che viene chiamato “punteggio di cambiamento” (change score), calcolato semplicemente sottraendo il punteggio iniziale da quello finale.
Questa pratica è molto diffusa nella ricerca psicologica. Se, ad esempio, si misura il livello di depressione di un paziente prima dell’inizio di una terapia cognitivo-comportamentale e successivamente a un ciclo di trattamento, appare del tutto naturale ricorrere al calcolo della differenza tra i due valori. Il punteggio di cambiamento sembra catturare esattamente ciò che ci interessa: quanto è migliorato il paziente? Tuttavia, come dimostrato in modo convincente da Tennant et al. (2022), questa apparente semplicità nasconde problemi metodologici profondi che possono condurre a conclusioni completamente errate riguardo agli effetti causali reali dei nostri interventi.
La criticità non riguarda i disegni sperimentali rigorosi, nei quali la randomizzazione garantisce il controllo delle differenze preesistenti tra i gruppi. In tali contesti, l’uso del punteggio di cambiamento è appropriato. Le difficoltà emergono invece negli studi osservazionali, dove il ricercatore non dispone di un controllo sperimentale diretto e i soggetti esposti a un determinato trattamento possono differire sistematicamente dai soggetti di controllo già prima dell’intervento. In psicologia, questa limitazione è particolarmente rilevante: molti fenomeni di interesse, come l’esposizione a eventi traumatici o le differenze negli stili genitoriali, non possono essere oggetto di manipolazione sperimentale, rendendo inevitabile il ricorso a disegni osservazionali e, di conseguenza, più complessa l’interpretazione causale dei punteggi di cambiamento.
25.1 La Natura dei punteggi di cambiamento
Per comprendere il problema, dobbiamo prima di tutto riconoscere che il punteggio di cambiamento non è una semplice misura come le altre. Quando calcoliamo \(\Delta Y = Y_1 - Y_0\), dove \(Y_0\) è la baseline e \(Y_1\) è la misura successiva, creiamo una variabile composita che contiene informazioni provenienti da entrambe le sue componenti. Questa caratteristica apparentemente innocua ha conseguenze profonde per l’analisi statistica e l’interpretazione causale.
Il problema fondamentale è che, per sua stessa definizione, il punteggio di cambiamento è matematicamente correlato alla misura di baseline. Anche se \(Y_0\) e \(Y_1\) fossero completamente indipendenti nella popolazione, il punteggio di cambiamento risulterebbe comunque correlato negativamente con \(Y_0\) con un coefficiente di circa -0.71.1 Si tratta di una correlazione spuria, un artefatto matematico che non riflette alcuna relazione sostanziale tra le variabili. Quando si utilizza questo punteggio di cambiamento in un’analisi di regressione, tale correlazione spuria può introdurre un bias sistematico nella stima delle relazioni causali, compromettendo l’accuratezza degli effetti del trattamento.
25.2 Tre scenari causali fondamentali
Per comprendere quando e perché i punteggi di cambiamento possono essere problematici, è necessario considerare la struttura causale che lega l’esposizione o il trattamento (\(X_0\)), la misura di baseline dell’outcome (\(Y_0\)) e la misura di follow-up (\(Y_1\)). Tennant et al. (2022) identificano tre scenari fondamentali, ciascuno dei quali comporta implicazioni analitiche distinte. Per illustrare questi scenari, useremo i grafi aciclici diretti (DAG) per rappresentare le relazioni causali tra le variabili.
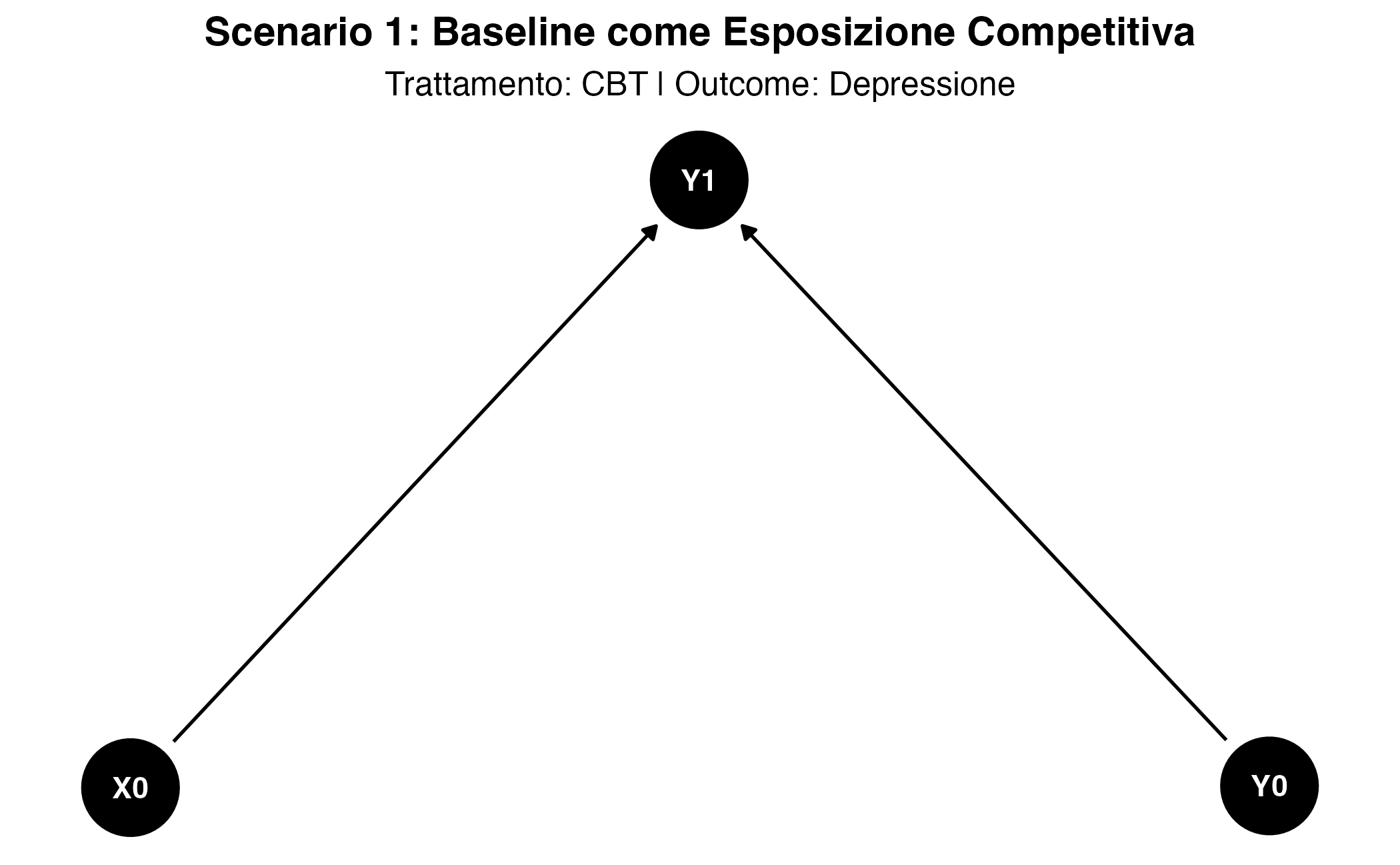
25.2.1 Scenario 1: la baseline come esposizione competitiva
Nel primo scenario, la misura baseline \(Y_0\) assume il ruolo concettuale di esposizione competitiva (o competing exposure). In questo modello, \(Y_0\) agisce come una causa diretta dell’esito al follow-up \(Y_1\), mentre è causalmente indipendente dall’esposizione o trattamento \(X_0\). Ciò significa che \(Y_0\) non è influenzata da \(X_0\), né essa stessa lo influenza, rappresentando invece un fattore preesistente che compete con \(X_0\) nel determinare l’esito finale. Si consideri, ad esempio, uno studio in cui pazienti con depressione vengono randomizzati per ricevere un intervento di terapia cognitivo-comportamentale (CBT) o un trattamento placebo. In questo disegno sperimentale, la procedura di randomizzazione assicura che il livello basale di depressione (\(Y_0\)) e l’assegnazione al trattamento (\(X_0\)) siano causalmente indipendenti. Pertanto, mentre \(Y_0\) esercita un’influenza diretta sul livello di depressione al follow-up (\(Y_1\)), esso non può essere un effetto né una causa di \(X_0\), configurandosi così come un’esposizione competitiva.
# Scenario 1: Y0 è un'esposizione competitiva
dag1 <- dagify(
Y1 ~ Y0 + X0,
exposure = "X0",
outcome = "Y1"
)
ggdag(dag1, text = TRUE, text_col = "white") +
theme_dag() +
labs(title = "Scenario 1: Baseline come Esposizione Competitiva",
subtitle = "Trattamento: CBT | Outcome: Depressione") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5))In questo scenario ideale, la stima dell’effetto causale del trattamento sulla variazione dell’outcome coincide con quella sull’outcome finale. Ciò implica che l’utilizzo del punteggio di cambiamento in un modello di regressione non introdurrebbe distorsioni (bias) nella stima dell’effetto del trattamento.
Tuttavia, dal punto vista della potenza statistica, l’approccio ottimale rimane l’analisi di covarianza (ANCOVA), in cui l’outcome finale (\(Y_1\)) viene regredito sul trattamento (\(X_0\)), aggiustando per il valore baseline (\(Y_0\)). Questo modello, infatti, è statisticamente più efficiente, in quanto riduce la variabilità residua e fornisce stime dell’effetto del trattamento con una maggiore precisione, pur rimanendo non distorto grazie al disegno randomizzato.
# Simulazione Scenario 1
n <- 1000
# In uno studio randomizzato, X0 è indipendente da Y0
X0 <- rbinom(n, 1, 0.5) # Randomizzazione 50-50
Y0 <- rnorm(n, mean = 20, sd = 5) # Depressione baseline
Y1 <- 0.7 * Y0 + (-3) * X0 + rnorm(n, sd = 3) # Effetto del trattamento = -3
# Calcolo change score
delta_Y <- Y1 - Y0
# Tre analisi
mod_change <- lm(delta_Y ~ X0)
mod_ancova <- lm(Y1 ~ X0 + Y0)
mod_simple <- lm(Y1 ~ X0)
# Risultati
tibble(
Analisi = c("Change Score", "ANCOVA", "Senza Controllo Baseline"),
Coefficiente = c(coef(mod_change)[2], coef(mod_ancova)[2], coef(mod_simple)[2]),
SE = c(summary(mod_change)$coef[2,2],
summary(mod_ancova)$coef[2,2],
summary(mod_simple)$coef[2,2])
) %>%
mutate(
IC_lower = Coefficiente - 1.96 * SE,
IC_upper = Coefficiente + 1.96 * SE
) %>%
ggplot(aes(x = Analisi, y = Coefficiente)) +
geom_hline(yintercept = -3, linetype = "dashed", color = "red", linewidth = 1) +
geom_pointrange(aes(ymin = IC_lower, ymax = IC_upper), size = 0.8) +
coord_flip() +
labs(title = "Confronto tra Metodi di Analisi - Scenario 1",
subtitle = "La linea rossa indica l'effetto causale vero (−3)",
y = "Stima dell'Effetto del Trattamento",
x = "") +
theme(plot.title = element_text(face = "bold")) +
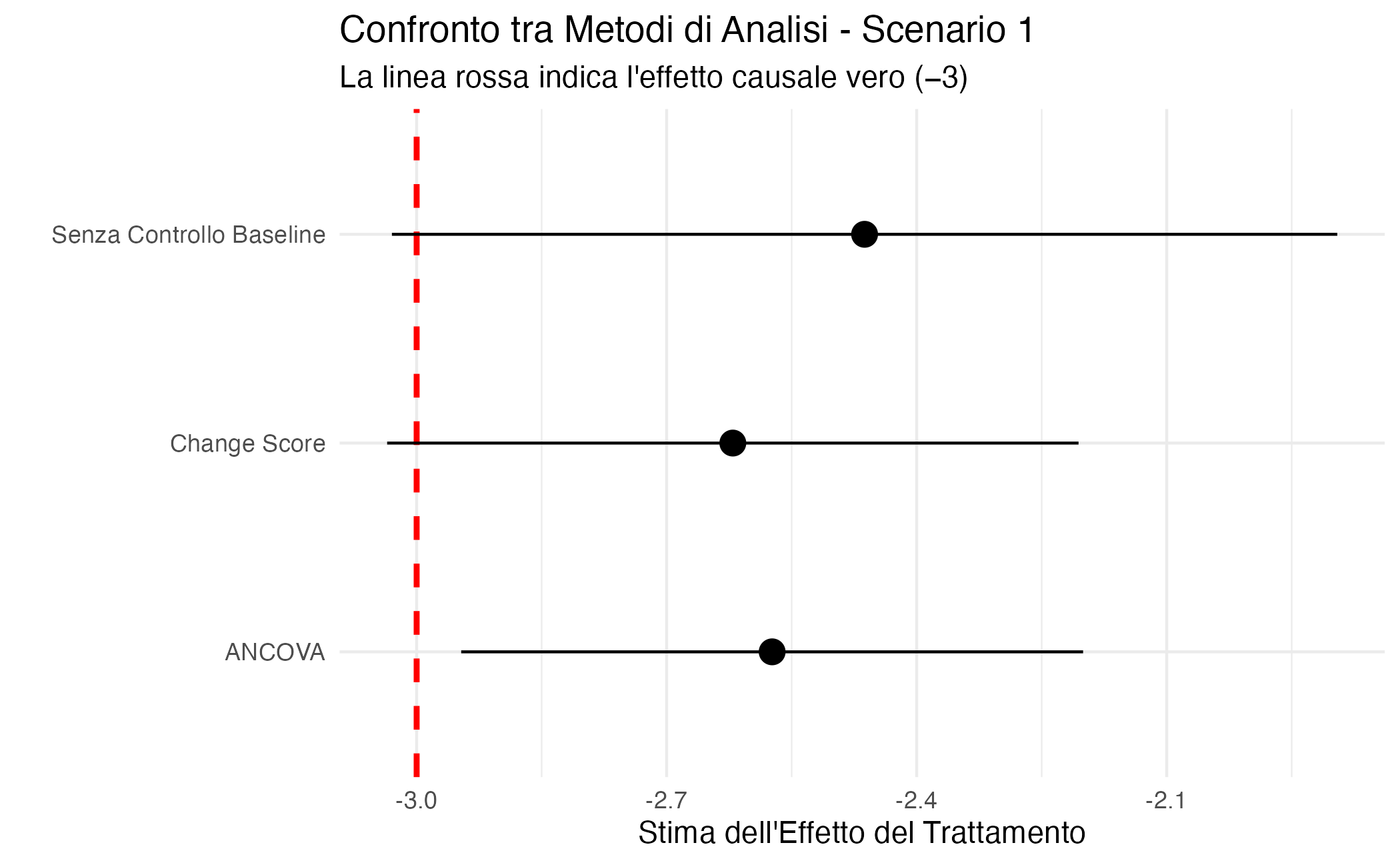
theme_minimal()Come si può osservare dalla simulazione, in questo scenario tutti e tre gli approcci forniscono stime non distorte dell’effetto del trattamento. Tuttavia, l’approccio ANCOVA presenta errori standard più piccoli, risultando quindi più preciso.
25.2.2 Scenario 2: la baseline come confoundente
Il secondo scenario presenta una sfida metodologica di maggiore complessità e rappresenta una condizione particolarmente diffusa nella ricerca psicologica osservazionale. In questa configurazione, la misura baseline \(Y_0\) assume il ruolo di variabile confondente: essa è influenzata da fattori preesistenti che determinano anche la probabilità di ricevere il trattamento \(X_0\), esercitando al contempo un effetto causale diretto sull’esito al follow-up \(Y_1\). Questa struttura causale emerge tipicamente in contesti non sperimentali, in cui l’assegnazione del trattamento è determinata dalle condizioni cliniche o caratteristiche individuali dei partecipanti.
Un esempio può chiarire questa dinamica. Si supponga di voler valutare l’efficacia di un programma di mindfulness nel ridurre i sintomi ansiosi. In questo contesto osservazionale, i soggetti che scelgono autonomamente di aderire al programma potrebbero presentare caratteristiche sistematicamente diverse rispetto al gruppo di controllo. È plausibile, ad esempio, che un livello basale di ansia più elevato rappresenti sia un fattore prognostico per i sintomi futuri, sia un determinante della motivazione a intraprendere un intervento. Quando il livello iniziale di ansia influisce sia sulla probabilità di ricevere il trattamento sia sull’esito successivo, si configura un classico caso di confondimento, in cui la stima dell’effetto terapeutico risulta compromessa senza un’adeguata correzione metodologica.
# Scenario 2: Y0 è un confounder
dag2 <- dagify(
Y1 ~ Y0 + X0,
X0 ~ Y0,
exposure = "X0",
outcome = "Y1"
)
ggdag(dag2, text = TRUE, text_col = "white") +
theme_dag() +
labs(title = "Scenario 2: Baseline come Confounder",
subtitle = "Comune negli studi osservazionali") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5))In questo scenario, l’impiego del punteggio di cambiamento conduce a stime dell’effetto terapeutico affette da una distorsione potenzialmente severa. L’origine del problema è di natura algebrica e causale: poiché il punteggio di cambiamento (\(D = Y_1 - Y_0\)) incorpora la misura baseline \(Y_0\) con segno negativo, la sua associazione con il trattamento \(X_0\) non cattura il solo effetto di \(X_0\) su \(Y_1\), ma riflette anche la relazione preesistente tra \(X_0\) e \(Y_0\). Poiché in questo modello \(Y_0\) è un antecedente causale di \(X_0\), tale relazione si traduce in un bias sistematico di notevole entità che può falsare la direzione stessa dell’effetto stimato.
# Simulazione Scenario 2
n <- 1000
# Y0 influenza X0 (confondimento)
Y0 <- rnorm(n, mean = 50, sd = 10)
X0 <- rbinom(n, 1, plogis((Y0 - 50) / 10)) # Chi ha più ansia cerca il trattamento
Y1 <- 0.6 * Y0 + (-5) * X0 + rnorm(n, sd = 4) # Vero effetto = -5
delta_Y <- Y1 - Y0
# Tre analisi
mod_change <- lm(delta_Y ~ X0)
mod_ancova <- lm(Y1 ~ X0 + Y0)
mod_simple <- lm(Y1 ~ X0)
# Visualizzazione risultati
tibble(
Analisi = c("Change Score", "ANCOVA", "Senza Controllo Baseline"),
Coefficiente = c(coef(mod_change)[2], coef(mod_ancova)[2], coef(mod_simple)[2]),
SE = c(summary(mod_change)$coef[2,2],
summary(mod_ancova)$coef[2,2],
summary(mod_simple)$coef[2,2])
) %>%
mutate(
IC_lower = Coefficiente - 1.96 * SE,
IC_upper = Coefficiente + 1.96 * SE,
Distorsione = abs(Coefficiente - (-5))
) %>%
ggplot(aes(x = Analisi, y = Coefficiente, color = Distorsione)) +
geom_hline(yintercept = -5, linetype = "dashed", color = "red", linewidth = 1) +
geom_pointrange(aes(ymin = IC_lower, ymax = IC_upper), size = 0.8) +
coord_flip() +
scale_color_gradient(low = "darkgreen", high = "darkred") +
labs(title = "Confronto tra Metodi di Analisi - Scenario 2",
subtitle = "La linea rossa indica l'effetto causale vero (−5)",
y = "Stima dell'Effetto del Trattamento",
x = "",
color = "Distorsione\nAssoluta") +
theme(plot.title = element_text(face = "bold"),
legend.position = "right") +
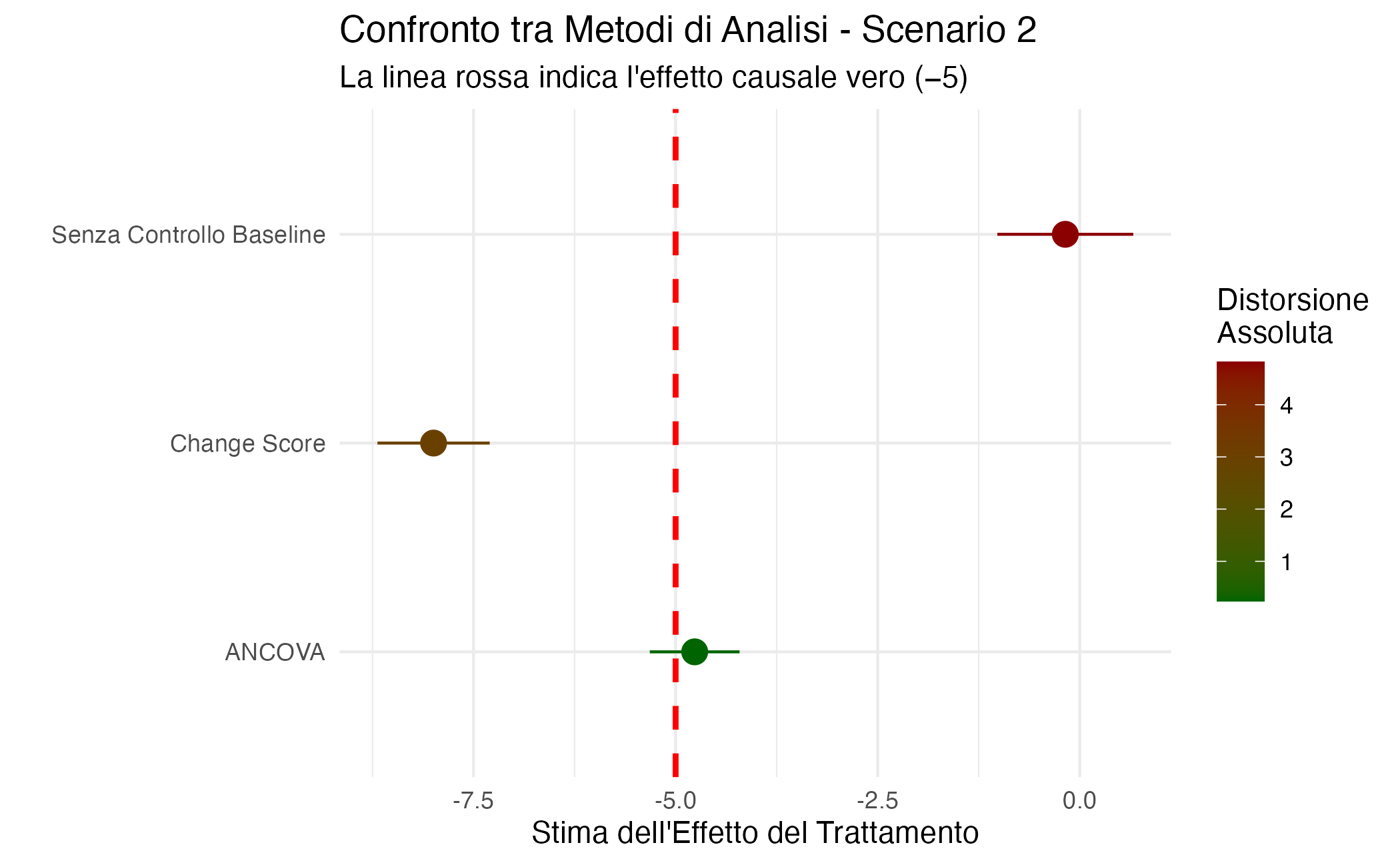
theme_minimal()I risultati della simulazione illustrano efficacemente la natura del problema: l’analisi basata sul punteggio di cambiamento sottostima in modo marcato l’effetto benefico del trattamento, mentre un modello che omette completamente il valore di base sovrastima in modo sistematico l’effetto. L’unico approccio in grado di stimare correttamente l’effetto causale è l’ANCOVA, che include contemporaneamente il trattamento e il valore baseline come predittori dell’esito finale. La superiorità di questo modello risiede nella sua capacità di bloccare il percorso di confondimento attraverso il condizionamento statistico su \(Y_0\), isolando così l’effetto causale diretto di \(X_0\) su \(Y_1\).
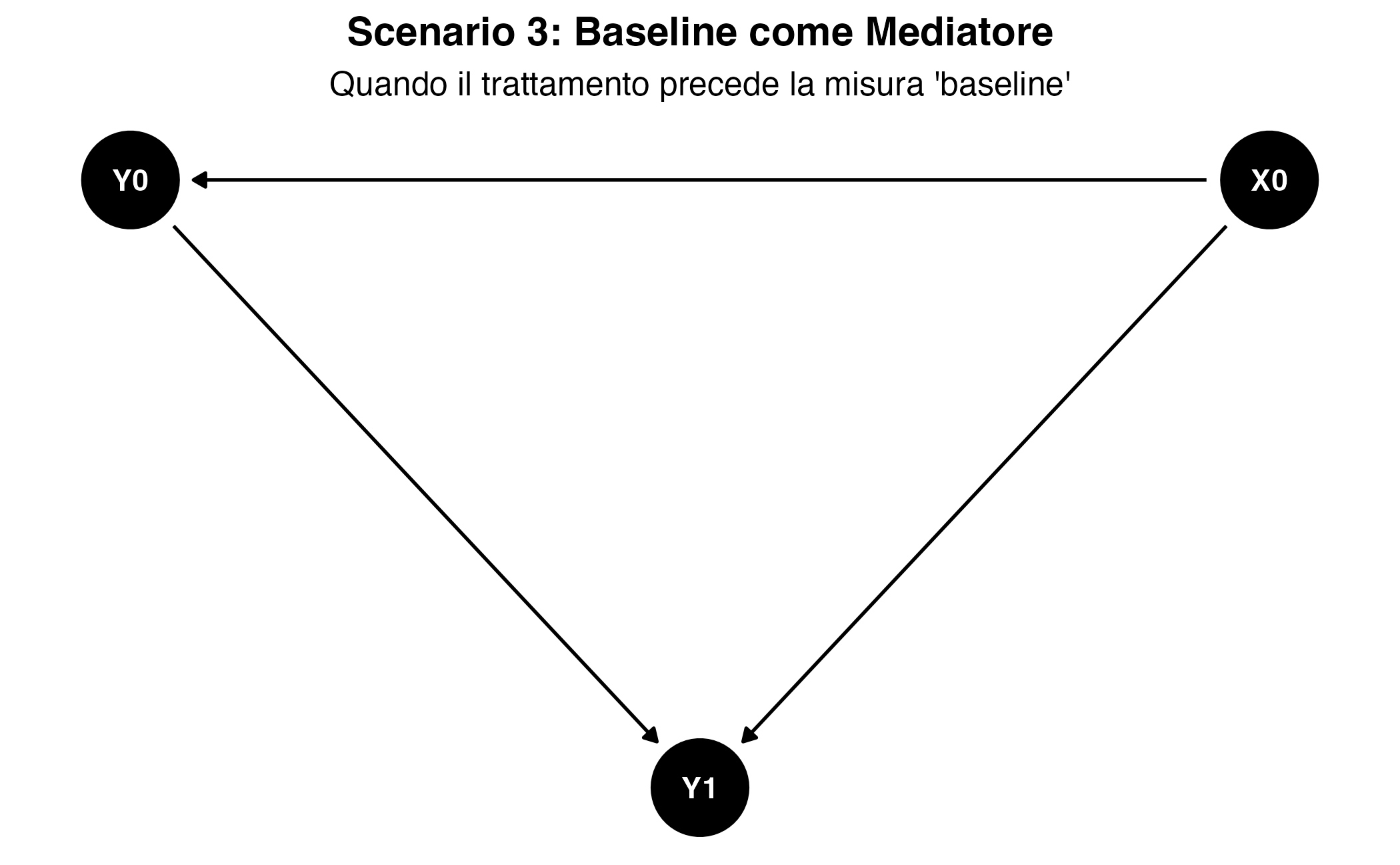
25.2.3 Scenario 3: la baseline come mediatore
Il terzo scenario introduce la configurazione più complessa dal punto di vista concettuale e metodologico. In questo modello, il trattamento \(X_0\) precede temporalmente e influenza causalmente sulla misura baseline \(Y_0\), la quale a sua volta determina l’esito al follow-up \(Y_1\). In questa architettura causale, \(Y_0\) non svolge più il ruolo di confondente, ma quello di mediatore lungo il percorso attraverso cui \(X_0\) esercita la sua influenza su \(Y_1\). Questa configurazione si realizza quando il trattamento inizia prima della misurazione baseline e i suoi effetti, essendo rapidi, sono già presenti al momento di tale rilevazione. In questo caso, la cosiddetta ‘baseline’ \(Y_0\) non rappresenta più lo stato puro pre-trattamento, ma cattura già una prima fase degli effetti dell’intervento, fungendo da mediatore precoce.
Un esempio può essere tratto dalla ricerca sugli interventi di esercizio fisico. Si supponga di valutare l’impatto di un programma di attività motoria sul benessere psicologico, dove il programma inizia prima della rilevazione baseline. In questo caso, il valore \(Y_0\) misurato come “baseline” catturerà già una parte degli effetti del trattamento. L’effetto causale totale del programma si articola quindi lungo due traiettorie: un effetto diretto sul benessere al follow-up (\(X_0 \rightarrow Y_1\)) e un effetto indiretto mediato dal miglioramento registrato già al baseline (\(X_0 \rightarrow Y_0 \rightarrow Y_1\)).
# Scenario 3: Y0 è un mediatore
dag3 <- dagify(
Y1 ~ Y0 + X0,
Y0 ~ X0,
exposure = "X0",
outcome = "Y1"
)
ggdag(dag3, text = TRUE, text_col = "white") +
theme_dag() +
labs(title = "Scenario 3: Baseline come Mediatore",
subtitle = "Quando il trattamento precede la misura 'baseline'") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5))In questo scenario, le diverse analisi stimano estimandi causali diversi. L’analisi del punteggio di cambiamento può produrre risultati particolarmente problematici, in quanto può stimare un effetto di segno opposto rispetto all’effetto causale totale vero. Ciò accade perché il punteggio di cambiamento, contenendo \(Y_0\) con segno negativo, distorce la relazione positiva tra \(X_0\) e \(Y_0\). L’approccio ANCOVA stima l’effetto diretto del trattamento controllando il mediatore, mentre l’analisi semplice che non include il valore di base stima l’effetto causale totale.
# Simulazione Scenario 3
n <- 1000
# X0 causa Y0 (mediazione)
X0 <- rbinom(n, 1, 0.5)
Y0 <- 30 + 4 * X0 + rnorm(n, sd = 5) # Effetto indiretto attraverso Y0
Y1 <- 0.7 * Y0 + 2 * X0 + rnorm(n, sd = 3) # Effetto diretto = 2
# Effetto totale = 2 + 4*0.7 = 4.8
delta_Y <- Y1 - Y0
# Tre analisi
mod_change <- lm(delta_Y ~ X0)
mod_ancova <- lm(Y1 ~ X0 + Y0)
mod_simple <- lm(Y1 ~ X0)
# Visualizzazione
tibble(
Analisi = c("Change Score", "ANCOVA (Effetto Diretto)", "Senza Controllo (Effetto Totale)"),
Coefficiente = c(coef(mod_change)[2], coef(mod_ancova)[2], coef(mod_simple)[2]),
SE = c(summary(mod_change)$coef[2,2],
summary(mod_ancova)$coef[2,2],
summary(mod_simple)$coef[2,2]),
Vero_Valore = c(NA, 2, 4.8)
) %>%
mutate(
IC_lower = Coefficiente - 1.96 * SE,
IC_upper = Coefficiente + 1.96 * SE
) %>%
ggplot(aes(x = Analisi, y = Coefficiente)) +
geom_pointrange(aes(ymin = IC_lower, ymax = IC_upper), size = 0.8) +
geom_point(aes(y = Vero_Valore), color = "red", size = 3, shape = 4) +
coord_flip() +
labs(title = "Confronto tra Metodi di Analisi - Scenario 3",
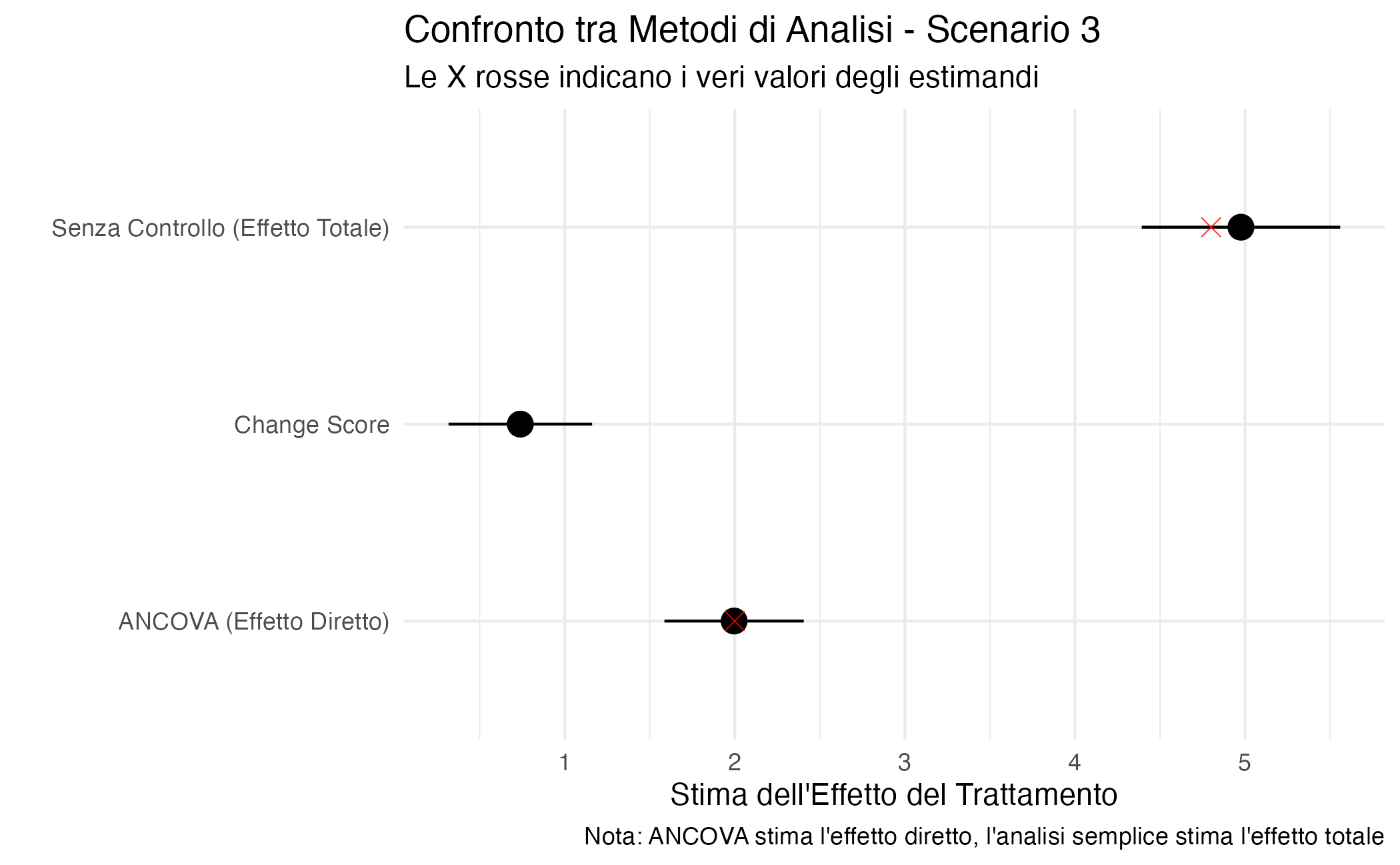
subtitle = "Le X rosse indicano i veri valori degli estimandi",
y = "Stima dell'Effetto del Trattamento",
x = "",
caption = "Nota: ANCOVA stima l'effetto diretto, l'analisi semplice stima l'effetto totale") +
theme(plot.title = element_text(face = "bold"),
plot.caption = element_text(hjust = 0)) +
theme_minimal()La simulazione illustra il problema: l’analisi del punteggio di cambiamento produce una stima negativa anche quando tutti gli effetti causali reali sono positivi. Ciò accade perché il punteggio di cambiamento cattura principalmente la differenza creata dall’effetto del trattamento su \(Y_0\), che poi viene parzialmente “trasmesso” a \(Y_1\) attraverso la persistenza naturale del benessere nel tempo. L’analisi ANCOVA stima correttamente l’effetto diretto, mentre l’analisi semplice stima l’effetto totale che include sia l’effetto diretto che quello mediato tramite \(Y_0\).
25.3 Un confronto visivo completo
Per apprezzare appieno le differenze tra i tre scenari e le relative implicazioni analitiche, è utile confrontare visivamente i risultati delle simulazioni fianco a fianco.
# Funzione per eseguire tutte le analisi
run_analysis <- function(scenario, Y0, X0, Y1) {
delta_Y <- Y1 - Y0
tibble(
Scenario = scenario,
Analisi = c("Change Score", "ANCOVA", "Semplice"),
Coefficiente = c(
coef(lm(delta_Y ~ X0))[2],
coef(lm(Y1 ~ X0 + Y0))[2],
coef(lm(Y1 ~ X0))[2]
),
SE = c(
summary(lm(delta_Y ~ X0))$coef[2,2],
summary(lm(Y1 ~ X0 + Y0))$coef[2,2],
summary(lm(Y1 ~ X0))$coef[2,2]
)
)
}
# Scenario 1: Esposizione competitiva (randomizzato)
n <- 1000
X0_s1 <- rbinom(n, 1, 0.5)
Y0_s1 <- rnorm(n, 20, 5)
Y1_s1 <- 0.7 * Y0_s1 + (-3) * X0_s1 + rnorm(n, sd = 3)
res1 <- run_analysis("Scenario 1:\nEsposizione\nCompetitiva", Y0_s1, X0_s1, Y1_s1)
# Scenario 2: Confounder
Y0_s2 <- rnorm(n, 50, 10)
X0_s2 <- rbinom(n, 1, plogis((Y0_s2 - 50) / 10))
Y1_s2 <- 0.6 * Y0_s2 + (-5) * X0_s2 + rnorm(n, sd = 4)
res2 <- run_analysis("Scenario 2:\nConfounder", Y0_s2, X0_s2, Y1_s2)
# Scenario 3: Mediatore
X0_s3 <- rbinom(n, 1, 0.5)
Y0_s3 <- 30 + 4 * X0_s3 + rnorm(n, sd = 5)
Y1_s3 <- 0.7 * Y0_s3 + 2 * X0_s3 + rnorm(n, sd = 3)
res3 <- run_analysis("Scenario 3:\nMediatore", Y0_s3, X0_s3, Y1_s3)
# Combinare e visualizzare
bind_rows(res1, res2, res3) %>%
mutate(
IC_lower = Coefficiente - 1.96 * SE,
IC_upper = Coefficiente + 1.96 * SE
) %>%
ggplot(aes(x = Analisi, y = Coefficiente, color = Analisi)) +
geom_hline(yintercept = 0, linetype = "dotted", alpha = 0.5) +
geom_pointrange(aes(ymin = IC_lower, ymax = IC_upper), size = 0.6) +
facet_wrap(~ Scenario, scales = "free_y") +
coord_flip() +
scale_color_manual(values = c("Change Score" = "#D55E00",
"ANCOVA" = "#009E73",
"Semplice" = "#0072B2")) +
labs(title = "Confronto tra Metodi di Analisi nei Tre Scenari Causali",
y = "Stima dell'Effetto del Trattamento (con IC 95%)",
x = "") +
theme(plot.title = element_text(face = "bold", size = 14),
legend.position = "none",
strip.text = element_text(face = "bold")) +
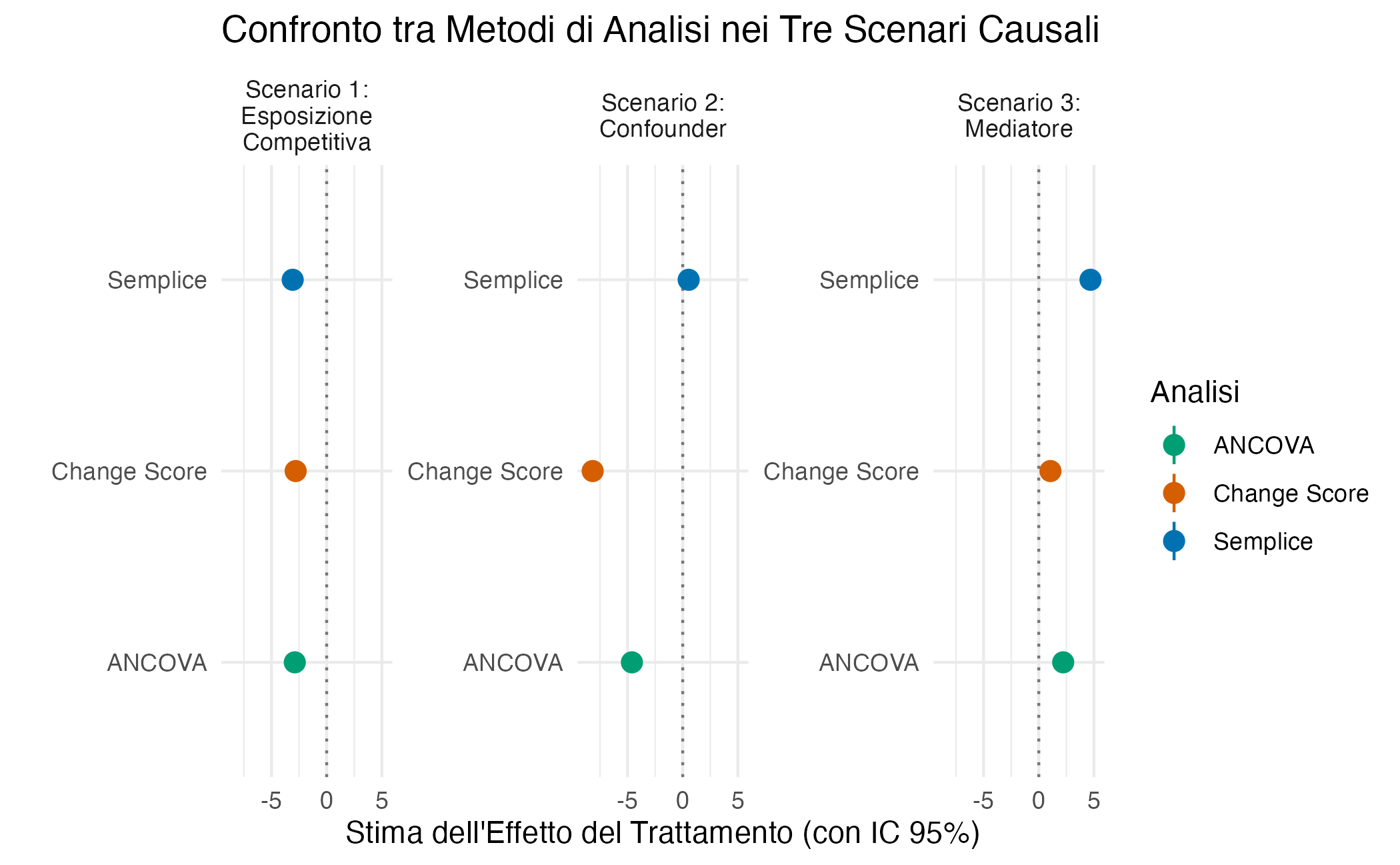
theme_minimal()L’ispezione visiva dei risultati consente di identificare pattern distintivi per ciascuno scenario: nello Scenario 1, tutti i metodi convergono verso stime simili, coerentemente con l’assenza di confondimento; nello Scenario 2, l’analisi del punteggio di cambiamento produce una stima gravemente distorta, dimostrando la sua vulnerabilità in presenza di variabili confondenti; nello Scenario 3, l’analisi del punteggio di cambiamento non solo fallisce nel recuperare l’effetto vero, ma genera una stima con segno opposto, invertendo così la direzione stessa della relazione causale.
25.4 Implicazioni pratiche per la ricerca psicologica
Le implicazioni metodologiche che emergono da questa analisi sono di notevole portata per la ricerca psicologica. Il principio cardine è che la scelta della strategia analitica deve essere guidata dalla struttura causale presupposta dal fenomeno in esame, e non da preferenze statistiche o convenzioni consolidate. Prima di selezionare un modello, è quindi necessario esplicitare e giustificare le proprie assunzioni causali: il trattamento è antecedente o successivo alla baseline? La misura baseline è un determinante dell’assegnazione al trattamento? La rilevanza di tali interrogativi è di natura concettuale e teorica, non puramente statistica, ed esige pertanto una riflessione approfondita sul disegno dello studio e sui meccanismi sottostanti al fenomeno indagato.
Nei disegni di ricerca randomizzati, dove la randomizzazione garantisce l’indipendenza tra l’assegnazione al trattamento e la misura baseline, i diversi metodi analitici tendono a convergere verso una stima coerente dell’effetto causale. Tuttavia, anche in questo contesto ideale, l’approccio ANCOVA risulta superiore grazie alla sua maggiore efficienza statistica.
La complessità metodologica aumenta considerevolmente negli studi osservazionali che costituiscono la parte predominante della ricerca in psicologia. In questi contesti, la scelta della procedura analitica non è più una questione di efficienza, ma di validità causale. La scelta del modello appropriato può fare la differenza tra un’inferenza sostanzialmente corretta e una conclusione gravemente distorta.
Quando sospettiamo che la misura di base possa essere un fattore confondente, ovvero possa influenzare sia la probabilità di ricevere il trattamento sia l’esito successivo, l’analisi ANCOVA non solo diventa preferibile, ma necessaria. Questo scenario si verifica comunemente nei contesti clinici in cui i trattamenti vengono assegnati in base alla gravità iniziale dei sintomi. Ignorare questo tipo di confondimento utilizzando i punteggi di cambiamento può portare a sottostimare o sovrastimare gli effetti del trattamento, con conseguenze potenzialmente serie per le decisioni di natura clinica.
Lo scenario di mediazione introduce problematiche concettuali di particolare complessità. Qualora il trattamento preceda temporalmente la cosiddetta misurazione “baseline” e produca effetti di natura persistente, è necessario operare una distinzione tra l’effetto causale totale del trattamento e il suo effetto diretto, non mediato dalla baseline medesima. Quale di questi effetti sia di maggiore interesse dipende dalla domanda di ricerca specifica. Se l’obiettivo è quantificare il beneficio complessivo attribuibile al trattamento, la stima appropriata sarà l’effetto totale, ottenibile attraverso un’analisi che non controlli per la baseline. Se invece vogliamo capire i meccanismi attraverso cui opera il trattamento, allora l’attenzione si sposterà sulla scomposizione in effetto diretto ed effetto indiretto mediato, il che richiede tecniche di analisi di mediazione più sofisticate.
25.4.1 Raccomandazioni pratiche
Alla luce di queste considerazioni, Tennant et al. (2022) formulano alcune raccomandazioni concrete per la pratica della ricerca. Il loro principale suggerimento è di abbandonare l’utilizzo sistematico dei punteggi di cambiamento come variabili dipendenti negli studi osservazionali. Sebbene radicata nella consuetudine e intuitivamente persuasiva, questa pratica comporta un rischio eccessivo di distorsione nelle inferenze causali.
L’applicazione dei punteggi di cambiamento rimane metodologicamente giustificabile esclusivamente nell’ambito di studi randomizzati con un disegno solido, sebbene persino in questo contesto esistano approcci alternativi—in particolare il modello ANCOVA—che offrono una superiore efficienza statistica.
Per gli studi osservazionali, la premessa metodologica fondamentale è l’articolazione esplicita delle assunzioni causali, formalizzabili mediante grafi aciclici diretti (DAG). Questi strumenti forniscono una rappresentazione visiva delle relazioni causali ipotizzate tra trattamento, misura baseline ed esito finale, orientando in modo sistematico la selezione della strategia analitica più appropriata. Qualora la misura baseline sia identificabile come un confondente, l’approccio ANCOVA—che include sia il trattamento sia la baseline tra i predittori dell’esito finale—costituisce generalmente la soluzione più valida. Nel caso in cui la baseline funga invece da mediatore, la scelta analitica deve essere guidata dall’obiettivo della ricerca: la stima dell’effetto totale richiede di non controllare per la baseline, mentre l’identificazione degli effetti diretti e indiretti richiede l’impiego di modelli di mediazione specifici.
È importante riconoscere, inoltre, che queste raccomandazioni non risolvono tutte le sfide dell’inferenza causale negli studi osservazionali. Restano infatti aperte sfide rilevanti, quali il confondimento non misurato, la corretta specificazione dei modelli e la violazione delle assunzioni. Tuttavia, evitare l’uso inappropriato dei punteggi di cambiamento rappresenta un passo importante verso analisi più rigorose e conclusioni più affidabili.
25.5 Un esempio dettagliato: studio sull’efficacia della psicoterapia
Per consolidare questi concetti, consideriamo un esempio completo e realistico. Supponiamo di voler valutare l’efficacia di un programma di terapia dialettico-comportamentale (DBT) per la riduzione dei sintomi della personalità borderline. Raccogliamo i dati di 500 pazienti che hanno cercato un trattamento in diverse cliniche nel corso di un anno, misurando la gravità dei loro sintomi all’inizio del trattamento (baseline) e dopo sei mesi (follow-up).
# Simulazione di uno studio realistico sulla DBT
n <- 500
# Creiamo variabili latenti che influenzano sia la ricerca di trattamento
# che la severità dei sintomi
motivazione <- rnorm(n, 0, 1)
supporto_sociale <- rnorm(n, 0, 1)
# Severità sintomi al baseline (scala 0-100)
# Influenzata da caratteristiche stabili
severita_baseline <- 60 + 10 * motivazione - 5 * supporto_sociale + rnorm(n, sd = 10)
severita_baseline <- pmin(pmax(severita_baseline, 0), 100) # Limitiamo tra 0 e 100
# Probabilità di iniziare la DBT dipende dalla severità e dalla motivazione
prob_dbt <- plogis((severita_baseline - 60) / 15 + 0.5 * motivazione)
riceve_dbt <- rbinom(n, 1, prob_dbt)
# Severità al follow-up
# Effetto vero della DBT: riduzione di 15 punti
# Persistenza dei sintomi: 0.6
# Effetto della motivazione e del supporto sociale continuano
severita_followup <- 0.6 * severita_baseline +
(-15) * riceve_dbt +
(-5) * motivazione +
3 * supporto_sociale +
rnorm(n, sd = 8)
severita_followup <- pmin(pmax(severita_followup, 0), 100)
# Creiamo il dataset
dati_studio <- tibble(
id = 1:n,
motivazione,
supporto_sociale,
severita_baseline,
riceve_dbt,
severita_followup,
change_score = severita_followup - severita_baseline
)
# Tre analisi
analisi_change <- lm(change_score ~ riceve_dbt, data = dati_studio)
analisi_ancova <- lm(severita_followup ~ riceve_dbt + severita_baseline, data = dati_studio)
analisi_semplice <- lm(severita_followup ~ riceve_dbt, data = dati_studio)
# Confronto risultati
risultati_esempio <- tibble(
Analisi = c("Punteggio di\nCambiamento",
"ANCOVA\n(Appropriata)",
"Semplice\n(Senza Baseline)"),
Coefficiente = c(
coef(analisi_change)[2],
coef(analisi_ancova)[2],
coef(analisi_semplice)[2]
),
SE = c(
summary(analisi_change)$coef[2,2],
summary(analisi_ancova)$coef[2,2],
summary(analisi_semplice)$coef[2,2]
),
p_value = c(
summary(analisi_change)$coef[2,4],
summary(analisi_ancova)$coef[2,4],
summary(analisi_semplice)$coef[2,4]
)
) %>%
mutate(
IC_lower = Coefficiente - 1.96 * SE,
IC_upper = Coefficiente + 1.96 * SE
)
# Visualizzazione
p1 <- ggplot(risultati_esempio, aes(x = Analisi, y = Coefficiente)) +
geom_hline(yintercept = -15, linetype = "dashed", color = "red", linewidth = 1) +
geom_pointrange(aes(ymin = IC_lower, ymax = IC_upper), size = 1) +
coord_flip() +
labs(title = "Stime dell'Effetto della DBT sui Sintomi Borderline",
subtitle = "La linea rossa indica l'effetto causale vero (−15 punti)",
y = "Effetto Stimato (punti di riduzione sulla scala)",
x = "") +
theme(plot.title = element_text(face = "bold")) +
theme_minimal()
# Distribuzione dei punteggi per gruppo
p2 <- dati_studio %>%
pivot_longer(cols = c(severita_baseline, severita_followup),
names_to = "Tempo",
values_to = "Severita") %>%
mutate(
Tempo = recode(Tempo,
"severita_baseline" = "Baseline",
"severita_followup" = "Follow-up"),
Gruppo = ifelse(riceve_dbt == 1, "DBT", "Nessun Trattamento")
) %>%
ggplot(aes(x = Tempo, y = Severita, group = id, color = Gruppo)) +
geom_line(alpha = 0.1) +
stat_summary(aes(group = Gruppo), fun = mean, geom = "line", linewidth = 2) +
stat_summary(aes(group = Gruppo), fun = mean, geom = "point", size = 3) +
scale_color_manual(values = c("DBT" = "#E69F00", "Nessun Trattamento" = "#56B4E9")) +
labs(title = "Traiettorie Individuali dei Sintomi",
y = "Severità Sintomi",
x = "") +
theme(plot.title = element_text(face = "bold"),
legend.position = "bottom") +
theme_minimal()
p1 / p2 + plot_annotation(
title = "Studio Osservazionale sull'Efficacia della DBT",
theme = theme(plot.title = element_text(size = 16, face = "bold"))
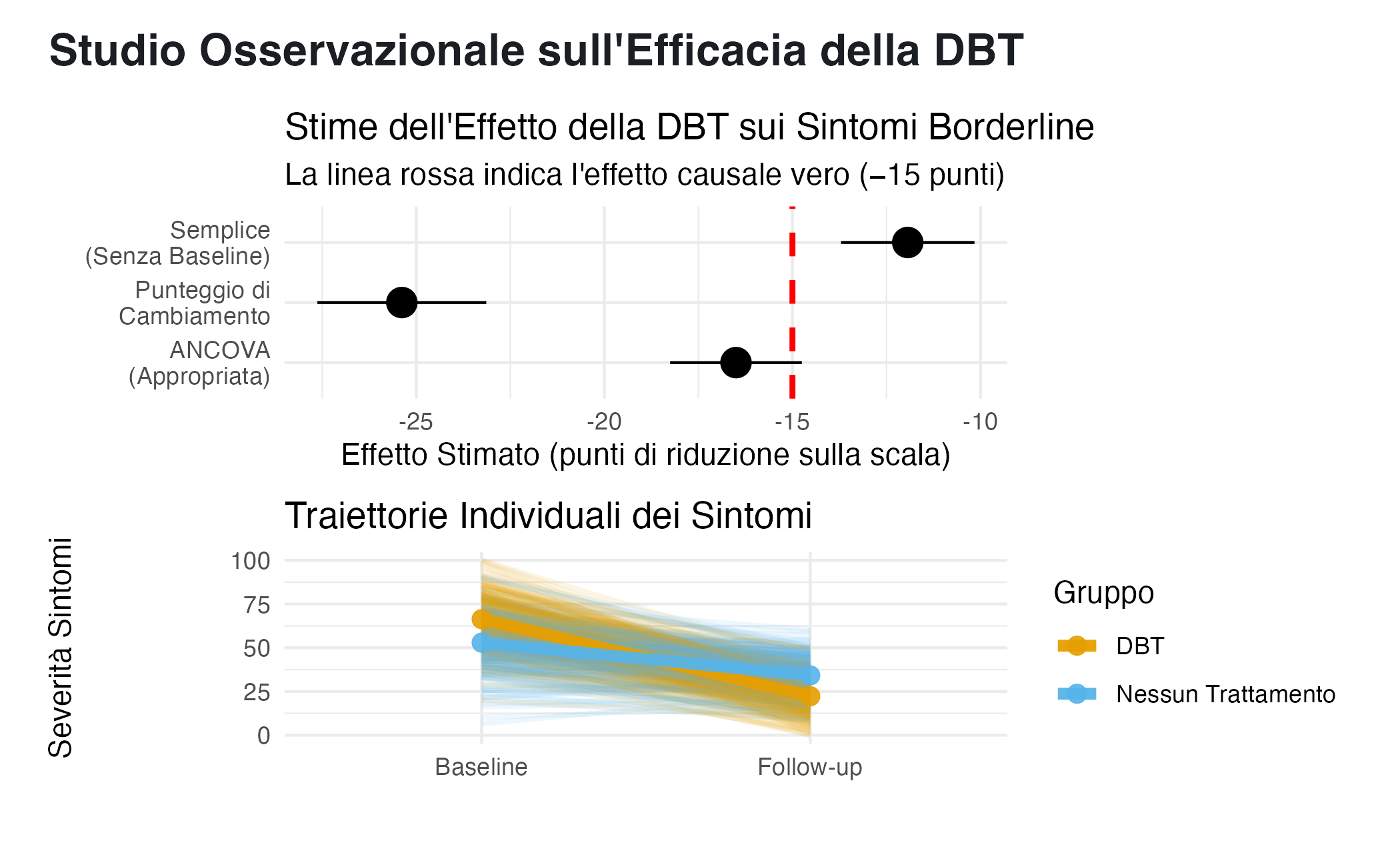
)Questo esempio illustra chiaramente il problema dell’analisi del punteggio di cambiamento in un contesto osservazionale realistico. L’analisi del punteggio di cambiamento sovrastima sostanzialmente l’effetto benefico della DBT, suggerendo una riduzione maggiore di quella reale (15 punti). Ciò accade perché i pazienti che hanno cercato il trattamento DBT tendevano ad avere sintomi più gravi all’inizio e una maggiore motivazione. Il punteggio di cambiamento cattura quindi non solo l’effetto del trattamento, ma anche:
- la regressione verso la media (chi parte da valori estremi tende naturalmente a migliorare);
- l’effetto confondente della motivazione, che influenza positivamente il cambiamento indipendentemente dal trattamento ricevuto.
L’analisi ANCOVA, che controlla per la gravità del disturbo alla baseline, fornisce una stima molto più accurata dell’effetto causale. Condizionando sulla gravità iniziale, l’analisi confronta pazienti con livelli simili di sintomi iniziali, isolando così l’effetto del trattamento dalle influenze confondenti della selezione e della regressione verso la media.
L’analisi semplice, che ignora completamente il valore di partenza, sottostima (o addirittura non rileva) l’effetto perché confronta direttamente i livelli assoluti al follow-up tra gruppi che differivano sistematicamente già alla baseline. Poiché il gruppo DBT partiva da una gravità molto più elevata, anche dopo il beneficio del trattamento potrebbe mantenere punteggi più alti rispetto al gruppo di controllo, mascherando così l’efficacia dell’intervento.
Riflessioni conclusive
Comprendere i processi di cambiamento è un obiettivo fondamentale della ricerca psicologica. Siamo chiamati a indagare costantemente come gli individui cambino, si adattino, superino le difficoltà e rispondano agli interventi terapeutici. Tuttavia, la misurazione accurata di tali trasformazioni e l’identificazione dei loro determinanti causali richiedono un approccio metodologico sofisticato che vada oltre la semplice differenza tra misurazioni ripetute.
I punteggi di cambiamento conservano indubbiamente una funzione descrittiva: forniscono una sintesi immediata dell’entità media della variazione di un determinato esito tra due momenti temporali in un campione. Il loro impiego è appropriato nel monitoraggio clinico individuale, dove possono informare le decisioni terapeutiche personalizzate. Tuttavia, la criticità emerge quando questi punteggi vengono utilizzati per trarre inferenze causali sull’efficacia di trattamenti o esposizioni, soprattutto in contesti osservazionali, dove le assunzioni necessarie per interpretazioni causali sono raramente verificate.
Fortunatamente, la metodologia contemporanea offre alternative robuste. Un’applicazione consapevole dell’ANCOVA, basata su una concettualizzazione rigorosa della struttura causale del fenomeno in esame, costituisce un solido framework analitico per gli studi longitudinali. I grafi aciclici diretti (DAG) si rivelano strumenti potenti per formalizzare le assunzioni causali e identificare le strategie di stima più appropriate, mentre l’analisi di mediazione formale consente di distinguere gli effetti totali, diretti e indiretti quando ciò è rilevante dal punto di vista teorico.
Noi ricercatori in psicologia abbiamo la responsabilità di adottare pratiche analitiche che rispettino la complessità causale dei fenomeni che studiamo. Questo impegno richiede uno sforzo continuo di aggiornamento metodologico, ma il guadagno in termini di validità delle nostre conclusioni giustifica ampiamente tale investimento intellettuale. Solo un’analisi appropriata può condurci a una comprensione autentica dei meccanismi che regolano il cambiamento psicologico e consentirci di tradurre questa conoscenza in interventi evidence-based per il miglioramento del benessere individuale e collettivo.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] ggdag_0.2.13 ragg_1.5.0 tinytable_0.13.0
#> [4] withr_3.0.2 systemfonts_1.3.1 patchwork_1.3.2
#> [7] ggdist_3.3.3 tidybayes_3.0.7 bayesplot_1.14.0
#> [10] ggplot2_4.0.0 reliabilitydiag_0.2.1 priorsense_1.1.1
#> [13] posterior_1.6.1 loo_2.8.0 rstan_2.32.7
#> [16] StanHeaders_2.32.10 brms_2.23.0 Rcpp_1.1.0
#> [19] sessioninfo_1.2.3 conflicted_1.2.0 janitor_2.2.1
#> [22] matrixStats_1.5.0 modelr_0.1.11 tibble_3.3.0
#> [25] dplyr_1.1.4 tidyr_1.3.1 rio_1.2.4
#> [28] here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-29
#> [7] snakecase_0.11.1 compiler_4.5.1 vctrs_0.6.5
#> [10] stringr_1.5.2 pkgconfig_2.0.3 arrayhelpers_1.1-0
#> [13] fastmap_1.2.0 backports_1.5.0 labeling_0.4.3
#> [16] ggraph_2.2.2 rmarkdown_2.30 purrr_1.1.0
#> [19] xfun_0.53 cachem_1.1.0 jsonlite_2.0.0
#> [22] tweenr_2.0.3 broom_1.0.10 parallel_4.5.1
#> [25] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [28] boot_1.3-32 lubridate_1.9.4 estimability_1.5.1
#> [31] knitr_1.50 zoo_1.8-14 pacman_0.5.1
#> [34] igraph_2.2.0 Matrix_1.7-4 splines_4.5.1
#> [37] timechange_0.3.0 tidyselect_1.2.1 viridis_0.6.5
#> [40] abind_1.4-8 codetools_0.2-20 curl_7.0.0
#> [43] dagitty_0.3-4 pkgbuild_1.4.8 lattice_0.22-7
#> [46] bridgesampling_1.1-2 S7_0.2.0 coda_0.19-4.1
#> [49] evaluate_1.0.5 survival_3.8-3 polyclip_1.10-7
#> [52] RcppParallel_5.1.11-1 pillar_1.11.1 tensorA_0.36.2.1
#> [55] checkmate_2.3.3 stats4_4.5.1 distributional_0.5.0
#> [58] generics_0.1.4 rprojroot_2.1.1 rstantools_2.5.0
#> [61] scales_1.4.0 xtable_1.8-4 glue_1.8.0
#> [64] emmeans_1.11.2-8 tools_4.5.1 graphlayouts_1.2.2
#> [67] mvtnorm_1.3-3 tidygraph_1.3.1 grid_4.5.1
#> [70] QuickJSR_1.8.1 colorspace_2.1-2 nlme_3.1-168
#> [73] ggforce_0.5.0 cli_3.6.5 textshaping_1.0.4
#> [76] svUnit_1.0.8 viridisLite_0.4.2 Brobdingnag_1.2-9
#> [79] V8_8.0.1 gtable_0.3.6 digest_0.6.37
#> [82] ggrepel_0.9.6 TH.data_1.1-4 htmlwidgets_1.6.4
#> [85] farver_2.1.2 memoise_2.0.1 htmltools_0.5.8.1
#> [88] lifecycle_1.0.4 MASS_7.3-65Bibliografia
Questo effetto deriva dal modo in cui il punteggio di cambiamento è definito: \(\Delta Y = Y_1 - Y_0\). Anche se \(Y_0\) e \(Y_1\) fossero statisticamente indipendenti, la differenza \(\Delta Y\) condivide con \(Y_0\) il termine \(Y_0\) stesso, generando meccanicamente una correlazione negativa tra le due variabili. In termini algebrici, se \(\mathrm{Cov}(Y_0, Y_1) = 0\) e \(\mathrm{Var}(Y_0) = \mathrm{Var}(Y_1)\), allora \[ \mathrm{Corr}(Y_0, \Delta Y) = \frac{\mathrm{Cov}(Y_0, Y_1 - Y_0)}{\sqrt{\mathrm{Var}(Y_0),\mathrm{Var}(\Delta Y)}} = -\frac{1}{\sqrt{2}} \approx -0.71. \] Questa correlazione è puramente matematica — non riflette alcuna relazione psicologica o causale reale — ma può generare interpretazioni fuorvianti se il punteggio di cambiamento viene trattato come variabile dipendente in modelli di regressione o analisi di gruppo.↩︎