39 Modellazione dell’eterogeneità: soggetti, popolazione e condizioni

Introduzione

Sulla scia del tutorial di Knight et al. (2023), in questo capitolo estendiamo il modello presentato in precedenza lungo tre direzioni complementari. Partiamo dal livello individuale, in cui stimiamo i parametri di ciascun partecipante (\(\alpha_i, \beta_i\)). Questo passaggio consente di mappare l’eterogeneità interindividuale (sensibilità al feedback e deriva motivazionale), ma le stime dei singoli rimangono isolate le une dalle altre.

Per superare questo limite introduciamo la versione gerarchica (multilevel): i parametri dei singoli sono considerati estratti da distribuzioni di popolazione (es. normali) descritte da iperparametri. In questo modo le informazioni vengono condivise tra individui, con il tipico effetto di shrinkage che stabilizza le stime, soprattutto quando i dati per soggetto sono pochi o rumorosi.

Infine, consideriamo il caso dei gruppi noti, stimando iperparametri separati per ciascuna condizione. Ciò permette di quantificare differenze sistematiche a livello di popolazione tra condizioni sperimentali, oltre alle differenze tra individui. Valuteremo i modelli con criteri predittivi (ELPD tramite LOO-CV), così da bilanciare in modo esplicito complessità e capacità di generalizzazione.

Obiettivi di apprendimento

Al termine del capitolo saprai:

modellare l’eterogeneità con tre granulosità (sample-level, person-level, gerarchico);
stimare e interpretare \((\alpha_i, \beta_i)\) e gli iper-parametri di popolazione;
valutare i modelli con ELPD/LOO e diagnosticare problemi (Pareto-k, divergenze);
tradurre risultati in implicazioni psicologiche (apprendimento vs drift) evitando conclusioni iperboliche;
costruire figure che mostrano shrinkage e differenze tra condizioni.

Panoramica del capitolo

Modello a livello individuale: stima di \(\alpha_i\) e \(\beta_i\) per ogni soggetto.
Modello gerarchico: parametri individuali estratti da distribuzioni di popolazione → shrinkage e maggiore robustezza.
Gruppi noti: iper-parametri specifici per condizione (approach vs avoidance).
Confronto predittivo: ELPD e LOO-CV per scegliere il modello.
Implicazioni psicologiche: quando e perché la gerarchia migliora l’inferenza.

Mappa concettuale

Granulosità del modello → Che cosa aggiunge → Quando usarlo

Sample-level → Parsimonia, ma ignora eterogeneità → Dati omogenei o teaser introduttivo.
Person-level → Parametri per soggetto → Profilazione individuale, dataset medi.
Gerarchico → Condivisione informazione + iperparametri → Dati scarsi/rumorosi per soggetto; inferenze di popolazione.
Gerarchico con gruppi → Stima differenze di condizione → Ipotesi sperimentali tra condizioni.

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

suppressPackageStartupMessages({
  library(cmdstanr)
  library(bayesplot)
  library(tidybayes)
  library(posterior)
  library(loo)
  library(patchwork)
  library(conflicted)
})

conflicts_prefer(loo::loo)
conflicts_prefer(dplyr::count)

39.1 Modello a livello individuale

Perché non basta un unico parametro per tutti?

Il modello sample-level produce una media “ecumenica” che appiattisce le differenze: va bene per un teaser, ma è rischioso per le inferenze psicologiche. Il modello person-level rende visibili (i) la sensibilità al feedback (\(\alpha\)) e (ii) la deriva motivazionale (\(\beta\)) idiosincratiche.

A differenza del modello sample-level, analizzato in precedenza, che stima un unico insieme di parametri (\((\alpha, \beta)\)) per l’intero campione, risultando così insensibile alle differenze individuali, il modello a livello individuale (o person-level) introduce un importante avanzamento concettuale e metodologico. Questo approccio stima parametri distinti, \(\alpha_i\) e \(\beta_i\), per ciascun partecipante, riconoscendo esplicitamente l’eterogeneità presente nella popolazione.

Nella sua formulazione, il modello assegna a ogni individuo un tasso di apprendimento \(\alpha_i\) e una deriva motivazionale \(\beta_i\) personalizzati. Questi parametri catturano, rispettivamente, la sensibilità specifica di un soggetto al feedback ricevuto e la sua inclinazione motivazionale intrinseca. Al contrario, il parametro \(\sigma\), che rappresenta la variabilità residua o il rumore decisionale, è solitamente considerato comune a tutti i partecipanti, in quanto misura un errore di processo ritenuto fondamentalmente simile tra gli individui.

L’adozione di un modello a livello individuale offre diversi vantaggi analitici. In primo luogo, consente di mappare con precisione la variabilità interindividuale nei processi cognitivi sottostanti l’aggiornamento degli obiettivi. In secondo luogo, permette di identificare profili comportamentali distinti, come, ad esempio, soggetti altamente reattivi al feedback contrapposti ad altri che mostrano un adattamento più contenuto. Infine, questo modello evita l’assunzione, spesso irrealistica, che tutti i partecipanti rispondano agli stimoli ambientali in modo identico e uniforme.

Tuttavia, è necessario notare che il modello a livello individuale, nella sua forma pura, non incorpora alcun meccanismo di “condivisione delle informazioni” tra i soggetti. Ogni partecipante viene modellato in modo completamente indipendente dagli altri. È proprio questa caratteristica a distinguerlo dal modello gerarchico (o multilevel), nel quale i parametri individuali sono concettualizzati come provenienti da una distribuzione di gruppo sovraordinata. Questa struttura gerarchica, che verrà esaminata in seguito, migliora notevolmente la robustezza e l’affidabilità delle stime, soprattutto quando si lavora con serie di dati limitate o particolarmente rumorose.

39.1.1 Preparazione dei dati

# Caricamento del dataset
dat <- rio::import("data/goal_data.csv")

# Ordina i dati per soggetto e per trial
dat <- dat |> 
  arrange(subject, trial)

# (Opzionale) Verifica che l'ordinamento sia corretto
str(dat)
#> 'data.frame':    600 obs. of  5 variables:
#>  $ subject    : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ condition  : chr  "approach" "approach" "approach" "approach" ...
#>  $ goal       : int  2 2 2 4 4 2 2 4 2 4 ...
#>  $ performance: int  0 2 2 4 2 0 4 2 4 4 ...
#>  $ trial      : int  1 2 3 4 5 6 7 8 9 10 ...

table(dat$subject)  # restituisce il numero di trial per soggetto
#> 
#>  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 
#> 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 
#> 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 
#> 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 
#> 53 54 55 56 57 58 59 60 
#> 10 10 10 10 10 10 10 10

Standardizzazione: cosa implica

Z-score su goal e performance allinea le scale ai prior (Normal(0,1)).
Interpretazione: \(\beta\) ≈ spostamento medio per trial in unità di SD; \(\alpha\) ≈ frazione di “errore” corretta per trial.
Non mischiare scaling per sottogruppi se poi confronti condizioni: usa un’unica scala globale.

# 1) Ordina per soggetto e trial
dat <- dat %>% arrange(subject, trial)

# 2) Salva scale originali (per eventuale back-transform)
goal_mean <- mean(dat$goal, na.rm = TRUE); goal_sd <- sd(dat$goal, na.rm = TRUE)
perf_mean <- mean(dat$performance, na.rm = TRUE); perf_sd <- sd(dat$performance, na.rm = TRUE)

# 3) Standardizza
dat <- dat %>%
  mutate(
    goal_z = (goal - goal_mean) / goal_sd,
    perf_z = (performance - perf_mean) / perf_sd
  )

# 4) Lista per Stan (condition è opzionale qui: non usata nel baseline)
stan_data <- list(
  subject       = dat$subject,
  trial         = dat$trial,
  observed_goal = dat$goal_z,
  performance   = dat$perf_z,
  Nsubj         = dplyr::n_distinct(dat$subject),
  Ntotal        = nrow(dat)
)

str(stan_data)
#> List of 6
#>  $ subject      : int [1:600] 1 1 1 1 1 1 1 1 1 1 ...
#>  $ trial        : int [1:600] 1 2 3 4 5 6 7 8 9 10 ...
#>  $ observed_goal: num [1:600] -2 -2 -2 -1.07 -1.07 ...
#>  $ performance  : num [1:600] -2.89 -1.99 -1.99 -1.1 -1.99 ...
#>  $ Nsubj        : int 60
#>  $ Ntotal       : int 600

39.1.2 Definizione del modello Stan

stancode <- "
data {
  int<lower=1> Ntotal;                 // es. 600
  int<lower=1> Nsubj;                  // es. 60
  array[Ntotal] int<lower=1> subject;  // indice soggetto (1..Nsubj)
  array[Ntotal] int<lower=1> trial;    // 1..T per ciascun soggetto (ordinati)
  vector[Ntotal] observed_goal;        // Z-score
  vector[Ntotal] performance;          // Z-score
}

parameters {
  vector[Nsubj] alpha;                 // guadagno per soggetto
  vector[Nsubj] beta;                  // drift per soggetto
  real<lower=1e-6> sigma;              // dev. std residua (comune)
}

transformed parameters {
  vector[Ntotal] ghat;                 // traiettoria predetta

  for (i in 1:Ntotal) {
    if (trial[i] == 1) {
      // reset a inizio soggetto: primo stato = prima osservazione
      ghat[i] = observed_goal[i];
    } else {
      int s = subject[i];
      // ricorsione: usa predizione e performance del trial precedente (stesso soggetto se i dati sono ordinati)
      ghat[i] = ghat[i - 1]
                + alpha[s] * (performance[i - 1] - ghat[i - 1])
                + beta[s];
    }
  }
}

model {
  // Priors semplici coerenti con z-score
  alpha ~ normal(0, 1);
  beta  ~ normal(0, 1);
  sigma ~ normal(0, 1);   // half-normal(1) per via del lower bound

  // Likelihood
  observed_goal ~ normal(ghat, sigma);
}

generated quantities {
  vector[Ntotal] yrep;
  vector[Ntotal] log_lik;

  for (i in 1:Ntotal) {
    yrep[i]   = normal_rng(ghat[i], sigma);
    log_lik[i] = normal_lpdf(observed_goal[i] | ghat[i], sigma);
  }
}
"

Intuizione: a ogni trial, il soggetto confronta la propria prestazione con l’obiettivo corrente. Il parametro \(\alpha_i\) regola l’entità della correzione verso la prestazione, mentre il parametro \(\beta_i\) spinge l’obiettivo verso l’alto o verso il basso, indipendentemente dall’errore. Se \(\alpha_i\) è prossimo a 0, il soggetto è inerte; se è prossimo a 1, il soggetto è aggressivo; se \(\beta_i\) è maggiore di 0, il soggetto è ambizioso; se è minore di 0, il soggetto è in fase di de-escalation.

Questo modello presuppone che i dati siano ordinati per soggetto e per trial, altrimenti la dinamica i - 1 non corrisponde al trial precedente dello stesso soggetto.

Esaminiamo in dettaglio il significato di alpha[subject[i]] e beta[subject[i]]. Nel modello Stan, ogni trial i è associato a un determinato soggetto. Tale informazione è contenuta nel vettore:

array[Ntotal] int<lower=1> subject;

stan_data$subject
#>   [1]  1  1  1  1  1  1  1  1  1  1  2  2  2  2  2  2  2  2  2  2  3  3  3  3  3
#>  [26]  3  3  3  3  3  4  4  4  4  4  4  4  4  4  4  5  5  5  5  5  5  5  5  5  5
#>  [51]  6  6  6  6  6  6  6  6  6  6  7  7  7  7  7  7  7  7  7  7  8  8  8  8  8
#>  [76]  8  8  8  8  8  9  9  9  9  9  9  9  9  9  9 10 10 10 10 10 10 10 10 10 10
#> [101] 11 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 13 13 13 13 13
#> [126] 13 13 13 13 13 14 14 14 14 14 14 14 14 14 14 15 15 15 15 15 15 15 15 15 15
#> [151] 16 16 16 16 16 16 16 16 16 16 17 17 17 17 17 17 17 17 17 17 18 18 18 18 18
#> [176] 18 18 18 18 18 19 19 19 19 19 19 19 19 19 19 20 20 20 20 20 20 20 20 20 20
#> [201] 21 21 21 21 21 21 21 21 21 21 22 22 22 22 22 22 22 22 22 22 23 23 23 23 23
#> [226] 23 23 23 23 23 24 24 24 24 24 24 24 24 24 24 25 25 25 25 25 25 25 25 25 25
#> [251] 26 26 26 26 26 26 26 26 26 26 27 27 27 27 27 27 27 27 27 27 28 28 28 28 28
#> [276] 28 28 28 28 28 29 29 29 29 29 29 29 29 29 29 30 30 30 30 30 30 30 30 30 30
#> [301] 31 31 31 31 31 31 31 31 31 31 32 32 32 32 32 32 32 32 32 32 33 33 33 33 33
#> [326] 33 33 33 33 33 34 34 34 34 34 34 34 34 34 34 35 35 35 35 35 35 35 35 35 35
#> [351] 36 36 36 36 36 36 36 36 36 36 37 37 37 37 37 37 37 37 37 37 38 38 38 38 38
#> [376] 38 38 38 38 38 39 39 39 39 39 39 39 39 39 39 40 40 40 40 40 40 40 40 40 40
#> [401] 41 41 41 41 41 41 41 41 41 41 42 42 42 42 42 42 42 42 42 42 43 43 43 43 43
#> [426] 43 43 43 43 43 44 44 44 44 44 44 44 44 44 44 45 45 45 45 45 45 45 45 45 45
#> [451] 46 46 46 46 46 46 46 46 46 46 47 47 47 47 47 47 47 47 47 47 48 48 48 48 48
#> [476] 48 48 48 48 48 49 49 49 49 49 49 49 49 49 49 50 50 50 50 50 50 50 50 50 50
#> [501] 51 51 51 51 51 51 51 51 51 51 52 52 52 52 52 52 52 52 52 52 53 53 53 53 53
#> [526] 53 53 53 53 53 54 54 54 54 54 54 54 54 54 54 55 55 55 55 55 55 55 55 55 55
#> [551] 56 56 56 56 56 56 56 56 56 56 57 57 57 57 57 57 57 57 57 57 58 58 58 58 58
#> [576] 58 58 58 58 58 59 59 59 59 59 59 59 59 59 59 60 60 60 60 60 60 60 60 60 60

Ogni elemento subject[i] ci dice a quale soggetto appartiene il trial i, usando un numero intero da 1 a Nsubj. Quindi se subject[137] == 24, significa che il 137-esimo trial appartiene al soggetto 24.

Ora, se abbiamo un vettore di parametri specifici per ogni soggetto

vector[Nsubj] alpha;
vector[Nsubj] beta;

allora

alpha[subject[i]] significa: prendi il valore del parametro alpha associato al soggetto a cui appartiene il trial i;
lo stesso vale per beta[subject[i]].

Per esempio, supponiamo che

subject = [1, 1, 1, 2, 2, 3, 3]
alpha = [0.5, 0.8, 1.1]  // Tre soggetti: 1, 2, 3

allora

alpha[subject[4]] = alpha[2] = 0.8, perché il 4° trial è del soggetto 2.
beta[subject[6]] = beta[3] = ..., perché il 6° trial è del soggetto 3.

In sintesi, la sintassi alpha[subject[i]] (e beta[subject[i]]) indica: “Nel trial i, usa il valore del parametro alpha (o beta) del soggetto indicato da subject[i]”. Questo metodo consente di associare in modo compatto ogni osservazione ai parametri della persona corrispondente.

39.1.3 Compilazione ed esecuzione del modello

stanmod <- cmdstan_model(
  write_stan_file(stancode),
  compile = TRUE
)

fit1 <- stanmod$sample(
  data = stan_data,
  iter_warmup = 1000,
  iter_sampling = 5000,
  chains = 4,
  parallel_chains = 4,
  refresh = 1000,
  seed = 4790
)

39.1.4 Analisi dei risultati

Questo modello genera un insieme di campioni posteriori per i parametri \(\alpha\) e \(\beta\), uno per ciascun partecipante.

I campioni vengono estratti in formato “draws_matrix” (per tabelle riassuntive):

standraws <- fit1$draws(format = "draws_matrix")

Statistiche descrittive compatte per \(\alpha_i\), \(\beta_i\) e \(\sigma\): media, mediana e intervalli di credibilità al 95% (2.5% - 97.5%):

standraws |> 
  subset_draws(variable = c("alpha", "beta", "sigma")) |> 
  summarise_draws(
    mean,
    ~ quantile(.x, probs = c(0.025, 0.5, 0.975))
  ) |> 
  print()
#> # A tibble: 121 × 5
#>    variable   mean   `2.5%` `50%` `97.5%`
#>    <chr>     <dbl>    <dbl> <dbl>   <dbl>
#>  1 alpha[1]  0.662  0.161   0.683   1.02 
#>  2 alpha[2]  0.181 -0.265   0.178   0.595
#>  3 alpha[3]  0.167 -0.251   0.186   0.507
#>  4 alpha[4]  0.300 -0.515   0.303   0.950
#>  5 alpha[5]  0.400  0.0561  0.399   0.744
#>  6 alpha[6]  0.586 -0.00103 0.613   1.04 
#>  7 alpha[7]  0.408  0.121   0.406   0.750
#>  8 alpha[8]  0.119 -0.0767  0.109   0.343
#>  9 alpha[9]  0.487  0.00886 0.487   0.927
#> 10 alpha[10] 0.811  0.440   0.811   1.11 
#> # ℹ 111 more rows

Checklist rapida

R-hat ≤ 1.01 e ESS > 400? ✓
Traceplot senza “stallo”? ✓
Posterior di \(\sigma\) non schiacciata verso 0? ✓

# Se qualche Rhat > 1.01 o ESS basso, considerare run più lunghi o reparametrizzazioni
fit1$summary(variables = c("alpha", "beta", "sigma")) |>
  dplyr::select(variable, rhat, ess_bulk, ess_tail) |>
  dplyr::arrange(dplyr::desc(rhat)) |>
  print(n = 10)
#> # A tibble: 121 × 4
#>    variable   rhat ess_bulk ess_tail
#>    <chr>     <dbl>    <dbl>    <dbl>
#>  1 alpha[34]  1.18     15.0     10.9
#>  2 beta[47]   1.17     15.8     17.1
#>  3 beta[34]   1.17     15.6     11.2
#>  4 alpha[47]  1.16     16.8     17.2
#>  5 beta[46]   1.16     17.0     18.5
#>  6 beta[56]   1.14     19.0     26.8
#>  7 alpha[56]  1.14     19.4     43.0
#>  8 beta[40]   1.12     21.2     71.7
#>  9 beta[32]   1.12     20.4     22.4
#> 10 beta[26]   1.12     20.7     27.6
#> # ℹ 111 more rows

Estrazione “tidy” dei parametri a livello di persona con la funzione tidybayes::spread_draws. Questo produce le colonne: .draw, subject, alpha, beta.

posteriors_person = spread_draws(fit1, alpha[subject], beta[subject])

Calcolo della media e dell’intervallo di credibilità al 95% per ciascun soggetto:

# Calcolo media e intervallo credibile al 95% per ciascun soggetto
CIs_person <- posteriors_person %>%
  group_by(subject) %>%
  summarise(
    across(c(alpha, beta), list(
      lower = ~quantile(.x, 0.025),
      mean  = ~mean(.x),
      upper = ~quantile(.x, 0.975)
    ), .names = "{.col}_{.fn}")
  ) %>%
  arrange(alpha_mean) %>%
  mutate(alpha_order = row_number()) %>%
  arrange(beta_mean) %>%
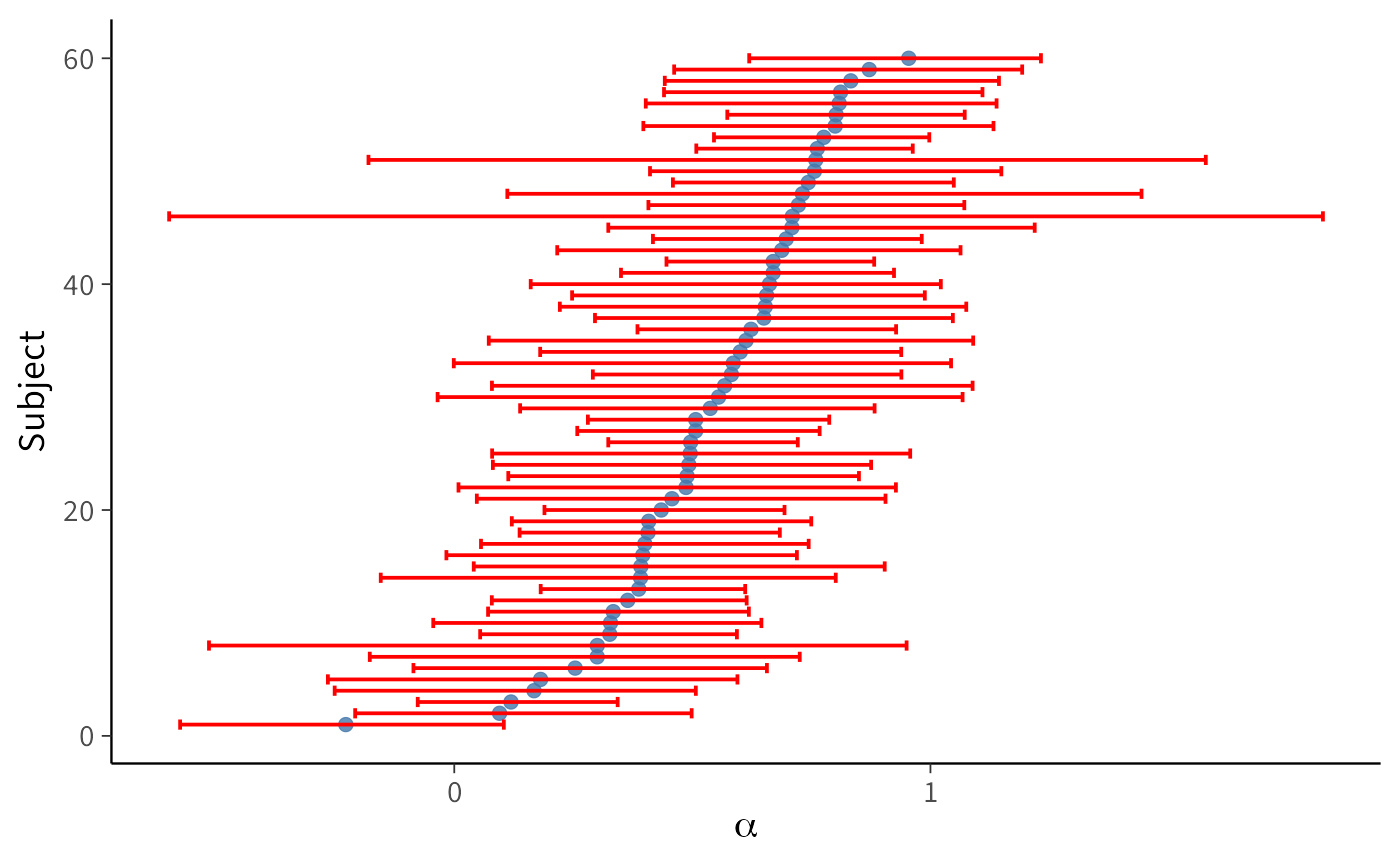
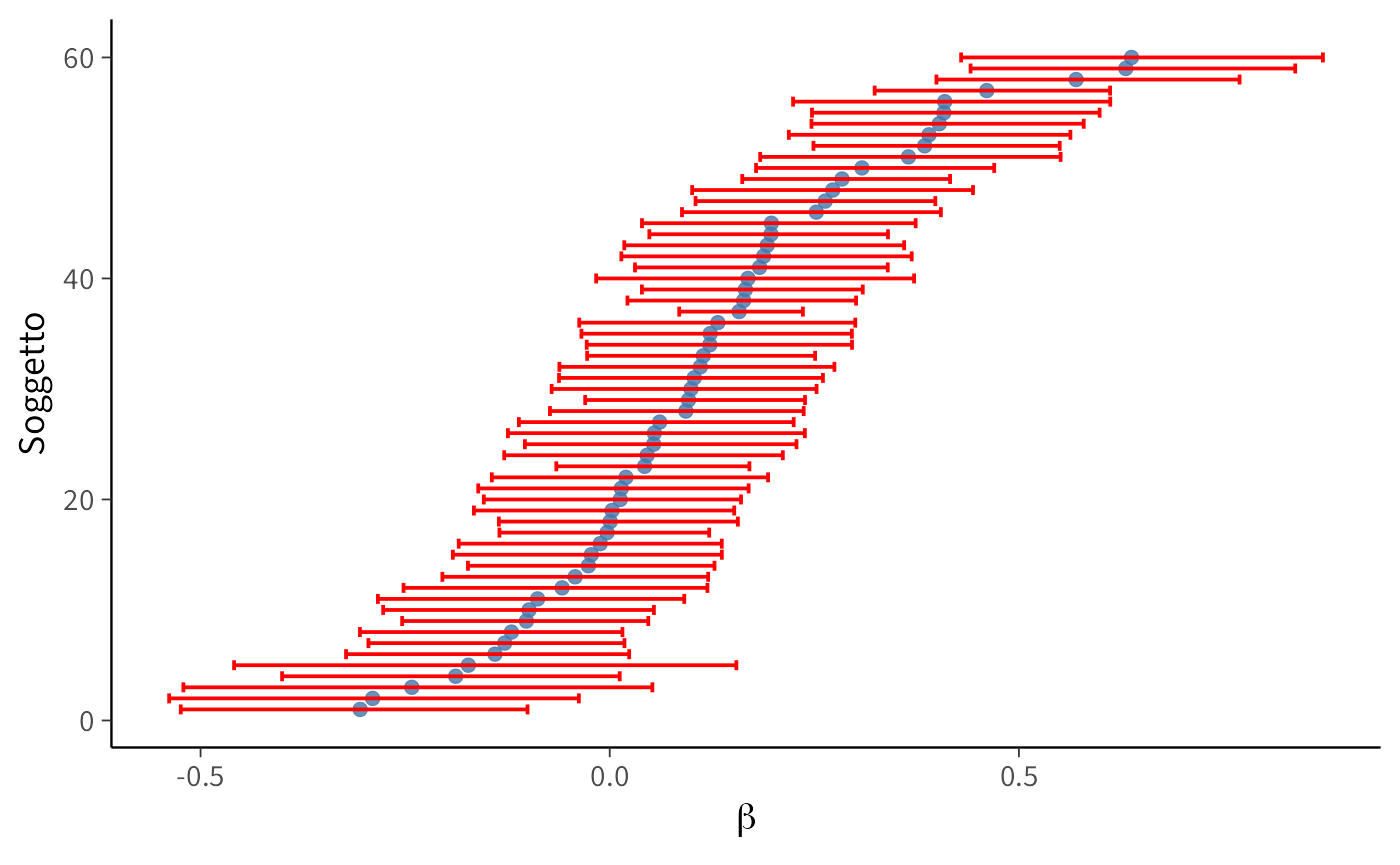
  mutate(beta_order = row_number())

Grafico 1: CI al 95% per \(\alpha_i\), ordinati per alpha_mean:

plot_person_alpha <- ggplot(data = CIs_person) +
  geom_point(aes(y = alpha_order, x = alpha_mean)) +
  geom_errorbar(
    aes(y = alpha_order, xmin = alpha_lower, xmax = alpha_upper),
    orientation = "y"
  ) +
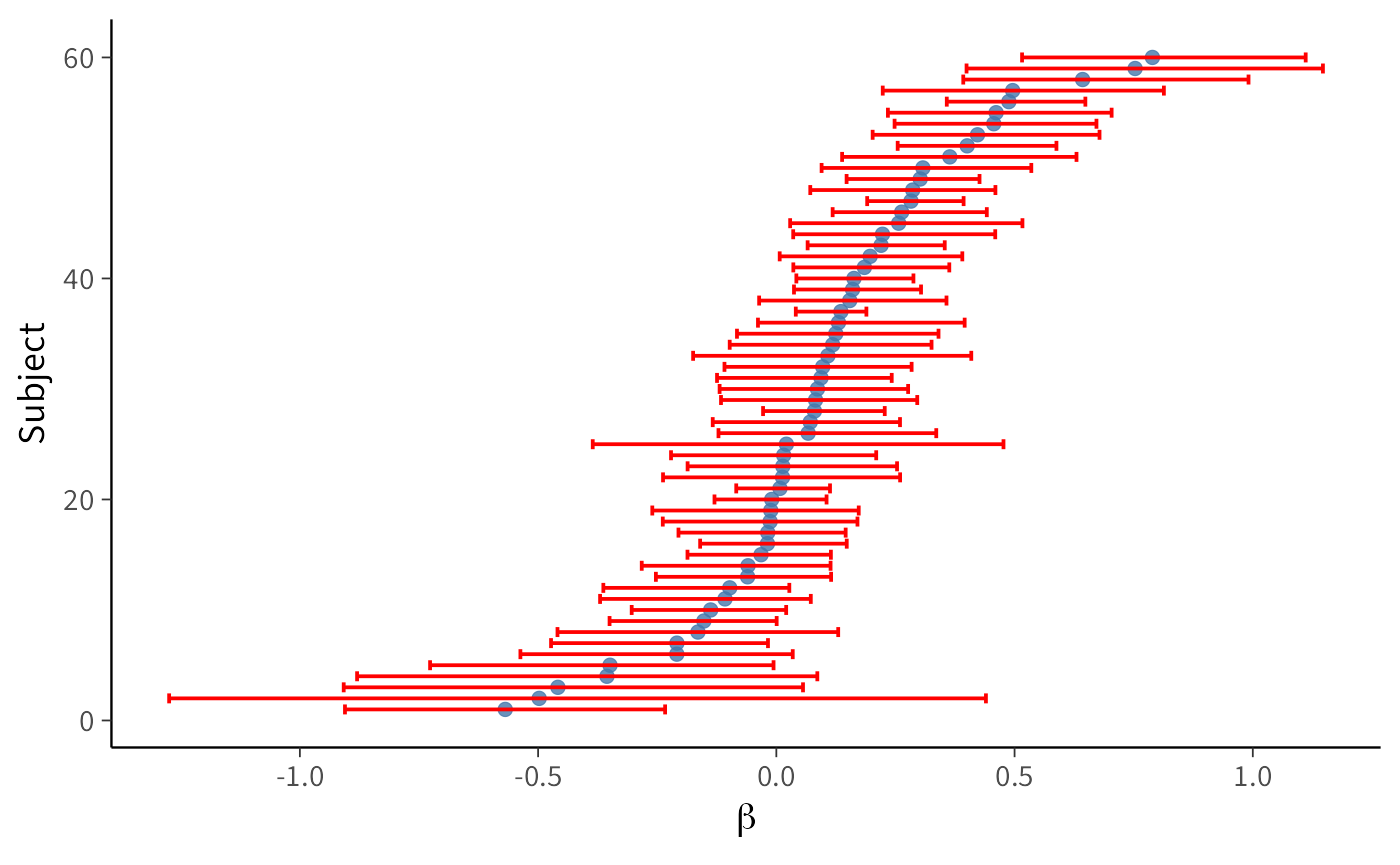
  labs(x = expression(alpha), y = "Subject")

Grafico 2: CI al 95% per \(\beta_i\), ordinati per beta_mean:

plot_person_beta <- ggplot(data = CIs_person) +
  geom_point(aes(y = beta_order, x = beta_mean)) +
  geom_errorbar(
    aes(y = beta_order, xmin = beta_lower, xmax = beta_upper),
    orientation = "y"
  ) +
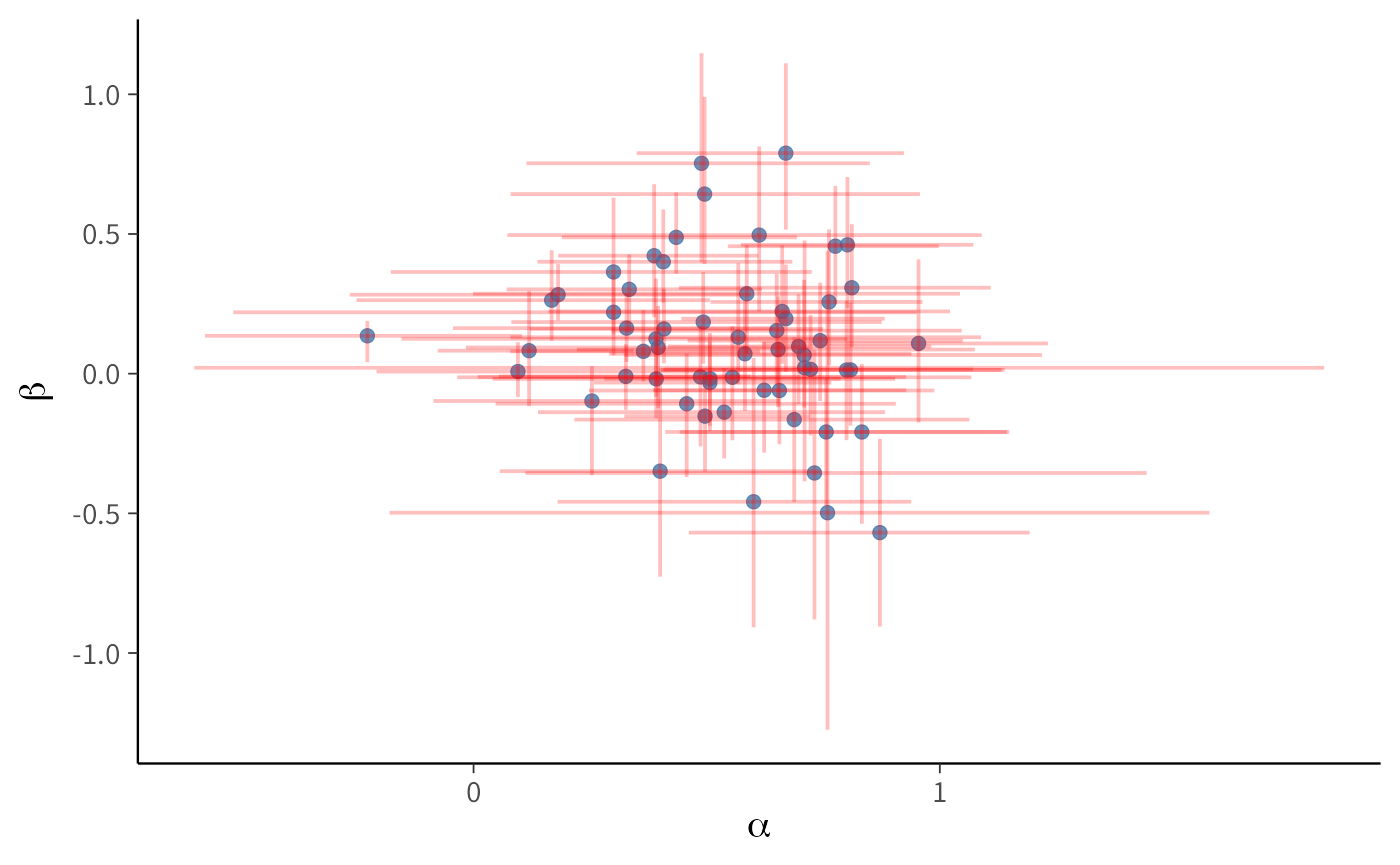
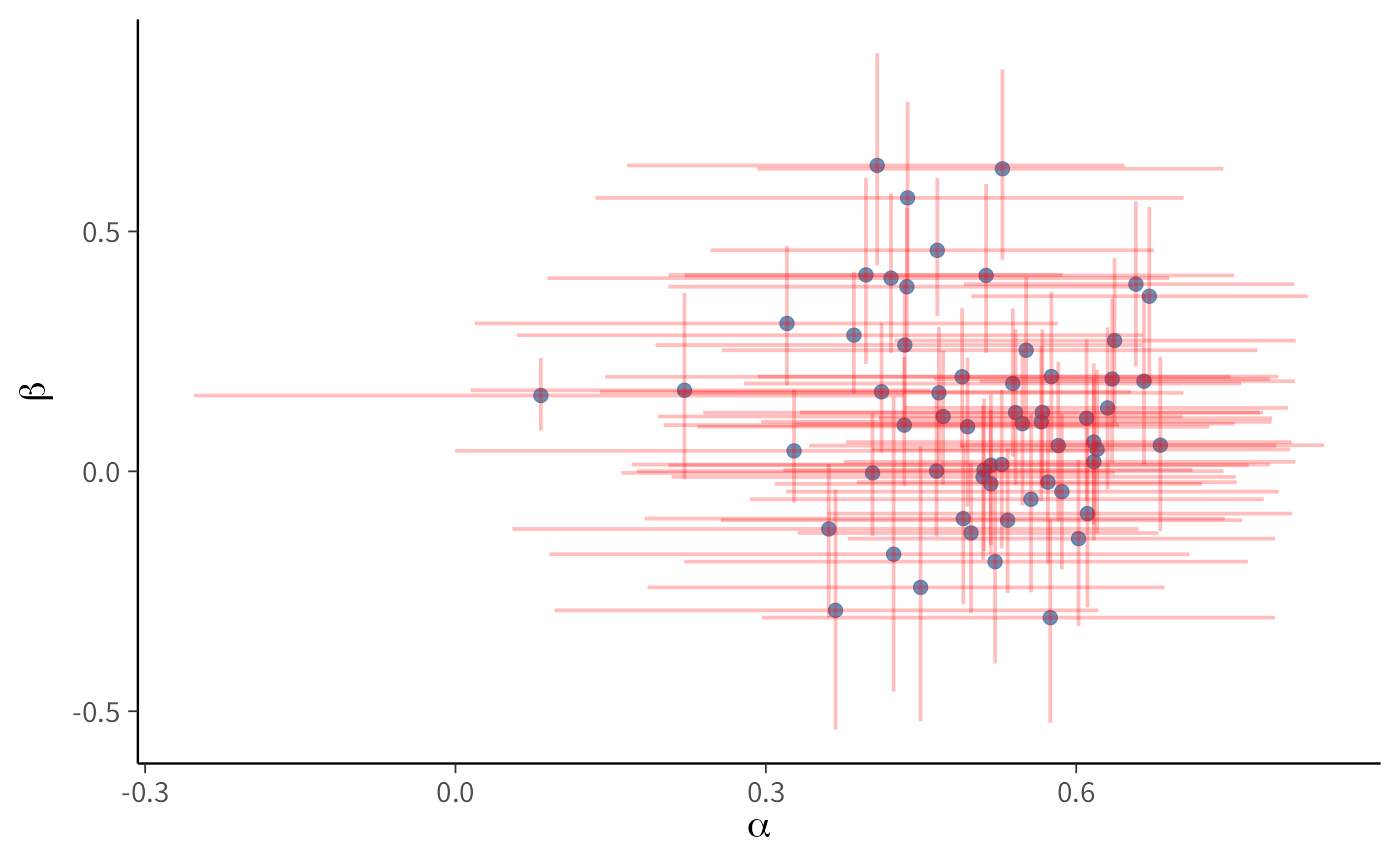
  labs(x = expression(beta), y = "Subject")

Grafico 3: Dispersione bivariata (alpha_mean vs beta_mean) + croci di CI 95%. Le barre verticali e orizzontali forniscono un’istantanea della (co)variabilità individuale:

plot_person_alphabeta <- ggplot(data = CIs_person) +
  geom_point(aes(x = alpha_mean, y = beta_mean)) +
  geom_errorbar(
    aes(x = alpha_mean, ymin = beta_lower, ymax = beta_upper),
    alpha = 0.25
  ) +
  geom_errorbar(
    aes(y = beta_mean, xmin = alpha_lower, xmax = alpha_upper),
    alpha = 0.25,
    orientation = "y"
  ) +
  labs(x = expression(alpha), y = expression(beta))

I grafici mostrano una marcata eterogeneità tra i partecipanti per quanto riguarda i parametri \(\alpha\) (tasso di apprendimento) e \(\beta\) (drift motivazionale), con intervalli di credibilità al 95% calcolati per ciascun \(\alpha_i\) e \(\beta_i\).

Per quanto riguarda \(\alpha\), i partecipanti mostrano valori distribuiti lungo quasi tutto l’intervallo [0,1]. Alcuni soggetti hanno un valore di \(\alpha\) molto vicino a 0 (bassa sensibilità al feedback), mentre altri si avvicinano a 1 (forte aggiornamento in risposta all’errore). L’ampiezza degli intervalli di credibilità varia, ma nella maggior parte dei casi fornisce stime sufficientemente informative.

Per quanto riguarda \(\beta\), i valori si distribuiscono attorno a 0, ma con marcate differenze individuali: alcuni soggetti mostrano un drift positivo (tendenza ad aumentare sistematicamente gli obiettivi), altri un drift negativo (tendenza a ridurli). Gli intervalli di credibilità confermano questa eterogeneità.

Il punto chiave è che questa variabilità non può essere colta dal modello sample-level. Infatti, stimando un unico \(\alpha\) e un unico \(\beta\) comuni a tutti, restituisce una sorta di “media” del comportamento dei partecipanti. In pratica:

un soggetto con \(\alpha \approx 0\) e uno con \(\alpha \approx 0.9\) verrebbero descritti dallo stesso parametro \(\alpha\), che potrebbe cadere a metà strada, ma non rappresenterebbe bene né l’uno né l’altro;
allo stesso modo, le derive motivazionali individuali \(\beta\) (positive, negative o vicine a zero) verrebbero tutte appiattite su un valore medio.

I grafici dimostrano quindi l’utilità del modello a livello individuale: esso permette di mappare differenze sostanziali tra i soggetti, che nel modello a livello di campione vengono perse.

In sintesi:

il modello sample-level offre una descrizione parsimoniosa, ma rischia di mascherare differenze psicologicamente rilevanti;
il modello person-level mostra che i partecipanti non solo differiscono per il grado di apprendimento dal feedback (\(\alpha\)), ma anche per la direzione e l’intensità della deriva motivazionale (\(\beta\));
questa eterogeneità costituisce un’informazione preziosa per comprendere i profili comportamentali individuali, impossibile da cogliere con un modello che assume parametri omogenei per l’intero campione.

39.2 Modello gerarchico

Il modello a livello individuale (person-level) stima parametri distinti \((\alpha_i, \beta_i)\) per ogni partecipante \(i\). In questa formulazione, ogni individuo possiede il proprio tasso di apprendimento \(\alpha_i\) e la propria deriva motivazionale \(\beta_i\), il che consente di mappare la variabilità interindividuale nei processi di aggiornamento degli obiettivi e di identificare profili comportamentali distinti. Il parametro \(\sigma\), che cattura la variabilità residua (rumore decisionale), rimane comune a tutti i soggetti in questa versione di base, ma può essere esteso a varianze specifiche per ciascun soggetto quando necessario.

Sebbene la stima separata dei parametri per ogni partecipante rappresenti un passo avanti nel riconoscere le differenze individuali, questo approccio presenta un limite cruciale: le stime restano concettualmente e statisticamente isolate. Analizzare i dati “soggetto per soggetto” equivale a condurre una serie di analisi indipendenti, senza riutilizzare l’informazione presente nel resto del campione.

Questa frammentazione ha tre conseguenze sfavorevoli:

riduce il potere statistico, perché ogni stima utilizza solo una frazione dei dati totali;
aumenta la variabilità delle stime, soprattutto quando il numero di osservazioni per soggetto è esiguo;
complica la generalizzazione a livello di popolazione, rendendo meno solide le conclusioni aggregate.

Un sintomo tipico è la presenza, per molti soggetti, di intervalli di credibilità molto ampi o di posteriori multi-modali su \(\alpha_i\) e/o su \(\beta_i\): segnali di informazione locale insufficiente e, talvolta, di non-identificabilità in specifiche regioni dello spazio dei parametri.

È in questo contesto che i modelli gerarchici mostrano il loro valore, “prestando” l’informazione a livello di popolazione per regolarizzare le stime individuali ed evitare valori estremi non supportati dai dati. I modelli gerarchici bayesiani (o multilevel) concettualizzano i parametri individuali non come entità indipendenti, ma come realizzazioni di una distribuzione di gruppo sovraordinata. In pratica, si introduce un pooling parziale: i parametri specifici del soggetto vengono tirati verso la tendenza della popolazione nella misura in cui i loro dati sono poco informativi.

Formalmente, \[ \alpha_i \sim \mathcal{N}(\mu_\alpha,\ \tau_\alpha^2),\qquad \beta_i \sim \mathcal{N}(\mu_\beta,\ \tau_\beta^2), \] dove \((\mu_\alpha,\tau_\alpha)\) e \((\mu_\beta,\tau_\beta)\) sono iperparametri che descrivono la popolazione. Questa struttura consente di bilanciare in modo ottimale le idiosincrasie individuali e le regolarità aggregate (Kruschke & Vanpaemel, 2015; Turner et al., 2013; Vincent, 2016). Il risultato è una regolarizzazione: le stime estreme vengono attenuate (shrinkage) verso la media della popolazione, riducendo il peso delle stime instabili o rumorose e producendo inferenze più robuste e interpretabili, specialmente con campioni piccoli o pochi trial per soggetto (Boehm et al., 2018; Rouder & Lu, 2005).

Intuizione: più i dati del soggetto \(i\) sono informativi, meno la stima di \((\alpha_i,\beta_i)\) viene “tirata” verso \((\mu_\alpha,\mu_\beta)\); con dati scarsi/rumorosi, lo shrinkage aumenta e protegge dall’overfitting.

39.2.1 Definizione del modello Stan

stancode <- "
data {
  int<lower=1> Ntotal;
  int<lower=1> Nsubj;
  array[Ntotal] int<lower=1> subject;
  array[Ntotal] int<lower=1> trial;
  vector[Ntotal] observed_goal;   // z-score
  vector[Ntotal] performance;     // z-score
}

parameters {
  // Iper-parametri di popolazione
  real alpha_mean;
  real<lower=0> alpha_sd;
  real beta_mean;
  real<lower=0> beta_sd;

  // Non-centrato: fattori standard per i soggetti
  vector[Nsubj] alpha_raw;
  vector[Nsubj] beta_raw;

  real<lower=1e-6> sigma;
}

transformed parameters {
  // Ricostruzione parametri individuali
  vector[Nsubj] alpha_unconstrained = alpha_mean + alpha_sd * alpha_raw;
  vector[Nsubj] beta  = beta_mean  + beta_sd  * beta_raw;

  // Vincolo morbido su alpha per stabilità
  vector[Nsubj] alpha = 0.95 * tanh(alpha_unconstrained);

  vector[Ntotal] ghat;

  for (i in 1:Ntotal) {
    if (trial[i] == 1) {
      ghat[i] = observed_goal[i];
    } else {
      int s = subject[i];
      ghat[i] = ghat[i - 1]
                + alpha[s] * (performance[i - 1] - ghat[i - 1])
                + beta[s];
    }
  }
}

model {
  // Iper-priori debolmente informativi (coerenti con z-score)
  alpha_mean ~ normal(0, 0.5);
  alpha_sd   ~ exponential(1);
  beta_mean  ~ normal(0, 0.5);
  beta_sd    ~ exponential(1);

  alpha_raw  ~ normal(0, 1);
  beta_raw   ~ normal(0, 1);

  sigma ~ student_t(3, 0, 0.5);

  // Likelihood
  observed_goal ~ normal(ghat, sigma);
}

generated quantities {
  vector[Ntotal] yrep;
  vector[Ntotal] log_lik;
  for (i in 1:Ntotal) {
    yrep[i]    = normal_rng(ghat[i], sigma);
    log_lik[i] = normal_lpdf(observed_goal[i] | ghat[i], sigma);
  }
}
"

Parametrizzazione tramite tanh per il tasso di apprendimento

La scelta di modellare il tasso di apprendimento \(\alpha\) mediante una trasformazione “tanh” (iperbolica tangente) è motivata da considerazioni sia teoriche che pratiche.

Dal punto di vista del modello dinamico, la stabilità del processo di aggiornamento ricorsivo richiede che il parametro \(\alpha\) si trovi nell’intervallo (0, 2). Tuttavia, quando si lavora con dati standardizzati, pratica comune per migliorare la convergenza degli algoritmi, è preferibile contenere \(\alpha\) in un intervallo più ristretto, tipicamente \((-1, 1),\) al fine di evitare aggiornamenti eccessivi che potrebbero destabilizzare le stime.

La funzione tanh fornisce una soluzione elegante a questo requisito, mappando in modo continuo e differenziabile qualsiasi valore reale (ad esempio, il valore di un parametro latente non vincolato) nell’intervallo (-1, 1). L’applicazione di un fattore moltiplicativo di 0.95 applicato all’output di tanh (cioè \(\alpha = 0.95 \cdot \text{tanh}(\cdot)\)) introduce un ulteriore margine di sicurezza numerica, ritirandosi leggermente dai limiti estremi dell’intervallo. Questa contrazione marginale si è rivelata efficace nel ridurre il verificarsi di divergenze durante il campionamento con la tecnica di Hamilton Monte Carlo (HMC), migliorando la stabilità e l’efficienza computazionale dell’inferenza.

Questa parametrizzazione garantisce quindi che i valori di \(\alpha\) siano sempre ben definiti e gestibili dal punto di vista numerico, facilitando un processo inferenziale robusto ed efficiente.

39.2.2 Differenza chiave rispetto al modello precedente

Nel Person-Level Model i parametri individuali sono stimati in modo indipendente, mentre qui valgono relazioni del tipo:

\[ \alpha_s \sim \mathcal{N}(\alpha_{\text{mean}}, \alpha_{\text{sd}}), \quad \beta_s \sim \mathcal{N}(\beta_{\text{mean}}, \beta_{\text{sd}}). \]

Questa struttura gerarchica introduce un vincolo statistico che collega i soggetti, generando un duplice vantaggio metodologico. Da un lato, essa preserva le differenze individuali, evitando l’assunzione irrealistica di parametri identici per tutti i partecipanti. Dall’altro lato, sfrutta sistematicamente le somiglianze tra i soggetti per ottenere stime più robuste a livello individuale e inferenze più precise sulla popolazione di riferimento.

39.2.3 Compilazione ed esecuzione

stanmod <- cmdstan_model(
  write_stan_file(stancode),
  compile = TRUE
)

fit2 <- stanmod$sample(
  data = stan_data,
  iter_warmup = 1000,
  iter_sampling = 4000,
  chains = 4, parallel_chains = 4,
  seed = 4790,
  refresh = 500,
  adapt_delta = 0.995,  # riduce divergenze
  max_treedepth = 15
)

39.2.4 Analisi dei risultati

Eseguiamo l’analisi dei risultati seguendo lo schema usato sopra.

# Estrazione dei campioni posteriori come matrice 
standraws <- fit2$draws(format = "draws_matrix")

# Statistiche descrittive aggregate
standraws |> 
  subset_draws(variable = c("alpha", "beta", "sigma", "alpha_mean", "beta_mean", "alpha_sd", "beta_sd")) |> 
  summarise_draws(
    mean,
    ~ quantile(.x, probs = c(0.025, 0.5, 0.975))
  )
#> # A tibble: 125 × 5
#>    variable   mean `2.5%` `50%` `97.5%`
#>    <chr>     <dbl>  <dbl> <dbl>   <dbl>
#>  1 alpha[1]  0.576 0.292  0.587   0.795
#>  2 alpha[2]  0.385 0.0594 0.393   0.664
#>  3 alpha[3]  0.320 0.0187 0.328   0.582
#>  4 alpha[4]  0.490 0.145  0.505   0.749
#>  5 alpha[5]  0.367 0.0957 0.371   0.621
#>  6 alpha[6]  0.552 0.257  0.563   0.775
#>  7 alpha[7]  0.467 0.215  0.471   0.704
#>  8 alpha[8]  0.221 0.0149 0.216   0.459
#>  9 alpha[9]  0.510 0.209  0.520   0.754
#> 10 alpha[10] 0.637 0.425  0.644   0.812
#> # ℹ 115 more rows

# Estrai le draw per i parametri individuali (alpha e beta per ciascun soggetto)
posteriors_person <- spread_draws(fit2, alpha[subject], beta[subject])

# Calcolo degli intervalli credibili per ciascun soggetto
CIs_person <- posteriors_person %>%
  group_by(subject) %>%
  summarise(
    across(c(alpha, beta), list(
      lower = ~quantile(.x, 0.025),
      mean  = ~mean(.x),
      upper = ~quantile(.x, 0.975)
    ), .names = "{.col}_{.fn}")
  ) %>%
  arrange(alpha_mean) %>%
  mutate(alpha_order = row_number()) %>%
  arrange(beta_mean) %>%
  mutate(beta_order = row_number())

# Grafico: intervalli credibili per alpha
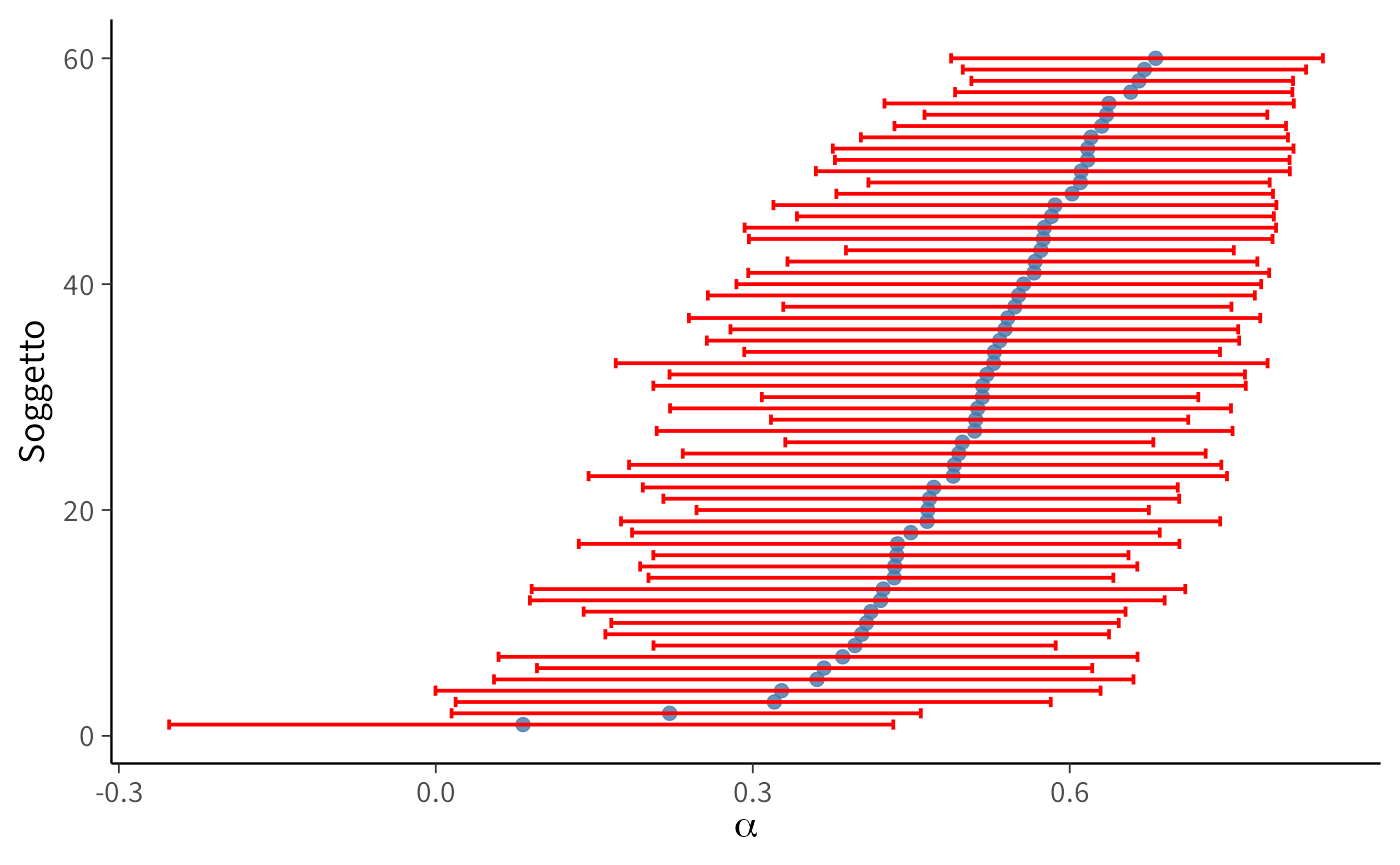
plot_person_alpha <- ggplot(CIs_person) +
  geom_point(aes(y = alpha_order, x = alpha_mean)) +
  geom_errorbar(
    aes(y = alpha_order, xmin = alpha_lower, xmax = alpha_upper),
    orientation = "y"
  ) +
  labs(x = expression(alpha), y = "Soggetto")

# Grafico: intervalli credibili per beta
plot_person_beta <- ggplot(CIs_person) +
  geom_point(aes(y = beta_order, x = beta_mean)) +
  geom_errorbar(
    aes(y = beta_order, xmin = beta_lower, xmax = beta_upper),
    orientation = "y"
  ) +
  labs(x = expression(beta), y = "Soggetto")

# Grafico: relazione tra alpha e beta per ciascun soggetto
plot_person_alphabeta <- ggplot(CIs_person) +
  geom_point(aes(x = alpha_mean, y = beta_mean)) +
  geom_errorbar(
    aes(x = alpha_mean, ymin = beta_lower, ymax = beta_upper),
    alpha = 0.25
  ) +
  geom_errorbar(
    aes(y = beta_mean, xmin = alpha_lower, xmax = alpha_upper),
    alpha = 0.25,
    orientation = "y"
  ) +
  labs(x = expression(alpha), y = expression(beta))

Infine, calcoliamo le stime a posteriori degli iper-parametri:

# Riassunto per alpha_mean e beta_mean con intervallo al 95%
standraws |>
  subset_draws(variable = c("alpha_mean", "beta_mean")) |>
  summarise_draws(
    mean,
    ~quantile(.x, probs = c(0.025, 0.975))
  )
#> # A tibble: 2 × 4
#>   variable    mean `2.5%` `97.5%`
#>   <chr>      <dbl>  <dbl>   <dbl>
#> 1 alpha_mean 0.621 0.521    0.732
#> 2 beta_mean  0.114 0.0495   0.176

39.2.4.1 Interpretazione

Il modello gerarchico bayesiano fornisce inferenze a due livelli:

Livello individuale: parametri \(\alpha_s\) e \(\beta_s\) per ciascun partecipante, con i relativi intervalli di credibilità.
Livello di popolazione: distribuzioni a priori/posteriori degli iperparametri \(\alpha_{\text{mean}}, \alpha_{\text{sd}}, \beta_{\text{mean}}, \beta_{\text{sd}}\) e del parametro residuo \(\sigma\).

I grafici relativi a \(\alpha\) e \(\beta\) evidenziano chiaramente l’eterogeneità interindividuale, mentre gli iperparametri descrivono la tendenza generale.

Rispetto a un modello puramente individuale, gli intervalli di credibilità delle stime soggettive risultano meno dispersi e più regolari. Questo fenomeno è noto come “shrinkage”: le stime dei singoli soggetti sono “attirate” verso la media della popolazione, riducendo l’impatto dei dati rumorosi o scarsi.

Nel grafico bivariato, lo shrinkage si traduce in una distribuzione più compatta dei punti attorno al centro della distribuzione collettiva. L’effetto principale è una maggiore robustezza delle inferenze: le stime estreme vengono mitigate, la variabilità non plausibile è penalizzata e la capacità di generalizzare a nuovi dati risulta rafforzata (Boehm et al., 2018).

39.3 Differenze tra i gruppi

In questo terzo modello, estendiamo la struttura gerarchica introducendo le condizioni sperimentali (approach vs avoidance). L’idea è che i parametri individuali \(\alpha_s\) e \(\beta_s\) non siano estratti da una distribuzione comune, ma da distribuzioni diverse a seconda del gruppo di appartenenza del soggetto.

In questo modo, per ciascuna condizione, è possibile stimare una media e una deviazione standard a livello di popolazione:

\(\alpha_{\text{mean},c}\) e \(\alpha_{\text{sd},c}\);
\(\beta_{\text{mean},c}, \beta_{\text{sd},c}\) con \(c \in \{1,2\}\);

39.3.1 Preparazione dei dati

# 1) Ordina per soggetto e trial
dat <- dat %>% arrange(subject, trial)

# 2) Codifica la condizione come intero (1 = approach, 2 = avoidance)
dat <- dat %>%
  mutate(cond_id = as.integer(factor(condition)))

# Verifica che ogni soggetto appartenga a una sola condizione
chk <- dat %>% distinct(subject, cond_id) %>% count(subject) %>% filter(n > 1)
stopifnot(nrow(chk) == 0)  # se fallisce, il design non è between-subject

# 3) Standardizza goal e performance su tutto il dataset
goal_mean <- mean(dat$goal, na.rm = TRUE); goal_sd <- sd(dat$goal, na.rm = TRUE)
perf_mean <- mean(dat$performance, na.rm = TRUE); perf_sd <- sd(dat$performance, na.rm = TRUE)

dat <- dat %>%
  mutate(
    goal_z = (goal - goal_mean) / goal_sd,
    perf_z = (performance - perf_mean) / perf_sd
  )

# 4) Vettore che assegna a ciascun soggetto la sua condizione
subjects <- sort(unique(dat$subject))
subj_cond <- dat %>%
  group_by(subject) %>%
  summarise(cond = first(cond_id), .groups = "drop") %>%
  arrange(subject) %>%
  pull(cond)

# 5) Lista per Stan
stan_data <- list(
  Ntotal        = nrow(dat),
  Nsubj         = length(subjects),
  C             = length(unique(dat$cond_id)),   # numero condizioni
  subject       = dat$subject,
  trial         = dat$trial,
  observed_goal = dat$goal_z,
  performance   = dat$perf_z,
  subj_cond     = subj_cond
)

str(stan_data)
#> List of 8
#>  $ Ntotal       : int 600
#>  $ Nsubj        : int 60
#>  $ C            : int 2
#>  $ subject      : int [1:600] 1 1 1 1 1 1 1 1 1 1 ...
#>  $ trial        : int [1:600] 1 2 3 4 5 6 7 8 9 10 ...
#>  $ observed_goal: num [1:600] -2 -2 -2 -1.07 -1.07 ...
#>  $ performance  : num [1:600] -2.89 -1.99 -1.99 -1.1 -1.99 ...
#>  $ subj_cond    : int [1:60] 1 2 2 1 2 1 2 1 2 1 ...

39.3.2 Definizione del modello Stan

stancode <- "
// Modello gerarchico con iper-parametri specifici per condizione
data {
  int<lower=1> Ntotal;
  int<lower=1> Nsubj;
  int<lower=1> C;                            // numero condizioni
  array[Ntotal] int<lower=1> subject;        // 1..Nsubj
  array[Ntotal] int<lower=1> trial;          // 1..T all'interno di soggetto
  vector[Ntotal] observed_goal;              // z-score
  vector[Ntotal] performance;                // z-score
  array[Nsubj] int<lower=1, upper=C> subj_cond; // condizione per soggetto
}

parameters {
  // Iper-parametri per condizione
  vector[C] alpha_mean;
  vector<lower=0>[C] alpha_sd;
  vector[C] beta_mean;
  vector<lower=0>[C] beta_sd;

  // Non-centrato: fattori standard per soggetti
  vector[Nsubj] alpha_raw;
  vector[Nsubj] beta_raw;

  real<lower=1e-6> sigma;
}

transformed parameters {
  vector[Nsubj] alpha_uncon;
  vector[Nsubj] beta;
  vector[Nsubj] alpha;           
  vector[Ntotal] ghat;

  // Ricostruzione dei parametri individuali in base alla condizione
  for (s in 1:Nsubj) {
    int c = subj_cond[s];
    alpha_uncon[s] = alpha_mean[c] + alpha_sd[c] * alpha_raw[s];
    beta[s]        = beta_mean[c]  + beta_sd[c]  * beta_raw[s];
    alpha[s]       = 0.95 * tanh(alpha_uncon[s]); // vincolo di stabilità
  }

  // Dinamica
  for (i in 1:Ntotal) {
    if (trial[i] == 1) {
      ghat[i] = observed_goal[i];
    } else {
      int s = subject[i];
      ghat[i] = ghat[i - 1]
                + alpha[s] * (performance[i - 1] - ghat[i - 1])
                + beta[s];
    }
  }
}

model {
  // Iper-priori debolmente informativi
  alpha_mean ~ normal(0, 0.5);
  alpha_sd   ~ exponential(1);
  beta_mean  ~ normal(0, 0.5);
  beta_sd    ~ exponential(1);

  alpha_raw  ~ normal(0, 1);
  beta_raw   ~ normal(0, 1);

  sigma ~ student_t(3, 0, 0.5);

  // Likelihood
  observed_goal ~ normal(ghat, sigma);
}

generated quantities {
  vector[Ntotal] yrep;
  vector[Ntotal] log_lik;
  for (i in 1:Ntotal) {
    yrep[i]    = normal_rng(ghat[i], sigma);
    log_lik[i] = normal_lpdf(observed_goal[i] | ghat[i], sigma);
  }
}
"

39.3.3 Come funziona la distinzione tra i gruppi

Assegnazione della condizione. Nel blocco data, il vettore subj_cond assegna a ciascun soggetto il numero della condizione (1 = approach, 2 = avoidance).
Parametri di gruppo. Gli iperparametri alpha_mean[c], alpha_sd[c], beta_mean[c], beta_sd[c] sono specifici per condizione. Ad esempio:
- alpha_mean[1] = media di \(\alpha\) per il gruppo approach
- alpha_mean[2] = media di \(\alpha\) per il gruppo avoidance
Parametri individuali. In transformed parameters, i parametri dei singoli soggetti vengono generati in base alla loro condizione di appartenenza. Di conseguenza, i soggetti approach e quelli avoidance condividono rispettivamente due diverse distribuzioni di partenza.

In sintesi, il modello permette di stimare non solo le differenze tra individui, ma anche le differenze sistematiche tra condizioni sperimentali.

39.3.4 Compilazione ed esecuzione

stanmod <- cmdstan_model(write_stan_file(stancode), compile = TRUE)

fit3 <- stanmod$sample(
  data = stan_data,
  iter_warmup = 1000,
  iter_sampling = 5000,
  chains = 4, parallel_chains = 4,
  seed = 123,
  adapt_delta = 0.999,   # ↑ riduce divergenze
  max_treedepth = 15
)

39.3.5 Risultati

39.3.5.1 Ispezione rapida delle variabili (opzionale)

draws_df <- as_draws_df(fit3$draws())   # oppure: fit3$draws(format = "df")
names(draws_df)[grepl("alpha_mean|beta_mean|alpha\\[|beta\\[", names(draws_df))]
#>   [1] "alpha_mean[1]" "alpha_mean[2]" "beta_mean[1]"  "beta_mean[2]" 
#>   [5] "beta[1]"       "beta[2]"       "beta[3]"       "beta[4]"      
#>   [9] "beta[5]"       "beta[6]"       "beta[7]"       "beta[8]"      
#>  [13] "beta[9]"       "beta[10]"      "beta[11]"      "beta[12]"     
#>  [17] "beta[13]"      "beta[14]"      "beta[15]"      "beta[16]"     
#>  [21] "beta[17]"      "beta[18]"      "beta[19]"      "beta[20]"     
#>  [25] "beta[21]"      "beta[22]"      "beta[23]"      "beta[24]"     
#>  [29] "beta[25]"      "beta[26]"      "beta[27]"      "beta[28]"     
#>  [33] "beta[29]"      "beta[30]"      "beta[31]"      "beta[32]"     
#>  [37] "beta[33]"      "beta[34]"      "beta[35]"      "beta[36]"     
#>  [41] "beta[37]"      "beta[38]"      "beta[39]"      "beta[40]"     
#>  [45] "beta[41]"      "beta[42]"      "beta[43]"      "beta[44]"     
#>  [49] "beta[45]"      "beta[46]"      "beta[47]"      "beta[48]"     
#>  [53] "beta[49]"      "beta[50]"      "beta[51]"      "beta[52]"     
#>  [57] "beta[53]"      "beta[54]"      "beta[55]"      "beta[56]"     
#>  [61] "beta[57]"      "beta[58]"      "beta[59]"      "beta[60]"     
#>  [65] "alpha[1]"      "alpha[2]"      "alpha[3]"      "alpha[4]"     
#>  [69] "alpha[5]"      "alpha[6]"      "alpha[7]"      "alpha[8]"     
#>  [73] "alpha[9]"      "alpha[10]"     "alpha[11]"     "alpha[12]"    
#>  [77] "alpha[13]"     "alpha[14]"     "alpha[15]"     "alpha[16]"    
#>  [81] "alpha[17]"     "alpha[18]"     "alpha[19]"     "alpha[20]"    
#>  [85] "alpha[21]"     "alpha[22]"     "alpha[23]"     "alpha[24]"    
#>  [89] "alpha[25]"     "alpha[26]"     "alpha[27]"     "alpha[28]"    
#>  [93] "alpha[29]"     "alpha[30]"     "alpha[31]"     "alpha[32]"    
#>  [97] "alpha[33]"     "alpha[34]"     "alpha[35]"     "alpha[36]"    
#> [101] "alpha[37]"     "alpha[38]"     "alpha[39]"     "alpha[40]"    
#> [105] "alpha[41]"     "alpha[42]"     "alpha[43]"     "alpha[44]"    
#> [109] "alpha[45]"     "alpha[46]"     "alpha[47]"     "alpha[48]"    
#> [113] "alpha[49]"     "alpha[50]"     "alpha[51]"     "alpha[52]"    
#> [117] "alpha[53]"     "alpha[54]"     "alpha[55]"     "alpha[56]"    
#> [121] "alpha[57]"     "alpha[58]"     "alpha[59]"     "alpha[60]"

39.3.5.2 Differenze tra condizioni sugli iper-parametri

L’obiettivo è verificare se i parametri di popolazione \(\alpha\) (tasso di aggiornamento) e \(\beta\) (drift/tendenza) differiscono tra le due condizioni sperimentali (approach vs avoidance). Per rispondere a questa domanda procediamo in quattro passaggi:

recuperiamo le etichette delle condizioni dal dataset;
calcoliamo il contrasto tra condizioni (\(\Delta =\) condizione\(_2\) − condizione\(_1\));
stimiamo la media della differenza, il 95% CrI e la probabilità a posteriori che la differenza sia negativa;
visualizziamo i risultati per facilitarne l’interpretazione.

39.3.5.2.1 Step 1. Etichette di condizione

cond_labels <- dat %>%
  distinct(cond_id, condition) %>%
  arrange(cond_id) %>%
  pull(condition)

cond_labels
#> [1] "approach"  "avoidance"
# Esempio: c("approach", "avoidance")

39.3.5.2.2 Step 2. Contrasto su α (media per condizione)

Calcoliamo \(\Delta_\alpha = \alpha_{\text{avoidance}} - \alpha_{\text{approach}}\).

delta_alpha <- fit3 |>
  spread_draws(alpha_mean[cond]) |>
  mutate(cond = factor(cond, levels = 1:2, labels = cond_labels)) |>
  pivot_wider(names_from = cond, values_from = alpha_mean, names_prefix = "alpha_mean_") |>
  mutate(delta_alpha_mean = alpha_mean_avoidance - alpha_mean_approach)

delta_alpha |> 
  summarise(
    mean   = mean(delta_alpha_mean),
    low95  = quantile(delta_alpha_mean, 0.025),
    upp95  = quantile(delta_alpha_mean, 0.975),
    p_lt0  = mean(delta_alpha_mean < 0)
  )
#> # A tibble: 1 × 4
#>     mean  low95   upp95 p_lt0
#>    <dbl>  <dbl>   <dbl> <dbl>
#> 1 -0.247 -0.481 -0.0349 0.989

39.3.5.2.3 Step 3. Contrasto su β (media per condizione)

In modo analogo, calcoliamo \(\Delta_\beta = \beta_{\text{avoidance}} - \beta_{\text{approach}}\).

delta_beta <- fit3 |>
  spread_draws(beta_mean[cond]) |>
  mutate(cond = factor(cond, levels = 1:2, labels = cond_labels)) |>
  pivot_wider(names_from = cond, values_from = beta_mean, names_prefix = "beta_mean_") |>
  mutate(delta_beta_mean = beta_mean_avoidance - beta_mean_approach)

delta_beta |> 
  summarise(
    mean   = mean(delta_beta_mean),
    low95  = quantile(delta_beta_mean, 0.025),
    upp95  = quantile(delta_beta_mean, 0.975),
    p_lt0  = mean(delta_beta_mean < 0)
  )
#> # A tibble: 1 × 4
#>     mean  low95   upp95 p_lt0
#>    <dbl>  <dbl>   <dbl> <dbl>
#> 1 -0.126 -0.251 0.00152 0.974

39.3.5.2.4 Step 4. Visualizzazione delle posterior

post_alpha <- fit3 |>
  spread_draws(alpha_mean[cond]) |>
  mutate(parameter = "alpha_mean",
         condition = factor(cond, levels = 1:2, labels = cond_labels)) |>
  rename(value = alpha_mean)

post_beta <- fit3 |>
  spread_draws(beta_mean[cond]) |>
  mutate(parameter = "beta_mean",
         condition = factor(cond, levels = 1:2, labels = cond_labels)) |>
  rename(value = beta_mean)

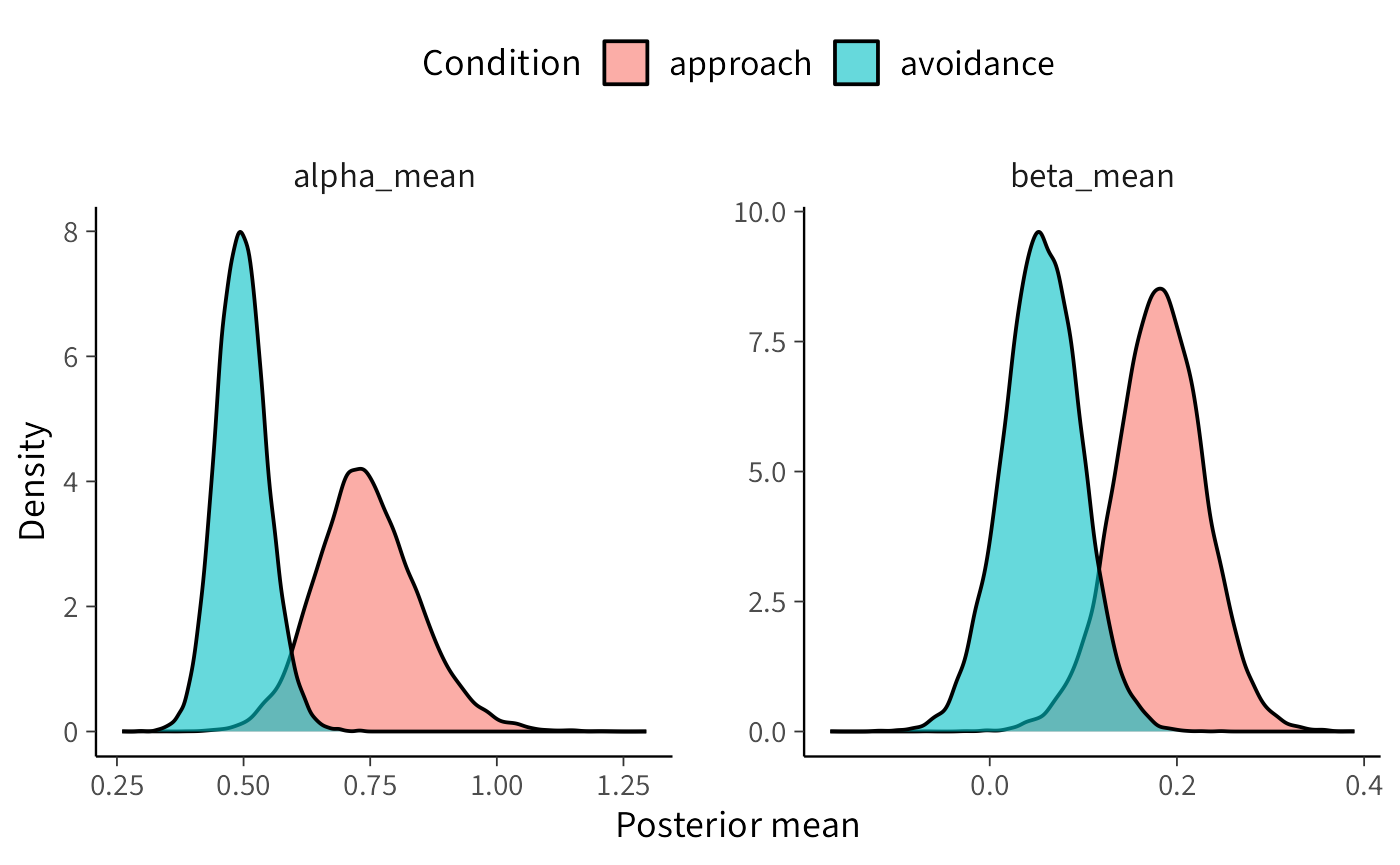
posterior_both <- bind_rows(post_alpha, post_beta)

ggplot(posterior_both, aes(x = value, fill = condition)) +
  geom_density(alpha = 0.6) +
  facet_wrap(~parameter, scales = "free") +
  labs(x = "Posterior mean", y = "Density", fill = "Condition") +
  theme(legend.position = "top")

39.3.5.2.5 Risultati numerici

prob_delta_alpha_neg <- mean(draws_df$`alpha_mean[2]` - draws_df$`alpha_mean[1]` < 0)
prob_delta_beta_neg  <- mean(draws_df$`beta_mean[2]` - draws_df$`beta_mean[1]` < 0)

cat("P(delta_alpha_mean < 0):", round(prob_delta_alpha_neg, 3), "\n")
#> P(delta_alpha_mean < 0): 0.989
cat("P(delta_beta_mean < 0):", round(prob_delta_beta_neg, 3), "\n")
#> P(delta_beta_mean < 0): 0.974

summary_df <- tibble(
  parameter = c("alpha_mean", "beta_mean"),
  delta_mean = c(
    mean(draws_df$`alpha_mean[2]` - draws_df$`alpha_mean[1]`),
    mean(draws_df$`beta_mean[2]` - draws_df$`beta_mean[1]`)
  ),
  lower_95 = c(
    quantile(draws_df$`alpha_mean[2]` - draws_df$`alpha_mean[1]`, 0.025),
    quantile(draws_df$`beta_mean[2]` - draws_df$`beta_mean[1]`, 0.025)
  ),
  upper_95 = c(
    quantile(draws_df$`alpha_mean[2]` - draws_df$`alpha_mean[1]`, 0.975),
    quantile(draws_df$`beta_mean[2]` - draws_df$`beta_mean[1]`, 0.975)
  ),
  prob_below_0 = c(prob_delta_alpha_neg, prob_delta_beta_neg)
)

summary_df
#> # A tibble: 2 × 5
#>   parameter  delta_mean lower_95 upper_95 prob_below_0
#>   <chr>           <dbl>    <dbl>    <dbl>        <dbl>
#> 1 alpha_mean     -0.247   -0.481 -0.0349         0.989
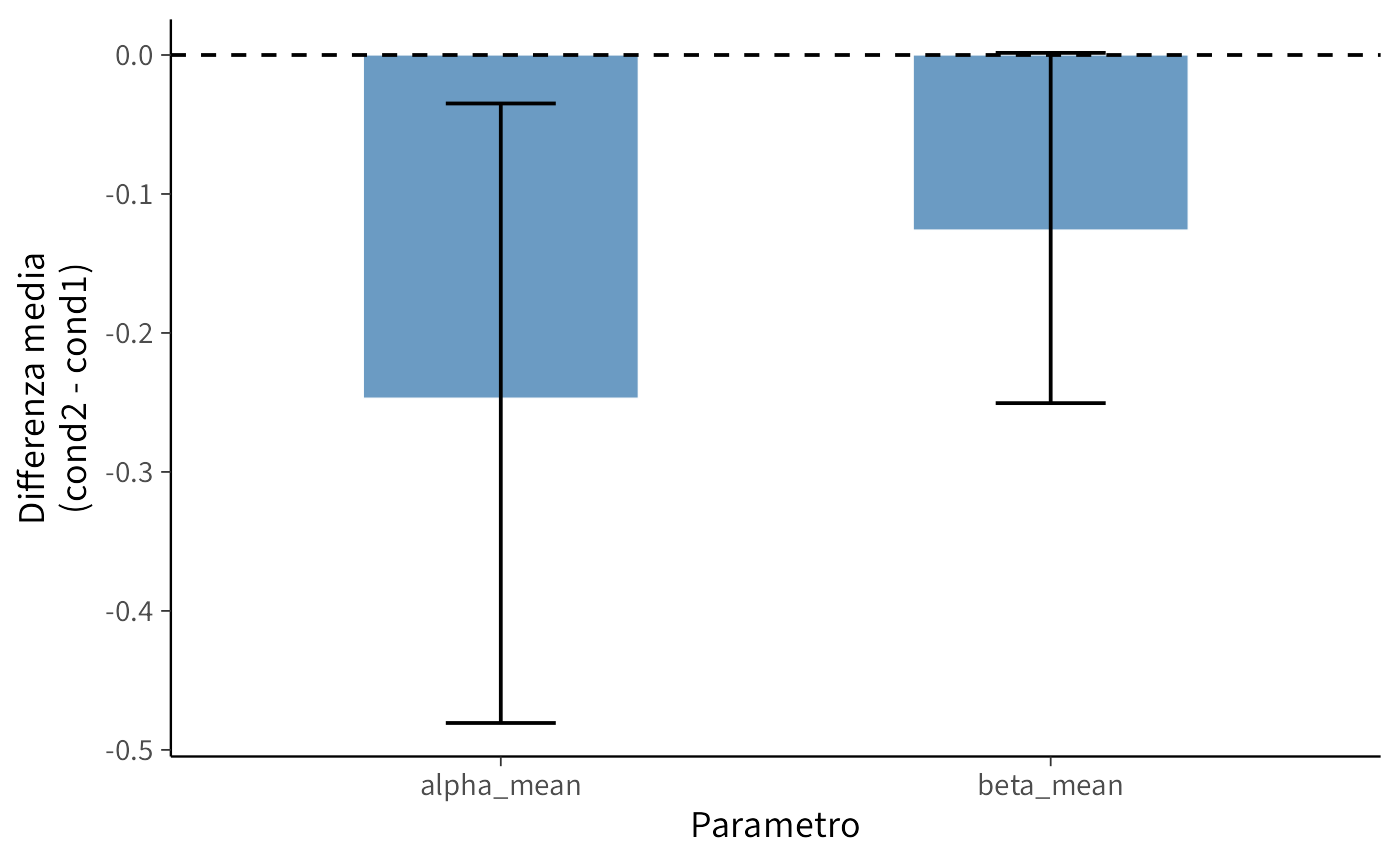
#> 2 beta_mean      -0.126   -0.251  0.00152        0.974

summary_df |> 
  ggplot(aes(x = parameter, y = delta_mean)) +
  geom_bar(stat = "identity", fill = "steelblue", width = 0.5) +
  geom_errorbar(aes(ymin = lower_95, ymax = upper_95), width = 0.2) +
  geom_hline(yintercept = 0, linetype = "dashed") +
  labs(
    x = "Parametro",
    y = "Differenza media\n(cond2 - cond1)"
  )

39.3.5.2.6 Interpretazione dei risultati

\(\Delta_\alpha\) (avoidance − approach) Media = −0.247; CrI 95% = [−0.481, −0.035]; \(P(\Delta<0) = 0.989\). → Evidenza forte che l’aggiornamento (\(\alpha\)) è più basso in avoidance. L’effetto è moderato (≈0.25 SD).
\(\Delta_\beta\) (avoidance − approach) Media = −0.126; CrI 95% = [−0.251, 0.002]; \(P(\Delta<0) = 0.974\). → La probabilità che \(\beta\) sia più basso in avoidance è elevata, ma l’intervallo credibile include lo zero. Evidenza suggestiva ma non conclusiva.

39.3.5.2.7 Significato sostantivo

Nella condizione di avoidance si osserva un rallentamento significativo nell’aggiornamento delle credenze, come evidenziato dal parametro \(\alpha\) più basso. Parallelamente, emerge una tendenza alla riduzione del parametro \(\beta\), sebbene con un grado di incertezza che ne impedisce una conclusione definitiva.

Questi risultati suggeriscono che la manipolazione sperimentale influisce prevalentemente sulla dinamica di apprendimento, mentre il suo eventuale effetto sulla componente di drift richiederà verifiche più approfondite attraverso raccolte dati più estese o modelli dotati di maggiore sensibilità discriminativa.

39.4 Confronto tra modelli

Per confrontare la capacità predittiva dei modelli è stata impiegata la cross-validazione leave-one-out (LOO-CV), che fornisce una stima della densità predittiva attesa (ELPD). Valori più elevati di ELPD indicano una superiore accuratezza predittiva fuori campione.

log_lik1 <- fit1$draws(variables = "log_lik", format = "matrix")
log_lik2 <- fit2$draws(variables = "log_lik", format = "matrix")
log_lik3 <- fit3$draws(variables = "log_lik", format = "matrix")

# Calcola LOO per ciascun modello
loo1 <- loo(log_lik1)
loo2 <- loo(log_lik2)
loo3 <- loo(log_lik3)

# Confronto tra i modelli
model_comparison <- loo_compare(loo1, loo2, loo3)
print(model_comparison)
#>        elpd_diff se_diff
#> model3   0.0       0.0  
#> model2  -4.7       3.9  
#> model1 -23.2       7.6

Il modello gerarchico con condizione (Modello 3) presenta le migliori prestazioni predittive secondo la metrica ELPD. Tuttavia, il confronto diretto con il modello gerarchico senza condizione (Modello 2) rivela una differenza di ELPD pari a -4.7 (SE = 3.9), un divario di entità contenuta rispetto all’incertezza campionaria. Sebbene si osservi una tendenza a favore del Modello 3, non è possibile stabilire con sufficiente sicurezza che l’inclusione della condizione produca un reale miglioramento delle prestazioni predittive.

Ben diverso è il caso del confronto con il modello non gerarchico (Modello 1), che mostra una perdita significativa di capacità predittiva con un ELPD inferiore di 23.3 unità (SE = 7.6) rispetto al Modello 3. In questo caso, la magnitudine della differenza, nettamente superiore all’errore standard, consente di concludere che il Modello 1 genera prestazioni predittive significativamente inferiori.

39.4.1 Cosa impariamo

Il confronto tra modelli ha messo in luce l’importanza cruciale della struttura gerarchica. I modelli gerarchici (Modelli 2 e 3) dimostrano una capacità descrittiva nettamente superiore rispetto al modello non gerarchico, confermando il valore epistemologico della condivisione delle informazioni tra i soggetti per ottenere stime più robuste e previsioni più accurate.

Per quanto riguarda l’effetto della condizione sperimentale, il modello che lo include (Modello 3) mostra una tendenza verso prestazioni migliori, sebbene il vantaggio predittivo rispetto al modello gerarchico semplice (Modello 2) non raggiunga una solidità statistica convincente. Questa conclusione è coerente con le stime parametriche, in cui la differenza tra le condizioni appare più marcata per il parametro \(\alpha\) rispetto al parametro \(\beta\).

La scelta del modello dipende quindi dagli obiettivi della ricerca. Se si privilegia la parsimonia, il modello 2 è già adeguato. Se invece l’obiettivo primario è quello di testare esplicitamente l’effetto della condizione, il modello 3 risulta preferibile, nonostante il reale guadagno predittivo rimanga incerto.

Riflessioni conclusive

Questo capitolo ha tracciato un percorso metodologico che, partendo dal livello individuale, conduce a una rappresentazione della collettività, incrementando progressivamente la complessità del modello in modo controllato e giustificato.

L’approccio person-level, stimando parametri specifici per ciascun soggetto \((\alpha_i, \beta_i)\), ha rivelato una marcata eterogeneità individuale sia nella velocità di aggiornamento che nella deriva decisionale. Tuttavia, questa flessibilità analitica presenta un costo metodologico sostanziale: l’assenza di condivisione delle informazioni tra i soggetti rende le stime particolarmente fragili quando il numero di osservazioni per partecipante è limitato.

Il modello gerarchico supera questa limitazione trattando i parametri individuali come realizzazioni di distribuzioni di popolazione. Questa architettura produce inferenze più stabili e generalizzabili, grazie al meccanismo dello “shrinkage”, che attenua le stime estreme non sufficientemente supportate dai dati. Il risultato è un duplice vantaggio: stime individuali più affidabili e un quadro generale della popolazione.

L’introduzione di iperparametri specifici per condizione permette, infine, di isolare differenze sistematiche tra gruppi a livello di popolazione. I risultati ottenuti indicano effetti credibili principalmente sul parametro \(\alpha\) (velocità di apprendimento), mentre l’evidenza riguardo al parametro \(\beta\) appare più incerta, in linea con l’ipotesi che la manipolazione sperimentale agisca principalmente sui processi di aggiornamento delle credenze.

Dal punto di vista predittivo, il confronto mediante ELPD/LOO-CV dimostra che la struttura gerarchica è un elemento cruciale: i modelli multilevel presentano una capacità predittiva sensibilmente superiore rispetto al modello non gerarchico. Il vantaggio del modello che include la condizione rispetto a quello gerarchico semplice, sebbene orientato nella direzione attesa, risulta modesto rispetto all’incertezza campionaria, rendendolo preferibile quando l’obiettivo è testare l’effetto sperimentale, ma meno decisivo in un’ottica di parsimonia.

Emergono tre messaggi metodologici fondamentali: la progettazione della struttura del modello dovrebbe riflettere le dipendenze naturali presenti nei dati, bilanciando complessità e vincoli; l’integrazione tra informazioni individuali e di popolazione produce stime più robuste e interpretazioni più chiare; la valutazione predittiva out-of-sample allinea la selezione del modello all’obiettivo della generalizzazione.

In sintesi, il passaggio da modelli basati sul livello della persona a gerarchie che incorporano gruppi noti non rappresenta solo un affinamento tecnico, ma un’evoluzione concettuale verso framework che catturano adeguatamente la struttura della popolazione, rispettano l’eterogeneità individuale e quantificano con rigore le differenze tra le condizioni. Questa architettura metodologica getta solide basi per le future estensioni, dall’identificazione di sottogruppi latenti alla modellazione di strutture temporali più sofisticate, mantenendo come principi guida la capacità predittiva e la coerenza psicologica delle ipotesi teoriche.

Informazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] cmdstanr_0.9.0        ragg_1.5.0            tinytable_0.13.0     
#>  [4] withr_3.0.2           systemfonts_1.3.1     patchwork_1.3.2      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#> [10] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.4            
#> [28] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      compiler_4.5.1        vctrs_0.6.5          
#> [10] stringr_1.5.2         pkgconfig_2.0.3       arrayhelpers_1.1-0   
#> [13] fastmap_1.2.0         backports_1.5.0       labeling_0.4.3       
#> [16] utf8_1.2.6            rmarkdown_2.30        ps_1.9.1             
#> [19] purrr_1.1.0           xfun_0.53             cachem_1.1.0         
#> [22] jsonlite_2.0.0        broom_1.0.10          parallel_4.5.1       
#> [25] R6_2.6.1              stringi_1.8.7         RColorBrewer_1.1-3   
#> [28] lubridate_1.9.4       estimability_1.5.1    knitr_1.50           
#> [31] zoo_1.8-14            R.utils_2.13.0        Matrix_1.7-4         
#> [34] splines_4.5.1         timechange_0.3.0      tidyselect_1.2.1     
#> [37] abind_1.4-8           yaml_2.3.10           codetools_0.2-20     
#> [40] curl_7.0.0            processx_3.8.6        pkgbuild_1.4.8       
#> [43] lattice_0.22-7        bridgesampling_1.1-2  S7_0.2.0             
#> [46] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [49] RcppParallel_5.1.11-1 pillar_1.11.1         tensorA_0.36.2.1     
#> [52] checkmate_2.3.3       stats4_4.5.1          distributional_0.5.0 
#> [55] generics_0.1.4        rprojroot_2.1.1       rstantools_2.5.0     
#> [58] scales_1.4.0          xtable_1.8-4          glue_1.8.0           
#> [61] emmeans_1.11.2-8      tools_4.5.1           data.table_1.17.8    
#> [64] mvtnorm_1.3-3         grid_4.5.1            QuickJSR_1.8.1       
#> [67] colorspace_2.1-2      nlme_3.1-168          cli_3.6.5            
#> [70] textshaping_1.0.4     svUnit_1.0.8          Brobdingnag_1.2-9    
#> [73] V8_8.0.1              gtable_0.3.6          R.methodsS3_1.8.2    
#> [76] digest_0.6.37         TH.data_1.1-4         htmlwidgets_1.6.4    
#> [79] farver_2.1.2          R.oo_1.27.1           memoise_2.0.1        
#> [82] htmltools_0.5.8.1     lifecycle_1.0.4       MASS_7.3-65

Bibliografia

Knight, E., Neal, A., Palada, H., & Ballard, T. (2023). A Tutorial on Bayesian Modeling of Change Across Time, Individuals, and Groups. Computational Brain & Behavior, 6(4), 697–718.