here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(
cmdstanr, HDInterval, lubridate, brms, bayesplot, posterior, tidyr, glmnet,
pROC
)36 Valutare la capacità predittiva: AUC e generalizzazione del modello
Introduzione
In una vasta gamma di contesti psicologici, dalla psicologia clinica alla neuroscienza cognitiva, ci troviamo spesso di fronte alla necessità di classificare gli individui in categorie distinte. Si pensi, ad esempio, alla distinzione tra pazienti e controlli sani in psicopatologia (ad es., Sideridis et al., 2006) o tra alta e bassa flessibilità cognitiva nella ricerca sui processi esecutivi (ad es., Caudek et al., 2020).
Questo compito di classificazione si basa tipicamente su indicatori osservabili, come punteggi psicometrici, parametri derivati da modelli computazionali o misure neurofisiologiche, a partire dai quali costruiamo un modello predittivo che stima la probabilità di appartenenza a ciascun gruppo.
Tuttavia, sviluppare un modello che descriva semplicemente bene i dati in nostro possesso non è sufficiente. La sfida scientifica e applicativa cruciale è duplice:
- quantificare con precisione la capacità del modello di discriminare tra i gruppi;
- verificare che questa capacità di distinzione si generalizzi oltre il campione specifico su cui il modello è stato addestrato, mantenendo la sua accuratezza quando applicato a nuovi dati.
In questo capitolo esploreremo come l’area sotto la curva ROC (AUC) emerga come una metrica fondamentale per valutare la performance discriminativa di un modello e come i principi di validazione e generalizzabilità siano indispensabili per trasformare un costrutto statistico in uno strumento di previsione clinicamente o teoricamente utile.
Panoramica del capitolo
- Scopo: valutare la capacità discriminativa di un modello (es. pazienti vs controlli) attraverso l’AUC.
- Concetto chiave: l’AUC misura la probabilità che un paziente ottenga un punteggio più alto di un controllo, indipendentemente dalla soglia.
- Validazione: l’AUC in-sample è spesso ottimistica; la cross-validation stima la capacità out-of-sample e riduce l’overfitting.
- Approccio bayesiano: produce una distribuzione a posteriori dell’AUC che quantifica l’incertezza e consente probabilità dirette (es. Pr(AUC > 0.8)).
- Messaggio finale: un buon modello deve generalizzare a nuovi dati, non solo adattarsi bene a quelli osservati.
36.1 Il problema della classificazione binaria
36.1.1 Un esempio intuitivo: separare due gruppi
Supponiamo che un ricercatore utilizzi un modello computazionale di apprendimento, come il modello di Rescorla-Wagner, per studiare le differenze tra un gruppo clinico e un gruppo di controllo. Supponiamo che il parametro \(\beta\), che rappresenta la sensibilità alle ricompense, mostri un andamento sistematico:
- i pazienti tendono ad avere valori di \(\beta\) più bassi, mentre i controlli mostrano valori più alti.
Un classificatore elementare potrebbe quindi stabilire una regola decisionale basata su una soglia:
“Se \(\beta > 1.2\), classifico il soggetto come controllo; altrimenti, come paziente”.
L’efficacia di questa regola dipende criticamente dal grado di sovrapposizione delle distribuzioni del parametro nei due gruppi:
- se le distribuzioni sono ampie e sovrapposte, la classificazione sarà incerta e soggetta a molti errori;
- se le distribuzioni sono ben separate, il modello potrà operare distinzioni accurate.
36.1.2 Misurare le performance: accuratezza, sensibilità e specificità
Per quantificare oggettivamente la capacità discriminativa di un classificatore binario, si ricorre alla matrice di confusione, che incrocia le previsioni del modello con la verità nota.
| Predetto: Paziente | Predetto: Controllo | |
|---|---|---|
| Reale: Paziente | Veri Positivi (TP) | Falsi Negativi (FN) |
| Reale: Controllo | Falsi Positivi (FP) | Veri Negativi (TN) |
Da questa tabella derivano tre metriche fondamentali:
Sensibilità: \(\frac{TP}{TP + FN}.\)
Interpretazione: la capacità del modello di identificare correttamente i pazienti. Una sensibilità alta significa pochi falsi negativi.Specificità: \(\frac{TN}{TN + FP}.\)
Interpretazione: la capacità del modello di identificare correttamente i controlli. Una specificità alta significa pochi falsi positivi.Accuratezza: \(\frac{TP + TN}{N}.\)
Interpretazione: la proporzione totale di classificazioni corrette.
Tuttavia, queste metriche presentano una limitazione cruciale: i loro valori dipendono strettamente dalla soglia di classificazione scelta (es. \(\beta > 1.2\)). Modificando la soglia, si alterano i compromessi tra sensibilità e specificità. È proprio per analizzare questo compromesso in modo completo e indipendente dalla soglia che introduciamo la curva ROC.
36.2 La curva ROC e l’AUC
36.2.1 Comprendere il compromesso fondamentale
Quando sviluppiamo un modello di classificazione, dobbiamo costantemente bilanciare due obiettivi:
- identificare correttamente i pazienti (sensibilità);
- evitare di classificare come pazienti i controlli sani (specificità).
La curva ROC (Receiver Operating Characteristic) visualizza questo compromesso. Possiamo immaginarla come una mappa che mostra, per ogni possibile soglia decisionale del nostro modello, il “costo” in falsi positivi che dobbiamo sostenere per ottenere un certo “guadagno” in veri positivi.
Assi della curva:
- Ascissa (X): Tasso di falsi positivi = 1 - specificità. “Quanti controlli sani stiamo erroneamente classificando come pazienti?”
-
Ordinate (Y): Tasso di veri positivi = sensibilità.
“Quanti pazienti reali stiamo correttamente identificando?”
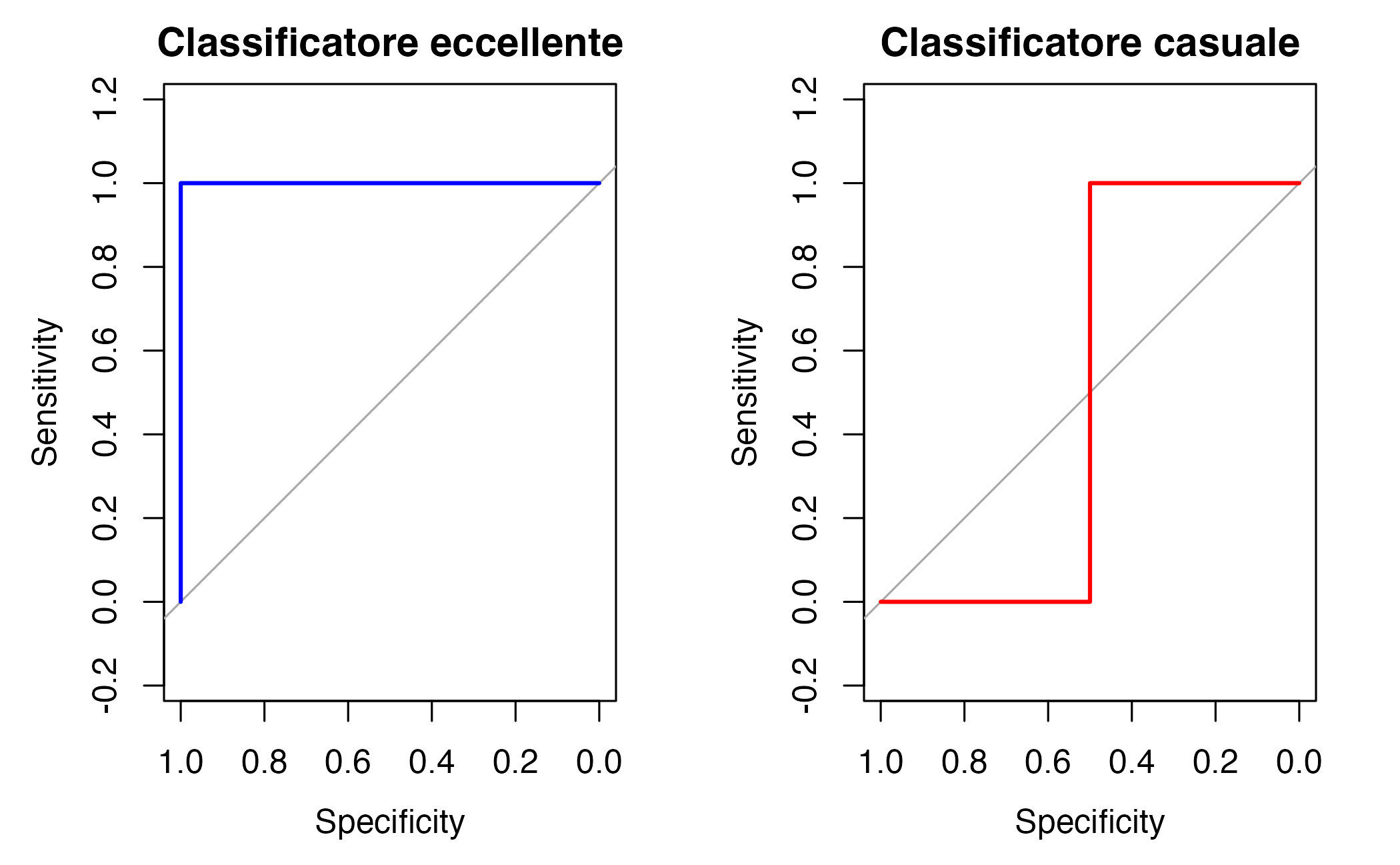
36.2.2 Interpretare la forma della curva
# Esempio visivo di diverse curve ROC
par(mfrow = c(1, 2))
# Curva di un classificatore perfetto
plot(roc(c(0,0,1,1), c(0.1,0.2,0.8,0.9)),
main = "Classificatore eccellente", col = "blue")
# Curva di un classificatore casuale
plot(roc(c(0,0,1,1), c(0.3,0.6,0.4,0.5)),
main = "Classificatore casuale", col = "red")Cosa osserviamo:
- Curva che “spinge” in alto a sinistra: il modello commette poche classificazioni errate tra i controlli (bassi falsi positivi) e identifica molti pazienti reali (alti veri positivi).
- Curva lungo la diagonale: Il modello non fa meglio di un lancio di moneta.
- Curve intermedie: maggiore è l’area sotto la curva, migliore è il compromesso complessivo.
36.2.3 L’AUC: una metrica sintetica e potente
L’Area Sotto la Curva (AUC) condensa in un singolo numero la performance complessiva del modello:
\[ \text{AUC} = P(\text{punteggio(paziente)} > \text{punteggio(controllo)}). \]
In pratica, se prendessimo un paziente e un controllo a caso, l’AUC rappresenta la probabilità che il nostro modello assegni al paziente un punteggio più alto (e quindi più “a rischio”) rispetto al controllo.
36.2.4 Scala interpretativa
# Scala qualitativa dell'AUC
scala_auc <- data.frame(
AUC = c("0.5", "0.6-0.7", "0.7-0.8", "0.8-0.9", "> 0.9"),
Interpretazione = c("Classificatore casuale", "Discriminazione scarsa",
"Discriminazione moderata", "Discriminazione buona",
"Discriminazione eccellente")
)
print(scala_auc)
#> AUC Interpretazione
#> 1 0.5 Classificatore casuale
#> 2 0.6-0.7 Discriminazione scarsa
#> 3 0.7-0.8 Discriminazione moderata
#> 4 0.8-0.9 Discriminazione buona
#> 5 > 0.9 Discriminazione eccellente36.3 Calcolare l’AUC: un esempio pratico in R
36.3.1 Contesto dello studio
Immaginiamo uno studio sulla depressione in cui un ricercatore vuole distinguere i pazienti depressi (codice 1) dai controlli sani (codice 0) sulla base di un punteggio di gravità derivato da un questionario psicometrico. I punteggi più alti indicano una sintomatologia più grave.
36.3.2 Dati simulati
# Dati dello studio
dati_studio <- data.frame(
soggetto = 1:10,
gruppo = rep(c("Paziente", "Controllo"), each = 5),
punteggio_gravita = c(0.85, 0.92, 0.38, 0.95, 0.82, # Pazienti
0.45, 0.52, 0.39, 0.61, 0.42) # Controlli
)
print(dati_studio)
#> soggetto gruppo punteggio_gravita
#> 1 1 Paziente 0.85
#> 2 2 Paziente 0.92
#> 3 3 Paziente 0.38
#> 4 4 Paziente 0.95
#> 5 5 Paziente 0.82
#> 6 6 Controllo 0.45
#> 7 7 Controllo 0.52
#> 8 8 Controllo 0.39
#> 9 9 Controllo 0.61
#> 10 10 Controllo 0.4236.3.3 L’algoritmo fondamentale: confronto a coppie
Per capire l’AUC, implementiamo il metodo della “forza bruta”, che conta tutte le coppie paziente-controllo.
calcola_auc_manual <- function(punteggi, etichette) {
# 1. Separazione dei gruppi
pazienti <- punteggi[etichette == 1]
controlli <- punteggi[etichette == 0]
n_pazienti <- length(pazienti)
n_controlli <- length(controlli)
cat("Pazienti:", pazienti, "\n")
cat("Controlli:", controlli, "\n")
cat("Numero di coppie da valutare:", n_pazienti, "×", n_controlli, "=",
n_pazienti * n_controlli, "\n\n")
# 2. Conteggio delle coppie concordanti
coppie_concordanti <- 0
cat("Coppie paziente > controllo:\n")
for(i in seq_along(pazienti)) {
for(j in seq_along(controlli)) {
if(pazienti[i] > controlli[j]) {
coppie_concordanti <- coppie_concordanti + 1
cat(" Paziente", i, "(", pazienti[i], ") > Controllo", j,
"(", controlli[j], ")\n")
}
}
}
# 3. Calcolo finale
auc <- coppie_concordanti / (n_pazienti * n_controlli)
cat("\nCoppie concordanti:", coppie_concordanti, "\n")
cat("AUC =", coppie_concordanti, "/", n_pazienti * n_controlli, "=",
round(auc, 3), "\n")
return(auc)
}
# Applicazione al nostro studio
punteggi <- dati_studio$punteggio_gravita
etichette <- ifelse(dati_studio$gruppo == "Paziente", 1, 0)
auc_calcolata <- calcola_auc_manual(punteggi, etichette)
#> Pazienti: 0.85 0.92 0.38 0.95 0.82
#> Controlli: 0.45 0.52 0.39 0.61 0.42
#> Numero di coppie da valutare: 5 × 5 = 25
#>
#> Coppie paziente > controllo:
#> Paziente 1 ( 0.85 ) > Controllo 1 ( 0.45 )
#> Paziente 1 ( 0.85 ) > Controllo 2 ( 0.52 )
#> Paziente 1 ( 0.85 ) > Controllo 3 ( 0.39 )
#> Paziente 1 ( 0.85 ) > Controllo 4 ( 0.61 )
#> Paziente 1 ( 0.85 ) > Controllo 5 ( 0.42 )
#> Paziente 2 ( 0.92 ) > Controllo 1 ( 0.45 )
#> Paziente 2 ( 0.92 ) > Controllo 2 ( 0.52 )
#> Paziente 2 ( 0.92 ) > Controllo 3 ( 0.39 )
#> Paziente 2 ( 0.92 ) > Controllo 4 ( 0.61 )
#> Paziente 2 ( 0.92 ) > Controllo 5 ( 0.42 )
#> Paziente 4 ( 0.95 ) > Controllo 1 ( 0.45 )
#> Paziente 4 ( 0.95 ) > Controllo 2 ( 0.52 )
#> Paziente 4 ( 0.95 ) > Controllo 3 ( 0.39 )
#> Paziente 4 ( 0.95 ) > Controllo 4 ( 0.61 )
#> Paziente 4 ( 0.95 ) > Controllo 5 ( 0.42 )
#> Paziente 5 ( 0.82 ) > Controllo 1 ( 0.45 )
#> Paziente 5 ( 0.82 ) > Controllo 2 ( 0.52 )
#> Paziente 5 ( 0.82 ) > Controllo 3 ( 0.39 )
#> Paziente 5 ( 0.82 ) > Controllo 4 ( 0.61 )
#> Paziente 5 ( 0.82 ) > Controllo 5 ( 0.42 )
#>
#> Coppie concordanti: 20
#> AUC = 20 / 25 = 0.836.3.3.1 Algoritmo passo per passo
Separiamo i due gruppi (pazienti e controlli) in base alle etichette note (1 = paziente, 0 = controllo).
-
Confrontiamo ogni coppia possibile paziente–controllo;
- se il punteggio del paziente è maggiore, il modello ha classificato correttamente la coppia.
- se è minore, la classificazione è errata.
- se i punteggi sono uguali, possiamo decidere di contare mezzo punto (qui li ignoriamo per semplicità).
Sommiamo le coppie corrette e dividiamo il risultato per il numero totale di coppie \((n_{\text{paz}} \times n_{\text{ctrl}})\).
Il risultato è la proporzione di coppie classificate correttamente, ovvero l’AUC.
36.3.4 Interpretazione concreta
AUC = 0.8 significa che, scegliendo a caso un paziente e un controllo, nell’80% dei casi il nostro modello assegna correttamente un punteggio più alto al paziente.
36.3.4.1 Approfondimento opzionale
L’algoritmo mostrato sopra ha una complessità di tipo \(O(n_{\text{paz}} \times n_{\text{ctrl}})\) e cresce rapidamente con il numero di osservazioni. Per dataset di grandi dimensioni, si utilizzano formule equivalenti basate sul rango dei punteggi, da cui deriva la connessione tra l’AUC e il test di Mann–Whitney U (o Wilcoxon rank-sum test).
Questo collegamento evidenzia come l’AUC sia, di fatto, una misura non parametrica della separazione tra le due distribuzioni di punteggi.
36.3.5 Versione ottimizzata con R
Nella pratica, per dataset più grandi si utilizzano funzioni ottimizzate:
36.4 Oltre l’AUC in-sample: il problema della generalizzazione
36.4.1 Il rischio dell’overfitting
Un’AUC apparentemente eccellente, calcolata sugli stessi dati utilizzati per sviluppare il modello (dati di training), può rivelarsi un’illusione. Questo fenomeno, noto come overfitting (o sovradattamento), si verifica quando il modello impara non solo le regolarità genuine dei dati, ma anche il rumore e le fluttuazioni casuali specifiche del campione utilizzato.
In termini pratici, un modello sovradattato:
- memorizza i dati di training invece di apprendere relazioni generalizzabili;
- mostra prestazioni eccellenti sui dati noti, ma deludenti su dati nuovi;
- cattura pattern spurii che non si ripeteranno in contesti reali.
36.4.2 Strategie per la validazione predittiva
Per stimare in modo realistico le prestazioni attese su nuovi individui, è essenziale adottare strategie di validazione rigorose:
- Hold-out validation: separazione iniziale dei dati in un set di addestramento (per sviluppare il modello) e un set di test (per valutarne le prestazioni).
- Cross-validation: suddivisione ripetuta dei dati in fold, alternando training e validazione su sottoinsiemi diversi.
- Validation esterna: applicazione del modello a un campione completamente indipendente.
36.4.3 La domanda cruciale per la ricerca psicologica
Nel contesto dei modelli psicologici, ciò si traduce in una domanda metodologica fondamentale:
Il mio modello distingue efficacemente pazienti e controlli solo nel campione specifico su cui è stato calibrato, oppure questa capacità discriminativa si mantiene quando viene applicato a soggetti nuovi provenienti dalla stessa popolazione?
Questa distinzione non è meramente tecnica, ma investe la validità ecologica e l’utilità clinica del modello. Un test diagnostico che non generalizza al di là del campione di sviluppo ha scarso valore applicativo, per quanto promettenti possano essere le sue prestazioni apparenti.
36.5 Una valutazione out-of-sample con cross-validation
36.5.1 L’idea fondamentale
Per evitare di sopravvalutare le prestazioni del nostro modello, dobbiamo testarlo su dati che non ha mai visto durante l’addestramento. La cross-validation a 10 fold è il metodo più affidabile per simulare questa situazione:
- dividiamo i dati in 10 gruppi (fold) di dimensioni simili;
- addestriamo il modello su 9 gruppi;
- testiamo sul gruppo rimanente;
- ripetiamo il processo 10 volte, cambiando ogni volta il gruppo di test;
- calcoliamo l’AUC media su tutte le previsioni “out-of-fold”.
36.5.2 Simulazione di dati psicologici realistici
# Simuliamo dati realistici per uno studio sulla depressione
set.seed(123)
n_soggetti <- 100 # 50 pazienti + 50 controlli
dati <- data.frame(
# Variabili demografiche e cliniche
eta = round(rnorm(n_soggetti, mean = 45, sd = 12)),
bdi = round(rnorm(n_soggetti, mean = 25, sd = 10)), # Beck Depression Inventory
ansia = round(rnorm(n_soggetti, mean = 18, sd = 8)), # Scala ansia
funz_cognitiva = round(rnorm(n_soggetti, mean = 85, sd = 15)), # Test neuropsicologico
# Gruppo: 1 = Paziente depresso, 0 = Controllo sano
gruppo = rep(c(1, 0), each = n_soggetti/2)
)
# Creiamo differenze reali tra gruppi nei predittori
dati$bdi[dati$gruppo == 1] <- dati$bdi[dati$gruppo == 1] + 10 # Pazienti hanno BDI più alto
dati$ansia[dati$gruppo == 1] <- dati$ansia[dati$gruppo == 1] + 9 # Pazienti hanno più ansia
dati$funz_cognitiva[dati$gruppo == 1] <- dati$funz_cognitiva[dati$gruppo == 1] - 12 # Pazienti hanno performance peggiore
# Prepariamo i dati per il modello
X <- as.matrix(dati[, c("eta", "bdi", "ansia", "funz_cognitiva")])
y <- dati$gruppo
cat("Distribuzione dei gruppi:\n")
#> Distribuzione dei gruppi:
table(y)
#> y
#> 0 1
#> 50 5036.5.3 Implementazione della cross-validation
# Configuriamo la cross-validation
set.seed(123)
n_fold <- 10
folds <- sample(rep(1:n_fold, length.out = nrow(X)))
# Vettore per raccogliere le previsioni out-of-sample
previsioni_oos <- numeric(nrow(X))
cat("Esecuzione della cross-validation...\n")
#> Esecuzione della cross-validation...
# Cross-validation
for (fold in 1:n_fold) {
cat("Fold", fold, "... ")
# Dividi in training e test
test_index <- which(folds == fold)
training_index <- which(folds != fold)
# Addestra il modello sul training set
modello <- cv.glmnet(
X[training_index, ],
y[training_index],
family = "binomial",
alpha = 0.5, # elastic net
nfolds = 5 # validazione interna per scegliere lambda
)
# Previsioni sul test set
previsioni_oos[test_index] <- predict(
modello,
X[test_index, ],
s = "lambda.min",
type = "response"
)[,1]
cat("completato\n")
}
#> Fold 1 ... completato
#> Fold 2 ... completato
#> Fold 3 ... completato
#> Fold 4 ... completato
#> Fold 5 ... completato
#> Fold 6 ... completato
#> Fold 7 ... completato
#> Fold 8 ... completato
#> Fold 9 ... completato
#> Fold 10 ... completato36.5.4 Risultati e interpretazione
# Calcoliamo l'AUC out-of-sample
auc_oos <- roc(y, previsioni_oos)$auc
auc_ci <- ci.auc(roc(y, previsioni_oos))
cat("\n--- RISULTATI ---\n")
#>
#> --- RISULTATI ---
cat("AUC out-of-sample:", round(auc_oos, 3), "\n")
#> AUC out-of-sample: 0.796
cat("Intervallo di confidenza 95%:", round(auc_ci[1], 3), "-", round(auc_ci[3], 3), "\n")
#> Intervallo di confidenza 95%: 0.708 - 0.883
# Visualizziamo le prestazioni
roc_curve <- roc(y, previsioni_oos)
plot(roc_curve, main = "Curva ROC - Prestazioni Out-of-Sample")
text(0.6, 0.2, paste("AUC =", round(auc_oos, 3)), cex = 1.2)
# Confrontiamo con AUC ottimistica (su tutto il dataset)
modello_ottimistico <- cv.glmnet(X, y, family = "binomial", alpha = 0.5)
previsioni_ottimistiche <- predict(modello_ottimistico, X, s = "lambda.min", type = "response")[,1]
auc_ottimistico <- roc(y, previsioni_ottimistiche)$auc
cat("AUC 'ottimistica' (in-sample):", round(auc_ottimistico, 3), "\n")
#> AUC 'ottimistica' (in-sample): 0.828
cat("Differenza:", round(auc_ottimistico - auc_oos, 3), "\n")
#> Differenza: 0.03236.5.5 Interpretazione dei risultati
L’AUC out-of-sample rappresenta la vera capacità generalizzabile del nostro modello. Nel nostro esempio simulato, ci aspettiamo un valore compreso tra 0.75 e 0.85, che indica una buona capacità discriminativa. La differenza tra l’AUC “ottimistica” (calcolata su tutti i dati) e l’AUC out-of-sample misura quanto il nostro modello fosse sovradattato ai dati di training.
Questo approccio fornisce una stima realistica di come il modello si comporterà quando verrà applicato a nuovi pazienti nella pratica clinica.
36.5.6 Perché questo approccio è il gold standard
L’AUC out-of-sample fornisce una stima realistica della capacità del modello di generalizzare a nuovi dati. Se questa AUC rimane alta (ad esempio, superiore a 0.8), possiamo ragionevolmente essere fiduciosi che il modello funzionerà bene nella pratica clinica.
36.6 Una prospettiva bayesiana sull’AUC
36.6.1 L’AUC come quantità incerta
Nel paradigma bayesiano, l’AUC non è un valore fisso ma una quantità incerta che deriva dalla nostra distribuzione a posteriori. Possiamo considerarla come una funzione dei parametri del modello che viene ricalcolata per ogni campione della catena MCMC.
36.6.2 Implementazione in Stan
Ecco un modello logistico gerarchico completo che calcola l’AUC a ogni iterazione:
stancode <- "
functions {
// AUC ingenua O(N^2) con gestione opzionale dei ties.
// Se vuoi ignorare i ties, chiama con ties_as_half = 0.
real calculate_auc(vector y_pred, array[] int y, int ties_as_half) {
int N = size(y);
int n_cases = sum(y);
int n_controls = N - n_cases;
if (n_cases == 0 || n_controls == 0) return not_a_number();
vector[n_cases] pos;
vector[n_controls] neg;
{
int ip = 1;
int ic = 1;
for (n in 1:N) {
if (y[n] == 1) {
pos[ip] = y_pred[n];
ip += 1;
} else {
neg[ic] = y_pred[n];
ic += 1;
}
}
}
real concordant = 0;
for (i in 1:n_cases) {
for (j in 1:n_controls) {
if (pos[i] > neg[j]) {
concordant += 1;
} else if (ties_as_half == 1 && pos[i] == neg[j]) {
concordant += 0.5; // mezzo punto ai pareggi
}
}
}
return concordant / (n_cases * n_controls);
}
}
data {
int<lower=1> N;
int<lower=1> K;
matrix[N, K] X;
array[N] int<lower=0, upper=1> y;
}
parameters {
vector[K] beta;
real alpha;
}
model {
beta ~ normal(0, 1);
alpha ~ normal(0, 2);
y ~ bernoulli_logit(alpha + X * beta);
}
generated quantities {
vector[N] eta = alpha + X * beta;
vector[N] y_pred = inv_logit(eta);
real auc = calculate_auc(y_pred, y, 1);
int auc_above_chance = (auc > 0.5);
array[N] int y_rep;
for (n in 1:N) {
y_rep[n] = bernoulli_logit_rng(eta[n]);
}
}
"mod <- cmdstan_model(
write_stan_file(stancode),
compile = TRUE
)Generare i dati per Stan.
# Colonne predittori usate
pred_cols <- c("eta", "bdi", "ansia", "funz_cognitiva")
# 1) Matrice X e vettore y (0/1)
X <- as.matrix(dati[, pred_cols])
y <- as.integer(dati$gruppo) # già 0/1 nel tuo esempio
# 2) Standardizzazione colonne di X
# Manteniamo l'intercetta separata in Stan, quindi NON si aggiunge la colonna di 1.
X_sc <- scale(X) # centriamo e scaliamo ogni predittore
# 3) Rimuoviamo eventuali NA (per sicurezza)
ok <- complete.cases(X_sc) & !is.na(y)
X_sc <- X_sc[ok, , drop = FALSE]
y <- y[ok]
# 4) Costruiamo la lista per Stan
stan_data <- list(
N = nrow(X_sc),
K = ncol(X_sc),
X = X_sc,
y = as.array(y) # Stan dichiara: array[N] int<lower=0,upper=1> y
)
str(stan_data)
#> List of 4
#> $ N: int 100
#> $ K: int 4
#> $ X: num [1:100, 1:4] -0.73324 -0.36889 1.63498 -0.00455 0.08653 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ : NULL
#> .. ..$ : chr [1:4] "eta" "bdi" "ansia" "funz_cognitiva"
#> $ y: int [1:100(1d)] 1 1 1 1 1 1 1 1 1 1 ...Fit del modello.
fit <- mod$sample(
data = stan_data,
iter_warmup = 1000,
iter_sampling = 2000,
chains = 4,
parallel_chains = 4,
seed = 4790,
refresh = 0
)
#> Running MCMC with 4 parallel chains...
#>
#> Chain 1 finished in 0.3 seconds.
#> Chain 2 finished in 0.3 seconds.
#> Chain 3 finished in 0.3 seconds.
#> Chain 4 finished in 0.3 seconds.
#>
#> All 4 chains finished successfully.
#> Mean chain execution time: 0.3 seconds.
#> Total execution time: 0.5 seconds.
36.6.3 Estrai AUC dai generated quantities (singolo fit)
# Nel modello Stan sono stati salvati: auc e auc_above_chance (0/1)
draws_aucs <- as_draws_df(fit$draws(variables = c("auc", "auc_above_chance")))
summ_auc <- tibble(
auc_mean = mean(draws_aucs$auc),
auc_q2.5 = quantile(draws_aucs$auc, 0.025),
auc_q50 = median(draws_aucs$auc),
auc_q97.5 = quantile(draws_aucs$auc, 0.975)
)
summ_auc
#> # A tibble: 1 × 4
#> auc_mean auc_q2.5 auc_q50 auc_q97.5
#> <dbl> <dbl> <dbl> <dbl>
#> 1 0.820 0.798 0.822 0.831
36.6.4 Calcola Pr(AUC > 0.8) (due modi)
# (A) Confronto diretto sui draw di 'auc'
pr_auc_gt_half_A <- mean(draws_aucs$auc > 0.8)
# (B) Usando l'indicatore 'auc_above_chance' creato in Stan (0/1)
pr_auc_gt_half_B <- mean(draws_aucs$auc_above_chance == 1)
cbind(
via_auc_draws = pr_auc_gt_half_A,
via_indicator_gq = pr_auc_gt_half_B
)
#> via_auc_draws via_indicator_gq
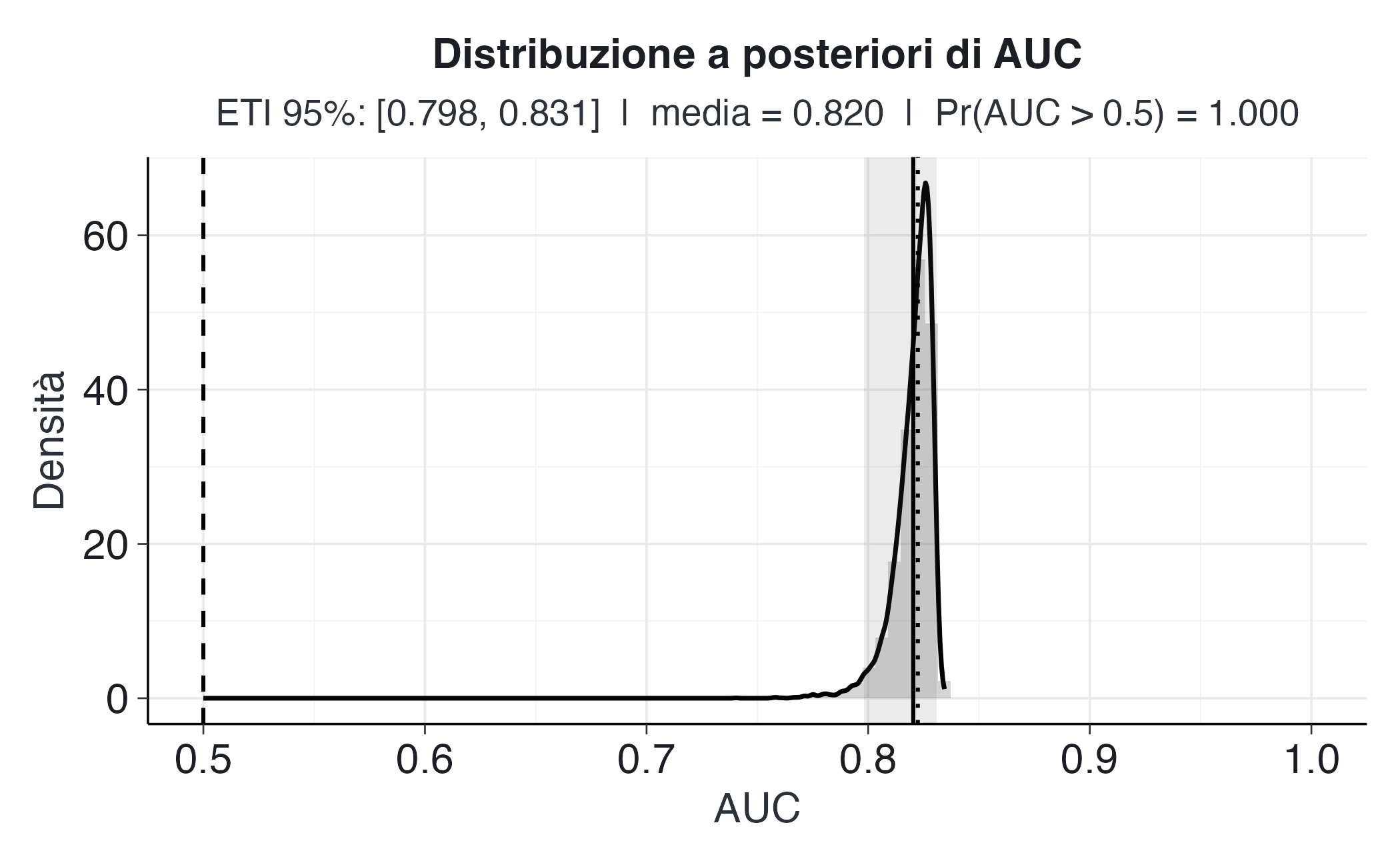
#> [1,] 0.967 1# Plot
ggplot(draws_aucs, aes(x = auc)) +
geom_histogram(aes(y = ..density..), bins = 60, alpha = 0.25) +
geom_density(adjust = 1.0, linewidth = 0.8) +
# Banda dell'intervallo di credibilità
annotate("rect",
xmin = summ_auc$q2.5, xmax = summ_auc$q97.5,
ymin = -Inf, ymax = Inf, alpha = 0.12) +
# Linee di riferimento
geom_vline(xintercept = 0.5, linetype = 2) +
geom_vline(xintercept = summ_auc$mean, color = "black") +
geom_vline(xintercept = summ_auc$q50, linetype = 3) +
coord_cartesian(xlim = c(0.5, 1)) +
labs(
title = "Distribuzione a posteriori di AUC",
subtitle = sprintf("ETI 95%%: [%.3f, %.3f] | media = %.3f | Pr(AUC > 0.5) = %.3f",
summ_auc$q2.5, summ_auc$q97.5, summ_auc$mean, summ_auc$pr_gt),
x = "AUC",
y = "Densità"
) 36.6.5 L’AUC in-sample come distribuzione a posteriori
Nel modello bayesiano presentato sopra, l’AUC viene calcolata all’interno di Stan come funzione dei parametri stimati a ogni iterazione della catena MCMC. Per ogni campione della distribuzione a posteriori del modello viene ricalcolata una stima dell’AUC, producendo così una distribuzione a posteriori dell’AUC invece di un singolo valore puntuale. Questa distribuzione riflette direttamente l’incertezza sui parametri del modello: se i coefficienti sono incerti, anche la capacità discriminativa del modello, rappresentata dall’AUC, sarà più o meno incerta.
L’AUC così calcolata è una stima “in-sample”, cioè misurata sugli stessi dati usati per adattare il modello. È quindi analoga all’AUC “ottimistica” del modello frequentista, con la differenza fondamentale che l’approccio bayesiano non fornisce una stima puntuale, ma una distribuzione di credibilità che quantifica esplicitamente l’incertezza.
In altre parole:
Nel caso frequentista, diremmo: “L’AUC è 0.82 (IC 95%: 0.76-0.87)”; nel caso bayesiano, possiamo dire: “L’AUC ha una probabilità del 98% di superare 0.5 e del 70% di superare 0.8”.
Questa formulazione è più informativa, in quanto si riferisce direttamente alla probabilità dei valori dell’AUC e non a una proprietà di ipotetiche ripetizioni dell’esperimento.
36.6.6 Perché serve la cross-validation bayesiana?
Come per i modelli frequentisti, anche nel caso bayesiano la valutazione “in-sample” può essere eccessivamente ottimistica: il modello tende a spiegare bene i dati che ha già visto, ma ciò non garantisce che possa generalizzare con la stessa efficacia a nuovi dati.
Per stimare la capacità di generalizzazione effettiva, è necessario ricorrere alla cross-validation bayesiana, che si basa sugli stessi principi della cross-validation classica, ma con una differenza sostanziale: invece di calcolare previsioni basate su coefficienti stimati una volta per tutte, si utilizzano predizioni integrate sulla distribuzione a posteriori dei parametri.
Nel caso più semplice (come una 10-fold cross-validation):
- si adatta il modello bayesiano su 9/10 dei dati (training set);
- per i soggetti del fold lasciato fuori, si calcolano le predizioni bayesiane, cioè la media delle probabilità predette su tutti i campioni della catena MCMC;
- si ripete il processo per tutti i fold;
- si combinano le predizioni “out-of-sample” e si calcola l’AUC risultante.
Questo approccio fornisce una stima non ottimistica e probabilisticamente coerente della capacità discriminativa del modello, in quanto tiene conto sia della variabilità dei dati sia dell’incertezza sui parametri.
36.6.7 Vantaggi della prospettiva bayesiana
Rispetto all’approccio frequentista, l’approccio bayesiano offre alcuni vantaggi concettuali e interpretativi importanti.
| Aspetto | Frequentista | Bayesiano |
|---|---|---|
| Tipo di stima | Valore puntuale | Distribuzione a posteriori |
| Incertezza su AUC | Intervallo di confidenza basato su assunzioni asintotiche | Intervallo di credibilità derivato dai campioni MCMC |
| Interpretazione | “Se ripetessi infinite volte l’esperimento…” | “Dato ciò che so, la probabilità che l’AUC superi 0.8 è X%” |
| Generalizzazione | Cross-validation o test set | Cross-validation bayesiana (predizione integrata sui parametri) |
| Costo computazionale | Basso | Più elevato, ma con maggiore informazione inferenziale |
In sintesi:
- l’AUC bayesiana in-sample descrive quanto bene il modello distingue i gruppi nei dati osservati, includendo l’incertezza parametrica;
- la cross-validation bayesiana estende questa analisi alla capacità del modello di generalizzare a nuovi dati, mantenendo la stessa coerenza probabilistica;
- anche se più costosa da implementare, essa rappresenta la forma più completa e coerente dal punto di vista teorico di valutazione predittiva bayesiana.
Riflessioni conclusive
- l’AUC misura la capacità discriminativa del modello indipendentemente dalla soglia di decisione;
- l’AUC “in-sample” può essere fuorviante: è necessario stimarla “out-of-sample”;
- L’approccio bayesiano permette di quantificare l’incertezza sull’AUC e di confrontare i modelli in base alla loro capacità predittiva (ad esempio, tramite ELPD o LOO-CV).
In psicologia, questo significa non solo valutare quanto bene un modello separa due gruppi, ma anche quanto è probabile che lo faccia con nuovi dati.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] pROC_1.19.0.1 glmnet_4.1-10 Matrix_1.7-4
#> [4] lubridate_1.9.4 HDInterval_0.2.4 cmdstanr_0.9.0
#> [7] ragg_1.5.0 tinytable_0.13.0 withr_3.0.2
#> [10] systemfonts_1.2.3 patchwork_1.3.2 ggdist_3.3.3
#> [13] tidybayes_3.0.7 bayesplot_1.14.0 ggplot2_4.0.0
#> [16] reliabilitydiag_0.2.1 priorsense_1.1.1 posterior_1.6.1
#> [19] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [22] brms_2.23.0 Rcpp_1.1.0 sessioninfo_1.2.3
#> [25] conflicted_1.2.0 janitor_2.2.1 matrixStats_1.5.0
#> [28] modelr_0.1.11 tibble_3.3.0 dplyr_1.1.4
#> [31] tidyr_1.3.1 rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 vctrs_0.6.5
#> [10] stringr_1.5.2 shape_1.4.6.1 pkgconfig_2.0.3
#> [13] arrayhelpers_1.1-0 fastmap_1.2.0 backports_1.5.0
#> [16] labeling_0.4.3 rmarkdown_2.30 ps_1.9.1
#> [19] purrr_1.1.0 xfun_0.53 cachem_1.1.0
#> [22] jsonlite_2.0.0 broom_1.0.10 parallel_4.5.1
#> [25] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [28] estimability_1.5.1 iterators_1.0.14 knitr_1.50
#> [31] zoo_1.8-14 pacman_0.5.1 splines_4.5.1
#> [34] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [37] yaml_2.3.10 codetools_0.2-20 processx_3.8.6
#> [40] curl_7.0.0 pkgbuild_1.4.8 lattice_0.22-7
#> [43] bridgesampling_1.1-2 S7_0.2.0 coda_0.19-4.1
#> [46] evaluate_1.0.5 survival_3.8-3 RcppParallel_5.1.11-1
#> [49] pillar_1.11.1 tensorA_0.36.2.1 foreach_1.5.2
#> [52] checkmate_2.3.3 stats4_4.5.1 distributional_0.5.0
#> [55] generics_0.1.4 rprojroot_2.1.1 rstantools_2.5.0
#> [58] scales_1.4.0 xtable_1.8-4 glue_1.8.0
#> [61] emmeans_1.11.2-8 tools_4.5.1 data.table_1.17.8
#> [64] mvtnorm_1.3-3 grid_4.5.1 QuickJSR_1.8.1
#> [67] colorspace_2.1-2 nlme_3.1-168 cli_3.6.5
#> [70] textshaping_1.0.3 svUnit_1.0.8 Brobdingnag_1.2-9
#> [73] V8_8.0.0 gtable_0.3.6 digest_0.6.37
#> [76] TH.data_1.1-4 htmlwidgets_1.6.4 farver_2.1.2
#> [79] memoise_2.0.1 htmltools_0.5.8.1 lifecycle_1.0.4
#> [82] MASS_7.3-65