Appendice L — Metropolis: esempio Normale–Normale

here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr)

In questa sezione di approfondimento applichiamo l’algoritmo di Metropolis a un caso in cui conosciamo la soluzione analitica: il modello Normale–Normale. L’obiettivo non è introdurre concetti nuovi, ma mostrare ancora una volta come l’algoritmo riesca a ricostruire una distribuzione a posteriori già nota, rafforzando l’intuizione costruita nel testo principale.

Supponiamo di voler stimare la media vera \(\mu\) di una popolazione. Abbiamo:

• un prior \(\mu \sim \mathcal{N}(30, 5^2)\),
• un insieme di dati \(y\) (30 osservazioni di punteggi BDI-II),
• una verosimiglianza normale con deviazione standard stimata dai dati.

Il modello è quindi:

\[ y_i \sim \mathcal{N}(\mu, \sigma^2), \qquad \mu \sim \mathcal{N}(30, 25). \]

L.1 Implementazione in R

Definizione delle funzioni prior, likelihood e posterior (non normalizzata):

prior <- function(mu) dnorm(mu, mean = 30, sd = 5)

likelihood <- function(mu, data) {
  sigma <- sd(data)
  prod(dnorm(data, mean = mu, sd = sigma))
}

posterior <- function(mu, data) {
  prior(mu) * likelihood(mu, data)
}

Algoritmo di Metropolis:

metropolis_for_normal <- function(nsamp, xinit, data) {
  samples <- numeric(nsamp)
  x_prev <- xinit
  for (i in seq_len(nsamp)) {
    x_star <- rnorm(1, mean = x_prev, sd = 0.5)
    if (runif(1) < min(1, posterior(x_star, data) / posterior(x_prev, data))) {
      x_prev <- x_star
    }
    samples[i] <- x_prev
  }
  samples
}

Dati osservati:

y <- c(
  26, 35, 30, 25, 44, 30, 33, 43, 22, 43,
  24, 19, 39, 31, 25, 28, 35, 30, 26, 31,
  41, 36, 26, 35, 33, 28, 27, 34, 27, 22
)

Esecuzione del campionamento:

set.seed(123)
samples <- metropolis_for_normal(100000, mean(y), y)

L.2 Confronto con la soluzione analitica

Nel caso Normale–Normale possiamo calcolare i parametri della distribuzione a posteriori esatta:

mu_prior <- 30; std_prior <- 5; var_prior <- std_prior^2
n <- length(y); sum_y <- sum(y); var_data <- var(y)

mu_post <- (mu_prior / var_prior + sum_y / var_data) / (1 / var_prior + n / var_data)
var_post <- 1 / (1 / var_prior + n / var_data)
std_post <- sqrt(var_post)

c(mu_post = mu_post, sd_post = std_post)
#> mu_post sd_post 
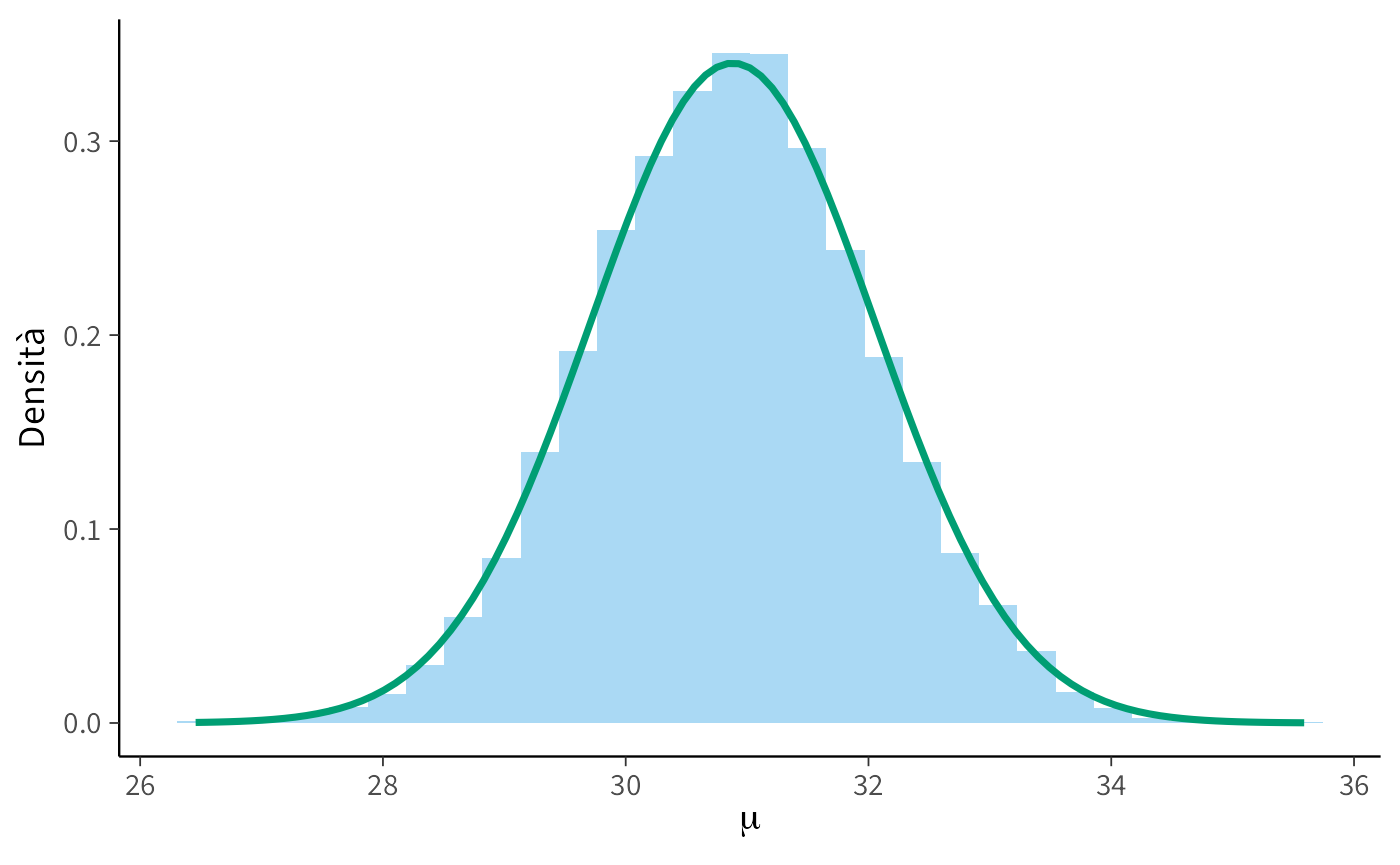
#>   30.88    1.17

Infine, confrontiamo graficamente l’istogramma dei campioni MCMC (dopo burn-in) con la densità analitica:

burnin <- 50000
post_samples <- samples[(burnin+1):length(samples)]

ggplot() +
  geom_histogram(
    aes(x = post_samples, y = after_stat(density)),
    bins = 30, fill = "#56B4E9", alpha = 0.5, color = NA
  ) +
  stat_function(
    fun = dnorm, args = list(mean = mu_post, sd = std_post),
    color = "#009E73", linewidth = 1.2
  ) +
  labs(x = expression(mu), y = "Densità") 

In conclusione, questo esempio conferma che l’algoritmo di Metropolis riesce a ricostruire accuratamente la distribuzione a posteriori anche in un modello con soluzione analitica nota. Dal punto di vista didattico, ciò offre un’ulteriore verifica intuitiva della validità dell’algoritmo.