42  Decisione ottimale e utilità attesa: l’approccio bayesiano

Introduzione

Ogni giorno ci troviamo di fronte a scelte che dobbiamo compiere in condizioni di incertezza. Quale metodo di studio adottare per prepararsi a un esame? Quale trattamento scegliere di fronte a una diagnosi medica complessa? Quale approccio terapeutico è meglio adottare quando un paziente presenta più disturbi? In ciascuna di queste situazioni, le nostre decisioni dipendono non solo dalle preferenze personali, ma anche dall’incertezza riguardo agli esiti futuri e dalla capacità di bilanciare obiettivi potenzialmente in conflitto tra loro.

L’analisi decisionale bayesiana offre un quadro teorico rigoroso per affrontare questo tipo di problemi, permettendoci di rendere espliciti e formalmente strutturati i ragionamenti che troppo spesso rimangono impliciti o intuitivi. L’idea di fondo è elegante nella sua semplicità: ogni alternativa possibile genera diversi esiti, ciascuno caratterizzato da una certa probabilità e da un valore associato in termini di utilità (quanto è desiderabile) o di perdita (quanto è costoso). La decisione migliore è quella che massimizza l’utilità attesa, oppure minimizza la perdita attesa, tenendo conto della distribuzione predittiva degli esiti e propagando in modo coerente tutta l’incertezza disponibile.

42.1 Modelli come strumenti di pensiero, non descrizioni del reale

È importante chiarire fin da subito la natura e la funzione di questo approccio. La teoria della decisione non pretende di essere una descrizione letterale di come le persone realmente prendono decisioni nella vita quotidiana: sappiamo bene che gli esseri umani si discostano frequentemente dalla razionalità bayesiana ideale, che le preferenze non sono sempre stabili e ben definite, che la capacità cognitiva è limitata e che le emozioni giocano un ruolo centrale. Tuttavia, come ha efficacemente sintetizzato George Box, “tutti i modelli sono sbagliati, ma alcuni sono utili”. La teoria della decisione non è un tentativo di imprigionare la complessità dell’esperienza umana in una formula matematica, ma piuttosto uno strumento analitico che ci permette di chiarire i trade-off impliciti nelle nostre scelte, di rendere trasparenti le assunzioni che stiamo facendo e di valutare sistematicamente la coerenza interna delle nostre preferenze.

In questo senso, l’approccio bayesiano alla decisione si configura come una forma di logica per il ragionamento sotto incertezza: non ci dice necessariamente come decidiamo, ma come dovremmo decidere se volessimo essere internamente coerenti con le informazioni disponibili e con le nostre preferenze dichiarate. Questa distinzione tra funzione descrittiva e funzione normativa è cruciale. Il valore dell’approccio non sta tanto nella sua accuratezza nel predire il comportamento effettivo, quanto nel fornire un punto di riferimento rispetto al quale comprendere dove e perché i processi decisionali reali si discostano dalla coerenza logica.

42.1.1 Decisioni umane nell’era dell’intelligenza artificiale

Negli ultimi anni, il dibattito sul ruolo della teoria della decisione ha assunto una nuova urgenza, in parte alimentato dal crescente utilizzo di sistemi di intelligenza artificiale nei processi decisionali. L’idea che “quasi ogni decisione potrebbe essere delegata a un algoritmo” ha suscitato comprensibili preoccupazioni riguardo alla perdita di agency umana e al rischio che interessi corporativi o politici possano plasmare le nostre scelte attraverso sistemi opachi. Di fronte a queste preoccupazioni, alcuni hanno reagito rifiutando in blocco l’idea stessa di formalizzare matematicamente le decisioni, considerandola intrinsecamente riduttiva o persino immorale.

Tuttavia, questa reazione rischia di confondere lo strumento con il suo uso. Il fatto che un approccio formale possa essere impiegato in modo problematico—come quando algoritmi decisionali vengono applicati senza trasparenza o riproducono discriminazioni sistemiche—non significa che dobbiamo rinunciare a tentare di comprendere razionalmente i nostri processi decisionali. Al contrario: è proprio quando affrontiamo decisioni complesse, potenzialmente assistite da tecnologie predittive, che diventa ancora più importante essere in grado di specificare esplicitamente quali sono i nostri obiettivi, come valutiamo i diversi esiti possibili, e quali assunzioni stiamo facendo. La formalizzazione non è un’abdicazione dell’autonomia umana, ma piuttosto uno strumento per esercitarla in modo più consapevole.

Quando, ad esempio, utilizziamo un sistema di intelligenza artificiale come supporto allo studio—uno dei temi che esploreremo in questo capitolo—non stiamo semplicemente delegando la decisione alla macchina. Stiamo piuttosto ponendo una domanda più sottile: dato che un certo strumento tecnologico può modificare sia i risultati attesi (ad esempio, il voto d’esame) sia i costi (ad esempio, il tempo necessario), come possiamo valutare se e quando tale strumento rappresenta effettivamente una scelta vantaggiosa? Per rispondere a questa domanda in modo rigoroso, abbiamo bisogno di un quadro che ci permetta di integrare previsioni probabilistiche, preferenze personali e criteri di scelta razionale. Questo è esattamente ciò che l’analisi decisionale bayesiana ci offre.

42.1.2 Il caso di studio: la scelta del metodo di studio

In questo capitolo applicheremo il quadro teorico della decisione bayesiana a un problema vicino all’esperienza degli studenti di psicologia: la scelta del metodo di studio. Considereremo tre possibili strategie, che si differenziano per impegno richiesto ed efficacia prevista:

  1. Metodo classico: studio individuale su testi ed esercizi, senza supporti interattivi.
  2. Metodo di gruppo: lo stesso approccio classico, arricchito da discussioni in piccoli gruppi per chiarire e consolidare i contenuti.
  3. Metodo con AI tutor: studio su testi integrato con spiegazioni alternative, chat interattiva ed esercizi generati automaticamente da un tutor basato su intelligenza artificiale.

Gli esiti che ci interessano sono due: il voto d’esame (\(g \in [0,100]\)) e le ore di studio necessarie (\(h \geq 0\)). Entrambi sono caratterizzati da incertezza, legata sia alle differenze individuali (abilità, motivazione, stile di apprendimento), sia alla variabilità intrinseca del processo di studio. È importante sottolineare che questa incertezza non è semplicemente un limite cognitivo da superare, ma una caratteristica intrinseca della realtà che stiamo modellando: anche con informazioni perfette sui parametri del modello, la variabilità individuale nelle risposte agli interventi educativi rimane una fonte irriducibile di imprevedibilità.

Il framework bayesiano ci consentirà di stimare la distribuzione congiunta di \((g,h)\) per ciascun metodo e di combinare voto e tempo in un’unica misura tramite una funzione di utilità. Per la discussione presente scegliamo la seguente funzione lineare:

\[ U(g,h;\lambda) = g - \lambda h, \]

dove \(\lambda \geq 0\) indica quanto “costa” un’ora di studio in termini di punti di voto. Questa specificazione, pur nella sua semplicità, rende esplicita una scelta di valore fondamentale: come bilanciare il risultato accademico con il tempo investito. Uno studente per cui \(\lambda = 0\) si preoccupa esclusivamente del voto massimo, indipendentemente dalle ore necessarie; uno studente con \(\lambda\) elevato valuta fortemente il proprio tempo e potrebbe preferire un metodo meno performante ma più efficiente. La bellezza di questo approccio risiede nel fatto che, una volta specificata la funzione di utilità, possiamo calcolare in modo sistematico l’utilità attesa di ciascun metodo, integrando l’incertezza attraverso simulazioni dalla distribuzione predittiva posteriore, e infine identificare l’opzione che ha maggiore probabilità di rappresentare la scelta ottimale per un dato profilo di preferenze.

42.1.3 Il valore della formalizzazione: rendere esplicito l’implicito

Prima di procedere con l’analisi tecnica, vale la pena soffermarsi sul valore stesso del tentativo di formalizzazione. Anche quando non riusciamo a definire perfettamente una funzione di utilità, o quando le nostre assunzioni risultano semplificate rispetto alla complessità del fenomeno reale, il solo fatto di dover esplicitare i nostri criteri di valutazione ci costringe a riflettere in modo più approfondito sui trade-off in gioco. Come nota la letteratura recente sulla comunicazione dell’incertezza statistica, molte ricerche che valutano l’efficacia di decisioni assistite da intelligenza artificiale non specificano chiaramente quale problema i partecipanti dovrebbero ottimizzare, lasciando così ambiguo il criterio stesso di successo. In assenza di una chiara formalizzazione del problema decisionale, è difficile distinguere tra scelte semplicemente diverse e scelte effettivamente subottimali.

La teoria della decisione, dunque, non è semplicemente uno strumento per calcolare la risposta “giusta” a un problema ben definito. È anche, e forse soprattutto, una metodologia per pensare che ci aiuta a identificare le domande rilevanti: quali sono i possibili esiti? Come li valutiamo? Quali informazioni sono rilevanti per la scelta? Come dovremmo aggiornare le nostre credenze di fronte a nuove evidenze? Quali assunzioni stiamo facendo tacitamente? Spesso, come vedremo nella discussione conclusiva, il valore maggiore non risiede nella risposta finale fornita dal modello, ma nel processo di riflessione innescato dal tentativo di modellizzazione.

Panoramica del capitolo

Il capitolo si articola nelle seguenti sezioni:

  • Le quattro fasi dell’analisi decisionale bayesiana.
  • Modellare la distribuzione predittiva degli esiti.
  • Formulare e interpretare una funzione di utilità.
  • Identificare la decisione ottimale.
  • Limiti del modello lineare e possibili estensioni.
  • Riflessioni conclusive sul ruolo dei modelli decisionali nella ricerca e nella pratica.
  • Per un’introduzione alla loss function, si rimanda al capitolo “Sampling the Imaginary” di Statistical Rethinking (McElreath, 2020).
here::here("code", "_common.R") |> 
  source()

# Additional packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, loo, cmdstanr, stringr, tidyr)

42.2 Schema in quattro passi

Seguendo l’impostazione proposta da Gelman et al. (2013), l’analisi decisionale bayesiana si articola in quattro fasi interconnesse: definizione del problema, modellazione degli esiti, specificazione della funzione di utilità e identificazione della decisione ottimale. Nel nostro caso, queste fasi vengono applicate alla scelta del metodo di studio più appropriato per preparare un esame di psicologia.

1. Definizione delle alternative e degli esiti

Le alternative decisionali disponibili sono tre: metodo classico (studio individuale tradizionale), studio di gruppo (approccio collaborativo), e AI tutor (studio assistito da intelligenza artificiale). Ogni decisione porta a due esiti di interesse che devono essere valutati congiuntamente: il voto d’esame \(g\) (compreso tra 0 e 100) e le ore di studio necessarie \(h\) (con \(h \geq 0\)). La natura bivariata degli esiti riflette il fatto che la qualità di un metodo di studio non può essere valutata considerando solo il risultato finale (il voto), ma deve tenere conto anche del costo in termini di tempo richiesto.

2. Modellazione della distribuzione predittiva

Per descrivere la variabilità dei risultati usiamo un modello statistico gerarchico che può essere stimato da dati storici (ad esempio, i registri di studenti dell’anno precedente o studi pilota). La scelta delle distribuzioni di probabilità riflette le caratteristiche intrinseche delle variabili in esame. Le ore di studio seguono una distribuzione lognormale, particolarmente adatta a variabili continue non negative che tendono a essere asimmetriche (la maggior parte degli studenti studia un numero “ragionevole” di ore, mentre alcuni valori estremi possono essere molto alti). Il voto, invece, dipende dalle ore in modo sublineare attraverso una trasformazione logaritmica, riflettendo il principio dei rendimenti decrescenti: inizialmente ogni ora extra di studio produce un guadagno sostanziale in termini di comprensione e preparazione, ma col tempo l’effetto marginale si attenua a causa di saturazione cognitiva e stanchezza.

3. Funzione di utilità

Per confrontare i metodi su un’unica scala di valutazione, combiniamo voto e ore in una funzione di utilità che quantifica la desiderabilità complessiva di ciascun esito. La forma più semplice è quella lineare:

\[ U(g,h;\lambda) = g - \lambda h, \]

dove \(\lambda \geq 0\) esprime il tasso marginale di sostituzione tra voto e tempo: quanto pesa un’ora di studio in termini di punti d’esame. Ad esempio, con \(\lambda=0\) lo studente si preoccupa esclusivamente di massimizzare il voto indipendentemente dal tempo investito, mentre con \(\lambda=2\) ogni ora di studio viene valutata come equivalente a una perdita di due punti d’esame. Questa parametrizzazione rende esplicita una scelta di valore che spesso rimane implicita nelle decisioni quotidiane: quanto è prezioso il nostro tempo rispetto al miglioramento della performance accademica?

4. Decisione ottimale

L’alternativa migliore è quella che massimizza l’utilità attesa, calcolata integrando l’incertezza sia sui parametri del modello (incertezza epistemica) sia sulla variabilità predittiva degli esiti per i futuri studenti (incertezza aleatoria). In pratica, questa integrazione si realizza tramite simulazioni dalla distribuzione predittiva posteriore: estraiamo campioni dai parametri stimati, generiamo predizioni per nuovi ipotetici studenti, e calcoliamo l’utilità per ciascuna realizzazione. Questo approccio Monte Carlo ci permette di ottenere un confronto robusto tra le opzioni disponibili che tiene conto di tutte le fonti di incertezza rilevanti.

42.3 Applicazione empirica: simulazione e analisi

42.3.1 Simulazione dei dati

Per illustrare concretamente il funzionamento dell’analisi decisionale bayesiana, iniziamo simulando un dataset. L’uso di dati simulati presenta un vantaggio pedagogico fondamentale: conosciamo i “veri” parametri del processo generativo e possiamo quindi verificare se il modello bayesiano riesce a recuperarli correttamente, validando così l’adeguatezza del nostro approccio inferenziale prima di applicarlo a dati reali.

Il campione simulato comprende 300 studenti, ciascuno assegnato casualmente a uno dei tre metodi di studio. La dimensione campionaria è stata scelta per bilanciare realismo (campioni troppo piccoli soffrirebbero di elevata incertezza) e praticità computazionale.

set.seed(1234)

# Numero di studenti
N <- 300
method_names <- c("classico", "AI", "gruppo")
d <- sample(1:3, N, replace = TRUE)  # Assegnazione casuale ai tre metodi

42.3.1.1 Distribuzione delle ore di studio

Per rendere l’esempio realistico, ipotizziamo che le ore di studio (\(H\)) seguano una distribuzione lognormale, che presenta diverse proprietà desiderabili: garantisce valori non negativi (non si può studiare un numero negativo di ore), ammette asimmetria positiva (la maggior parte degli studenti si colloca in una fascia “normale” mentre alcuni outlier studiano molto di più), e ha una coda destra relativamente pesante (valori estremi sono rari ma possibili).

Ciascun metodo è caratterizzato da parametri propri che riflettono differenze nella struttura temporale richiesta:

mu_h_true    <- log(c(8, 10, 16))   # mediane: ~8, ~10, ~16 ore
sigma_h_true <- c(0.30, 0.30, 0.50)

Questi valori riflettono uno scenario plausibile:

  • Metodo classico: mediana di ~8 ore, variabilità contenuta (σ = 0.30). Rappresenta l’approccio tradizionale più snello ma con risultati più standardizzati.
  • Metodo AI: mediana di ~10 ore, variabilità contenuta (σ = 0.30). L’AI tutor richiede un investimento temporale leggermente superiore per familiarizzare con lo strumento, ma mantiene prevedibilità nei tempi.
  • Metodo gruppo: mediana di ~16 ore, variabilità elevata (σ = 0.50). Lo studio collaborativo richiede sostanzialmente più tempo (coordinamento, discussioni, velocità dettata dal gruppo) e presenta maggiore eterogeneità (dipende fortemente dalla composizione e dinamica del gruppo).

42.3.1.2 Modello per il voto d’esame

Il voto d’esame (\(G\)) dipende dalle ore di studio attraverso una relazione a rendimenti decrescenti, modellata tramite la funzione logaritmica. Questa scelta riflette un principio consolidato nella psicologia dell’apprendimento: l’efficacia marginale dello studio diminuisce progressivamente. Le prime ore sono estremamente produttive (si acquisiscono i concetti fondamentali, si costruisce una struttura di conoscenza), ma col tempo l’apprendimento incrementale rallenta a causa di saturazione cognitiva, stanchezza, e rendimenti decrescenti dell’attenzione.

# Parametri veri per il voto
alpha_true   <- c(55, 78, 58)    # Intercette (livello base di preparazione)
beta_true    <- c(5.5, 7.5, 6.5) # Pendenze (efficienza di apprendimento)
sigma_g_true <- 5.5               # Deviazione standard residua

Questi parametri codificano differenze qualitative sostanziali tra i metodi:

  • Metodo classico: intercetta bassa (α = 55) e efficienza moderata (β = 5.5). Rappresenta l’approccio meno performante: parte da una base di conoscenza limitata e converte le ore di studio in apprendimento con efficienza contenuta.
  • Metodo AI: intercetta elevata (α = 78) ed efficienza elevata (β = 7.5). Il tutor AI fornisce una base di conoscenza solida fin dall’inizio (spiegazioni personalizzate, esempi mirati) e massimizza l’efficacia di ogni ora investita. Questo è il metodo più performante in assoluto.
  • Metodo gruppo: intercetta intermedia (α = 58) ed efficienza buona (β = 6.5). La discussione collettiva offre benefici in termini di comprensione profonda, ma non raggiunge l’ottimizzazione del tutor AI.

42.3.1.3 Costo orario e generazione dei dati

Specifichiamo il costo orario in termini di punti d’esame:

lambda <- 0.8  # Ogni ora "costa" 0.8 punti di voto

Questo valore riflette uno scenario in cui il tempo ha un valore moderato ma non trascurabile. Uno studente con \(\lambda = 0.8\) è disposto a “sacrificare” 0.8 punti di voto pur di risparmiare un’ora di studio (ad esempio, per lavorare, riposare, o dedicarsi ad altre attività).

Generiamo ora le osservazioni simulate applicando il processo generativo specificato:

# Generazione delle ore di studio
h <- rlnorm(N, meanlog = mu_h_true[d], sdlog = sigma_h_true[d])

# Valore atteso del voto (dipende dalle ore con rendimenti decrescenti)
mu <- alpha_true[d] + beta_true[d] * log1p(h)

# Generazione del voto (con variabilità individuale)
g <- rnorm(N, mu, sigma_g_true)

# Vincolo ai limiti della scala di valutazione [0, 100]
g <- pmin(pmax(g, 0), 100)

# Costruzione del dataframe
df_sim <- data.frame(
  method = factor(method_names[d], levels = method_names),
  g = g,
  h = h
)

42.3.1.4 Visualizzazione delle utilità simulate

Calcoliamo l’utilità vera per ciascuno studente e visualizziamo come si distribuisce nei tre gruppi:

u_true <- g - lambda * h
df_sim$u <- u_true

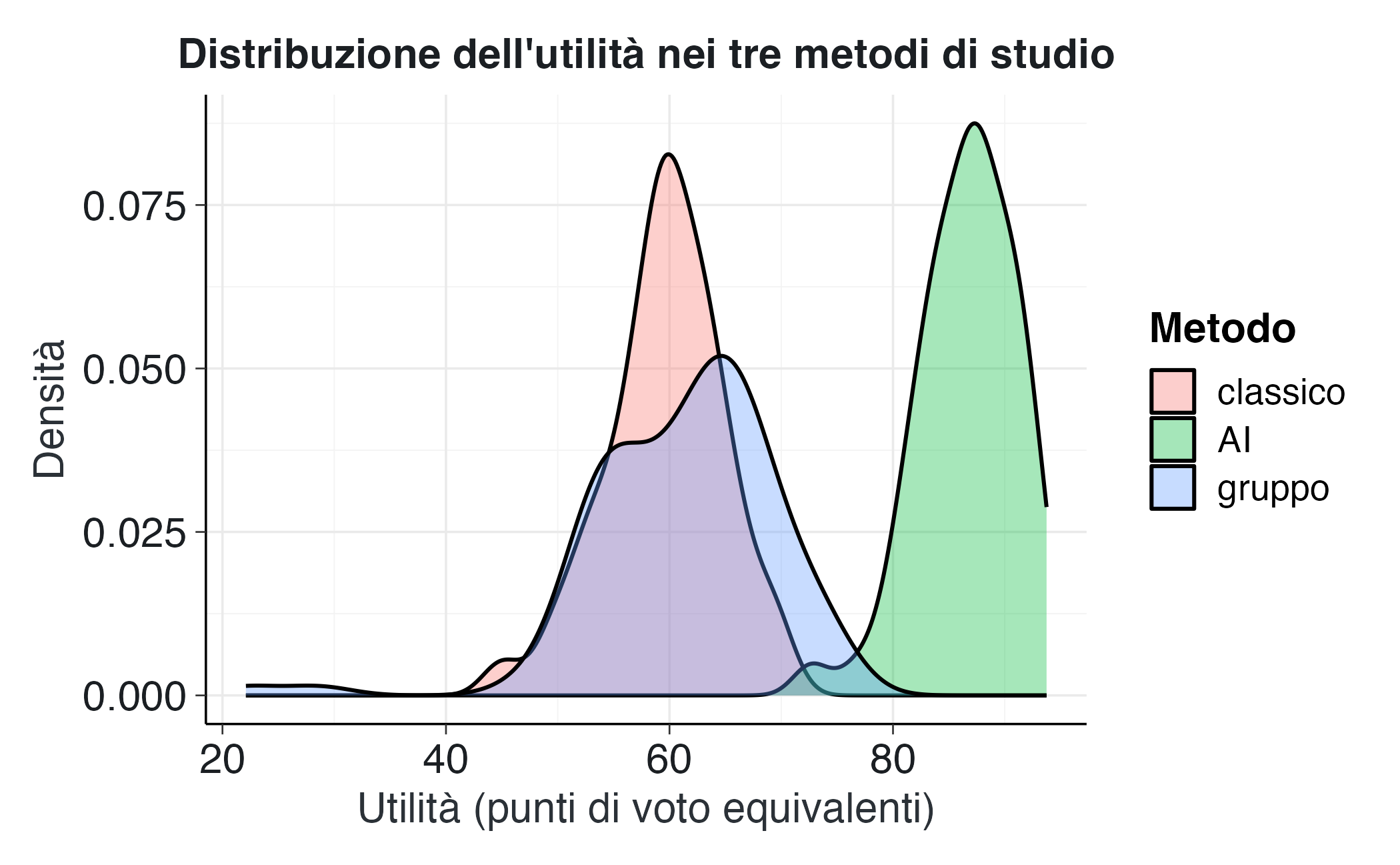
ggplot(df_sim, aes(x = u, fill = method)) +
  geom_density(alpha = 0.35) +
  labs(
    title = "Distribuzione dell'utilità nei tre metodi di studio",
    x = "Utilità (punti di voto equivalenti)",
    y = "Densità",
    fill = "Metodo"
  )

Questo primo grafico ci permette di visualizzare immediatamente la struttura del problema. Ci aspettiamo di osservare tre distribuzioni con centri e dispersioni diverse, riflettendo i differenti trade-off tra voto e tempo caratteristici di ciascun metodo. Il metodo AI dovrebbe mostrare una distribuzione spostata verso destra (utilità più elevate), mentre il metodo classico e quello di gruppo dovrebbero collocarsi più a sinistra. La sovrapposizione parziale tra le distribuzioni evidenzia che, a livello individuale, la scelta ottimale può variare: alcuni studenti potrebbero ottenere risultati eccellenti anche con metodi mediamente meno performanti.

42.3.2 Stima del modello bayesiano

Ora formuliamo e stimiamo il modello bayesiano che descrive formalmente le relazioni tra metodo di studio, ore investite e voto conseguito. Il modello si compone di due sottostrutture che riflettono la natura bivariata degli esiti:

Modello per le ore di studio: \[ H_i \sim \text{LogNormal}(\mu_{h,d_i}, \sigma_{h,d_i}), \] dove \(d_i \in \{1, 2, 3\}\) indica il metodo scelto dallo studente \(i\). Ogni metodo ha quindi parametri di locazione (\(\mu_h\), sulla scala logaritmica) e di scala (\(\sigma_h\)) propri, permettendo di catturare differenze sia nella tendenza centrale che nella variabilità delle ore richieste.

Modello per il voto: \[ G_i \sim \text{Normal}(\alpha_{d_i} + \beta_{d_i} \log(1 + H_i), \sigma_g), \] dove \(\alpha_d\) rappresenta il livello base di preparazione (l’“intercetta” sulla scala del voto), \(\beta_d\) quantifica l’efficienza di apprendimento (quanto voto si guadagna aumentando di un’unità il logaritmo delle ore), e \(\sigma_g\) è la deviazione standard residua, che assumiamo omoschedastica (comune a tutti i metodi). La trasformazione \(\log(1 + H)\) implementa rendimenti decrescenti: il primo termine della serie di Taylor è lineare, ma la concavità della funzione logaritmica cattura il fatto che raddoppiare le ore non raddoppia il voto.

È importante notare che questi due modelli possono essere stimati separatamente senza perdita di informazione: le ore di studio dipendono solo dal metodo (sono generate prima della realizzazione del voto), mentre il voto è condizionato alle ore ma, dato \(H\), non fornisce informazione aggiuntiva sui parametri del modello per \(H\). Questa indipendenza condizionale semplifica notevolmente la stima e migliora la convergenza dell’algoritmo MCMC.

42.3.2.1 Stima del modello per le ore di studio

Iniziamo stimando il modello per le ore:

# Modello per le ore di studio
fit_h <- brm(
  bf(h ~ 0 + method,                # Media dipende dal metodo (no intercetta globale)
     sigma ~ 0 + method),           # Anche la varianza dipende dal metodo
  data = df_sim,
  family = lognormal(),
  prior = c(
    prior(normal(2, 1), class = "b"),            # Prior per mu_h (scala log)
    prior(normal(-1, 1), class = "b", dpar = "sigma")  # Prior per log(sigma_h)
  ),
  iter = 2000, 
  warmup = 1000, 
  chains = 4,
  cores = 4,
  control = list(adapt_delta = 0.95),  # Maggiore accuratezza nella fase di adattamento
  seed = 123
)
# Verifica convergenza
summary(fit_h)
#>  Family: lognormal 
#>   Links: mu = identity; sigma = log 
#> Formula: h ~ 0 + method 
#>          sigma ~ 0 + method
#>    Data: df_sim (Number of observations: 300) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>                      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
#> methodclassico           2.10      0.04     2.03     2.17 1.00     6228
#> methodAI                 2.30      0.03     2.24     2.35 1.00     5877
#> methodgruppo             2.82      0.06     2.70     2.93 1.00     5948
#> sigma_methodclassico    -1.11      0.08    -1.25    -0.96 1.00     6165
#> sigma_methodAI          -1.21      0.07    -1.35    -1.07 1.00     5427
#> sigma_methodgruppo      -0.62      0.07    -0.75    -0.48 1.00     5121
#>                      Tail_ESS
#> methodclassico           2565
#> methodAI                 2771
#> methodgruppo             2870
#> sigma_methodclassico     2261
#> sigma_methodAI           3020
#> sigma_methodgruppo       2696
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

I diagnostici di convergenza principali da verificare sono:

  • Rhat ≈ 1.00: Indica convergenza tra le catene. Valori maggiori di 1.01 segnalano potenziali problemi.
  • ESS (Effective Sample Size) > 1000: Misura il numero effettivo di campioni indipendenti. Valori bassi indicano autocorrelazione elevata.
  • Absence of divergences: Le transizioni divergenti segnalano difficoltà nell’esplorazione dello spazio dei parametri.

Se i valori diagnostici sono soddisfacenti, possiamo procedere con la stima del secondo modello.

42.3.2.2 Stima del modello per il voto

# Modello per il voto (condizionato alle ore osservate)
fit_g <- brm(
  bf(g ~ 0 + method + method:log1p(h)),  # Intercette + pendenze specifiche per metodo
  data = df_sim,
  family = gaussian(),
  prior = c(
    # Prior per le intercette (alpha)
    prior(normal(70, 20), class = "b", coef = "methodclassico"),
    prior(normal(70, 20), class = "b", coef = "methodAI"),
    prior(normal(70, 20), class = "b", coef = "methodgruppo"),
    # Prior per le pendenze (beta)
    prior(normal(10, 5), class = "b", coef = "methodclassico:log1ph"),
    prior(normal(10, 5), class = "b", coef = "methodAI:log1ph"),
    prior(normal(10, 5), class = "b", coef = "methodgruppo:log1ph"),
    # Prior per la deviazione standard residua
    prior(exponential(0.1), class = "sigma")
  ),
  iter = 2000, 
  warmup = 1000, 
  chains = 4,
  cores = 4,
  control = list(adapt_delta = 0.95),
  seed = 123
)
# Verifica convergenza
summary(fit_g)
#>  Family: gaussian 
#>   Links: mu = identity 
#> Formula: g ~ 0 + method + method:log1p(h) 
#>    Data: df_sim (Number of observations: 300) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>                       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
#> methodclassico           55.03      3.71    48.04    62.64 1.00     1794
#> methodAI                 79.23      4.02    71.51    87.00 1.00     1972
#> methodgruppo             57.07      2.83    51.30    62.49 1.00     2171
#> methodclassico:log1ph     5.15      1.66     1.79     8.23 1.00     1801
#> methodAI:log1ph           6.52      1.67     3.35     9.69 1.00     1959
#> methodgruppo:log1ph       6.80      0.97     4.96     8.79 1.00     2143
#>                       Tail_ESS
#> methodclassico            1887
#> methodAI                  2478
#> methodgruppo              1883
#> methodclassico:log1ph     1850
#> methodAI:log1ph           2514
#> methodgruppo:log1ph       1886
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     4.95      0.20     4.57     5.37 1.00     3093     2497
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Una volta stimati entrambi i modelli, possiamo confrontare i parametri stimati con i valori veri utilizzati nella simulazione. Questo passaggio di validazione è essenziale in un contesto didattico: ci rassicura che il modello è specificato correttamente e che l’inferenza bayesiana funziona come previsto. In un’analisi con dati reali, non avremmo accesso ai “veri” valori, ma la validazione su dati simulati ci dà fiducia nell’affidabilità della procedura.

42.3.3 Distribuzione predittiva e calcolo dell’utilità attesa

Ora che abbiamo stimato i parametri, possiamo generare previsioni per nuovi ipotetici studenti che adotteranno ciascuno dei tre metodi. Questo processo simula la distribuzione predittiva posteriore degli esiti \((G, H)\), integrando sia l’incertezza sui parametri (incertezza epistemica: quanto siamo sicuri delle stime?) sia la variabilità individuale (incertezza aleatoria: quanto variano i risultati tra studenti simili?).

La procedura si articola in due passi che rispecchiano la struttura causale del processo:

42.3.3.1 Passo 1: Simulazione delle ore di studio

Per ciascun metodo, generiamo predizioni delle ore che un nuovo studente investirebbe:

# Creiamo un dataset con i tre metodi
newdata <- data.frame(method = factor(method_names, levels = method_names))

# Simuliamo le ore di studio dalla distribuzione predittiva
H_pred <- posterior_predict(fit_h, newdata = newdata, ndraws = 4000)
# H_pred è una matrice 4000 × 3: ogni riga è un'estrazione dalla posteriore,
# ogni colonna corrisponde a un metodo

Ogni riga di H_pred rappresenta una possibile realizzazione del numero di ore per i tre metodi, generata da un particolare set di parametri estratti dalla distribuzione posteriore.

42.3.3.2 Passo 2: Simulazione dei voti condizionati alle ore

Per ciascun metodo e per ciascuna realizzazione delle ore simulate al passo precedente, generiamo una predizione del voto conseguito:

n_draws <- nrow(H_pred)
n_methods <- length(method_names)

# Matrice per contenere le predizioni dei voti
G_pred <- matrix(NA, nrow = n_draws, ncol = n_methods)

# Per ogni metodo
for (j in 1:n_methods) {
  # Creiamo un dataset che abbina il metodo j con le ore simulate per quel metodo
  newdata_g <- data.frame(
    method = factor(rep(method_names[j], n_draws), levels = method_names),
    h = H_pred[, j]  # Ore simulate al passo precedente
  )
  
  # Generiamo i voti condizionati a queste ore
  G_pred[, j] <- posterior_predict(
    fit_g, 
    newdata = newdata_g, 
    ndraws = 1,           # Un solo draw per riga (già abbiamo variabilità da H_pred)
    draw_ids = 1:n_draws  # Usiamo gli stessi draw della posteriore di H
  )[, 1]
}

Questo approccio è corretto perché rispetta la struttura di dipendenza: prima si determina quanto tempo si studierà (dipende solo dal metodo), poi si osserva il voto conseguito (dipende dal tempo investito e dal metodo).

42.3.3.3 Calcolo dell’utilità attesa

Ora possiamo calcolare l’utilità per ciascuna simulazione, applicando la funzione di utilità specificata:

# Calcolo dell'utilità: U = g - λh
U_pred <- G_pred - lambda * H_pred

# Conversione in formato tidy per la visualizzazione
U_df <- as.data.frame(U_pred)
colnames(U_df) <- method_names

U_long <- U_df |>
  mutate(draw = row_number()) |>
  pivot_longer(
    cols = all_of(method_names), 
    names_to = "metodo", 
    values_to = "utilità"
  )

42.3.3.4 Visualizzazione delle distribuzioni di utilità

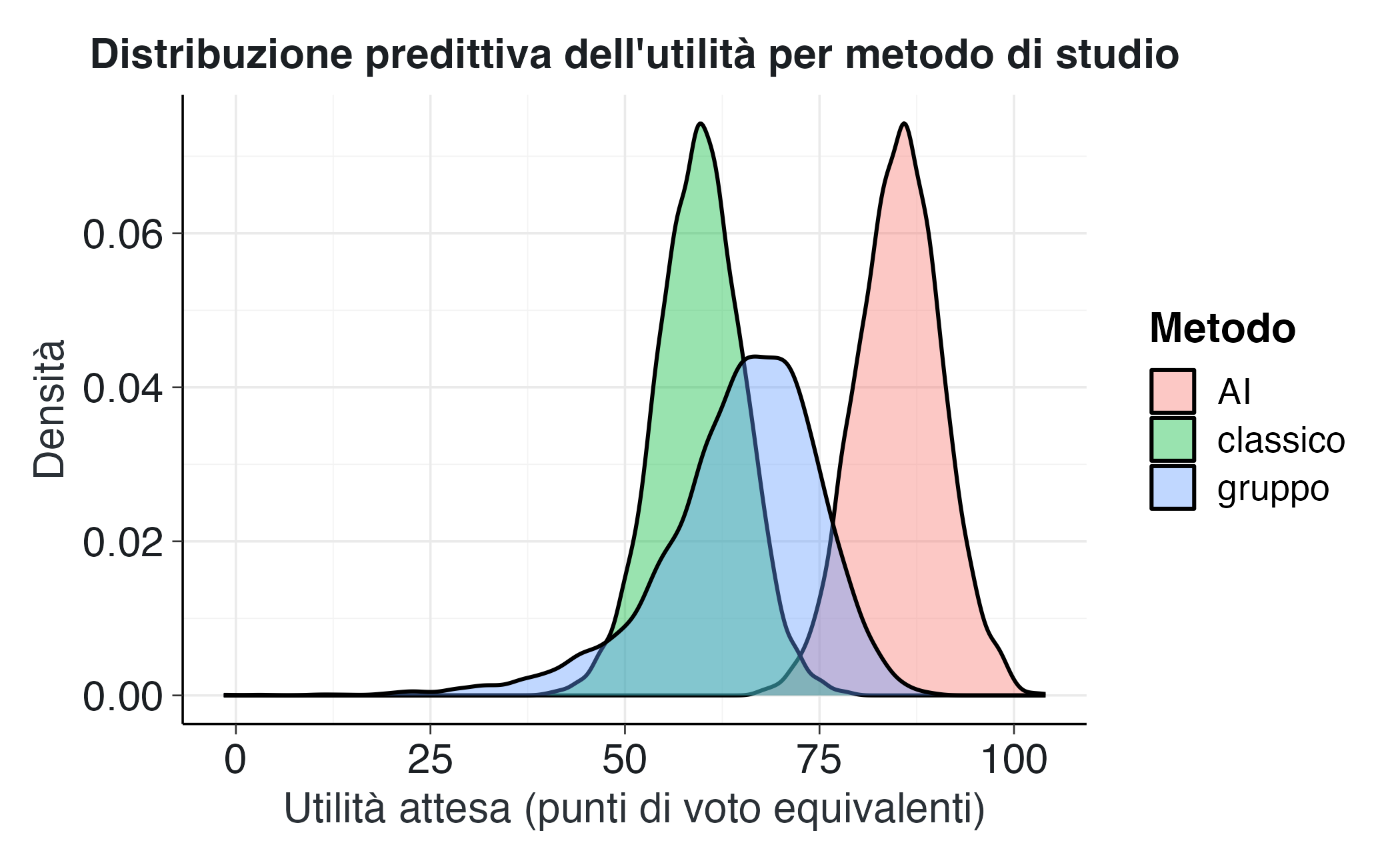
ggplot(U_long, aes(x = utilità, fill = metodo)) +
  geom_density(alpha = 0.4) +
  labs(
    title = "Distribuzione predittiva dell'utilità per metodo di studio",
    x = "Utilità attesa (punti di voto equivalenti)",
    y = "Densità",
    fill = "Metodo"
  )

Questo grafico è cruciale per l’interpretazione. Mostra come si distribuiscono le utilità attese tenendo conto di tutta l’incertezza disponibile. Alcuni aspetti chiave da osservare:

  • Posizione delle distribuzioni: Una distribuzione spostata verso destra indica maggiore utilità attesa. Se il metodo AI è chiaramente a destra rispetto agli altri, significa che in media produce risultati superiori per questo valore di \(\lambda\).
  • Dispersione: Una distribuzione più stretta indica prevedibilità; una più larga indica maggiore variabilità nei risultati (maggiore rischio).
  • Sovrapposizione: Le aree di sovrapposizione evidenziano che, a livello individuale, la scelta ottimale può variare. Non esiste una soluzione universalmente ottimale per tutti gli studenti.

42.3.4 Identificazione della decisione ottimale

Per identificare quale metodo sia ottimale in media, calcoliamo per ogni simulazione quale dei tre metodi produce la massima utilità. Questo ci fornisce una distribuzione di probabilità sulla decisione ottimale che quantifica la nostra incertezza:

# Per ogni draw, identifichiamo il metodo con utilità massima
best_method <- apply(U_pred, 1, which.max)
best_method_names <- method_names[best_method]

# Probabilità posteriore che ciascun metodo sia ottimale
prob_best <- table(best_method_names) / length(best_method_names)
print("Probabilità posteriore di essere il metodo ottimale:")
#> [1] "Probabilità posteriore di essere il metodo ottimale:"
print(prob_best)
#> best_method_names
#>       AI classico   gruppo 
#>   0.9792   0.0005   0.0203

Questo approccio ci fornisce non solo una risposta punto (“il metodo AI è il migliore”), ma anche una quantificazione completa dell’incertezza associata. Ad esempio:

  • Se il metodo AI ha probabilità 0.85 di essere ottimale, ciò significa che nel 15% delle simulazioni dalla posteriore un altro metodo risulta preferibile. Questa incertezza residua riflette sia l’incertezza parametrica (non conosciamo i parametri con certezza infinita) sia la variabilità predittiva (anche con parametri noti perfettamente, i risultati individuali variano).
  • Se le probabilità fossero più equilibrate (ad esempio, 0.40-0.35-0.25), ciò indicherebbe sostanziale incertezza sulla scelta ottimale, suggerendo che ulteriori dati potrebbero essere preziosi per ridurre l’ambiguità.
  • Se un metodo avesse probabilità ≈ 1.00, la conclusione sarebbe molto robusta: praticamente tutte le realizzazioni plausibili dei parametri portano alla stessa raccomandazione.

È importante interpretare queste probabilità nel contesto della funzione di utilità specificata. Queste sono probabilità condizionate a \(\lambda = 0.8\): se il costo del tempo cambia, cambiano anche le conclusioni.

42.3.5 Analisi di sensibilità: il ruolo di \(\lambda\)

Un aspetto fondamentale dell’analisi decisionale bayesiana è riconoscere esplicitamente che la scelta ottimale dipende dalla funzione di utilità specificata. Nel nostro caso, il parametro \(\lambda\) codifica una preferenza soggettiva fondamentale: quanto vale il tempo rispetto ai punti di voto. Diverse persone hanno valori diversi di \(\lambda\):

  • Uno studente a tempo pieno con poche altre responsabilità potrebbe avere \(\lambda\) basso (il tempo è relativamente abbondante).
  • Uno studente lavoratore con vincoli temporali stringenti potrebbe avere \(\lambda\) elevato (il tempo è estremamente prezioso).
  • Uno studente che punta a voti altissimi per ottenere una borsa di studio potrebbe avere \(\lambda\) molto basso (il voto ha priorità assoluta).

È quindi cruciale esplorare come cambiano le conclusioni al variare di questo parametro. Conduciamo un’analisi di sensibilità sistematica:

# Range di valori di lambda da esplorare
lambda_values <- seq(0, 2, by = 0.1)
results <- data.frame()

# Per ciascun valore di lambda
for (lambda_val in lambda_values) {
  # Ricalcoliamo le utilità
  U_temp <- G_pred - lambda_val * H_pred
  
  # Identifichiamo il metodo ottimale per ogni draw
  best <- method_names[apply(U_temp, 1, which.max)]
  
  # Calcoliamo le probabilità
  probs <- table(best) / nrow(U_temp)
  
  # Costruiamo un dataframe con i risultati
  prob_df <- data.frame(
    metodo = method_names,
    probabilità = as.numeric(probs[method_names]),
    lambda = lambda_val
  )
  
  # Gestiamo il caso in cui un metodo non sia mai ottimale
  prob_df$probabilità[is.na(prob_df$probabilità)] <- 0
  
  results <- rbind(results, prob_df)
}

Visualizziamo i risultati:

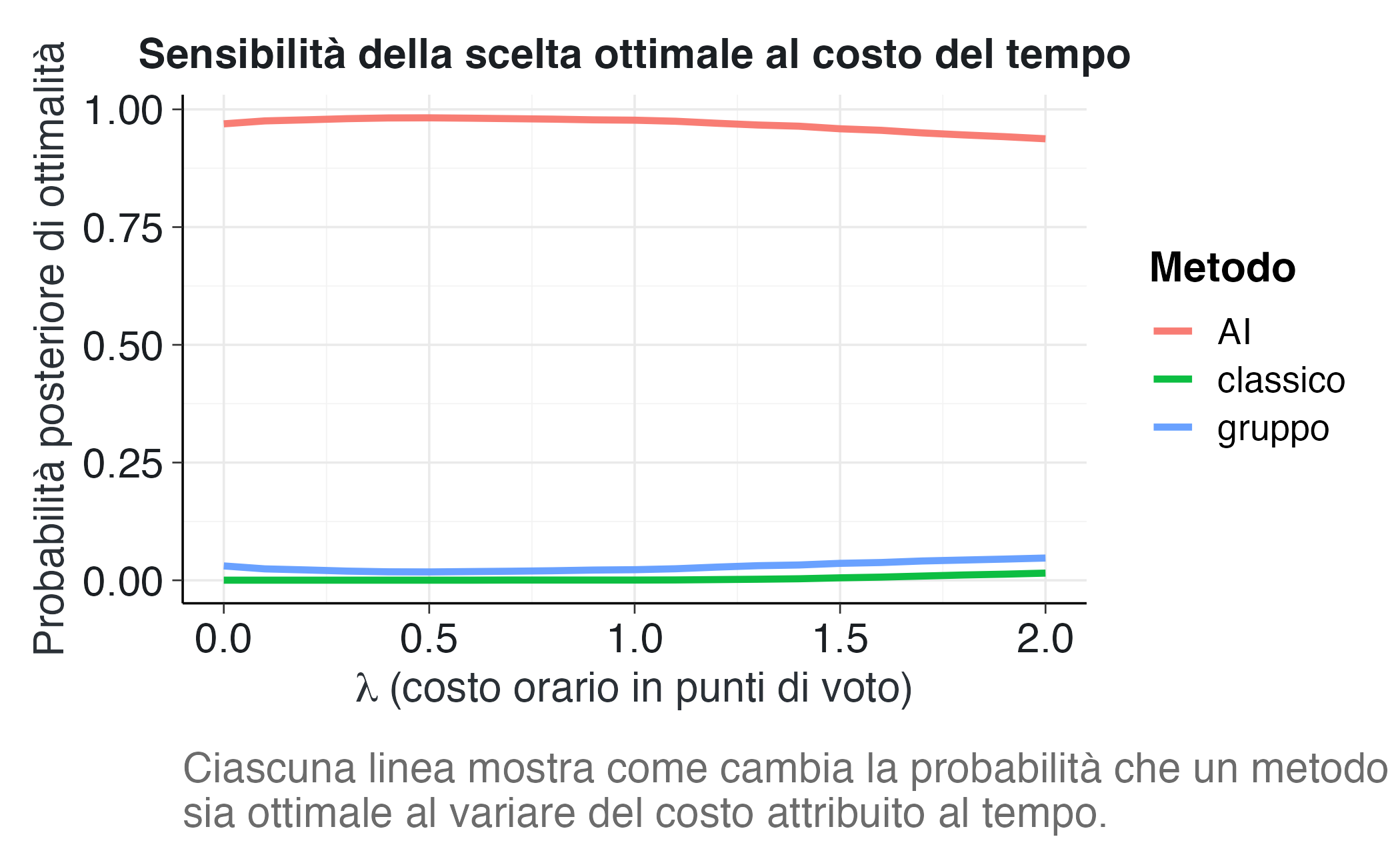
ggplot(results, aes(x = lambda, y = probabilità, color = metodo)) +
  geom_line(linewidth = 1.2) +
  labs(
    title = "Sensibilità della scelta ottimale al costo del tempo",
    x = expression(lambda ~ "(costo orario in punti di voto)"),
    y = "Probabilità posteriore di ottimalità",
    color = "Metodo",
    caption = "Ciascuna linea mostra come cambia la probabilità che un metodo\nsia ottimale al variare del costo attribuito al tempo."
  )

42.3.5.1 Interpretazione dell’analisi di sensibilità

Questo grafico è particolarmente informativo e merita un’analisi attenta:

Regione \(\lambda \approx 0\) (tempo trascurabile): Quando il tempo ha costo quasi nullo, la decisione si basa esclusivamente sul voto atteso. In questa regione, il metodo che produce i voti più alti domina, indipendentemente dalle ore richieste. Se osserviamo che il metodo AI o gruppo prevale qui, ciò conferma che questi metodi producono voti mediamente più alti del metodo classico.

Regione intermedia (\(\lambda \approx 0.5-1.5\)): Questa è la regione in cui il trade-off tra voto e tempo diventa cruciale. Possono emergere incroci tra le curve, indicando punti di indifferenza: valori di \(\lambda\) per cui due metodi hanno uguale probabilità di essere ottimali. Questi punti sono particolarmente rilevanti: identificano soglie oltre le quali cambia la raccomandazione. Ad esempio, se le curve di AI e gruppo si incrociano a \(\lambda \approx 1.2\), ciò significa che: - Per \(\lambda < 1.2\) (tempo relativamente poco costoso), preferire AI - Per \(\lambda > 1.2\) (tempo molto costoso), potrebbe diventare preferibile un metodo più rapido

Regione \(\lambda\) elevato (tempo molto prezioso): Quando il tempo è estremamente costoso, diventa ottimale il metodo che richiede meno ore, anche se produce voti inferiori. Il metodo classico, pur essendo meno performante, potrebbe dominare in questa regione se è significativamente più rapido.

Robustezza della conclusione: Se una curva domina (rimane sopra le altre) su un ampio range di \(\lambda\), la conclusione è robusta rispetto alle preferenze individuali. Se invece le curve si incrociano più volte, ciò suggerisce che la raccomandazione ottimale è fortemente dipendente dalle preferenze specifiche dello studente, e sarebbe opportuno personalizzare il consiglio.

42.3.6 Confronti alternativi: efficienza a parità di ore e a parità di voto

Oltre a confrontare le utilità attese nell’approccio generale appena discusso, possiamo esplorare domande più specifiche che riflettono prospettive decisionali complementari. Questi confronti alternativi sono utili perché:

  1. Offrono intuizioni più dirette e interpretabili per chi ha difficoltà con il concetto astratto di “utilità”
  2. Permettono di valutare i metodi da angolature diverse, arricchendo la comprensione
  3. Possono essere più rilevanti per studenti con vincoli specifici (budget temporale fisso, voto minimo richiesto)

42.3.6.1 Confronto a ore costanti: efficienza nella conversione del tempo

Supponiamo che uno studente abbia un vincolo temporale rigido (ad esempio, può dedicare solo 15 ore allo studio a causa di impegni lavorativi). La domanda diventa: a parità di tempo investito, quale metodo produce il voto più alto?

Questo confronto isola l’efficienza pura nella conversione del tempo in apprendimento, neutralizzando le differenze nel tempo richiesto.

# Fissiamo un budget temporale
H_fixed <- 15

# Estraiamo i parametri stimati del modello per i voti
draws_g <- as_draws_df(fit_g)

# Per ciascun metodo, calcoliamo la distribuzione predittiva del voto
# condizionata a h = H_fixed
G_at_H <- lapply(method_names, function(m) {
  # Estraiamo i parametri specifici per questo metodo
  alpha <- draws_g[[paste0("b_method", m)]]
  beta <- draws_g[[paste0("b_method", m, ":log1ph")]]
  sigma <- draws_g$sigma
  
  # Valore atteso del voto per h = H_fixed
  mu <- alpha + beta * log1p(H_fixed)
  
  # Aggiungiamo la variabilità predittiva individuale
  rnorm(length(mu), mu, sigma)
})

names(G_at_H) <- method_names
G_df <- as.data.frame(G_at_H)

# Conversione in formato tidy
G_long <- G_df |>
  pivot_longer(everything(), names_to = "metodo", values_to = "voto")

Visualizziamo le distribuzioni:

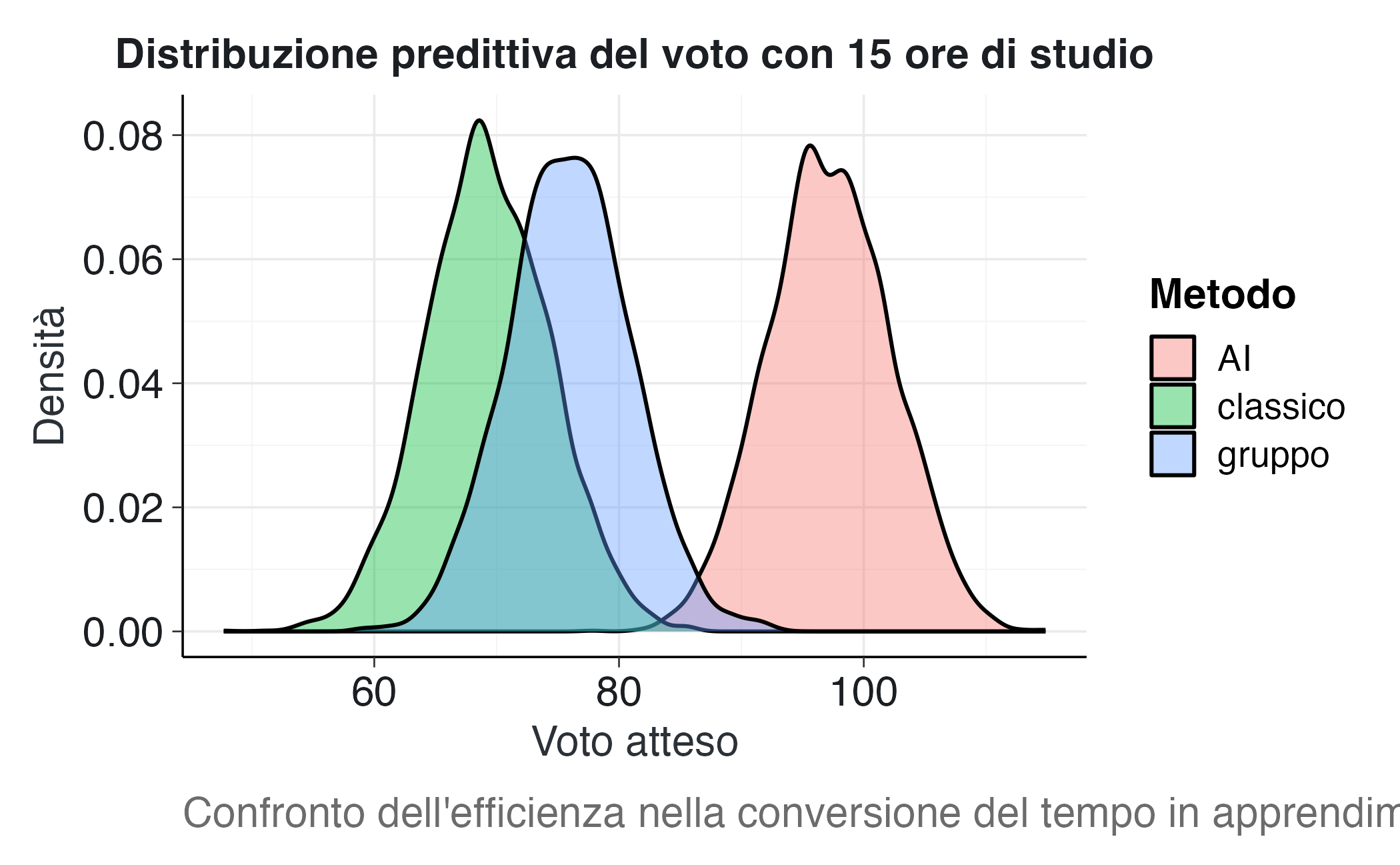
ggplot(G_long, aes(x = voto, fill = metodo)) +
  geom_density(alpha = 0.4) +
  labs(
    title = sprintf("Distribuzione predittiva del voto con %d ore di studio", H_fixed),
    x = "Voto atteso",
    y = "Densità",
    fill = "Metodo",
    caption = "Confronto dell'efficienza nella conversione del tempo in apprendimento."
  )

Interpretazione:

  • Se il metodo AI produce una distribuzione spostata significativamente a destra, ciò dimostra la sua superiorità in termini di efficienza: a parità di tempo, genera voti più alti.
  • La dispersione delle distribuzioni indica la prevedibilità: una distribuzione stretta significa risultati più consistenti.
  • Questo confronto è particolarmente rilevante per studenti con vincoli temporali rigidi: se ho solo 15 ore disponibili, quale metodo mi dà le migliori chances di un buon voto?

Possiamo anche calcolare metriche sintetiche:

G_df |>
  pivot_longer(everything(), names_to = "metodo", values_to = "voto") |>
  group_by(metodo) |>
  summarize(
    media = mean(voto),
    mediana = median(voto),
    sd = sd(voto),
    q05 = quantile(voto, 0.05),
    q95 = quantile(voto, 0.95)
  ) |>
  arrange(desc(media))
#> # A tibble: 3 × 6
#>   metodo   media mediana    sd   q05   q95
#>   <chr>    <dbl>   <dbl> <dbl> <dbl> <dbl>
#> 1 AI        97.2    97.2  5.02  89.0 106. 
#> 2 gruppo    76.0    76.0  5.01  67.8  84.1
#> 3 classico  69.3    69.1  5.06  60.9  77.7

Queste statistiche riassuntive permettono confronti diretti: quanto guadagno in voto atteso scegliendo AI invece di classico? Quanto rischio (variabilità) devo accettare con il metodo gruppo?

42.3.6.2 Confronto a voto costante: efficienza temporale

Un’altra prospettiva complementare è fissare un voto obiettivo e chiedersi: quante ore servono per raggiungerlo con ciascun metodo? Questo confronto valuta l’efficienza temporale: se tutti e tre i metodi possono portarmi a 80/100, quale ci arriva più rapidamente?

Questa prospettiva è rilevante per studenti che hanno un target chiaro (ad esempio, raggiungere la sufficienza, ottenere un voto per una borsa di studio) e vogliono minimizzare il tempo necessario.

Fissiamo alcuni voti obiettivo rappresentativi:

G_targets <- c(75, 80, 85)  # Buono, Ottimo, Eccellente

Dalla formula del modello, \(G = \alpha + \beta \log(1 + H)\), possiamo invertire per ottenere le ore richieste:

\[ H_{\text{req}} = \exp\left(\frac{G_0 - \alpha}{\beta}\right) - 1 \]

dove \(G_0\) è il voto obiettivo. Implementiamo questa inversione:

# Funzione: ore necessarie per raggiungere G0
Hreq_fun <- function(G0, alpha, beta) {
  # Proteggiamo contro valori impossibili (G0 < alpha implicherebbe h < 0)
  pmax(exp((G0 - alpha) / beta) - 1, 0)
}

# Per ciascun voto target, calcoliamo la distribuzione posteriore delle ore richieste
out <- lapply(G_targets, function(G0) {
  # Per ciascun metodo, calcoliamo H_req su tutti i draw della posteriore
  Hreq_mat <- sapply(method_names, function(m) {
    alpha_m <- draws_g[[paste0("b_method", m)]]
    beta_m  <- draws_g[[paste0("b_method", m, ":log1ph")]]
    Hreq_fun(G0, alpha_m, beta_m)
  })
  
  # Convertiamo in tibble e aggiungiamo metadati
  as_tibble(Hreq_mat) |> 
    mutate(G0 = G0, .draw = row_number())
}) |> 
  bind_rows()

Riassumiamo con statistiche robuste:

Hreq_summary <- out |>
  pivot_longer(all_of(method_names), names_to = "metodo", values_to = "Hreq") |>
  group_by(G0, metodo) |>
  summarize(
    mediana = median(Hreq),
    q25 = quantile(Hreq, 0.25),
    q75 = quantile(Hreq, 0.75),
    media = mean(Hreq),
    .groups = "drop"
  )

print(Hreq_summary)
#> # A tibble: 9 × 6
#>      G0 metodo   mediana     q25     q75    media
#>   <dbl> <chr>      <dbl>   <dbl>   <dbl>    <dbl>
#> 1    75 AI         0       0       0       0.0348
#> 2    75 classico  46.8    34.5    75.1   Inf     
#> 3    75 gruppo    13.0    12.2    13.7    12.9   
#> 4    80 AI         0.143   0       0.585   0.335 
#> 5    80 classico 125.     78.0   257.    Inf     
#> 6    80 gruppo    28.1    26.4    30.2    28.6   
#> 7    85 AI         1.45    0.761   2.05    1.41  
#> 8    85 classico 329.    174.    887.    Inf     
#> 9    85 gruppo    59.9    53.3    68.8    62.9

Visualizziamo i confronti:

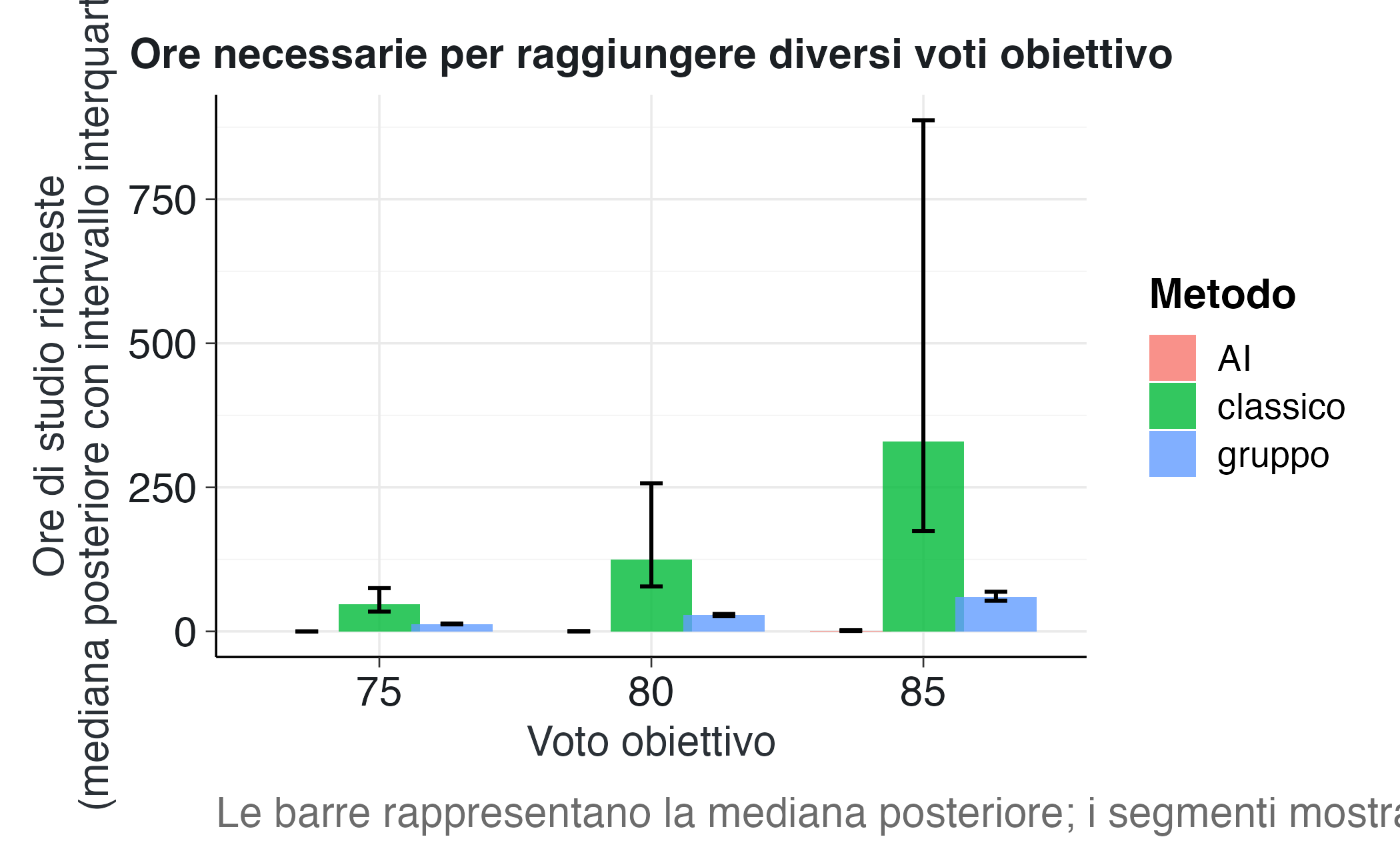
ggplot(Hreq_summary, aes(x = factor(G0), y = mediana, fill = metodo)) +
  geom_col(position = position_dodge(width = 0.8), alpha = 0.8) +
  geom_errorbar(
    aes(ymin = q25, ymax = q75),
    position = position_dodge(width = 0.8),
    width = 0.25
  ) +
  labs(
    title = "Ore necessarie per raggiungere diversi voti obiettivo",
    x = "Voto obiettivo",
    y = "Ore di studio richieste\n(mediana posteriore con intervallo interquartile)",
    fill = "Metodo",
    caption = "Le barre rappresentano la mediana posteriore; i segmenti mostrano l'IQR."
  )

42.3.6.3 Interpretazione dei confronti a voto costante

Efficienza assoluta: Il metodo che richiede meno ore (barre più basse) per raggiungere lo stesso voto è più efficiente temporalmente. Se AI mostra consistentemente barre più basse, ciò dimostra superiorità nell’efficienza di apprendimento.

Sensibilità al livello di ambizione: Osservando come cambiano i rapporti tra metodi al variare del voto obiettivo, possiamo identificare pattern interessanti:

  • Se i rapporti rimangono costanti, l’efficienza relativa è indipendente dall’ambizione
  • Se invece convergono o divergono, ciò indica effetti di interazione: alcuni metodi potrebbero essere particolarmente efficaci per voti alti ma non per voti bassi

Incertezza nelle stime: Gli intervalli interquartili (IQR) quantificano l’incertezza sulle ore necessarie. IQR ampi indicano maggiore incertezza, che può derivare da:

  • Incertezza sui parametri del modello (pochi dati, alta variabilità)
  • Eterogeneità individuale reale (alcuni studenti ci arrivano rapidamente, altri lentamente)

Confronti specifici: Possiamo calcolare esplicitamente il risparmio temporale. Ad esempio, per un voto di 80:

# Estraiamo i valori per G0 = 80
H80 <- Hreq_summary |> filter(G0 == 80)

# Calcoliamo le differenze rispetto al metodo peggiore
metodo_peggiore <- H80 |> slice_max(mediana, n = 1)
metodo_migliore <- H80 |> slice_min(mediana, n = 1)

risparmio <- metodo_peggiore$mediana - metodo_migliore$mediana

cat(sprintf(
  "Per raggiungere un voto di 80, il metodo %s richiede circa %.1f ore in meno rispetto al metodo %s (un risparmio del %.0f%%).",
  metodo_migliore$metodo,
  risparmio,
  metodo_peggiore$metodo,
  100 * risparmio / metodo_peggiore$mediana
))
#> Per raggiungere un voto di 80, il metodo AI richiede circa 124.5 ore in meno rispetto al metodo classico (un risparmio del 100%).

42.3.7 Sintesi interpretativa

Integrando tutti i confronti effettuati, emergono conclusioni ricche e sfaccettate:

Efficienza a parità di ore: Il metodo AI tende a produrre voti significativamente più alti quando gli studenti investono lo stesso numero di ore. Questo riflette la sua efficacia intrinseca: spiegazioni personalizzate, feedback immediato, esercizi adattivi. Tuttavia, il vantaggio può ridursi parzialmente se l’AI tutor richiede tempo aggiuntivo per familiarizzazione.

Efficienza a parità di voto: I metodi che necessitano meno ore per raggiungere lo stesso obiettivo sono temporalmente più efficienti. Il grafico mostra chiaramente queste differenze e permette di quantificare il risparmio temporale. Ad esempio, se l’AI permette di raggiungere 80/100 con 10 ore invece di 16, il risparmio di 6 ore ha valore significativo.

Incertezza e variabilità individuale: Gli intervalli interquartili evidenziano che non c’è una separazione netta: esiste sempre sovrapposizione tra le distribuzioni dei diversi metodi. Questo sottolinea un punto cruciale: la scelta ottimale può variare a livello individuale. Alcuni studenti potrebbero ottenere risultati eccellenti anche con il metodo classico (ad esempio, se hanno ottima autodisciplina e motivazione intrinseca), mentre altri potrebbero beneficiare enormemente della struttura e del supporto offerti dall’AI tutor o dal gruppo.

Dipendenza dalle preferenze: L’analisi di sensibilità su \(\lambda\) dimostra che la raccomandazione ottimale dipende fortemente dalle preferenze individuali riguardo al trade-off voto-tempo. Non esiste una “risposta giusta” universale: la scelta migliore deve essere contestualizzata rispetto ai vincoli e agli obiettivi dello studente specifico.

Valore dell’approccio bayesiano: Anziché fornire una risposta categorica (“il metodo X è il migliore”), l’analisi decisionale bayesiana ci permette di caratterizzare completamente la distribuzione delle utilità, di quantificare l’incertezza, e di esplorare come le conclusioni cambiano al variare delle assunzioni. Questo approccio più sfumato è più onesto intellettualmente e più utile praticamente: aiuta il decisore a comprendere in quali condizioni una certa scelta è preferibile.

In definitiva, il confronto tra metodi diventa un esercizio ricco e multidimensionale: non ci fermiamo a dire “chi è il migliore”, ma vediamo in quali condizioni, per quali profili di preferenze, e con che grado di certezza un metodo può risultare più vantaggioso. Questa prospettiva è coerente con l’idea fondamentale che la teoria della decisione non fornisce risposte assolute, ma piuttosto un quadro strutturato per ragionare sistematicamente sui trade-off in presenza di incertezza.

42.3.8 Verso modelli più realistici: oltre la funzione di utilità lineare

La funzione di utilità lineare qui adottata,

\[ U(g,h;\lambda) = g - \lambda h, \quad \lambda \geq 0, \]

presenta il pregio di una notevole semplicità interpretativa: ogni ora di studio viene infatti associata a un “costo” costante, pari a \(\lambda\) punti di voto. Tuttavia, questa formulazione poggia su due ipotesi semplificatrici che possono discostarsi dal comportamento effettivo degli studenti.

In primo luogo, la linearità nel voto implica che il valore marginale di ciascun punto sia identico a qualsiasi livello della scala di valutazione, equiparando ad esempio il passaggio da 60 a 61 a quello da 90 a 91. In realtà, è plausibile che i voti presentino rendimenti decrescenti: guadagnare punti in prossimità della sufficienza viene spesso percepito come più rilevante che incrementare il punteggio in regioni già elevate della scala. Allo stesso modo, potrebbero esistere soglie minime al di sotto delle quali un esito viene considerato inaccettabile (ad esempio, bocciare un esame), indipendentemente dal tempo risparmiato.

In secondo luogo, la linearità nel tempo presuppone che il disagio associato a un’ora aggiuntiva di studio rimanga invariato, indipendentemente dal numero di ore già dedicate. Tuttavia, l’esperienza soggettiva suggerisce che la fatica tende ad aumentare in modo più che proporzionale con il numero di ore: le prime ore di studio sono relativamente tollerabili, mentre dopo molte ore la concentrazione cala e il costo psicologico aumenta. Funzioni con esponente maggiore di 1 (come \(h^2\) o \(h^{1.5}\)) potrebbero catturare meglio questa progressione non lineare.

Ulteriori aspetti rilevanti includono:

  • Obiettivi personali e avversione alle perdite: gli studenti potrebbero mostrare avversione alle perdite, attribuendo un peso maggiore al mancato raggiungimento di un traguardo rispetto al superamento dello stesso. Questo suggerirebbe l’uso di funzioni di utilità asimmetriche rispetto a un punto di riferimento.

  • Gestione del rischio e dell’incertezza: alcuni individui potrebbero preferire metodi che offrono risultati più stabili, anche se meno brillanti in media. Questo richiederebbe di considerare non solo il valore atteso dell’utilità, ma anche la sua variabilità o il comportamento in scenari sfavorevoli (ad esempio, attraverso misure come il valore a rischio o l’utilità attesa penalizzata per la varianza).

  • Eterogeneità delle preferenze: il trade-off tra voto e tempo può variare notevolmente tra diversi profili di studenti. Uno studente lavoratore part-time ha vincoli temporali molto più stringenti rispetto a uno studente a tempo pieno. Modelli gerarchici permettono di stimare tale variabilità individuale preservando una struttura comune.

42.3.8.1 Un approccio progressivo alla complessità

Per un ricercatore che si accinga ad affrontare questo tipo di analisi, si raccomanda un approccio progressivo. È preferibile iniziare con il modello lineare, apprezzabile per la sua trasparenza e facilità di comunicazione. Solo dopo un’attenta analisi esplorativa dei dati—che potrebbe rivelare, ad esempio, pattern di non linearità o effetti soglia—dovrebbe essere contemplata l’introduzione di complessità aggiuntive. Come notato nella letteratura metodologica, il valore di un modello non risiede solo nella sua capacità predittiva, ma anche nella sua interpretabilità e nella facilità con cui può essere comunicato e criticato.

Il tentativo stesso di formalizzare il problema, anche se imperfetto, ci costringe a rendere esplicite le nostre assunzioni e a riflettere sui trade-off impliciti. Questo processo di esplicitazione è spesso più prezioso del risultato finale: ci aiuta a identificare quali aspetti del fenomeno abbiamo colto, quali abbiamo semplificato, e dove potrebbe essere necessario raccogliere ulteriori dati o raffinare il modello. In questo senso, l’analisi decisionale bayesiana non è tanto una ricetta da applicare meccanicamente, quanto una disciplina del pensiero che ci aiuta a navigare la complessità in modo strutturato.

Riflessioni conclusive

In questo capitolo abbiamo esplorato come l’analisi decisionale bayesiana offra un quadro coerente per integrare tre componenti fondamentali del processo decisionale: le previsioni sugli esiti, attraverso distribuzioni predittive che riflettono la nostra incertezza; la formalizzazione delle preferenze, mediante funzioni di utilità che quantificano la desiderabilità dei risultati; e infine un criterio di scelta razionale, rappresentato dalla massimizzazione dell’utilità attesa.

Abbiamo iniziato con un modello semplice, caratterizzato da una funzione di utilità lineare sia nel voto che nel tempo. Questa scelta, sebbene semplificata, si è rivelata preziosa per introdurre i concetti cardine del metodo: tradurre in valori numerici il grado di soddisfazione associato a diversi esiti, calcolare utilità attese che incorporino l’incertezza predittiva, e confrontare in modo sistematico alternative complesse. Successivamente, abbiamo discusso come estendere questo modello per cogliere aspetti più realistici, quali la presenza di rendimenti decrescenti, costi marginali crescenti, il ruolo degli obiettivi personali, l’avversione al rischio, e la possibile eterogeneità delle preferenze tra individui.

42.3.9 Modelli come strumenti, non dogmi

Un tema ricorrente in questo capitolo, e una lezione fondamentale dell’approccio bayesiano, è che i modelli sono strumenti di pensiero piuttosto che descrizioni letterali della realtà. Come richiamato nell’introduzione attraverso l’aforisma di Box—“tutti i modelli sono sbagliati, ma alcuni sono utili”—non dovremmo aspettarci che una funzione di utilità lineare catturi perfettamente la complessità delle preferenze umane, né che un modello lognormale per le ore di studio descriva esattamente ogni possibile pattern di comportamento. L’obiettivo non è la perfezione descrittiva, ma piuttosto la creazione di un punto di riferimento rispetto al quale possiamo organizzare le nostre intuizioni, identificare pattern nei dati, e valutare sistematicamente le implicazioni di diverse scelte.

Questa distinzione tra funzione descrittiva e funzione normativa è essenziale. Quando utilizziamo la teoria della decisione per valutare se un metodo di studio supportato da intelligenza artificiale sia preferibile a un approccio tradizionale, non stiamo affermando che gli studenti reali calcoleranno effettivamente utilità attese in modo bayesiano. Stiamo piuttosto costruendo un benchmark logico: se uno studente avesse preferenze chiaramente specificate (quanto vale un punto in più di voto rispetto a un’ora di tempo?) e credenze coerenti sull’efficacia dei diversi metodi (basate, ad esempio, su evidenze empiriche), quale scelta sarebbe internamente coerente con quelle premesse? La risposta a questa domanda non ci dice necessariamente come le persone decidono, ma ci fornisce un punto di partenza per capire dove e perché le scelte reali si discostano da quella coerenza ideale.

42.3.10 Il valore della formalizzazione: oltre il risultato finale

Una delle lezioni più importanti di questo capitolo riguarda il valore intrinseco del processo di formalizzazione, indipendentemente dal risultato finale. Come discusso nell’introduzione, anche quando non riusciamo a specificare perfettamente una funzione di utilità, o quando le nostre assunzioni risultano necessariamente semplificate, il solo fatto di dover rendere espliciti i nostri criteri di valutazione ci costringe a riflettere in modo più approfondito sui trade-off in gioco.

Consideriamo, ad esempio, il processo di definizione della funzione \(U(g,h;\lambda) = g - \lambda h\). La scelta di questa forma funzionale richiede che ci poniamo domande precise: quanto conta il voto rispetto al tempo? Il rapporto di scambio è costante o varia? Esistono soglie critiche? Anche se le nostre risposte iniziali sono imperfette o provvisorie, queste domande ci aiutano a identificare quali informazioni sarebbero rilevanti per migliorare la decisione. Se, ad esempio, ci rendiamo conto che non sappiamo quanto valga un’ora di tempo in termini di punti di voto, questo ci spinge a riflettere più attentamente sulle nostre priorità, o magari a condurre un’analisi di sensibilità per esplorare come la scelta ottimale cambi al variare di questo parametro.

Questo aspetto è particolarmente rilevante nel contesto della ricerca empirica. Come osservato nella letteratura recente, molti studi che valutano l’efficacia di decisioni assistite da sistemi di intelligenza artificiale non specificano chiaramente quale problema i partecipanti dovrebbero ottimizzare. Senza una formalizzazione esplicita del problema decisionale, diventa difficile distinguere tra scelte diverse (che riflettono preferenze o credenze differenti) e scelte subottimali (che violano la coerenza interna date certe preferenze). La teoria della decisione, in questo senso, non è solo uno strumento per calcolare la risposta “giusta”, ma anche una metodologia per rendere esplicite le assunzioni che altrimenti rimarrebbero implicite e quindi non criticabili.

42.3.11 Teoria della decisione e agency umana nell’era dell’IA

Un tema che ha attraversato implicitamente tutto il capitolo, e che merita una riflessione conclusiva più esplicita, riguarda il rapporto tra formalizzazione decisionale e autonomia umana, specialmente nel contesto del crescente utilizzo di sistemi di intelligenza artificiale come supporto alle decisioni.

Come accennato nell’introduzione, negli ultimi anni si è diffusa una comprensibile preoccupazione riguardo al rischio che la delega sistematica di decisioni a algoritmi possa erodere la nostra capacità di esercitare un giudizio autonomo, riducendo gli esseri umani a semplici esecutori di raccomandazioni generate da sistemi opachi. Di fronte a questo rischio, alcuni hanno reagito rifiutando in blocco qualsiasi tentativo di formalizzare matematicamente le decisioni, considerandolo intrinsecamente riduttivo o addirittura come un’abdicazione della responsabilità umana.

Tuttavia, questa reazione rischia di essere controproducente. Il fatto che un approccio formale possa essere usato in modo problematico—ad esempio, quando algoritmi decisionali vengono imposti senza trasparenza o riproducono discriminazioni sistemiche—non significa che dobbiamo rinunciare a comprendere razionalmente i nostri processi decisionali. Al contrario, è proprio quando le decisioni sono mediate o assistite da tecnologie predittive che diventa ancora più importante essere in grado di specificare esplicitamente quali sono i nostri obiettivi, come valutiamo i diversi esiti, e quali assunzioni stiamo facendo.

Consideriamo l’esempio discusso in questo capitolo: la valutazione di un sistema di AI tutor per il supporto allo studio. La domanda non è se “delegare” la decisione all’intelligenza artificiale, ma piuttosto come valutare sistematicamente se e quando tale strumento tecnologico rappresenta effettivamente una scelta vantaggiosa per uno studente con determinate preferenze e vincoli. Per rispondere a questa domanda in modo rigoroso, abbiamo bisogno di un quadro che ci permetta di:

  1. Formulare previsioni strutturate sull’efficacia relativa dei diversi metodi (quanto è probabile che l’AI tutor aumenti il voto? Di quanto riduce o aumenta il tempo necessario?);
  2. Esplicitare le preferenze (quanto conta il voto rispetto al tempo? Esistono vincoli temporali rigidi?);
  3. Integrare l’incertezza in modo coerente, riconoscendo che sia le previsioni sull’efficacia sia le realizzazioni individuali sono soggette a variabilità.

Lungi dal rappresentare una rinuncia all’autonomia, questo approccio è piuttosto un modo per esercitare l’autonomia in modo più consapevole. La formalizzazione non ci dice cosa dovremmo valorizzare—questa rimane una scelta profondamente personale—ma ci aiuta a verificare se le nostre decisioni sono coerenti con i valori che affermiamo di avere e con le informazioni disponibili.

42.3.12 Verso un uso riflessivo della teoria della decisione

Alla luce di queste considerazioni, emerge l’importanza di un approccio riflessivo all’uso della teoria della decisione, specialmente nel contesto della ricerca psicologica e delle scienze sociali. Questo significa:

  1. Riconoscere i limiti intrinseci del modello: Ogni specificazione di una funzione di utilità, di una distribuzione predittiva, o di un criterio di ottimalità comporta semplificazioni rispetto alla complessità del fenomeno reale. È importante rendere espliciti questi limiti e valutare la robustezza delle conclusioni rispetto a specificazioni alternative.

  2. Distinguere tra descrizione e prescrizione: La teoria della decisione non pretende di descrivere come le persone realmente decidono, ma piuttosto di fornire un benchmark normativo per valutare la coerenza interna delle scelte. Questa distinzione permette di apprezzare il valore del metodo senza cadere nell’errore di considerarlo una teoria psicologica completa.

  3. Valorizzare il processo oltre il risultato: Come discusso, spesso il valore maggiore della formalizzazione risiede nel processo stesso—nelle domande che ci costringe a porci, nelle assunzioni che ci obbliga a rendere esplicite—piuttosto che nella risposta finale fornita dal modello.

  4. Mantenere apertura alla pluralità di approcci: Non esiste una singola funzione di utilità o un unico modo di formulare un problema decisionale. È spesso utile esplorare diverse specificazioni, confrontare i risultati, e riflettere su cosa le differenze ci dicono sui trade-off in gioco.

  5. Usare l’analisi di sensibilità come strumento di riflessione: Invece di cercare di specificare la funzione di utilità “corretta”, è spesso più produttivo esplorare come le conclusioni cambiano al variare dei parametri chiave (come \(\lambda\) nel nostro esempio). Questo ci aiuta a identificare quali preferenze sono cruciali per la decisione e quali invece hanno un impatto limitato.

42.3.13 Il vantaggio distintivo dell’approccio bayesiano

L’approccio bayesiano alla teoria della decisione offre alcuni vantaggi distintivi che meritano di essere sottolineati. In primo luogo, la capacità di propagare coerentemente l’incertezza da tutte le fonti—incertezza sui parametri del modello, variabilità predittiva degli esiti, incertezza sulla specificazione della funzione di utilità—fino alla quantificazione finale dell’utilità attesa. Questo permette non solo di identificare l’opzione mediamente migliore, ma anche di valutare la robustezza di questa conclusione, esprimendo ad esempio la probabilità che una data alternativa sia da preferire.

In secondo luogo, l’approccio bayesiano si integra naturalmente con una concezione progressiva della conoscenza: man mano che raccogliamo nuovi dati o affiniamo le nostre misurazioni, possiamo aggiornare le nostre credenze sui parametri rilevanti e di conseguenza rivedere le nostre valutazioni sulle decisioni ottimali. Non siamo costretti a dichiarare fin dall’inizio che abbiamo la risposta definitiva; possiamo invece costruire la nostra comprensione in modo iterativo, partendo da modelli semplici e introducendo complessità solo dove i dati lo giustificano.

Infine, il framework bayesiano facilita la comunicazione trasparente dell’incertezza. Invece di fornire raccomandazioni categoriche (“il metodo X è il migliore”), possiamo presentare distribuzioni di probabilità sulle decisioni ottimali, visualizzazioni che mostrano come le conclusioni cambiano al variare delle assunzioni, e analisi di sensibilità che aiutano i decisori a comprendere quali fattori sono più rilevanti per le loro scelte. Questa trasparenza è particolarmente importante quando le decisioni hanno implicazioni significative per il benessere delle persone.

42.3.14 Considerazioni etiche e sociali

Non possiamo concludere questa riflessione senza accennare brevemente alle implicazioni etiche e sociali dell’uso della teoria della decisione, specialmente nel contesto della crescente automazione dei processi decisionali. Come osservato nella letteratura critica, gli algoritmi decisionali possono perpetuare o amplificare disuguaglianze esistenti quando vengono applicati senza un’attenta riflessione sui valori che incorporano e sugli effetti distributivi che producono.

Tuttavia, la risposta a questi rischi reali non dovrebbe essere il rifiuto categorico della formalizzazione, ma piuttosto una sua applicazione più riflessiva e democratica. Quando rendiamo espliciti i criteri di ottimalità, le funzioni di utilità, e le previsioni sui cui si basano le decisioni, rendiamo anche più facile sottoporli a scrutinio critico. Possiamo chiederci: chi ha definito questa funzione di utilità? Quali gruppi sociali beneficiano e quali vengono penalizzati da questa particolare specificazione? Le previsioni sui cui si basa il modello sono equamente accurate per diversi sottogruppi della popolazione?

In questo senso, la formalizzazione matematica non è antitetica alla responsabilità etica, ma può anzi facilitarla rendendo esplicite scelte che altrimenti rimarrebbero opache e non criticabili. Naturalmente, questo richiede che i modelli siano accompagnati da una riflessione critica sui loro presupposti e da meccanismi di governance che assicurino che i criteri di ottimalità riflettano effettivamente i valori di coloro che saranno affettati dalle decisioni.

42.3.15 Conclusioni

In definitiva, l’analisi decisionale bayesiana si configura non solo come una tecnica per supportare scelte ottimali in condizioni di incertezza, ma anche e soprattutto come una metodologia per rendere esplicito, trasparente e criticabile il processo attraverso cui valutiamo e confrontiamo le alternative a nostra disposizione. Il suo valore non risiede tanto nella capacità di fornire risposte definitive a problemi complessi, quanto nell’offrire un linguaggio comune e un quadro strutturato per riflettere collettivamente sui trade-off, sull’incertezza, e sulle assunzioni che inevitabilmente caratterizzano ogni processo decisionale.

Nel contesto specifico della psicologia e delle scienze sociali, dove i fenomeni studiati sono intrinsecamente complessi e le decisioni hanno spesso implicazioni profonde per il benessere delle persone, questo approccio riflessivo alla formalizzazione diventa particolarmente prezioso. Ci aiuta a navigare la tensione tra la necessità di strutturare il pensiero attraverso modelli formali e il riconoscimento dell’irriducibile complessità dell’esperienza umana. Ci permette di beneficiare della chiarezza e della coerenza che la matematica può offrire, senza cadere nella trappola di reificare i modelli o di confondere la mappa con il territorio.

In qualità di ricercatori e professionisti sul campo, il nostro compito non è semplicemente applicare meccanicamente le tecniche dell’analisi decisionale, ma piuttosto usarle come strumenti per pensare in modo più efficace ai problemi che ci interessano, mantenendo sempre viva la consapevolezza che i modelli sono costruzioni umane fallibili e perfettibili, al servizio di una comprensione più profonda e di decisioni più sagge.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] stringr_1.5.2         cmdstanr_0.9.0        ragg_1.5.0           
#>  [4] tinytable_0.13.0      withr_3.0.2           systemfonts_1.3.1    
#>  [7] patchwork_1.3.2       ggdist_3.3.3          tidybayes_3.0.7      
#> [10] bayesplot_1.14.0      ggplot2_4.0.0         reliabilitydiag_0.2.1
#> [13] priorsense_1.1.1      posterior_1.6.1       loo_2.8.0            
#> [16] rstan_2.32.7          StanHeaders_2.32.10   brms_2.23.0          
#> [19] Rcpp_1.1.0            sessioninfo_1.2.3     conflicted_1.2.0     
#> [22] janitor_2.2.1         matrixStats_1.5.0     modelr_0.1.11        
#> [25] tibble_3.3.0          dplyr_1.1.4           tidyr_1.3.1          
#> [28] rio_1.2.4             here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-29      
#>  [7] snakecase_0.11.1      compiler_4.5.1        reshape2_1.4.4       
#> [10] vctrs_0.6.5           pkgconfig_2.0.3       arrayhelpers_1.1-0   
#> [13] fastmap_1.2.0         backports_1.5.0       labeling_0.4.3       
#> [16] utf8_1.2.6            rmarkdown_2.30        ps_1.9.1             
#> [19] purrr_1.1.0           xfun_0.53             cachem_1.1.0         
#> [22] jsonlite_2.0.0        broom_1.0.10          parallel_4.5.1       
#> [25] R6_2.6.1              stringi_1.8.7         RColorBrewer_1.1-3   
#> [28] lubridate_1.9.4       estimability_1.5.1    knitr_1.50           
#> [31] zoo_1.8-14            pacman_0.5.1          Matrix_1.7-4         
#> [34] splines_4.5.1         timechange_0.3.0      tidyselect_1.2.1     
#> [37] abind_1.4-8           yaml_2.3.10           codetools_0.2-20     
#> [40] processx_3.8.6        curl_7.0.0            pkgbuild_1.4.8       
#> [43] plyr_1.8.9            lattice_0.22-7        bridgesampling_1.1-2 
#> [46] S7_0.2.0              coda_0.19-4.1         evaluate_1.0.5       
#> [49] survival_3.8-3        RcppParallel_5.1.11-1 pillar_1.11.1        
#> [52] tensorA_0.36.2.1      checkmate_2.3.3       stats4_4.5.1         
#> [55] distributional_0.5.0  generics_0.1.4        rprojroot_2.1.1      
#> [58] rstantools_2.5.0      scales_1.4.0          xtable_1.8-4         
#> [61] glue_1.8.0            emmeans_1.11.2-8      tools_4.5.1          
#> [64] data.table_1.17.8     mvtnorm_1.3-3         grid_4.5.1           
#> [67] QuickJSR_1.8.1        colorspace_2.1-2      nlme_3.1-168         
#> [70] cli_3.6.5             textshaping_1.0.4     svUnit_1.0.8         
#> [73] Brobdingnag_1.2-9     V8_8.0.1              gtable_0.3.6         
#> [76] digest_0.6.37         TH.data_1.1-4         htmlwidgets_1.6.4    
#> [79] farver_2.1.2          memoise_2.0.1         htmltools_0.5.8.1    
#> [82] lifecycle_1.0.4       MASS_7.3-65

Bibliografia

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis (3rd ed.). Chapman; Hall/CRC.
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.