11  Modello di Poisson

Introduzione

Questo capitolo fornisce un approfondimento tematico che non trova spazio nel manuale didattico principale, ma che affronta questioni metodologiche di particolare importanza per la ricerca psicologica. Estendiamo l’approccio bayesiano a una classe di dati ampiamente diffusa nella pratica sperimentale e clinica: i conteggi.

Nei capitoli precedenti abbiamo visto come utilizzare Stan per analizzare un problema familiare, quello delle proporzioni, introducendo l’odds ratio come primo esempio pratico. Qui allarghiamo l’orizzonte a un’altra categoria di dati molto comune in psicologia: il numero di occorrenze di un evento in un intervallo di tempo o spazio. In tutti questi contesti, il modello probabilistico di riferimento è spesso la distribuzione di Poisson, che descrive il numero di eventi osservati quando il tasso medio di occorrenza è costante.

Il modello di Poisson è un banco di prova ideale per consolidare due aspetti fondamentali dell’inferenza bayesiana: la coerenza logica del metodo, che rimane invariata anche quando cambia la verosimiglianza, e la versatilità di Stan come strumento di calcolo, che semplifica la realizzazione di modelli altrimenti difficili da sviluppare manualmente.

Attraverso un esempio concreto di ambito psicologico, mostreremo come specificare e stimare un modello di Poisson in Stan, acquisendo familiarità con questo tipo di dati e rafforzando la comprensione della logica bayesiana in un contesto applicativo diverso, in preparazione ai modelli multilivello che affronteremo in seguito.

Panoramica del capitolo

  • Capire quando usare un modello di Poisson (conteggi non negativi, tendenzialmente rari, indipendenti dato il tasso).
  • Scrivere un modello in Stan con parametri su scala naturale (qui: lambda come tasso medio).
  • Impostare prior debolmente informative su lambda o sul suo log (per mantenere positività e stabilità numerica).
  • Eseguire stima MCMC con cmdstanr e leggere i diagnostici di convergenza.
  • Fare posterior predictive checks (PPC) per valutare l’adeguatezza del modello.

In questo capitolo non vogliamo solo calcolare una media dal campione, ma imparare a stimare il tasso medio di occorrenza nella popolazione a partire dai dati osservati, esprimendo anche la nostra incertezza su quel tasso. Traduciamo un modello teorico (Poisson con prior Gamma) in un modello computazionale in Stan, e verifichiamo che Stan fornisce gli stessi risultati della soluzione analitica, così da prendere confidenza con il workflow MCMC. È una “palestra” semplice che prepara a modelli più complessi, dove le formule chiuse non ci saranno.

here::here("code", "_common.R") |> 
  source()

if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayesplot, ggplot2, tidyverse, tibble)
conflicts_prefer(posterior::ess_bulk)
conflicts_prefer(posterior::ess_tail)
conflicts_prefer(dplyr::count)

11.1 Dal modello teorico al modello computazionale

Quando raccogliamo dati in psicologia, non ci interessa soltanto descrivere ciò che è accaduto nel nostro campione, ma soprattutto comprendere e stimare il processo che genera i dati. Un modello statistico non si limita a fotografare i risultati osservati: formula ipotesi sul meccanismo che li produce — ad esempio, con quale frequenza tende a comparire un certo comportamento in condizioni simili.

Un caso reale aiuta a chiarire l’idea. In uno studio di ecological momentary assessment condotto da Tilley & Rees (2014) su pazienti con disturbo ossessivo-compulsivo (OCD), un partecipante (“John”) registrava il numero di compulsioni compiute in diverse finestre temporali della giornata, ciascuna della durata di circa due ore. L’obiettivo clinico era stimare quanto frequentemente questi comportamenti si manifestassero nel corso di una giornata tipo e come potesse variare il ritmo nel tempo.

I dati raccolti per una singola giornata possono essere sintetizzati come segue:

Finestra temporale (ore) Descrizione del contesto Compulsioni osservate
10:00–12:00 Routine mattutina (pulizia e ordine) 4
12:00–14:00 Dopo pranzo, controlli domestici 3
14:00–16:00 Guida e checking su strada 5
16:00–18:00 Relax pomeridiano 2
18:00–20:00 Preparazione cena 3
20:00–22:00 Routine serale (chiusura casa) 4

Totale giornata: 21 eventi.

In R, questi dati si rappresentano come:

y <- c(4, 3, 5, 2, 3, 4)

Abbiamo quindi N = 6 osservazioni, ognuna relativa a una finestra di due ore. La semplice media campionaria, ad esempio \(\bar y = 3.5\), descrive la frequenza osservata oggi, ma la domanda sostantiva è diversa:

qual è il tasso medio con cui questo tipo di comportamento tende a verificarsi in condizioni simili?

Chiamiamo questo parametro \(\lambda\): rappresenta il numero medio di eventi attesi per finestra di due ore per una giornata tipica di questa persona. Nel modello bayesiano stimiamo \(\lambda\) tenendo conto sia della variabilità tra finestre sia dell’esiguità del campione.

11.1.1 Perché serve un modello probabilistico?

I dati osservati sono un piccolo campione e possono variare da una raccolta all’altra. Un modello probabilistico ci permette di separare il segnale dal rumore, chiarendo quanto dell’andamento osservato sia dovuto al caso e quanto rifletta una regolarità, e consente di quantificare l’incertezza della stima di \(\lambda\) invece di limitarci a una media.

11.1.2 Il modello di Poisson

Per conteggi di eventi in un intervallo, il modello naturale è la distribuzione di Poisson: \[ y_i \sim \text{Poisson}(\mu_i), \qquad \mu_i = \lambda \cdot t_i, \] dove \(y_i\) è il numero di eventi nella finestra \(i\), \(t_i\) la durata della finestra e \(\lambda\) il tasso medio. Con finestre tutte uguali (\(t_i = 1\)): \[ P(y_i \mid \lambda) = \frac{\lambda^{y_i} e^{-\lambda}}{y_i!}, \qquad \mathbb{E}[y_i]=\lambda,\quad \mathrm{Var}(y_i)=\lambda. \] In parole semplici, \(\lambda\) è quanti eventi in media ci aspettiamo per finestra.

  • Clinica: numero di episodi compulsivi o attacchi di panico in un periodo.
  • Sviluppo: parole nuove prodotte in un giorno.
  • Cognitiva: risposte corrette in prove a tempo.
  • Sociale: interazioni osservate in una sessione.

In tutti i casi, il modello di Poisson aiuta a stimare il tasso medio e la relativa incertezza.

11.1.3 La distribuzione a priori

Nell’approccio bayesiano dobbiamo dichiarare cosa riteniamo plausibile per \(\lambda\) prima di osservare i dati. Nel caso di John non ci aspettiamo tassi estremi: nelle finestre EMA della giornata il numero di compulsioni oscilla tra 2 e 5, quindi un valore medio plausibile è attorno a 3–4 eventi per finestra. Possiamo tradurlo con una Gamma con media 3.5 e deviazione standard 1.5:

mu_prior <- 3.5
sd_prior <- 1.5
alpha_prior <- (mu_prior / sd_prior)^2
beta_prior  <-  mu_prior / sd_prior^2

Questa prior riflette l’idea che, prima di vedere i dati, consideriamo plausibile un tasso vicino a 3–4, senza escludere del tutto valori più bassi o più alti.

11.1.3.1 Verifica predittiva a priori

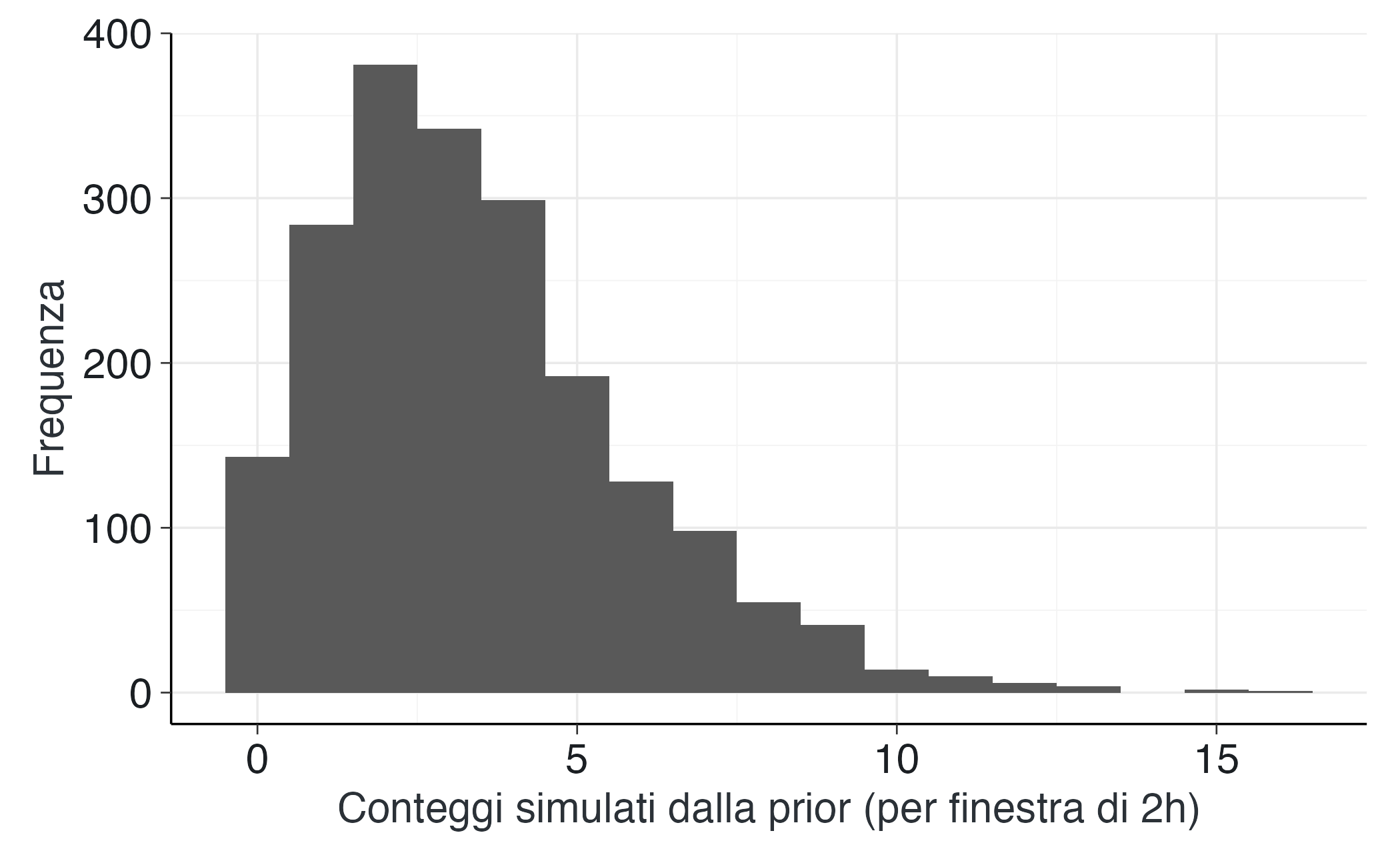
Prima di procedere con la stima del modello, è fondamentale valutare quali implicazioni comporti la scelta delle distribuzioni a priori sui dati generabili. È utile chiedersi: con quale frequenza le prior generano valori nulli? Quante volte producono valori superiori a 8? Se le simulazioni restituiscono sistematicamente valori irrealistici per il contesto psicologico in esame, sarà necessario ricalibrare le prior, modificandone la localizzazione o l’ampiezza.

set.seed(42)
lambda_prior_draws <- rgamma(2000, shape = alpha_prior, rate = beta_prior)
y_ppc_prior <- rpois(2000, lambda = lambda_prior_draws)

tibble(y_ppc_prior) |>
  ggplot(aes(y_ppc_prior)) +
  geom_histogram(binwidth = 1) +
  labs(x = "Conteggi simulati dalla prior (per finestra di 2h)", y = "Frequenza")

11.1.4 Perché usiamo Stan?

In questo caso specifico, sarebbe possibile calcolare la distribuzione a posteriori in forma analitica (si tratta, infatti, di una distribuzione Gamma), ma abbiamo scelto deliberatamente di utilizzare Stan per un motivo didattico fondamentale: acquisire familiarità con un flusso di lavoro standardizzato e generalizzabile. Questo approccio ci permette di esercitarci nella formalizzazione del modello, nel campionamento MCMC, nell’analisi della convergenza, nell’analisi delle distribuzioni a posteriori, nel confronto tra modelli e nelle verifiche predittive.

Questo esercizio metodologico rappresenta una palestra essenziale per prepararci ad affrontare situazioni reali più complesse in cui le soluzioni analitiche non saranno disponibili e in cui l’utilizzo di strumenti computazionali avanzati diventerà indispensabile.

11.1.5 Obiettivi del modello in Stan

Vogliamo stimare \(\lambda\), quantificare l’incertezza e verificare che i campioni generati da Stan coincidano con la soluzione analitica disponibile.

11.2 Scrivere il modello in Stan

stan_code <- "
data {
  int<lower=0> N;
  array[N] int<lower=0> y;
  real<lower=0> alpha_prior;
  real<lower=0> beta_prior;
}
parameters {
  real<lower=0> lambda;
}
model {
  // Prior: Gamma(shape=alpha_prior, rate=beta_prior)
  lambda ~ gamma(alpha_prior, beta_prior);
  // Likelihood: Poisson(lambda) per tutte le finestre (stessa durata)
  y ~ poisson(lambda);
}
generated quantities {
  // Parametri della posterior coniugata (per confronto didattico)
  real alpha_post = alpha_prior + sum(y);
  real beta_post  = beta_prior + N;
  // Log-likelihood per eventuale PSIS-LOO
  array[N] real log_lik;
  for (i in 1:N) log_lik[i] = poisson_lpmf(y[i] | lambda);
}
"

Compiliamo e prepariamo i dati con la prior coerente con il caso clinico:

mod <- cmdstan_model(write_stan_file(stan_code))
# Dati e prior
N <- length(y)

# Lista dati per Stan - DEVI INCLUIRE alpha_prior e beta_prior!
stan_data <- list(
  N = N,
  y = y,
  alpha_prior = alpha_prior,  # Questo mancava!
  beta_prior = beta_prior     # Questo mancava!
)

cat("Parametri passati a Stan:\n")
#> Parametri passati a Stan:
cat("alpha_prior =", alpha_prior, "\n")
#> alpha_prior = 5.44
cat("beta_prior =", beta_prior, "\n")
#> beta_prior = 1.56

Avviamo il campionamento:

fit <- mod$sample(
  data = stan_data,
  seed = 123,
  chains = 4,
  parallel_chains = 4,
  iter_sampling = 3000,
  iter_warmup = 2000,
  refresh = 0
)

11.3 Analizzare i risultati

11.3.2 Verifica della correttezza implementativa

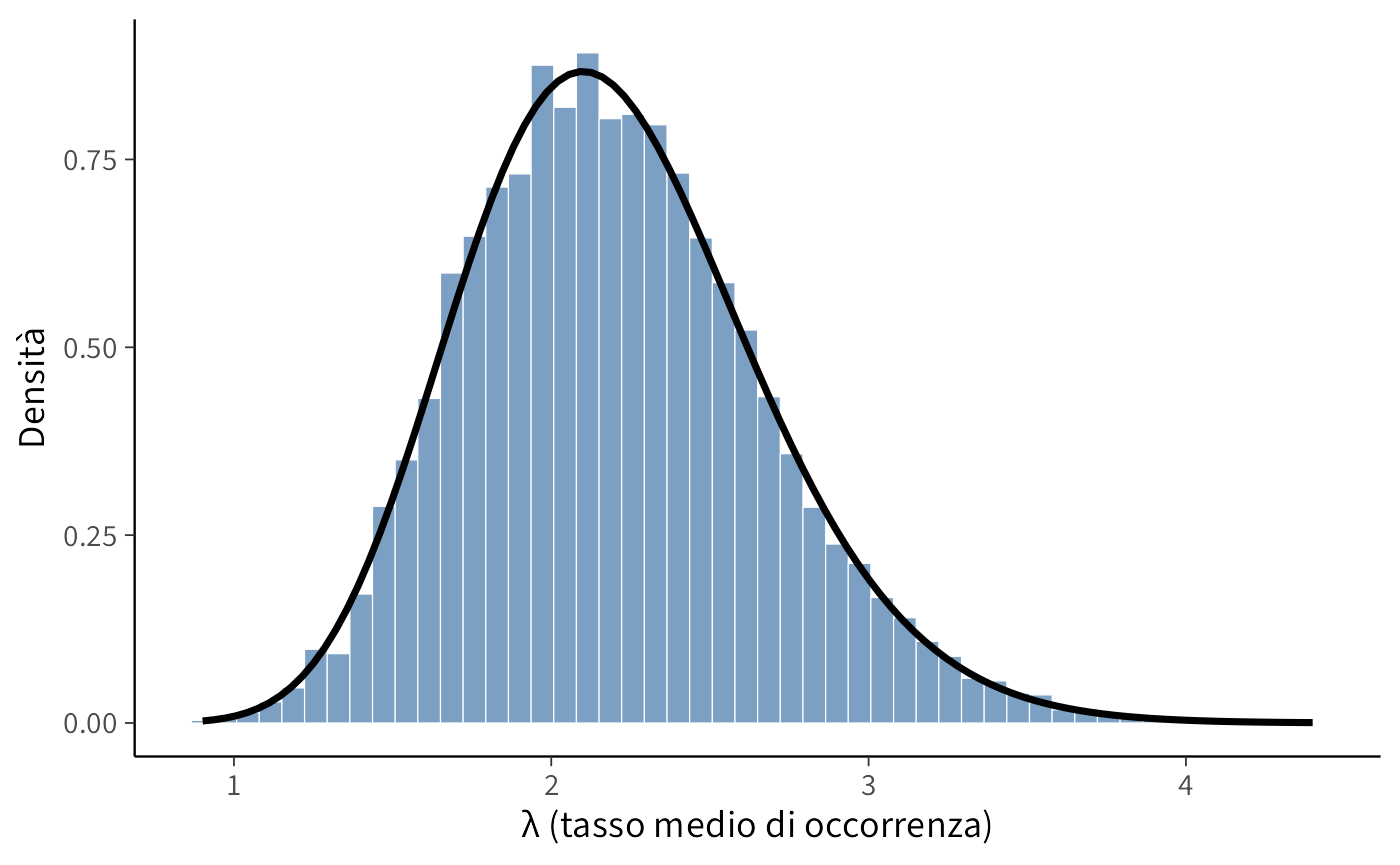
La proprietà di coniugazione del modello Gamma-Poisson ci permette di verificare l’accuratezza dell’implementazione MCMC confrontando i campioni ottenuti con Stan con la soluzione analitica esatta:

lambda_samples <- as.numeric(fit$draws("lambda"))

# Parametri teorici
alpha_post_teorico <- alpha_prior + sum(y)
beta_post_teorico <- beta_prior + N

ggplot(data.frame(lambda = lambda_samples), aes(x = lambda)) +
  geom_histogram(aes(y = after_stat(density)), bins = 30, alpha = 0.7, 
                 fill = "lightblue", color = "white") +
  stat_function(
    fun = function(x) dgamma(x, shape = alpha_post_teorico, rate = beta_post_teorico),
    linewidth = 1.2,
    color = "darkred"
  ) +
  labs(x = "λ", y = "Densità", 
       title = "Confronto: MCMC vs Soluzione Teorica",
       subtitle = paste("Media teorica:", round(alpha_post_teorico/beta_post_teorico, 3),
                       "| Media MCMC:", round(mean(lambda_samples), 3)))

La sostanziale sovrapposizione tra l’istogramma dei campioni MCMC e la curva teorica della distribuzione Gamma - considerando le inevitabili fluttuazioni di campionamento - conferma la correttezza dell’implementazione del modello in Stan. Questo controllo incrociato rappresenta una pratica essenziale per validare il workflow computazionale, particolarmente utile quando ci si prepara ad affrontare modelli più complessi privi di soluzioni analitiche chiuse.

11.3.3 Intervalli di credibilità

La distribuzione a posteriori ci permette di quantificare l’incertezza sul parametro \(\lambda\) attraverso intervalli di credibilità. Calcoliamo ad esempio un intervallo al 94%:

cred_interval <- quantile(lambda_samples, probs = c(0.03, 0.5, 0.97))
cred_interval
#>   3%  50%  97% 
#> 2.32 3.48 4.89

L’interpretazione di questi quantili è particolarmente informativa:

  • Mediana (50%): rappresenta il valore centrale della distribuzione a posteriori, offrendo una stima robusta del tasso di compulsioni tipico.
  • Limiti del 94%: i quantili al 3% e 97% delimitano un intervallo che contiene con alta probabilità il vero valore del parametro.

A differenza degli intervalli di confidenza frequentisti, l’intervallo di credibilità bayesiano ammette un’interpretazione probabilistica diretta: possiamo affermare che, dati i nostri priori e le osservazioni, esiste una probabilità del 94% che il vero valore di \(\lambda\) sia compreso tra questi estremi. Questa caratteristica rende gli intervalli di credibilità particolarmente utili per la comunicazione dei risultati in contesti applicativi.

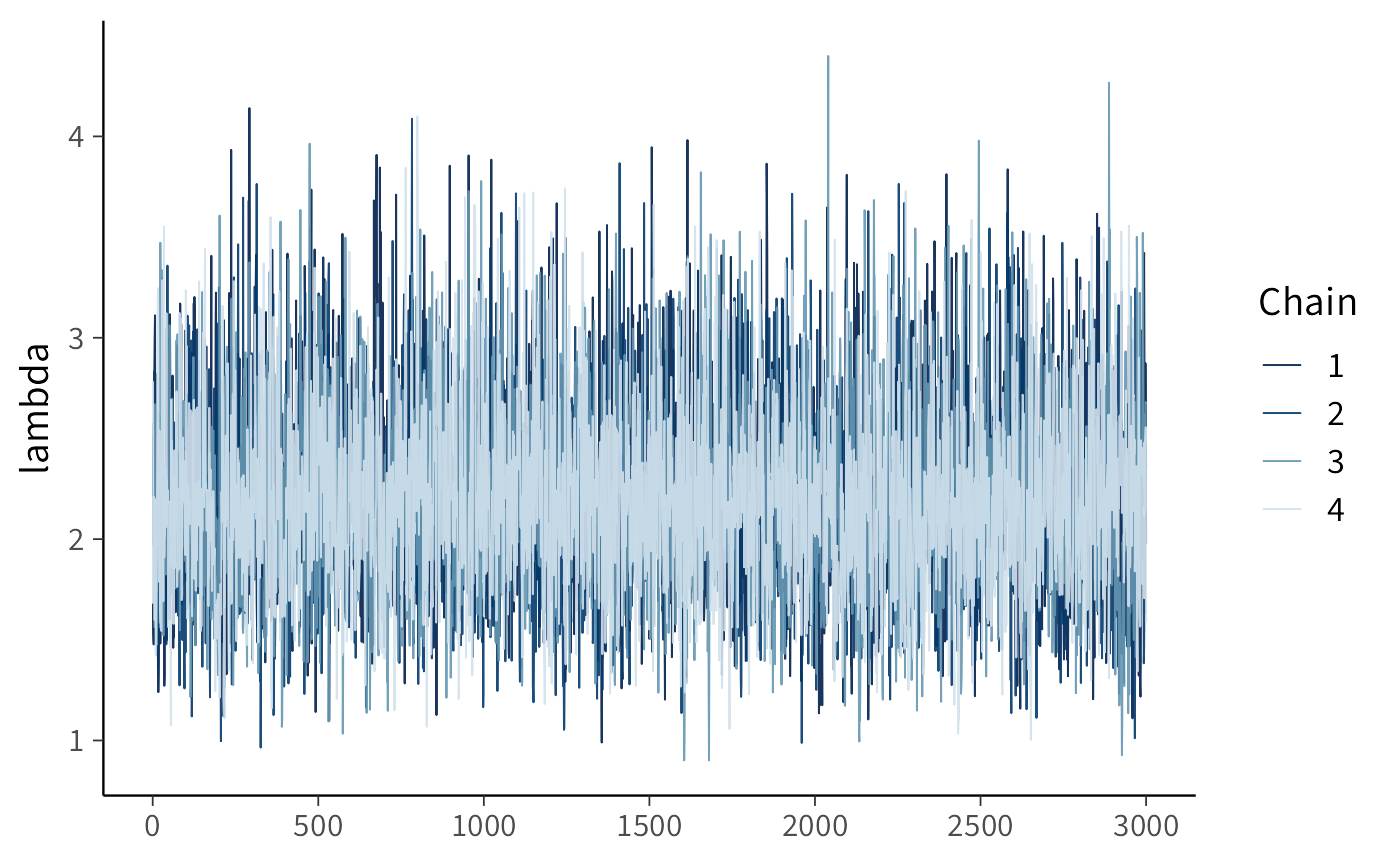
11.3.4 Diagnostica essenziale

Al termine del campionamento, verifichiamo la qualità delle stime attraverso indicatori essenziali:

posterior::summarise_draws(fit$draws("lambda"), rhat, ess_bulk, ess_tail)
#> # A tibble: 1 × 4
#>   variable  rhat ess_bulk ess_tail
#>   <chr>    <dbl>    <dbl>    <dbl>
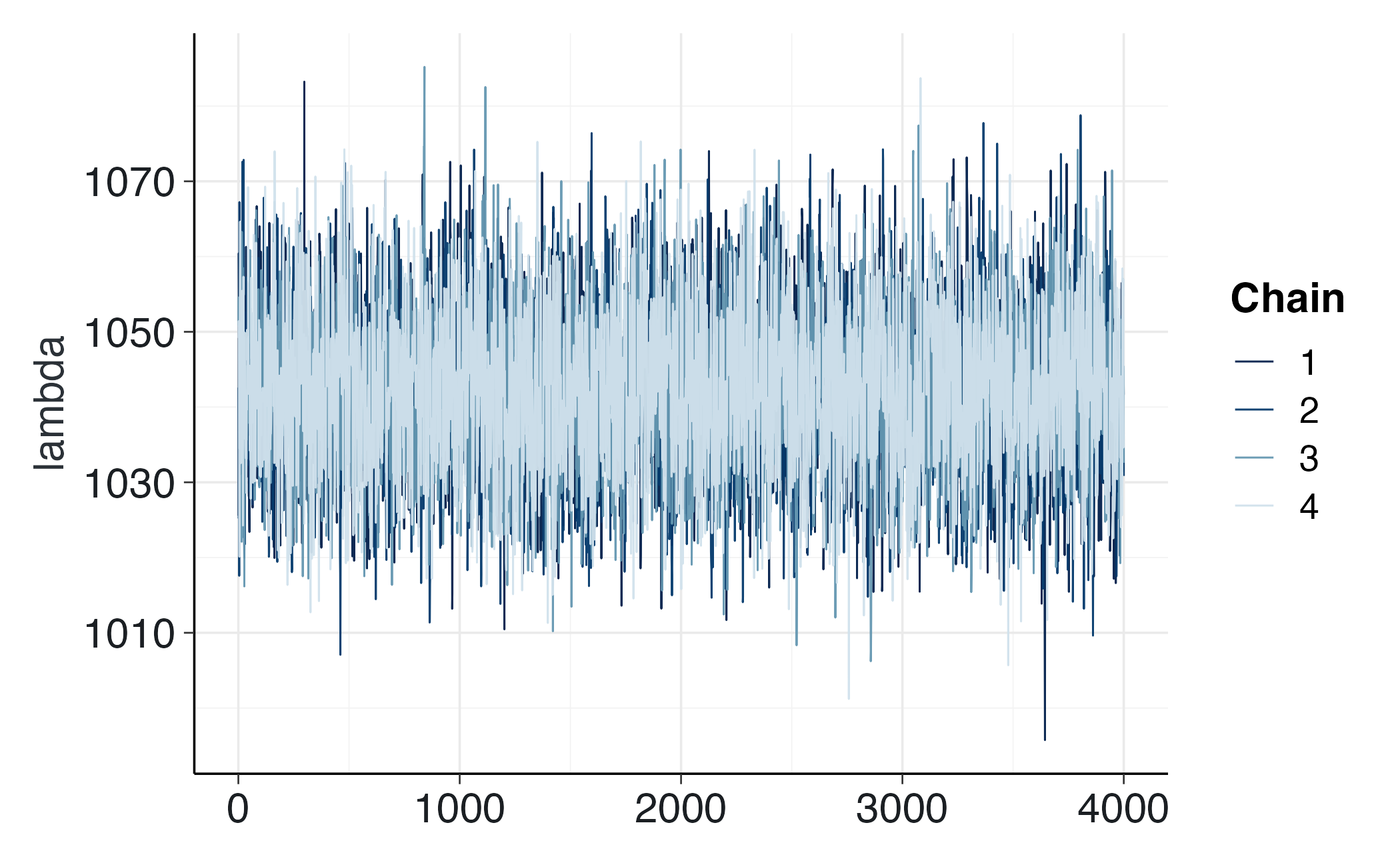
#> 1 lambda    1.00    4522.    5741.
bayesplot::mcmc_trace(fit$draws("lambda"))

Se \(\hat R \approx 1\), ESS è elevato e le catene sono ben mescolate, possiamo fidarci delle stime. Se \(\hat R > 1.01\) o ESS è basso, è necessario aumentare il numero di warm-up/campioni, innalzare adapt_delta o verificare la compatibilità delle prior con i dati osservati.

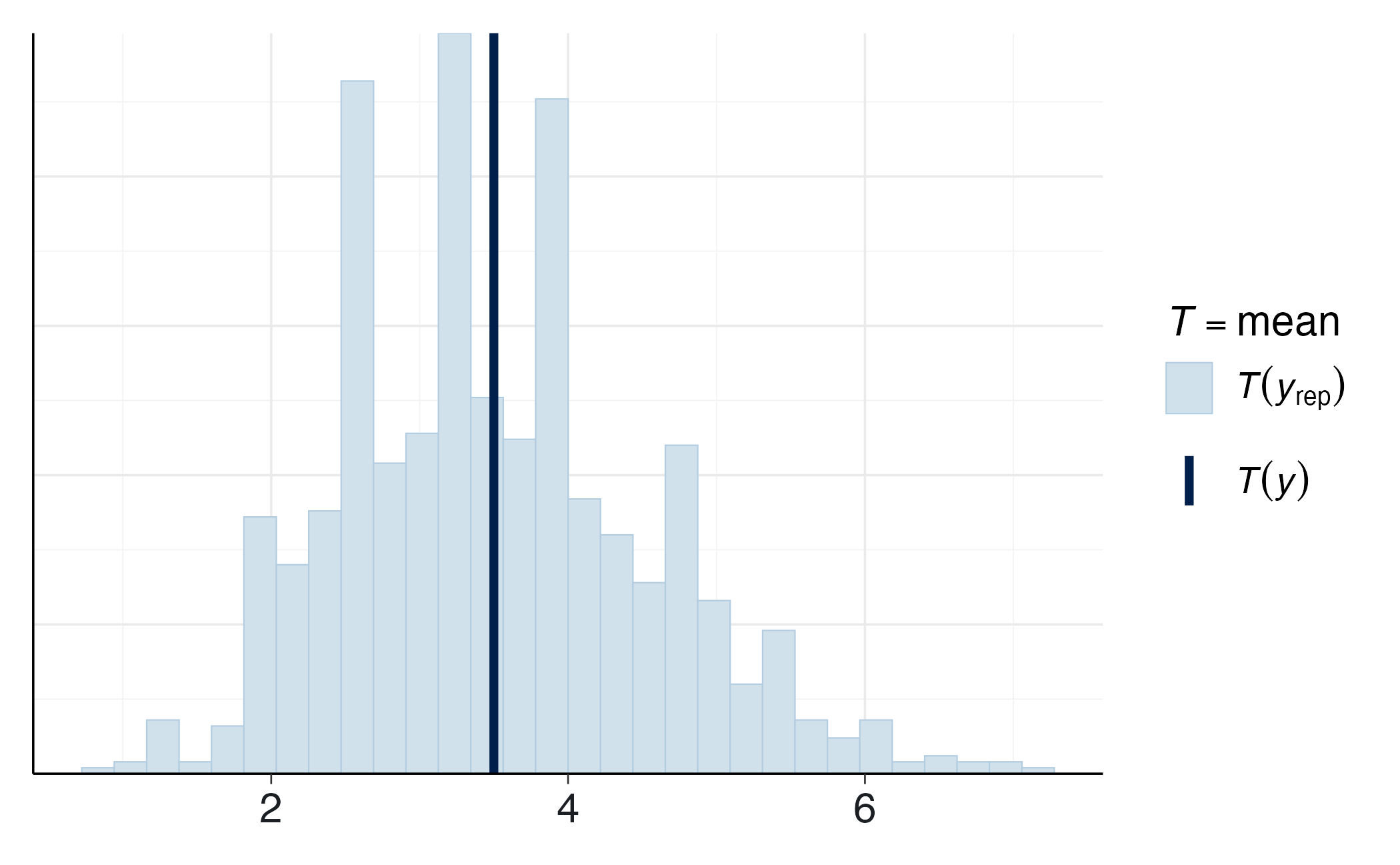
11.3.5 Verifica predittiva e coerenza psicologica

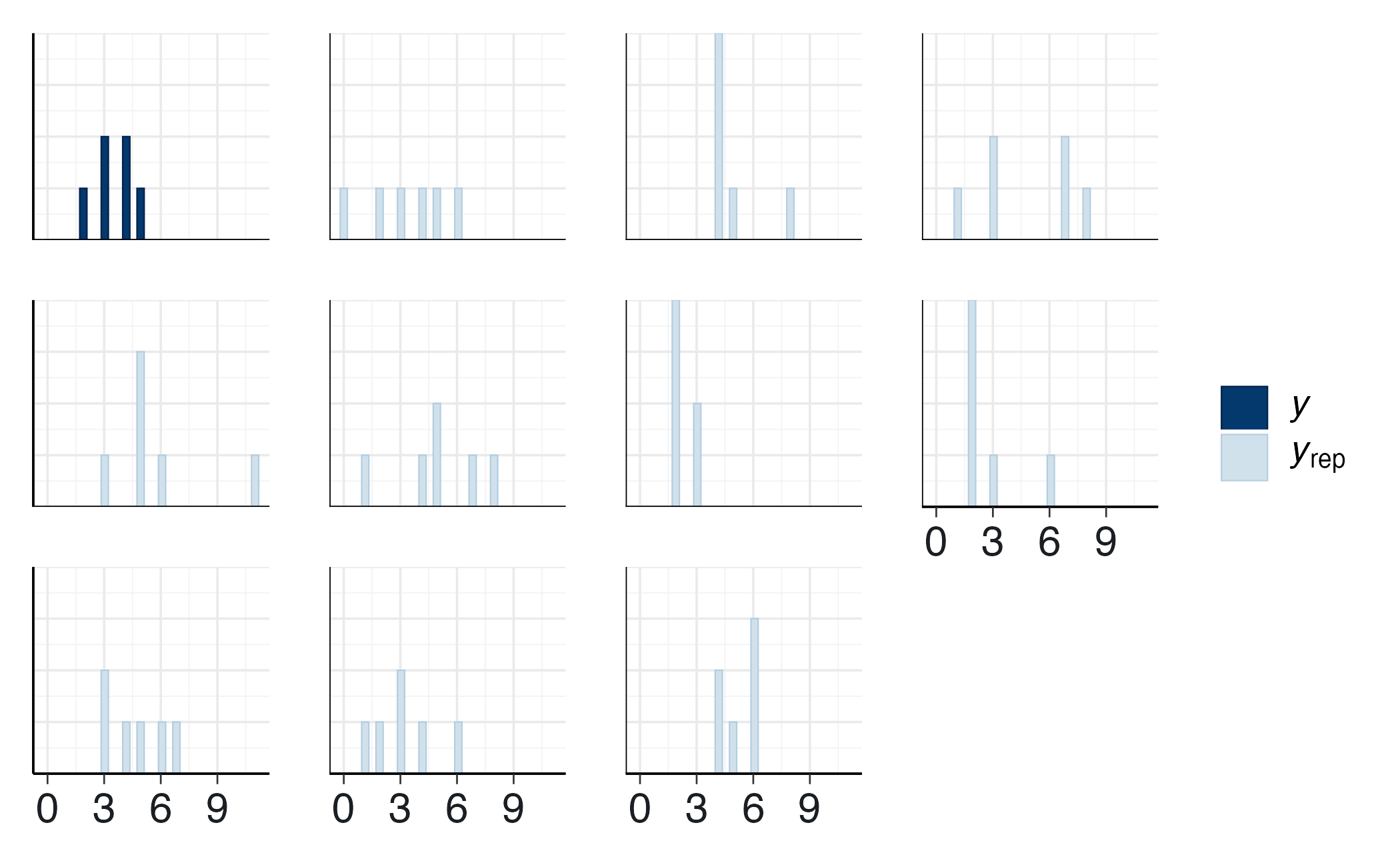
Le verifiche predittive a posteriori confrontano i dati simulati dal modello con quelli effettivamente osservati, offrendo anche un’importante validazione psicologica: se il modello riproduce la variabilità comportamentale tipica (2-5 compulsioni per finestra), la rappresentazione probabilistica risulta coerente con il fenomeno reale.

set.seed(123)
# Matrice yrep: righe = repliche, colonne = finestre
yrep <- replicate(1000, rpois(N, sample(lambda_samples, 1))) |> t()

# PPC grafici (alcuni esempi)
bayesplot::ppc_stat(y, yrep, stat = "mean")

bayesplot::ppc_stat(y, yrep, stat = "sd")

bayesplot::ppc_hist(y, yrep[1:10, ])

# Verifiche quantitative (p-value bayesiani)
p_max <- mean(apply(yrep, 1, max) >= max(y))
p_sum <- mean(rowSums(yrep)        >= sum(y))
tibble(`PPC max (≥ osservato)` = p_max, `PPC somma (≥ osservato)` = p_sum)
#> # A tibble: 1 × 2
#>   `PPC max (≥ osservato)` `PPC somma (≥ osservato)`
#>                     <dbl>                     <dbl>
#> 1                   0.806                     0.507

Se il modello generasse sistematicamente valori estremi (0 o >7), l’assunzione Poissoniana di varianza uguale alla media risulterebbe inadeguata. In tali casi sarebbe necessario considerare modelli con sovradispersione (es. Binomiale Negativa), che accomodano una varianza maggiore della media pur mantenendo un’interpretazione analoga in termini di tasso medio. Questa estensione esula tuttavia dagli obiettivi della presente trattazione.

Questa esercitazione usa un dataset pubblico del Washington Post sulle sparatorie mortali da parte della polizia negli Stati Uniti. L’obiettivo è metodologico: mostrare un caso reale in cui il modello di Poisson con prior Gamma è una buona “palestra” per il workflow bayesiano. Il tema è sensibile: valuta se proporlo in aula e anticipa il contesto etico. Nota anche che l’ipotesi di tasso costante nel tempo è semplificativa; i conteggi reali presentano trend e possibili variazioni stagionali, quindi il modello Poisson i.i.d. è pedagogico, non definitivo.

Domanda della ricerca

Come spiegato nella documentazione del dataset, i dati registrano ogni sparatoria mortale a partire dal 1° gennaio 2015. Stimiamo, per gli anni completi disponibili, un tasso medio annuo \(\lambda\) e la sua incertezza (l’anno corrente non è incluso perché incompleto).

Importazione e pre-processing

# URL del dataset
url <- "https://raw.githubusercontent.com/washingtonpost/data-police-shootings/master/v2/fatal-police-shootings-data.csv"

# Importa i dati
fps_dat <- read_csv(url, show_col_types = FALSE) |>
  mutate(date = lubridate::ymd(date),
         year = lubridate::year(date))

# Esplora e filtra (escludi l'anno corrente, incompleto)
colnames(fps_dat)
#>  [1] "id"                         "date"                      
#>  [3] "threat_type"                "flee_status"               
#>  [5] "armed_with"                 "city"                      
#>  [7] "county"                     "state"                     
#>  [9] "latitude"                   "longitude"                 
#> [11] "location_precision"         "name"                      
#> [13] "age"                        "gender"                    
#> [15] "race"                       "race_source"               
#> [17] "was_mental_illness_related" "body_camera"               
#> [19] "agency_ids"                 "year"
fps <- fps_dat |>
  filter(year != lubridate::year(Sys.Date()))

# Conta le occorrenze per anno
year_counts <- fps |>
  count(year, name = "events") |>
  arrange(year)

print(year_counts)
#> # A tibble: 10 × 2
#>     year events
#>    <dbl>  <int>
#>  1  2015    995
#>  2  2016    959
#>  3  2017    984
#>  4  2018    992
#>  5  2019    993
#>  6  2020   1021
#>  7  2021   1050
#>  8  2022   1097
#>  9  2023   1164
#> 10  2024   1175

Modello di Poisson (pooling completo)

Assumiamo \(y_t \sim \text{Poisson}(\lambda)\), \(t=1,\dots,n\), con \(\lambda\) costante sul periodo (assunzione semplificativa ma utile didatticamente).

Prior

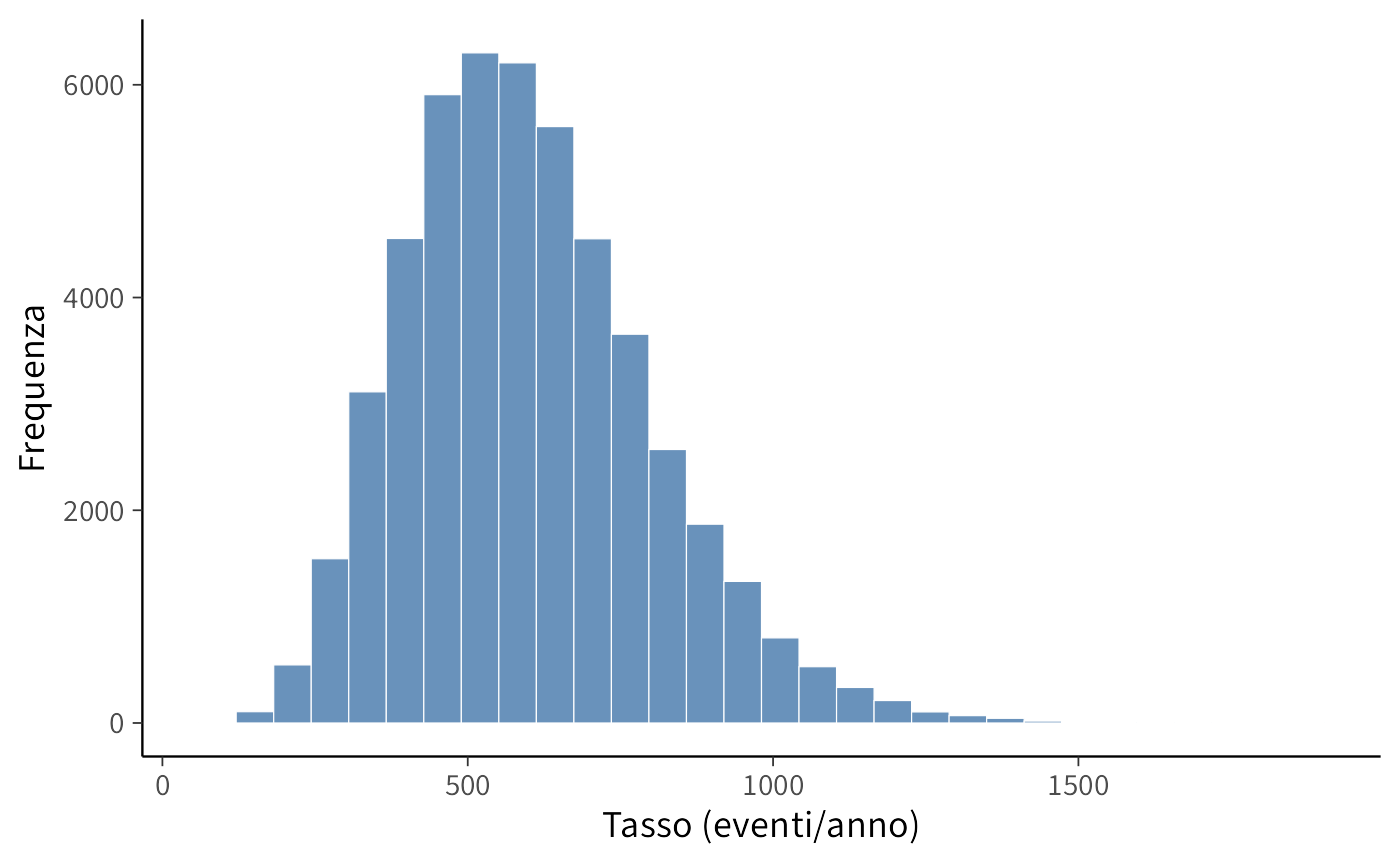
Usiamo una prior Gamma debolmente informativa con media 600 eventi/anno e deviazione standard 200:

mu    <- 600
sigma <- 200
alpha_prior <- (mu / sigma)^2
beta_prior  <-  mu / sigma^2

# Visualizza la prior con una breve simulazione
set.seed(2)
x_draws <- rgamma(50000, shape = alpha_prior, rate = beta_prior)
ggplot(data.frame(x = x_draws), aes(x = x)) +
  geom_histogram(bins = 30) +
  labs(x = "Tasso (eventi/anno)", y = "Frequenza")

Stan: stima di λ

stan_code <- "
data {
  int<lower=1> N;                 // numero di anni
  array[N] int<lower=0> y;        // conteggi annuali
  real<lower=0> alpha_prior;      // shape
  real<lower=0> beta_prior;       // rate
}
parameters {
  real<lower=0> lambda;           // tasso medio annuo
}
model {
  lambda ~ gamma(alpha_prior, beta_prior); // prior
  y ~ poisson(lambda);                     // verosimiglianza
}
generated quantities {
  real log_lik = poisson_lpmf(y | lambda);
}
"
y_vec <- year_counts$events

stan_data <- list(
  N = length(y_vec),
  y = as.integer(y_vec),
  alpha_prior = alpha_prior,
  beta_prior  = beta_prior
)

#| output: false
mod <- cmdstan_model(write_stan_file(stan_code))

#| output: false
fit <- mod$sample(
  data = stan_data,
  iter_warmup = 1000,
  iter_sampling = 4000,
  chains = 4,
  seed = 123,
  refresh = 0
)
#> Running MCMC with 4 chains, at most 10 in parallel...
#> Chain 1 finished in 0.0 seconds.
#> Chain 2 finished in 0.0 seconds.
#> Chain 3 finished in 0.0 seconds.
#> Chain 4 finished in 0.0 seconds.
#> 
#> All 4 chains finished successfully.
#> Mean chain execution time: 0.0 seconds.
#> Total execution time: 0.2 seconds.

# Riassunti senza fissare numeri nel testo (i dati si aggiornano nel tempo)
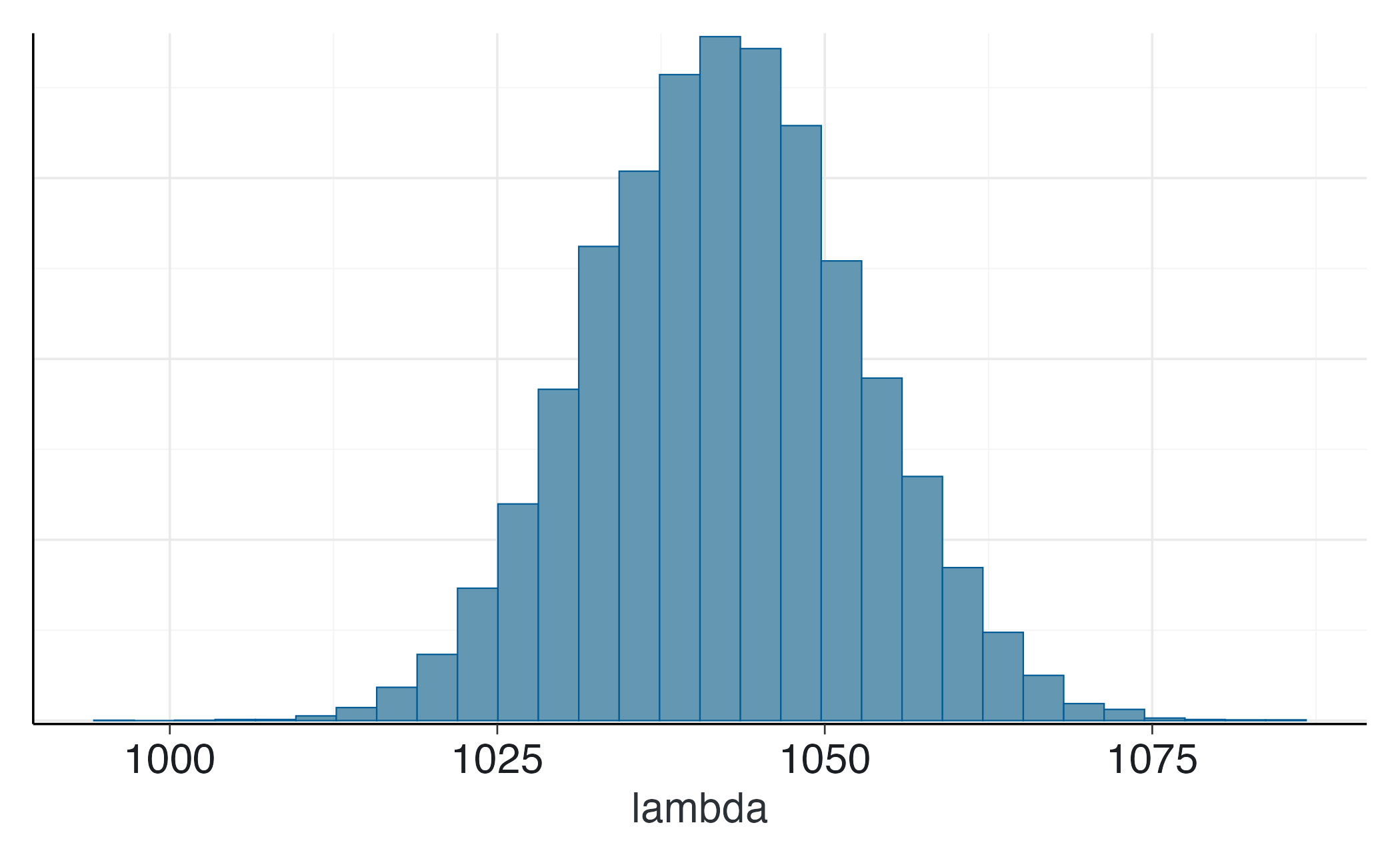
fit$summary("lambda")
#> # A tibble: 1 × 10
#>   variable  mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>    <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 lambda   1042.  1042.  10.3  10.4 1026. 1060.  1.00    6111.    8233.
posterior::summarise_draws(
  fit$draws("lambda"),
  mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)
#> # A tibble: 1 × 6
#>   variable  mean    sd `2.5%` `50%` `97.5%`
#>   <chr>    <dbl> <dbl>  <dbl> <dbl>   <dbl>
#> 1 lambda   1042.  10.3  1023. 1042.   1063.
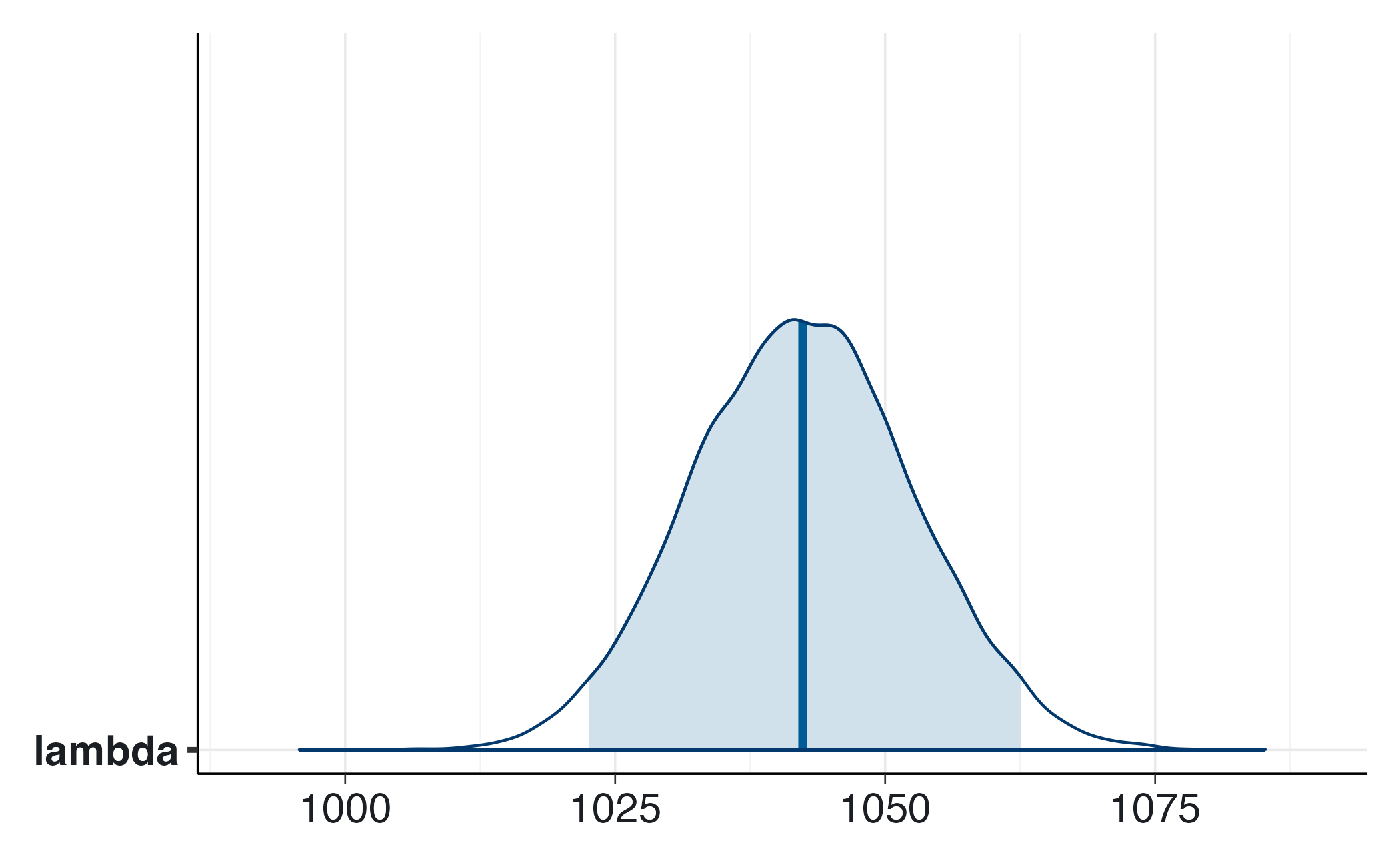
bayesplot::mcmc_hist(fit$draws("lambda")) 

bayesplot::mcmc_areas(fit$draws("lambda"), prob = 0.95)


# Diagnostica
posterior::summarize_draws(fit$draws("lambda"), "rhat", "ess_bulk", "ess_tail")
#> # A tibble: 1 × 4
#>   variable  rhat ess_bulk ess_tail
#>   <chr>    <dbl>    <dbl>    <dbl>
#> 1 lambda    1.00    6111.    8233.
bayesplot::mcmc_trace(fit$draws("lambda"))

Derivazione analitica (Gamma–Poisson)

Con prior \(\lambda \sim \text{Gamma}(\alpha,\beta)\) e \(y_1,\dots,y_n \stackrel{iid}{\sim} \text{Poisson}(\lambda)\), la posterior è: \[ \lambda \mid \mathbf{y} \sim \text{Gamma}!\left(\alpha + \sum_{t=1}^n y_t,; \beta + n\right). \] Quindi media posteriore \((\alpha+\sum y)/(\beta+n)\) e intervallo credibile con i quantili Gamma:

data_vec <- y_vec
n        <- length(data_vec)
sum_y    <- sum(data_vec)

alpha_post <- alpha_prior + sum_y
beta_post  <- beta_prior  + n

post_mean <- alpha_post / beta_post
ci95      <- qgamma(c(0.025, 0.975), shape = alpha_post, rate = beta_post)

cat("Posterior mean λ:", round(post_mean, 1), "\n")
#> Posterior mean λ: 1042
cat("95% CrI: [", round(ci95[1], 1), ", ", round(ci95[2], 1), "]\n")
#> 95% CrI: [ 1022 ,  1062 ]

11.4 Riflessioni conclusive

L’esempio del modello di Poisson ha esteso l’applicazione dell’inferenza bayesiana a una classe di dati diversa da proporzioni e medie, dimostrandone la versatilità nell’ambiente Stan. La struttura logica rimane coerente: attraverso la specificazione di distribuzioni a priori e di una verosimiglianza di Poisson, si ottiene una distribuzione a posteriori che quantifica l’incertezza residua sui parametri di interesse.

Dal punto di vista applicativo, i dati di conteggio sono una tipologia molto diffusa in psicologia. Il caso di John mostra come una serie di compulsioni osservate possa essere tradotta in un modello probabilistico che descrive in modo trasparente il comportamento del soggetto, preservandone la variabilità naturale e l’incertezza di misura. Il parametro λ non rappresenta una semplice stima puntuale, ma incarna una caratteristica psicologicamente significativa: il ritmo medio di manifestazione del sintomo in un contesto ecologico. La sua distribuzione a posteriori si aggiorna dinamicamente con l’acquisizione di nuovi dati, consentendo una valutazione clinica personalizzata del cambiamento sintomatologico. Le quantità predittive, come la probabilità di osservare al massimo due compulsioni nella prossima finestra, forniscono inoltre indicazioni operative direttamente utilizzabili nella pianificazione terapeutica.

Dal punto di vista didattico, questo esempio conferma la continuità tra la modellazione teorica e la pratica della ricerca. Il modello di Poisson, nella sua apparente semplicità, funge da ponte concettuale verso architetture più sofisticate, quali i modelli gerarchici per i dati longitudinali, le strutture dinamiche per i tassi temporalmente variabili e le estensioni che permettono di considerare la sovradispersione. La lezione fondamentale è che un modello probabilistico, pur nella sua essenzialità, fornisce una rappresentazione quantitativa e interpretabile di processi psicologici complessi, esplicitando l’incertezza, integrando le conoscenze pregresse e offrendo un linguaggio formale per quantificare l’evidenza empirica in termini di probabilità.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] lubridate_1.9.4       forcats_1.0.1         stringr_1.5.2        
#>  [4] purrr_1.1.0           readr_2.1.5           tidyverse_2.0.0      
#>  [7] cmdstanr_0.9.0        ragg_1.5.0            tinytable_0.13.0     
#> [10] withr_3.0.2           systemfonts_1.3.1     patchwork_1.3.2      
#> [13] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#> [16] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [19] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [22] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [25] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [28] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [31] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.4            
#> [34] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      ggridges_0.5.7        compiler_4.5.1       
#> [10] reshape2_1.4.4        vctrs_0.6.5           crayon_1.5.3         
#> [13] pkgconfig_2.0.3       arrayhelpers_1.1-0    fastmap_1.2.0        
#> [16] backports_1.5.0       labeling_0.4.3        utf8_1.2.6           
#> [19] rmarkdown_2.30        tzdb_0.5.0            ps_1.9.1             
#> [22] bit_4.6.0             xfun_0.53             cachem_1.1.0         
#> [25] jsonlite_2.0.0        broom_1.0.10          parallel_4.5.1       
#> [28] R6_2.6.1              stringi_1.8.7         RColorBrewer_1.1-3   
#> [31] estimability_1.5.1    knitr_1.50            zoo_1.8-14           
#> [34] pacman_0.5.1          Matrix_1.7-4          splines_4.5.1        
#> [37] timechange_0.3.0      tidyselect_1.2.1      abind_1.4-8          
#> [40] yaml_2.3.10           codetools_0.2-20      processx_3.8.6       
#> [43] curl_7.0.0            pkgbuild_1.4.8        plyr_1.8.9           
#> [46] lattice_0.22-7        bridgesampling_1.1-2  S7_0.2.0             
#> [49] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [52] RcppParallel_5.1.11-1 pillar_1.11.1         tensorA_0.36.2.1     
#> [55] checkmate_2.3.3       stats4_4.5.1          distributional_0.5.0 
#> [58] generics_0.1.4        vroom_1.6.6           rprojroot_2.1.1      
#> [61] hms_1.1.3             rstantools_2.5.0      scales_1.4.0         
#> [64] xtable_1.8-4          glue_1.8.0            emmeans_1.11.2-8     
#> [67] tools_4.5.1           data.table_1.17.8     mvtnorm_1.3-3        
#> [70] grid_4.5.1            QuickJSR_1.8.1        colorspace_2.1-2     
#> [73] nlme_3.1-168          cli_3.6.5             textshaping_1.0.4    
#> [76] svUnit_1.0.8          Brobdingnag_1.2-9     V8_8.0.1             
#> [79] gtable_0.3.6          digest_0.6.37         TH.data_1.1-4        
#> [82] htmlwidgets_1.6.4     farver_2.1.2          memoise_2.0.1        
#> [85] htmltools_0.5.8.1     lifecycle_1.0.4       bit64_4.6.0-1        
#> [88] MASS_7.3-65

Bibliografia

Tilley, P. M., & Rees, C. S. (2014). A clinical case study of the use of ecological momentary assessment in obsessive compulsive disorder. Frontiers in Psychology, 5, 339.