28 Modelli multilivello
Introduzione
Questo capitolo approfondisce gli aspetti implementativi dell’esempio presentato nel capitolo 23 del manuale didattico, dedicato ai modelli multilivello.
Nei capitoli precedenti abbiamo esaminato il confronto tra le medie di gruppi indipendenti, assumendo che ogni osservazione fosse statisticamente indipendente dalle altre. Tuttavia, questa ipotesi è spesso irrealistica nel contesto della ricerca psicologica. Infatti, una parte essenziale del lavoro dello psicologo consiste nel comprendere sia le differenze tra le persone (differenze interindividuali), sia le variazioni all’interno della stessa persona nel tempo o nelle diverse situazioni (differenze intraindividuali).
Le analisi tradizionali, come l’ANOVA o la regressione lineare classica, tendono però a trascurare la struttura multilivello dei dati, trattando tutte le osservazioni come indipendenti. In presenza di misurazioni ripetute o di gruppi naturalmente nidificati (per esempio, studenti all’interno di classi, pazienti all’interno di centri clinici o momenti di osservazione all’interno della stessa persona), tale assunzione viene violata, compromettendo la validità delle inferenze.
Questa semplificazione può condurre a conclusioni fuorvianti. Si consideri, ad esempio, uno studio sull’umore giornaliero: in media, le persone potrebbero sembrare più felici durante il fine settimana, ma alcune potrebbero invece sperimentare maggiore solitudine o disagio proprio in quei giorni. Ignorare queste differenze individuali significa trascurare un’informazione psicologica cruciale, ovvero il modo in cui ogni individuo si discosta dal comportamento medio della popolazione.
28.1 L’approccio idiografico e l’analisi personalizzata
Negli ultimi anni è cresciuta la consapevolezza che ogni individuo è un caso a sé. L’approccio idiografico cerca di modellare le caratteristiche di ogni persona singolarmente. Tuttavia, le analisi idiografiche pure richiedono un gran numero di dati per ciascun soggetto e spesso non sono praticabili negli studi reali.
I modelli multilivello bayesiani offrono un compromesso elegante. Questi modelli permettono di stimare gli effetti specifici per ogni individuo, ma sfruttano anche l’informazione condivisa all’interno del gruppo. Ciò è possibile grazie al meccanismo di shrinkage, che “bilancia” le stime individuali con la tendenza generale. Ne vedremo il funzionamento più avanti.
28.2 I tre approcci: complete pooling, no pooling, e partial pooling
Quando analizziamo i dati gerarchici, come le misurazioni ripetute sullo stesso individuo o i dati delle persone in gruppi, possiamo scegliere diverse strategie. Per fare un esempio, consideriamo uno studio sugli effetti della deprivazione del sonno su dieci partecipanti, valutati più volte ciascuno.
Il primo approccio è il complete pooling. In questo caso, trattiamo tutti i dati come se fossero stati raccolti da un’unica entità, ignorando completamente la struttura gerarchica. È come se tutti e dieci i partecipanti fossero, in realtà, la stessa persona.
All’estremo opposto, troviamo il no pooling. In questo caso, si stima un effetto completamente separato per ogni partecipante, come se non ci fosse alcuna informazione comune o relazione tra loro. Ogni individuo è considerato un’entità unica e indipendente.
Infine, il partial pooling, noto anche come modello multilivello, rappresenta una via di mezzo e spesso è la soluzione più equilibrata. In questo approccio, stimiamo comunque effetti individuali per ciascun partecipante, ma li “regolarizziamo”, ovvero li avviciniamo alla media complessiva del gruppo. Ciò significa che le stime per ciascun partecipante sono influenzate sia dai dati specifici di ciascun partecipante, sia dalla tendenza generale osservata nell’intero gruppo.
Nelle prossime sezioni, esploreremo come implementare ciascuno di questi tre modelli utilizzando il pacchetto brms in R, fornendo un’applicazione pratica di questi concetti teorici.
28.2.1 Un esempio guidato: l’effetto della deprivazione del sonno sulle prestazioni psicomotorie
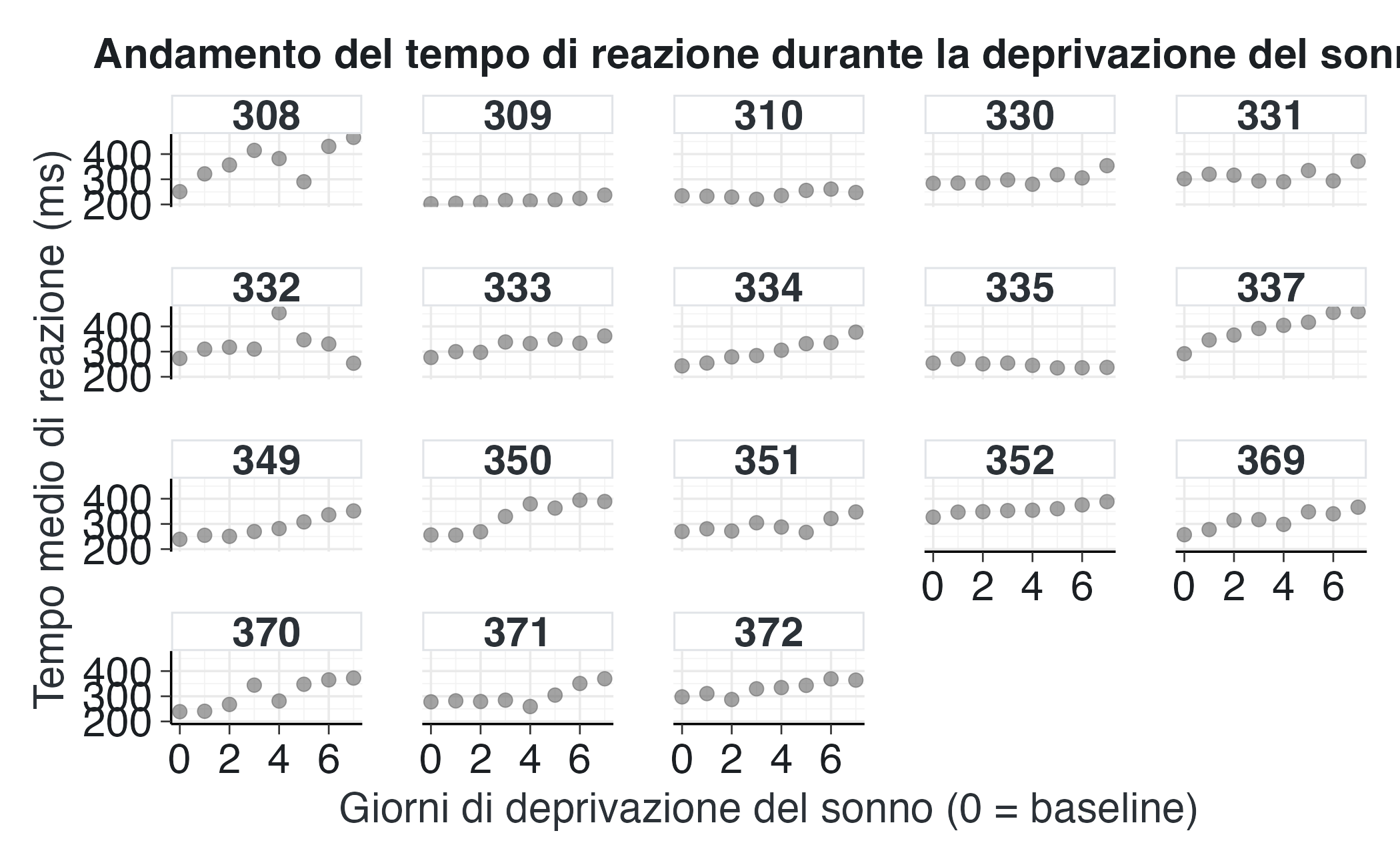
Per illustrare l’utilità dei modelli multilivello nell’analisi di dati longitudinali, utilizzeremo un dataset derivato dallo studio di Belenky et al. (2003), il quale ha esaminato l’effetto cumulativo della restrizione del sonno sulla vigilanza psicomotoria. In questo studio, i partecipanti hanno svolto per dieci giorni un compito di reazione agli stimoli visivi ripetuto più volte, dopo aver dormito solo tre ore per notte. La variabile di interesse è il tempo medio di reazione (in millisecondi), registrato ogni giorno per ciascun partecipante.
Il dataset ha una struttura tipicamente multilivello: ogni soggetto ha fornito osservazioni ripetute nel tempo, pertanto ci si aspetta una forte correlazione intraindividuale. L’analisi mira a quantificare sia l’effetto medio della deprivazione del sonno sia le differenze individuali nella traiettoria del tempo di reazione.
Per semplicità, caricheremo direttamente il file già elaborato sleep2.csv, in cui sono stati rimossi i primi due giorni (fase di adattamento e addestramento). Inoltre, è stata creata una nuova variabile, days_deprived, che parte da 0 (baseline) e aumenta nei giorni successivi di deprivazione del sonno.
Questa visualizzazione evidenzia sia la tendenza generale all’aumento del tempo di reazione sia la variabilità tra i soggetti riguardo al modo in cui le prestazioni si degradano nel tempo. I modelli multilivello ci permetteranno di formalizzare queste osservazioni, stimando congiuntamente l’effetto medio della deprivazione del sonno e le differenze tra i partecipanti in termini di velocità e intensità di tale effetto.
28.2.2 Relazione tra tempo di reazione e deprivazione del sonno
L’analisi dei dati relativi alla deprivazione del sonno ha rivelato che, con l’unica eccezione del soggetto 335, il tempo medio di reazione tende ad aumentare progressivamente con l’aumentare di ogni giorno deprivazione aggiuntivo. Questo suggerisce che un modello di regressione lineare potrebbe essere utile per descrivere le prestazioni di ciascun partecipante.
La regressione lineare è definita dalla seguente equazione:
\[ E(Y) = \beta_0 + \beta_1 X, \] dove:
- \(Y\) rappresenta la variabile dipendente (il tempo di reazione medio);
- \(\beta_0\) è l’intercetta, ovvero il tempo di reazione stimato il primo giorno (baseline, senza deprivazione del sonno);
- \(\beta_1\) è il coefficiente di pendenza che rappresenta la variazione stimata del tempo di reazione per ogni giorno di deprivazione aggiuntivo;
- \(X\) indica il numero di giorni di deprivazione del sonno.
I parametri \(\beta_0\) e \(\beta_1\) vengono stimati dai dati e la loro interpretazione fornisce informazioni chiave sulle dinamiche delle prestazioni psicomotorie.
28.2.3 Scelta del modello di regressione
Un aspetto cruciale dell’analisi è la scelta della struttura modellistica da adottare per descrivere i dati. Bisogna considerare le seguenti opzioni.
Complete Pooling: questo approccio utilizza un unico modello di regressione lineare per tutti i partecipanti, assumendo che la relazione tra deprivazione del sonno e tempo di reazione sia identica per tutti. In pratica, si stima una singola intercetta (\(\beta_0\)) e una singola pendenza (\(\beta_1\)) comuni a tutti i soggetti. Sebbene sia semplice, questo metodo ignora completamente le differenze individuali.
No Pooling: in questo caso, si stima un modello di regressione lineare separato per ciascun partecipante, consentendo a ogni soggetto di avere la propria intercetta e la propria pendenza. Questo approccio riconosce pienamente le variazioni individuali, ma potrebbe risultare eccessivamente complesso e sensibile al rumore nei dati, soprattutto quando il numero di punti di osservazione per soggetto è ridotto.
Partial Pooling: questo approccio intermedio, spesso implementato attraverso i modelli multilivello, bilancia i due estremi descritti in precedenza. Si assume una relazione media condivisa tra i soggetti (ad esempio, una pendenza media), ma si consente una variazione individuale attorno a questa media. Il partial pooling sfrutta le informazioni condivise tra i partecipanti, migliorando la robustezza delle stime, soprattutto in presenza di un numero ridotto di dati per ciascun soggetto.
28.3 Complete pooling: un modello unico per tutti
L’approccio del complete pooling presuppone che tutti i partecipanti seguano la stessa relazione tra la variabile indipendente (ad esempio, giorni di deprivazione del sonno) e quella dipendente (ad esempio, tempo di reazione). In altre parole, si stima un’unica intercetta e un’unica pendenza per l’intero campione, ignorando le differenze individuali. Questo approccio può essere utile come modello di partenza, ma è spesso irrealistico in psicologia, dove i soggetti tendono a mostrare andamenti diversi.
Per adattare questo modello in R, utilizziamo la funzione brm():
cp_model <- brm(
Reaction ~ days_deprived,
data = sleep2,
family = gaussian(),
chains = 2, iter = 1000,
backend = "cmdstanr",
refresh = 0
)fixef(cp_model)
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 268.0 7.60 253.47 282.4
#> days_deprived 11.4 1.87 7.93 15.3Il modello stima che il tempo di reazione iniziale (al giorno 0) sia di circa 268 ms e che aumenti di circa 11 ms per ogni giorno di deprivazione del sonno.
28.3.1 Limiti dell’approccio
Questo approccio presenta diverse criticità. In primo luogo, ignora il fatto che lo stesso soggetto viene misurato più volte, il che significa che l’indipendenza delle osservazioni non viene rispettata. Di conseguenza, gli errori standard dei coefficienti potrebbero risultare irrealistici, portando a una sottostima dell’incertezza. Inoltre, il modello non considera la perdita di informazione individuale, in quanto ogni soggetto potrebbe avere la propria intercetta e la propria pendenza, aspetti che non vengono presi in considerazione in questa analisi.
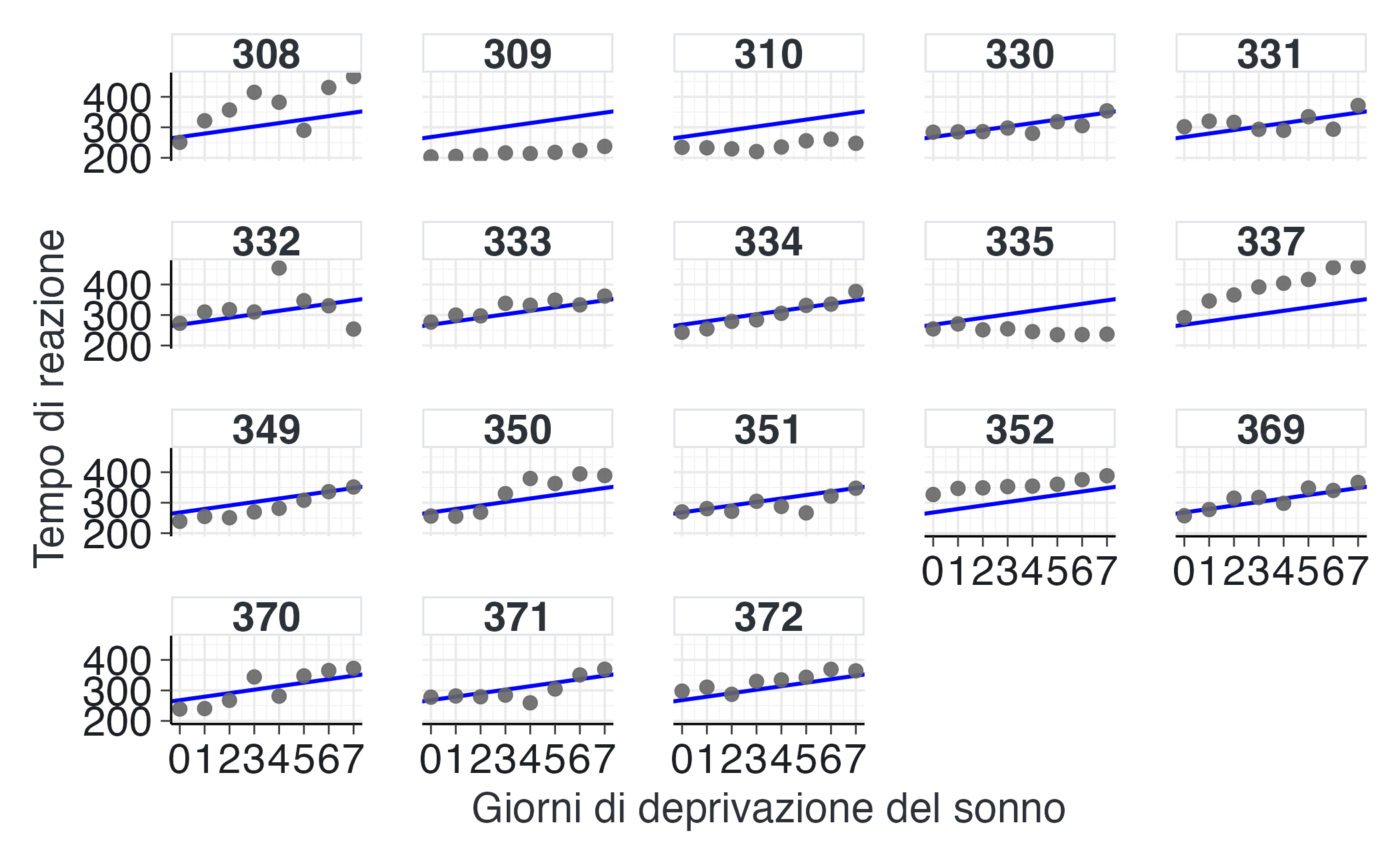
Per visualizzare meglio questi risultati, possiamo aggiungere le previsioni del modello al grafico che abbiamo già creato.
Il grafico mostra che il modello attuale non si adatta in modo ottimale ai dati raccolti. Ciò evidenzia la necessità di adottare un approccio diverso per modellare in modo più accurato le relazioni presenti nei dati.
28.4 No Pooling: un modello per ciascun partecipante
L’approccio del no pooling stima una retta di regressione distinta per ogni soggetto, trattando ciascuno di essi come un caso indipendente. Questo approccio consente di cogliere al meglio le differenze individuali, ma ignora completamente l’informazione condivisa tra i soggetti. Si tratta del metodo più vicino a un’analisi idiografica pura. In questo modo, ogni partecipante ha la propria intercetta e la propria pendenza. Tuttavia, le stime non sono regolarizzate, pertanto i soggetti con pochi dati possono produrre stime molto rumorose.
28.4.1 Implementazione con brm() mediante un loop
# Otteniamo i livelli unici dei soggetti
subjects <- unique(sleep2$Subject)
# Inizializziamo una lista per salvare i modelli
subject_models <- list()
subject_coefs <- tibble()
# Loop sui soggetti
for (id in subjects) {
data_i <- filter(sleep2, Subject == id)
fit <- brm(
Reaction ~ days_deprived,
data = data_i,
family = gaussian(),
chains = 2, iter = 1000, refresh = 0,
backend = "cmdstanr",
silent = TRUE
)
subject_models[[as.character(id)]] <- fit
coef_i <- fixef(fit)[, "Estimate"]
subject_coefs <- bind_rows(subject_coefs, tibble(
Subject = id,
intercept = coef_i[1],
slope = coef_i[2]
))
}Questo approccio evidenzia efficacemente le differenze individuali sia nella pendenza, che riflette il tasso di peggioramento, sia nell’intercetta, corrispondente al livello basale di reazione. Tuttavia, questo approccio non sfrutta l’informazione condivisa all’interno del gruppo, limitando così la sua efficacia inferenziale. Inoltre, le stime risultano particolarmente instabili per i soggetti con un numero limitato di osservazioni.
Nel prossimo passo, vedremo un compromesso tra il no pooling e il complete pooling: il partial pooling, tipico dei modelli multilivello bayesiani.
28.5 Partial pooling: un compromesso tra individuo e gruppo
Nel modellare i dati psicologici, dobbiamo scegliere se trattare ogni partecipante come un caso a sé stante (no pooling) o considerare tutti i dati come provenienti da un unico gruppo omogeneo (complete pooling). Il partial pooling è un approccio intermedio: ogni soggetto ha le proprie stime, ma queste sono influenzate anche dai dati degli altri soggetti. Ciò si realizza con i modelli multilivello o a effetti misti.
28.5.1 Il concetto di shrinkage
Nel partial pooling, le stime individuali subiscono un fenomeno di contrazione verso la media del gruppo noto come shrinkage. Questo meccanismo opera come una sorta di regolarizzazione statistica che stabilizza le stime, particolarmente utile quando i dati individuali sono limitati o affetti da rumore. Operativamente, il modello bilancia dinamicamente le fonti di informazione: per i partecipanti con un numero limitato di osservazioni, privilegia l’informazione di gruppo; quando invece sono disponibili numerosi dati individuali, attribuisce maggiore peso all’evidenza specifica del soggetto.
28.5.2 Implementazione con brm()
L’obiettivo consiste nello specificare un modello che accomodi eterogeneità individuale sia nel livello basale (intercetta) che nel tasso di cambiamento (pendenza).
# Modello multilivello (partial pooling)
pp_model <- brm(
Reaction ~ 1 + days_deprived + (1 + days_deprived | Subject),
data = sleep2,
family = gaussian(),
chains = 2, iter = 2000, seed = 123,
backend = "cmdstanr",
refresh = 0
)Qui la sintassi 1 + days_deprived | Subject specifica che a ciascun soggetto viene associata un’intercetta unica e una pendenza specifica per la variabile days_deprived.
Costruiamo le predizioni del modello per ciascun soggetto, considerando l’intero range di giorni di deprivazione, e procediamo alla visualizzazione dei risultati:
28.6 Il ruolo dei modelli multilivello in psicologia
28.6.1 Una sintesi tra nomotetico e idiografico
La ricerca psicologica si è tradizionalmente articolata in due prospettive epistemologiche distinte: l’approccio nomotetico, volto all’identificazione di principi generali applicabili a tutta la popolazione, e l’approccio idiografico, focalizzato sull’indagine delle caratteristiche distintive di ciascun individuo. I modelli multilivello rappresentano una sintesi metodologica che supera questa dicotomia, riconoscendo che le traiettorie individuali (dimensione idiografica) si sviluppano all’interno di contesti collettivi che ne influenzano l’andamento (dimensione nomotetica).
Questa integrazione consente di indagare sistematicamente le differenze individuali, preservando al contempo la capacità di generalizzazione a livello di popolazione e offrendo un contributo metodologicamente robusto alla comprensione del comportamento umano.
Tuttavia, l’applicazione di questi modelli richiede una riflessione critica sulle assunzioni teoriche su cui si basano. Come evidenziato da (richters2021incredible?), gran parte della ricerca psicologica adotta implicitamente un’«assunzione ergonomica» che presuppone un’omogeneità psicologica fondamentale tra gli individui. Questa premessa, sebbene sia funzionale all’aggregazione dei dati e alla stima degli effetti medi, rischia di mascherare le sostanziali eterogeneità, producendo quello che l’autore chiama “causal debris”: una proliferazione di risultati significativi, ma teoricamente frammentari e difficili da replicare.
La capacità dei modelli multilivello di stimare simultaneamente effetti medi e variazioni individuali non garantisce che tali effetti riflettano processi causali omogenei tra i partecipanti. In assenza di una solida base teorica che specifichi quali meccanismi siano plausibilmente condivisi e in che modo possano variare, si rischia di interpretare le differenze qualitative come semplici deviazioni quantitative da un effetto medio.
Pertanto, l’implementazione di modelli multilivello in psicologia richiede un’attenzione critica alla plausibilità teorica dell’omogeneità assunta, affiancando all’analisi statistica l’esplorazione di approcci complementari, quali la modellizzazione idiografica pura o l’identificazione di sottogruppi teoricamente fondati. Solo attraverso questa integrazione metodologica è possibile cogliere appieno la complessità e la variabilità che caratterizzano i fenomeni psicologici.
28.7 Interpretazione del modello
Dopo aver stimato un modello multilivello, è importante saperlo leggere e interpretare. In particolare, analizzeremo tre componenti fondamentali: gli effetti fissi (la media del gruppo), gli effetti casuali (le deviazioni individuali) e la varianza tra soggetti.
28.7.1 Effetti fissi: la media del gruppo
fixef(pp_model)
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 267.9 9.09 250.20 286.4
#> days_deprived 11.5 1.95 7.72 15.5Questo comando restituisce le stime degli effetti fissi a livello di popolazione:
- l’intercetta corrisponde al tempo di reazione medio stimato in condizioni basali (giorno 0, senza deprivazione di sonno);
- il coefficiente di
days_deprivedindica l’incremento medio del tempo di reazione associato a ogni giorno aggiuntivo di deprivazione di sonno.
Questi parametri rappresentano gli effetti “nomotetici” del modello, descrivendo le relazioni medie che caratterizzano l’intera popolazione di riferimento.
28.7.2 Effetti casuali: le deviazioni individuali
ranef(pp_model)$Subject
#> , , Intercept
#>
#> Estimate Est.Error Q2.5 Q97.5
#> 308 24.754 15.8 -4.113 57.02
#> 309 -59.221 16.6 -92.099 -28.59
#> 310 -39.815 14.9 -69.778 -11.60
#> 330 0.919 15.1 -28.436 30.08
#> 331 17.447 15.7 -13.441 48.88
#> 332 29.633 16.2 -0.272 61.70
#> 333 12.871 15.5 -17.235 44.26
#> 334 -17.473 15.6 -49.469 12.81
#> 335 -17.245 15.6 -47.889 13.58
#> 337 44.654 16.4 13.507 75.40
#> 349 -26.089 15.6 -57.449 4.23
#> 350 -5.884 16.1 -37.797 25.12
#> 351 -5.946 15.3 -38.501 24.12
#> 352 45.968 16.2 16.817 80.10
#> 369 1.058 15.0 -29.863 31.03
#> 370 -18.069 16.0 -50.287 12.79
#> 371 -7.354 15.3 -38.538 23.03
#> 372 17.499 15.4 -12.578 48.52
#>
#> , , days_deprived
#>
#> Estimate Est.Error Q2.5 Q97.5
#> 308 8.515 3.66 1.53 16.011
#> 309 -8.107 3.77 -15.67 -0.825
#> 310 -7.341 3.64 -14.75 -0.281
#> 330 -2.292 3.52 -9.40 4.382
#> 331 -3.679 3.64 -11.18 3.478
#> 332 -4.763 3.82 -12.66 2.419
#> 333 0.295 3.60 -6.88 7.094
#> 334 3.671 3.69 -3.37 11.171
#> 335 -12.075 3.69 -19.45 -5.105
#> 337 10.078 3.74 2.82 17.293
#> 349 2.029 3.60 -4.52 9.120
#> 350 8.047 3.63 1.09 15.468
#> 351 -2.300 3.51 -9.38 4.388
#> 352 -0.494 3.79 -7.76 6.682
#> 369 1.726 3.51 -4.89 8.820
#> 370 5.431 3.66 -1.54 13.243
#> 371 0.250 3.43 -6.18 7.081
#> 372 0.641 3.54 -6.50 7.390Questo comando restituisce, per ciascun partecipante, l’entità con cui i suoi parametri si discostano dalla media di popolazione.
In particolare, vengono riportati:
- gli scostamenti dell’intercetta, che riflettono differenze nei tempi di reazione di base tra i soggetti;
- gli scostamenti della pendenza, che mostrano quanto ciascun individuo sia più o meno sensibile, rispetto alla media del gruppo, all’effetto della deprivazione di sonno.
Queste deviazioni individuali, note come effetti casuali stimati, quantificano la componente specifica di ciascun partecipante che non è spiegata dagli effetti fissi del modello. Esse consentono di osservare come ogni individuo si discosti sistematicamente dal comportamento medio del gruppo.
28.7.3 Varianza tra soggetti: quanta differenza c’è nel campione
VarCorr(pp_model)$Subject
#> $sd
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 33.6 8.04 20.85 53.5
#> days_deprived 7.4 1.83 4.39 11.6
#>
#> $cor
#> , , Intercept
#>
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 1.000 0.000 1.000 1.000
#> days_deprived 0.185 0.302 -0.408 0.764
#>
#> , , days_deprived
#>
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 0.185 0.302 -0.408 0.764
#> days_deprived 1.000 0.000 1.000 1.000
#>
#>
#> $cov
#> , , Intercept
#>
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 1194 605.2 435 2857
#> days_deprived 39 83.6 -137 205
#>
#> , , days_deprived
#>
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept 39.0 83.6 -137.2 205
#> days_deprived 58.1 30.5 19.3 134L’output riporta la dispersione (deviazioni standard, varianze e covarianze) e la correlazione tra gli effetti casuali dell’intercetta e della pendenza. Queste informazioni descrivono l’eterogeneità tra i partecipanti e il modo in cui le loro differenze nei tempi di reazione si associano all’effetto della deprivazione di sonno.
La deviazione standard dell’intercetta è di circa 33.6 ms (IC 95%: 20.9 – 53.5), indicando una notevole variabilità nei tempi di reazione di base: alcuni soggetti sono sistematicamente più rapidi, altri più lenti, anche prima dell’intervento della manipolazione sperimentale.
La deviazione standard della pendenza è pari a 7.4 ms (IC 95%: 4.4 – 11.6), suggerendo che esistono differenze di rilievo anche nella sensibilità individuale alla deprivazione di sonno. In altre parole, i soggetti non reagiscono tutti allo stesso modo: alcuni mostrano un rallentamento marcato, altri quasi nullo.
La correlazione tra intercetta e pendenza è stimata a 0.18, ma con un intervallo di credibilità ampio (–0.41, 0.76). Questa incertezza indica che non vi è una prova consistente di un legame tra i tempi di reazione di base e l’entità dell’effetto della deprivazione: non possiamo affermare con certezza che chi parte più lento tenda anche ad aumentare di più i tempi con il sonno ridotto.
La matrice di covarianza, anch’essa presente nell’output, completa il quadro informativo: la covarianza tra intercetta e pendenza è stimata attorno a 39, sebbene con un ampio intervallo di credibilità (–137, 205). Questo parametro quantifica la relazione sistematica tra i due effetti casuali: un valore positivo indicherebbe che soggetti con tempi di reazione basali più elevati tendono a mostrare incrementi più marcati in condizioni di deprivazione, mentre la sostanziale sovrapposizione dello zero nell’intervallo di credibilità suggerisce che, nei nostri dati, le due dimensioni potrebbero variare in modo indipendente.
Nel complesso, il modello rivela una marcata eterogeneità tra gli individui, sia nei livelli di prestazione iniziale sia nella risposta alla manipolazione. Questa diversità rappresenta la variabilità idiografica del campione: ciascun individuo presenta un proprio profilo di funzionamento, distinguibile ma connesso a un quadro di gruppo condiviso.
In sintesi:
| Comando | Cosa restituisce | Significato |
|---|---|---|
fixef(pp_model) |
Effetti fissi (intercetta e pendenza medie) | Relazioni medie a livello di popolazione |
ranef(pp_model)$Subject |
Deviazioni individuali dagli effetti fissi | Specificità di ciascun soggetto rispetto alla media |
VarCorr(pp_model) |
Varianza e correlazione degli effetti casuali | Entità e struttura della variabilità individuale |
Queste funzioni consentono di interpretare il modello multilivello in modo esaustivo: non solo identificano le tendenze centrali, ma anche l’entità delle differenze individuali rispetto a tali tendenze. Questa duplice lettura costituisce l’essenza del partial pooling.
Riflessioni conclusive
I modelli multilivello costituiscono uno strumento metodologico fondamentale per la ricerca psicologica, particolarmente adatto all’analisi di dati con struttura gerarchica, come quelli derivanti da misurazioni ripetute sugli stessi individui. Il loro principale vantaggio risiede nella capacità di integrare informazioni provenienti da diversi livelli di analisi, consentendo di stimare congiuntamente le tendenze generali a livello di popolazione e le variazioni specifiche a livello individuale.
In questo capitolo è stato introdotto il concetto di “partial pooling”, che si colloca a metà strada tra due approcci estremi: il “complete pooling”, che presuppone l’omogeneità totale tra i soggetti, e il “no pooling”, che analizza ogni individuo in modo completamente isolato. Il partial pooling rappresenta un compromesso ottimale tra queste due prospettive, consentendo, da un lato, di modellare sistematicamente la variabilità interindividuale e, dall’altro, di sfruttare strategicamente l’informazione condivisa nel campione per ottenere stime più robuste.
Il fenomeno dello shrinkage, ovvero la contrazione delle stime individuali verso la media di gruppo, rappresenta una caratteristica essenziale di questo approccio. Questo meccanismo di regolarizzazione statistica non rappresenta un limite metodologico, ma un elemento funzionale che previene il sovradattamento e riduce l’incertezza delle stime, risultando particolarmente vantaggioso quando i dati individuali sono limitati o rumorosi.
Dal punto di vista epistemologico, i modelli multilivello superano la tradizionale dicotomia tra approccio nomotetico e idiografico. Questi modelli, infatti, permettono di rispondere simultaneamente a domande relative alle relazioni medie a livello di popolazione e all’identificazione delle specifiche caratteristiche individuali, riconoscendo la coesistenza di pattern generali e di differenze sistematiche tra i soggetti.
L’applicazione al dataset sleepstudy ha mostrato in modo concreto come modellare gli effetti della deprivazione di sonno sui tempi di reazione, distinguendo chiaramente l’effetto medio nella popolazione dalla variabilità interindividuale nella risposta alla deprivazione. L’analisi ha dimostrato che è possibile stimare i parametri specifici per ciascun partecipante, mantenendo al contempo la coerenza con il principio del partial pooling.
Questi modelli trovano ampia applicazione in vari ambiti della psicologia, dalla psicometria allo studio delle traiettorie di sviluppo, e costituiscono la base concettuale per i successivi modelli di crescita latente. Rappresentano inoltre il quadro metodologico di riferimento per affrontare il tema dell’affidabilità tra osservatori, che verrà approfondito in seguito.
In sintesi, i modelli multilivello offrono un approccio rigoroso e sofisticato per l’analisi dei dati psicologici, che coniuga il rigore metodologico con l’attenzione necessaria alla complessità dei fenomeni umani. La loro adozione contribuisce significativamente allo sviluppo di una psicologia scientifica che sia in grado di cogliere sia le regolarità generali sia le specificità individuali che caratterizzano il comportamento umano.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] kableExtra_1.4.0 cmdstanr_0.9.0 lme4_1.1-37
#> [4] Matrix_1.7-4 car_3.1-3 carData_3.0-5
#> [7] ragg_1.5.0 tinytable_0.13.0 withr_3.0.2
#> [10] systemfonts_1.3.1 patchwork_1.3.2 ggdist_3.3.3
#> [13] tidybayes_3.0.7 bayesplot_1.14.0 ggplot2_4.0.0
#> [16] reliabilitydiag_0.2.1 priorsense_1.1.1 posterior_1.6.1
#> [19] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [22] brms_2.23.0 Rcpp_1.1.0 sessioninfo_1.2.3
#> [25] conflicted_1.2.0 janitor_2.2.1 matrixStats_1.5.0
#> [28] modelr_0.1.11 tibble_3.3.0 dplyr_1.1.4
#> [31] tidyr_1.3.1 rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] RColorBrewer_1.1-3 tensorA_0.36.2.1 rstudioapi_0.17.1
#> [4] jsonlite_2.0.0 magrittr_2.0.4 TH.data_1.1-4
#> [7] estimability_1.5.1 farver_2.1.2 nloptr_2.2.1
#> [10] rmarkdown_2.30 vctrs_0.6.5 memoise_2.0.1
#> [13] minqa_1.2.8 htmltools_0.5.8.1 distributional_0.5.0
#> [16] curl_7.0.0 broom_1.0.10 Formula_1.2-5
#> [19] htmlwidgets_1.6.4 sandwich_3.1-1 emmeans_1.11.2-8
#> [22] zoo_1.8-14 lubridate_1.9.4 cachem_1.1.0
#> [25] lifecycle_1.0.4 pkgconfig_2.0.3 R6_2.6.1
#> [28] fastmap_1.2.0 rbibutils_2.3 snakecase_0.11.1
#> [31] digest_0.6.37 colorspace_2.1-2 ps_1.9.1
#> [34] rprojroot_2.1.1 textshaping_1.0.4 labeling_0.4.3
#> [37] timechange_0.3.0 abind_1.4-8 compiler_4.5.1
#> [40] S7_0.2.0 backports_1.5.0 inline_0.3.21
#> [43] QuickJSR_1.8.1 pkgbuild_1.4.8 R.utils_2.13.0
#> [46] MASS_7.3-65 tools_4.5.1 R.oo_1.27.1
#> [49] glue_1.8.0 nlme_3.1-168 grid_4.5.1
#> [52] checkmate_2.3.3 generics_0.1.4 gtable_0.3.6
#> [55] R.methodsS3_1.8.2 data.table_1.17.8 xml2_1.4.0
#> [58] pillar_1.11.1 stringr_1.5.2 splines_4.5.1
#> [61] lattice_0.22-7 survival_3.8-3 tidyselect_1.2.1
#> [64] knitr_1.50 reformulas_0.4.1 arrayhelpers_1.1-0
#> [67] gridExtra_2.3 V8_8.0.1 svglite_2.2.1
#> [70] stats4_4.5.1 xfun_0.53 bridgesampling_1.1-2
#> [73] stringi_1.8.7 yaml_2.3.10 pacman_0.5.1
#> [76] boot_1.3-32 evaluate_1.0.5 codetools_0.2-20
#> [79] cli_3.6.5 RcppParallel_5.1.11-1 xtable_1.8-4
#> [82] Rdpack_2.6.4 processx_3.8.6 coda_0.19-4.1
#> [85] svUnit_1.0.8 parallel_4.5.1 rstantools_2.5.0
#> [88] Brobdingnag_1.2-9 viridisLite_0.4.2 mvtnorm_1.3-3
#> [91] scales_1.4.0 purrr_1.1.0 rlang_1.1.6
#> [94] multcomp_1.4-28