6 Distribuzione predittiva a posteriori
Introduzione
Questo materiale costituisce un approfondimento del capitolo 18 del manuale didattico, dedicato alla validazione della capacità predittiva dei modelli bayesiani.
Nel manuale didattico abbiamo esaminato due aspetti fondamentali dell’inferenza bayesiana: da un lato, la costruzione delle distribuzioni a posteriori dei parametri di interesse; dall’altro, la verifica dei prior mediante i controlli predittivi, per accertare la compatibilità delle nostre assunzioni iniziali con la realtà psicologica oggetto di studio.
Ora compiamo un passo ulteriore. La domanda non è più soltanto se i prior siano ragionevoli, ma se l’intero modello, dopo aver incorporato i dati osservati, sia in grado di generare previsioni plausibili per nuovi individui, nuove sedute o nuove prove. È questo spostamento di prospettiva a definire il concetto di distribuzione predittiva a posteriori.
Se un modello rappresenta in modo credibile il processo che ha generato i dati, allora deve essere in grado di fare due cose: adattarsi ai dati raccolti e simulare dati nuovi con caratteristiche simili. In psicologia, ciò significa, ad esempio, prevedere il punteggio di uno studente a un questionario d’ansia che non ha partecipato allo studio, stimare la probabilità di un ricordo corretto in una prova di memoria per un nuovo partecipante o quantificare la riduzione attesa dei sintomi depressivi dopo un ciclo di terapia cognitivo-comportamentale.
Spesso, la distribuzione predittiva a posteriori è persino più interessante della distribuzione a posteriori dei parametri. Mentre quest’ultima quantifica la nostra incertezza riguardo a quantità latenti, come la media dei punteggi BDI in una popolazione, la distribuzione predittiva a posteriori risponde a domande più applicative: qual è la probabilità che un nuovo paziente raggiunga una remissione clinicamente significativa? Quale gamma di punteggi possiamo attenderci nella prossima somministrazione del test di Stroop?
La differenza fondamentale tra queste due distribuzioni risiede nel tipo di incertezza che catturano. La distribuzione a posteriori dei parametri riflette solo l’incertezza epistemica riguardo ai valori latenti del modello. Al contrario, la distribuzione predittiva a posteriori combina questa incertezza epistemica con quella intrinseca al processo di campionamento, fornendo così una visione più completa e realistica di ciò che possiamo effettivamente osservare in contesti applicativi.
In questo approfondimento, esploreremo le procedure per costruire la distribuzione predittiva a posteriori, le strategie per interpretarla e le metodologie per impiegarla nella validazione empirica dei modelli psicologici.
Panoramica del capitolo
- Previsione bayesiana: incorporare incertezza parametrica e variabilità intrinseca.
- Verifica di coerenza: valutare l’adeguatezza del modello ai dati osservati.
- Caso beta-binomiale: applicazione pratica del framework predittivo.
6.1 La distribuzione predittiva a posteriori
6.1.1 Dall’aggiornamento bayesiano alle previsioni
Dopo aver osservato i dati \(y\) e aggiornato le nostre credenze sui parametri \(\theta\) tramite il teorema di Bayes, otteniamo la distribuzione a posteriori \(p(\theta \mid y)\). Ma spesso il nostro obiettivo non è solo stimare i parametri: vogliamo fare previsioni su nuove osservazioni future.
Date le nostre conoscenze aggiornate sui parametri, cosa possiamo dire su dati futuri \(\tilde{y}\) non ancora osservati?
6.1.2 Definizione e significato
La distribuzione predittiva a posteriori risponde precisamente a questa domanda. Rappresenta la distribuzione probabilistica di una nuova osservazione \(\tilde{y}\), condizionata ai dati già osservati \(y\).
Definizione formale:
\[ p(\tilde{y} \mid y) = \int p(\tilde{y} \mid \theta)\, p(\theta \mid y)\, d\theta. \tag{6.1}\] dove:
- \(\tilde{y}\): osservazione futura che vogliamo prevedere;
- \(p(\tilde{y} \mid \theta)\): modello di verosimiglianza (come i dati dipendono dai parametri);
- \(p(\theta \mid y)\): distribuzione a posteriori (credenze aggiornate sui parametri).
L’Equazione 6.1 calcola una media ponderata: per ogni possibile valore di \(\theta\), genera una previsione per \(\tilde{y}\), poi combina tutte queste previsioni pesandole secondo quanto ciascun valore di \(\theta\) è plausibile dopo aver osservato i dati.
6.1.3 Perché è importante
La distribuzione predittiva a posteriori riveste un’importanza cruciale nell’analisi bayesiana per molteplici ragioni. In primo luogo, essa incorpora sistematicamente l’incertezza parametrica, considerando non un singolo valore stimato di \(\theta\), ma l’intero spettro dei valori plausibili alla luce dei dati osservati. In secondo luogo, essa quantifica l’incertezza predittiva, fornendo non una semplice stima puntuale, ma la distribuzione di probabilità completa per i possibili esiti futuri.
Inoltre, la distribuzione predittiva a posteriori consente le verifiche predittive (posterior predictive checks), ovvero il confronto tra le previsioni del modello e i dati effettivamente osservati, al fine di valutare l’adeguatezza del modello stesso. Infine, dal punto di vista decisionale, la distribuzione predittiva a posteriori costituisce la base per scelte informate, offrendo probabilità complete e calibrate per diversi scenari futuri, aspetto essenziale in contesti applicativi in cui è necessario quantificare non solo gli esiti attesi, ma anche i rischi associati.
Scenario: abbiamo somministrato un test a 100 studenti e vogliamo prevedere il risultato di un nuovo studente.
- Se ignoriamo l’incertezza su \(\theta\) e utilizziamo solo la stima puntuale \(\hat{\theta}\), finiamo per sottostimare l’incertezza reale: trattiamo \(\hat{\theta}\) come se fosse nota con certezza.
- La distribuzione predittiva a posteriori, invece, tiene conto del fatto che il vero valore di \(\theta\) potrebbe trovarsi, ad esempio, tra 0.65 e 0.75. Di conseguenza, le previsioni per il nuovo studente riflettono questa incertezza, producendo un intervallo di risultati plausibili più ampio e realistico.
6.1.4 Intuizione: la distribuzione predittiva come media ponderata di previsioni
Il modo più efficace per comprendere l’Equazione 6.1 è considerarla come un processo in tre fasi, che possiamo illustrare attraverso un esperimento mentale nel contesto del modello beta-binomiale.
Contesto applicativo Supponiamo di voler prevedere il numero di risposte corrette che uno studente fornirà in un test futuro, dopo aver analizzato le prestazioni di un gruppo di studenti precedenti.
Fase 1: esplorazione dello spazio dei parametri. Definiamo una griglia di valori plausibili per \(\theta\): \[ \theta = 0, 0.01, 0.02, \ldots, 0.99, 1 \] in modo da coprire l’intero spettro delle possibili abilità.
Fase 2: generazione delle previsioni condizionate. Per ciascun valore di \(\theta'\) della griglia, calcoliamo la distribuzione binomiale condizionata su \(\theta'\). Essa rappresenta ciò che prevedremmo se fossimo certi che l’abilità dello studente fosse esattamente \(\theta'\):
\[ p(\tilde y \mid \theta') = \binom{n_{\text{new}}}{\tilde y} (\theta')^{\tilde y} (1-\theta')^{n_{\text{new}}-\tilde y}, \]
- con \(\theta' = 0.7\): la previsione si concentra prevalentemente su 6–8 successi;
- con \(\theta' = 0.3\): la previsione si focalizza principalmente su 2–4 successi.
Fase 3: combinazione delle previsioni attraverso i pesi bayesiani. Le diverse previsioni vengono poi pesate in base alla loro plausibilità a posteriori \(p(\theta' \mid y)\):
- se \(p(\theta' = 0.7 \mid y)\) è elevata, la previsione corrispondente riceve un peso sostanziale;
- se \(p(\theta' = 0.2 \mid y)\) è trascurabile, la previsione associata contribuisce solo marginalmente.
Sintesi del processo. La probabilità finale di osservare \(\tilde{y} = k\) successi è una media ponderata di tutte le probabilità condizionate \(p(\tilde y = k \mid \theta')\), dove i pesi sono determinati dalla distribuzione a posteriori \(p(\theta' \mid y)\). Il risultato è la distribuzione predittiva a posteriori, che incorpora contemporaneamente:
- la variabilità dei dati (descritta dal modello binomiale);
- e l’incertezza sui parametri (descritta dalla distribuzione a posteriori di \(\theta\)).
Ciascun valore di \(\theta\) genera una specifica previsione per \(\tilde{y}\); il compito della distribuzione a posteriori è determinare quanto contributo attribuire a ciascuna di queste previsioni alternative.
6.1.5 Confronto: distribuzioni a posteriori concentrate vs. distribuzioni a posteriori disperse
L’incertezza parametrica esercita un’influenza determinante sulla forma della distribuzione predittiva, come mostrato nei due scenari seguenti.
Scenario 1: distribuzione a posteriori concentrata (ad esempio, \(\theta \approx 0.70 \pm 0.03\)).
In questa situazione, tutti i valori plausibili del parametro \(\theta\) si collocano in un intervallo ristretto. Di conseguenza, le previsioni condizionate generate dai diversi valori di \(\theta\) sono sostanzialmente simili tra loro. Il risultato è una distribuzione predittiva concentrata e di forma regolare, che nel caso di \(n_{\text{new}} = 10\) domande assegna la maggior parte della massa probabilistica ai valori compresi tra 6 e 8 successi.
Scenario 2: distribuzione a posteriori dispersa (ad esempio, \(\theta\) plausibilmente compreso tra 0.4 e 0.8).
Quando l’incertezza parametrica è elevata, i valori plausibili di \(\theta\) coprono un’ampia gamma di possibilità. Il processo di media ponderata combina quindi previsioni molto eterogenee: alcuni valori di \(\theta\) (intorno a 0.4) predicono approssimativamente 4 successi, mentre altri (intorno a 0.8) predicono circa 8 successi. Il risultato è una distribuzione predittiva più dispersa e con code più pesanti, la quale riflette adeguatamente la maggiore incertezza sul parametro latente.
Caso con distribuzione a posteriori concentrata: \(\theta \sim \text{Beta}(70, 30)\) dopo 70 successi osservati su 100 prove - Parametri della distribuzione a posteriori: \(\mathbb{E}[\theta] \approx 0.70\), \(\text{SD}[\theta] \approx 0.045\). - Distribuzione della distribuzione predittiva: massa probabilistica concentrata su 6-8 successi. - \(\text{P}(0 \text{ successi}) \approx 0.0001\%\) (evento estremamente improbabile). - \(\text{P}(10 \text{ successi}) \approx 0.03\%\) (evento molto raro).
Caso con distribuzione a posteriori dispersa: \(\theta \sim \text{Beta}(7, 7)\) dopo 7 successi osservati su 14 prove. - Parametri della distribuzione a posteriori: \(\mathbb{E}[\theta] = 0.50\), \(\text{SD}[\theta] \approx 0.13\) (elevata incertezza). - Distribuzione predittiva: massa probabilistica distribuita su 3-7 successi. - \(\text{P}(0 \text{ successi}) \approx 0.1\%\) (raro ma non trascurabile). - \(\text{P}(10 \text{ successi}) \approx 0.1\%\) (analogamente raro). - code della distribuzione marcatamente più pesanti rispetto al caso concentrato.
Questo confronto mostra come l’incertezza sui parametri si propaghi in modo sistematico all’incertezza predittiva, con implicazioni fondamentali per l’interpretazione dei risultati e la pianificazione di studi futuri.
6.1.6 Le due fonti di incertezza predittiva
La maggiore dispersione osservabile nella distribuzione predittiva quando la posterior è ampia deriva dalla combinazione sistematica di due distinte fonti di incertezza:
-
Variabilità intrinseca (aleatory uncertainty):
- Rappresenta la variabilità naturale del processo generativo dei dati
- Anche conoscendo con esattezza il parametro \(\theta\), l’esito \(\tilde{y}\) mantiene una componente stocastica inevitabile
- Esempio: anche supponendo di conoscere con precisione il valore di \(\theta = 0.7\), uno studente potrebbe ottenere 6, 7 o 8 risposte corrette su 10 a causa della variabilità campionaria intrinseca.
-
Incertezza epistemica (epistemic uncertainty):
- Deriva dalla nostra conoscenza imperfetta del parametro latente \(\theta\).
- Rappresenta l’incertezza sulla stima del parametro stesso, che potrebbe assumere valori come 0.65, 0.70, 0.75…
- Questa incertezza parametrica si propaga direttamente alle previsioni attraverso il processo di integrazione bayesiana che considera tutti i valori plausibili di \(\theta\).
La distribuzione predittiva a posteriori NON è la distribuzione di \(\tilde{y}\) per un singolo valore di \(\theta\) (quello più probabile, per esempio). È la media ponderata di tutte le possibili distribuzioni condizionate, dove i pesi riflettono la plausibilità a posteriori di ciascun parametro.
6.1.7 Implicazioni pratiche
La relazione tra l’incertezza parametrica e la dispersione predittiva ha importanti conseguenze operative. Quando le informazioni a disposizione sono limitate, una distribuzione a posteriori ampia genera necessariamente previsioni conservative e poco precise. Questa situazione riflette un’onesta ammissione epistemica: “Non disponiamo di conoscenze sufficienti sul parametro \(\theta\), quindi le nostre previsioni devono rimanere caute”. In questo contesto, le code della distribuzione predittiva risultano più pesanti, assegnando probabilità rilevanti anche agli eventi apparentemente estremi.
Al contrario, quando le informazioni sono abbondanti, una distribuzione a posteriori concentrata produce previsioni più focalizzate e precise. Questo scenario corrisponde all’affermazione: “La nostra conoscenza di \(\theta\) è sufficientemente solida da permetterci di fare previsioni affidabili”. In queste condizioni, gli eventi estremi diventano statisticamente molto improbabili, il che riflette una maggiore certezza sui meccanismi alla base del fenomeno studiato.
Previsioni del tempo a confronto.
Scenario informativo limitato: con un solo giorno di osservazioni storiche (distribuzione a posteriori dispersa), la previsione è cauta: “La temperatura oscillerà probabilmente tra i 10° e i 30° domani”. La distribuzione predittiva è ampia a causa dell’elevata incertezza epistemica.
Scenario informativo ricco: con trent’anni di dati climatici per lo stesso periodo (distribuzione a posteriori concentrata), la previsione diventa più precisa: “La temperatura di domani si attesterà probabilmente tra i 18° e i 22°”. La distribuzione predittiva è più focalizzata grazie alla minore incertezza parametrica.
In entrambi i casi, la variabilità intrinseca del sistema meteorologico rimane invariata, ma nel secondo scenario, la minore incertezza epistemica consente previsioni notevolmente più accurate.
6.1.8 Confronto tra distribuzioni predittive a priori e a posteriori
Per comprendere appieno il valore della distribuzione predittiva a posteriori, è utile metterla a confronto con la sua controparte a priori.
| Caratteristica | Predittiva a priori | Predittiva a posteriori |
|---|---|---|
| Formula | \(p(\tilde{y}) = \int p(\tilde{y} \mid \theta) p(\theta) d\theta\) | \(p(\tilde{y} \mid y) = \int p(\tilde{y} \mid \theta) p(\theta \mid y) d\theta\) |
| Pesi | \(p(\theta)\) (credenze iniziali) | \(p(\theta \mid y)\) (credenze aggiornate) |
| Contesto | Prima di osservare i dati | Dopo aver osservato i dati |
| Finalità | Verificare la coerenza delle assunzioni iniziali | Effettuare previsioni informate dall’evidenza empirica |
| Incertezza | Tipicamente elevata (scarsa informazione) | Ridotta grazie all’apporto dei dati |
Evoluzione dall’a priori all’a posteriori:
Prior vago → Predittiva a priori dispersa
↓ [acquisizione dati osservati]
Posteriori concentrata → Predittiva a posteriori focalizzata- Verifica predittiva a priori: “Le mie assunzioni iniziali generano dati empiricamente plausibili?”
- Verifica predittiva a posteriori: “Il modello aggiornato riproduce adeguatamente i dati osservati e formula previsioni ragionevoli per nuove osservazioni?”
Se combinate, queste due procedure forniscono un framework integrato per la validazione metodologica del modello, coprendo l’intero processo inferenziale bayesiano.
6.1.9 Messaggio conclusivo
La distribuzione predittiva a posteriori rappresenta lo strumento bayesiano per eccellenza per la previsione. A differenza degli approcci che si basano esclusivamente su stime puntuali di \(\theta\), questa distribuzione:
- integra sistematicamente l’intera gamma di incertezza parametrica;
- quantifica in modo esaustivo l’incertezza predittiva attraverso distribuzioni complete;
- riflette fedelmente l’apprendimento ottenuto dai dati osservati;
- guadagna progressivamente in precisione con l’aumentare delle informazioni disponibili.
Possiamo immaginare la distribuzione predittiva a posteriori come un processo di deliberazione collettiva:
- ogni membro della comunità scientifica (valore specifico di \(\theta\)) avanza una previsione;
- i ricercatori più credibili (elevata densità a posteriori) esercitano una maggiore influenza;
- la previsione finale emerge come sintesi ponderata di tutte le prospettive;
- quando il consenso è ampio (posteriori concentrata), le previsioni risultano nette e definite;
- in presenza di opinioni divergenti (posteriori dispersa), le previsioni mantengono un appropriato grado di cautela.
Questa caratteristica di sintesi dell’incertezza rende la distribuzione predittiva a posteriori particolarmente preziosa per la ricerca psicologica, dove la complessità dei fenomeni studiati richiede strumenti in grado di rappresentare adeguatamente i margini di incertezza insiti nei processi inferenziali.
6.2 Il modello Beta-Binomiale
Poniamoci ora l’obiettivo di costruire in pratica la distribuzione predittiva a posteriori nel caso del modello beta-binomiale, il quale ci consente di illustrare il meccanismo quantitativo di questo processo in una situazione particolarmente semplice. Consideriamo un esperimento binomiale consistente in \(n\) prove indipendenti, dove osserviamo il numero di successi \(y\) (ad esempio, il numero di teste nel lancio di una moneta). Per costruire la distribuzione predittiva a posteriori seguiamo un percorso costituito da tre fasi.
-
Specificazione della distribuzione a priori La conoscenza iniziale riguardante la probabilità di successo \(p\) viene formalizzata attraverso una distribuzione Beta(\(\alpha, \beta\)), laddove:
- il parametro \(\alpha\) rappresenta un numero pseudo-osservato di successi;
- il parametro \(\beta\) rappresenta un numero pseudo-osservato di insuccessi.
Questa parametrizzazione consente di incorporare conoscenze pregresse nella forma di un’“evidenza virtuale”.
-
Aggiornamento bayesiano alla distribuzione a posteriori Dopo l’osservazione di \(y\) successi in \(n\) prove, la distribuzione a posteriori si ottiene mediante aggiornamento coniugato:
\[ p \mid y \sim \text{Beta}(\alpha + y, \beta + n - y). \]
La distribuzione a posteriori caratterizza completamente l’incertezza residua sul parametro \(p\) condizionatamente ai dati osservati.
3. Costruzione della distribuzione predittiva a posteriori
Per prevedere il numero di successi \(y_{\text{new}}\) in \(n_{\text{new}}\) prove future, è necessario integrare l’incertezza sul parametro \(p\) - rappresentata dalla distribuzione a posteriori - con la variabilità intrinseca del processo di campionamento, formalizzata dalla distribuzione binomiale. Questo obiettivo si ottiene mediante un procedimento di simulazione iterativa.
Si estrae casualmente un valore del parametro \(p\) dalla distribuzione a posteriori, ottenendo \(p^{(s)} \sim \text{Beta}(\alpha + y, \beta + n - y)\). Utilizzando questo valore campionato, si genera una realizzazione \(y_{\text{new}}^{(s)}\) dalla corrispondente distribuzione binomiale condizionata, secondo \(y_{\text{new}}^{(s)} \sim \text{Binomial}(n_{\text{new}}, p^{(s)})\). Ripetendo questo processo per un numero elevato di iterazioni, si ottiene una sequenza di valori predetti.
La distribuzione empirica dei valori \(y_{\text{new}}^{(s)}\) così generati approssima la distribuzione predittiva a posteriori teorica, sintetizzando in modo completo sia l’incertezza epistemica sul parametro \(p\) sia la variabilità aleatoria del processo binomiale sottostante.
6.2.1 Un esempio numerico
6.2.1.1 I dati e le nostre conoscenze iniziali
- Dati osservati: supponiamo di avere osservato 70 successi su 100 prove (ad esempio, 70 teste su 100 lanci di moneta).
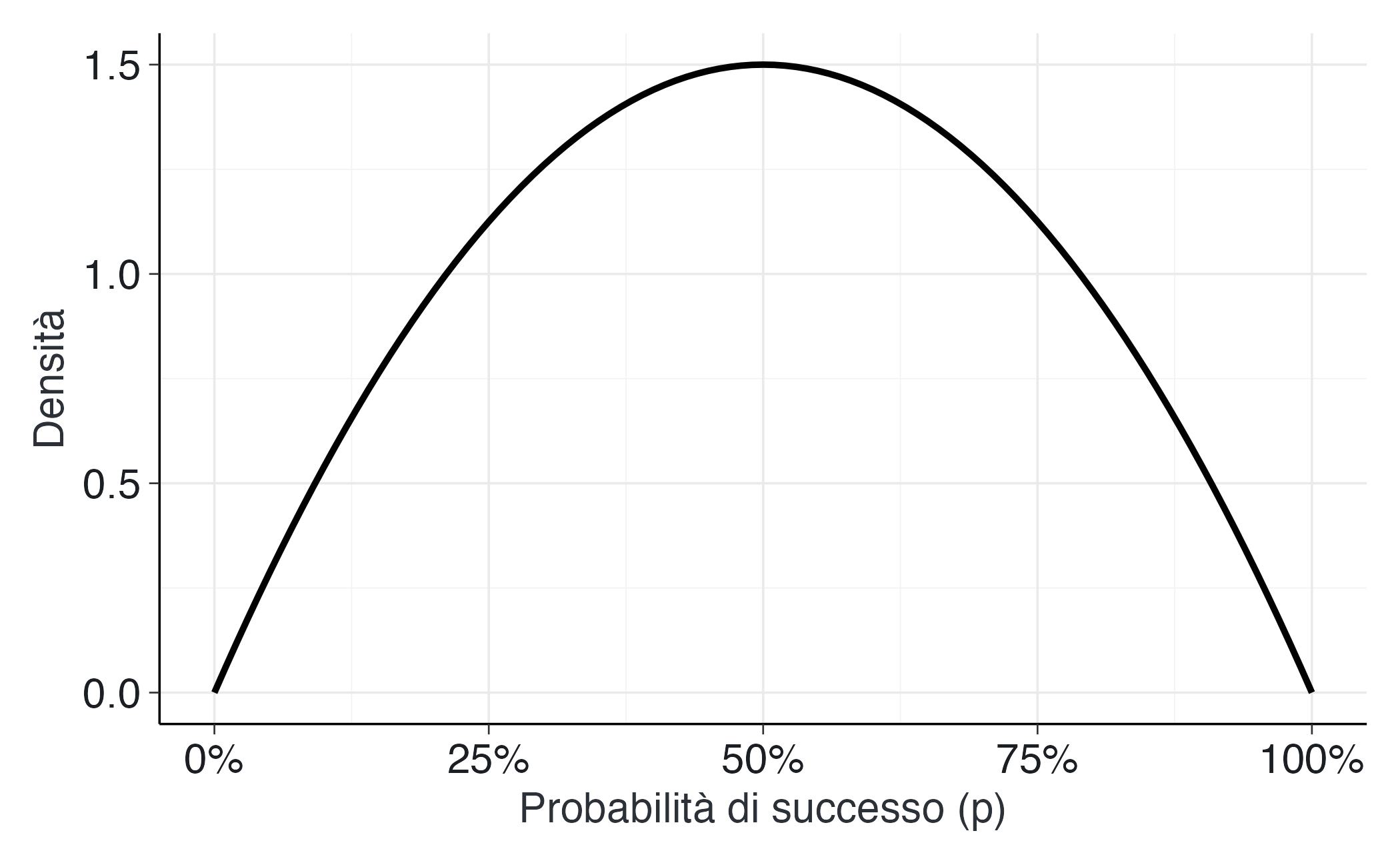
- Conoscenza iniziale (prior): usiamo una distribuzione \(Beta(2, 2)\). Questa prior è “debolmente informativa”, ovvero suggerisce che pensiamo che la moneta sia probabilmente equilibrata (p ≈ 0.5), ma siamo aperti ad altre possibilità.
6.2.1.2 Aggiornamento delle nostre conoscenze
Dopo aver visto i dati, aggiorniamo le nostre convinzioni sulla probabilità di successo \(p\):
alpha_posterior = 2 + 70 = 72
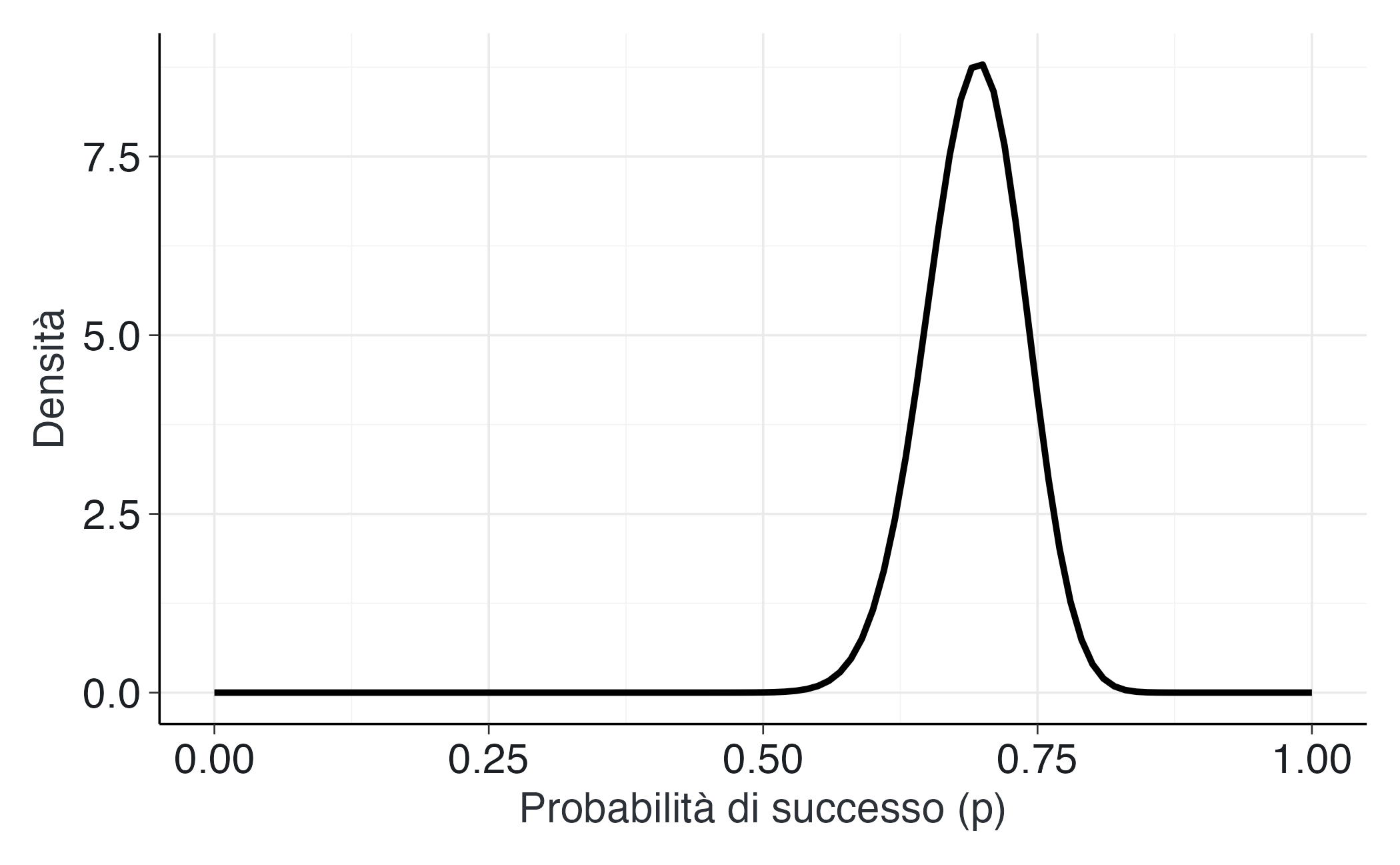
beta_posterior = 2 + (100 - 70) = 32Ora crediamo che \(p\) segua una distribuzione \(Beta(72, 32)\), che è centrata attorno a 0.7.
6.2.1.3 Simulazione delle previsioni
Vogliamo prevedere cosa succederà in 10 lanci futuri.
# Dati osservati
successi_osservati <- 70
lanci_totali <- 100
# Prior (conoscenza iniziale)
alpha_prior <- 2
beta_prior <- 2
# Posterior (conoscenza aggiornata)
alpha_post <- alpha_prior + successi_osservati
beta_post <- beta_prior + (lanci_totali - successi_osservati)
# Simuliamo 1000 valori plausibili per p
valori_p <- rbeta(1000, alpha_post, beta_post)
# Per ogni valore di p, simuliamo 10 lanci futuri
successi_futuri <- rbinom(1000, size = 10, prob = valori_p)
# Calcoliamo le proporzioni di successo
proporzioni_future <- successi_futuri / 106.2.1.4 Spiegazione passo per passo
Abbiamo osservato 70 successi su 100 prove. Con un prior \(Beta(2,2)\), la distribuzione a posteriori risulta una \(Beta(72,32)\). Questo significa che, sebbene non possiamo determinare il valore esatto della probabilità di successo \(p\), possiamo quantificarne l’incertezza in modo probabilistico: è molto plausibile che \(p\) si collochi attorno a 0.7, con una dispersione attorno a questo valore centrale definita dalla distribuzione \(Beta(72,32)\).
Per rappresentare questa incertezza, estraiamo 1000 valori da una distribuzione \(Beta(72,32)\): valori_p <- rbeta(1000, 72, 32). Ciascun valore estratto è un candidato possibile per \(p\), compatibile con i dati osservati e con la nostra conoscenza iniziale. Si noti che i valori estratti nell’intervallo [0, 1] non hanno tutti la stessa probabilità di essere campionati; la probabilità di essere campionati dipende dalla densità \(Beta(72,32)\).
A questo punto, ci chiediamo: quali risultati potremmo realisticamente aspettarci in una sequenza futura di 10 lanci? Per rispondere, procediamo nel modo seguente: per ciascuno dei valori di \(p\) campionati in precedenza, generiamo una distribuzione binomiale con parametro \(n = 10\). Da ciascuna di queste distribuzioni campioniamo quindi un singolo valore \(y\), che rappresenta il numero di successi attesi in 10 prove future. È importante notare che i possibili valori \(y\) nell’intervallo \([0, 10]\) non sono tutti equiprobabili, ma ciascuno ha una probabilità di realizzazione determinata dalla specifica distribuzione binomiale condizionata al valore di \(p'\) preso in considerazione. Ripetendo questo processo 1000 volte con l’istruzione successi_futuri <- rbinom(1000, size = 10, prob = valori_p), otteniamo un campione rappresentativo della distribuzione predittiva a posteriori.
Infine, per ottenere risultati immediatamente interpretabili come probabilità di successo nei lanci futuri, trasformiamo il numero di successi in proporzioni dividendo per 10: proporzioni_future <- successi_futuri / 10. In altre parole, otteniamo un quadro di ciò che possiamo aspettarci, tenendo insieme due fonti di incertezza: da un lato non conosciamo il valore esatto di \(p\); dall’altro, anche conoscendo \(p\), i risultati dei lanci rimarrebbero comunque soggetti al caso.
Il vettore proporzioni_future riassume queste possibilità: non una singola previsione puntuale, ma un’intera distribuzione di esiti futuri, coerente con i dati raccolti e con il modello bayesiano adottato.
6.2.1.5 Visualizziamo i risultati
Distribuzione iniziale (prima di osservare i dati):
# Distribuzione iniziale (prima di osservare i dati) — PRIOR
ggplot(data.frame(x = c(0, 1)), aes(x = x)) +
stat_function(
fun = dbeta,
args = list(shape1 = alpha_prior, shape2 = beta_prior),
linewidth = 1.1,
) +
scale_x_continuous(labels = scales::label_percent(accuracy = 1)) +
labs(x = "Probabilità di successo (p)", y = "Densità") Conoscenza aggiornata (dopo aver osservato i dati):
# Conoscenza aggiornata (dopo aver osservato i dati) — POSTERIOR
ggplot(data.frame(x = c(0, 1)), aes(x = x)) +
stat_function(
fun = dbeta,
args = list(shape1 = alpha_post, shape2 = beta_post),
linewidth = 1.1
) +
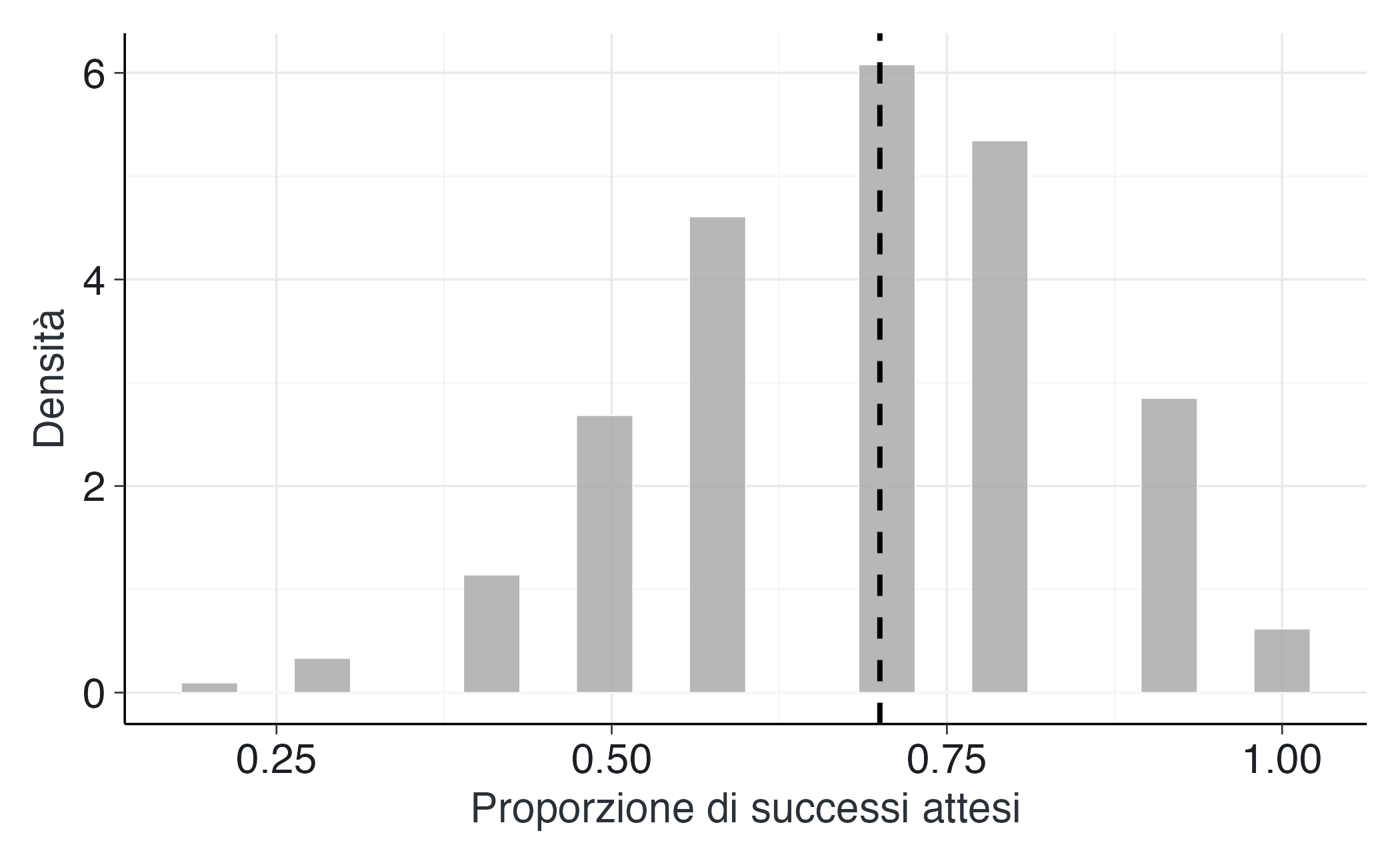
labs(x = "Probabilità di successo (p)", y = "Densità")Previsioni per i prossimi 10 lanci:
# Previsioni per i prossimi 10 lanci — Posterior predictive
ggplot(data.frame(proporzioni = proporzioni_future), aes(x = proporzioni)) +
geom_histogram(
aes(y = after_stat(density)),
bins = 20,
fill = modern_palette$grey5,
color = modern_palette$white,
alpha = 0.85,
linewidth = 0.2
) +
geom_vline(
aes(xintercept = successi_osservati / lanci_totali),
linewidth = 0.9,
linetype = "dashed"
) +
labs(x = "Proporzione di successi attesi", y = "Densità")6.2.1.6 Interpretazione dei risultati
La nostra conoscenza del parametro \(p\) risulta ora concentrata attorno al valore 0.7, come evidenziato dal grafico in rosso. Le previsioni per i prossimi 10 lanci mostrano una maggiore variabilità, dovuta alla combinazione di due fattori: persiste un certo grado di incertezza sul valore esatto di \(p\), e anche ammettendo di conoscerlo perfettamente, i risultati di 10 lanci presentano comunque una fluttuazione intrinseca. Il fatto che il risultato osservato del 70% di successi cada nella regione più probabile delle nostre previsioni indica che il modello adottato è ragionevole e può essere utilizzato per le previsioni future.
In termini pratici, se si dovesse formulare una previsione per i prossimi 10 lanci, l’intervallo più plausibile si collocherebbe tra 6 e 8 successi, anche se non si possono escludere esiti di 5 o 9 successi, a causa della variabilità casuale.
Potrebbe sembrare ovvio che la distribuzione predittiva a posteriori riproduca fedelmente i dati osservati nel nostro esempio. In realtà, questo risultato positivo non è affatto scontato ed è importante dal punto di vista metodologico: attesta la buona calibrazione del nostro modello.
Nel caso che abbiamo discusso, abbiamo scelto un modello binomiale con un prior Beta perché ci permette di illustrare chiaramente la logica alla base della distribuzione predittiva a posteriori in un caso particolarmente semplice. È tuttavia cruciale riconoscere che la ricerca psicologica opera tipicamente con modelli di complessità ben superiore. In questi contesti applicativi, la corrispondenza tra i dati osservati e quelli generati tramite la distribuzione predittiva non può mai essere data per scontata, ma deve sempre essere oggetto di verifica empirica.
Riflessioni conclusive
Le distribuzioni predittive a posteriori rappresentano il naturale completamento del percorso iniziato con i prior. Se i prior predictive checks ci consentono di controllare la plausibilità delle nostre assunzioni iniziali, i posterior predictive checks ci permettono di verificare la plausibilità del modello alla luce dei dati.
Dal punto di vista applicativo, questo approccio rafforza la trasparenza e la robustezza delle nostre inferenze. Non ci limitiamo a riportare valori puntuali o intervalli di credibilità per i parametri, ma mostriamo esplicitamente quali dati il nostro modello ritiene plausibili e li confrontiamo con i dati effettivamente raccolti. Questo rende la comunicazione dei risultati più chiara e intuitiva, anche per chi non ha familiarità con la statistica bayesiana.
In sintesi, le distribuzioni predittive a posteriori ci ricordano che la forza dell’approccio bayesiano non risiede soltanto nella stima dei parametri, ma soprattutto nella capacità di prevedere e spiegare i fenomeni. Nei capitoli successivi, vedremo come questa logica si estenda anche al confronto sistematico tra modelli, aprendo la strada a un approccio più rigoroso e cumulativo alla psicologia.
Consideriamo i dati della SWLS somministrata a un campione di studenti, ottenendo per ciascuno uno score complessivo. Per semplicità, vogliamo “dichiarare positivo” lo studente se il punteggio SWLS supera una determinata soglia (ad esempio, 20 su 35). In questo modo otteniamo una variabile dicotomica (0/1), che useremo come “successo” in un modello binomiale.
-
Dati e conteggio dei successi
- Carica il dataset con le risposte SWLS.
- Costruisci la variabile binaria (ad esempio
SWLS_dich) che vale 1 se lo score ≥ 20, e 0 altrimenti.
- Calcola il numero di successi (numero di persone che superano la soglia) e il numero totale di osservazioni (N).
- Carica il dataset con le risposte SWLS.
-
Modello beta-binomiale (approccio manuale via simulazione)
-
Specifica una distribuzione Beta(a, b) come prior per la probabilità di successo \(p\). Scegli una coppia \((a, b)\) relativamente poco informativa, ad esempio (2,2) o (1,1).
- Osservando \(y\) successi su \(n\) soggetti, aggiorna i parametri a posteriori: \[
a_{\text{post}} = a + y,
\quad
b_{\text{post}} = b + (n - y).
\]
- Simula un gran numero di campioni di \(p\) dalla distribuzione Beta\(\bigl(a_{\text{post}},\, b_{\text{post}}\bigr)\).
- Per ciascun campione di \(p\), genera un valore \(\tilde{y}\) da una Binomiale\(\bigl(n_{\text{new}}, p\bigr)\), dove \(n_{\text{new}}\) è la dimensione di un ipotetico nuovo campione (che puoi scegliere, ad esempio, uguale a \(n\) oppure un valore diverso). Otterrai così una posterior predictive distribution per \(\tilde{y}\).
- Infine, calcola statistiche descrittive (media, varianza, intervalli) e/o disegna un istogramma di \(\tilde{y}\) o della proporzione \(\tilde{y}/n_{\text{new}}\).
-
Specifica una distribuzione Beta(a, b) come prior per la probabilità di successo \(p\). Scegli una coppia \((a, b)\) relativamente poco informativa, ad esempio (2,2) o (1,1).
-
Replicare con brms
-
Usa il pacchetto brms per costruire un modello binomiale. Per esempio:
library(brms) # Crea un data frame con la variabile dicotomica df_binom <- data.frame( successes = y, # conteggio dei successi failures = n - y ) # Modello binomiale con prior Beta(a,b) approssimato tramite logit fit_brms <- brm( bf(successes | trials(n) ~ 1), data = df_binom, family = binomial(link = "logit"), prior = c( prior(beta(2, 2), class = "Intercept", dpar = "mu") # NOTA: la specifica di una "beta(2,2)" diretta sull'intercetta # è un'approssimazione, tipicamente serve passare a una scala logit. # In brms, di solito si usa prior su scale normali dell'intercetta. ), seed = 123 )(Le specifiche del
priorpotrebbero richiedere una formulazione differente se vuoi rispettare esattamente la corrispondenza con Beta(a,b). In ogni caso, l’idea è mostrare come definire un prior e costruire un modello binomiale conbrms.) -
Verifica la convergenza e poi estrai la posterior predictive distribution con le funzioni di brms:
pp_check(fit_brms, nsamples = 100)Questo ti mostrerà come i dati predetti dal modello (in termini di binomiale) si confrontano con i dati osservati.
-
-
Confronto e interpretazione
- Metti a confronto i risultati della simulazione “manuale” (Beta-Binomial) e quelli ottenuti con brms. Noterai che le distribuzioni predittive dovrebbero essere coerenti, se hai impostato un prior per brms simile a quello del modello Beta-Binomiale.
- Discuti brevemente se la distribuzione predittiva a posteriori acquisita è plausibile rispetto ai dati osservati. Ad esempio, la probabilità di osservare \(\tilde{y}\) simile a \(y\) dovrebbe essere relativamente alta se il modello è appropriato.
- Se vuoi, puoi cambiare \(n_{\text{new}}\) (es. previsione su 200 soggetti futuri) per vedere come la variabilità della previsione si “ridimensiona” o cresce a seconda della taglia del campione.
- Metti a confronto i risultati della simulazione “manuale” (Beta-Binomial) e quelli ottenuti con brms. Noterai che le distribuzioni predittive dovrebbero essere coerenti, se hai impostato un prior per brms simile a quello del modello Beta-Binomiale.
-
Costruzione del dataset
-
Se la SWLS varia tra 5 e 35, e la soglia è 20, puoi fare:
-
-
Approccio Beta-Binomial manuale
Prior: \((a, b) = (2, 2)\)
Posterior: \((a_{\text{post}}, b_{\text{post}}) = (2 + y,\, 2 + n - y)\).
-
Generazione dei campioni:
-
Statistiche:
-
Grafici (istogramma e densità):
hist(prop_pred, freq=FALSE, col='lightblue', main='Posterior Predictive Distribution: prop. di successi')
-
Modello con brms
Usa la sintassi di una binomiale con offset o con
trials(n).-
Specifica un prior che approssimi Beta(2,2) sullo scale logit, ad esempio:
# Beta(2,2) ha media ~ 0.5, varianza relativamente ampia. # Approssimandola su scala logit ~ normal(0, 2.2) # (valore indicativo: la normal(0, 2) su logit copre un intervallo ampio). prior_approx <- prior(normal(0, 2), class = "Intercept") Esegui
pp_check(fit_brms)e interpreta.
-
Interpretazione
- Se la soglia scelta per la SWLS cattura un “buon livello di soddisfazione”, potresti aspettarti una certa % di successi.
- Se i dati futuri simulati sono coerenti con i dati reali — ad esempio, la media di \(\tilde{y}\) è vicina a \(y\) — allora il modello sembra descrivere bene la realtà. Altrimenti, potresti rivedere la soglia o la specifica del prior.
- Se la soglia scelta per la SWLS cattura un “buon livello di soddisfazione”, potresti aspettarti una certa % di successi.
L’elemento chiave è che la distribuzione predittiva a posteriori (posterior predictive distribution) non si limita a considerare un solo valore di \(p\), bensì campiona molteplici valori plausibili (dalla posterior), e per ciascuno simula un potenziale outcome. Così facendo, si riflette pienamente l’incertezza residua sul parametro e l’aleatorietà del processo binomiale.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] ragg_1.5.0 tinytable_0.13.0 withr_3.0.2
#> [4] systemfonts_1.3.1 patchwork_1.3.2 ggdist_3.3.3
#> [7] tidybayes_3.0.7 bayesplot_1.14.0 ggplot2_4.0.0
#> [10] reliabilitydiag_0.2.1 priorsense_1.1.1 posterior_1.6.1
#> [13] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [16] brms_2.23.0 Rcpp_1.1.0 sessioninfo_1.2.3
#> [19] conflicted_1.2.0 janitor_2.2.1 matrixStats_1.5.0
#> [22] modelr_0.1.11 tibble_3.3.0 dplyr_1.1.4
#> [25] tidyr_1.3.1 rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] svUnit_1.0.8 tidyselect_1.2.1 farver_2.1.2
#> [4] S7_0.2.0 fastmap_1.2.0 TH.data_1.1-4
#> [7] tensorA_0.36.2.1 digest_0.6.37 timechange_0.3.0
#> [10] estimability_1.5.1 lifecycle_1.0.4 survival_3.8-3
#> [13] magrittr_2.0.4 compiler_4.5.1 rlang_1.1.6
#> [16] tools_4.5.1 knitr_1.50 labeling_0.4.3
#> [19] bridgesampling_1.1-2 htmlwidgets_1.6.4 curl_7.0.0
#> [22] pkgbuild_1.4.8 RColorBrewer_1.1-3 abind_1.4-8
#> [25] multcomp_1.4-28 purrr_1.1.0 grid_4.5.1
#> [28] stats4_4.5.1 colorspace_2.1-2 xtable_1.8-4
#> [31] inline_0.3.21 emmeans_1.11.2-8 scales_1.4.0
#> [34] MASS_7.3-65 cli_3.6.5 mvtnorm_1.3-3
#> [37] rmarkdown_2.30 generics_0.1.4 RcppParallel_5.1.11-1
#> [40] cachem_1.1.0 stringr_1.5.2 splines_4.5.1
#> [43] parallel_4.5.1 vctrs_0.6.5 V8_8.0.1
#> [46] Matrix_1.7-4 sandwich_3.1-1 jsonlite_2.0.0
#> [49] arrayhelpers_1.1-0 glue_1.8.0 codetools_0.2-20
#> [52] distributional_0.5.0 lubridate_1.9.4 stringi_1.8.7
#> [55] gtable_0.3.6 QuickJSR_1.8.1 pillar_1.11.1
#> [58] htmltools_0.5.8.1 Brobdingnag_1.2-9 R6_2.6.1
#> [61] textshaping_1.0.4 rprojroot_2.1.1 evaluate_1.0.5
#> [64] lattice_0.22-7 backports_1.5.0 memoise_2.0.1
#> [67] broom_1.0.10 snakecase_0.11.1 rstantools_2.5.0
#> [70] gridExtra_2.3 coda_0.19-4.1 nlme_3.1-168
#> [73] checkmate_2.3.3 xfun_0.53 zoo_1.8-14
#> [76] pkgconfig_2.0.3