30  Errore di specificazione e bias da variabile omessa

Finora abbiamo presentato la regressione lineare come uno strumento per descrivere le relazioni tra le variabili. Abbiamo visto come stimare i suoi parametri, come interpretarli e come implementarli sia in R che in Stan. In tutte queste applicazioni, però, abbiamo dato per scontato un punto cruciale: che il modello fosse specificato correttamente.

Nella pratica, però, questa condizione è raramente soddisfatta. Può accadere che una variabile rilevante non sia stata inclusa nel modello o che la forma funzionale ipotizzata non descriva adeguatamente la relazione reale. In questi casi parliamo di errore di specificazione del modello.

Una delle conseguenze più importanti è il cosiddetto bias da variabile omessa: quando si omette un predittore correlato sia con la variabile dipendente sia con altri predittori inclusi nel modello, le stime dei coefficienti risultano distorte. Questo non è un semplice problema tecnico, ma una questione sostanziale: in tali condizioni, infatti, si finisce per attribuire a un predittore un effetto che in realtà appartiene a un altro, producendo un’interpretazione errata dei meccanismi che hanno generato i dati.

In questo capitolo analizzeremo il significato dell’errore di specificazione, mostreremo matematicamente come nasce il bias da variabile omessa e discuteremo le sue implicazioni nella ricerca psicologica. Comprendere questi limiti è fondamentale non solo per interpretare correttamente i risultati della regressione, ma anche per formulare modelli più adeguati e consapevoli.

Panoramica del capitolo

  • Bias da variabile omessa: escludere una variabile rilevante altera sistematicamente i coefficienti.
  • Condizioni del bias.
  • Implicazioni: i coefficienti OLS non sono interpretabili in chiave causale; la regressione è fenomenologica.
  • Prospettiva: privilegiare modelli meccanicistici (es., Rescorla–Wagner, DDM, dinamici EMA).

Per seguire al meglio questo capitolo è utile avere:

  • una conoscenza di base della regressione lineare semplice e del concetto di coefficiente di regressione.
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, cmdstanr, tidybayes, loo, patchwork)

30.1 Errore di specificazione e bias da variabile omessa

Esaminiamo nel dettaglio quali sono le condizioni per l’errore di specificazione e quali sono le conseguenze del bias da variabile omessa.

30.1.1 Idea chiave

Se il vero modello è

\[ Y=\beta_0+\beta_1X_1+\beta_2X_2+\varepsilon,\qquad \mathbb{E}[\varepsilon\mid X_1,X_2]=0, \] ma stimiamo erroneamente il modello che omette \(X_2\),

\[ Y=\alpha_0+\alpha_1X_1+u, \] allora il coefficiente su \(X_1\) risulta distorto quando:

  1. \(X_2\) ha effetto diretto su \(Y\) (\(\beta_2\neq 0\));
  2. \(X_2\) è correlata con \(X_1\) (\(\mathrm{Corr}(X_1,X_2)\neq 0\)).

L’errore di specificazione emerge, in altre parole, solo quando si verificano congiuntamente due condizioni: deve essere omessa dal modello una variabile che influenza direttamente la variabile dipendente e questa stessa variabile deve essere correlata con almeno uno dei predittori inclusi. Ne consegue che non si commette tale errore né quando si omette una variabile irrilevante per \(Y\), né quando si omette una variabile che, pur influenzando \(Y\), risulta incorrelata con tutti i predittori presenti nel modello.

30.1.2 Dimostrazione

Per semplificare la trattazione, senza perdere in generalità, lavoriamo con variabili standardizzate.

30.1.2.1 Passo 1 — Standardizzazione delle variabili

Siano \(\mu_1,\mu_2,\mu_Y\) le medie e \(\sigma_1,\sigma_2,\sigma_Y\) le deviazioni standard delle variabili originali. Definiamo le variabili standardizzate:

\[ Z_1=\frac{X_1-\mu_1}{\sigma_1},\qquad Z_2=\frac{X_2-\mu_2}{\sigma_2},\qquad Z_Y=\frac{Y-\mu_Y}{\sigma_Y}. \]

Per costruzione, si ha:

  • \(\mathrm{Var}(Z_1)=\mathrm{Var}(Z_2)=1\),
  • \(\mathrm{Cov}(Z_1,Z_2)=\rho_{12}=\mathrm{Corr}(X_1,X_2)\).

Il modello vero standardizzato è

\[ Z_Y=\gamma_1 Z_1+\gamma_2 Z_2+\varepsilon_z,\qquad \mathbb{E}[\varepsilon_z\mid Z_1,Z_2]=0, \] dove i coefficienti standardizzati sono:

\[ \gamma_1=\beta_1\,\frac{\sigma_1}{\sigma_Y},\qquad \gamma_2=\beta_2\,\frac{\sigma_2}{\sigma_Y}. \]

30.1.2.2 Passo 2 — Stima con variabile omessa

Stimiamo ora la regressione erronea che omette \(Z_2\):

\[ Z_Y=\delta_1 Z_1 + \text{errore}. \] dove \(u\) è il termine d’errore del modello incompleto. Lo stimatore OLS di \(\delta_1\) è:

\[ \hat\delta_1=\frac{\mathrm{Cov}(Z_1,Z_Y)}{\mathrm{Var}(Z_1)}=\mathrm{Cov}(Z_1,Z_Y), \] poiché \(\mathrm{Var}(Z_1)=1\).

Sostituiamo \(Z_Y\) con l’espressione del modello vero:

\[ \begin{align} \mathrm{Cov}(Z_1,Z_Y) &=\mathrm{Cov}\big(Z_1,\gamma_1Z_1+\gamma_2Z_2+\varepsilon_z\big)\notag\\ &=\gamma_1\underbrace{\mathrm{Var}(Z_1)}_{=1} +\gamma_2\,\mathrm{Cov}(Z_1,Z_2) +\underbrace{\mathrm{Cov}(Z_1,\varepsilon_z)}_{=0}. \end{align} \]

Dunque:

\[ \boxed{\;\hat\delta_1=\gamma_1+\gamma_2\,\rho_{12}\;}. \]

Interpretazione: lo stimatore univariato \(\hat\delta_1\) non cattura solo l’effetto diretto standardizzato di \(Z_1\) (\(\gamma_1\)), ma somma ad esso un termine spurio \(\gamma_2\rho_{12}\), che riflette l’influenza della variabile omessa \(Z_2\) attraverso la sua correlazione con \(Z_1\).

30.1.3 Passo 3 — Ritorno ai coefficienti originali

Per collegare il risultato ai coefficienti non standardizzati, ricordiamo le relazioni:

\[ \hat\delta_1=\frac{\sigma_1}{\sigma_Y}\,\hat\alpha_1,\qquad \gamma_1=\beta_1\,\frac{\sigma_1}{\sigma_Y},\qquad \gamma_2=\beta_2\,\frac{\sigma_2}{\sigma_Y}. \]

Sostituendo nella formula standardizzata \(\hat\delta_1=\gamma_1+\gamma_2\rho_{12}\) otteniamo:

\[ \frac{\sigma_1}{\sigma_Y}\,\hat\alpha_1 =\beta_1\frac{\sigma_1}{\sigma_Y} +\beta_2\frac{\sigma_2}{\sigma_Y}\rho_{12}. \] Moltiplicando entrambi i membri per \(\sigma_Y/\sigma_1\) e ricordando che \(\rho_{12}= \mathrm{Cov}(X_1,X_2)/(\sigma_1\sigma_2)\), si arriva alla forma non standardizzata:

\[ \boxed{\;\hat\alpha_1=\beta_1+\beta_2\,\frac{\mathrm{Cov}(X_1,X_2)}{\mathrm{Var}(X_1)}\;}. \]

Espressione del bias: in media, lo stimatore \(\hat\alpha_1\) differisce dal parametro vero \(\beta_1\) per una quantità pari a:

\[ \boxed{\;\mathbb{E}[\hat\alpha_1]-\beta_1 =\beta_2\,\frac{\mathrm{Cov}(X_1,X_2)}{\mathrm{Var}(X_1)}\;} \]

equivalente, nella versione standardizzata, a:

\[ \boxed{\;\mathbb{E}[\hat\delta_1]-\gamma_1=\gamma_2\rho_{12}\;}. \]

Questa è l’espressione analitica del bias da variabile omessa.

30.1.4 Interpretazione didattica

Il bias da variabile omessa si verifica solo quando sono presenti entrambe le seguenti condizioni:

  1. \(\beta_2 \neq 0\) – la variabile omessa \(X_2\) influisce realmente su \(Y\),
  2. \(\rho_{12} \neq 0\) – la variabile omessa \(X_2\) è correlata con \(X_1\).

Se una delle due condizioni non sussiste, il bias si annulla.

Direzione del bias (scala standardizzata): Poiché \(\mathrm{Bias}(\hat\delta_1)=\gamma_2\rho_{12}\), la distorsione può essere positiva o negativa:

  • \(\gamma_2>0\) e \(\rho_{12}>0\) ⇒ sovrastima dell’effetto di \(X_1\);
  • \(\gamma_2>0\) e \(\rho_{12}<0\) ⇒ sottostima dell’effetto di \(X_1\).

30.1.5 La rilevanza per la psicologia

La regressione multipla è un modello essenzialmente descrittivo o fenomenologico: fotografa le associazioni tra le variabili senza necessariamente catturare i meccanismi causali che le producono. Nella ricerca psicologica, l’omissione di variabili rilevanti è spesso inevitabile, dato che è impossibile conoscere o misurare tutti i fattori che determinano il comportamento. Di conseguenza, i coefficienti stimati possono risultare sistematicamente distorti, offrendo un’interpretazione fuorviante delle relazioni sottostanti (Wilms et al., 2021).

Come evidenziato da Wilms et al. (2021), il bias da variabile omessa non è un semplice dettaglio tecnico, ma una minaccia sostanziale alla validità della ricerca. Le simulazioni presentate nell’articolo, coerentemente con quelle discusse in precedenza, mostrano chiaramente che, quando omettiamo una variabile che influenza sia il predittore che l’esito, le nostre stime possono sovrastimare l’effetto reale (falsi positivi), sottostimare l’effetto reale (falsi negativi) o addirittura invertirne il segno, suggerendo un effetto positivo dove è negativo, o viceversa.

In altre parole, i risultati di una regressione su dati osservazionali possono catturare associazioni spurie anziché effetti genuini. Questa difficoltà è particolarmente rilevante in psicologia, in quanto, nella pratica, non abbiamo mai accesso al “modello vero”, ovvero alla reale struttura causale che genera i dati, e non possiamo quindi escludere con certezza che le nostre stime non siano distorte da variabili omesse.

La lezione fondamentale è chiara: la regressione standard non è adatta per trarre inferenze causali a partire da dati osservazionali. Affermare che “\(X\) causa \(Y\)” sulla base di un coefficiente di regressione è metodologicamente insostenibile se non possiamo escludere l’esistenza di una terza variabile, non misurata, che influenzi sia \(X\) che \(Y\).

30.1.6 Oltre i modelli associativi: strategie per l’inferenza causale

L’articolo di Wilms et al. (2021) non si limita a illustrare il problema, ma esplora anche strategie metodologiche per affrontare la sfida dell’inferenza causale. Tali approcci rappresentano un vero e proprio cambio di paradigma rispetto all’uso ingenuo della regressione descrittiva.

1. Disegni sperimentali e quasi-sperimentali. Il modo più diretto per garantire l’esogeneità di un predittore è la randomizzazione sperimentale. Tuttavia, quando gli esperimenti non sono praticabili, è possibile ricorrere a disegni quasi-sperimentali. Wilms et al. (2021) citano in particolare:

  • variabili strumentali (IV): un approccio che sfrutta una variabile esogena (lo strumento) che influenza l’esito esclusivamente attraverso il predittore di interesse, consentendo di isolare la componente di variazione esogena del predittore stesso;
  • regressione della discontinuità (RDD): un disegno che sfrutta soglie amministrative o criteri di assegnazione arbitrari per allocare i partecipanti a condizioni differenti, trattando gli individui prossimi alla soglia come se fossero assegnati in modo casuale.

Questi metodi mirano esplicitamente a risolvere il problema dell’endogeneità, ossia la correlazione tra i predittori e il termine d’errore del modello, da cui deriva il bias da variabile omessa.

2. Modelli formali dei processi psicologici. Un approccio complementare e, per molti versi, più ambizioso, consiste nell’abbandonare i modelli puramente associativi a favore di modelli formali. Questi modelli non si limitano a descrivere le correlazioni tra le variabili osservate, ma cercano di specificare in modo esplicito i meccanismi causali ipotizzati che generano i dati.

Alcuni esempi discussi in questo manuale includono:

  • il modello di apprendimento di Rescorla–Wagner, che formalizza l’aggiornamento delle aspettative in funzione della discrepanza tra esiti attesi ed esiti osservati;
  • il Drift Diffusion Model (DDM), che rappresenta il processo decisionale come un accumulo sequenziale di evidenza fino al raggiungimento di una soglia di risposta;
  • i modelli dinamici per dati EMA (Ecological Momentary Assessment), progettati per catturare l’evoluzione temporale degli stati psicologici (ad esempio l’umore) e le loro interdipendenze nel tempo.

A differenza di una regressione che cerca semplicemente di “predire” \(Y\) da \(X\), questi modelli forniscono una rappresentazione esplicita del processo generativo sottostante. Il loro obiettivo non è solo la descrizione statistica, ma anche la comprensione meccanicistica: il modello produce delle previsioni su come i dati dovrebbero apparire se il meccanismo ipotizzato fosse vero. La valutazione del modello consiste quindi nel verificare quanto tali previsioni siano coerenti con i dati osservati.

In conclusione, la consapevolezza dei limiti della regressione multipla non costituisce un vicolo cieco, ma bensì un punto di partenza. Essa stimola l’adozione di una metodologia più rigorosa e articolata, che integri strategie di disegno robuste per l’inferenza causale con lo sviluppo di teorie formalizzate dei processi psicologici. È proprio questa combinazione che può favorire una scienza psicologica più cumulativa, esplicativa e teoricamente solida.

Esaminiamo come segno e magnitudo del bias cambino al variare della correlazione tra regressori (\(\rho_{12}\)) e dell’effetto dell’omessa (\(\beta_2\)). La heatmap visualizza \(\hat\alpha_1-\beta_1\).

set.seed(1)
n <- 3000; beta1 <- 1; sig <- 1
rho_seq <- seq(-.9,.9,length=19); b2_seq <- seq(-1.5,1.5,length=19)

grid <- expand.grid(rho=rho_seq, b2=b2_seq)

sim_once <- function(rho, beta2){
  X1 <- rnorm(n)
  X2 <- rho*X1 + sqrt(1-rho^2)*rnorm(n)   # Corr(X1,X2)=rho
  Y  <- beta1*X1 + beta2*X2 + rnorm(n,0,sig)
  coef(lm(Y ~ X1))[2] - beta1             # ritorna uno scalare, senza nome
}

grid$bias <- mapply(sim_once, grid$rho, grid$b2)  # <-- niente t(), niente [, "bias"]

ggplot(grid, aes(x=rho, y=b2, fill=bias)) +
  geom_tile() + scale_fill_gradient2() +
  labs(x=expression(rho[12]), y=expression(beta[2]), fill="Bias",
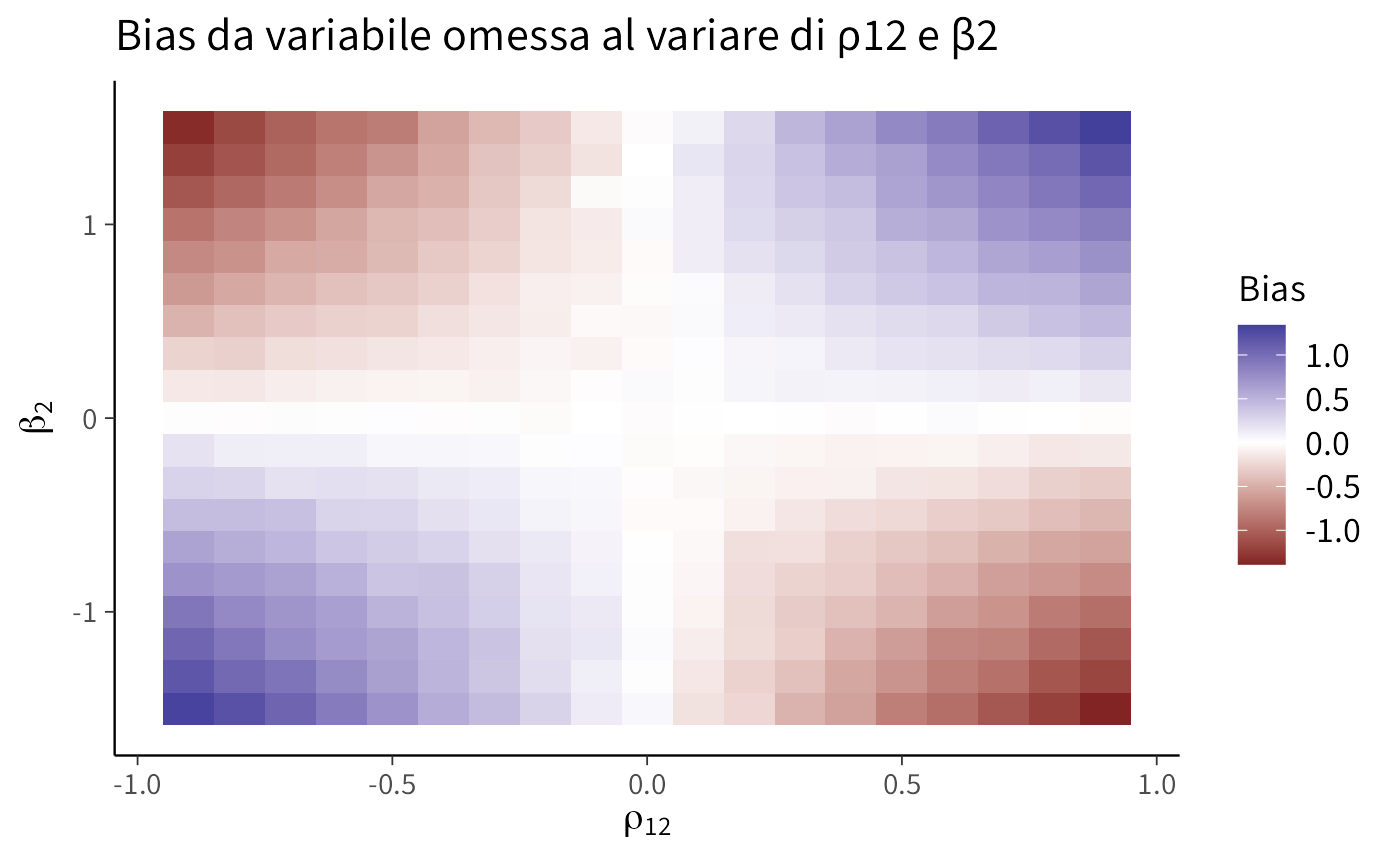
       title="Bias da variabile omessa al variare di ρ12 e β2")

Commento e interpretazione. L’asse orizzontale riporta la correlazione tra i regressori \(\rho_{12}=\mathrm{Corr}(X_1,X_2)\); l’asse verticale l’effetto dell’omessa \(X_2\) su \(Y\) (\(\beta_2\)). Il riempimento (“Bias”) è \(\hat\alpha_1-\beta_1\), cioè di quanto il coefficiente sul regressore incluso \(X_1\) sovrastima (valori > 0) o sottostima (valori < 0) il suo valore vero.

  • Segno del bias. Il bias è (in media) \(\beta_2\,\rho_{12}\). Quadranti:

    • \(\beta_2>0,\ \rho_{12}>0\) → positivo (sovrastima);
    • \(\beta_2>0,\ \rho_{12}<0\) → negativo (sottostima);
    • \(\beta_2<0,\ \rho_{12}>0\) → negativo;
    • \(\beta_2<0,\ \rho_{12}<0\) → positivo.

    Le bande di colore cambiano segno attraversando le linee \(\rho_{12}=0\) o \(\beta_2=0\), dove il bias si annulla (zona chiara).

  • Magnitudo. Aumenta con \(|\beta_2|\) e \(|\rho_{12}|\): gli angoli (|ρ|≈0.9, |β₂|≈1.5) mostrano i bias maggiori. La diagonale basso-sinistra → alto-destra evidenzia bias positivo; l’altra diagonale bias negativo.

  • Simmetria e teoria. La mappa è sostanzialmente simmetrica perché il bias teorico è \(\beta_2\rho_{12}\). Le piccole irregolarità dipendono dal rumore Monte Carlo della simulazione (con \(n\) finito).

  • Lettura pratica. Se anche solo una tra correlazione tra regressori (\(\rho_{12}\)) o effetto dell’omessa (\(\beta_2\)) è prossima a zero, il bias è trascurabile (aree chiare lungo gli assi). Quando entrambi sono lontani da zero, l’OLS nel modello omesso è fuorviante.

Riflessioni conclusive

In questo capitolo abbiamo visto che la validità delle stime di regressione dipende in modo cruciale dalla corretta specificazione del modello. In particolare, abbiamo discusso il bias da variabile omessa, mostrando come l’esclusione di un predittore rilevante possa alterare i coefficienti stimati per le altre variabili, portando a interpretazioni potenzialmente fuorvianti.

Il problema non è affatto marginale. Nella ricerca psicologica, infatti, i costrutti di interesse sono spesso complessi e difficili da misurare, e non è possibile includere tutti i fattori rilevanti. In queste condizioni, le stime di regressione rischiano di catturare associazioni spurie anziché effetti genuini. Essere consapevoli di questi limiti è quindi essenziale per interpretare i risultati con la dovuta cautela.

La lezione fondamentale è che la regressione, in quanto modello essenzialmente descrittivo, non deve essere confusa con una spiegazione causale. La regressione fornisce un metodo per sintetizzare le associazioni osservate nei dati, ma può indurre in errore se non è accompagnata da una riflessione critica sulle variabili omesse e sulla struttura del fenomeno in esame.

Nei prossimi due capitoli affronteremo direttamente il problema dell’inferenza causale: se il bias da variabile omessa è un rischio onnipresente nelle analisi osservative, dato che non è possibile conoscere tutte le variabili che influenzano un fenomeno psicologico, come è possibile ottenere conclusioni causali affidabili? Vedremo che esistono strategie per affrontare questa sfida, ma che esse richiedono un cambiamento di prospettiva rispetto all’approccio puramente descrittivo della regressione tradizionale.

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.2
#> 
#> Matrix products: default
#> BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] cmdstanr_0.8.0        ragg_1.5.0            tinytable_0.15.1     
#>  [4] withr_3.0.2           systemfonts_1.3.1     patchwork_1.3.2      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#> [10] ggplot2_4.0.1         reliabilitydiag_0.2.1 priorsense_1.2.0     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.4            
#> [28] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-29      
#>  [7] snakecase_0.11.1      compiler_4.5.2        vctrs_0.6.5          
#> [10] stringr_1.6.0         pkgconfig_2.0.3       arrayhelpers_1.1-0   
#> [13] fastmap_1.2.0         backports_1.5.0       labeling_0.4.3       
#> [16] rmarkdown_2.30        ps_1.9.1              purrr_1.2.0          
#> [19] xfun_0.54             cachem_1.1.0          jsonlite_2.0.0       
#> [22] broom_1.0.11          parallel_4.5.2        R6_2.6.1             
#> [25] stringi_1.8.7         RColorBrewer_1.1-3    lubridate_1.9.4      
#> [28] estimability_1.5.1    knitr_1.50            zoo_1.8-14           
#> [31] pacman_0.5.1          Matrix_1.7-4          splines_4.5.2        
#> [34] timechange_0.3.0      tidyselect_1.2.1      abind_1.4-8          
#> [37] yaml_2.3.12           codetools_0.2-20      processx_3.8.6       
#> [40] curl_7.0.0            pkgbuild_1.4.8        lattice_0.22-7       
#> [43] bridgesampling_1.2-1  S7_0.2.1              coda_0.19-4.1        
#> [46] evaluate_1.0.5        survival_3.8-3        RcppParallel_5.1.11-1
#> [49] pillar_1.11.1         tensorA_0.36.2.1      checkmate_2.3.3      
#> [52] stats4_4.5.2          distributional_0.5.0  generics_0.1.4       
#> [55] rprojroot_2.1.1       rstantools_2.5.0      scales_1.4.0         
#> [58] xtable_1.8-4          glue_1.8.0            emmeans_2.0.0        
#> [61] tools_4.5.2           mvtnorm_1.3-3         grid_4.5.2           
#> [64] QuickJSR_1.8.1        colorspace_2.1-2      nlme_3.1-168         
#> [67] cli_3.6.5             textshaping_1.0.4     svUnit_1.0.8         
#> [70] Brobdingnag_1.2-9     V8_8.0.1              gtable_0.3.6         
#> [73] digest_0.6.39         TH.data_1.1-5         htmlwidgets_1.6.4    
#> [76] farver_2.1.2          memoise_2.0.1         htmltools_0.5.9      
#> [79] lifecycle_1.0.4       MASS_7.3-65

Bibliografia

Wilms, R., Mäthner, E., Winnen, L., & Lanwehr, R. (2021). Omitted variable bias: A threat to estimating causal relationships. Methods in Psychology, 5, 100075.