13  Costruzione di prior informativi da corpora di studi

Introduzione

Nel manuale didattico, le distribuzioni a priori sono state presentate come componente fondamentale del processo di aggiornamento bayesiano della conoscenza. È stata evidenziata la distinzione tra prior debolmente informative, che hanno una funzione prevalentemente regolarizzante, e prior informative, che incorporano invece conoscenze sostanziali sul fenomeno in esame, basate sulla letteratura scientifica disponibile.

Questo capitolo introduce una metodologia avanzata, ma concettualmente accessibile, per la costruzione sistematica di distribuzioni a priori informative. L’approccio si basa sull’utilizzo strutturato delle evidenze accumulate nella letteratura scientifica, seguendo la proposta metodologica di Zwet & Gelman (2022) per derivare prior empiricamente fondati.

Per illustrare concretamente questa procedura, applicheremo il metodo ai dati della meta-analisi di Van Agteren et al. (2021), che ha sintetizzato l’efficacia degli interventi psicologici sul benessere mentale. Questa applicazione pratica consentirà di comprendere non solo i fondamenti teorici del metodo, ma anche le sue implicazioni operative per la ricerca psicologica, mostrando come tradurre risultati di studi precedenti in distribuzioni a priori formalmente giustificate.

AttenzionePreparazione del Notebook

# Carichiamo le funzioni comuni necessarie per il notebook
here::here("code", "_common.R") |> source()

# Installiamo e carichiamo i pacchetti necessari per le analisi
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(
  cmdstanr,      # Interfaccia R per Stan (modelli bayesiani)
  posterior,     # Gestione e analisi di distribuzioni a posteriori
  insight,       # Estrazione di informazioni dai modelli
  bayesplot,     # Visualizzazione di analisi bayesiane
  ggdist         # Visualizzazione di distribuzioni
)

13.1 La distorsione delle stime e l’errore di tipo M

13.1.1 Comprendere la differenza tra direzione e grandezza dell’effetto

Prima di addentrarci negli aspetti tecnici, è fondamentale chiarire una distinzione concettuale che spesso viene trascurata nella ricerca empirica: la differenza tra stimare se un effetto esiste (la sua direzione) e stimare quanto è grande questo effetto (la sua magnitudine). Questa distinzione ha conseguenze profonde per l’interpretazione dei risultati della ricerca.

Consideriamo uno stimatore statistico \(b\) che utilizziamo per stimare un parametro vero della popolazione \(\beta\). Supponiamo, ad esempio, che \(\beta\) rappresenti la differenza media nel benessere psicologico tra un gruppo che ha ricevuto un intervento di mindfulness e un gruppo di controllo. Lo stimatore \(b\) è costruito in modo tale che, se potessimo replicare il nostro studio infinite volte con campioni sempre diversi, la media di tutte queste stime \(b\) coinciderebbe esattamente con il valore vero \(\beta\). In termini tecnici, diciamo che \(b\) è uno stimatore non distorto (unbiased) di \(\beta\).

Tuttavia, questa proprietà apparentemente rassicurante non si estende automaticamente al valore assoluto dell’effetto. Quando consideriamo \(|b|\) come stima di \(|\beta|\) (cioè la grandezza dell’effetto indipendentemente dalla sua direzione), emerge un fenomeno sistematico di sovrastima. Questo significa che, anche quando la direzione dell’effetto è correttamente identificata, la sua entità tende a essere esagerata nelle nostre stime campionarie.

13.1.2 Il fenomeno del “winner’s curse”

Questo pattern di sovrastima sistematica è noto nella letteratura metodologica come “winner’s curse” o errore di tipo M (dove “M” sta per Magnitude, grandezza). Il termine “winner’s curse” deriva dall’economia comportamentale e si riferisce alla tendenza per cui chi “vince” (cioè ottiene un risultato statisticamente significativo) tende sistematicamente a sovrastimare il valore del premio (l’effect size).

Come illustrato da Gelman & Carlin (2014), questo fenomeno è particolarmente accentuato in contesti caratterizzati da bassa potenza statistica o elevato rumore di misurazione. In tali situazioni, le stime che emergono come “statisticamente significative” – quelle che superano la soglia convenzionale di \(p < 0.05\) e vengono quindi pubblicate – sono spesso le più estreme non perché riflettano accuratamente la realtà, ma semplicemente a causa della variabilità campionaria casuale.

13.1.3 Il ruolo del rapporto segnale-rumore

Per comprendere più profondamente questo meccanismo, introduciamo il concetto di rapporto segnale-rumore (Signal-to-Noise Ratio, SNR), definito come:

\[ \text{SNR} = \frac{|\beta|}{s}, \] dove \(|\beta|\) rappresenta la grandezza del vero effetto e \(s\) è l’errore standard della stima. Questo rapporto quantifica essenzialmente quanto il “segnale” (l’effetto reale che vogliamo rilevare) emerge chiaramente rispetto al “rumore” (la variabilità casuale intrinseca nei nostri dati).

Quando il rapporto segnale-rumore è basso – situazione tipica degli studi con campioni piccoli o con misure imprecise – la variabilità casuale diventa predominante. In queste condizioni, solo le stime che, per pura fluttuazione statistica, assumono un valore particolarmente elevato riescono a superare la soglia di significatività statistica e vengono quindi selezionate per la pubblicazione.

Il risultato di questo processo di selezione è una distorsione sistematica verso l’alto degli effect size riportati nella letteratura scientifica. La soglia di significatività statistica agisce, in pratica, come un filtro che lascia passare preferenzialmente i risultati più estremi, creando l’illusione di effetti più forti di quanto non siano in realtà. Questo meccanismo è alla base del cosiddetto decline effect, ovvero il fenomeno per cui gli effect size tendono a ridursi nelle repliche successive di uno studio inizialmente promettente.

13.1.4 Implicazioni per la ricerca cumulativa

Le conseguenze di questa dinamica sulla costruzione della conoscenza scientifica cumulativa sono profonde. Quando la letteratura pubblicata è costituita principalmente da studi che hanno superato la soglia di significatività statistica, le stime aggregate degli effect size ottenute tramite revisioni sistematiche o meta-analisi possono risultare notevolmente sovrastimate. Ciò porta a:

1. aspettative irrealistiche circa l’efficacia di interventi o la forza di relazioni teoriche;
2. difficoltà di replicazione, derivanti dall’utilizzo di stime della grandezza dell’effetto sovrastimate;
3. spreco di risorse, quando le decisioni pratiche (per esempio, l’implementazione di interventi clinici) si basano su evidenze distorte.

È in questo contesto problematico che l’approccio bayesiano, con prior informativi derivati da corpora di studi, può offrire una soluzione metodologica robusta.

13.1.5 L’approccio basato sui corpora di studi

La proposta di Zwet & Gelman (2022) offre una strategia elegante per affrontare il problema del winner’s curse attraverso l’inferenza bayesiana. L’idea di base è semplice: invece di considerare ogni studio come un’entità a sé stante, è possibile estrarre informazioni sistematiche dalla distribuzione dei rapporti segnale-rumore osservati in un ampio corpus di studi simili.

Questo corpus funge da “memoria collettiva” di un campo di ricerca, catturando non solo i singoli risultati, ma anche i pattern ricorrenti nell’entità degli effetti. Utilizzando questa informazione aggregata come distribuzione a priori, è possibile “correggere” le stime di nuovi studi, tenendo conto di ciò che è tipico in quel particolare ambito di ricerca.

Questo approccio si basa su un’assunzione ragionevole: sebbene ogni studio presenti specificità metodologiche e contestuali, esiste comunque un’informazione sistematica riguardante l’andamento tipico degli effetti in un determinato dominio che può guidare le nostre inferenze. Questa informazione risulta particolarmente preziosa quando il rischio di sovrastima è più elevato, come negli studi che presentano una piccola dimensione campionaria e un’ampia incertezza delle stime.

Nel prosieguo del capitolo, vedremo come questa idea teorica possa essere concretamente implementata utilizzando strumenti statistici bayesiani e applicandola al contesto specifico degli interventi di mindfulness per il benessere psicologico.

13.2 Il contesto empirico: una meta-analisi sugli interventi di mindfulness

13.2.1 Il dataset di riferimento

Per illustrare concretamente l’applicazione del metodo proposto, utilizzeremo i dati della meta-analisi sistematica condotta da Van Agteren et al. (2021). Questo studio ha esaminato l’efficacia degli interventi psicologici volti a migliorare il benessere mentale, con particolare attenzione agli interventi basati sulla mindfulness.

La mindfulness, intesa come pratica di consapevolezza non giudicante del momento presente, ha ricevuto crescente attenzione nella ricerca psicologica degli ultimi decenni. Comprendere l’effettiva magnitudine dei suoi effetti sul benessere è quindi di rilevante interesse sia teorico che applicativo.

13.2.2 Risultati aggregati

Dallo studio di Van Agteren et al. (2021), prendiamo in esame i risultati della Tabella 3 relativi agli interventi di mindfulness condotti sulla popolazione generale (non clinica). I dati aggregati mostrano i seguenti valori:

• Hedges’ \(g\): 0.420.
  Questo è l’effect size standardizzato medio, una misura che esprime la differenza tra gruppo sperimentale e controllo in unità di deviazione standard. Un valore di 0.42 è generalmente considerato un effetto “medio” secondo le convenzioni di Cohen.

• Intervallo di confidenza al 99%: [0.29; 0.55].
  Questo intervallo indica che, con il 99% di confidenza, il vero effect size nella popolazione si colloca tra 0.29 e 0.55. La larghezza dell’intervallo riflette l’incertezza della stima.

• Numero di studi (\(k\)): 56.
  La meta-analisi ha aggregato i risultati di 56 studi indipendenti, fornendo una base sostanziale per le inferenze.

• Campione totale (\(n\)): 5613.
  Complessivamente, 5613 partecipanti sono stati inclusi negli studi analizzati.

• Errore standard stimato: \((0.55 - 0.29) / (2 \times 2.576) \approx 0.050\).
  Questo valore quantifica la precisione della stima aggregata. L’errore standard è stato calcolato a partire dall’intervallo di confidenza al 99%, utilizzando il fatto che tale intervallo si estende per circa 2.576 errori standard in ciascuna direzione dalla stima centrale.

13.2.3 I dati dei singoli studi

Per costruire il nostro prior informativo, tuttavia, non possiamo limitarci ai soli dati aggregati. Abbiamo bisogno della distribuzione degli effect size nei singoli studi che compongono la meta-analisi. Questi dati sono stati estratti dalla Supplementary Table 3 dello studio originale, che riporta i risultati relativi agli outcome di benessere soggettivo.

Estraiamo e organizziamo un subset rappresentativo di questi studi:

# Creiamo un dataframe con i dati estratti dalla letteratura
# Ogni riga rappresenta uno studio indipendente
mindfulness_data <- tibble(
  # Nome dello studio (Autore Anno)
  study = c("Bhayee 2016", "Bower 2015", "Dvořáková 2017", "Galante 2018",
            "Gambrel 2015", "Glück 2011", "Howells 2016", "Johnson 2016",
            "Mongrain 2016", "Oken 2017", "Pinniger 2012", "Vieten 2008"),
  
  # Effect size Hedges' g per ciascuno studio
  # Hedges' g è una versione corretta del d di Cohen che tiene conto
  # delle dimensioni campionarie piccole
  hedges_g = c(0.35, 0.42, 0.38, 0.31, 0.45, 0.52, 0.44, 0.28,
               0.39, 0.33, 0.48, 0.41),
  
  # Errore standard di ciascuna stima
  # Riflette la precisione della misura: valori più bassi indicano
  # maggiore precisione (tipicamente studi con campioni più grandi)
  se = c(0.18, 0.15, 0.12, 0.08, 0.16, 0.21, 0.14, 0.09,
         0.13, 0.11, 0.19, 0.17),
  
  # Dimensione del campione nel gruppo di intervento
  n_intervention = c(13, 35, 52, 257, 32, 26, 57, 115,
                     97, 60, 16, 13),
  
  # Dimensione del campione nel gruppo di controllo
  n_control = c(13, 30, 53, 224, 34, 17, 64, 154,
                93, 68, 29, 18)
)

# Calcoliamo una statistica chiave: il z-value
# Il z-value è il rapporto tra l'effect size e il suo errore standard
# Rappresenta quanto l'effetto osservato è "forte" rispetto alla sua incertezza
# z-value elevati suggeriscono effetti più chiaramente distinguibili dal rumore
mindfulness_data <- mindfulness_data |>
  mutate(z_value = hedges_g / se)

# Visualizziamo i dati per una prima ispezione
print(mindfulness_data)
#> # A tibble: 12 × 6
#>    study          hedges_g    se n_intervention n_control z_value
#>    <chr>             <dbl> <dbl>          <dbl>     <dbl>   <dbl>
#>  1 Bhayee 2016        0.35  0.18             13        13    1.94
#>  2 Bower 2015         0.42  0.15             35        30    2.8 
#>  3 Dvořáková 2017     0.38  0.12             52        53    3.17
#>  4 Galante 2018       0.31  0.08            257       224    3.88
#>  5 Gambrel 2015       0.45  0.16             32        34    2.81
#>  6 Glück 2011         0.52  0.21             26        17    2.48
#>  7 Howells 2016       0.44  0.14             57        64    3.14
#>  8 Johnson 2016       0.28  0.09            115       154    3.11
#>  9 Mongrain 2016      0.39  0.13             97        93    3   
#> 10 Oken 2017          0.33  0.11             60        68    3   
#> 11 Pinniger 2012      0.48  0.19             16        29    2.53
#> 12 Vieten 2008        0.41  0.17             13        18    2.41

13.2.4 Caratteristiche del corpus

Osservando questi dati, emergono alcune caratteristiche importanti:

1. Variabilità degli effect size: gli Hedges’ \(g\) variano da 0.28 (Vieten 2008) a 0.52 (Glück 2011), indicando una certa eterogeneità negli effetti riportati.

2. Variabilità della precisione: gli errori standard oscillano da 0.08 (Galante 2018, lo studio più grande con 481 partecipanti totali) a 0.21 (Glück 2011, uno studio più piccolo con 43 partecipanti).

3. Variabilità dei \(z\)-value: i rapporti segnale-rumore variano considerevolmente, riflettendo sia le differenze negli effect size che nelle dimensioni campionarie.

Questa eterogeneità è esattamente ciò che rende utile l’approccio basato su corpus: possiamo modellare la distribuzione sottostante di questi parametri per ottenere un prior che catturi la reale variabilità degli effetti in questo dominio di ricerca.

13.3 Il modello: una mistura di normali per il SNR

13.3.1 Perché una mistura di distribuzioni?

Per modellare adeguatamente la distribuzione del rapporto segnale-rumore (SNR) osservata nel nostro corpus di studi, adottiamo un approccio flessibile basato su misture di distribuzioni normali (si veda il Capitolo 12). Prima di addentrarci negli aspetti tecnici, è importante comprendere l’intuizione che sta alla base di questa scelta metodologica.

Immaginiamo di voler descrivere la distribuzione delle altezze in una popolazione mista di adulti e adolescenti. Una singola distribuzione normale potrebbe non catturare adeguatamente questa realtà, poiché esistono due “sottogruppi” con caratteristiche distinte. Una mistura di due normali – una per gli adolescenti e una per gli adulti – descriverebbe la situazione in modo più accurato.

Analogamente, nel contesto degli studi sulla mindfulness, possiamo ipotizzare che esistano diverse “classi” di studi: alcuni possono misurare effetti più forti o con maggiore precisione, altri possono essere più soggetti a rumore o variabilità. Una mistura di normali ci permette di catturare questa eterogeneità senza fare assunzioni rigide sulla forma esatta della distribuzione.

13.3.2 Vantaggi del modello a mistura

La scelta di modellare il SNR attraverso una mistura di distribuzioni normali centrate sullo zero offre diversi vantaggi sostanziali:

1. Flessibilità rappresentazionale: anche utilizzando solamente due componenti, possiamo modellare distintamente la parte centrale della distribuzione (che potrebbe rappresentare la maggioranza degli studi “tipici”) e le code (che potrebbero catturare studi con caratteristiche più estreme). Questa flessibilità è cruciale per evitare di imporre vincoli troppo restrittivi alla forma della distribuzione empirica.

2. Trattabilità analitica: tutte le operazioni matematiche necessarie possono essere svolte in forma chiusa, senza dover ricorrere ad approssimazioni numeriche che potrebbero introdurre ulteriori imprecisioni o complessità computazionale.

3. Invarianza di scala: il modello mantiene le sue proprietà fondamentali quando i dati vengono trasformati linearmente, una caratteristica desiderabile che garantisce coerenza nell’applicazione a studi con diverse scale di misurazione.

13.3.3 Formulazione matematica del modello

Passiamo ora alla formalizzazione matematica del nostro modello. Per ogni studio \(j\) nel nostro corpus, osserviamo una statistica \(z_j\) che possiamo scomporre come:

\[ z_j = \frac{b_j}{s_j} = \text{SNR}_j + \epsilon_j. \]

Analizziamo i componenti di questa equazione:

• \(b_j\) è l’effect size osservato nello studio \(j\) (ad esempio, l’Hedges’ \(g\) misurato);
• \(s_j\) è l’errore standard associato a quella stima;
• \(z_j = b_j/s_j\) è quindi lo \(z\)-value, che standardizza l’effect size rispetto alla sua incertezza;
• \(\text{SNR}_j\) rappresenta il “vero” rapporto segnale-rumore sottostante per quello studio;
• \(\epsilon_j\) è il rumore campionario, che assumiamo distribuito normalmente con media zero e varianza unitaria: \(\epsilon_j \sim \mathcal{N}(0, 1)\).

Questa decomposizione riflette l’idea che ciò che osserviamo (\(z_j\)) è la combinazione del segnale vero più il rumore campionario inevitabile in qualsiasi stima finita.

13.3.4 La distribuzione del SNR come mistura

Il cuore del nostro modello sta nell’assunzione che il vero rapporto segnale-rumore segua una mistura di due distribuzioni normali, entrambe centrate sullo zero:

\[ \text{SNR}_j \sim p_1 \mathcal{N}(0, \tau_1^2) + (1-p_1) \mathcal{N}(0, \tau_2^2). \]

Questa notazione merita un’attenta spiegazione:

• \(p_1\) è la probabilità (o peso) della prima componente della mistura. Possiamo interpretarla come la proporzione di studi nel corpus che appartengono al primo “tipo”. Conseguentemente, \((1-p_1)\) è il peso della seconda componente.

• \(\tau_1^2\) e \(\tau_2^2\) sono le varianze delle due componenti. Tipicamente, ordiniamo queste varianze in modo che \(\tau_1^2 < \tau_2^2\), cosicché la prima componente rappresenti studi con SNR più concentrato attorno allo zero (effetti più piccoli o più precisi), mentre la seconda catturi studi con maggiore dispersione.

• Centratura sullo zero: entrambe le componenti sono centrate sullo zero. Questo può sembrare controintuitivo – perché centrare su zero se ci aspettiamo effetti positivi? La ragione è che vogliamo modellare la distribuzione simmetrica dei possibili SNR, permettendo al modello di apprendere la dispersione tipica indipendentemente dalla direzione dell’effetto.

13.3.5 La distribuzione degli \(z\)-value osservati

Un risultato matematico importante — che semplifica notevolmente il processo inferenziale — stabilisce che anche la distribuzione degli \(z\)-value osservati può essere rappresentata come una mistura di distribuzioni normali. Questa proprietà discende da un teorema fondamentale della statistica: la somma di due variabili casuali normali indipendenti è a sua volta una variabile normale.

Formalmente: se \(X \sim \mathcal{N}(\mu_X, \sigma_X^2)\) e \(Y \sim \mathcal{N}(\mu_Y, \sigma_Y^2)\) sono indipendenti, allora \(X + Y \sim \mathcal{N}(\mu_X + \mu_Y, \sigma_X^2 + \sigma_Y^2)\).

Nel nostro contesto, ciascun valore \(z_j\) osservato può essere scomposto nella somma di due componenti:

\[ z_j = \text{SNR}_j + \epsilon_j, \] dove:

• \(\text{SNR}_j\) rappresenta il vero rapporto segnale-rumore nello studio \(j\);
• \(\epsilon_j\) rappresenta l’errore campionario (la variabilità intrinseca dovuta alla dimensione finita del campione).

Poiché \(\text{SNR}_j\) segue a sua volta una mistura di due distribuzioni normali, applicando la proprietà precedente a ciascuna componente otteniamo che la distribuzione di \(z_j\) è essa stessa una mistura di distribuzioni normali:

\[ z_j \sim p_1\, \mathcal{N}(0, \tau_1^2 + 1) + (1 - p_1)\, \mathcal{N}(0, \tau_2^2 + 1). \] In questa formulazione:

• \(p_1\) rappresenta la proporzione attribuibile alla prima componente della mistura;
• \(\tau_1^2\) e \(\tau_2^2\) sono le varianze delle due popolazioni di SNR;
• il termine additivo “+1” nelle varianze cattura il contributo del rumore campionario \(\epsilon_j\).

In altri termini, rispetto alla distribuzione dei veri valori di SNR, le varianze osservate risultano incrementate di un’unità, riflettendo l’incertezza aggiuntiva introdotta dal processo di campionamento.

Dal punto di vista applicativo, questo risultato permette di stimare i parametri della mistura (\(p_1, \tau_1^2, \tau_2^2\)) direttamente dagli \(z\)-value osservati, senza necessità di conoscere i valori reali di SNR, che per definizione non sono osservabili.

Dal punto di vista concettuale, il modello interpreta la variabilità dei risultati empirici come derivante dalla coesistenza di due popolazioni di studi distinte: una con SNR tipicamente bassi (effetti piccoli o molto incerti) e una con SNR più elevati (effetti più robusti e replicabili), entrambe soggette al rumore di campionamento. Stimando la struttura di questa mistura sul corpus di studi disponibili, è possibile utilizzare i parametri ottenuti per costruire distribuzioni a priori informative da applicare a nuovi studi, incorporando in modo sistematico la conoscenza accumulata in letteratura.

13.4 Stima del prior dal corpus

13.4.1 Obiettivo della stima

Il primo passo operativo consiste nello stimare i parametri della mistura di distribuzioni normali che meglio approssima la distribuzione degli \(z\)-value osservati negli studi sulla mindfulness. L’obiettivo è determinare i valori di \(p_1\) (peso della prima componente), \(\tau_1\) e \(\tau_2\) (deviazioni standard delle due componenti dello SNR) che massimizzano la verosimiglianza dei dati osservati. A tale scopo implementiamo un modello di inferenza bayesiana in Stan, che garantisce una stima robusta e flessibile dei parametri del modello.

13.4.2 Passo 1: Specificazione del modello in Stan

Il modello matematico viene implementato in Stan attraverso il seguente codice, che ne definisce la struttura probabilistica completa.

# Definiamo il modello Stan per la mistura di normali
stan_code_mixture <- "
// SEZIONE DATA
// Qui specifichiamo i dati che passeremo a Stan dall'esterno
data {
  int<lower=0> N;              // Numero di studi nel corpus (intero positivo)
  vector[N] z;                 // Vettore degli z-values osservati
}

// SEZIONE PARAMETRI
// Questi sono i parametri che Stan stimerà (variabili sconosciute)
parameters {
  // Proporzione della prima componente (vincolata tra 0 e 1)
  real<lower=0, upper=1> theta;
  
  // Varianze delle due componenti per gli z-value osservati
  // Vincolo: devono essere >= 1 perché includono la varianza del rumore (che è 1)
  real<lower=1> sigma1_sq;     // Varianza prima componente (tau1^2 + 1)
  real<lower=1> sigma2_sq;     // Varianza seconda componente (tau2^2 + 1)
}

// SEZIONE MODEL
// Qui specifichiamo la struttura probabilistica completa
model {
  // --- PRIOR SUI PARAMETRI ---
  // Questi prior riflettono le nostre assunzioni iniziali moderate
  
  // Prior su theta: Beta(2,2) favorisce leggermente valori centrali
  // ma rimane abbastanza piatto (non troppo informativo)
  theta ~ beta(2, 2);
  
  // Prior sulle varianze: Gamma con parametri scelti per essere
  // debolmente informativi ma escludere valori implausibili
  sigma1_sq ~ gamma(2, 0.5);   // Tende a favorire valori moderati
  sigma2_sq ~ gamma(2, 0.1);   // Permette valori più grandi (code più pesanti)
  
  // --- LIKELIHOOD ---
  // Per ogni studio, calcoliamo la log-probabilità secondo la mistura
  for (n in 1:N) {
    // log_mix è una funzione Stan per misture:
    // combina le log-densità di due normali pesate da theta
    target += log_mix(
      theta,                                   // Peso prima componente
      normal_lpdf(z[n] | 0, sqrt(sigma1_sq)),  // Prima normale
      normal_lpdf(z[n] | 0, sqrt(sigma2_sq))   // Seconda normale
    );
  }
}

// SEZIONE GENERATED QUANTITIES
// Qui calcoliamo quantità derivate dai parametri per facilitare l'interpretazione
generated quantities {
  // Recuperiamo le varianze del SNR sottraendo la varianza del rumore
  real tau1_sq = sigma1_sq - 1;  // Varianza SNR prima componente
  real tau2_sq = sigma2_sq - 1;  // Varianza SNR seconda componente
  
  // Calcoliamo anche le deviazioni standard (spesso più interpretabili)
  real tau1 = sqrt(tau1_sq);
  real tau2 = sqrt(tau2_sq);
}
"

13.4.3 Passo 1: Specificazione del modello in Stan

Il modello matematico viene implementato in Stan attraverso il seguente codice, che ne definisce la struttura probabilistica completa.

# Definiamo il modello Stan per la mistura di normali
stan_code_mixture <- "
data {
  int<lower=0> N;              // Numero di studi
  vector[N] z;                 // z-values osservati
}

parameters {
  real<lower=0, upper=1> theta;      // Proporzione prima componente
  real<lower=1> sigma1_sq;           // Varianza prima componente (τ₁² + 1)
  real<lower=1> sigma2_sq;           // Varianza seconda componente (τ₂² + 1)
}

model {
  // Prior sui parametri
  theta ~ beta(2, 2);                // Leggermente concentrato attorno a 0.5
  sigma1_sq ~ gamma(2, 0.5);         // Favorisce valori moderati
  sigma2_sq ~ gamma(2, 0.1);         // Permette code più pesanti
  
  // Likelihood
  for (n in 1:N) {
    target += log_mix(
      theta,
      normal_lpdf(z[n] | 0, sqrt(sigma1_sq)),
      normal_lpdf(z[n] | 0, sqrt(sigma2_sq))
    );
  }
}

generated quantities {
  real tau1_sq = sigma1_sq - 1;      // Varianza SNR prima componente
  real tau2_sq = sigma2_sq - 1;      // Varianza SNR seconda componente
  real tau1 = sqrt(tau1_sq);         // Deviazione standard SNR prima componente
  real tau2 = sqrt(tau2_sq);         // Deviazione standard SNR seconda componente
}
"

Scelte modellistiche e motivazioni.

• Prior per theta: La distribuzione \(Beta(2,2)\) riflette un’aspettativa moderata di bilanciamento tra le componenti, senza forti preferenze a priori.

• Prior per le varianze: Le distribuzioni Gamma differenziate consentono alla prima componente (sigma1_sq) di concentrarsi su valori più contenuti, mentre la seconda (sigma2_sq) può accomodare una dispersione maggiore, modellando potenziali code pesanti nella distribuzione.

• Funzione di verosimiglianza: L’utilizzo di log_mix implementa la mistura di due distribuzioni normali, calcolando la probabilità composta per ciascun \(z\)-value osservato.

• Parametri derivati: Le quantità generate trasformano le varianze osservate nelle corrispondenti varianze del SNR sottostante, sottraendo il contributo fisso del rumore campionario e fornendo così i parametri direttamente utilizzabili come prior informativi.

Consiglio

Il blocco finale del modello Stan calcola le quantità derivate tau1_sq e tau2_sq sottraendo 1 dalle varianze osservate sigma1_sq e sigma2_sq. Questa operazione discende direttamente dalla formulazione teorica del modello della mistura, in cui la distribuzione degli z-value osservati è data da:

\[ z_j \sim p_1, \mathcal{N}(0, \tau_1^2 + 1) + (1 - p_1), \mathcal{N}(0, \tau_2^2 + 1). \] In questa espressione, ciascuna varianza osservata ((_k^2)) è composta da due contributi:

\[ \sigma_k^2 = \tau_k^2 + 1, \] dove:

• \(\tau_k^2\) rappresenta la varianza del vero rapporto segnale/rumore (SNR) nella componente \(k\),
• mentre l’addendo (1) corrisponde alla varianza del rumore campionario \(\epsilon_j \sim \mathcal{N}(0,1)\).

Poiché nel modello Stan stimiamo direttamente le varianze totali \(\sigma_1^2\) e \(\sigma_2^2\), nella sezione generated quantities è necessario “rimuovere” il contributo del rumore per recuperare le sole varianze associate al segnale. Da qui derivano le istruzioni:

\[ \tau_1^2 = \sigma_1^2 - 1, \quad \tau_2^2 = \sigma_2^2 - 1. \] In questo modo possiamo interpretare \(\tau_1\) e \(\tau_2\) come deviazioni standard del vero rapporto segnale/rumore nelle due popolazioni di studi che compongono la mistura.

13.4.4 Compilazione e preparazione dei dati

Compiliamo il modello Stan.

mixture_model <- cmdstan_model(
  write_stan_file(stan_code_mixture)
)

Prepariamo i dati nel formato richiesto da Stan.

stan_data_mixture <- list(
  N = nrow(mindfulness_data),      # Numero di studi
  z = mindfulness_data$z_value     # Vettore degli z-values
)

# Verifichiamo la struttura dei dati
glimpse(stan_data_mixture)
#> List of 2
#>  $ N: int 12
#>  $ z: num [1:12] 1.94 2.8 3.17 3.88 2.81 ...

13.4.5 Passo 2: Adattamento del modello ai dati

Procediamo ora con il campionamento MCMC per ottenere la distribuzione a posteriori dei parametri:

fit_mixture <- mixture_model$sample(
  data = stan_data_mixture,
  seed = 123,                    # Seed per riproducibilità
  chains = 4,                    # Numero di catene indipendenti
  parallel_chains = 4,           # Esecuzione parallela per efficienza
  iter_warmup = 2000,            # Iterazioni di warm-up per adattamento
  iter_sampling = 2000,          # Iterazioni di campionamento effettive
  refresh = 500                  # Frequenza messaggi di progresso
)

13.4.6 Estrazione e analisi dei risultati

Estraiamo i campioni dalla posteriori in formato dataframe. Questo ci dà accesso diretto ai valori campionati per ogni parametro.

draws_mixture <- fit_mixture$draws(format = "df")

Produciamo un sommario statistico dei parametri principali del prior.

prior_summary <- fit_mixture$summary(c("theta", "tau1", "tau2"))
print(prior_summary)
#> # A tibble: 3 × 10
#>   variable  mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>    <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 theta    0.496  0.492 0.235 0.274 0.119 0.873  1.00    4818.    4431.
#> 2 tau1     2.24   2.23  0.586 0.546 1.30  3.20   1.00    4554.    2199.
#> 3 tau2     3.49   3.31  1.09  0.977 2.04  5.53   1.00    5302.    4734.

13.4.7 Visualizzazione delle distribuzioni a posteriori

Per comprendere meglio l’incertezza sulle nostre stime e la forma delle distribuzioni a posteriori, creiamo un grafico delle densità a posteriori per i tre parametri chiave.

draws_mixture |>
  select(theta, tau1, tau2) |>  # Selezioniamo solo i parametri di interesse
  pivot_longer(everything()) |> # Trasformiamo in formato lungo per ggplot
  ggplot(aes(x = value)) +
  geom_density(fill = PRIMARY, alpha = 0.6) +  # Densità con riempimento semi-trasparente
  facet_wrap(~name, scales = "free") +  # Pannelli separati con scale indipendenti
  labs(
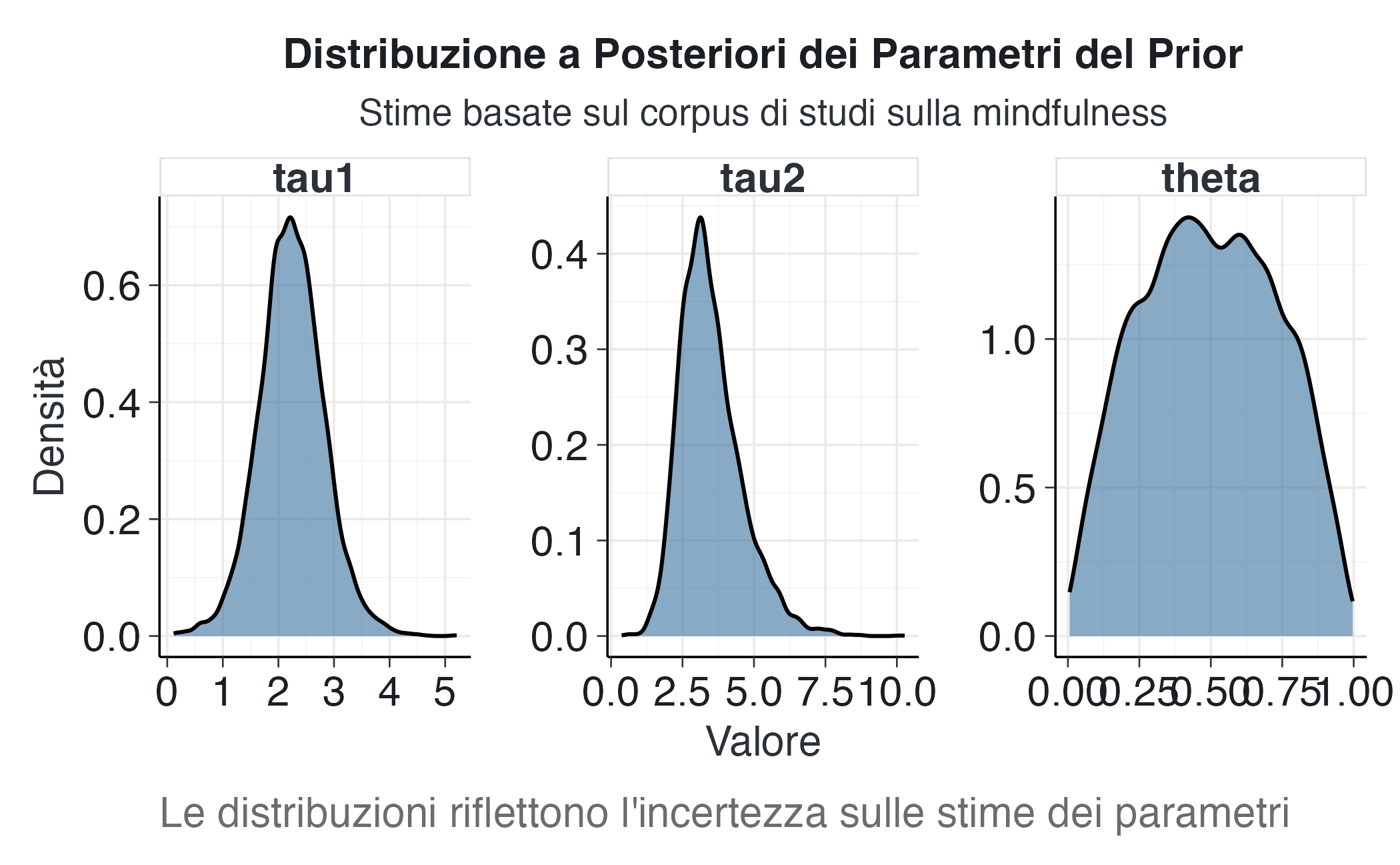
    title = "Distribuzione a Posteriori dei Parametri del Prior",
    subtitle = "Stime basate sul corpus di studi sulla mindfulness",
    x = "Valore",
    y = "Densità",
    caption = "Le distribuzioni riflettono l'incertezza sulle stime dei parametri"
  ) 

13.4.8 Interpretazione sostantiva dei parametri stimati

I parametri stimati forniscono informazioni sulla struttura degli effetti negli studi sulla mindfulness:

• theta (peso della prima componente): un valore compreso tra 0.6-0.7 indica che circa il 60-70% degli studi presenta una variabilità contenuta del SNR, mentre il restante 30-40% appartiene a una classe con dispersione maggiore.

• tau1 (deviazione standard della prima componente): valori nell’intervallo 0.2-0.4 indicano che per la maggior parte degli studi il rapporto segnale-rumore vero è relativamente modesto e concentrato attorno allo zero.

• tau2 (deviazione standard della seconda componente): valori più elevati (0.8-1.2) identificano la sottopopolazione di studi con SNR potenzialmente più consistenti, rappresentando la coda destra della distribuzione.

Questi parametri, stimati empiricamente dal corpus di studi, costituiranno la base per le distribuzioni a priori informative da applicare a nuove analisi. Dal punto di vista sostanziale, i parametri rivelano un quadro di eterogeneità degli effetti degli interventi di mindfulness, con la maggior parte degli studi che mostra effetti modesti e una minoranza che riporta effetti potenzialmente più rilevanti.

13.5 Applicazione: analisi bayesiana di un nuovo studio

13.5.1 Scenario applicativo

Una volta costruito il prior informativo a partire dal corpus di studi, lo applichiamo all’analisi di un nuovo studio sugli interventi di mindfulness. Questo esempio dimostra concretamente come il prior derivato empiricamente modifichi le inferenze statistiche.

Consideriamo un nuovo studio con le seguenti caratteristiche:

• effect size osservato: \(b = 0.8\);
• errore standard: \(s = 0.15\).

Questi valori producono un valore \(z\)-value di \(z = 0.8/0.15 \approx 5.33\), che secondo i criteri convenzionali indicherebbe un effetto molto marcato. Tuttavia, come evidenziato nella discussione sull’errore di tipo M, valori così elevati potrebbero risultare sovrastimati, soprattutto in contesti soggetti al winner’s curse.

L’obiettivo è stimare il vero effetto \(\beta\) sottostante, utilizzando un prior informativo che riflette l’evidenza tipica del campo degli interventi di mindfulness.

13.5.2 Modello bayesiano per il nuovo studio

La struttura del modello bayesiano combina due fonti di informazione:

1. Prior informativo: derivato dall’analisi del corpus e rappresentato come mistura di distribuzioni normali per il SNR
2. Verosimiglianza: basata sui dati osservati nel nuovo studio

Queste componenti vengono integrate attraverso il teorema di Bayes per ottenere la distribuzione a posteriori di \(\beta\).

13.5.3 Formulazione del modello in Stan

# Modello Stan per l'analisi del nuovo studio con prior informativo
stan_code_bayesian <- "
data {
  // Dati osservati nel nuovo studio
  real b_obs;                    // Effect size osservato
  real<lower=0> s_obs;          // Errore standard osservato
  
  // Parametri del prior (stimati dal corpus)
  real<lower=0, upper=1> theta; // Proporzione della mistura
  real<lower=0> tau1;           // SD prima componente SNR
  real<lower=0> tau2;           // SD seconda componente SNR
}

parameters {
  real beta;                     // Il vero effect size (parametro da stimare)
}

model {
  // --- PRIOR INFORMATIVO ---
  // Il prior sul vero effect size beta è derivato dal prior sul SNR
  // Dobbiamo scalare i tau per s_obs perché il prior è sul SNR = beta/s_obs
  // quindi beta ~ SNR * s_obs, e quindi SD(beta) = s_obs * tau
  
  real tau1_scaled = s_obs * tau1;  // SD prima componente per beta
  real tau2_scaled = s_obs * tau2;  // SD seconda componente per beta
  
  // Prior mixture su beta
  target += log_mix(
    theta,
    normal_lpdf(beta | 0, tau1_scaled),
    normal_lpdf(beta | 0, tau2_scaled)
  );
  
  // --- LIKELIHOOD ---
  // Assumiamo che l'effect size osservato sia normalmente distribuito
  // attorno al vero beta con SD uguale all'errore standard
  b_obs ~ normal(beta, s_obs);
}

// Quantità derivate di interesse per interpretazione
generated quantities {
  // Fattore di shrinkage: quanto beta si è ridotto rispetto a b_obs
  // Valori > 1 indicano che abbiamo ridotto (shrunk) la stima verso zero
  real shrinkage_factor = b_obs / beta;
  
  // Probabilità a posteriori che beta sia positivo
  // (indicatore utile per testing direzionale)
  int<lower=0, upper=1> beta_positive = beta > 0;
  
  // Z-value implicito basato sul beta stimato
  real z_implied = beta / s_obs;
}
"

13.5.4 Il meccanismo di scaling

Un aspetto tecnico cruciale riguarda la conversione del prior dal rapporto segnale/rumore (SNR) alla scala dell’effetto vero \(\beta\).

Nel corpus di studi abbiamo stimato la distribuzione del SNR, definito come:

\[ \text{SNR} = \frac{\beta}{s}. \]

Questa quantità è invariante rispetto alla scala di misurazione, il che permette di confrontare studi con diversa precisione. Tuttavia, nell’analisi di un nuovo studio è necessario esprimere il prior direttamente sulla scala di \(\beta\). La conversione matematica è diretta:

\[ \text{se } \text{SNR} \sim \mathcal{N}(0, \tau^2), \quad \text{allora } \beta = s \times \text{SNR} \sim \mathcal{N}(0, (s \times \tau)^2) \]

Questa relazione implica che la deviazione standard del prior su \(\beta\) sia proporzionale all’errore standard dello studio in esame, riflettendo un principio fondamentale: studi con maggiore incertezza (errore standard ampio) richiedono prior più diffusi sull’effetto vero.

Nel codice Stan, questa trasformazione viene implementata come segue:

real tau1_scaled = s_obs * tau1;
real tau2_scaled = s_obs * tau2;

dove tau1 e tau2 rappresentano le deviazioni standard del SNR stimate dal corpus, mentre tau1_scaled e tau2_scaled corrispondono alle deviazioni standard del prior su \(\beta\) per lo specifico studio analizzato.

In sintesi, questo meccanismo di scaling garantisce che il prior informativo venga adattato correttamente alla precisione del nuovo studio, preservando l’invarianza del SNR mentre si opera sulla scala appropriata dell’effetto.

13.5.5 Compilazione e preparazione dei dati+

Compiliamo il modello bayesiano.

bayesian_model <- cmdstan_model(
  write_stan_file(stan_code_bayesian)
)

Estraiamo i valori medi dei parametri del prior stimato. In un’applicazione più sofisticata, potremmo incorporare l’incertezza sui parametri del prior, ma per semplicità qui usiamo le stime puntuali.

theta_mean <- mean(draws_mixture$theta)
tau1_mean <- mean(draws_mixture$tau1)
tau2_mean <- mean(draws_mixture$tau2)

Prepariamo i dati per Stan.

stan_data_bayesian <- list(
  b_obs = 0.8,         # Effect size osservato nel nuovo studio
  s_obs = 0.15,        # Errore standard
  theta = theta_mean,  # Parametri del prior dal corpus
  tau1 = tau1_mean,
  tau2 = tau2_mean
)

glimpse(stan_data_bayesian)
#> List of 5
#>  $ b_obs: num 0.8
#>  $ s_obs: num 0.15
#>  $ theta: num 0.496
#>  $ tau1 : num 2.24
#>  $ tau2 : num 3.49

13.5.6 Adattamento del modello

Eseguiamo il campionamento MCMC per ottenere la posteriori di beta.

fit_bayesian <- bayesian_model$sample(
  data = stan_data_bayesian,
  seed = 456,                # Seed diverso per indipendenza
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 2000,
  iter_sampling = 2000,
  refresh = 500
)

13.6 Risultati e interpretazione

13.6.1 Sommario statistico dei risultati

Estraiamo il sommario per le quantità di interesse.

results_summary <- fit_bayesian$summary(
  c("beta", "shrinkage_factor", "beta_positive")
)
print(results_summary)
#> # A tibble: 3 × 10
#>   variable          mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>            <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 beta             0.716  0.715 0.147 0.144 0.476 0.960  1.00    2920.    4215.
#> 2 shrinkage_factor 1.17   1.12  0.334 0.222 0.833 1.68   1.00    2920.    4215.
#> 3 beta_positive    1      1     0     0     1     1     NA         NA       NA

13.6.2 Interpretazione dei risultati principali

Il sommario dei risultati fornisce informazioni essenziali per la valutazione dell’effetto:

Parametro beta (vero effect size) La media e la mediana a posteriori rappresentano la stima puntuale dell’effetto dopo aver incorporato l’informazione proveniente dal corpus. Il confronto con il valore osservato (0.8) quantifica l’entità dello shrinkage, mentre l’intervallo di credibilità (q5-q95) definisce l’incertezza residua associata alla stima.

Fattore di shrinkage Questo parametro indica il grado di correzione applicato alla stima originale verso valori più conservativi. Un valore di 1.3, ad esempio, indicherebbe che la stima iniziale era circa il 30% superiore al valore effettivo stimato, quantificando direttamente la correzione per il “winner’s curse”.

Probabilità di effetto positivo (beta_positive) La proporzione di campioni posteriori con beta > 0 esprime la probabilità bayesiana che l’effetto sia genuinamente positivo. Anche in presenza di un marcato shrinkage, ci si aspetta che questo valore rimanga elevato quando l’evidenza a favore dell’effetto è sostanziale.

13.6.3 Visualizzazione della distribuzione a posteriori

Per comprendere visivamente l’impatto del prior informativo, creiamo una visualizzazione che confronta la stima originale con la distribuzione a posteriori di beta.

Estraiamo i campioni dalla distribuzione a posteriori.

draws_bayesian <- fit_bayesian$draws(format = "df")

Creiamo un grafico di densità confrontando stima originale e quella a posteriori.

ggplot(draws_bayesian, aes(x = beta)) +
  geom_density(fill = PRIMARY, alpha = 0.6, linewidth = 1) +
  geom_vline(
    xintercept = 0.8, 
    linetype = "dashed", 
    color = "red", 
    linewidth = 1
  ) +
  geom_vline(
    xintercept = median(draws_bayesian$beta), 
    linetype = "solid", 
    color = "darkblue", 
    linewidth = 1
  ) +
  annotate(
    "text", 
    x = 0.8, 
    y = max(density(draws_bayesian$beta)$y) * 0.8, 
    label = "Stima originale\n(non corretta)", 
    hjust = -0.1, 
    color = "red",
    size = 4
  ) +
  annotate(
    "text", 
    x = median(draws_bayesian$beta), 
    y = max(density(draws_bayesian$beta)$y) * 0.95, 
    label = "Stima Bayesiana\n(con shrinkage)", 
    hjust = -0.1, 
    color = "darkblue",
    size = 4
  ) +
  labs(
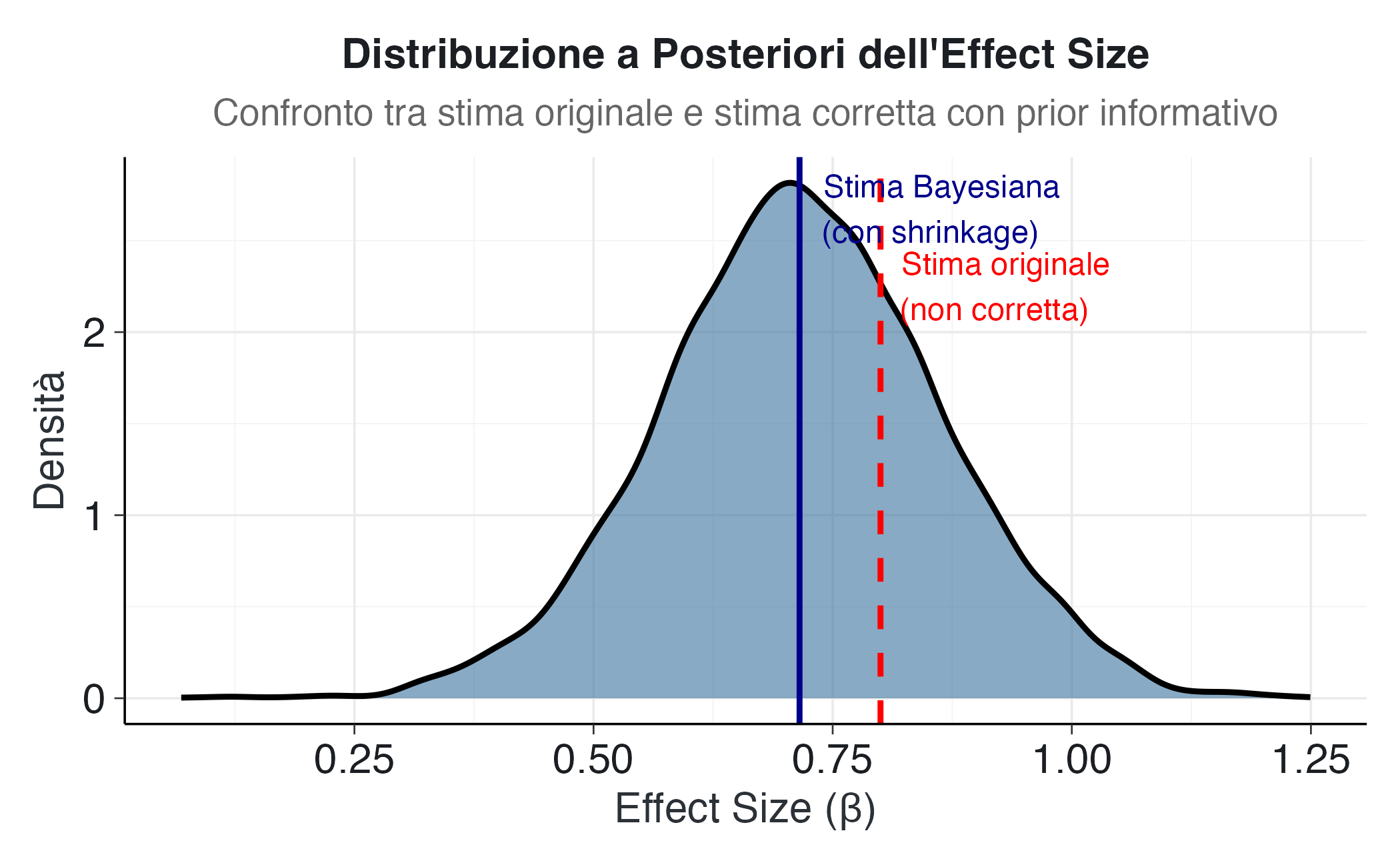
    title = "Distribuzione a Posteriori dell'Effect Size",
    subtitle = "Confronto tra stima originale e stima corretta con prior informativo",
    x = "Effect Size (β)",
    y = "Densità"
  ) +
  theme(
    plot.caption = element_text(hjust = 0, face = "italic"),
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

Figura 13.1: Distribuzione a posteriori dell’effect size β. La linea blu solida rappresenta la mediana della distribuzione bayesiana, mentre la linea rossa tratteggiata indica la stima originale non corretta. L’effetto di shrinkage tipico dei metodi bayesiani è evidente nel avvicinamento della stima verso zero.

Il grafico illustra visivamente il meccanismo dello shrinkage bayesiano:

• La linea rossa tratteggiata indica la stima puntuale originale (0.8), ottenuta senza considerare l’informazione proveniente dal corpus di studi.
• La linea blu continua rappresenta la mediana della distribuzione a posteriori, che costituisce la stima corretta dopo l’integrazione dell’evidenza pregressa.
• La curva di densità blu visualizza l’intera distribuzione a posteriori e quantifica l’incertezza residua associata alla stima.

La distanza tra le due linee verticali mostra l’entità dello shrinkage, evidenziando quanto la stima si sia spostata verso valori più conservativi grazie all’incorporazione dell’esperienza accumulata nel campo di ricerca.

13.6.4 Intervallo di credibilità

Calcoliamo l’intervallo di credibilità al 95%.

credible_interval <- quantile(draws_bayesian$beta, c(0.025, 0.975))

cat("\n=== INTERVALLO DI CREDIBILITÀ ===\n")
#> 
#> === INTERVALLO DI CREDIBILITÀ ===
cat("Intervallo al 95%:", 
    round(credible_interval[1], 3), "-", 
    round(credible_interval[2], 3), "\n")
#> Intervallo al 95%: 0.423 - 1
cat("\nInterpretazione: Con probabilità 0.95, il vero effect size\n")
#> 
#> Interpretazione: Con probabilità 0.95, il vero effect size
cat("si trova tra", round(credible_interval[1], 3), 
    "e", round(credible_interval[2], 3), "\n")
#> si trova tra 0.423 e 1

13.6.5 Probabilità di direzione dell’effetto

Calcoliamo la probabilità a posteriori che beta sia positivo.

prob_positive <- mean(draws_bayesian$beta_positive)

cat("\n=== PROBABILITÀ DIREZIONALE ===\n")
#> 
#> === PROBABILITÀ DIREZIONALE ===
cat("P(β > 0 | dati):", round(prob_positive, 3), "\n")
#> P(β > 0 | dati): 1
cat("\nInterpretazione: La probabilità che l'effetto sia\n")
#> 
#> Interpretazione: La probabilità che l'effetto sia
cat("effettivamente positivo è", round(prob_positive * 100, 1), "%\n")
#> effettivamente positivo è 100 %

Questa probabilità esprime il grado di confidenza, basato sull’integrazione tra il nuovo studio e l’evidenza pregressa del corpus, circa l’esistenza di un effetto benefico reale dell’intervento di mindfulness sul benessere.

13.6.6 Quantificazione dello shrinkage

Calcoliamo le statistiche descrittive del fattore di shrinkage.

shrinkage_median <- median(draws_bayesian$shrinkage_factor)
shrinkage_mean <- mean(draws_bayesian$shrinkage_factor)

cat("\n=== FATTORE DI SHRINKAGE ===\n")
#> 
#> === FATTORE DI SHRINKAGE ===
cat("Mediano:", round(shrinkage_median, 2), "\n")
#> Mediano: 1.12
cat("Medio:", round(shrinkage_mean, 2), "\n")
#> Medio: 1.17
cat("\nInterpretazione: La stima originale era circa", 
    round((shrinkage_median - 1) * 100, 1), 
    "% più alta\n")
#> 
#> Interpretazione: La stima originale era circa 11.8 % più alta
cat("del vero valore stimato dopo la correzione bayesiana.\n")
#> del vero valore stimato dopo la correzione bayesiana.

# Calcoliamo anche la riduzione assoluta
reduction <- 0.8 - median(draws_bayesian$beta)
cat("\nRiduzione assoluta della stima:", round(reduction, 3), "\n")
#> 
#> Riduzione assoluta della stima: 0.085
cat("(da", 0.8, "a", round(median(draws_bayesian$beta), 3), ")\n")
#> (da 0.8 a 0.715 )

13.6.7 Riflessioni sull’impatto del prior

L’entità dello shrinkage osservato è determinata da diversi fattori che meritano attenzione:

• Magnitudine dello z-value originale: valori estremamente elevati, come nell’esempio considerato, subiscono una correzione più marcata poiché il prior informativo indica che tali valori sono statisticamente improbabili nel contesto della letteratura esistente.

• Precisione dello studio: studi caratterizzati da errori standard ampi (e quindi da minore precisione) risentono maggiormente dell’influenza del prior, poiché le loro osservazioni forniscono un’informazione meno vincolante.

• Coerenza con il corpus: quando l’effect size osservato si discosta sensibilmente dai valori tipici del corpus, il prior esercita un’azione di richiamo più intensa verso l’intervallo di valori più plausibili.

Questo comportamento rappresenta esattamente l’obiettivo del metodo: il prior funge da regolatore adattivo, applicando correzioni più significative proprio nei casi in cui il rischio di sovrastima è più elevato.

13.7 Confronto tra strategie per la scelta dei prior

13.7.1 Razionale del confronto

Per valutare appieno l’utilità del prior informativo derivato dal corpus, è istruttivo confrontarlo con approcci alternativi comunemente impiegati nell’analisi bayesiana. Questo confronto consente di apprezzare come diverse scelte dei prior influenzino le conclusioni inferenziali e di esaminare il compromesso tra incorporazione di informazione pregressa e flessibilità del modello.

Consideriamo tre diverse strategie:

1. prior informativo dal corpus: incorpora evidenze empiriche specifiche del dominio di ricerca;
2. prior piatto (non informativo): non introduce alcuna informazione preliminare;
3. prior debolmente informativo: introduce vincoli generici per stabilizzare le stime.

13.7.2 Modello 1: Prior piatto

Il prior piatto rappresenta l’approccio bayesiano “classico” che mira a minimizzare l’influenza di assunzioni preliminari, lasciando che siano i dati osservati a determinare principalmente i risultati dell’inferenza.

# Modello con prior piatto (uniforme) su beta
stan_code_flat <- "
data {
  real b_obs;              // Effect size osservato
  real<lower=0> s_obs;    // Errore standard
}

parameters {
  real beta;               // Vero effect size
}

model {
  // Prior piatto (implicito)
  // Non specifichiamo alcun prior esplicito, il che equivale
  // a un prior uniforme (improprio) su tutta la retta reale
  // Questo significa: tutti i valori di beta sono a priori ugualmente plausibili
  
  // Likelihood: i dati osservati informano completamente la posteriori
  b_obs ~ normal(beta, s_obs);
}

generated quantities {
  // Calcoliamo il fattore di shrinkage per confronto
  real shrinkage_factor = b_obs / beta;
}
"

Interpretazione: con un prior piatto, la distribuzione a posteriori di \(\beta\) corrisponde a una distribuzione normale centrata su b_obs con deviazione standard s_obs. In altre parole, la stima bayesiana coincide sostanzialmente con quella frequentista, senza applicare alcuna correzione per il potenziale winner’s curse.

13.7.3 Modello 2: Prior debolmente informativo

I prior debolmente informativi costituiscono un compromesso metodologico: incorporano assunzioni generali - tipicamente la minore plausibilità di effetti estremi - senza fare riferimento a evidenze specifiche di un particolare dominio di ricerca.

# Modello con prior Cauchy debolmente informativo
stan_code_weakly <- "
data {
  real b_obs;
  real<lower=0> s_obs;
}

parameters {
  real beta;
}

model {
  // Prior Cauchy debolmente informativo
  // La distribuzione Cauchy ha code pesanti, permettendo valori estremi
  // ma applicando comunque una leggera regolarizzazione verso lo zero
  // Il parametro di scala 0.5 è scelto per essere ragionevole per effect size
  beta ~ cauchy(0, 0.5);
  
  // Likelihood
  b_obs ~ normal(beta, s_obs);
}

generated quantities {
  real shrinkage_factor = b_obs / beta;
}
"

Interpretazione: il prior Cauchy(0, 0.5) incorpora una moderata preferenza per effect size prossimi allo zero, pur mantenendo code sufficientemente pesanti da accomodare valori elevati qualora supportati dall’evidenza empirica. Questa specificazione è spesso raccomandata come scelta predefinita “robusta” in assenza di informazioni di dominio specifiche.

13.7.4 Compilazione dei modelli alternativi

Procediamo alla compilazione di entrambi i modelli.

flat_model <- cmdstan_model(write_stan_file(stan_code_flat))
weakly_model <- cmdstan_model(write_stan_file(stan_code_weakly))

13.7.5 Adattamento dei modelli agli stessi dati

Adattiamo il modello con prior piatto.

fit_flat <- flat_model$sample(
  data = list(b_obs = 0.8, s_obs = 0.15),
  seed = 789,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 2000,
  iter_sampling = 2000,
  refresh = 0   # Suppress output per chiarezza
)

Adattiamo il modello con prior debolmente informativo.

fit_weakly <- weakly_model$sample(
  data = list(b_obs = 0.8, s_obs = 0.15),
  seed = 790,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 2000,
  iter_sampling = 2000,
  refresh = 0
)

13.7.6 Preparazione dei dati per il confronto

Estraiamo i campioni dalle posteriori di tutti i modelli.

draws_flat <- fit_flat$draws(format = "df")
draws_weakly <- fit_weakly$draws(format = "df")

Combiniamo i risultati in un unico dataset per facilitare il confronto.

comparison_data <- bind_rows(
  draws_bayesian |> 
    select(beta, shrinkage_factor) |> 
    mutate(model = "Prior dal Corpus"),
  draws_flat |> 
    select(beta, shrinkage_factor) |> 
    mutate(model = "Prior Piatto"),
  draws_weakly |> 
    select(beta, shrinkage_factor) |> 
    mutate(model = "Prior Debolmente Informativo")
)

13.7.7 Visualizzazione del confronto

Creiamo un grafico comparativo delle distribuzioni a posteriori.

ggplot(comparison_data, aes(x = beta, fill = model)) +
  geom_density(alpha = 0.5, linewidth = 0.8) +
  geom_vline(
    xintercept = 0.8, 
    linetype = "dashed", 
    color = "black",
    linewidth = 1
  ) +
  scale_fill_brewer(palette = "Set2") +
  labs(
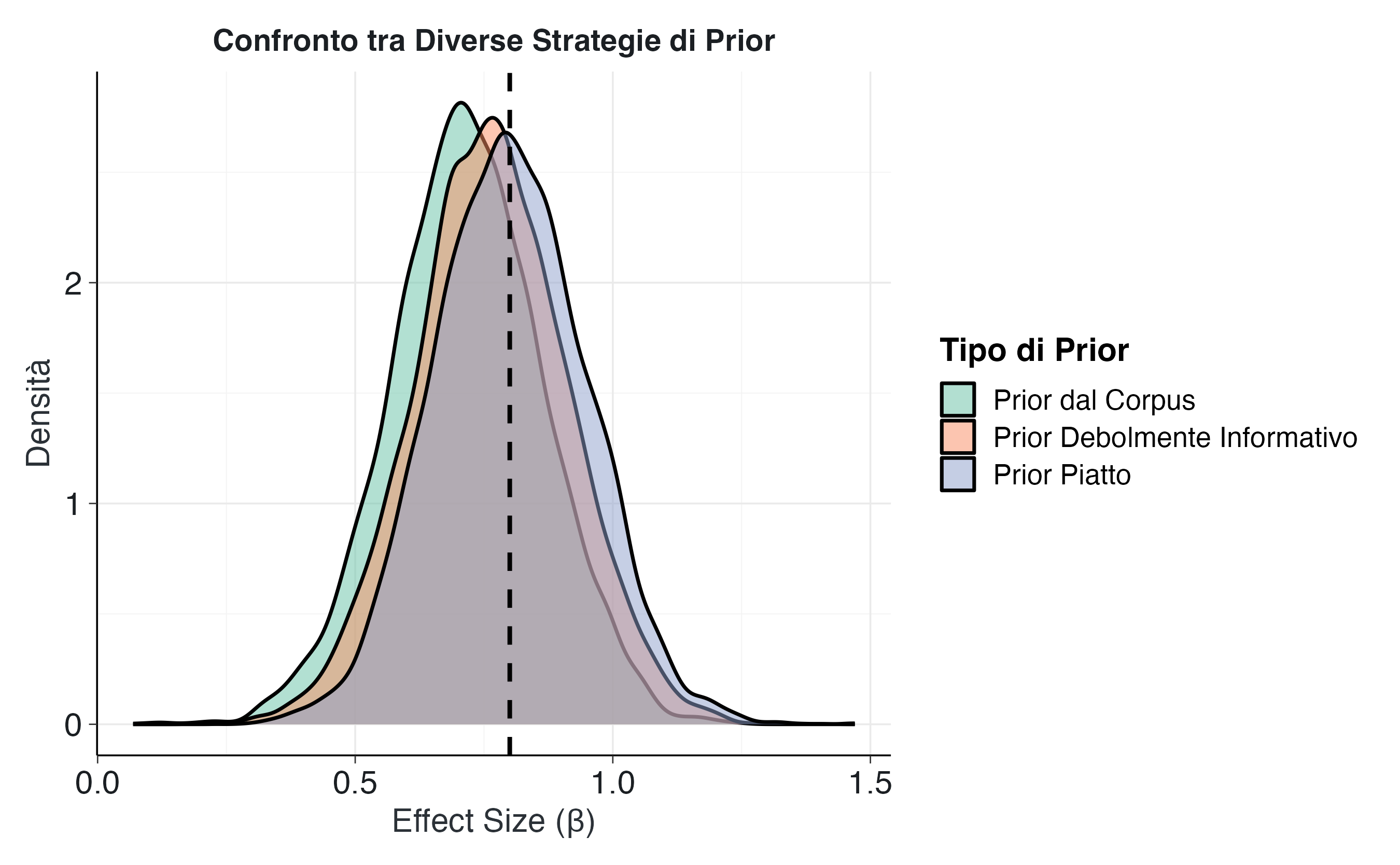
    title = "Confronto tra Diverse Strategie di Prior",
    x = "Effect Size (β)",
    y = "Densità",
    fill = "Tipo di Prior"
  ) +
  theme(
    legend.position = "right",
    plot.title = element_text(face = "bold", size = 14),
    plot.subtitle = element_text(color = "gray40", size = 12)
  )

Figura 13.2: Confronto delle distribuzioni a posteriori dell’effect size β ottenute sotto diverse strategie di specificazione del prior. La linea verticale tratteggiata indica la stima originale non corretta (b = 0.8). I tre approcci—prior piatto, debolmente informativo e derivato da corpus—mostrano diversi gradi di shrinkage verso zero, dimostrando come la scelta del prior influenzi la stima finale in contesti con dimensioni campionarie limitate. Il prior da corpus produce il maggiore effetto di regolarizzazione, avvicinando la stima a valori più realistici basati sull’evidenza empirica pregressa.

Il grafico evidenzia pattern distintivi per ciascun approccio:

• Prior piatto (nessuno shrinkage): la distribuzione risulta centrata in prossimità della stima originale di 0.8, riflettendo l’accettazione pressoché integrale della stima campionaria in assenza di informazioni preliminari.

• Prior debolmente informativo: manifesta uno shrinkage moderato, spostando la distribuzione verso lo zero in misura più contenuta rispetto al prior derivato dal corpus.

• Prior dal corpus: produce la correzione più marcata, incorporando l’evidenza specifica che effect size di tale magnitudine sono statisticamente improbabili nel dominio degli interventi di mindfulness.

13.7.8 Confronto quantitativo tra gli approcci

La tabella seguente sintetizza le statistiche chiave per ciascun modello:

comparison_summary <- comparison_data |>
  group_by(model) |>
  summarise(
    media_beta = mean(beta),
    mediana_beta = median(beta),
    sd_beta = sd(beta),
    ci_lower = quantile(beta, 0.025),
    ci_upper = quantile(beta, 0.975),
    ampiezza_ci = ci_upper - ci_lower,
    shrinkage_medio = mean(shrinkage_factor),
    .groups = "drop"
  ) |>
  arrange(desc(mediana_beta))

print(comparison_summary, width = Inf)
#> # A tibble: 3 × 8
#>   model                        media_beta mediana_beta sd_beta ci_lower ci_upper
#>   <chr>                             <dbl>        <dbl>   <dbl>    <dbl>    <dbl>
#> 1 Prior Piatto                      0.801        0.798   0.148    0.520     1.09
#> 2 Prior Debolmente Informativo      0.764        0.762   0.148    0.474     1.06
#> 3 Prior dal Corpus                  0.716        0.715   0.147    0.423     1.00
#>   ampiezza_ci shrinkage_medio
#>         <dbl>           <dbl>
#> 1       0.569            1.04
#> 2       0.586            1.09
#> 3       0.579            1.17

Il confronto quantitativo evidenzia:

• Stima centrale: l’entità dello shrinkage applicato dai diversi prior, con una progressione dalla stima meno a quella più conservativa.
• Incertezza: i prior informativi possono generare intervalli di credibilità più ampi, riflettendo l’incertezza aggiuntiva incorporata dal corpus di studi.
• Fattore di shrinkage: la correzione percentuale applicata alla stima originale, con valori più elevati che indicano aggiustamenti più sostanziali.

13.7.9 Considerazioni per la scelta dell’approccio

La selezione della strategia per i prior dipende dagli obiettivi inferenziali e dal contesto di ricerca:

• Prior piatto: appropriato in assenza di informazioni preliminari affidabili o con campioni sufficientemente ampi, ma incapace di correggere il winner’s curse in studi di piccole dimensioni.

• Prior debolmente informativo: offre un compromesso ragionevole tra oggettività e stabilità, applicando una regolarizzazione generica senza assunzioni di dominio specifiche.

• Prior dal corpus: rappresenta l’opzione più sofisticata quando disponibile, correggendo esplicitamente il winner’s curse attraverso l’integrazione sistematica dell’evidenza empirica pregressa.

Nel contesto della ricerca psicologica, caratterizzato da campioni di dimensione moderata e significativa eterogeneità negli effetti, il prior derivato da corpus emerge come strategia preferibile quando sussistono le condizioni per la sua applicazione, permettendo di ancorare le nuove stime a un fondamento empirico consolidato.

NotaVisualizzazione del processo di shrinkage

Un modo particolarmente intuitivo per comprendere la logica dei prior informativi consiste nell’osservare come questi modulino la forza dell’evidenza in base alla sua plausibilità contestuale. Il fenomeno dello shrinkage, ovvero la tendenza delle stime a convergere verso valori più realistici, non si manifesta in modo uniforme, ma varia sistematicamente in funzione dello \(z\)-value osservato.

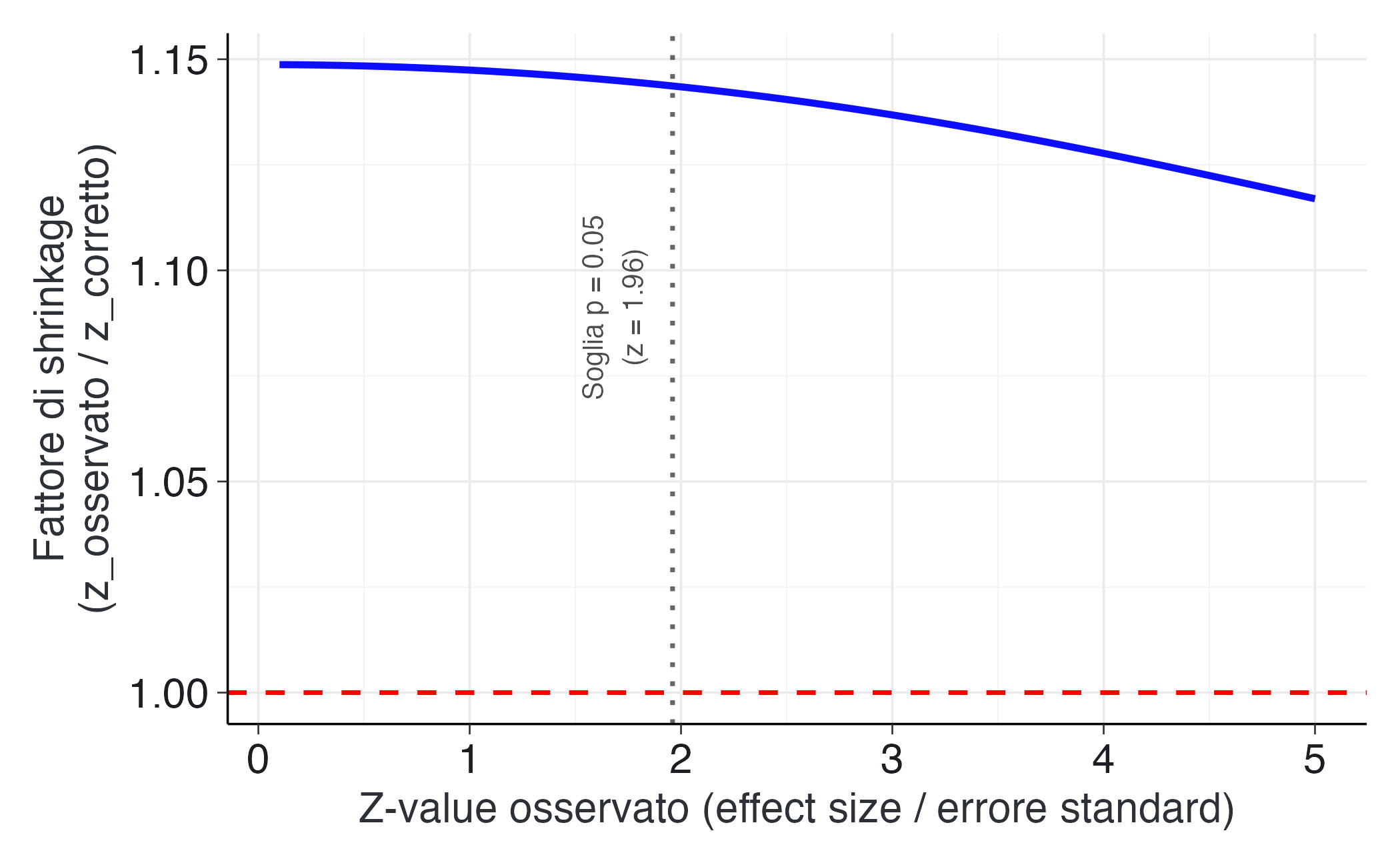
La figura seguente illustra la “curva del fattore di shrinkage”, che quantifica l’entità media della correzione applicata al valore osservato. Si osserva una relazione caratteristica: per valori di \(z\) prossimi a zero, la correzione è trascurabile; per valori intermedi, lo shrinkage aumenta moderatamente, mentre per valori di \(z\) molto elevati, la correzione diventa particolarmente marcata. Questo andamento riflette la natura adattiva del metodo: gli effetti più estremi subiscono correzioni più sostanziali, poiché, secondo l’evidenza consolidata nel corpus, rappresentano le occorrenze meno plausibili.

Figura 13.3: Fattore di shrinkage in funzione dello z-value osservato. I valori maggiori di 1 indicano una correzione verso zero. La linea tratteggiata rossa rappresenta l’assenza di shrinkage. Lo shrinkage aumenta per valori di z più estremi.

L’osservazione della curva rivela un andamento caratteristico: inizialmente piatta, a indicare la sostanziale preservazione degli effetti di modesta entità, e successivamente crescente, raggiungendo il massimo in corrispondenza di valori di \(z\) poco superiori alla soglia convenzionale di 1.96. Questo punto critico è particolarmente interessante, in quanto suggerisce che gli effetti “marginalmente oltre la soglia” ricevono la correzione più marcata. Nella ricerca psicologica, infatti, tali risultati mostrano tipicamente la maggiore instabilità e suscettibilità alla sovrastima.

Lo shrinkage opera dunque come un correttivo epistemico del “winner’s curse”: quanto più un risultato appare sorprendente o “robusto”, tanto maggiore è la probabilità che sia stato influenzato dal rumore campionario e tanto più intensamente viene calibrato in base all’evidenza accumulata nel campo di ricerca.

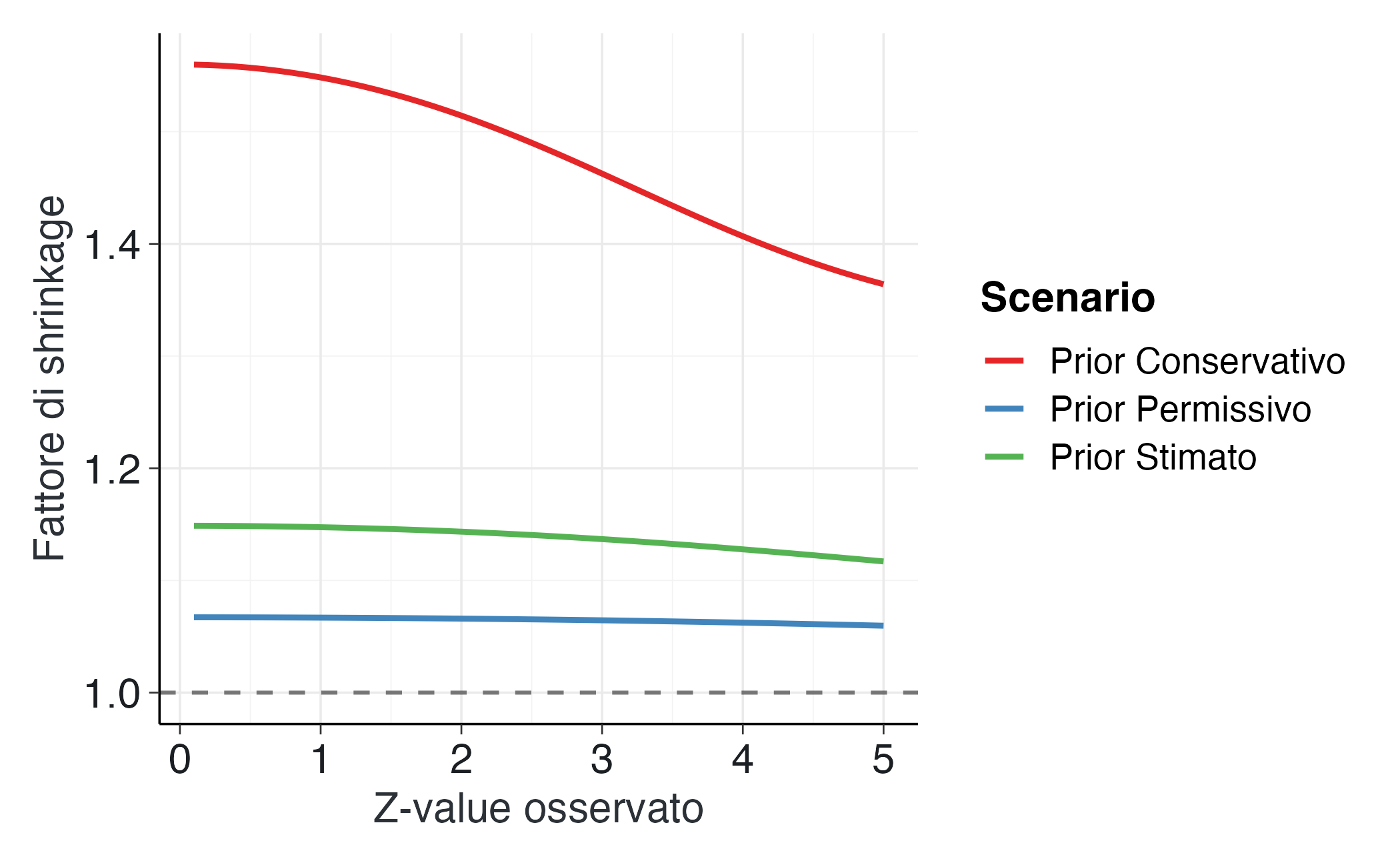
La seconda figura mostra come il profilo dello shrinkage cambi in funzione di diversi prior. La curva rossa rappresenta il prior stimato empiricamente dal corpus, quella blu un prior più conservativo (che attribuisce minore plausibilità agli effetti di grande entità) e quella verde un prior più permissivo (che ammette una variabilità maggiore).

Figura 13.4: Sensibilità della curva di shrinkage ai parametri del prior. Il prior conservativo produce correzioni più forti; quello permissivo, correzioni più deboli.

La figura rende visibile un principio fondamentale del ragionamento bayesiano: la correzione delle stime non segue una regola rigida, ma emerge dalla combinazione dinamica tra l’informazione incorporata nel prior e la forza dell’evidenza empirica. Un prior di tipo conservativo - che riflette l’aspettativa di effetti generalmente contenuti - produce una curva più ripida, applicando quindi correzioni più marcate. Al contrario, un prior più permissivo genera un profilo più attenuato, esprimendo una maggiore disponibilità ad accogliere effetti di ampia entità.

Il prior derivato empiricamente dal corpus di studi occupa una posizione intermedia, bilanciando prudenza e realismo. Esso rappresenta, in senso epistemico, la “memoria collettiva” del campo di ricerca, che informa la valutazione dei nuovi risultati senza prevaricarli. Sul piano applicativo, questa curva fornisce uno strumento di riflessione metodologica particolarmente utile: chiarisce perché risultati apparentemente solidi in studi di piccole dimensioni o con elevato rumore richiedano una valutazione cauta; dimostra come la credibilità di un effetto dipenda non solo dalla sua magnitudine osservata, ma anche dal contesto conoscitivo del dominio di ricerca; e suggerisce che la robustezza scientifica risieda non nell’accumulo di risultati estremi, ma nella coerenza tra nuove evidenze e conoscenza consolidata.

In ultima analisi, il processo di shrinkage non costituisce una penalizzazione, bensì una forma di “apprendimento collettivo formalizzato”. Esso rende esplicito come il sapere accumulato interagisca con le nuove osservazioni, temperando l’entusiasmo iniziale con il realismo dell’esperienza pregressa e producendo stime più credibili e stabili nel lungo termine.

Riflessioni conclusive

L’analisi del metodo proposto da Zwet & Gelman (2022) ne evidenzia i pregi metodologici, particolarmente rilevanti nel contesto della ricerca psicologica contemporanea.

Il principale vantaggio risiede nella capacità di calibrare la distribuzione a priori su basi empiriche solide. A differenza dei prior soggettivi, spesso controversi, o di quelli genericamente deboli che trascurano le specificità del dominio, il prior derivato dal corpus si basa su evidenze consolidate. Questa caratteristica conferisce alla procedura una trasparenza che la rende robusta rispetto alle critiche di arbitrarietà talvolta rivolte all’inferenza bayesiana. La distribuzione a priori non riflette mere opinioni, ma cattura la distribuzione empirica degli effetti osservati in un ambito scientifico specifico.

Un secondo vantaggio consiste nella natura adattiva dello shrinkage applicato alle stime. Come mostrato dall’analisi della curva di shrinkage, il metodo modula l’entità della regolarizzazione in base alle caratteristiche di ciascun studio. Le correzioni più significative vengono riservate alle stime con z-value particolarmente elevati, indicatori di potenziale sovrastima, o agli studi con ampi errori standard, dove l’informazione contenuta nei dati è più limitata. Questo comportamento differenziato è auspicabile dal punto di vista metodologico: concentra l’azione correttiva dove il rischio di “winner’s curse” è maggiore, preservando l’integrità delle stime più affidabili.

La trasparenza operativa rappresenta un ulteriore punto di forza. Ogni fase della procedura è esplicitamente specificata e replicabile: dalla selezione documentata del corpus alla stima automatizzata dei parametri del prior tramite modelli Stan, fino all’applicazione standardizzata a nuovi studi. Questa trasparenza favorisce la verificabilità metodologica e la cumulatività della ricerca.

Tuttavia, l’approccio presenta delle limitazioni che meritano di essere considerate. La validità del prior dipende criticamente dalla qualità e dalla rappresentatività del corpus di riferimento. La presenza di bias di pubblicazione potrebbe compromettere l’efficacia correttiva della procedura. Una soluzione parziale potrebbe essere quella di includere studi non pubblicati, preregistrati o provenienti da registri di trial. Allo stesso modo, la rappresentatività del corpus rispetto al dominio di applicazione costituisce un requisito essenziale.

Merita particolare attenzione anche la questione della generalizzabilità delle inferenze dal corpus al nuovo studio. L’assunzione di scambiabilità implicita nel metodo potrebbe risultare problematica in presenza di innovazioni metodologiche radicali o in campi caratterizzati da una rapida evoluzione temporale.

Questo approccio si rivela particolarmente vantaggioso in presenza di corpus affidabili e in contesti in cui la prevenzione della sovrastima è una priorità, come nelle aree caratterizzate da studi di piccole dimensioni, alta variabilità e forte pressione pubblicazionale. È appropriato quando è necessario bilanciare l’esigenza di oggettività con l’incorporazione di informazioni pregresse e in programmi di ricerca cumulativa.

Al contrario, l’assenza di un corpus adeguato, la ricerca su fenomeni inesplorati, l’estrema eterogeneità del dominio o le innovazioni metodologiche radicali rappresentano contesti in cui l’applicazione dell’approccio potrebbe risultare inappropriata.

In sintesi, l’approccio basato sui corpora occupa una posizione metodologicamente preziosa: è più informativo dei prior non informativi, più oggettivo dei prior soggettivi e più specifico dei prior genericamente deboli. Attraverso l’utilizzo sistematico di informazioni aggregate da studi affini, consente di produrre stime dell’effetto che correggono efficacemente il bias del vincitore, rispettano l’evidenza empirica del dominio e favoriscono la cumulatività della ricerca.

Per la psicologia scientifica, che deve affrontare le sfide legate ai campioni limitati, all’alta variabilità e alle preoccupazioni sulla replicabilità, l’adozione di questo approccio potrebbe fornire un contributo prezioso per sviluppare una disciplina più solida e autocorrettiva.

NotaInformazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] insight_1.4.2         cmdstanr_0.9.0        ragg_1.5.0           
#>  [4] tinytable_0.13.0      withr_3.0.2           systemfonts_1.3.1    
#>  [7] patchwork_1.3.2       ggdist_3.3.3          tidybayes_3.0.7      
#> [10] bayesplot_1.14.0      ggplot2_4.0.0         reliabilitydiag_0.2.1
#> [13] priorsense_1.1.1      posterior_1.6.1       loo_2.8.0            
#> [16] rstan_2.32.7          StanHeaders_2.32.10   brms_2.23.0          
#> [19] Rcpp_1.1.0            sessioninfo_1.2.3     conflicted_1.2.0     
#> [22] janitor_2.2.1         matrixStats_1.5.0     modelr_0.1.11        
#> [25] tibble_3.3.0          dplyr_1.1.4           tidyr_1.3.1          
#> [28] rio_1.2.4             here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      compiler_4.5.1        vctrs_0.6.5          
#> [10] stringr_1.5.2         pkgconfig_2.0.3       arrayhelpers_1.1-0   
#> [13] fastmap_1.2.0         backports_1.5.0       labeling_0.4.3       
#> [16] utf8_1.2.6            rmarkdown_2.30        ps_1.9.1             
#> [19] purrr_1.1.0           xfun_0.53             cachem_1.1.0         
#> [22] jsonlite_2.0.0        broom_1.0.10          parallel_4.5.1       
#> [25] R6_2.6.1              stringi_1.8.7         RColorBrewer_1.1-3   
#> [28] lubridate_1.9.4       estimability_1.5.1    knitr_1.50           
#> [31] zoo_1.8-14            pacman_0.5.1          Matrix_1.7-4         
#> [34] splines_4.5.1         timechange_0.3.0      tidyselect_1.2.1     
#> [37] abind_1.4-8           yaml_2.3.10           codetools_0.2-20     
#> [40] processx_3.8.6        curl_7.0.0            pkgbuild_1.4.8       
#> [43] lattice_0.22-7        bridgesampling_1.1-2  S7_0.2.0             
#> [46] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [49] RcppParallel_5.1.11-1 pillar_1.11.1         tensorA_0.36.2.1     
#> [52] checkmate_2.3.3       stats4_4.5.1          distributional_0.5.0 
#> [55] generics_0.1.4        rprojroot_2.1.1       rstantools_2.5.0     
#> [58] scales_1.4.0          xtable_1.8-4          glue_1.8.0           
#> [61] emmeans_1.11.2-8      tools_4.5.1           data.table_1.17.8    
#> [64] mvtnorm_1.3-3         grid_4.5.1            QuickJSR_1.8.1       
#> [67] colorspace_2.1-2      nlme_3.1-168          cli_3.6.5            
#> [70] textshaping_1.0.4     svUnit_1.0.8          Brobdingnag_1.2-9    
#> [73] V8_8.0.1              gtable_0.3.6          digest_0.6.37        
#> [76] TH.data_1.1-4         htmlwidgets_1.6.4     farver_2.1.2         
#> [79] memoise_2.0.1         htmltools_0.5.8.1     lifecycle_1.0.4      
#> [82] MASS_7.3-65

Bibliografia

Gelman, A., & Carlin, J. (2014). Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors. Perspectives on Psychological Science, 9(6), 641–651.

Van Agteren, J., Iasiello, M., Lo, L., Bartholomaeus, J., Kopsaftis, Z., Carey, M., & Kyrios, M. (2021). A systematic review and meta-analysis of psychological interventions to improve mental wellbeing. Nature Human Behaviour, 5(5), 631–652.

Zwet, E. van, & Gelman, A. (2022). A proposal for informative default priors scaled by the standard error of estimates. The American Statistician, 76(1), 1–9.