# Il modello di Rescorla–Wagner {#sec-dynamic-models-rescorla-wagner}
## Introduzione {.unnumbered .unlisted}
Questo capitolo approfondisce la discussione del *modello di Rescorla–Wagner (RW)* con *regola di scelta Softmax* [@rescorla1972theory; cfr. capitolo 24 del manuale], come naturale estensione del modello di revisione degli obiettivi discusso nel capitolo precedente. Nel modello precedente l’aggiornamento era un *termine additivo* guidato da una discrepanza osservata; qui, invece, l’aggiornamento è esplicitamente *guidato dall’errore di predizione del rinforzo* (*reward prediction error*, RPE), ovvero la differenza tra il rinforzo ottenuto e quello attese. Questa formulazione è più *psicologicamente plausibile* e allineata all’evidenza in psicologia e nelle neuroscienze: *si impara proporzionalmente a quanto l’esito sorprende le aspettative*.
Accanto al livello di *apprendimento* (aggiornamento dei valori associativi $Q$), introduciamo il livello *decisionale*: le scelte non sono deterministiche, ma riflettono un compromesso tra *sfruttamento* dell’opzione migliore ed *esplorazione* di alternative. Con due opzioni, la Softmax si riduce a una *logistica della differenza* $Q_B-Q_A$, modulata dal parametro di *inverse temperature* $\tau$: valori alti di $\tau$ rendono le scelte più coerenti con $Q$, mentre valori bassi le rendono più esplorative.
Questa distinzione *apprendimento–decisione* è cruciale: consente di *separare* il meccanismo che aggiorna le aspettative (parametro $lr$) da quello che le traduce in probabilità di scelta (parametro $\tau$). Nei paragrafi successivi mostreremo come *simulare* dati (ad esempio, il *probabilistic reversal learning*), *stimare* i parametri con *Stan* e *interpretare* i profili individuali e di gruppo.
::: {.callout-caution collapse=true title="Preparazione del Notebook"}
```{r}
#| echo: false
#| message: false
#| warning: false
# Setup comune del manuale
here::here("code", "_common.R") |> source()
library(cmdstanr)
```
:::
## Il modello di Rescorla–Wagner
Il modello di *Rescorla–Wagner (RW)* è uno dei modelli più influenti nello studio dell’apprendimento associativo. Esso descrive come gli individui aggiornino le proprie aspettative in base all’esperienza, introducendo un meccanismo semplice ma potente che spiega fenomeni quali l’acquisizione, l’estinzione e il blocking.
L’idea di fondo è che l’apprendimento si realizzi attraverso l’aggiornamento della *forza associativa* $Q_t(s)$ di uno stimolo $s$ al tempo $t$, in funzione della discrepanza tra ciò che ci si aspettava e ciò che è stato effettivamente osservato.
### Aggiornamento delle aspettative
Dopo ogni prova, la stima del valore viene modificata secondo la regola:
$$
Q_{t+1}(s) \;=\; Q_t(s) \;+\; \alpha \, \delta_t ,
$$
dove
$$
\delta_t \;=\; R_t - Q_t(s)
$$
è l’*errore di previsione* (*prediction error*), cioè la differenza tra la ricompensa ottenuta $R_t$ e l’aspettativa precedente $Q_t(s)$.
Quando l'errore di previsione $\delta_t$ assume valori positivi, indica una ricompensa superiore alle attese, determinando così un rafforzamento dell'associazione appresa. Al contrario, un valore negativo di $\delta_t$ segnala una ricompensa inferiore al previsto, con conseguente indebolimento dell'associazione. Nel caso in cui $\delta_t$ sia nullo, l'esito corrisponde esattamente all'aspettativa, e non si verifica quindi alcun aggiornamento delle credenze.
Il parametro $ \alpha \in [0,1] $ rappresenta il tasso di apprendimento (qui lo indichiamo con `lr`). Con `lr` alto l’aggiornamento è rapido; con `lr` basso è lento e più “conservativo”.
::: {.callout-note collapse=true title="Variante (facoltativa): tassi distinti per PE positivo/negativo"}
In alcune applicazioni si usano due tassi distinti $\alpha^+$ e $\alpha^-$ per apprendere diversamente da buone e cattive notizie. Questa distinzione consente di modellare la diversa sensibilità di individui o gruppi alle ricompense inattese rispetto alle punizioni o ai premi. Nel contesto del presente tutorial, al fine di privilegiare la chiarezza espositiva, viene mantenuto un unico parametro `lr` che aggrega entrambe le componenti di apprendimento.
:::
### Dalla valutazione alla decisione
La differenziazione nei valori attesi $Q_t(A)$ e $Q_t(B)$ non determina necessariamente un comportamento puramente deterministico. Gli individui mostrano infatti una caratteristica alternanza tra *sfruttamento* - selezione dell'opzione dal valore atteso più elevato - ed *esplorazione* - campionamento di alternative potenzialmente subottimali.
In uno scenario decisionale binario ($A$ vs. $B$), questa dinamica viene formalizzata attraverso una funzione logistica applicata alla differenza di valore:
$$
P(\text{scegliere B}) = \text{inv\_logit}\!\big(\tau \,[Q_t(B)-Q_t(A)]\big).
$$
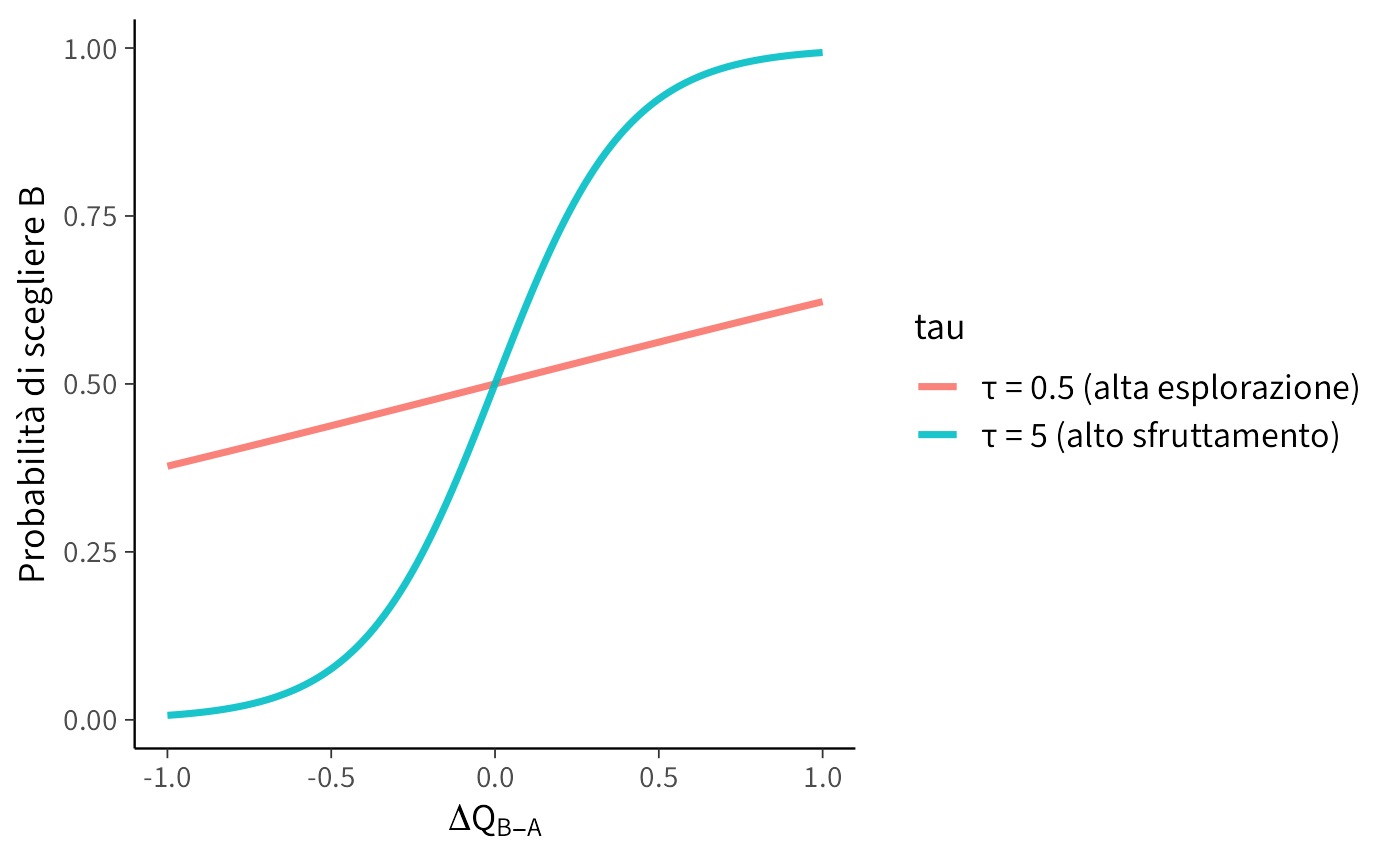
Il parametro $\tau$ (temperatura) regola il bilanciamento tra esplorazione e sfruttamento: valori elevati di $\tau$ producono scelte quasi deterministiche anche in presenza di minime differenze di valore, mentre valori bassi di $\tau$ generano comportamenti più esplorativi e stocastici.
In definitiva, il modello di Rescorla-Wagner fornisce una descrizione formale e compatta di come gli individui imparano in modo flessibile dalle proprie esperienze, adattando aspettative e decisioni in risposta ai cambiamenti dell'ambiente.
::: {.callout-caution collapse=true title="Approfondimento: esplorazione vs. sfruttamento (logit a 2 opzioni)"}
Con due opzioni, la *Softmax* si riduce a una *logistica* sulla differenza di valore. Useremo quindi $\Delta Q = Q_B - Q_A$ e modelleremo la probabilità di scegliere *B* come
$$
P(B) = \text{inv\_logit}\big(\tau \,\Delta Q\big),
$$
dove $\tau>0$ (*inverse temperature*) regola il compromesso esplorazione–sfruttamento:
* *$\tau$ basso* → comportamento *esplorativo*: anche differenze modeste non portano scelte deterministiche.
* *$\tau$ alto* → comportamento di *sfruttamento*: piccole differenze in $\Delta Q$ bastano per preferenze quasi certe.
Nel grafico seguente mostriamo la relazione tra $\Delta Q$ e $P(B)$ per due valori di $\tau$.
```{r}
# Differenze di valore (coerenti con Q in [0,1] → ΔQ in [-1, 1])
dq <- seq(-1, 1, length.out = 201)
# Logit a 2 opzioni (equivalente alla Softmax con K=2)
p_choose_B <- function(dq, tau) plogis(tau * dq)
df <- data.frame(
dq = rep(dq, 2),
prob_B = c(p_choose_B(dq, tau = 0.5),
p_choose_B(dq, tau = 5)),
tau = factor(rep(c("τ = 0.5 (alta esplorazione)",
"τ = 5 (alto sfruttamento)"),
each = length(dq)))
)
ggplot(df, aes(x = dq, y = prob_B, color = tau)) +
geom_line(size = 1.2) +
labs(
x = expression(Delta*Q[B-A]),
y = "Probabilità di scegliere B"
)
```
**Lettura del grafico**
* Se $\Delta Q = 0.5$:
* con $\tau = 0.5$, $P(B) \approx \text{inv\_logit}(0.25) \approx 0.56$ → decisione ancora esplorativa;
* con $\tau = 5$, $P(B) \approx \text{inv\_logit}(2.5) \approx 0.92$ → prevale lo sfruttamento.
* Se $\Delta Q = 1$:
* con $\tau = 0.5$, $P(B) \approx \text{inv\_logit}(0.5) \approx 0.62$;
* con $\tau = 5$, $P(B) \approx \text{inv\_logit}(5) \approx 0.993$, scelta quasi deterministica.
Questo esempio mostra come $\tau$ controlli la transizione tra esplorazione e sfruttamento nel *caso binario* (logit), coerente con il modello Stan usato nel tutorial.
:::
### Identificabilità e scaling
Nella funzione Softmax conta solo la *differenza* tra i valori di $Q$. Se aggiungiamo la stessa costante $c$ a entrambi, le probabilità di scelta rimangono invariate. Per questo motivo, il livello assoluto dei valori $Q$ non è identificabile: solo le differenze relative influenzano le scelte.
Per evitare ambiguità si adottano convenzioni di *scaling*, come inizializzare i valori di $Q$ in modo simmetrico (ad esempio $Q_0(A) = Q_0(B) = 0.5$), mantenere i rinforzi nell'intervallo ${0,1}$ o fissare un valore di riferimento o un vincolo su $\beta$. Queste scelte non modificano il comportamento del modello, ma lo rendono ben definito dal punto di vista matematico.
Nel presente tutorial il rinforzo è codificato come $R_t \in {0,1}$, pertanto i valori $Q$ convergono naturalmente verso stime di probabilità di ricompensa comprese tra 0 e 1. Se invece i rinforzi fossero codificati come ${-1,+1}$, i valori $Q$ si collocherebbero nell’intervallo $[-1,+1]$, e l'interpretazione dovrebbe essere adeguata di conseguenza.
## Simulazione
Simuliamo i dati di un compito di "Probabilistic Reversal Learning" (PRL), in cui il partecipante deve scegliere ripetutamente tra due stimoli. Uno degli stimoli, detto "ricco", fornisce una ricompensa con probabilità $p = 0.7$, mentre l'altro, detto "povero", ha una probabilità di ricompensa di $1 - p = 0.3$.
A metà dell'esperimento, le probabilità si invertono (*reversal*): lo stimolo inizialmente ricco diventa povero e quello povero diventa ricco. Il compito del partecipante è riconoscere questo cambiamento e adattare le proprie scelte per ottenere il maggior numero possibile di ricompense.
```{r}
# Simulatore PRL (RW + logit) allineato al modello Stan (choice in 0/1)
simulate_prl_rw_binary <- function(
n_trials = 160,
p_reward_rich = 0.7,
reversal_trial = 80, # se NULL, nessun reversal
lr = 0.15, # learning rate unico
tau = 2, # inverse temperature (decision noise)
Q0 = c(A = 0.0, B = 0.0),
seed = 1234
){
stopifnot(length(Q0) == 2, all(c("A","B") %in% names(Q0)))
set.seed(seed)
Q <- Q0
choice <- integer(n_trials) # 0 = A, 1 = B
reward <- integer(n_trials) # 0/1
rich_is_A <- rep.int(1L, n_trials) # 1 = A ricco, 0 = B ricco (inizio A ricco)
if (!is.null(reversal_trial)) {
rich_is_A[(reversal_trial + 1):n_trials] <- 0L
}
Q_A <- Q_B <- pB_seq <- pe_seq <- numeric(n_trials)
for (t in seq_len(n_trials)) {
# probabilità di scegliere B (softmax logit a due opzioni)
pB <- plogis(tau * (Q["B"] - Q["A"]))
choice[t] <- rbinom(1, 1, pB) # 1=B, 0=A
a_idx <- if (choice[t] == 1L) 2L else 1L
# probabilità di ricompensa per l’opzione scelta
chosen_is_rich <- (choice[t] == 0L && rich_is_A[t] == 1L) ||
(choice[t] == 1L && rich_is_A[t] == 0L)
pr <- if (chosen_is_rich) p_reward_rich else (1 - p_reward_rich)
reward[t] <- rbinom(1, 1, pr)
# prediction error e aggiornamento RW
pe <- reward[t] - Q[a_idx]
Q[a_idx] <- Q[a_idx] + lr * pe
Q_A[t] <- Q["A"]
Q_B[t] <- Q["B"]
pB_seq[t] <- pB
pe_seq[t] <- pe
}
tibble::tibble(
trial = seq_len(n_trials),
choice = choice, # 0=A, 1=B
reward = reward, # 0/1
rich_is_A = rich_is_A, # 0/1
Q_A = Q_A, Q_B = Q_B, pB = pB_seq, pe = pe_seq
)
}
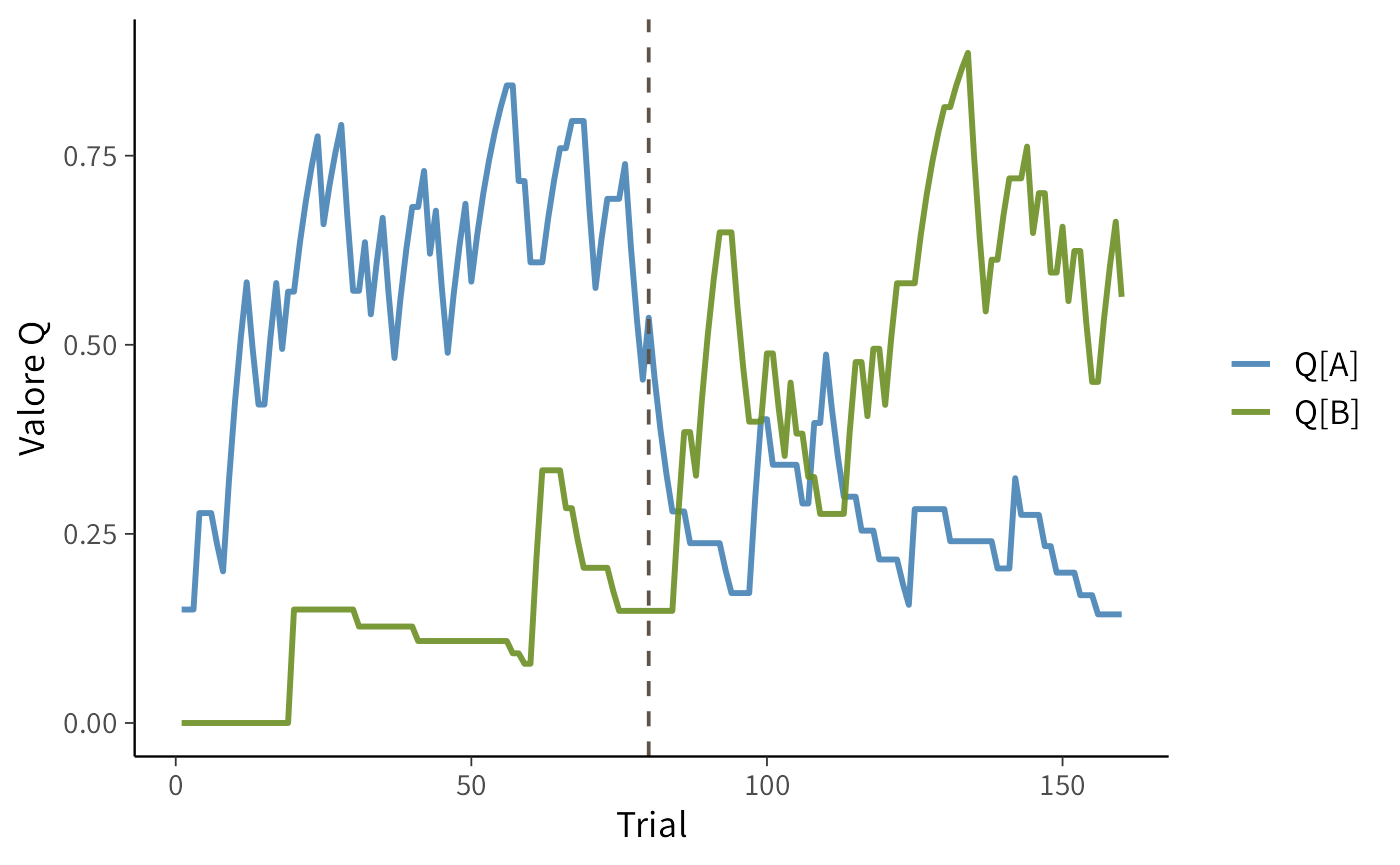
sim <- simulate_prl_rw_binary()
```
Visualizziamo l’evoluzione dei valori associativi $Q$:
```{r echo=FALSE}
sim_long <- sim |>
select(trial, Q_A, Q_B) |>
pivot_longer(
cols = c(Q_A, Q_B),
names_to = "stimolo",
values_to = "Q"
)
ggplot(sim_long, aes(x = trial, y = Q, color = stimolo)) +
geom_line(linewidth = 1) +
geom_vline(xintercept = 80, linetype = 2, color = "#5d5349") +
scale_color_manual(
values = c(Q_A = "#4682B4", Q_B = "#6B8E23"),
labels = c(Q_A = "Q[A]", Q_B = "Q[B]")
) +
labs(
x = "Trial", y = "Valore Q",
color = NULL
) +
theme(plot.title = element_text(hjust = 0.5))
```
### Interpretazione del grafico
Nella prima parte dell'esperimento (trial 1-80), lo stimolo "ricco", rappresentato dalla linea blu, riceve ricompense più frequenti e accumula progressivamente un valore $Q$ più alto rispetto allo stimolo "povero", rappresentato dalla linea verde.
Quando si verifica il *reversal* (linea verticale tratteggiata), le probabilità di rinforzo si invertono: lo stimolo blu smette di essere vantaggioso e il suo valore $Q$ diminuisce, mentre quello verde aumenta man mano che diventa la scelta più remunerativa.
Questo andamento illustra il principio fondamentale del modello di Rescorla–Wagner, secondo cui i valori associativi $Q$ vengono aggiornati prova per prova in base all’errore di previsione (*prediction error*, PE):
$$
Q_{\text{nuovo}} = Q_{\text{vecchio}} + lr \times (reward - Q_{\text{vecchio}}).
$$
Il termine $(reward - Q_{\text{vecchio}})$ rappresenta la differenza tra il risultato ottenuto e quello atteso.
Quando il feedback è migliore del previsto (PE > 0), il valore $Q$ aumenta; quando è peggiore (PE < 0), diminuisce. L'entità dell'aggiornamento dipende dal parametro di apprendimento "learning rate" (`lr`): un valore alto porta a un adattamento rapido ma instabile, mentre un valore basso produce aggiustamenti graduali e stabili.
Il parametro `tau` controlla invece la sensibilità delle scelte alle differenze tra i valori $Q$. Con un valore di tau grande, le scelte diventano più deterministiche (si tende a preferire quasi sempre lo stimolo con il valore più alto), mentre con un valore di `tau` piccolo, prevale un comportamento più esplorativo o rumoroso.
## Stima bayesiana con Stan
Nella simulazione conoscevamo i parametri generativi (`lr = 0.15`, `tau = 2`). Nella pratica, invece, disponiamo soltanto dei *dati osservati*: per ogni trial sappiamo quale scelta è stata effettuata (`choice = 0` per A, `choice = 1` per B) e se il feedback ricevuto è stato positivo o negativo (`reward = 1` oppure `0`).
I valori interni del modello — i $Q$ associati agli stimoli e i parametri che li governano — non sono direttamente osservabili: devono essere *inferiti* a partire dal comportamento.
L’ipotesi di base è che le scelte derivino da un processo di tipo *Rescorla–Wagner* combinato con una regola di scelta logistica (*softmax*). L’obiettivo dell’analisi è stimare, usando i soli dati comportamentali, due parametri fondamentali:
* il *learning rate* `lr`, che determina la rapidità con cui i valori $Q$ si aggiornano dopo ciascun feedback;
* l’*inverse temperature* `tau`, che quantifica quanto le scelte seguono i valori $Q$ in modo coerente (valori alti implicano scelte più deterministiche, valori bassi scelte più esplorative).
### Codice Stan
```{r}
stancode_rw <- "
data {
int<lower=1> nTrials; // numero di prove
array[nTrials] int<lower=0,upper=1> choice; // scelte osservate (0=A, 1=B)
array[nTrials] real<lower=0,upper=1> reward; // ricompense osservate (0/1)
}
transformed data {
vector[2] initV = rep_vector(0.0, 2); // valori Q iniziali
}
parameters {
real<lower=0,upper=1> lr; // learning rate
real<lower=0,upper=3> tau; // inverse temperature (softmax / decision noise)
}
model {
vector[2] v = initV; // valori Q correnti
real pe; // prediction error
real p; // probabilità di scelta =1 (stimolo B)
// Priors deboli ma informative
lr ~ beta(2, 10); // learning rate vicino a valori piccoli
tau ~ lognormal(log(2), 0.5); // inverse temperature positiva
for (t in 1:nTrials) {
// Probabilità di scegliere B: logit della differenza Q_B - Q_A
p = inv_logit(tau * (v[2] - v[1]));
choice[t] ~ bernoulli(p);
// Prediction error e aggiornamento
int a = choice[t] + 1; // 0→1 (A), 1→2 (B)
pe = reward[t] - v[a];
v[a] += lr * pe;
}
}
"
```
I prior scelti sono debolmente informativi ma coerenti con compiti PRL tipici (apprendimento moderato e scelte non eccessivamente rumorose). Possono essere resi più o meno conservativi in base al compito.
### Commento al codice Stan
All’inizio dell’esecuzione, i due valori $Q[1]$ e $Q[2]$ (associati agli stimoli A e B) sono fissati a zero: rappresentano l’aspettativa iniziale del partecipante, cioè una condizione di indifferenza tra le due opzioni.
Al trial $t$, il modello calcola la probabilità di scegliere B confrontando i due valori di $Q$:
$$
p(B) = \text{inv\_logit}\big(\tau \cdot (Q_B - Q_A)\big).
$$
Quando $Q_B$ supera $Q_A$, la probabilità di scegliere B aumenta. Il parametro `tau` controlla quanto questa differenza incide sulle scelte: con valori elevati, anche piccole differenze tra i due Q portano a decisioni quasi certe; con valori bassi, le scelte restano più esplorative e meno determinate.
La riga `choice[t] ~ bernoulli(p)` specifica la *verosimiglianza*: confronta la scelta osservata con la probabilità prevista dal modello. Se la scelta è coerente con le aspettative derivanti dai $Q$, la probabilità (e quindi il “credito” del modello) aumenta; se è incoerente, diminuisce.
Dopo la scelta, si osserva il feedback e si calcola l'errore di previsione (*prediction error*, PE):
$$
PE = reward[t] - Q[\text{scelta}],
$$
ovvero, la differenza tra il risultato ottenuto e quello atteso.
Infine, solo il valore $Q$ corrispondente all’opzione scelta viene aggiornato secondo la regola di apprendimento di Rescorla–Wagner:
$$
Q_{\text{nuovo}} = Q_{\text{vecchio}} + lr \cdot PE.
$$
Se il feedback è migliore del previsto (PE > 0), il valore aumenta; se è peggiore (PE < 0), diminuisce. L’entità dell’aggiornamento dipende dal *learning rate* `lr`: un valore alto produce cambiamenti rapidi, uno basso genera un apprendimento più graduale.
::: {.callout-note collapse=true title="Esempio intuitivo"}
Supponiamo che in un certo momento i valori stimati siano $Q_A = 0.6$ e $Q_B = 0.3$, con `tau = 2`. La differenza tra i due è $Q_B - Q_A = -0.3$, quindi l’argomento della funzione logit è $-0.6$. Ne consegue:
$$
p(B) = \text{inv_logit}(-0.6) \approx 0.35.
$$
Il modello prevede dunque che il partecipante scelga lo stimolo $A$ con una probabilità di circa il 65%.
Se il partecipante sceglie effettivamente $A$, l’osservazione è coerente con le aspettative del modello e la verosimiglianza risulta elevata. Se invece sceglie $B$, l’evento è meno probabile ma comunque possibile: in tal caso, dopo aver osservato il feedback, il modello aggiorna i valori interni $Q$ per ridurre la discrepanza tra previsione e risultato.
:::
In questo tutorial useremo i dati simulati in precedenza:
```{r}
stan_data <- list(
nTrials = nrow(sim),
choice = as.integer(sim$choice),
reward = as.numeric(sim$reward) # 0/1 come real per coerenza con <lower=0,upper=1>
)
glimpse(stan_data)
```
Compiliamo il modello e eseguiamo il campionamento:
```{r}
#| output: false
mod_rw <- cmdstanr::cmdstan_model(write_stan_file(stancode_rw))
fit_rw <- mod_rw$sample(
data = stan_data,
seed = 42,
chains = 4,
parallel_chains = 4,
iter_warmup = 1000,
iter_sampling = 4000,
refresh = 200
)
```
Calcoliamo le diagnostiche di campionamento:
```{r}
fit_rw$cmdstan_diagnose() # controlli rapidi cmdstan
```
Esaminiamo la distribuzione a posteriori dei parametri:
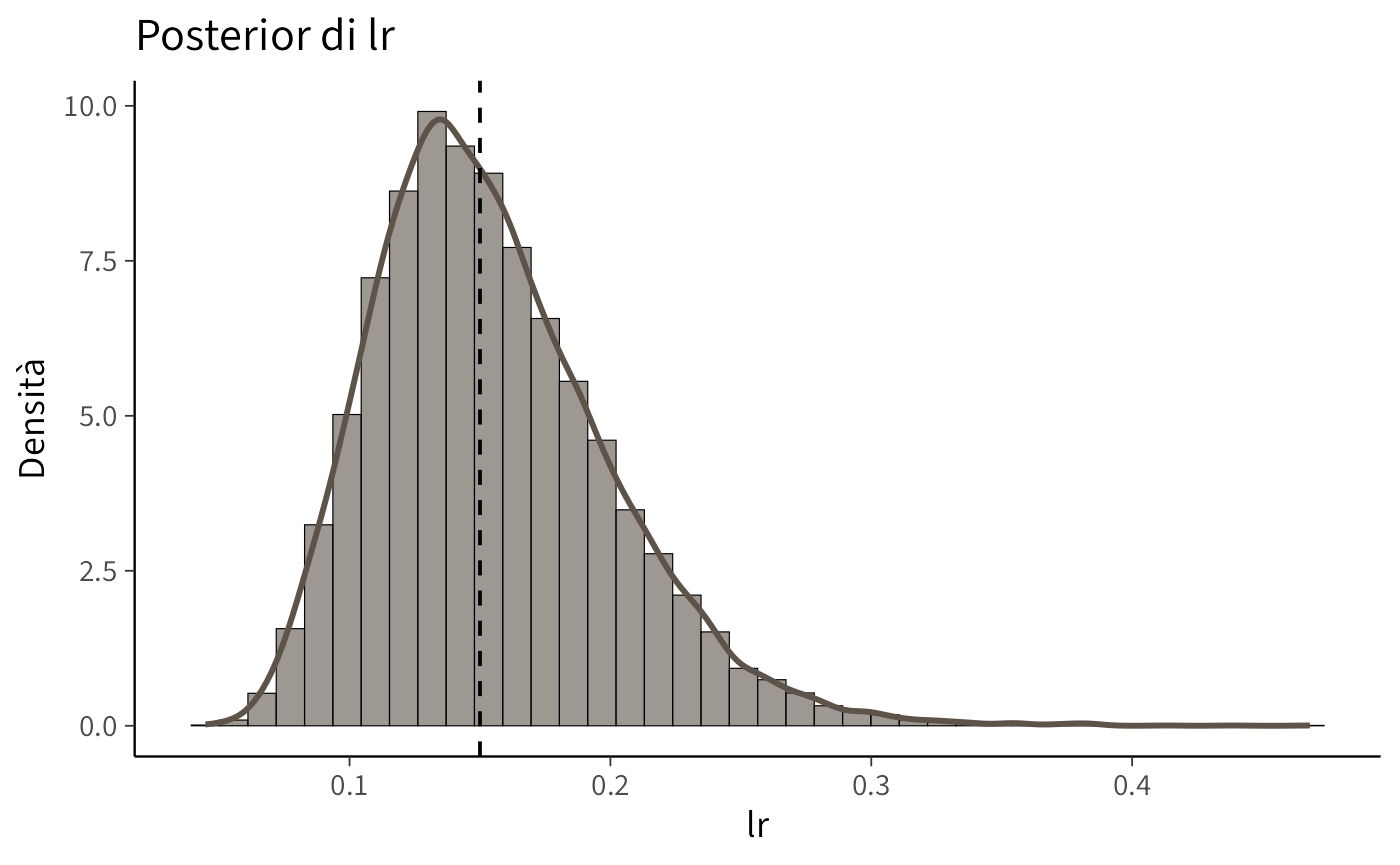
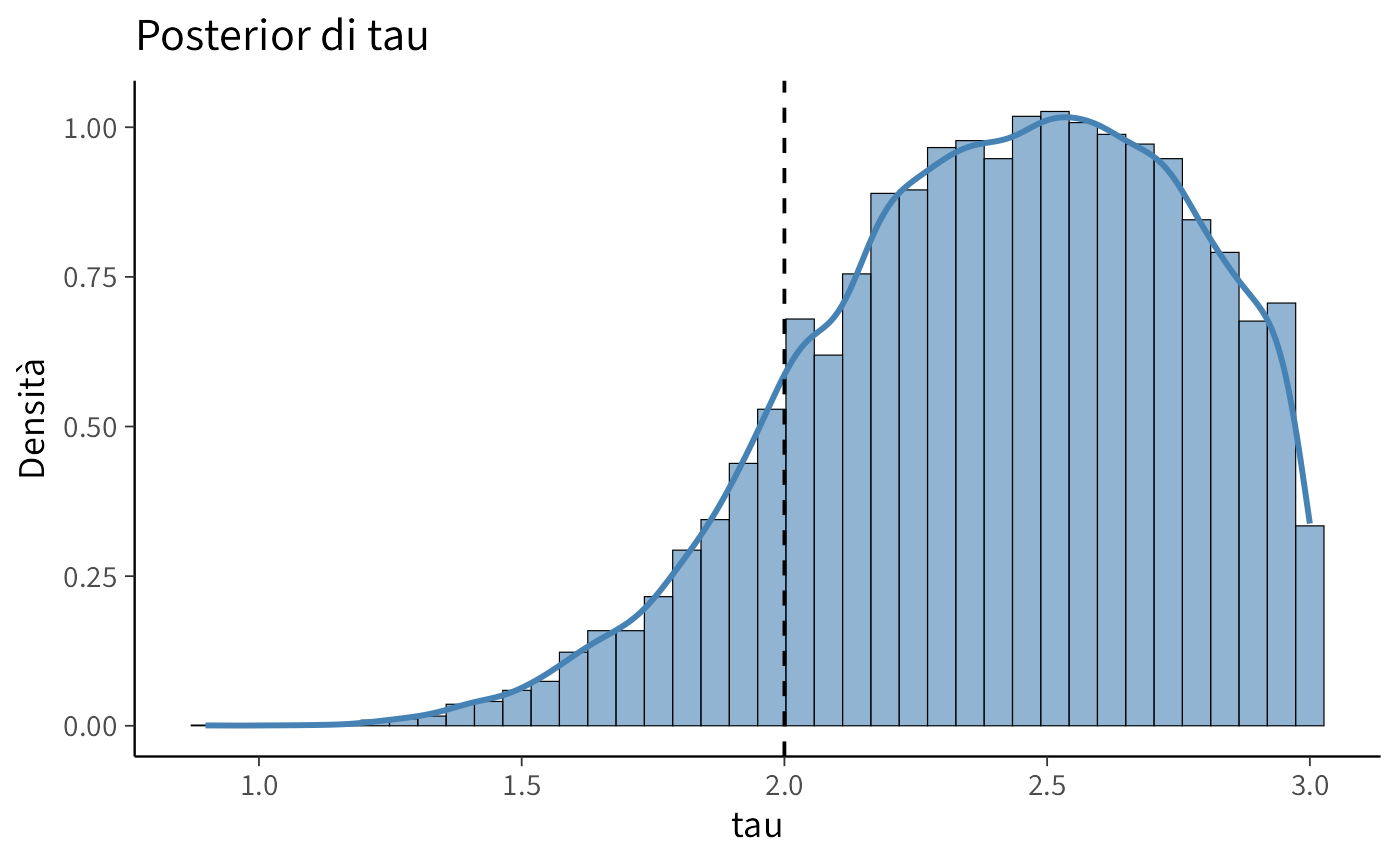
```{r}
fit_rw$summary(c("lr","tau"))
```
## Interpretazione dei risultati
Le distribuzioni a posteriori mostrano quanto bene il modello è riuscito a recuperare i parametri generativi utilizzati nella simulazione (`lr = 0.15`, `tau = 2`).
Il parametro `lr` (*learning rate*) determina la velocità con cui il soggetto aggiorna le proprie aspettative dopo ogni feedback. Valori elevati indicano un apprendimento rapido: anche un singolo esito può modificare sensibilmente la stima del valore di uno stimolo. Valori bassi, invece, producono un apprendimento più lento e conservativo: le esperienze passate continuano a influenzare a lungo le scelte, rendendo l’adattamento ai cambiamenti più graduale.
Il parametro `tau` (*inverse temperature*) controlla invece quanto le scelte seguono in modo coerente i valori stimati $Q$. Con un valore alto di `tau`, il comportamento è quasi deterministico: basta una piccola differenza tra $Q_A$ e $Q_B$ per generare una preferenza netta. Con un valore basso di `tau`, le scelte appaiono più esplorative o rumorose: anche stimoli con un valore inferiore vengono scelti occasionalmente.
```{r}
draws_df <- fit_rw$draws(c("lr","tau")) |>
as_draws_df() |>
tibble::as_tibble()
cols <- c(lr = "#5d5349", tau = "#4682B4")
plot_post <- function(draws, param, col) {
ggplot(draws, aes(x = .data[[param]])) +
geom_histogram(aes(y = after_stat(density)), bins = 40,
fill = col, color = "black", alpha = 0.6) +
geom_density(color = col, linewidth = 1) +
labs(x = param, y = "Densità", title = paste("Posterior di", param))
}
p_lr <- plot_post(draws_df, "lr", cols["lr"])
p_tau <- plot_post(draws_df, "tau", cols["tau"])
```
```{r}
true_vals <- c(lr = 0.15, tau = 2)
p_lr + geom_vline(xintercept = true_vals["lr"], linetype = 2)
p_tau + geom_vline(xintercept = true_vals["tau"], linetype = 2)
```
Nei grafici delle distribuzioni posteriori, le linee tratteggiate rappresentano i valori reali utilizzati nella simulazione, mentre le distribuzioni colorate riflettono l'incertezza del modello riguardo alle possibili stime dei parametri. Quando una distribuzione è centrata sulla linea tratteggiata e risulta concentrata, significa che il modello ha recuperato il parametro in modo accurato. Distribuzioni più ampie o spostate indicano invece una maggiore incertezza o relazioni di compensazione tra i parametri: ad esempio, un `lr` leggermente diverso può essere controbilanciato da un `tau` più alto o più basso, producendo previsioni simili.
Questo fenomeno di *trade-off* è comune nei dataset brevi o con bassa variabilità nelle scelte, in cui più combinazioni di parametri possono descrivere in modo equivalente i dati osservati. È quindi importante verificare la qualità del campionamento (ad esempio, tramite le statistiche R-hat e ESS) e valutare l'adattamento del modello con analisi predittive posteriori (*posterior predictive checks*).
## Dal parametro allo stile cognitivo
I parametri del modello non rappresentano solo grandezze numeriche, ma descrivono diverse modalità di apprendimento e di presa di decisioni.
Il learning rate (`lr`) riflette la rapidità con cui una persona aggiorna le proprie aspettative in base ai risultati ricevuti. Un individuo con un valore di learning rate alto è molto sensibile ai singoli feedback: reagisce prontamente agli esiti e può adattarsi rapidamente a un cambiamento delle contingenze (*reversal*). Per esempio, bastano pochi esiti negativi perché abbandoni lo stimolo che in precedenza sembrava più vantaggioso. Al contrario, un valore basso di `lr` indica un apprendimento più cauto e conservativo: l'individuo integra lentamente le nuove informazioni e tende a mantenere le proprie scelte abituali anche di fronte a segnali contrari, modificando il proprio comportamento solo dopo un'evidenza più consistente.
L'*inverse temperature* (`tau`) descrive invece quanto le scelte siano coerenti con i valori stimati $Q$. Con un valore di `tau` alto, il comportamento diventa quasi deterministico: lo stimolo con il valore più alto viene scelto quasi sempre. Questo profilo corrisponde a uno stile orientato allo sfruttamento, volto a massimizzare subito i guadagni. Con un valore di `tau` basso, invece, le scelte appaiono più esplorative o rumorose: anche quando una delle due opzioni è chiaramente migliore, il soggetto talvolta opta per l'altra. Questo stile, apparentemente "incoerente", può però rivelarsi vantaggioso in ambienti incerti o mutevoli, in quanto favorisce l'esplorazione di alternative potenzialmente più redditizie.
### Messaggio chiave
L’approccio bayesiano consente di stimare, per ciascun individuo, un profilo che integra due dimensioni fondamentali: *apprendimento*, cioè la velocità con cui aggiorna le proprie aspettative, e *decisione*, ovvero quanto coerentemente agisce in base a tali aspettative.
Differenze sistematiche nei parametri tra gruppi sperimentali (ad esempio, tra stimoli emotivi e stimoli neutri) o tra popolazioni cliniche e di controllo possono rivelare *stili cognitivi distinti*. Un *learning rate* basso (`lr`) può indicare difficoltà nell’adattarsi a nuovi feedback, mentre valori estremi di *inverse temperature* (`tau`) possono riflettere scelte eccessivamente rigide o, al contrario, troppo esplorative.
In questa prospettiva, anche un modello computazionale essenziale come quello di *Rescorla–Wagner* con regola di scelta logistica non si limita a descrivere il comportamento osservato, ma offre una *chiave di lettura psicologica* per comprendere i meccanismi cognitivi che lo generano.
## Contextual bandits
Nel modello di *Rescorla–Wagner* con regola logistica, come visto nel tutorial, i parametri principali, ovvero il learning rate (`lr`), che regola la velocità con cui i valori $Q$ vengono aggiornati, e l’inverse temperature (`tau`), che governa la coerenza delle scelte rispetto a tali valori, sono assunti come stabili per tutto il compito.
La famiglia dei *banditi contestuali* (*contextual bandits*) estende questo schema introducendo la possibilità che i parametri varino in funzione del *contesto sperimentale*. Lo stesso meccanismo di apprendimento e decisione (RW + logit) viene quindi applicato separatamente a condizioni diverse, come nel caso di stimoli *food* e *neutral* in un campione di pazienti con anoressia, oppure a gruppi differenti, come pazienti clinici e controlli.
Questa estensione si è rivelata particolarmente utile nello studio dei disturbi alimentari. Analisi recenti hanno mostrato che i *deficit di apprendimento in anoressia nervosa non sono generalizzati*, ma *specifici del contesto alimentare*: nelle prove con stimoli legati al cibo, le persone con anoressia tendono a mostrare un *learning rate* più basso, cioè aggiornano più lentamente le proprie aspettative; negli stessi compiti con stimoli neutri, invece, i parametri risultano simili a quelli dei controlli [@colpizzi2025food].
Questi risultati indicano che la vulnerabilità non riguarda un deficit globale nei meccanismi di apprendimento, ma un'alterazione selettiva e dipendente dal contesto che contribuisce al mantenimento del disturbo.
Formalmente, per ciascun contesto $c \in {\text{food}, \text{neutral}}$, il modello è espresso come:
$$
P_c(B_t)=\text{inv\_logit}!\big(\tau_c [Q_{c,t}(B)-Q_{c,t}(A)]\big),
$$
$$
Q_{c,t+1}(s)=Q_{c,t}(s)+lr_c ,[R_{c,t}-Q_{c,t}(s)].
$$
Il confronto tra $lr_{\text{food}}$ e $lr_{\text{neutral}}$ (e, analogamente, tra $\tau_{\text{food}}$ e $\tau_{\text{neutral}}$) consente di quantificare con precisione le differenze legate al contesto.
## Riflessioni conclusive {.unlisted .unnumbered}
Il modello di Rescorla-Wagner con regola logistica separa chiaramente l'apprendimento dalla decisione: il parametro `lr` governa la velocità con cui le aspettative si aggiornano in base all'errore di previsione, mentre il parametro `tau` controlla quanto le scelte seguono in modo coerente i valori appresi. Questa distinzione permette di spiegare lo stesso comportamento con meccanismi diversi (apprendimento rapido ma scelte esplorative, oppure apprendimento lento ma scelte deterministiche), evitando letture unidimensionali della "prestazione".
La scomposizione fornisce anche informazioni utili dal punto di vista clinico. Nel caso dell'anoressia nervosa, ad esempio, i deficit non sono globali, ma dipendono dal contesto: di fronte a stimoli "food" si osserva un `lr` ridotto, mentre con stimoli "neutral" i parametri sono allineati ai controlli [@colpizzi2025food]. In altre parole, il problema non è quanto si impara in generale, ma da cosa e quando le scelte sfruttano ciò che si è appreso.
Operativamente, il modello RW permette di: (i) quantificare le differenze nei meccanismi di apprendimento (`lr`) tra condizioni o gruppi; (ii) valutare le eventuali variazioni nello stile decisionale (`tau`); (iii) collegare queste differenze a ipotesi psicologiche e cliniche mirate (es. sensibilità al feedback, equilibrio esplorazione-sfruttamento). L'inferenza bayesiana rende questi confronti espliciti e trasferibili da uno studio all'altro, tramite stime a posteriori, incertezze e *posterior predictive checks*.
In sintesi, il modello RW non si limita a descrivere matematicamente le curve di apprendimento, ma propone una *teoria verificabile* sui processi cognitivi che le generano. Esso funge da ponte esplicativo tra il comportamento osservato e i meccanismi mentali ipotizzati, consentendo di individuare alterazioni contestuali specifiche. Questa formalizzazione è ciò che trasforma un pattern comportamentale in un'ipotesi precisa e falsificabile su *come* si apprende e *come* si decide, gettando le basi per interventi che distinguono sistematicamente tra le due componenti.
::: {.callout-note collapse=true title="Informazioni sull'ambiente di sviluppo"}
```{r}
sessionInfo()
```
:::
## Bibliografia {.unnumbered .unlisted}
