here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(ggdist)Appendice K — Modello coniugato Gamma-Poisson
Introduzione
Nei capitoli principali abbiamo introdotto l’idea di distribuzioni coniugate con il caso Beta–Binomiale, un laboratorio ideale per capire la logica dell’aggiornamento bayesiano in situazioni semplici. In questa appendice presentiamo un esempio parallelo: il modello Gamma–Poisson, particolarmente adatto per dati di conteggio, cioè quando osserviamo il numero di volte in cui si verifica un certo evento.
La struttura è analoga: la verosimiglianza è data dalla distribuzione di Poisson e la prior coniugata è una distribuzione Gamma. Grazie alla proprietà di coniugazione, il posterior risulta anch’esso una Gamma, ottenuta semplicemente aggiornando i parametri iniziali con i dati osservati. Questo ci permette di seguire passo passo la stessa logica vista nel caso binomiale: le assunzioni iniziali e l’evidenza empirica si combinano in modo trasparente, modificando i parametri della distribuzione senza alterarne la forma.
Lo scopo di questa appendice non è introdurre nuovo materiale concettuale, ma rafforzare l’intuizione su come funziona la coniugazione in un contesto diverso. Chi desidera un primo contatto pratico con i modelli per dati di conteggio troverà qui un esempio utile; chi preferisce concentrarsi sul flusso principale del manuale può considerare questa sezione come un approfondimento facoltativo.
Panoramica del capitolo
- Comprendere la distribuzione di Poisson come un modello probabilistico adatto per descrivere eventi rari in un intervallo di tempo o spazio fisso.
- Sapere applicare il metodo basato su griglia per derivare la distribuzione a posteriori del parametro \(\lambda\) della distribuzione di Poisson.
- Conoscere il modello coniugato Gamma-Poisson, dimostrando come la distribuzione a priori Gamma si combini con la verosimiglianza di Poisson per produrre una distribuzione a posteriori Gamma.
- Sapere come calcolare e interpretare le probabilità utilizzando la distribuzione a posteriori.
K.1 Distribuzione di Poisson
La distribuzione di Poisson descrive fenomeni di conteggio, ovvero situazioni in cui si desidera conoscere il numero di volte in cui un certo evento si verifica in un intervallo di tempo o di spazio prestabilito. L’idea di fondo è semplice: immaginiamo che gli eventi si verifichino con una frequenza media costante e che ogni evento avvenga in modo indipendente dagli altri.
Se una variabile casuale \(Y\) segue una distribuzione di Poisson con parametro \(\lambda\), la probabilità di osservare un certo numero \(y_i\) di eventi è data da:
\[ f(y_i \mid \lambda) = \frac{e^{-\lambda} \lambda^{y_i}}{y_i!}, \quad y_i \in \{0,1,2,\dots\},\ \lambda > 0, \] dove il parametro \(\lambda\) rappresenta il tasso medio di occorrenza degli eventi.
Una caratteristica importante della distribuzione di Poisson è che la sua media e la sua varianza coincidono:
\[ E(Y) = \lambda, \qquad \text{Var}(Y) = \lambda. \] Ciò significa che, se in media si osservano 2 eventi per intervallo, anche la varianza attesa di questo valore sarà pari a 2.
K.1.1 Un esempio psicologico
Per rendere l’idea più concreta, immaginiamo un paziente affetto da disturbo ossessivo-compulsivo. Supponiamo che, in media, compia due azioni compulsive all’ora. In questo caso, il parametro della distribuzione di Poisson è \(\lambda = 2\).
La formula ci permette di calcolare la probabilità di osservare esattamente k eventi in un’ora. Ad esempio:
- la probabilità di osservare 0 eventi è \(\frac{e^{-2} \cdot 2^0}{0!} = e^{-2} \approx 0.1353\);
- la probabilità di osservare 1 evento è \(\frac{e^{-2} \cdot 2^1}{1!} = 2e^{-2} \approx 0.2707\);
- la probabilità di osservare 2 eventi è \(\frac{e^{-2} \cdot 2^2}{2!} = 2e^{-2} \approx 0.2707\).
K.1.2 Calcoli in R
Possiamo svolgere questi calcoli direttamente con R, utilizzando la funzione dpois:
lam_true <- 2
k_values <- 0:9
probabilities <- dpois(k_values, lambda = lam_true)
for (i in seq_along(k_values)) {
cat(sprintf("Probabilità di %d eventi: %.4f\n", k_values[i], probabilities[i]))
}
#> Probabilità di 0 eventi: 0.1353
#> Probabilità di 1 eventi: 0.2707
#> Probabilità di 2 eventi: 0.2707
#> Probabilità di 3 eventi: 0.1804
#> Probabilità di 4 eventi: 0.0902
#> Probabilità di 5 eventi: 0.0361
#> Probabilità di 6 eventi: 0.0120
#> Probabilità di 7 eventi: 0.0034
#> Probabilità di 8 eventi: 0.0009
#> Probabilità di 9 eventi: 0.0002Questo codice calcola la probabilità di osservare tra 0 e 9 eventi in un’ora, dato che il tasso medio è 2. Si noti che i valori più probabili sono 1 o 2 eventi all’ora, mentre la probabilità di osservare molti più eventi diminuisce rapidamente.
K.1.3 Visualizzazione grafica
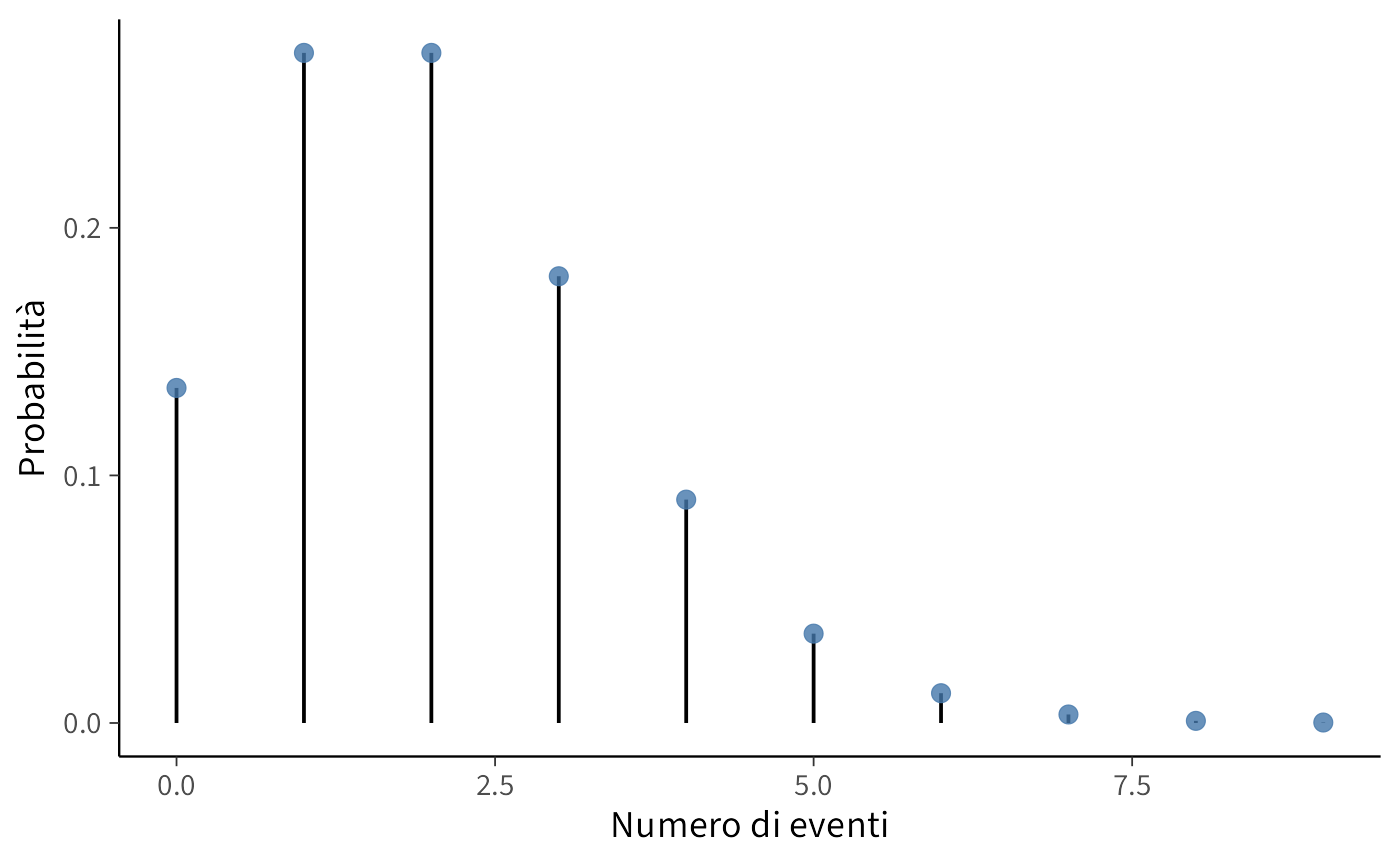
Un modo ancora più intuitivo per comprendere la distribuzione di Poisson è osservare il suo grafico. Il seguente codice permette di rappresentare la funzione di massa di probabilità (PMF) per \(\lambda = 2\):
lambd <- 2
x <- 0:9
y <- dpois(x, lambda = lambd)
df <- data.frame(
numero_eventi = x,
probabilita = y
)
ggplot(df, aes(x = numero_eventi, y = probabilita)) +
geom_segment(aes(x = numero_eventi, xend = numero_eventi, y = 0, yend = probabilita)) +
geom_point(size = 3) +
labs(x = "Numero di eventi",
y = "Probabilità") +
theme(plot.title = element_text(hjust = 0.5))
Il grafico mostra chiaramente che i valori centrati attorno a 2 hanno una probabilità maggiore, mentre la probabilità diminuisce rapidamente per valori più alti.
K.2 Distribuzione Gamma
Per costruire un modello bayesiano con dati di tipo Poisson, è necessario scegliere una distribuzione a priori per il parametro di tasso \(\lambda\). La scelta più comune, nonché la più conveniente dal punto di vista matematico, è la distribuzione Gamma. Questa distribuzione, infatti, è coniugata alla Poisson, il che significa che, partendo da una distribuzione a priori Gamma e aggiornandola con dati che seguono una distribuzione di Poisson, la distribuzione a posteriori appartiene ancora alla famiglia delle Gamma. In pratica, la coniugatezza ci permette di aggiornare le nostre credenze in modo semplice e diretto, senza dover affrontare calcoli complicati.
La densità della distribuzione Gamma è definita dalla formula:
\[ f(x \mid \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\beta x}, \quad x > 0. \] In questa formula compaiono due parametri fondamentali:
- \(\alpha\) (forma): controlla la forma della distribuzione. Con valori piccoli, la distribuzione è molto asimmetrica e concentrata vicino allo zero; aumentando il valore di \(\alpha\), la distribuzione diventa più regolare e tende a assumere una forma simile a quella di una distribuzione normale.
- \(\beta\) (tasso o “rate”): regola la scala della distribuzione. Con valori alti, la probabilità si concentra su valori più piccoli di \(x\); con valori bassi, invece, la distribuzione si allarga e assegna probabilità a valori più grandi.
Alcuni esempi aiutano a chiarire:
- con \(\alpha = 2\) e \(\beta = 3\), la distribuzione descrive un processo in cui gli eventi sono relativamente rari, ma non impossibili;
- con \(\alpha = 10\) e \(\beta = 1\), invece, la distribuzione è molto più concentrata e simmetrica, a indicare un processo più regolare e prevedibile.
In R possiamo calcolare la densità della distribuzione Gamma con la funzione dgamma:
dgamma(x, shape = alpha, rate = beta)Ad esempio, per una Gamma con \(\alpha = 2\) e \(\beta = 3\) possiamo scrivere:
alpha <- 2
beta <- 3
ggplot(data.frame(x = c(0, 3)), aes(x = x)) +
stat_function(
fun = dgamma,
args = list(shape = alpha, rate = beta)
) +
labs(
x = "x",
y = "Densità di probabilità"
) +
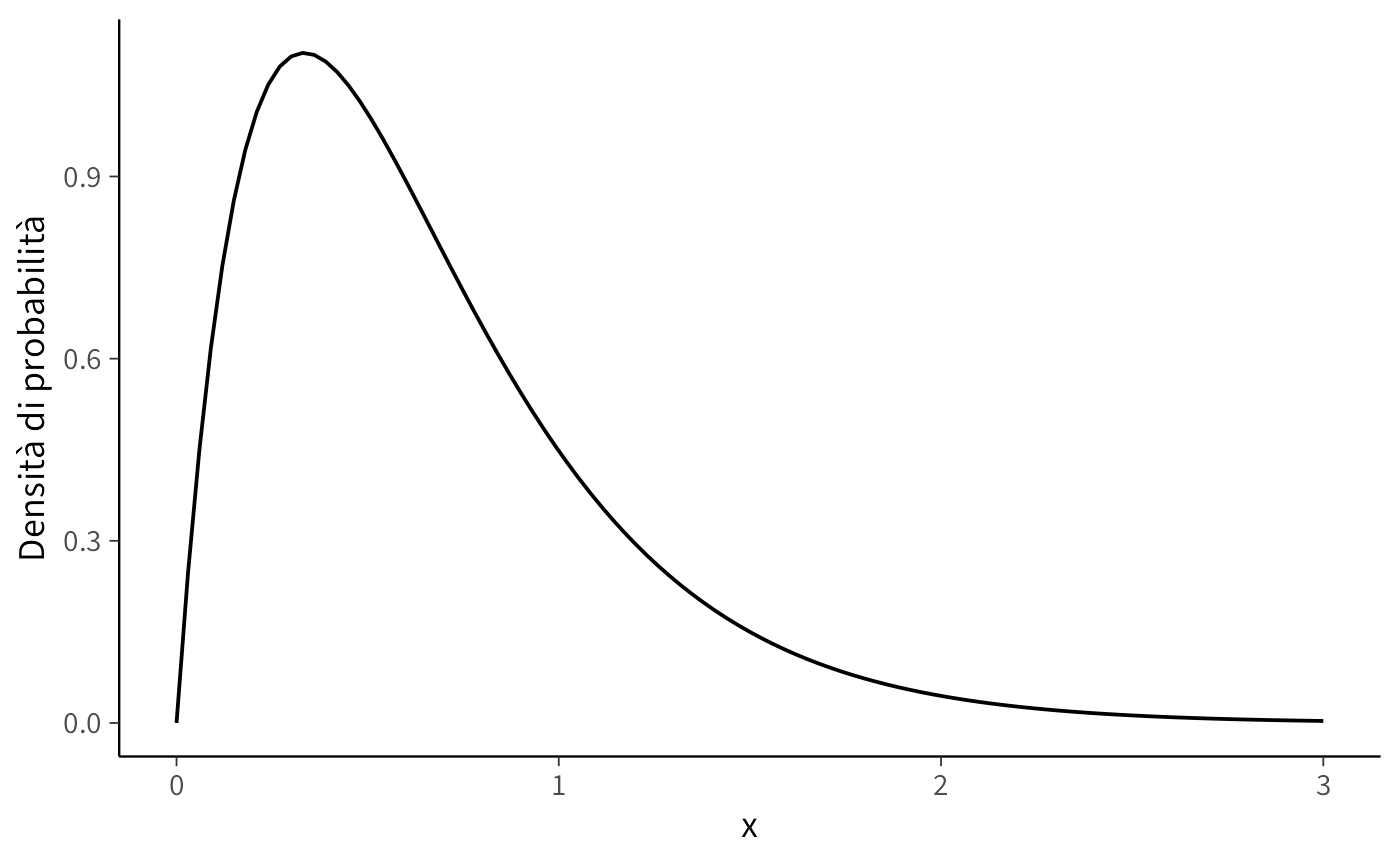
theme(plot.title = element_text(hjust = 0.5))
Il grafico mostra come la distribuzione si concentri intorno ai valori piccoli di x, ma lasci comunque una coda lunga verso destra. È proprio questa flessibilità a rendere la distribuzione gamma molto utile come modello a priori: può descrivere sia situazioni in cui ci si aspetta valori piccoli ma incerti, sia casi in cui si prevedono valori medi o alti con maggiore regolarità.
K.3 La coppia coniugata Gamma–Poisson
Abbiamo esaminato separatamente due elementi: la distribuzione di Poisson, che descrive il numero di eventi osservati, e la distribuzione Gamma, che abbiamo scelto come distribuzione a priori per il parametro di tasso \(\lambda\). Ora possiamo unirli per costruire un modello bayesiano completo.
Il cuore del ragionamento è il seguente:
- i dati osservati (\(y_1, y_2, ..., y_N\)) sono modellati come una distribuzione di Poisson con parametro \(\lambda\);
- la nostra conoscenza a priori su \(\lambda\) è rappresentata da una distribuzione Gamma con parametri \(\alpha_{\text{prior}}\) e \(\beta_{\text{prior}}\).
Questa combinazione è molto conveniente, perché la Gamma è coniugata alla Poisson. Ma cosa significa, concretamente, “coniugata”? Significa che, dopo aver osservato i dati, la distribuzione a posteriori di \(\lambda\) rimane della stessa famiglia della distribuzione a priori, ovvero una distribuzione Gamma. In altre parole, se si parte da una distribuzione Gamma e la si aggiorna con dati di tipo Poisson, si ottiene ancora una distribuzione Gamma, ma i valori dei parametri cambiano, incorporando l’informazione proveniente dai dati.
K.3.1 La distribuzione a posteriori
La regola di Bayes ci dice che:
\[ p(\lambda \mid y) \propto p(\lambda) \cdot p(y \mid \lambda). \] Sostituendo le due distribuzioni (Gamma per la prioritaria e Poisson per la verosimiglianza), si ottiene ancora una distribuzione Gamma. I parametri aggiornati sono:
\[ \alpha_{\text{post}} = \alpha_{\text{prior}} + \sum_{i=1}^N y_i , \]
\[ \beta_{\text{post}} = \beta_{\text{prior}} + N . \] Dunque, la nostra credenza su \(\lambda\) dopo aver osservato i dati è rappresentata da una distribuzione:
\[ \lambda \mid y \sim \text{Gamma}(\alpha_{\text{post}}, \beta_{\text{post}}) \]
K.3.2 Intuizione
Il meccanismo di aggiornamento bayesiano ammette un’interpretazione particolarmente intuitiva nel caso della distribuzione di Poisson. I parametri della distribuzione a posteriori, \(\alpha_{\text{post}}\) e \(\beta_{\text{post}}\), si ottengono semplicemente aggiornando quelli a priori, ovvero \(\alpha_0\) e \(\beta_0\), con le informazioni contenute nei dati.
il parametro di forma, \(\alpha_{\text{post}} = \alpha_0 + \sum_{i=1}^N y_i\), cresce con il numero totale di eventi osservati; Ogni evento è considerato come un’unità di “evidenza” a favore di un certo tasso \(\lambda\), spostando la distribuzione a posteriori verso valori più alti man mano che si accumulano le osservazioni.
il parametro rate (tasso), \(\beta_{\text{post}} = \beta_0 + N\), aumenta con il numero di intervalli osservati, N. Questo parametro controlla la dispersione della distribuzione: valori più alti di \(\beta\) corrispondono a una minore varianza e, quindi, a una maggiore certezza nella stima di \(\lambda\). Ogni nuovo intervallo di osservazione, indipendentemente dal numero di eventi in esso registrati, restringe la distribuzione a posteriori, perfezionando la stima.
K.3.3 Un esempio numerico
Riprendiamo l’esempio visto in precedenza con i dati:
y <- c(2, 1, 3, 2, 2, 1, 1, 1)Abbiamo \(N = 8\) osservazioni, e come prior scegliamo \(\alpha_{\text{prior}} = 9\) e \(\beta_{\text{prior}} = 2\).
Calcoliamo i nuovi parametri:
Il risultato è \(\alpha_{\text{post}} = 22\) e \(\beta_{\text{post}} = 10\). La nostra distribuzione a posteriori è quindi una Gamma(22, 10), che rappresenta la nuova convinzione su \(\lambda\) dopo aver osservato i dati.
K.3.4 Visualizzare la distribuzione a posteriori
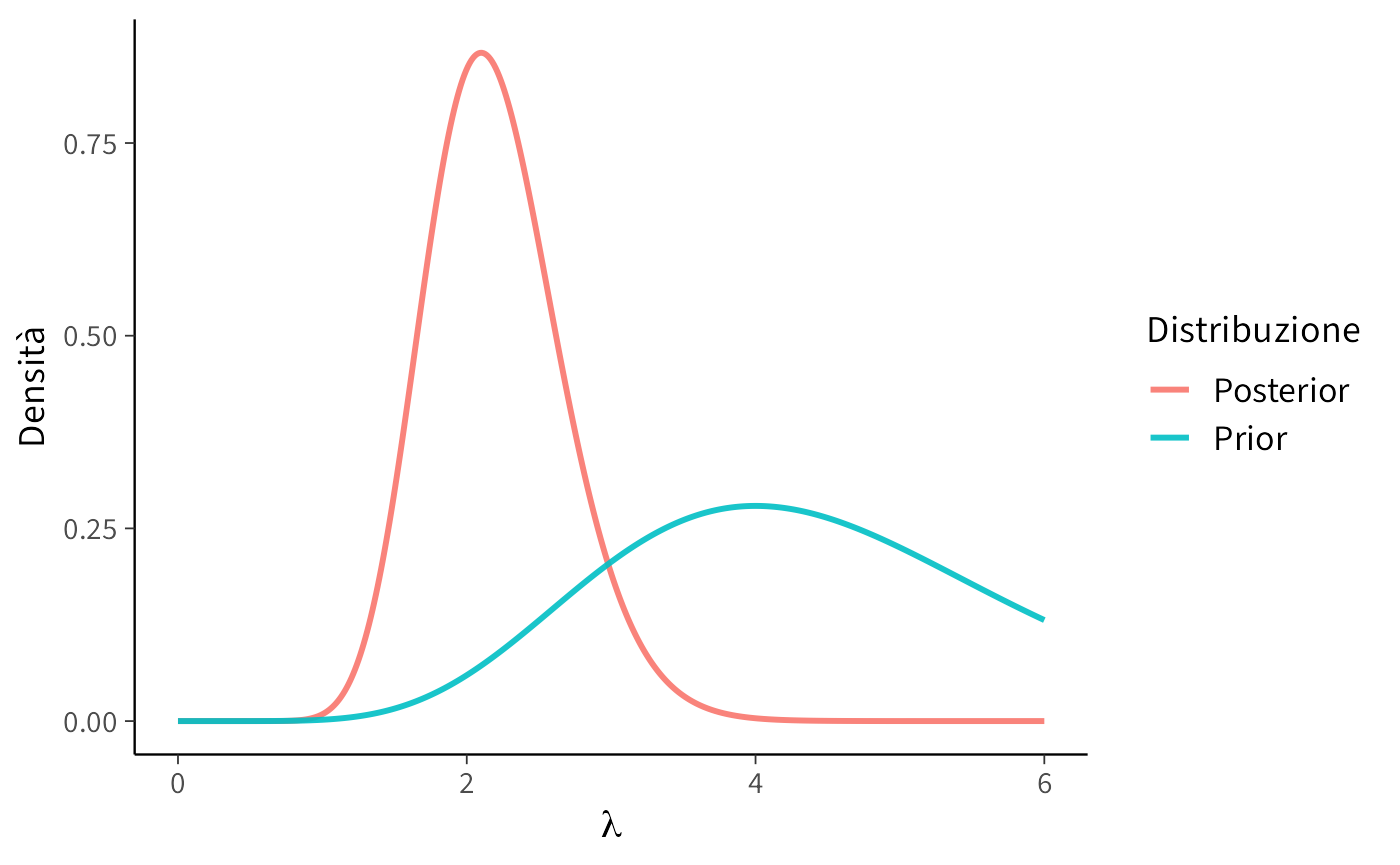
Possiamo visualizzare il cambiamento confrontando la prior e la posterior:
x <- seq(0, 6, length.out = 500)
prior_density <- dgamma(x, shape = 9, rate = 2)
post_density <- dgamma(x, shape = alpha_post, rate = beta_post)
df <- data.frame(
x = rep(x, 2),
densita = c(prior_density, post_density),
Distribuzione = rep(c("Prior", "Posterior"), each = length(x))
)
ggplot(df, aes(x = x, y = densita, color = Distribuzione)) +
geom_line(size = 1) +
labs(
x = expression(lambda),
y = "Densità"
) +
theme(plot.title = element_text(hjust = 0.5))
Il grafico mostra chiaramente che la posterior è più concentrata: osservare gli otto dati ci ha reso più sicuri del valore di \(\lambda\). Inoltre, il centro della distribuzione si è spostato verso il valore suggerito dai dati, integrando così le informazioni empiriche con le credenze iniziali.
K.3.5 Metodo basato su griglia
Ora che abbiamo introdotto il modello Gamma–Poisson, possiamo provare a calcolare la distribuzione a posteriori del parametro \(\lambda\) non con formule chiuse, ma con un procedimento puramente numerico. Questo approccio prende il nome di metodo su griglia (grid approximation), ed è molto utile come strumento didattico, in quanto mostra, passo dopo passo, il funzionamento dell’aggiornamento bayesiano, trasformando le regole matematiche in un algoritmo semplice da eseguire al computer.
L’idea è la seguente:
- fissiamo una griglia di possibili valori per \(\lambda\);
- calcoliamo la probabilità di ciascun valore secondo la prioria;
- calcoliamo, per gli stessi valori, la verosimiglianza dei dati osservati;
- moltiplichiamo i due risultati per ottenere la distribuzione a posteriori (non ancora normalizzata);
- normalizziamo in modo che la somma totale sia pari a 1.
K.3.5.1 I dati e la prior
Prendiamo gli stessi dati già usati in precedenza, cioè il numero di compulsioni osservate in otto intervalli di tempo:
y <- c(2, 1, 3, 2, 2, 1, 1, 1)La priori scelta per \(\lambda\) è una Gamma con parametri \(\alpha = 9\) e \(\beta = 2\), che riflette la nostra convinzione iniziale che il tasso medio sia intorno a 4–5 eventi, con un certo margine di incertezza.
Creiamo una griglia di valori plausibili di \(\lambda\), ad esempio da 0 a 10, divisa in 1000 punti:
Questa curva rappresenta ciò che crediamo possibile prima di vedere i dati.
K.3.5.2 La verosimiglianza
La seconda componente è la verosimiglianza, cioè quanto ciascun valore ipotetico di \(\lambda\) rende probabili i dati osservati. Per una Poisson, la verosimiglianza è il prodotto delle probabilità individuali:
\[ \mathcal{L}(\lambda) = \prod_{i=1}^N P(Y = y_i \mid \lambda). \]
In R possiamo calcolarla in modo vettoriale:
Così, per ogni punto della griglia otteniamo il valore della verosimiglianza: se il dato osservato è molto coerente con un certo \(\lambda\), la verosimiglianza sarà alta; altrimenti sarà vicina a zero.
K.3.5.3 La distribuzione a posteriori
Il passo successivo è combinare priori e verosimiglianza. La regola di Bayes ci dice che:
\[ p(\lambda \mid y) \propto p(\lambda) \cdot \mathcal{L}(\lambda). \] In pratica, moltiplichiamo i valori calcolati ai due passi precedenti:
posterior_unnormalized <- prior * likelihoodQuesto ci dà una curva che ha la forma giusta, ma che non è ancora una vera distribuzione di probabilità: non somma a 1.
K.3.5.4 Normalizzazione
Per trasformarla in una distribuzione valida, dobbiamo normalizzare, cioè dividere per la somma totale (che qui approssimiamo come una somma numerica sulla griglia):
grid_width <- lambda_grid[2] - lambda_grid[1]
normalization_factor <- sum(posterior_unnormalized) * grid_width
posterior <- posterior_unnormalized / normalization_factorOra abbiamo davvero la distribuzione a posteriori di \(\lambda\).
K.3.5.5 Interpretazione e confronto visivo
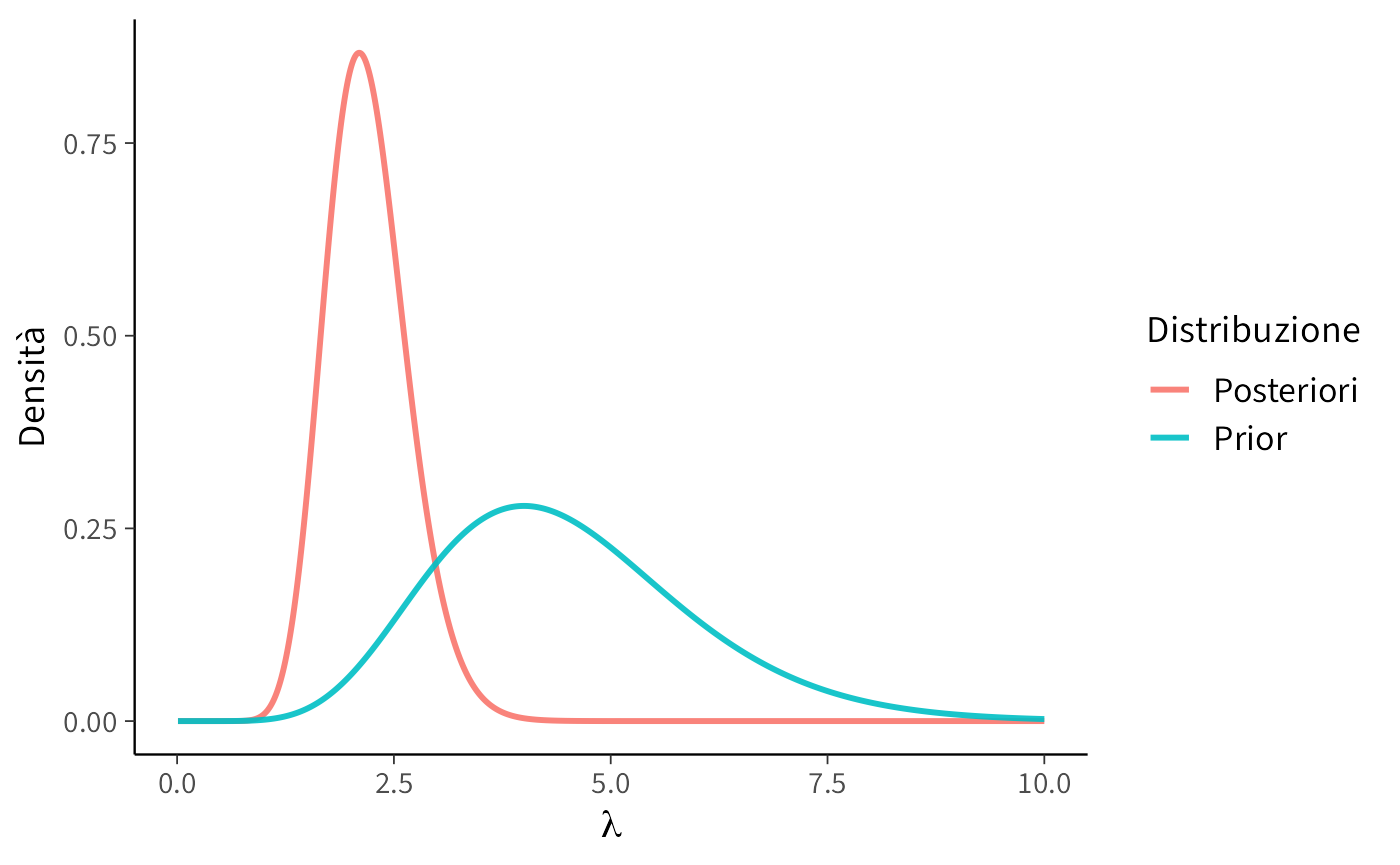
A questo punto possiamo confrontare la priori e la posteriori in un unico grafico:
df <- data.frame(
lambda = lambda_grid,
Prior = prior,
Posteriori = posterior
)
df_long <- pivot_longer(df, cols = c("Prior", "Posteriori"),
names_to = "Distribuzione",
values_to = "Densita")
ggplot(df_long, aes(x = lambda, y = Densita, color = Distribuzione)) +
geom_line(size = 1) +
labs(x = expression(lambda),
y = "Densità")
Il grafico rivela due aspetti fondamentali:
- la posteriori è spostata rispetto alla priori, perché i dati suggeriscono valori di \(\lambda\) più bassi di quanto ci aspettassimo inizialmente;
- la posteriori è anche più concentrata, cioè meno incerta: dopo aver osservato i dati, non solo abbiamo aggiornato la nostra convinzione, ma siamo anche diventati più sicuri del valore plausibile di \(\lambda\).
K.3.6 Perché è utile il metodo a griglia?
Questo metodo non è molto efficiente nei problemi complessi (dove i parametri sono numerosi e lo spazio da esplorare è vasto), ma è molto utile a scopo didattico. Ci mostra infatti in modo visivo e intuitivo il funzionamento dell’aggiornamento bayesiano: partiamo da una convinzione iniziale (la prior), la confrontiamo con i dati (la likelihood) e otteniamo una nuova convinzione aggiornata (la posterior).
Nei prossimi capitoli vedremo come affrontare lo stesso problema con strumenti più generali, come il campionamento MCMC in Stan, che diventano indispensabili quando i modelli si complicano e il metodo su griglia non è più praticabile.
Riflessioni conclusive
Il modello Gamma–Poisson ci mostra che la logica delle famiglie coniugate non è limitata al caso dei dati binari, ma si estende in modo naturale a dati di altra natura, come i conteggi. Anche in questo caso, il teorema di Bayes fornisce un aggiornamento semplice e cumulativo: i parametri della distribuzione prior si modificano alla luce dei dati, producendo un posterior facilmente interpretabile.
Dal punto di vista didattico, questo esempio ha il valore di rendere più generale l’intuizione acquisita con il Beta–Binomiale, mostrando la ricorrenza della coniugazione in contesti diversi. Dal punto di vista applicativo, invece, è bene sottolineare che la coniugazione rimane un caso speciale. Nella maggior parte delle situazioni psicologiche reali non possiamo contare su soluzioni analitiche così eleganti, ed è per questo che nei capitoli principali del manuale ci concentriamo su metodi computazionali più generali, come il campionamento MCMC.
In sintesi, il modello Gamma–Poisson è un’utile illustrazione supplementare: non rappresenta un passaggio essenziale per la comprensione del manuale, ma offre un’occasione per consolidare le idee chiave e per intravedere la varietà di applicazioni in cui l’approccio bayesiano può essere adottato.
Bibliografia
Scholz, U., Stadler, G., Berli, C., Lüscher, J., & Knoll, N. (2021). How do people experience and respond to social control from their partner? Three daily diary studies. Frontiers in Psychology, 11, 613546.