here::here("code", "_common.R") |>
source()
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayesplot, ggplot2, dplyr, tibble, stringr)
conflicts_prefer(posterior::ess_bulk)
conflicts_prefer(posterior::ess_tail)14 Modello gerarchico beta-binomiale
Introduzione
In questo capitolo introdurremo il concetto di struttura gerarchica nell’inferenza bayesiana usando il modello beta-binomiale. In questo contesto, concetti chiave come la scambiabilità, gli iperparametri, la concentrazione e lo shrinkage possono essere osservati in modo particolarmente chiaro, prima di passare, in seguito, al caso gaussiano che, pur condividendo la stessa logica di base, richiede strumenti computazionali più sofisticati e meno trasparenti dal punto di vista analitico.
Nella ricerca psicologica è frequente incontrare situazioni sperimentali in cui, per ciascun partecipante, viene registrata una sequenza di esiti dicotomici, generalmente classificati come successi o insuccessi, ottenuti in un numero prefissato di prove. Questo paradigma sperimentale solleva tre questioni analitiche fondamentali: la stima della probabilità di successo del singolo individuo, la descrizione della tendenza centrale della popolazione di riferimento e la quantificazione dell’eterogeneità tra i soggetti.
La risposta a tali interrogativi risulta particolarmente problematica quando il numero di prove a disposizione di ciascun partecipante è limitato. In queste condizioni, le proporzioni osservate mostrano una notevole instabilità e sono fortemente influenzate dalle fluttuazioni campionarie casuali. Il modello gerarchico beta-binomiale affronta queste criticità inferenziali producendo stime più robuste a livello individuale mediante un meccanismo di shrinkage che attenua le stime estreme riportandole verso la media di gruppo e quantificando, al contempo, la variabilità effettiva tra gli individui a livello di popolazione.
In questo capitolo, le probabilità di successo individuali vengono interpretate come realizzazioni scambiabili tratte da una distribuzione Beta comune. I conteggi dei successi per ciascun individuo sono modellati tramite distribuzioni binomiali condizionate a tali probabilità, mentre gli iperparametri della distribuzione Beta vengono stimati direttamente dai dati.
Nel Capitolo 28, dedicato ai modelli gaussiani a effetti misti, ritroveremo la stessa struttura concettuale in una forma continua: i parametri individuali saranno considerati come estrazioni da una distribuzione normale, la verosimiglianza assumerà una forma gaussiana e il grado di concentrazione sarà espresso dalla deviazione standard degli effetti casuali. Il principio unificante resta invariato: gli individui condividono tratti comuni pur mantenendo una propria specificità e questa condivisione di informazioni produce un pooling parziale naturale delle stime che combina la stabilità delle inferenze di gruppo con la sensibilità alle differenze individuali.
In sintesi, il modello beta-binomiale può essere considerato come l’equivalente discreto del modello gaussiano a effetti misti. La probabilità individuale \(p_i\) svolge lo stesso ruolo del parametro continuo \(\theta_j\) nei modelli gaussiani; la distribuzione Beta si comporta come l’analogo discreto della distribuzione Normale; e il parametro di concentrazione \(\kappa\) rappresenta l’equivalente della deviazione standard degli effetti casuali.
In questa prospettiva, il modello beta-binomiale, oltre al suo valore intrinseco, offre la possibilità di esaminare un caso di studio in cui i meccanismi di pooling e di regolarizzazione possono essere osservati in modo trasparente prima di essere generalizzati ai modelli lineari gerarchici più complessi (si vedano Gelman et al., 2013; McElreath, 2020).
Panoramica del capitolo
- Specificare un modello beta–binomiale gerarchico.
- Spiegare il ruolo della probabilità media nella popolazione \(\mu\) e concentrazione \(\kappa\).
- Interpretare lo shrinkage e collegarlo al numero di prove per soggetto.
- Leggere le principali diagnostiche MCMC.
- Confrontare la prestazione media con un valore di riferimento (es. 0.5).
14.1 Perché adottare una struttura gerarchica
L’analisi di dati psicologici raccolti su più individui pone una sfida metodologica fondamentale: come conciliare il rispetto delle differenze individuali con l’esigenza di formulare conclusioni valide a livello della popolazione? Da un lato, ciascun partecipante presenta caratteristiche uniche che meritano di essere rappresentate; dall’altro, l’obiettivo della ricerca è spesso quello di comprendere tendenze generali che trascendono il singolo caso. I modelli gerarchici bayesiani offrono una soluzione elegante a questa sfida, integrando entrambe le prospettive in un unico quadro inferenziale coerente.
La logica alla base di questi modelli è insieme semplice e potente. Ogni individuo contribuisce con i propri dati alla stima del proprio parametro specifico, ma al tempo stesso partecipa alla definizione del profilo generale della popolazione. Questo profilo collettivo, a sua volta, esercita un’influenza regolatrice sulle stime individuali. Il risultato è un equilibrio dinamico: quando disponiamo di poche osservazioni per un determinato soggetto, la stima del suo parametro tende ad avvicinarsi alla media del gruppo; quando invece le prove sono numerose, prevale l’evidenza empirica specifica di quel partecipante. Questo fenomeno, noto come shrinkage (letteralmente “restringimento” o “contrazione”), non è un artificio statistico imposto dall’esterno, ma emerge naturalmente dalla struttura probabilistica del modello.
14.1.1 Il principio di scambiabilità
Il fondamento concettuale di questo approccio risiede nel principio di scambiabilità. In assenza di informazioni che permettano di distinguere sistematicamente alcuni individui dagli altri – ad esempio, in base a covariate come l’età, il livello di istruzione o l’appartenenza a gruppi clinici – è metodologicamente appropriato trattare i parametri individuali come realizzazioni indipendenti provenienti da una distribuzione comune. In termini psicologici, questo equivale a riconoscere che tutti gli individui del campione appartengono alla medesima popolazione di riferimento, pur manifestando variabilità individuale.
Consideriamo un esempio concreto. Supponiamo di analizzare la precisione del riconoscimento delle espressioni facciali. Se non abbiamo ragioni teoriche o empiriche per ritenere che alcuni individui appartengano a sottogruppi sistematicamente diversi (per esempio, in base all’età o alla formazione), possiamo considerare le loro probabilità di successo come scambiabili. Questo significa che, prima di osservare i dati, non possiamo distinguere a priori le performance dei partecipanti: ciascuno ha la stessa probabilità di mostrare un dato livello di abilità. Il modello gerarchico cattura questa intuizione rappresentando tutti i partecipanti come provenienti da una distribuzione comune che descrive il livello medio di abilità della popolazione, pur preservando le differenze individuali attorno a tale valore centrale.
Naturalmente, quando sono disponibili covariate rilevanti o si identificano sottogruppi teoricamente motivati, il modello può essere esteso in modo naturale includendo predittori che spiegano parte della variabilità tra i soggetti. Tuttavia, la logica strutturale di base rimane inalterata: il modello continua a operare una regolarizzazione gerarchica, ora condizionata alle caratteristiche osservate dei partecipanti.
14.2 Struttura del modello e parametrizzazione
Il modello gerarchico adotta una struttura generativa articolata su due livelli, che riflette la natura dei dati e le nostre assunzioni sulla popolazione.
Livello individuale (likelihood). Per ciascun partecipante \(i\), il numero di successi \(y_i\) ottenuti su \(n_i\) prove segue una distribuzione binomiale con probabilità di successo \(p_i\):
\[y_i \sim \text{Binomiale}(n_i, p_i).\]
Questa componente del modello descrive il processo di generazione dei dati osservati per ogni singolo individuo.
Livello di popolazione (distribuzione dei parametri). Le probabilità individuali \(p_i\) non sono parametri indipendenti, ma vengono estratte in modo scambiabile da una distribuzione Beta comune, caratterizzata dagli iperparametri \(\alpha\) e \(\beta\):
\[p_i \sim \text{Beta}(\alpha, \beta).\]
Questa distribuzione rappresenta la variabilità tra individui nella popolazione. Gli iperparametri \(\alpha\) e \(\beta\) determinano la forma della distribuzione Beta e, quindi, il modo in cui le probabilità individuali si distribuiscono attorno a un valore tipico.
Prior sugli iperparametri. A completare la specificazione, \(\alpha\) e \(\beta\) ricevono distribuzioni a priori debolmente informative che riflettono la nostra conoscenza preliminare (solitamente vaga) sulla popolazione.
14.2.1 Una parametrizzazione più interpretabile
Sebbene la parametrizzazione tradizionale in termini di \(\alpha\) e \(\beta\) sia matematicamente naturale, risulta spesso poco intuitiva. Una rappresentazione alternativa, basata sulla media e sulla concentrazione, facilita notevolmente l’interpretazione:
Media di popolazione: \(\mu = \frac{\alpha}{\alpha + \beta}\) rappresenta la probabilità media di successo nella popolazione, ossia il livello tipico di performance atteso.
Concentrazione: \(\kappa = \alpha + \beta\) quantifica il grado di omogeneità tra i partecipanti. Valori elevati di \(\kappa\) indicano che le probabilità individuali tendono a concentrarsi strettamente attorno alla media \(\mu\), segnalando una popolazione relativamente omogenea. Valori bassi di \(\kappa\), al contrario, permettono una maggiore dispersione e riflettono una popolazione più eterogenea.
Questa parametrizzazione rende più semplice specificare prior significative e interpretare i risultati del modello in termini sostanziali.
14.3 Il meccanismo di shrinkage bayesiano
Uno degli aspetti più eleganti del modello gerarchico emerge quando esaminiamo la distribuzione a posteriori dei parametri individuali. Quando gli iperparametri \(\alpha\) e \(\beta\) sono noti (o stimati dai dati), la coniugazione tra la distribuzione Beta e la binomiale produce una distribuzione a posteriori che ha una forma particolarmente illuminante.
La stima a posteriori di \(p_i\) può essere espressa come una media ponderata tra due fonti di informazione:
\[\mathbb{E}[p_i \mid y_i, \alpha, \beta] = w_i \cdot \hat{p}_i + (1 - w_i) \cdot \mu,\] dove:
- \(\hat{p}_i = y_i/n_i\) è la proporzione empirica osservata per il soggetto \(i\);
- \(\mu = \alpha/(\alpha + \beta)\) è la media di popolazione;
- \(w_i = \frac{n_i}{n_i + \kappa}\) è il peso assegnato ai dati individuali.
Il peso \(w_i\) rivela in modo esplicito il meccanismo di shrinkage. Questo peso quantifica la fiducia che il modello ripone nell’evidenza individuale rispetto all’informazione proveniente dal gruppo. Osserviamo che:
quando \(n_i\) è piccolo (poche prove per quel soggetto), \(w_i\) è vicino a zero e la stima si avvicina fortemente alla media di popolazione \(\mu\). In altre parole, in assenza di dati sufficienti, “prendiamo in prestito” informazione dal gruppo.
quando \(n_i\) è grande (molte prove disponibili), \(w_i\) si avvicina a uno e la stima privilegia la proporzione empirica individuale \(\hat{p}_i\).
il parametro di concentrazione \(\kappa\) modula l’intensità di questo effetto: una maggiore concentrazione (popolazione più omogenea) aumenta l’attrazione verso la media di gruppo, mentre una minore concentrazione (maggiore eterogeneità) riduce questa regolarizzazione.
Questo bilanciamento automatico tra informazione individuale e informazione di gruppo costituisce l’essenza dello shrinkage bayesiano e rappresenta uno dei principali vantaggi dei modelli gerarchici. Il modello “apprende” dai dati quanto peso assegnare a ciascuna fonte di informazione, producendo stime che sono al contempo sensibili alle specificità individuali e informate dal contesto della popolazione.
14.4 Un’applicazione pratica: lo studio sulla terapia tattile
14.4.1 Il contesto sperimentale
Per illustrare concretamente il funzionamento del modello gerarchico beta-binomiale, esaminiamo uno studio sperimentale di Rosa et al. (1998), che ha indagato l’efficacia della cosiddetta “terapia tattile”. Questo controverso approccio terapeutico si basa sull’assunto che alcuni operatori sanitari, specificamente addestrati, siano in grado di percepire e manipolare il cosiddetto “campo energetico umano” che circonda il corpo.
Per verificare questa affermazione, i ricercatori hanno progettato un esperimento in condizioni controllate. Ventotto praticanti del Therapeutic Touch dovevano identificare, senza alcun contatto visivo o fisico, quale delle due mani di un partecipante era stata avvicinata dallo sperimentatore. Il disegno prevedeva che ciascun operatore completasse dieci prove indipendenti, ottenendo in ciascuna un risultato binario: identificazione corretta o errore.
Dal punto di vista statistico, l’obiettivo inferenziale si articola su due livelli complementari:
Livello individuale: stimare la probabilità di successo specifica di ciascun operatore, riconoscendo che potrebbero esistere differenze individuali nell’abilità (ammesso che tale abilità esista).
Livello di popolazione: stimare la probabilità media di successo dell’intero gruppo di operatori, per valutare se complessivamente la performance si discosti dalla pura casualità.
Entrambi i parametri possono essere interpretati in base al confronto con il valore di riferimento di 0.5, che rappresenta la performance attesa per puro caso in un compito a due alternative forzate. Se gli operatori possedessero effettivamente la capacità dichiarata, si dovrebbero osservare probabilità di successo sistematicamente superiori a tale valore.
Questo contesto sperimentale si presta idealmente all’applicazione di un modello gerarchico, poiché combina l’interesse per le specificità individuali con la necessità di trarre conclusioni sulla popolazione generale, in un dominio dove la performance casuale costituisce un punto di riferimento teoricamente cruciale.
14.4.2 Preparazione e ispezione dei dati
Procediamo innanzitutto all’importazione dei dati e alla loro organizzazione. Il dataset contiene le risposte di ciascun operatore per ogni singola prova.
# Importazione dei dati
url <- "https://raw.githubusercontent.com/boboppie/kruschke-doing_bayesian_data_analysis/master/2e/TherapeuticTouchData.csv"
tt_dat <- read.csv(url)
tt_dat %>% glimpse()
#> Rows: 280
#> Columns: 2
#> $ y <int> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0,…
#> $ s <chr> "S01", "S01", "S01", "S01", "S01", "S01", "S01", "S01", "S01", "S01"…Aggreghiamo quindi i dati per operatore, calcolando le statistiche sufficienti necessarie per il modello: il numero totale di successi e il numero di prove completate. Includiamo anche la proporzione empirica di successi come riferimento descrittivo iniziale.
by_subject <- tt_dat %>%
group_by(s) %>%
summarise(
y = sum(y),
n_trials = n(),
prop_emp = y / n_trials,
.groups = "drop"
) %>%
arrange(s)
by_subject %>% head()
#> # A tibble: 6 × 4
#> s y n_trials prop_emp
#> <chr> <int> <int> <dbl>
#> 1 S01 1 10 0.1
#> 2 S02 2 10 0.2
#> 3 S03 3 10 0.3
#> 4 S04 3 10 0.3
#> 5 S05 3 10 0.3
#> 6 S06 3 10 0.314.4.3 Verifica predittiva a priori
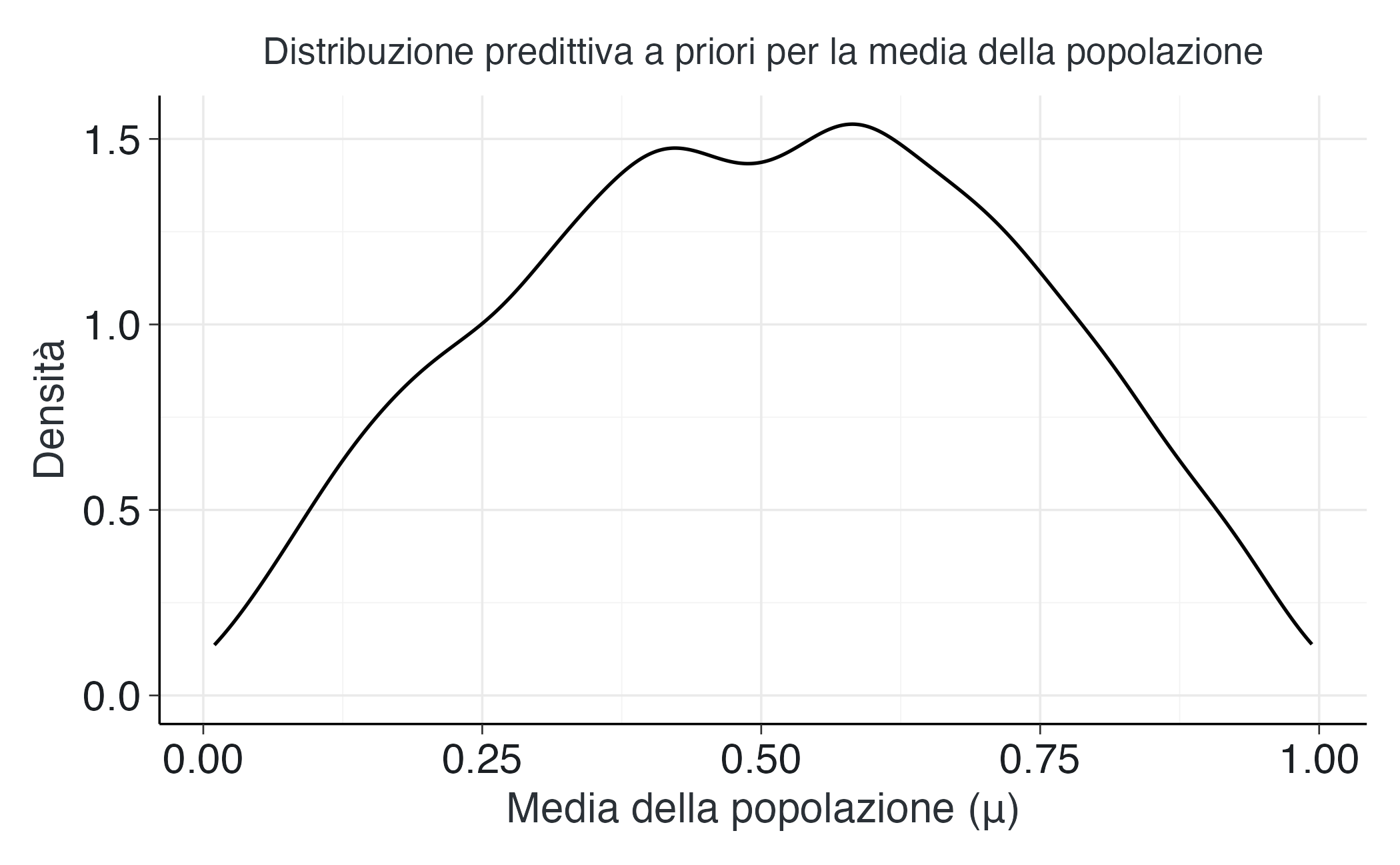
Prima di adattare il modello ai dati, è buona pratica verificare che le distribuzioni a priori scelte generino previsioni ragionevoli. In altre parole, vogliamo assicurarci che le nostre prior non escludano a priori scenari plausibili né favoriscano eccessivamente valori estremi.
Per gli iperparametri \(\alpha\) e \(\beta\) adottiamo distribuzioni Gamma debolmente informative, specificate nella parametrizzazione shape-rate: \(\alpha \sim \text{Gamma}(2, 2)\) e \(\beta \sim \text{Gamma}(2, 2)\). Queste prior consentono una vasta di configurazioni possibili per la distribuzione Beta della popolazione, senza imporre vincoli troppo restrittivi.
Generiamo campioni dalla distribuzione predittiva a priori per visualizzare le implicazioni di queste scelte:
set.seed(1)
a_draw <- rgamma(2000, shape = 2, rate = 2)
b_draw <- rgamma(2000, shape = 2, rate = 2)
mu_draw <- a_draw / (a_draw + b_draw)
kappa_draw <- a_draw + b_draw
tibble(mu = mu_draw, kappa = kappa_draw) %>%
ggplot(aes(x = mu)) +
geom_density(linewidth = 0.6) +
labs(x = "Media della popolazione (μ)",
y = "Densità",
subtitle = "Distribuzione predittiva a priori per la media della popolazione")Come possiamo osservare, la distribuzione a priori per la media della popolazione \(\mu\) risulta relativamente piatta e si distribuisce su un ampio intervallo di valori, senza concentrarsi in modo inappropriato su alcuna regione particolare. Questo comportamento riflette un atteggiamento epistemico prudente: prima di osservare i dati, non imponiamo forti vincoli sulla performance media degli operatori.
Allo stesso modo, le distribuzioni implicite per il parametro di concentrazione \(\kappa\) non impongono né un’omogeneità estrema (che costringerebbe tutti gli operatori a essere quasi identici) né una variabilità eccessiva (che impedirebbe al modello di condividere informazioni tra gli individui). Qualora si desideri un controllo ancora più esplicito su questi aspetti, è possibile specificare prior direttamente sulla parametrizzazione \((\mu, \kappa)\).
14.4.4 Implementazione del modello in Stan
Traduciamo ora la struttura generativa del modello in codice Stan. L’architettura del programma riflette direttamente la struttura gerarchica descritta in precedenza.
Blocco data: specifica i dati osservati che forniamo al modello: il numero di operatori, i successi ottenuti da ciascuno e il numero di prove completate.
Blocco parameters: dichiara i parametri da stimare – gli iperparametri \(\alpha\) e \(\beta\) che caratterizzano la distribuzione Beta di popolazione e le probabilità individuali \(p_i\) per ciascun operatore, vincolate all’intervallo \([0,1]\).
Blocco model: specifica le distribuzioni a priori per gli iperparametri e la struttura gerarchica del modello. Qui definiamo esplicitamente che le probabilità individuali sono estratte da una distribuzione Beta comune e che i dati osservati seguono una distribuzione binomiale condizionata a tali probabilità.
Blocco generated quantities: calcola quantità derivate di interesse, in particolare la media della popolazione \(\mu = \alpha/(\alpha + \beta)\), che utilizzeremo per confrontare la performance media con la soglia casuale di 0.5.
stan_code <- "
data {
int<lower=1> N; // numero di operatori
array[N] int<lower=0> y; // successi per operatore
array[N] int<lower=1> n_trials; // prove per operatore
}
parameters {
real<lower=0> alpha; // parametro shape della Beta
real<lower=0> beta; // parametro shape della Beta
array[N] real<lower=0, upper=1> p; // probabilità individuali
}
model {
alpha ~ gamma(2, 2); // prior su alpha
beta ~ gamma(2, 2); // prior su beta
// Livello di popolazione: le probabilità individuali seguono una Beta comune
for (i in 1:N) {
p[i] ~ beta(alpha, beta);
}
// Livello individuale: verosimiglianza binomiale
for (i in 1:N) {
y[i] ~ binomial(n_trials[i], p[i]);
}
}
generated quantities {
real overall_p = alpha / (alpha + beta); // media di popolazione
}
"Procediamo alla compilazione del modello:
mod <- cmdstanr::cmdstan_model(write_stan_file(stan_code))Prepariamo i dati nel formato richiesto da Stan:
stan_data <- list(
N = nrow(by_subject),
y = as.integer(by_subject$y),
n_trials = as.integer(by_subject$n_trials)
)E infine avviamo il campionamento MCMC utilizzando l’algoritmo di default (NUTS, No-U-Turn Sampler):
set.seed(84735)
fit <- mod$sample(
data = stan_data,
chains = 4,
parallel_chains = 4,
iter_warmup = 1000,
iter_sampling = 2000,
adapt_delta = 0.9,
max_treedepth = 12,
refresh = 0
)14.4.5 Diagnostica della convergenza
Al termine del campionamento, è essenziale verificare che l’algoritmo MCMC abbia raggiunto la convergenza. Esaminiamo le principali diagnostiche per gli iperparametri e per un sottoinsieme rappresentativo delle probabilità individuali:
posterior::summarise_draws(
fit$draws(variables = c("alpha", "beta", "overall_p", "p[1]", "p[2]", "p[3]")),
"mean", "sd", "rhat", "ess_bulk", "ess_tail"
)
#> # A tibble: 6 × 6
#> variable mean sd rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 alpha 2.30 0.625 1.00 6375. 5674.
#> 2 beta 2.83 0.777 1.00 6916. 5882.
#> 3 overall_p 0.449 0.0453 1.00 9668. 6381.
#> 4 p[1] 0.217 0.105 1.00 13325. 5691.
#> 5 p[2] 0.283 0.116 1.00 14168. 5108.
#> 6 p[3] 0.349 0.120 1.00 13573. 5489.Gli indici \(\hat{R}\) prossimi a 1.00 indicano che le catene hanno raggiunto una distribuzione stazionaria comune, mentre valori di dimensione campionaria effettiva (ESS) dell’ordine delle migliaia confermano che disponiamo di un numero sufficiente di campioni indipendenti per l’inferenza. In presenza di problemi di convergenza, questi indicatori mostrerebbero segnali d’allarme che richiederebbero un intervento correttivo.
14.4.6 Analisi dello shrinkage e interpretazione dei risultati
Uno degli aspetti più illuminanti dell’analisi consiste nell’esaminare visivamente il fenomeno dello shrinkage. Estraiamo le stime a posteriori delle probabilità individuali e confrontiamole graficamente con le proporzioni empiriche osservate.
# Estrazione delle distribuzioni a posteriori
draws_p <- fit$draws("p")
draws_mu <- fit$draws("overall_p")
mu_hat <- posterior::summarise_draws(draws_mu, "mean")$mean
# Calcolo delle statistiche riassuntive per le probabilità individuali
sum_p <- posterior::summarise_draws(draws_p, "mean", "median", "sd") %>%
mutate(s = as.integer(stringr::str_extract(variable, "\\d+"))) %>%
arrange(s)
# Calcolo degli intervalli di credibilità al 90%
qs <- posterior::summarise_draws(draws_p, ~ quantile2(.x, probs = c(0.05, 0.95))) %>%
mutate(s = as.integer(stringr::str_extract(variable, "\\d+"))) %>%
arrange(s)
sum_p <- sum_p %>%
left_join(qs %>% select(s, q5 = `q5`, q95 = `q95`), by = "s")
# Integrazione con i dati osservati
df_shrink <- by_subject %>%
mutate(s_idx = as.integer(stringr::str_extract(s, "\\d+"))) %>%
arrange(s_idx) %>%
select(s, s_idx, prop_emp, n_trials) %>%
inner_join(
sum_p %>% select(s, post_mean = mean, post_med = median,
post_q05 = q5, post_q95 = q95),
by = join_by(s_idx == s)
) %>%
arrange(prop_emp) %>%
mutate(s_ord = factor(s, levels = s))Creiamo ora una visualizzazione che mostra simultaneamente le proporzioni empiriche, le stime a posteriori e l’entità della contrazione verso la media di popolazione:
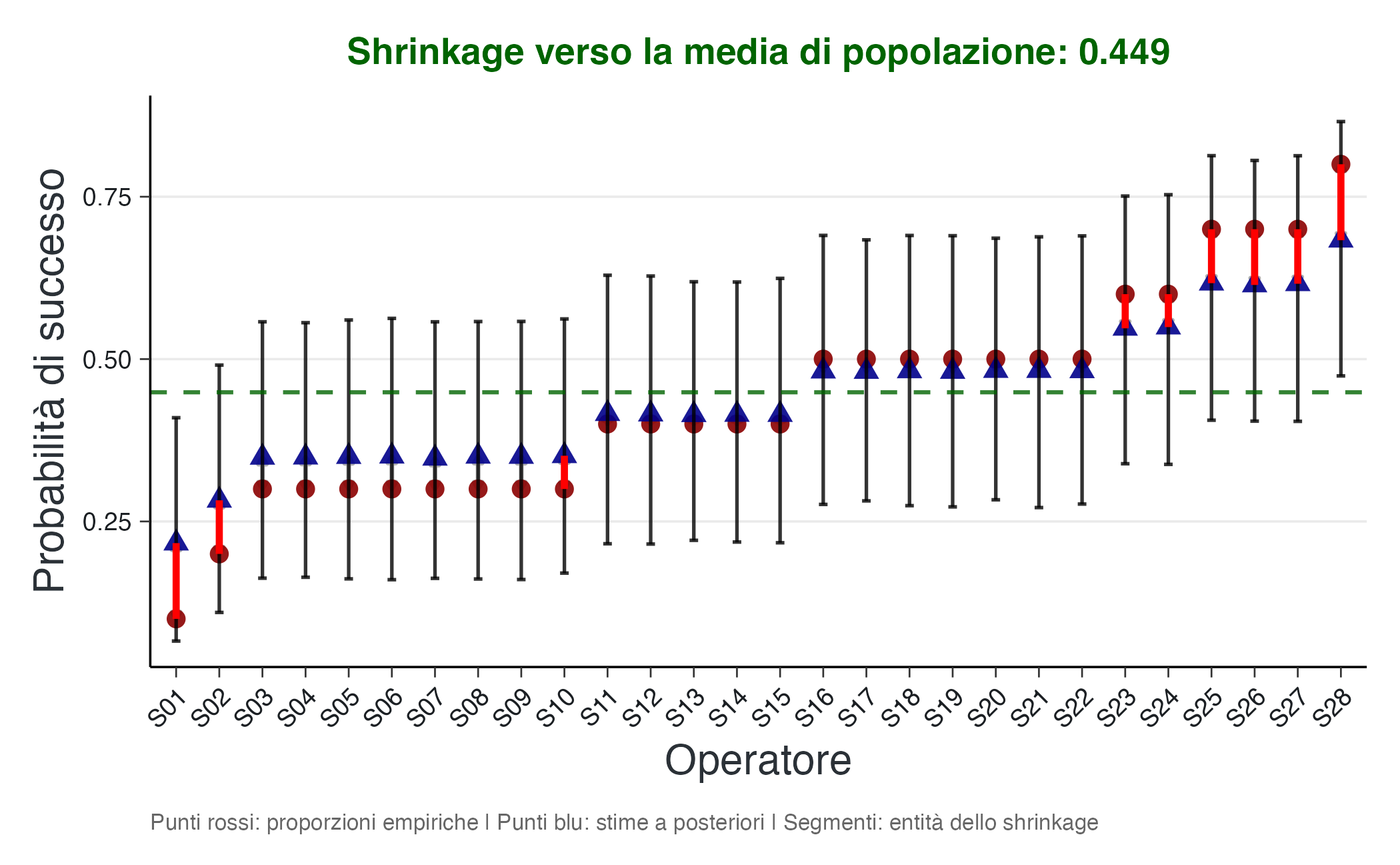
ggplot(df_shrink, aes(x = s_ord)) +
# Segmenti più visibili per lo shrinkage
geom_segment(aes(xend = s_ord, y = prop_emp, yend = post_mean),
linewidth = 0.8, alpha = 0.9, color = "darkgray",
arrow = arrow(length = unit(0.1, "cm"), ends = "both", type = "closed")) +
# Punti per le stime empiriche
geom_point(aes(y = prop_emp), size = 3, alpha = 0.9, color = "darkred",
shape = 16) +
# Punti per le stime a posteriori
geom_point(aes(y = post_mean), size = 3, color = "darkblue", shape = 17) +
# Intervalli di credibilità
geom_errorbar(aes(ymin = post_q05, ymax = post_q95),
width = 0.2, alpha = 0.8, linewidth = 0.6) +
# Media di popolazione
geom_hline(yintercept = mu_hat, linetype = "dashed", alpha = 0.8,
color = "darkgreen", linewidth = 0.7) +
labs(x = "Operatore",
y = "Probabilità di successo",
subtitle = sprintf("Shrinkage verso la media di popolazione: %.3f", mu_hat),
caption = "Punti rossi: proporzioni empiriche | Punti blu: stime a posteriori | Segmenti: entità dello shrinkage") +
theme(panel.grid.minor = element_blank(),
panel.grid.major.x = element_blank(),
axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1, size = 9),
axis.text.y = element_text(size = 9),
plot.caption = element_text(size = 8, color = "gray40", hjust = 0),
plot.subtitle = element_text(face = "bold", color = "darkgreen")) +
scale_x_discrete(labels = function(x) gsub("s", "Op. ", x)) +
# Evidenzia i segmenti di shrinkage più ampi
geom_segment(data = df_shrink %>%
mutate(shrinkage_magnitude = abs(prop_emp - post_mean)) %>%
filter(shrinkage_magnitude > quantile(abs(prop_emp - post_mean), 0.7)),
aes(xend = s_ord, y = prop_emp, yend = post_mean),
linewidth = 1.2, alpha = 1, color = "red")In questa visualizzazione, i punti rossi rappresentano le proporzioni empiriche (i dati grezzi), mentre i triangoli blu mostrano le stime a posteriori prodotte dal modello gerarchico. I segmenti verticali collegano ciascuna coppia di stime, rendendo visibile l’entità dello shrinkage. Gli intervalli di credibilità al 90% (barre verticali) quantificano l’incertezza associata a ciascuna stima a posteriori.
L’effetto di contrazione emerge chiaramente: le stime a posteriori sono sistematicamente “attratte” verso la media della popolazione (linea tratteggiata), con un effetto più marcato per gli operatori con proporzioni empiriche più estreme. Questo comportamento è particolarmente pronunciato per gli operatori che hanno ottenuto solo successi o solo insuccessi nelle dieci prove: in questi casi, la proporzione empirica suggerirebbe probabilità pari a 0 o 1, ma il modello gerarchico, riconoscendo la limitatezza del campione (solo dieci prove), produce stime più moderate e realistiche.
Con soli dieci trial per partecipante, la regolarizzazione operata dal modello gerarchico sembra sostanziale, ma è metodologicamente appropriata. In pratica, il modello ci sta dicendo: “Attenzione, dieci prove sono poche per essere certi che questa performance estrema rifletta la vera abilità dell’operatore; teniamo conto anche di ciò che sappiamo sugli altri partecipanti”. Questo bilanciamento automatico tra l’evidenza individuale e l’informazione di gruppo rappresenta uno dei principali vantaggi dell’approccio gerarchico.
14.4.7 Verifica predittiva a posteriori
Un ulteriore passo essenziale consiste nel valutare l’adeguatezza complessiva del modello mediante una verifica predittiva a posteriori. L’idea di fondo è semplice: se il modello è adeguato, dovrebbe essere in grado di generare dati simulati simili ai dati realmente osservati.
Procediamo campionando dalla distribuzione predittiva a posteriori: per ciascuna iterazione MCMC, si genera un dataset replicato completo utilizzando i valori degli iperparametri campionati in quell’iterazione. Quindi, confrontiamo le statistiche sintetiche dei dati osservati con la distribuzione di queste stesse statistiche calcolate sui dati replicati.
In particolare, ci concentriamo sulla media complessiva delle proporzioni individuali, una statistica naturale per valutare la tendenza centrale della performance.
set.seed(123)
draws <- posterior::as_draws_df(fit$draws(c("alpha", "beta")))
S <- 1000
idx <- sample(seq_len(nrow(draws)), S, replace = TRUE)
yrep_mean <- numeric(S)
yobs_mean <- mean(by_subject$y / by_subject$n_trials)
for (s in seq_len(S)) {
# Estrai i valori degli iperparametri per questa iterazione
a <- draws$alpha[idx[s]]
b <- draws$beta[idx[s]]
# Genera probabilità individuali dalla distribuzione Beta di popolazione
p_ <- rbeta(nrow(by_subject), a, b)
# Genera dati replicati dalla verosimiglianza binomiale
y_ <- rbinom(nrow(by_subject), size = by_subject$n_trials, prob = p_)
# Calcola la statistica di interesse per questo dataset replicato
yrep_mean[s] <- mean(y_ / by_subject$n_trials)
}
# Visualizzazione
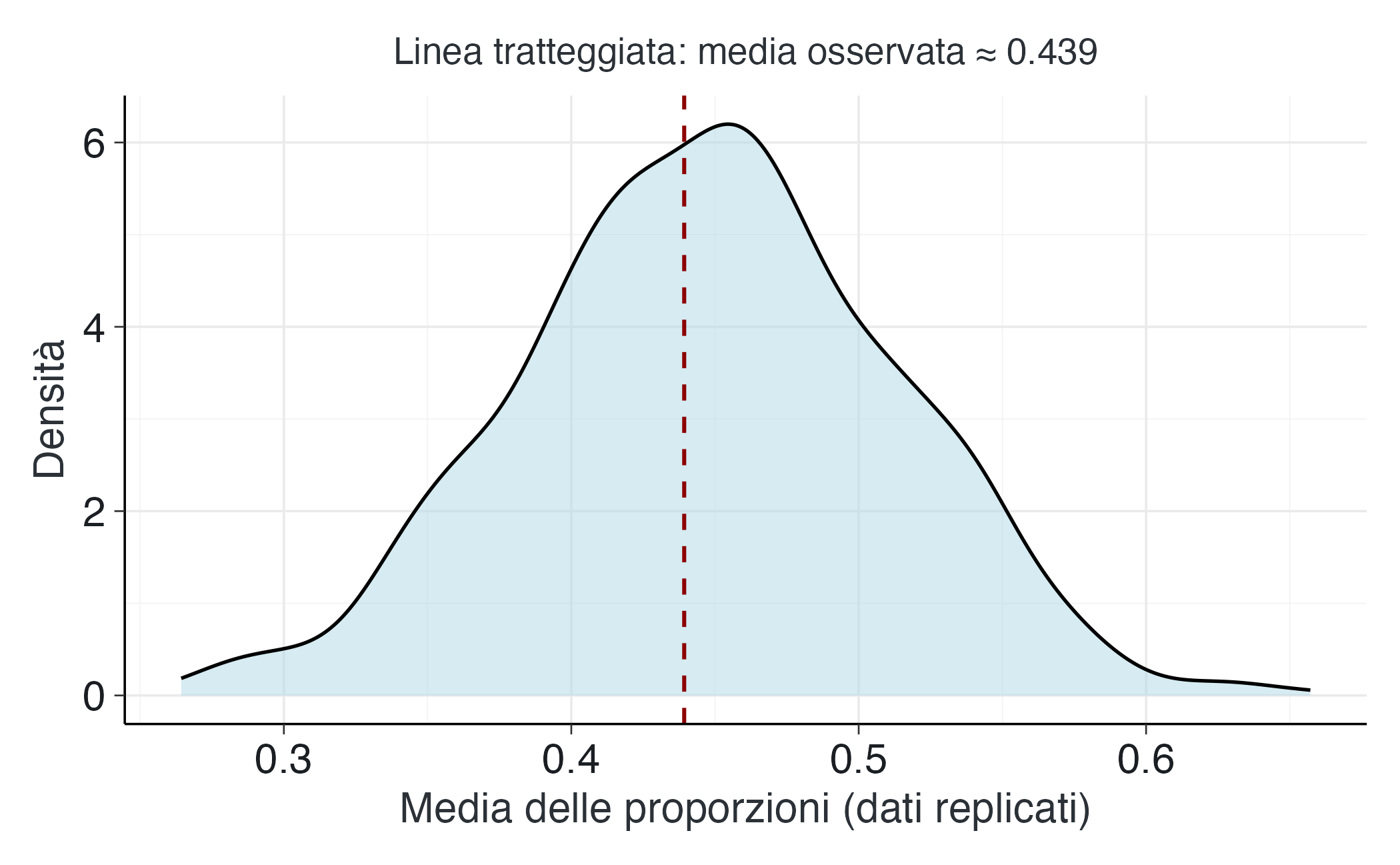
tibble(yrep_mean = yrep_mean) %>%
ggplot(aes(x = yrep_mean)) +
geom_density(linewidth = 0.6, fill = "lightblue", alpha = 0.5) +
geom_vline(xintercept = yobs_mean, linetype = "dashed", color = "darkred") +
labs(x = "Media delle proporzioni (dati replicati)",
y = "Densità",
subtitle = sprintf("Linea tratteggiata: media osservata ≈ %.3f", yobs_mean))La distribuzione delle medie replicate (in blu) rappresenta la variabilità che ci aspetteremmo di osservare in campioni futuri generati dallo stesso processo, secondo quanto stimato dal modello. La linea tratteggiata rossa indica il valore effettivamente osservato nei dati reali.
Se il valore osservato cade in una regione di alta densità della distribuzione predittiva – come accade in questo caso – possiamo concludere che il modello è adeguato nel riprodurre questa caratteristica dei dati. Se invece il valore osservato cadesse in una coda estrema della distribuzione predittiva, ciò costituirebbe un segnale d’allarme, suggerendo che il modello potrebbe non catturare adeguatamente alcuni aspetti importanti del processo generativo dei dati.
Eventuali discrepanze sistematiche potrebbero indicare la necessità di rivedere le assunzioni del modello – ad esempio, riconsiderando le distribuzioni a priori sulla concentrazione, o valutando se l’ipotesi di scambiabilità semplice sia appropriata, oppure esplorando l’inclusione di covariate per modellare fonti di eterogeneità non catturate dalla struttura gerarchica di base.
14.4.8 Valutazione dell’efficacia della terapia tattile
L’obiettivo principale dello studio era determinare se i praticanti del Therapeutic Touch fossero in grado di identificare il campo energetico umano a un tasso superiore a quello atteso per puro caso (0.5). Per rispondere a questa domanda, possiamo esaminare direttamente la distribuzione a posteriori della probabilità media di successo nella popolazione, overall_p (o \(\mu\)).
Calcoliamo gli intervalli di credibilità (IC) per questo parametro chiave:
# Calcolo dell'intervallo di credibilità per l'accuratezza media
draws_mu <- fit$draws("overall_p")
mu_summary <- posterior::summarise_draws(
draws_mu,
mean = ~mean(.x),
sd = ~sd(.x),
~quantile2(.x, probs = c(0.025, 0.05, 0.25, 0.5, 0.75, 0.95, 0.975))
)
print(mu_summary)
#> # A tibble: 1 × 10
#> variable mean sd q2.5 q5 q25 q50 q75 q95 q97.5
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 overall_p 0.449 0.0453 0.361 0.375 0.418 0.449 0.479 0.523 0.537# Possiamo anche calcolare la probabilità a posteriori che l'accuratezza media sia > 0.5
prob_above_chance <- posterior::summarise_draws(
draws_mu,
prob_above_0.5 = ~mean(.x > 0.5)
)
print(prob_above_chance)
#> # A tibble: 1 × 2
#> variable prob_above_0.5
#> <chr> <dbl>
#> 1 overall_p 0.134Interpretazione: l’intervallo di credibilità al 95% per l’accuratezza media della popolazione (\(\mu\)) è [0.361, 0.537]. Questo intervallo contiene il valore di riferimento 0.5, sebbene la maggior parte della massa della distribuzione (il 79% dell’IC) si trovi al di sotto di esso. La probabilità a posteriori che l’accuratezza media sia maggiore di 0.5 è solo del %.
Conclusione sull’efficacia: i dati non forniscono prove convincenti a sostegno dell’efficacia del Therapeutic Touch. La performance media del gruppo di operatori non è statisticamente distinguibile dal caso, con una lieve tendenza verso performance peggiori rispetto al valore atteso di 0.5. Questo risultato, ottenuto da un modello che tiene conto della variabilità individuale, fornisce una risposta robusta alla domanda di ricerca originale, in linea con le conclusioni dello studio di Rosa et al. (1998).
14.4.9 Vantaggi del modello gerarchico in questo contesto
L’adozione di un modello gerarchico beta-binomiale in questo scenario sperimentale offre diversi vantaggi metodologici decisivi rispetto agli approcci non gerarchici:
Stime robuste per soggetti con dati limitati: con solo 10 prove per operatore, le proporzioni empiriche grezze sono stime molto instabili delle reali abilità individuali. Il modello gerarchico, attraverso il meccanismo di shrinkage, produce stime più conservative e realistiche, in particolare per quegli operatori con proporzioni empiriche estreme (0 o 1). Ciò previene conclusioni fuorvianti sulle abilità individuali basate su evidenze aneddotiche.
Inferenza simultanea a più livelli: il modello ci permette di trarre conclusioni sia a livello individuale (le abilità specifiche \(p_i\)) che a livello di popolazione (l’accuratezza media \(\mu\) e l’eterogeneità \(\kappa\)), il tutto all’interno di un unico quadro coerente. Un approccio che analizzasse ogni operatore separatamente non potrebbe fornire una stima affidabile della tendenza centrale della popolazione.
Quantificazione dell’eterogeneità: il parametro di concentrazione \(\kappa\) (o la varianza equivalente della distribuzione Beta) fornisce una misura quantitativa di quanto gli operatori differiscano tra loro in termini di abilità percepita. Questo dato è informativo di per sé: un valore basso di \(\kappa\) indicherebbe una popolazione molto eterogenea, mentre un valore alto indicherebbe operatori molto simili tra loro.
Gestione automatica dell’incertezza: il modello propaga l’incertezza in modo appropriato a tutti i livelli della gerarchia. Gli intervalli di credibilità delle probabilità individuali incorporano l’incertezza sia sulla stima del singolo operatore che sugli iperparametri della popolazione, producendo intervalli più calibrati e realistici.
Pooling parziale delle informazioni: a differenza di un approccio che aggrega tutti i dati (ignorando le differenze individuali) o che analizza ogni soggetto separatamente (ignorando le similarità), il modello gerarchico trova un bilanciamento ottimale tra questi due estremi. Il grado di pooling è determinato dai dati stessi: maggiore è il numero di prove per soggetto, minore è lo shrinkage verso la media.
In sintesi, la struttura gerarchica si rivela particolarmente adatta a questo tipo di dati sperimentali in psicologia, in cui si raccolgono osservazioni multiple per ogni partecipante, ma il numero di osservazioni per partecipante è spesso limitato. Questo modello fornisce stime più affidabili a livello individuale e offre una valutazione più sfumata degli effetti a livello della popolazione, mantenendo comunque una corretta calibrazione dell’incertezza statistica.
14.5 Dal modello beta-binomiale ai modelli gaussiani gerarchici
Ora che abbiamo sviluppato una comprensione concreta del funzionamento dei modelli gerarchici attraverso il caso beta-binomiale, possiamo anticipare un’importante transizione: l’estensione ai modelli gaussiani a effetti misti per dati continui.
Questa transizione, pur comportando un cambiamento nella formalizzazione matematica, mantiene inalterata la struttura concettuale che abbiamo esplorato. La tabella seguente evidenzia le corrispondenze tra i due framework:
| Aspetto | Modello Beta-Binomiale | Modello Gaussiano Gerarchico |
|---|---|---|
| Parametri individuali | \(p_i\) (probabilità di successo) | \(\theta_j\) (effetti casuali) |
| Distribuzione di popolazione | \(\text{Beta}(\alpha, \beta)\) | \(\text{Normale}(\mu, \sigma_\theta)\) |
| Parametro di concentrazione | \(\kappa = \alpha + \beta\) | Deviazione standard \(\sigma_\theta\) |
| Verosimiglianza | \(y_i \sim \text{Binomiale}(n_i, p_i)\) | \(y_{ij} \sim \text{Normale}(\theta_j, \sigma_y)\) |
| Meccanismo di shrinkage | Regolato da \(w_i = n_i/(n_i + \kappa)\) | Regolato da \(\sigma_\theta\) e dall’informazione disponibile |
Il principio fondamentale rimane invariato: il modello stima simultaneamente i parametri individuali e le caratteristiche della distribuzione della popolazione. Il fenomeno dello shrinkage emerge naturalmente come conseguenza della struttura gerarchica e bilancia automaticamente l’evidenza individuale con l’informazione di gruppo.
Nel caso gaussiano:
- le probabilità di successo \(p_i\) vengono sostituite da effetti casuali \(\theta_j\), che rappresentano le deviazioni individuali rispetto alla media di gruppo;
- la distribuzione Beta viene sostituita da una distribuzione Normale per gli effetti casuali;
- il parametro di concentrazione \(\kappa\) trova il suo analogo nella deviazione standard \(\sigma_\theta\): valori piccoli di \(\sigma_\theta\) indicano maggiore omogeneità (shrinkage più forte), mentre valori grandi permettono maggiore eterogeneità.
Sebbene le formule matematiche specifiche differiscano, la logica inferenziale sottostante rimane identica: la condivisione dell’informazione tra le unità, la regolarizzazione delle stime individuali attraverso l’informazione di gruppo e l’adattamento automatico del grado di regolarizzazione in funzione della quantità di dati disponibili.
Riflessioni conclusive
L’impiego del modello gerarchico beta-binomiale come punto di partenza pedagogico offre numerosi vantaggi. La proprietà di coniugazione tra la distribuzione Beta e quella binomiale, unita alla parametrizzazione intuitiva in termini di media \(\mu\) e concentrazione \(\kappa\), rende particolarmente trasparente il meccanismo dello shrinkage. Attraverso la formula del peso \(w_i = n_i/(n_i + \kappa)\), possiamo vedere letteralmente come il modello bilanci automaticamente l’informazione individuale e quella di gruppo.
Questa trasparenza concettuale ci permette di comprendere in profondità perché la struttura gerarchica sia la soluzione metodologicamente più appropriata per gestire la tensione fondamentale tra specificità individuale e generalizzazione a livello di popolazione. Questo non è un compromesso arbitrario, ma una conseguenza naturale del principio di scambiabilità e della struttura probabilistica del modello.
Una volta consolidata questa intuizione attraverso il caso beta-binomiale, il lettore sarà ben preparato a riconoscere gli stessi principi operativi nei modelli gaussiani a effetti misti, trasferendo la comprensione acquisita dall’analisi di dati discreti binomiali a quella di variabili continue senza dover ricominciare da zero con la logica inferenziale di base. I dettagli matematici possono cambiare, ma la filosofia statistica rimane invariata: condividere l’informazione in modo intelligente per migliorare le inferenze sia a livello individuale che a livello di popolazione.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] stringr_1.5.2 cmdstanr_0.9.0 ragg_1.5.0
#> [4] tinytable_0.13.0 withr_3.0.2 systemfonts_1.3.1
#> [7] patchwork_1.3.2 ggdist_3.3.3 tidybayes_3.0.7
#> [10] bayesplot_1.14.0 ggplot2_4.0.0 reliabilitydiag_0.2.1
#> [13] priorsense_1.1.1 posterior_1.6.1 loo_2.8.0
#> [16] rstan_2.32.7 StanHeaders_2.32.10 brms_2.23.0
#> [19] Rcpp_1.1.0 sessioninfo_1.2.3 conflicted_1.2.0
#> [22] janitor_2.2.1 matrixStats_1.5.0 modelr_0.1.11
#> [25] tibble_3.3.0 dplyr_1.1.4 tidyr_1.3.1
#> [28] rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 vctrs_0.6.5
#> [10] pkgconfig_2.0.3 arrayhelpers_1.1-0 fastmap_1.2.0
#> [13] backports_1.5.0 labeling_0.4.3 utf8_1.2.6
#> [16] rmarkdown_2.30 ps_1.9.1 purrr_1.1.0
#> [19] xfun_0.53 cachem_1.1.0 jsonlite_2.0.0
#> [22] broom_1.0.10 parallel_4.5.1 R6_2.6.1
#> [25] stringi_1.8.7 RColorBrewer_1.1-3 lubridate_1.9.4
#> [28] estimability_1.5.1 knitr_1.50 zoo_1.8-14
#> [31] pacman_0.5.1 Matrix_1.7-4 splines_4.5.1
#> [34] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [37] yaml_2.3.10 codetools_0.2-20 processx_3.8.6
#> [40] curl_7.0.0 pkgbuild_1.4.8 lattice_0.22-7
#> [43] bridgesampling_1.1-2 S7_0.2.0 coda_0.19-4.1
#> [46] evaluate_1.0.5 survival_3.8-3 RcppParallel_5.1.11-1
#> [49] pillar_1.11.1 tensorA_0.36.2.1 checkmate_2.3.3
#> [52] stats4_4.5.1 distributional_0.5.0 generics_0.1.4
#> [55] rprojroot_2.1.1 rstantools_2.5.0 scales_1.4.0
#> [58] xtable_1.8-4 glue_1.8.0 emmeans_1.11.2-8
#> [61] tools_4.5.1 data.table_1.17.8 mvtnorm_1.3-3
#> [64] grid_4.5.1 QuickJSR_1.8.1 colorspace_2.1-2
#> [67] nlme_3.1-168 cli_3.6.5 textshaping_1.0.4
#> [70] svUnit_1.0.8 Brobdingnag_1.2-9 V8_8.0.1
#> [73] gtable_0.3.6 digest_0.6.37 TH.data_1.1-4
#> [76] htmlwidgets_1.6.4 farver_2.1.2 memoise_2.0.1
#> [79] htmltools_0.5.8.1 lifecycle_1.0.4 MASS_7.3-65