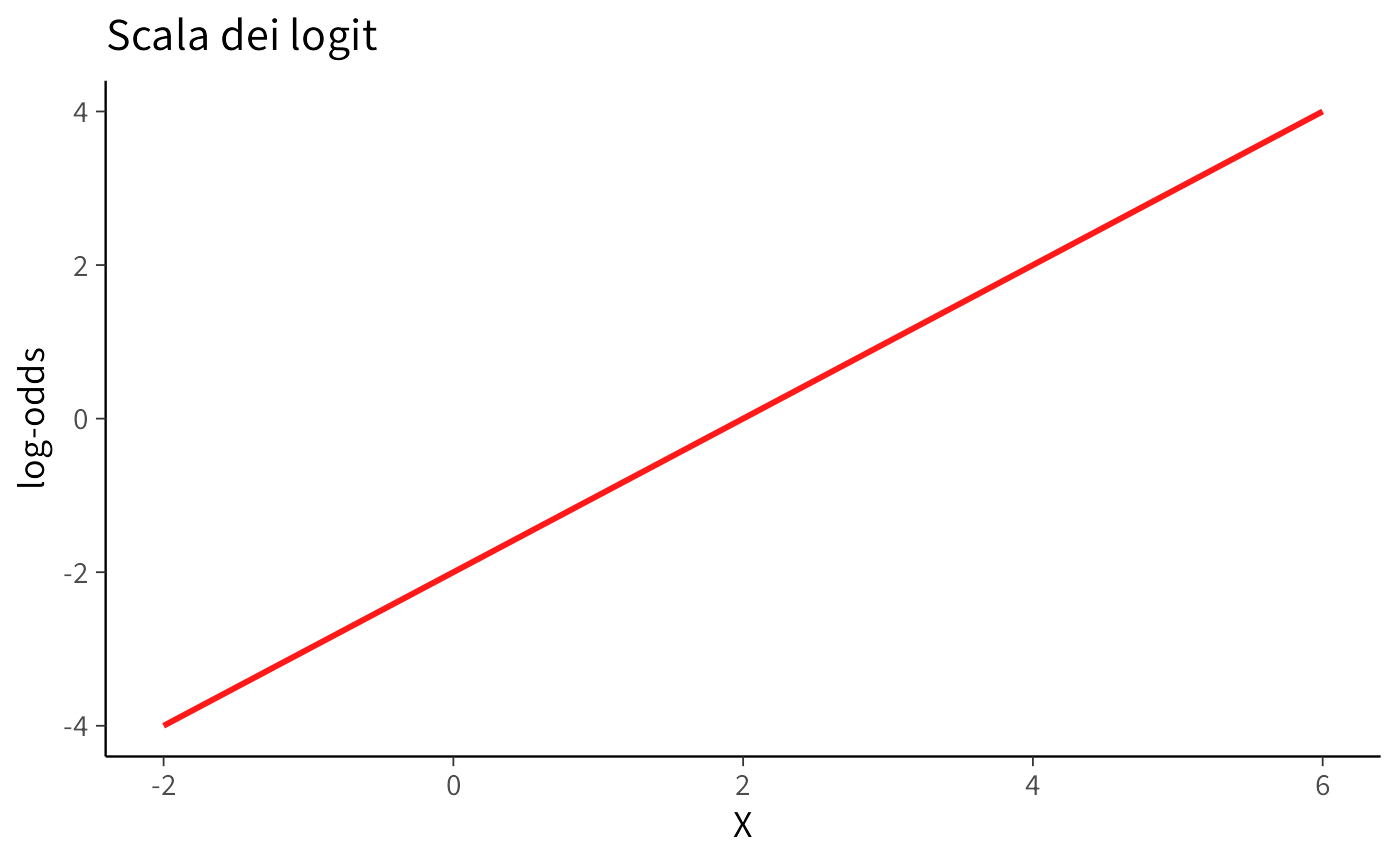here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, cmdstanr, posterior, brms, bayestestR, insight)30 Regressione logistica con Stan
Introduzione
La regressione logistica è un’estensione del modello lineare che consente di analizzare esiti dicotomici, ovvero variabili che assumono soltanto due valori (per esempio: successo/insuccesso, presenza/assenza, risposta corretta/errata). Situazioni di questo tipo sono molto frequenti nella ricerca psicologica: si pensi alle risposte a domande con risposta “vero” o “falso”, alla presenza o assenza di un sintomo clinico o alla scelta tra due alternative in un compito sperimentale.
A differenza della regressione lineare, non si modella direttamente la variabile dipendente, ma una trasformazione della probabilità di successo attraverso la funzione logit, definita come il logaritmo naturale del rapporto tra la probabilità di successo e quella di insuccesso. Questa parametrizzazione presenta due vantaggi: conserva la linearità nella relazione tra predittori e risultato trasformato e garantisce che le probabilità stimate rimangano nell’intervallo [0, 1], rispettando i vincoli probabilistici intrinseci al fenomeno in esame.
In questo capitolo ci concentreremo sulla regressione logistica bivariata, caratterizzata dall’inclusione di un singolo predittore di natura continua o categoriale. L’obiettivo è duplice: da un lato, acquisire familiarità con la stima bayesiana dei parametri del modello mediante l’utilizzo di Stan; dall’altro, sviluppare la capacità di interpretare i coefficienti stimati attraverso diverse scale metriche: probabilistica, odds ratio e risk ratio. In particolare, vedremo come un coefficiente unico possa assumere significati diversi a seconda della scala di lettura adottata e come il caso del predittore dicotomico costituisca una specializzazione del modello con variabile continua.
La regressione logistica rappresenta dunque un primo passo nell’ambito dei modelli lineari generalizzati (GLM), estendendo le possibilità dell’analisi statistica oltre i confini della regressione lineare tradizionale e gettando le basi per l’analisi di scenari di ricerca più complessi.
Panoramica del capitolo
- specificare una regressione logistica con un predittore continuo;
- interpretare i coefficienti sulla scala dei logit, degli odds e delle probabilità, ricavando in modo chiaro le relazioni algebriche tra \(RD\), \(OR\) e \(RR\);
- stimare il modello con approccio frequentista (glm) e bayesiano (brms/Stan), comprendendo l’effetto dei priori e leggendo le distribuzioni a posteriori;
- produrre predizioni posteriori su una griglia di valori di \(x\) e rappresentare l’incertezza con curve e intervalli credibili;
- valutare l’adeguatezza del modello attraverso i posterior predictive checks.
- Leggere il capitolo dedicato alla regressione statistica di Applied regression analysis and generalized linear models (Fox, 2015).
30.1 Il modello di regressione logistica
Consideriamo un campione di \(n\) unità sperimentali, ciascuna caratterizzata da un esito binario \(y_i \in \{0,1\}\) e un predittore continuo \(x_i\). Il modello di regressione logistica assume la seguente forma:
\[ \begin{aligned} y_i &\sim \mathrm{Bernoulli}(p_i), \\ \mathrm{logit}(p_i) &= \alpha + \beta x_i. \end{aligned} \]
In questa parametrizzazione, \(p_i\) rappresenta la probabilità di successo per dell’\(i\)-esima osservazione. Il parametro \(\alpha\) corrisponde al log-odds di successo quando \(x_i = 0\), mentre \(\beta\) quantifica la variazione attesa del log-odds per ogni incremento unitario del predittore \(x\).
Trasformando sulla scala degli odds, si ottiene:
\[ \mathrm{odds}(x) = \frac{p(x)}{1-p(x)} = \exp(\alpha + \beta x). \]
Il confronto tra due valori consecutivi del predittore, \(x=a\) e \(x=a+1\), rivela che:
\[ \frac{\mathrm{odds}(a+1)}{\mathrm{odds}(a)} = e^{\beta}. \]
Pertanto, l’esponenziale di \(\beta\) corrisponde all’odds ratio (OR): il fattore moltiplicativo che descrive la variazione degli odds associata a un incremento unitario di \(x\). Ad esempio, un coefficiente \(\beta = 1.0\) produce un OR di circa \(2.7\), indicando che ogni unità aggiuntiva di \(x\) moltiplica gli odds di successo per \(2.7\).
Nel modello logistico \(\log\!\big(\tfrac{p(x)}{1-p(x)}\big)=\alpha+\beta x\), gli odds in corrispondenza di un valore \(x\) sono dati da \(\tfrac{p(x)}{1-p(x)}=\exp(\alpha+\beta x)\). Confrontando due valori distinti del predittore, \(x=a\) e \(x=b\), l’odds ratio che confronta \(b\) rispetto ad \(a\) è definito come
\[ OR(b\,\text{vs}\,a) =\frac{\tfrac{p(b)}{1-p(b)}}{\tfrac{p(a)}{1-p(a)}} =\frac{\exp(\alpha+\beta b)}{\exp(\alpha+\beta a)} =\exp\!\big(\beta(b-a)\big). \]
Nel caso specifico di una variazione unitaria (\(b=a+1\)), si ottiene
\[ OR(a+1\,\text{vs}\,a)=\exp(\beta). \]
Questa relazione mette in luce due proprietà fondamentali del modello. In primo luogo, l’odds ratio dipende esclusivamente dalla differenza \(b-a\), risultando indipendente dal livello base \(a\). In un modello logistico bivariato, l’OR associato a un incremento fisso rimane costante lungo tutto l’asse delle ascisse. In secondo luogo, l’interpretazione di \(\beta\) è strettamente legata alla scala di misurazione di \(x\): quando \(x\) è una variabile dummy \(\{0,1\}\), \(\beta\) rappresenta il log-odds ratio tra i due gruppi e \(\exp(\beta)\) l’OR corrispondente; se \(x\) subisce un incremento di 10 unità, \(\exp(10\beta)\) esprime l’OR per tale variazione; se \(x\) è standardizzato (ad esempio in punteggi z), \(\exp(\beta)\) rappresenta l’OR associato a un incremento di una deviazione standard.
30.2 Risk difference, odds ratio e risk ratio
Consideriamo due valori distinti del predittore, \(x=a\) e \(x=b\), e indichiamo con
\[ p_a = \text{logit}^{-1}(\alpha + \beta a), \qquad p_b = \text{logit}^{-1}(\alpha + \beta b) \] le probabilità di successo corrispondenti. La differenza tra i due livelli può essere quantificata attraverso tre misure distinte ma coerenti.
La risk difference (RD), o differenza assoluta di rischio, è definita come \[ RD = p_b - p_a . \] Questa misura esprime la variazione assoluta nella probabilità di successo tra i due livelli del predittore.
L’odds ratio (OR) è dato da \[ OR = \frac{p_b/(1-p_b)}{p_a/(1-p_a)} = \exp\!\bigl(\beta(b-a)\bigr). \] Questo rapporto descrive la variazione relativa negli odds di successo associata al passaggio da \(a\) a \(b\).
Il risk ratio (RR), o rapporto di rischio, è definito come \[ RR = \frac{p_b}{p_a}. \] Questa misura, particolarmente utilizzata in epidemiologia, esprime il rapporto diretto tra le probabilità di successo ai due livelli del predittore.
Ciascuna di queste misure fornisce una prospettiva diversa ma complementare sull’effetto del predittore, con proprietà matematiche e campi di applicazione specifici.
30.2.1 Scala delle probabilità e la regola del “dividere per 4”
La relazione funzionale tra il predittore \(x\) e la probabilità \(p(x)\) è data dalla curva logistica:
\[ p(x) = \frac{e^{\alpha + \beta x}}{1 + e^{\alpha + \beta x}}. \]
La variazione nella probabilità associata a un incremento unitario di \(x\),
\[ \Delta p = p(x+1) - p(x), \]
non è costante ma dipende dal valore iniziale di \(x\). Questa variazione risulta minima nelle regioni estreme della curva, quando \(p\) si avvicina a 0 o 1, mentre raggiunge il suo massimo nella regione centrale, in corrispondenza di \(p \approx 0.5\), dove la curva presenta la massima pendenza.
Analiticamente, la derivata della funzione logistica è data da
\[ \frac{dp}{dx} = \beta \, p(x)\,[1 - p(x)]. \]
Il termine \(p(x)(1-p(x))\), che rappresenta la varianza della distribuzione Bernoulli sottostante, assume il valore massimo di \(0.25\) quando \(p=0.5\). Di conseguenza, la massima variazione istantanea della probabilità per unità di \(x\) risulta
\[ \max \frac{dp}{dx} = \frac{\beta}{4}. \]
Questo risultato costituisce la regola del dividere per 4: un’euristica che fornisce una stima approssimata dell’effetto massimo di \(\beta\) sulla scala probabilistica. Ad esempio, con \(\beta=1.0\), l’incremento massimo di probabilità per unità di \(x\) è circa 0.25 (25 punti percentuali), osservabile quando \(p=0.5\). Sebbene questa approssimazione non sia esatta per tutti i valori di \(x\), offre un’intuizione immediata sull’ordine di grandezza dell’effetto del coefficiente \(\beta\) sulla probabilità di successo.
30.2.2 Sintesi
Il coefficiente \(\beta\) della regressione logistica ha interpretazioni coerenti su scale diverse:
- sulla scala logit è la variazione lineare dei log-odds;
- sulla scala odds il suo esponenziale è l’odds ratio, il moltiplicatore degli odds;
- sulla scala probabilità descrive variazioni non costanti, con massimo effetto pari a circa \(\beta/4\) quando \(p=0.5\).
Queste interpretazioni non sono alternative ma complementari: lo stesso coefficiente viene letto in tre linguaggi diversi, offrendo prospettive complementari sul legame tra \(x\) e la probabilità di successo.
30.2.3 Visualizzazione delle tre scale
Per fissare meglio le idee, possiamo rappresentare graficamente l’effetto del coefficiente \(\beta\) sulle tre scale: logit, odds e probabilità. Useremo valori simulati per poter confrontare direttamente i tre casi.
30.2.3.1 Come leggere i tre grafici
- Scala logit: la relazione con \(x\) è lineare. Ogni unità in più di \(x\) aumenta i log-odds di \(\beta\).
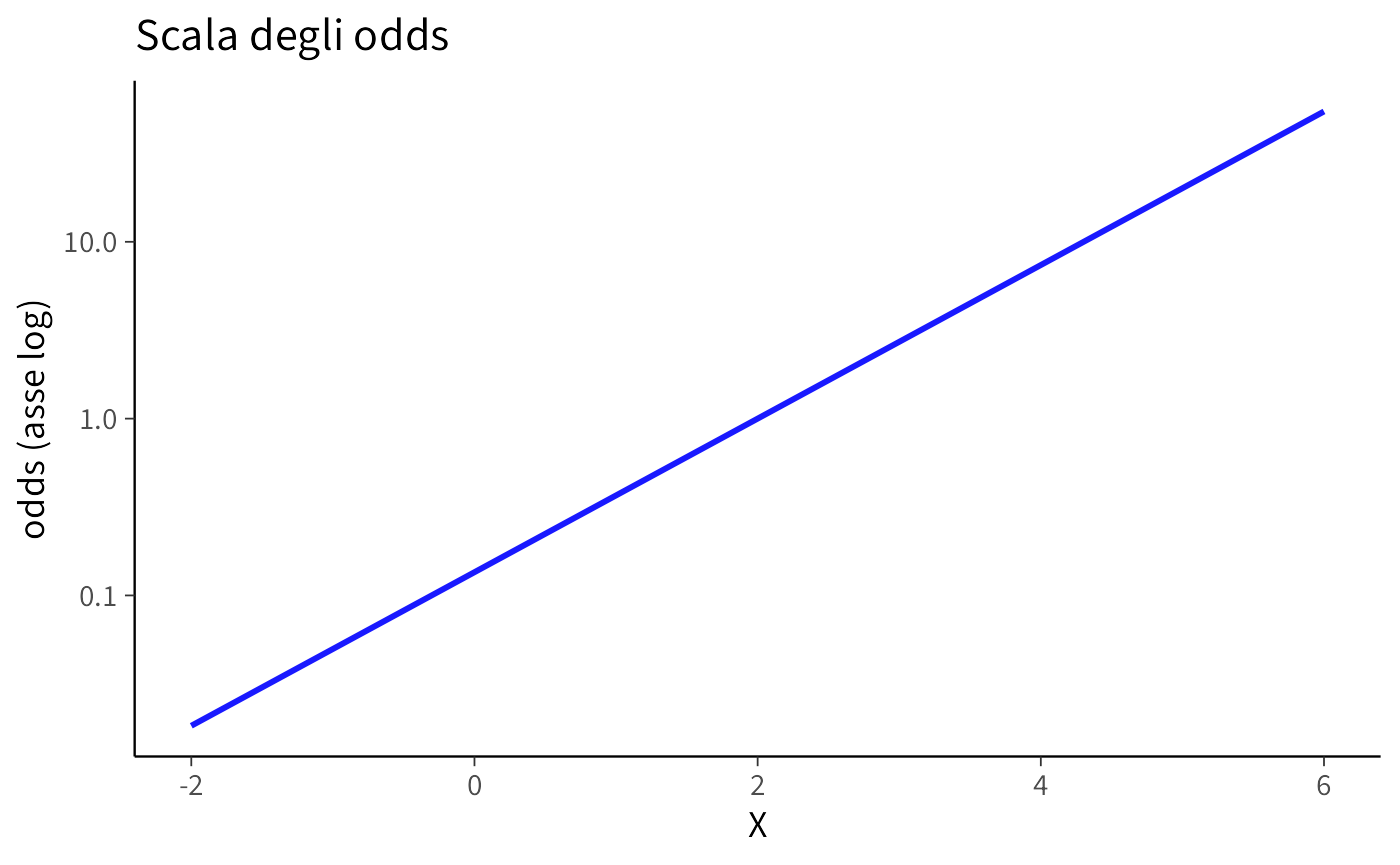
- Scala odds: la crescita è esponenziale. In questo caso, \(\exp(\beta)\) indica di quanto si moltiplicano gli odds per ogni unità aggiuntiva di \(x\).
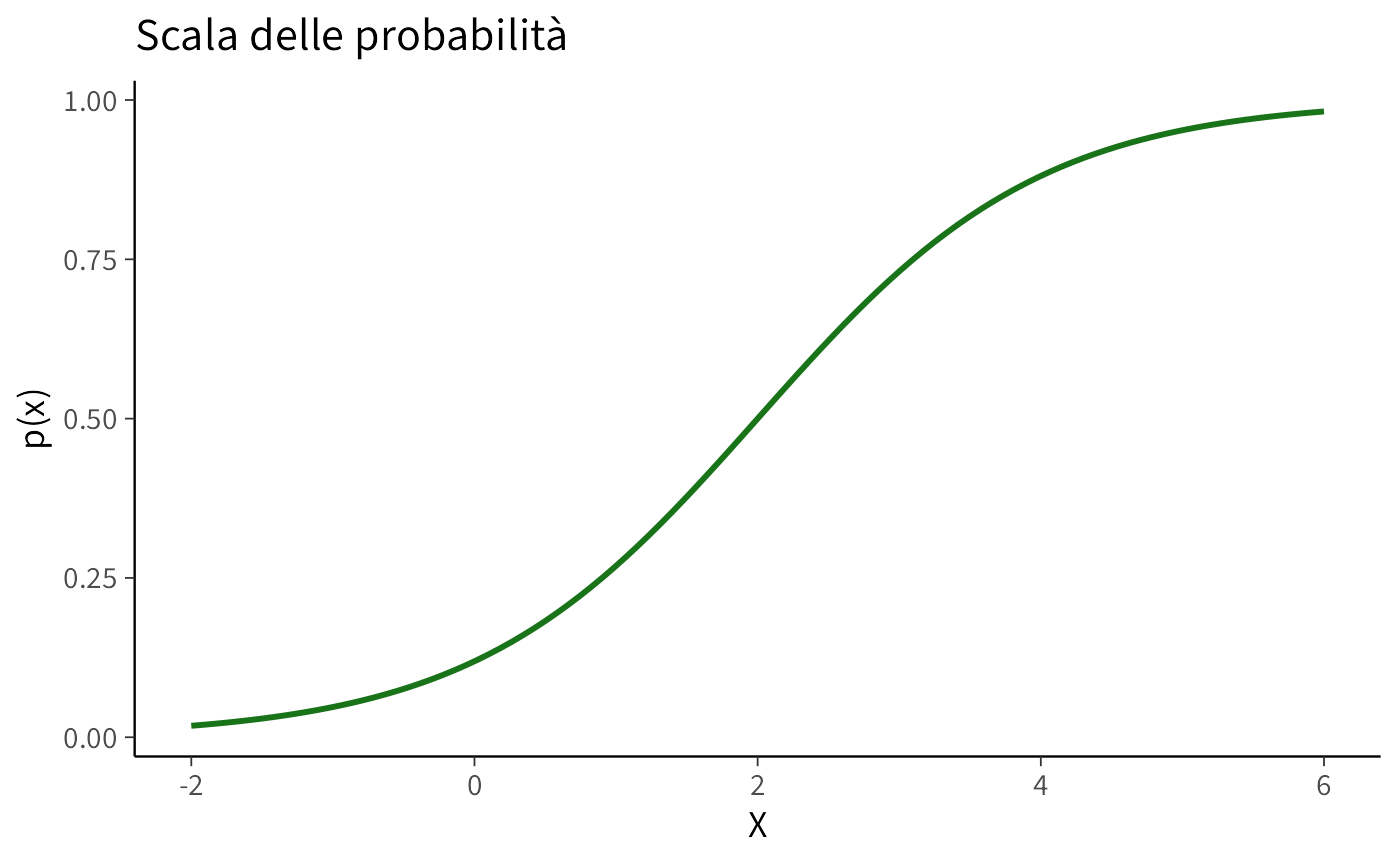
- Scala probabilità: la curva è sigmoide e rimane sempre compresa tra 0 e 1. L’effetto di \(\beta\) non è costante: è massimo quando \(p \approx 0.5\), e minimo ai margini, quando la curva è piatta.
30.2.4 Interpretazione didattica
La regressione logistica cattura una relazione non lineare tra il predittore \(x\) e la probabilità di successo \(p(x)\), generando una caratteristica curva sigmoide. Questa presenta un andamento asintotico: per valori estremamente bassi di \(x\) la probabilità converge a 0, mentre per valori elevati tende a 1, con la transizione più marcata nella regione centrale dove la curva manifesta la massima pendenza.
Il segno del coefficiente β determina la direzionalità dell’effetto. Un valore di \(\beta > 0\) indica che, con l’aumentare di \(x\), crescono sistematicamente i log-odds, gli odds e la probabilità di successo, producendo una curva monotona crescente. Al contrario, un valore di \(\beta\) inferiore a 0 segnala una relazione inversa, con la curva che assume un andamento decrescente.
La medesima relazione può essere interpretata anche attraverso scale metriche alternative che offrono una prospettiva complementare. Sulla scala delle probabilità, si osserva la variazione assoluta di p(x), che dipende dal punto di partenza lungo la curva. Sulla scala degli odds, l’effetto si manifesta attraverso un moltiplicatore costante, \(OR = e^{\beta}\), per ogni incremento unitario di \(x\). Sulla scala logit, la relazione assume invece una forma linearmente additiva, con \(\beta\) che rappresenta il cambiamento costante nei log-odds.
A completare il quadro interpretativo ci sono la risk difference (RD), che quantifica la differenza assoluta di probabilità tra due livelli di x, e il risk ratio (RR), che ne esprime il rapporto relativo. Sebbene queste misure non derivino direttamente dal coefficiente β come l’odds ratio, costituiscono metriche di immediata comprensione in numerosi contesti applicativi, in particolare in ambito epidemiologico e clinico.
La potenza euristica della regressione logistica risiede proprio nella sua capacità di unificazione: un unico modello matematico genera simultaneamente tre diverse chiavi di lettura - logit, odds e probabilità - che, se integrate sinergicamente, consentono di caratterizzare in modo completo e coerente l’influenza di una variabile indipendente su un esito binario.
30.3 Esempio numerico
Simuliamo dei dati con un predittore discreto \(X\) e una variabile dicotomica \(Y\), in cui la probabilità di successo cresce con \(X\). Applichiamo quindi la regressione logistica e tracciamo la curva stimata, confrontandola con le proporzioni empiriche osservate.
# Fissiamo il seme per riproducibilità
set.seed(42)
# Numero di osservazioni
n <- 1000
# Predittore X: estraiamo numeri interi fra 0 e 9 con uguale probabilità
X <- sample(0:9, n, replace = TRUE)
# Definiamo una funzione logistica che restituisce plogis(alpha + beta * x),
# cioè la trasformazione inversa del logit
logistic <- function(x, beta0, beta1) plogis(beta0 + beta1 * x)
# Parametri veri del modello usato per simulare i dati
beta0 <- -2 # intercetta
beta1 <- 1 # coefficiente
# Calcoliamo la probabilità di successo associata a ciascun valore di X
p <- logistic(X, beta0, beta1)
# Generiamo i dati binari (0/1) da una distribuzione binomiale di Bernoulli
Y <- rbinom(n, size = 1, prob = p)
# Creiamo un data frame con i dati simulati
df <- tibble::tibble(X = X, Y = Y)
head(df)
#> # A tibble: 6 × 2
#> X Y
#> <int> <int>
#> 1 0 0
#> 2 4 1
#> 3 0 0
#> 4 8 1
#> 5 9 1
#> 6 3 0Stima del modello di regressione logistica con funzione glm():
# Creiamo una griglia di valori di X su cui calcolare le probabilità predette
x_vals <- seq(min(df$X), max(df$X), length.out = 100)
# Data frame per le predizioni
pred_df <- data.frame(X = x_vals)
# Calcoliamo le probabilità predette dal modello (scala di risposta, cioè probabilità)
pred_df$pred <- predict(logit_model, newdata = pred_df, type = "response")Grafico finale:
ggplot(df, aes(x = X, y = Y)) +
# Per ogni valore di X mostriamo la proporzione empirica di successi (punti blu)
stat_summary(fun = mean, geom = "point", color = "blue") +
# Sovrapponiamo la curva logistica stimata dal modello (linea rossa)
geom_line(data = pred_df, aes(x = X, y = pred), color = "red") +
# Etichette degli assi
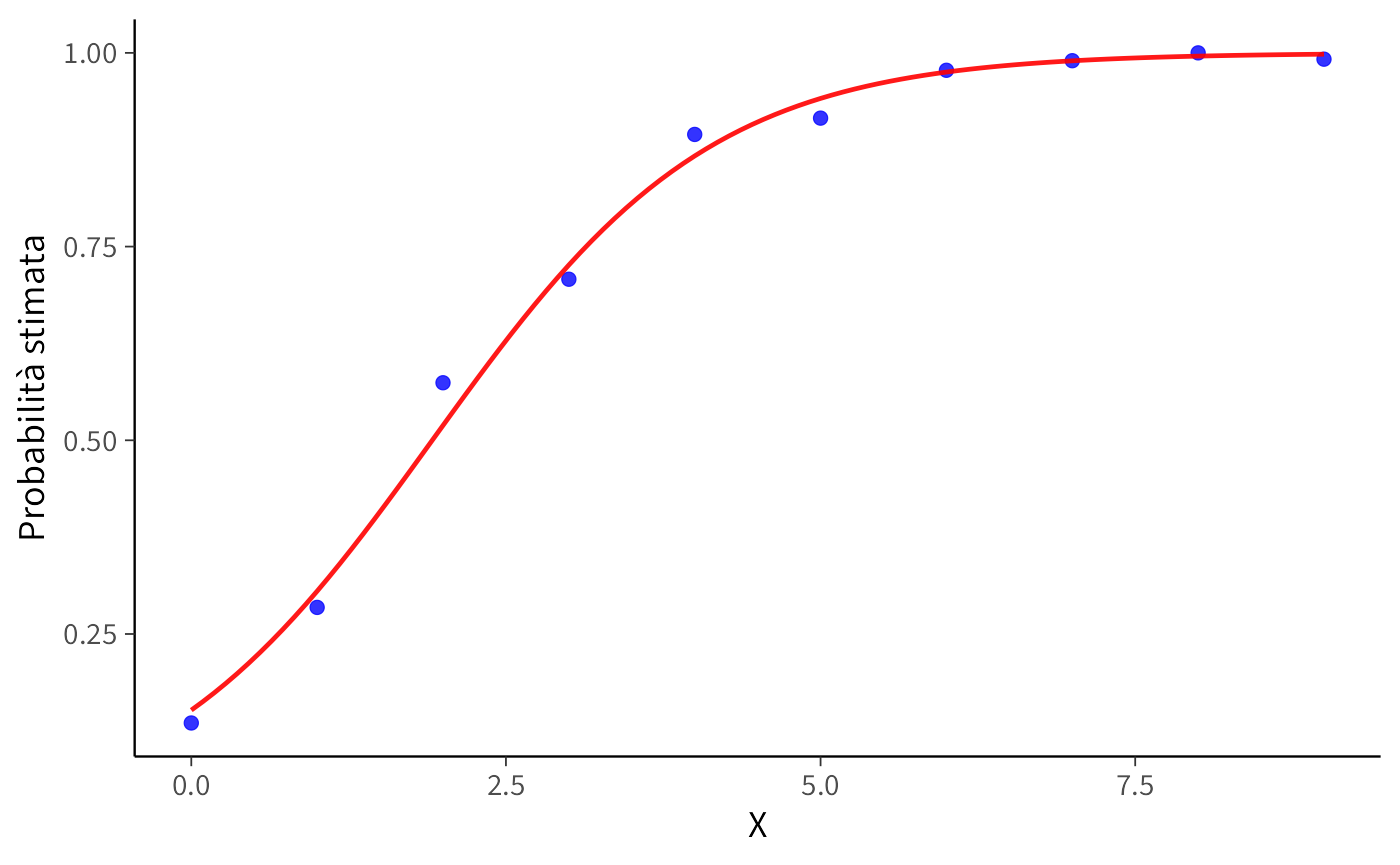
labs(x = "X", y = "Probabilità stimata")In questo esempio i punti blu rappresentano la proporzione empirica di successi per ciascun valore di \(X\), mentre la linea rossa mostra la curva logistica stimata dal modello. La forma sigmoide emerge naturalmente e garantisce che le probabilità rimangano sempre comprese tra 0 e 1.
30.4 Stima bayesiana con Stan
Finora abbiamo stimato i coefficienti \(\alpha\) e \(\beta\) con la funzione glm(), ottenendo valori puntuali secondo il metodo della massima verosimiglianza. Con Stan possiamo costruire lo stesso modello in chiave bayesiana, specificando priori debolmente informativi. Ciò ci permette di ottenere l’intera distribuzione a posteriori dei parametri, invece di un singolo valore di stima, e di quantificare direttamente l’incertezza.
Un dettaglio importante è che i risultati di Stan possono differire leggermente da quelli di glm(). La ragione è proprio la presenza dei priori: anche se scelti molto larghi (qui, per esempio, normal(0, 2.5)), essi esercitano un piccolo “effetto di contrazione” verso lo zero, soprattutto con campioni finiti. In assenza di priori (o con dati molto abbondanti), le due stime coincidono. Questa differenza è preziosa dal punto di vista didattico, perché mostra come l’approccio frequentista possa essere considerato un caso limite di quello bayesiano.
30.4.1 Il modello in Stan
Il modello di regressione logistica per un predittore continuo si scrive così:
stan_code <- '
data {
int<lower=0> N; // numero di osservazioni
array[N] int<lower=0, upper=1> y; // esiti (0/1)
vector[N] x; // predittore
}
parameters {
real alpha; // intercetta
real beta; // coefficiente di regressione
}
model {
// prior deboli
alpha ~ normal(0, 2.5);
beta ~ normal(0, 2.5);
// verosimiglianza
y ~ bernoulli_logit(alpha + beta * x);
}
generated quantities {
real OR = exp(beta); // odds ratio
}
'Questo modello assume gli stessi dati simulati nell’esempio precedente. Prepariamo i dati:
Compiliamo e eseguiamo il campionamento:
mod <- cmdstan_model(write_stan_file(stan_code))fit <- mod$sample(
data = stan_data,
seed = 123,
chains = 4, parallel_chains = 4,
iter_warmup = 1000, iter_sampling = 2000
)30.4.2 Risultati
Esaminiamo ora i coefficienti stimati dal modello bayesiano:
fit$summary(variables = c("alpha","beta","OR"))
#> # A tibble: 3 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 alpha -1.72 -1.72 0.171 0.170 -2.01 -1.45 1.00 2674. 2762.
#> 2 beta 0.901 0.899 0.0621 0.0620 0.802 1.01 1.00 2688. 2860.
#> 3 OR 2.47 2.46 0.154 0.153 2.23 2.74 1.00 2688. 2860.L’output fornisce per ciascun parametro la media posteriore, la deviazione standard e gli intervalli di credibilità. Il coefficiente \(\beta\) presenta un intervallo di credibilità interamente positivo, in linea con la struttura generativa dei dati, mentre l’odds ratio stimato si colloca completamente al di sopra di 1. Questo risultato suggerisce una relazione positiva tra il predittore e l’outcome: all’aumentare di \(X\) si osserva un incremento sistematico della probabilità di successo.
30.4.3 Interpretazione sulle tre scale
Le distribuzioni posteriori dei parametri \(\alpha\) e \(\beta\) possono essere interpretate attraverso le tre scale metriche precedentemente introdotte.
Scala dei logit
L’intercetta \(\alpha\) rappresenta i log-odds quando \(x=0\). Una stima posteriore di \(\alpha \approx -2\) con CrI 95% [-2.2, -1.8] indica che al valore di riferimento del predittore la probabilità di successo è marcatamente bassa. Il coefficiente \(\beta\), con valore centrale di 1 e CrI 95% [0.9, 1.1], segnala che ogni incremento unitario di \(x\) determina un aumento di circa un punto nei log-odds di successo.
Scala degli odds
Mediante l’esponenziazione di \(\beta\) si ottiene l’odds ratio. Con \(\beta \approx 1\), la distribuzione posteriore di \(OR\) risulta centrata attorno a 2.7, con CrI 95% [2.5, 3.0]. Questo intervallo di credibilità indica che, con elevata probabilità, un incremento unitario di \(x\) moltiplica gli odds di successo per un fattore compreso tra 2.5 e 3.
Scala delle probabilità
Applicando la trasformazione logistica si ricava \(p(x) = \text{logit}^{-1}(\alpha + \beta x)\). Campionando dalla distribuzione congiunta a posteriori dei parametri è possibile generare un insieme di curve sigmoidi plausibili, che rappresentano l’incertezza inferenziale in modo completo. Nella regione centrale della curva, dove \(p \approx 0.5\), la pendenza raggiunge il suo massimo teorico di circa \(\beta/4\). Con \(\beta \approx 1\), questo si traduce in un incremento massimo di probabilità di circa 25 punti percentuali per ogni unità aggiuntiva di \(x\).
30.4.4 Quantità derivate: RD, OR, RR
Possiamo anche confrontare due valori specifici del predittore, ad esempio \(x=0\) e \(x=1\), e derivare da ciascun draw posteriore tre misure di interesse:
# Estrazione dei campioni posteriori
post <- as_draws_df(fit)
# Confronto tra x=0 e x=1
x_a <- 0
x_b <- 1
post <- post %>%
mutate(
p_a = plogis(alpha + beta * x_a),
p_b = plogis(alpha + beta * x_b),
RD = p_b - p_a,
OR = exp(beta * (x_b - x_a)),
RR = p_b / p_a
)
posterior_summary <- tibble(
quantity = c("p_a (x=0)", "p_b (x=1)", "RD (p_b - p_a)", "OR", "RR"),
mean = c(mean(post$p_a), mean(post$p_b),
mean(post$RD), mean(post$OR), mean(post$RR)),
q2.5 = c(quantile(post$p_a, .025), quantile(post$p_b, .025),
quantile(post$RD, .025), quantile(post$OR, .025), quantile(post$RR, .025)),
q97.5 = c(quantile(post$p_a, .975), quantile(post$p_b, .975),
quantile(post$RD, .975), quantile(post$OR, .975), quantile(post$RR, .975))
)
posterior_summary
#> # A tibble: 5 × 4
#> quantity mean q2.5 q97.5
#> <chr> <dbl> <dbl> <dbl>
#> 1 p_a (x=0) 0.153 0.112 0.198
#> 2 p_b (x=1) 0.307 0.255 0.359
#> 3 RD (p_b - p_a) 0.153 0.137 0.170
#> 4 OR 2.47 2.20 2.80
#> 5 RR 2.02 1.79 2.32In questa rappresentazione, \(p_a\) e \(p_b\) indicano le probabilità predette corrispondenti a due diversi valori del predittore \(x\). La risk difference costituisce la differenza assoluta tra queste probabilità, mentre l’odds ratio corrisponde a \(e^\beta\), e il risk ratio esprime il rapporto diretto tra \(p_b\) e \(p_a\). Ciascuna di queste quantità, essendo derivata dalla distribuzione posteriore dei parametri, possiede a sua volta una distribuzione di probabilità completa, caratterizzata da propri intervalli di credibilità che ne quantificano l’incertezza inferenziale.
30.4.5 Visualizzazione dell’incertezza
Per rappresentare adeguatamente la variabilità predittiva del modello, è possibile visualizzare un campione di curve estratte dalla distribuzione a posteriori, affiancandole alla curva media:
x_grid <- seq(0, 9, length.out = 100)
pred_curves <- post %>%
slice_sample(n = 200) %>%
mutate(.draw = row_number()) %>%
expand_grid(x = x_grid) %>%
mutate(p = plogis(alpha + beta * x))
pred_mean <- post %>%
expand_grid(x = x_grid) %>%
group_by(x) %>%
summarise(p = mean(plogis(alpha + beta * x)), .groups = "drop")
ggplot() +
geom_line(data = pred_curves, aes(x = x, y = p, group = .draw),
alpha = 0.1, color = "grey") +
geom_line(data = pred_mean, aes(x = x, y = p),
color = "black", size = 1) +
labs(
x = "X", y = "Probabilità stimata"
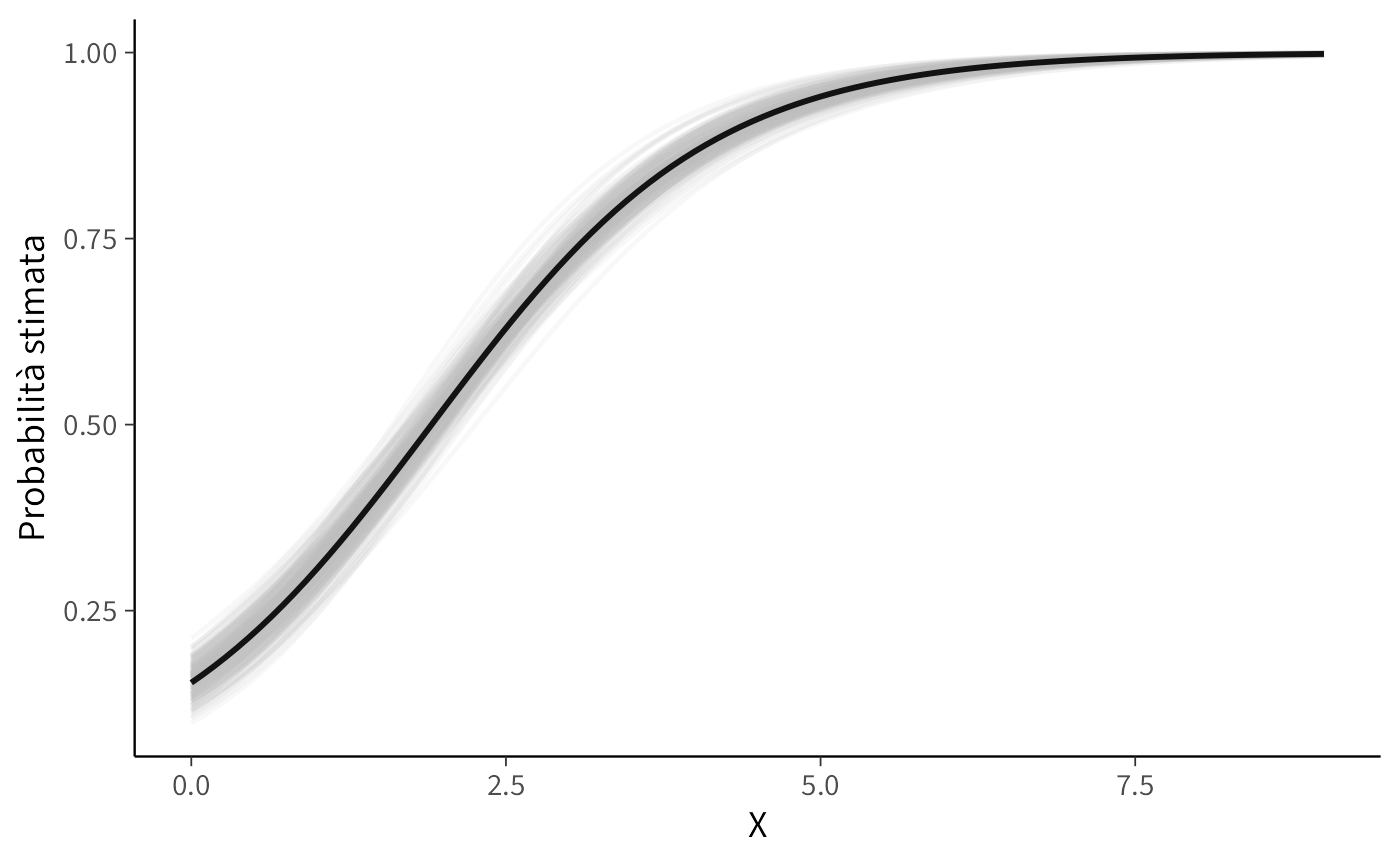
)La visualizzazione risultante evidenzia come i dati supportino un’intera famiglia di relazioni logistiche plausibili. La curva nera rappresenta la relazione media posteriore, mentre il ventaglio di curve grigie rende tangibile l’incertezza inferenziale, mostrando l’intero spettro di andamenti compatibili con l’evidenza empirica.
30.4.6 Sintesi
Rispetto all’approccio tradizionale tramite la funzione glm(), il framework bayesiano implementato con Stan offre una rappresentazione inferenziale più completa e trasparente. Oltre alle stime puntuali e agli errori standard, fornisce distribuzioni posteriori complete per tutti i parametri del modello e per qualsiasi quantità derivabile da essi. Questa ricchezza informativa consente di fare affermazioni probabilisticamente fondate, come l’asserzione che “con probabilità posteriore del 95%, l’odds ratio è compreso tra 2,5 e 3,0” o che “l’effetto massimo sulla scala probabilistica ammonta a circa 25 punti percentuali per ogni unità incrementale di \(x\)”.
In definitiva, la regressione logistica in ottica bayesiana non si limita a riprodurre i risultati dell’approccio frequentista, ma li potenzia attraverso una caratterizzazione completa dell’incertezza e inferenze direttamente interpretabili in termini di probabilità soggettive, offrendo un quadro più solido per le decisioni scientifiche.
| Scala | Quantità | Media [CrI 95%] |
|---|---|---|
| Logit | α (log-odds a x=0) | -1.721 [-2.068, -1.399] |
| Logit | β (incremento di log-odds per +1 in X) | 0.901 [0.787, 1.031] |
| Odds | OR = exp(β) per +1 in X | 2.467 [2.196, 2.804] |
| Probabilità | p(x=0) | 0.153 [0.112, 0.198] |
| Probabilità | p(x=1) | 0.307 [0.255, 0.359] |
| Probabilità | RD = p(x=1) - p(x=0) | 0.153 [0.137, 0.170] |
| Probabilità | RR = p(x=1) / p(x=0) | 2.020 [1.787, 2.320] |
| Probabilità | Pendenza massima ≈ β/4 (a p≈0.5) | 0.225 [0.197, 0.258] |
30.5 Collegamento con il caso a due gruppi
Quando il predittore \(x\) assume la forma di una variabile dicotomica, codificata come 0 per un gruppo di riferimento e 1 per il gruppo sperimentale, il modello di regressione logistica si riduce esattamente al caso del confronto tra due proporzioni. In questo scenario specifico otteniamo:
\[ p_{\text{ref}} = \text{logit}^{-1}(\alpha), \qquad p_{\text{work}} = \text{logit}^{-1}(\alpha + \gamma), \] da cui derivano naturalmente
\[ RD = p_{\text{work}} - p_{\text{ref}}, \qquad OR = \exp(\gamma), \qquad RR = \frac{p_{\text{work}}}{p_{\text{ref}}}. \] Il confronto fra due gruppi, dunque, non è un modello a sé stante, ma un caso particolare all’interno del quadro generale della regressione logistica. Questo ponte concettuale è importante perché mostra come il caso elementare del confronto tra due proporzioni si inserisca nello stesso quadro teorico della regressione logistica con predittori continui. Questa continuità metodologica getta le basi per il successivo capitolo, che sarà interamente dedicato all’approfondimento analitico del confronto tra proporzioni nel contesto bayesiano.
Riflessioni conclusive
La regressione logistica estende in modo naturale il modello lineare agli esiti binari: linearizza la relazione tramite il logit, mantiene l’interpretabilità dei coefficienti e rispetta i vincoli probabilistici. Il medesimo coefficiente può essere letto su tre scale complementari: come variazione dei log-odds (logit), come odds ratio tramite esponenziazione, e come cambiamento della probabilità (massimo ≈ \(\beta/4\) attorno a \(p=0.5\)). Questa tripla lettura non duplica l’informazione, ma la completa, permettendo di rispondere a domande diverse con lo stesso modello.
L’inferenza bayesiana (via Stan) aggiunge ciò che spesso manca nelle stime puntuali: una descrizione esplicita dell’incertezza sui parametri e sulle quantità derivate (OR, RD, RR, predizioni). Le distribuzioni a posteriori, insieme ai posterior predictive checks, rendono trasparenti robustezza inferenziale e l’adeguatezza del modello.
Per la psicologia, dove abbondano gli esiti 0/1 (corretto/errato, presenza/assenza, scelta A/B), la regressione logistica offre un ponte chiaro tra ipotesi teoriche e dati osservati, consentendo di quantificare gli effetti, confrontare le condizioni e formulare previsioni interpretabili dal punto di vista applicativo (sia in ambito clinico che sperimentale).
Più che un punto d’arrivo, è una porta d’accesso ai GLM: lo stesso impianto si può generalizzare a più predittori, interazioni, predittori categorici/continui e si può arrivare fino a estensioni gerarchiche e a modelli con link e distribuzioni diverse. Nei capitoli successivi useremo questo quadro unificato per affrontare scenari più complessi, mantenendo coerenza formale e leggibilità dei risultati.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] knitr_1.50 glue_1.8.0 insight_1.4.2
#> [4] bayestestR_0.17.0 cmdstanr_0.9.0 ragg_1.5.0
#> [7] tinytable_0.13.0 withr_3.0.2 systemfonts_1.3.1
#> [10] patchwork_1.3.2 ggdist_3.3.3 tidybayes_3.0.7
#> [13] bayesplot_1.14.0 ggplot2_4.0.0 reliabilitydiag_0.2.1
#> [16] priorsense_1.1.1 posterior_1.6.1 loo_2.8.0
#> [19] rstan_2.32.7 StanHeaders_2.32.10 brms_2.23.0
#> [22] Rcpp_1.1.0 sessioninfo_1.2.3 conflicted_1.2.0
#> [25] janitor_2.2.1 matrixStats_1.5.0 modelr_0.1.11
#> [28] tibble_3.3.0 dplyr_1.1.4 tidyr_1.3.1
#> [31] rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 vctrs_0.6.5
#> [10] stringr_1.5.2 pkgconfig_2.0.3 arrayhelpers_1.1-0
#> [13] fastmap_1.2.0 backports_1.5.0 labeling_0.4.3
#> [16] utf8_1.2.6 rmarkdown_2.30 ps_1.9.1
#> [19] purrr_1.1.0 xfun_0.53 cachem_1.1.0
#> [22] jsonlite_2.0.0 broom_1.0.10 parallel_4.5.1
#> [25] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [28] lubridate_1.9.4 estimability_1.5.1 zoo_1.8-14
#> [31] pacman_0.5.1 Matrix_1.7-4 splines_4.5.1
#> [34] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [37] yaml_2.3.10 codetools_0.2-20 processx_3.8.6
#> [40] curl_7.0.0 pkgbuild_1.4.8 lattice_0.22-7
#> [43] bridgesampling_1.1-2 S7_0.2.0 coda_0.19-4.1
#> [46] evaluate_1.0.5 survival_3.8-3 RcppParallel_5.1.11-1
#> [49] pillar_1.11.1 tensorA_0.36.2.1 checkmate_2.3.3
#> [52] stats4_4.5.1 distributional_0.5.0 generics_0.1.4
#> [55] rprojroot_2.1.1 rstantools_2.5.0 scales_1.4.0
#> [58] xtable_1.8-4 emmeans_1.11.2-8 tools_4.5.1
#> [61] data.table_1.17.8 mvtnorm_1.3-3 grid_4.5.1
#> [64] QuickJSR_1.8.1 colorspace_2.1-2 nlme_3.1-168
#> [67] cli_3.6.5 textshaping_1.0.4 svUnit_1.0.8
#> [70] Brobdingnag_1.2-9 V8_8.0.1 gtable_0.3.6
#> [73] digest_0.6.37 TH.data_1.1-4 htmlwidgets_1.6.4
#> [76] farver_2.1.2 memoise_2.0.1 htmltools_0.5.8.1
#> [79] lifecycle_1.0.4 MASS_7.3-65