here::here("code", "_common.R") |>
source()
library(igraph)
library(ggraph)
library(tidygraph)
# Funzione per calcolare la lunghezza media del codice di Huffman
huffman_encoding <- function(probabilities) {
# Crea la "coda con priorità" iniziale come lista di liste
heap <- lapply(names(probabilities), function(sym) list(probabilities[[sym]], list(sym, "")))
# Funzione per ordinare la heap per probabilità (peso)
sort_heap <- function(heap) {
heap[order(sapply(heap, function(x) x[[1]]))]
}
# Costruzione dell'albero di Huffman
while (length(heap) > 1) {
heap <- sort_heap(heap)
lo <- heap[[1]]
hi <- heap[[2]]
heap <- heap[-c(1, 2)]
# Aggiunge i prefissi "0" e "1" ai codici
for (i in seq_along(lo)[-1]) {
lo[[i]][[2]] <- paste0("0", lo[[i]][[2]])
}
for (i in seq_along(hi)[-1]) {
hi[[i]][[2]] <- paste0("1", hi[[i]][[2]])
}
merged <- c(list(lo[[1]] + hi[[1]]), lo[-1], hi[-1])
heap <- append(heap, list(merged))
}
# Estrai la lista finale dei simboli e codici
final <- heap[[1]][-1]
names(final) <- sapply(final, function(x) x[[1]])
# Crea dizionario con codici
huffman_dict <- lapply(final, function(x) x[[2]])
# Calcolo della lunghezza media del codice
avg_length <- sum(mapply(function(sym, code) {
probabilities[[sym]] * nchar(code)
}, names(huffman_dict), huffman_dict))
return(list(avg_length = avg_length, codes = huffman_dict))
}42 Entropia e informazione di Shannon
Introduzione
In ambito probabilistico, l’entropia fornisce una misura quantitativa del grado di incertezza o imprevedibilità di un sistema. Si consideri, a titolo esemplificativo, il tentativo di prevedere la risposta di uno studente a un test a scelta multipla. In assenza di informazioni specifiche sulla sua preparazione, l’ipotesi più conservativa è che tutte le opzioni siano equiprobabili, una condizione che corrisponde al massimo livello di incertezza. Al contrario, qualora si sapesse che lo studente è molto preparato e fornisce quasi sempre la risposta corretta, l’incertezza risulterebbe drasticamente ridotta. È questa quantificazione sistematica dell’incertezza a costituire l’essenza del concetto di entropia.
Dal punto di vista qualitativo, l’entropia può essere interpretata come il livello di “sorpresa” attesa associata al verificarsi di un evento. La sua proprietà fondamentale è di raggiungere il valore massimo in condizioni di massima indeterminazione, ovvero quando tutti gli esiti possibili sono equiprobabili. Viceversa, l’entropia si annulla quando un esito possiede probabilità prossima all’unità, rendendo il risultato di fatto certo e prevedibile.
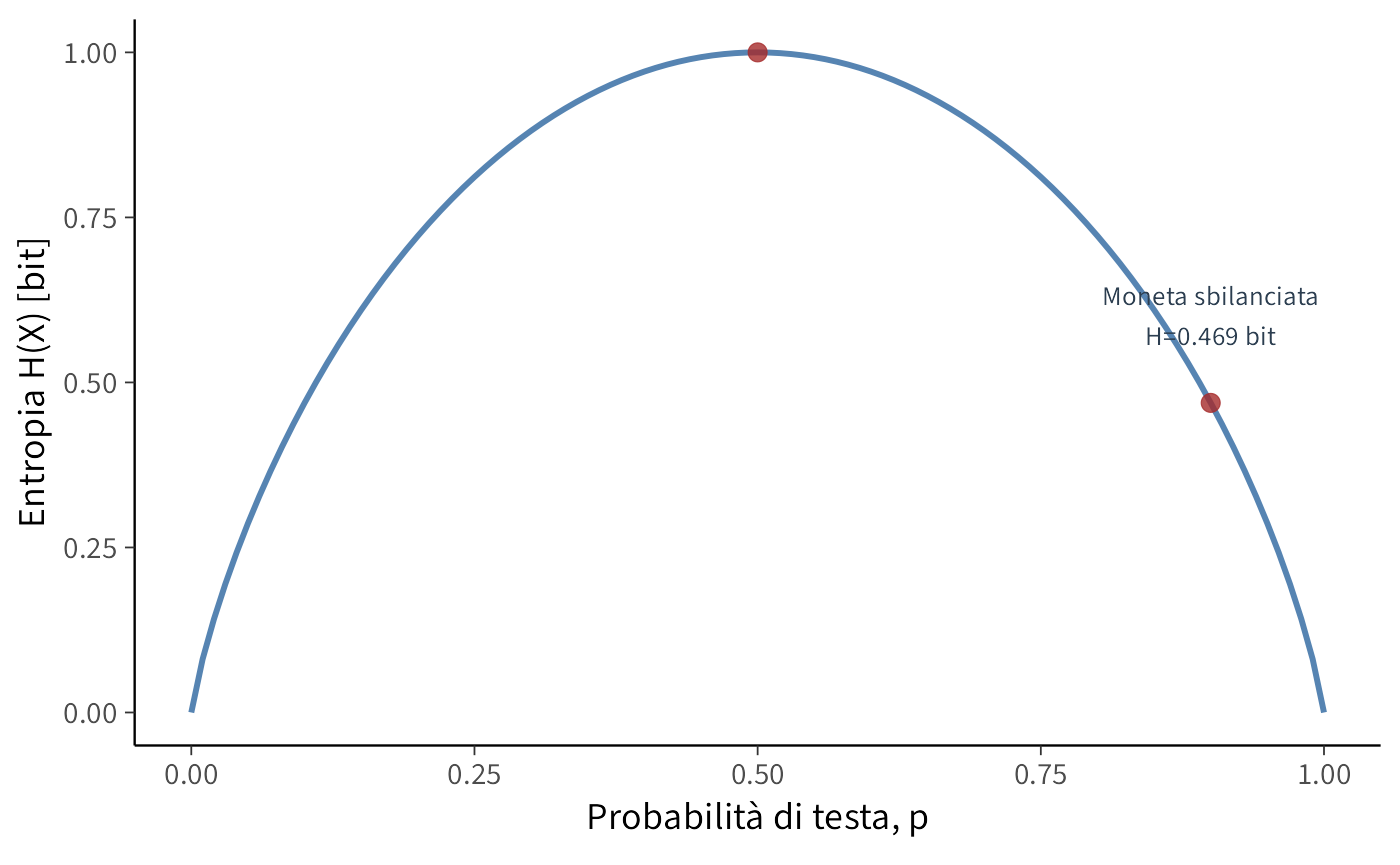
Un esempio tratto dalla psicologia sperimentale può chiarire ulteriormente questa dualità: il lancio di una moneta non truccata \((p = 0.5)\) riflette un’elevata entropia a causa dell’intrinseca imprevedibilità del risultato. All’opposto, il comportamento stereotipato di un paziente che fornisce invariabilmente la medesima risposta a uno stimolo rappresenta una situazione a entropia pressoché nulla, caratterizzata da un’altissima prevedibilità.
Panoramica del capitolo
- Introdurre il concetto di informazione e la sua unità di misura (bit).
- Definire l’entropia come media della sorpresa di Shannon.
- Interpretare l’entropia in termini di incertezza e numero di alternative equiprobabili.
- Stimare l’entropia da distribuzioni teoriche e da campioni osservati.
- Collegare l’entropia alla codifica di Huffman e al limite teorico di compressione.
- Per i concetti di base sulla teoria dell’informazione, si rimanda ai primi due capitoli di Information Theory: A Tutorial Introduction (Stone, 2022).
42.1 Che cos’è l’informazione?
Un bit costituisce l’unità elementare di informazione, corrispondente alla scelta tra due alternative ugualmente probabili. Ogni raddoppio del numero di opzioni disponibili richiede un bit aggiuntivo per identificarle univocamente. Il logaritmo in base 2 (\(\log_2\)) quantifica esattamente il numero di bit necessari per distinguere tra un dato numero di alternative.
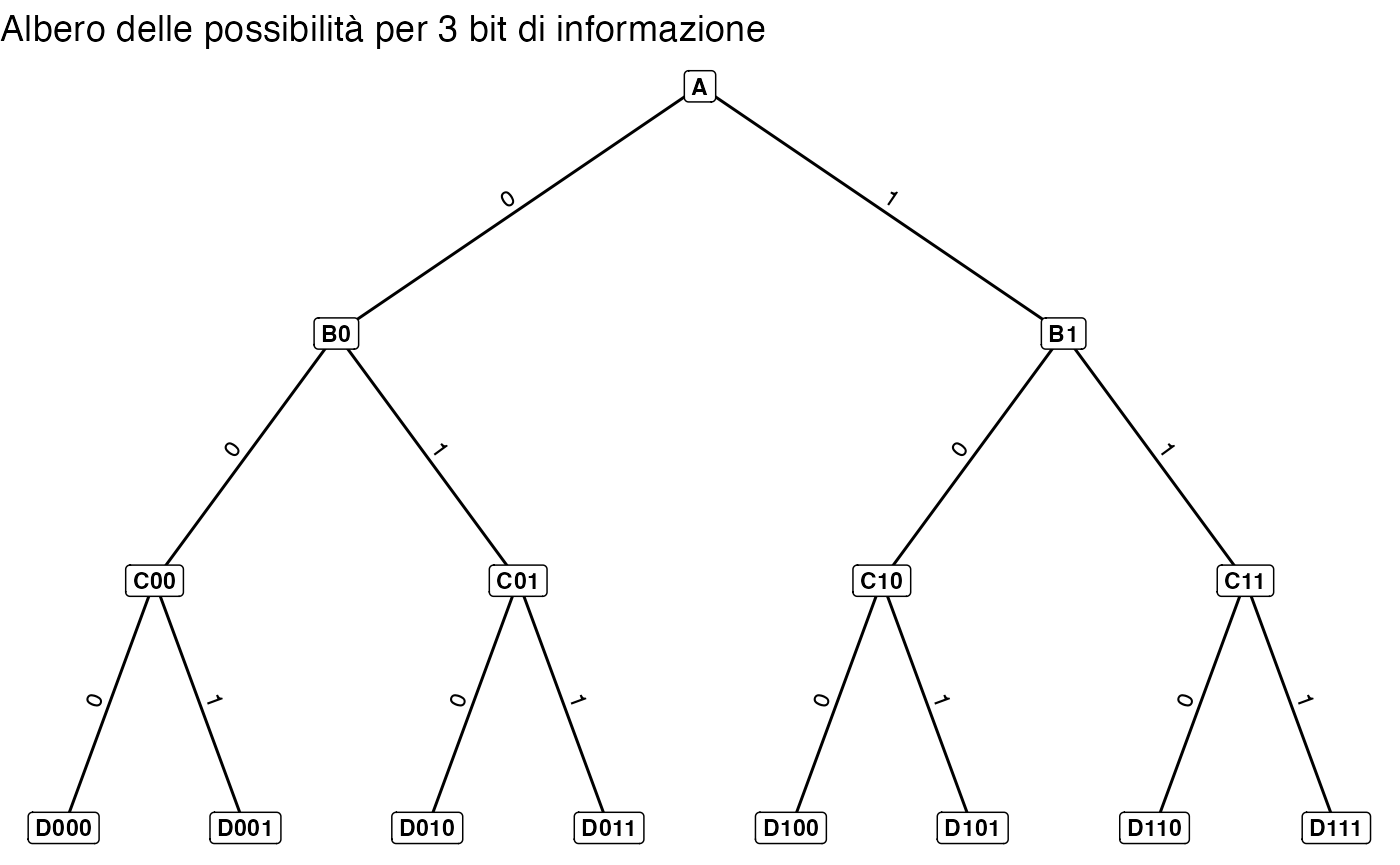
42.1.1 Dalle scelte ai bit: un esempio visivo
Per comprendere come l’informazione venga misurata in bit, consideriamo un esempio spaziale. Immaginiamo di trovarci a un incrocio con due strade possibili. Ogni scelta tra destra e sinistra può essere codificata con un singolo bit (ad esempio, 0 per sinistra, 1 per destra).
Estendiamo questo concetto a un percorso con più incroci sequenziali, come mostrato nel diagramma seguente. Ogni percorso completo è univocamente descritto da una sequenza di bit, dove ciascuno rappresenta una decisione binaria presa a un incrocio. Ad esempio, per raggiungere la destinazione D011, la sequenza corretta è 0-1-1.
42.1.1.1 Relazione tra destinazioni e bit
Ogni decisione binaria lungo il percorso aggiunge un bit alla descrizione della destinazione. Se sono disponibili \(m\) destinazioni distinte, il numero di bit necessari per identificarne una in modo univoco è dato da:
\[ n = \log_2 m \]
Nell’esempio illustrato, le destinazioni finali sono otto. Pertanto, sono necessari esattamente \(\log_2 8 = 3\) bit (ovvero, tre decisioni binarie) per specificarne una.
42.1.1.2 Il significato di un bit
In questo contesto, un bit risponde a una domanda elementare del tipo: “Devo andare a destra o a sinistra?”. È l’unità di risoluzione dell’incertezza in uno scenario decisionale binario.
42.1.1.3 Perché i logaritmi?
Il logaritmo in base 2 calcola l’esponente a cui elevare 2 per ottenere un numero dato. In altre parole, fornisce il numero di decisioni binarie (bit) necessarie per selezionare un’opzione tra \(m\) possibilità. Nell’esempio, per specificare il percorso per D011 a partire da A, sono necessarie le risposte a tre distinte domande binarie.
Sintesi:
- Per raggiungere
D011daAoccorrono tre decisioni binarie successive. - Ogni decisione è codificata da un bit (0/1), producendo la sequenza
011. - Rispondere alla domanda “Come si arriva a
D011?” richiede pertanto 3 bit di informazione.
In conclusione, esiste una relazione diretta e logaritmica tra il numero di alternative e l’informazione necessaria per selezionarne una. Ogni bit aggiuntivo raddoppia lo spazio delle possibilità, permettendo di distinguere tra un numero sempre maggiore di percorsi o esiti.
42.2 La sorpresa e l’informazione di Shannon
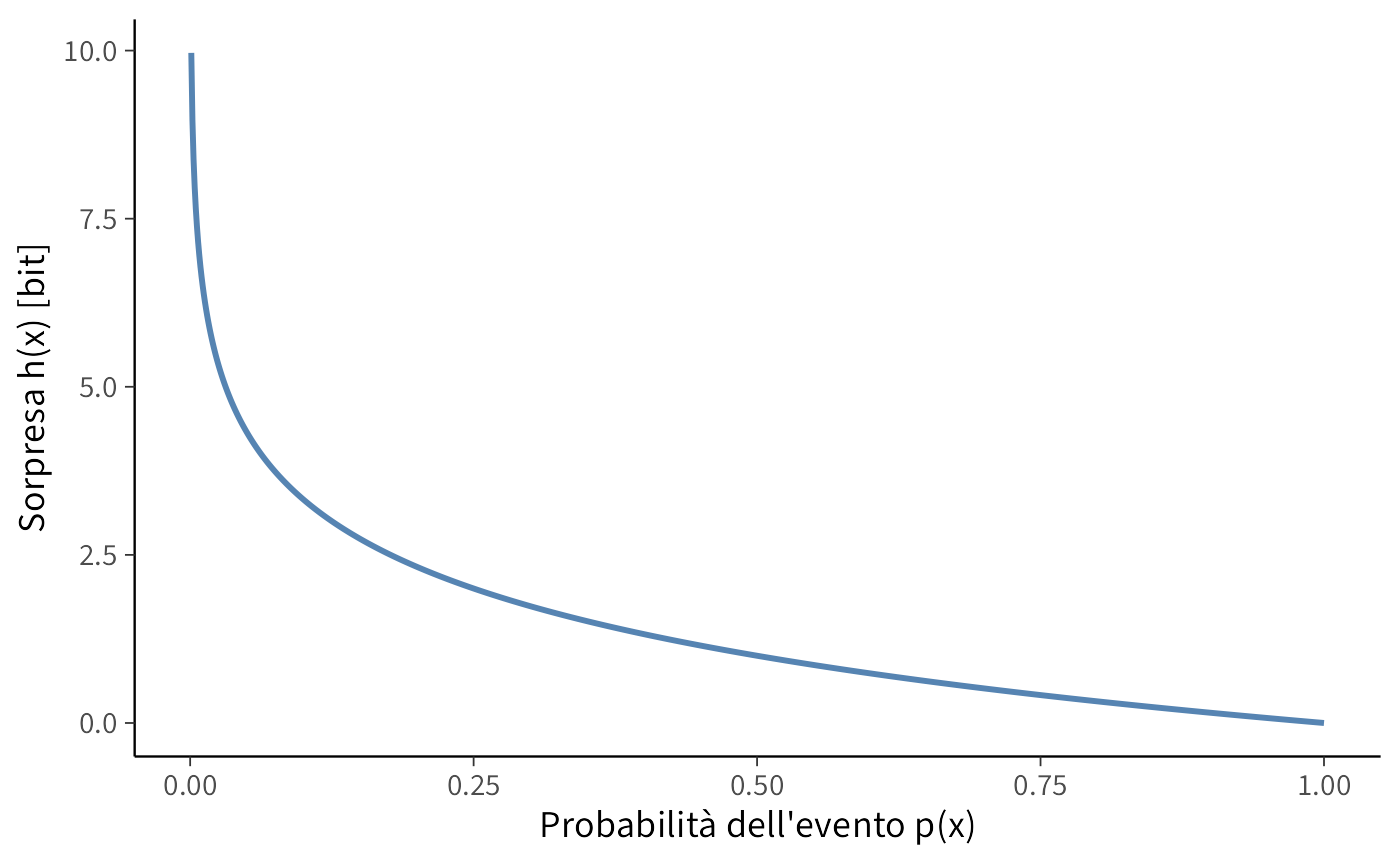
Introduciamo ora un elemento cruciale: la probabilità dell’evento. Eventi con probabilità diverse veicolano quantità di informazione differenti. Un evento molto probabile suscita poca sorpresa e fornisce poca informazione; un evento raro, al contrario, produce una sorpresa maggiore e trasmette più informazione.
Shannon formalizzò questa intuizione definendo l’informazione (o “sorpresa”) associata a un evento \(x\) come:
\[ h(x) = \log_2 \frac{1}{p(x)} = -\log_2 p(x) \ \text{bit}. \tag{42.1}\]
Questa relazione mostra come l’informazione sia inversamente proporzionale alla probabilità: minore è \(p(x)\), maggiore è \(h(x)\).1
Consideriamo tre eventi con probabilità 0.5, 0.25 e 0.10. La loro sorpresa corrisponde rispettivamente a 1.00, 2.00 e 3.32 bit. Man mano che la probabilità diminuisce, l’informazione—misurata in bit—aumenta. Un’osservazione inattesa “pesa” di più, modificando in misura maggiore la nostra conoscenza del sistema.
42.2.1 Entropia come informazione attesa
Finora abbiamo considerato la sorpresa di un singolo evento. Per descrivere l’incertezza complessiva di un sistema che può produrre esiti diversi, dobbiamo calcolare la sorpresa media attesa, considerando tutti i possibili risultati e le loro probabilità. Questa è l’entropia.
Matematicamente, l’entropia è la media pesata dell’informazione di Shannon per tutti i possibili esiti di una variabile casuale \(X\):
\[ H(X) = \mathbb{E}[h(X)] = \sum_{x \in \mathcal{X}} p(x) \cdot \left[-\log_2 p(x)\right]. \tag{42.2}\]
L’entropia non si riferisce a un evento specifico, ma alla sorpresa media che ci aspettiamo osservando ripetutamente la variabile.
- Se la distribuzione è perfettamente equilibrata (es. uniforme), l’entropia è massima: ogni osservazione fornisce una quantità simile e relativamente alta di informazione.
- Se la distribuzione è sbilanciata (es. moneta fortemente truccata), l’entropia è più bassa: la prevedibilità aumenta e l’informazione media per osservazione diminuisce.
Il grafico seguente illustra come la sorpresa di Shannon vari in funzione della probabilità dell’evento:
42.2.2 Interpretazione dell’entropia
Poiché l’entropia rappresenta la sorpresa media attesa, può essere interpretata come il numero medio di bit necessari per descrivere un’osservazione della variabile \(X\).
Quando l’entropia è espressa in bit, possiamo convertirla in un numero equivalente di alternative equiprobabili:
\[ m = 2^{H(X)}. \tag{42.3}\]
Un’entropia di \(H(X)\) bit corrisponde quindi alla stessa incertezza che avremmo se dovessimo distinguere tra \(m\) esiti tutti ugualmente probabili. In questo senso, l’entropia quantifica l’informazione contenuta in una variabile esprimendola in termini del numero di scelte binarie necessarie per descriverla.
42.2.3 Proprietà fondamentali dell’entropia
L’entropia raggiunge il suo massimo quando tutti gli esiti possibili sono equiprobabili. In questa condizione di massima indeterminazione, l’incertezza è totale: non disponiamo di alcuna informazione che ci permetta di prevedere il risultato meglio del puro caso.
All’estremo opposto, l’entropia è minima (pari a zero) quando il risultato è deterministico, ovvero quando un evento ha probabilità 1 e tutti gli altri probabilità 0. In questo caso non sussiste alcuna incertezza, l’osservazione non produce sorpresa e non fornisce informazione aggiuntiva.
Una proprietà cruciale è l’additività per eventi indipendenti: l’entropia congiunta di due o più variabili casuali indipendenti è pari alla somma delle loro entropie individuali. Questa caratteristica discende direttamente dall’additività dei logaritmi nella definizione di Shannon e riflette il fatto che, per eventi indipendenti, l’incertezza totale è la semplice somma delle incertezze dei singoli componenti.
42.3 Stimare l’entropia
Nelle sezioni precedenti abbiamo definito l’entropia come la sorpresa media attesa associata all’osservazione di una variabile casuale, fondandola sul concetto di informazione di Shannon. Passiamo ora dalla teoria alla pratica, illustrando come calcolare l’entropia sia a partire da una distribuzione di probabilità teorica, sia da dati osservati.
42.3.1 Entropia di una distribuzione di probabilità
Consideriamo una variabile casuale discreta \(X\) in grado di assumere valori \(x_1, x_2, \dots, x_n\), ciascuno con probabilità \(p(x) = \Pr\{X = x\}\). L’informazione, o “sorpresa”, associata all’osservazione di un particolare esito \(x\) è definita come:
\[ h(x) = -\log_2 p(x). \] Questa funzione cattura l’intuizione per cui eventi improbabili (\(p(x)\) piccolo) producono un’alta sorpresa, mentre eventi certi (\(p(x) = 1\)) non forniscono alcuna informazione nuova.
Per quantificare l’incertezza complessiva della variabile \(X\), calcoliamo il valore atteso della sorpresa su tutti i suoi possibili esiti. Si ottiene così la definizione di entropia di Shannon:
\[ H(X) = \mathbb{E}[h(X)] = -\sum_{x \in \mathcal{X}} p(x) \log_2 p(x). \tag{42.4}\] Ogni termine della sommatoria, \(-p(x)\log_2 p(x)\), rappresenta il contributo informativo medio dell’esito \(x\), ponderato per la sua probabilità di occorrenza.
Proprietà fondamentali:
- L’entropia è massima per una distribuzione uniforme, quando tutti gli esiti sono equiprobabili e l’incertezza è massima.
- L’entropia diminuisce quando la distribuzione diventa più squilibrata; esiti ad alta probabilità riducono la sorpresa media.
- L’entropia è zero se un esito è certo (\(p(x)=1\)), poiché non sussiste alcuna incertezza.
In sintesi, \(H(X)\) misura l’incertezza media di \(X\) e può essere interpretata come il numero medio di bit necessari per codificare un’osservazione della variabile.
- La sommatoria calcola il contributo di ogni possibile esito.
- Il logaritmo in base 2 quantifica l’informazione in bit.
- Il segno negativo compensa il fatto che i logaritmi di probabilità (\(0 \leq p(x) \leq 1\)) sono valori non positivi.
42.3.2 Entropia in un campione osservato
Finora abbiamo considerato l’entropia nel caso ideale in cui la distribuzione di probabilità teorica è nota. Nella pratica della ricerca psicologica, tuttavia, lavoriamo tipicamente con un campione di dati osservati. In questo scenario, possiamo stimare l’entropia calcolando le frequenze relative di ciascun valore distinto e utilizzandole come stime empiriche delle probabilità sottostanti.
La stima risultante quantifica il grado di incertezza o imprevedibilità presente nella distribuzione campionaria. Un campione con frequenze uniformi tra i diversi valori presenterà un’entropia stimata elevata, riflettendo un’alta incertezza. Al contrario, un campione in cui un singolo valore domina nettamente gli altri mostrerà un’entropia stimata bassa, indicando una distribuzione più prevedibile e concentrata.
42.3.2.1 Interpretazione finale
L’entropia \(H(X)\) quantifica l’incertezza media di una distribuzione di probabilità. Essa può essere interpretata come il numero medio di bit necessari per codificare un’osservazione di \(X\). In altri termini, l’entropia misura la quantità media di informazione che otteniamo osservando la realizzazione di una variabile casuale: un’entropia più elevata corrisponde a una maggiore imprevedibilità del fenomeno studiato.
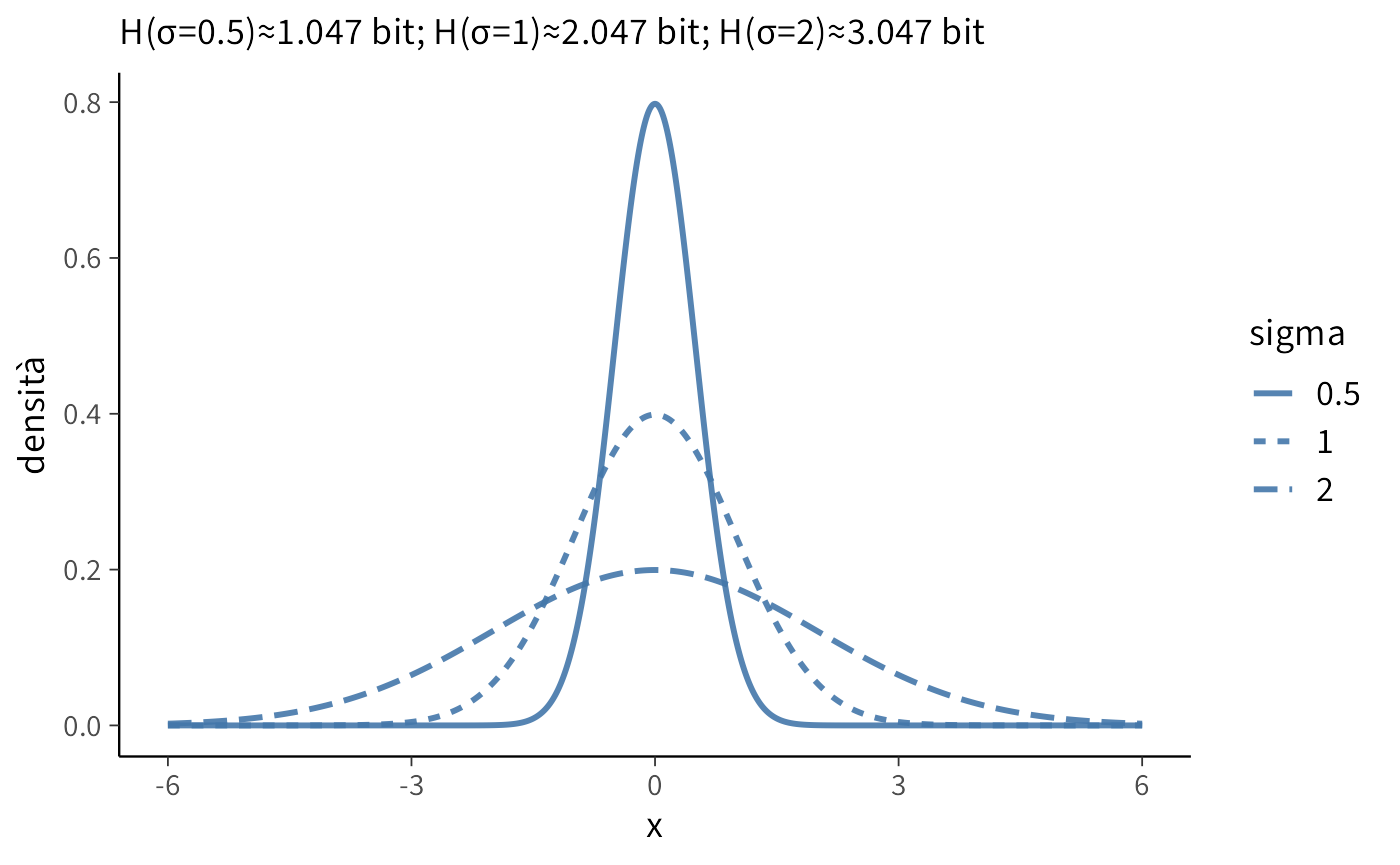
42.3.3 Entropia di variabili casuali continue
Il concetto di entropia si estende naturalmente alle variabili casuali continue sostituendo la sommatoria con un integrale. Questa generalizzazione, nota come entropia differenziale, è necessaria poiché variabili continue assumono valori in un insieme non numerabile, dove le probabilità puntuali sono nulle e la densità di probabilità diventa l’oggetto rilevante.
Per una variabile continua \(X\) con funzione di densità \(p(x)\), l’entropia differenziale è definita come:
\[ H(X) = -\int_{\mathcal{X}} p(x) \log_2 p(x) \, dx, \tag{42.5}\]
dove l’integrale è calcolato sull’intero supporto \(\mathcal{X}\) della variabile.
Analogamente al caso discreto, l’entropia differenziale misura l’incertezza media della distribuzione:
- Una densità molto concentrata (es. un picco stretto) implica bassa entropia, indicando prevedibilità.
- Una densità dispersa (es. distribuzione uniforme su un ampio intervallo) comporta alta entropia, riflettendo maggiore imprevedibilità.
Il segno negativo compensa la negatività del logaritmo per valori \(0 < p(x) \leq 1\), garantendo che l’entropia sia non negativa e mantenendo l’interpretazione in termini di bit necessari per la codifica.
42.4 La codifica di Huffman
Abbiamo visto che l’entropia \(H(X)\) misura la sorpresa media di una variabile casuale \(X\). Un risultato fondamentale dell’informazione teorica è che l’entropia rappresenta anche il limite inferiore teorico per la lunghezza media di un codice binario che rappresenti gli esiti di \(X\) senza perdite. In altre parole, è impossibile progettare un sistema di codifica che utilizzi in media meno di \(H(X)\) bit per simbolo.
L’algoritmo di Huffman, sviluppato da David A. Huffman nel 1952, fornisce un metodo pratico per costruire un codice che si avvicina asintoticamente a questo limite teorico.
42.4.1 L’intuizione fondamentale
Il principio è semplice e intuitivo: assegnare codici brevi agli eventi comuni e codici più lunghi agli eventi rari. Questa strategia di ottimizzazione rispecchia il nostro comportamento quotidiano quando abbreviamo parole frequenti nei messaggi (“tvb”, “xké”) mentre scriviamo per esteso termini meno comuni.
42.4.2 L’algoritmo passo dopo passo
L’obiettivo è costruire un albero binario dove le foglie rappresentano i simboli da codificare:
- Inizializzazione: Creare una lista di nodi, ciascuno contenente un simbolo e la sua probabilità.
- Fusione iterativa: Unire ripetutamente i due nodi con probabilità più bassa in un nuovo nodo, la cui probabilità è la somma delle probabilità dei figli.
- Terminazione: Procedere finché non rimane un unico nodo (la radice dell’albero).
-
Assegnazione dei codici: Percorrere l’albero dalla radice a ciascuna foglia, assegnando
0ai rami sinistri e1ai rami destri. La sequenza risultante è il codice di Huffman per quel simbolo.
La proprietà cruciale di questo codice è che è un codice prefisso: nessun codice costituisce il prefisso di un altro, eliminando ogni ambiguità in fase di decodifica.
42.4.3 Esempio concreto
Consideriamo un messaggio con quattro simboli e le seguenti frequenze:
| Simbolo | Frequenza | Probabilità |
|---|---|---|
| A | 20 | ~0.47 |
| B | 10 | ~0.23 |
| C | 8 | ~0.19 |
| D | 5 | ~0.12 |
Costruzione dell’albero:
- Unire D(5) e C(8) → N1(13)
- Unire B(10) e N1(13) → N2(23)
- Unire A(20) e N2(23) → Radice(43)
L’albero risultante è:
(Radice:43)
/ \
0/ \1
(A:20) (N2:23)
/ \
0/ \1
(B:10) (N1:13)
/ \
0/ \1
(D:5) (C:8)Assegnazione dei codici:
- A:
0(1 bit) - B:
10(2 bit) - D:
110(3 bit) - C:
111(3 bit)
Notiamo come il simbolo più frequente (A) ottenga il codice più breve, mentre quelli meno frequenti (C, D) ricevano codici più lunghi.
42.4.4 Confronto con il limite teorico
Calcoliamo l’efficienza della codifica:
Lunghezza media del codice: \[ L = (0.47\cdot 1) + (0.23\cdot 2) + (0.19\cdot 3) + (0.12\cdot 3) \approx 1.9 \ \text{bit} \]
Entropia della distribuzione: \[ H(X) = -\sum p(x)\log_2 p(x) \approx 1.85 \ \text{bit} \]
Il codice di Huffman (1.9 bit/simbolo) si avvicina notevolmente al limite teorico dell’entropia (1.85 bit/simbolo). La piccola differenza è dovuta al vincolo che i codici devono avere lunghezza intera, mentre l’entropia rappresenta un valore medio continuo.
42.4.4.1 In sintesi
| Concetto | Significato Teorico | Analogia Psicologica (Approssimativa) |
|---|---|---|
| Entropia H(X) | Limite teorico assoluto di compressione. Misura l’incertezza/intrinseca. | Il “carico cognitivo” minimo necessario per rappresentare uno stimolo. |
| Codifica di Huffman | Metodo pratico per costruire un codice ottimale che si avvicina al limite H(X). |
Una strategia cognitiva efficiente per categorizzare informazioni (es. etichette mentali corte per concetti comuni). |
| Lunghezza media L | Il risultato pratico ottenuto con Huffman. | Il reale “costo” cognitivo della strategia adottata. |
| Differenza (L - H(X)) | Quanto il metodo pratico si discosta dal limite teorico ideale. | Quanto la nostra strategia cognitiva è efficiente rispetto all’ideale. |
In sintesi, l’algoritmo di Huffman costituisce un ponte tra teoria e pratica, dimostrando in modo concreto come il principio astratto dell’entropia—il limite teorico di compressione—possa essere realizzato attraverso una strategia di codifica efficiente. Questo meccanismo di ottimizzazione fornisce un’analogia potente per comprendere come la mente umana potrebbe elaborare le informazioni in modo economicamente vantaggioso, privilegiando le rappresentazioni concise per gli stimoli più frequenti al fine di ottimizzare le risorse cognitive.
42.5 Applicazioni psicologiche dell’entropia
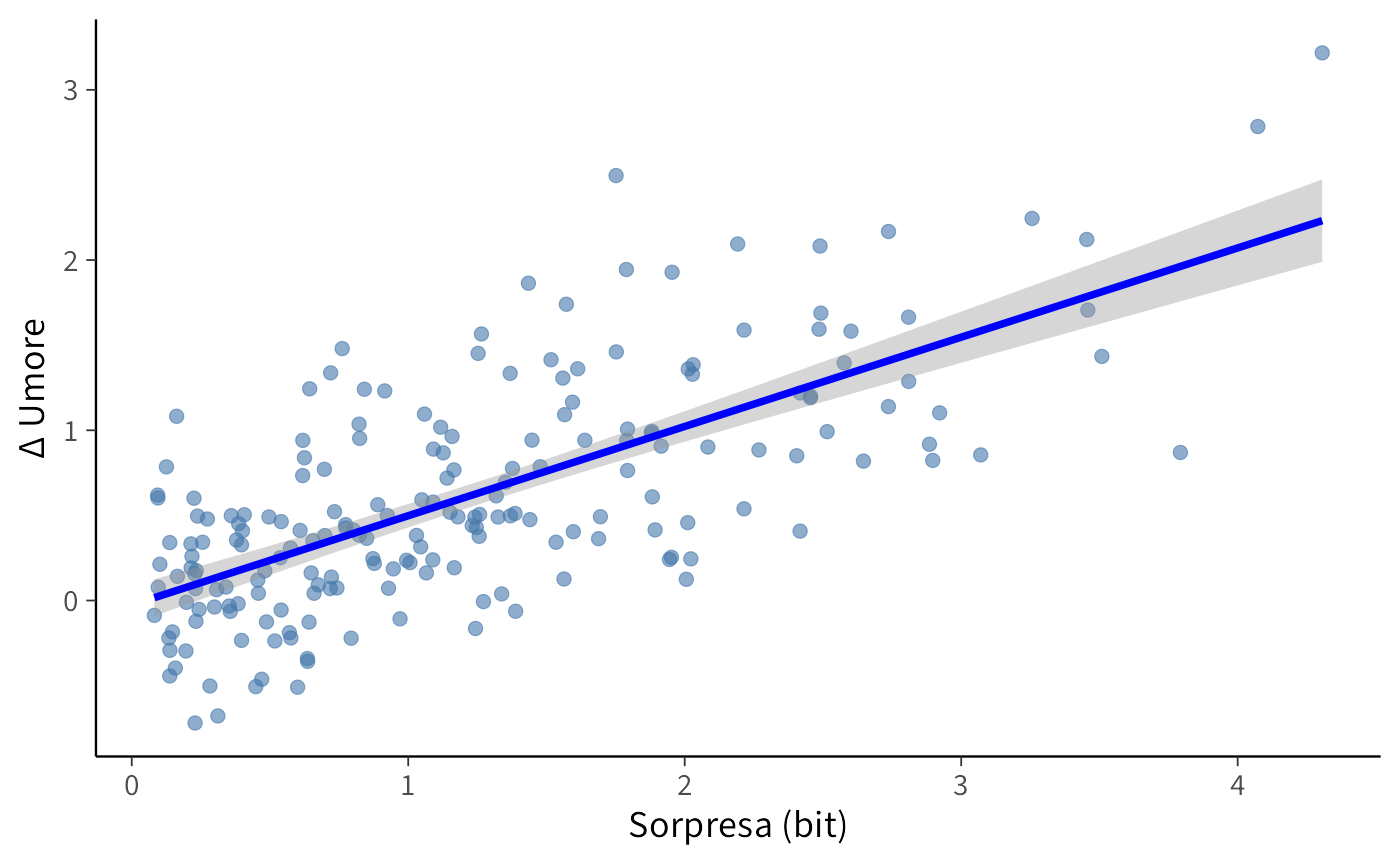
Il concetto di entropia, nella sua accezione di misura della sorpresa media associata a un evento, trova applicazione diretta nello studio di numerosi fenomeni psicologici. In particolare, la sorpresa—formalizzabile attraverso l’informazione di Shannon—è stata collegata a specifici correlati emotivi, meccanismi di apprendimento e processi di modulazione motivazionale.
Un esempio paradigmatico è fornito da Spector (1956), il quale indagò l’effetto della probabilità a priori sulla soddisfazione percepita in seguito a una promozione lavorativa. I risultati dimostrarono che esiti inizialmente giudicati improbabili—e dunque più sorprendenti al loro verificarsi—generavano un impatto emotivo significativamente più intenso rispetto a esiti ampiamente attesi. Questo suggerisce che l’entropia non costituisce una mera astrazione matematica, ma un indicatore predittivo della potenziale intensità di una risposta affettiva.
Ricerche più recenti, condotte sia in contesti sperimentali controllati che in setting ecologici, hanno ulteriormente consolidato questa relazione. Studi di neuroscienze cognitive, ad esempio, hanno evidenziato come eventi ad alta sorpresa modulino l’attività di regioni cerebrali implicate nell’elaborazione emotiva, come l’amigdala e la corteccia prefrontale ventromediale, influenzando tanto l’umore immediato quanto i successivi processi di apprendimento. Parallelamente, analisi basate su dati di Ecological Momentary Assessment (EMA) mostrano come la probabilità soggettiva di un evento si correli sistematicamente con le fluttuazioni dell’umore, rivelando che episodi rari e inattesi inducono oscillazioni emotive di maggiore ampiezza.
Nel loro insieme, questi risultati illustrano come l’entropia possa essere impiegata in psicologia non solo come strumento descrittivo per caratterizzare distribuzioni di probabilità, ma anche come variabile esplicativa in modelli che esplorano l’intreccio tra aspettative, sorpresa ed esperienza emotiva. È proprio questo nesso fondamentale a preparare il terreno per l’introduzione della divergenza di Kullback-Leibler, che estenderà il discorso al confronto tra modelli nell’ambito dell’inferenza bayesiana.
Riflessioni conclusive
In questo capitolo abbiamo esplorato la capacità dell’entropia di quantificare l’incertezza e l’informazione in sistemi complessi. Attraverso esempi che spaziano dal lancio di una moneta alla codifica efficiente dei messaggi, abbiamo visto come questo potente strumento matematico possa essere applicato in modo concreto e intuitivo.
Abbiamo appreso che l’entropia misura l’incertezza: situazioni massimamente imprevedibili, come il risultato del lancio di una moneta equilibrata, presentano un’entropia elevata, mentre comportamenti stereotipati e deterministici sono caratterizzati da un’entropia prossima allo zero. Abbiamo inoltre scoperto come l’informazione coincida con la sorpresa, per cui eventi rari e inaspettati—formalizzati dall’informazione di Shannon—veicolano un contenuto informativo maggiore rispetto a eventi comuni e attesi. Infine, abbiamo compreso che l’entropia stabilisce un limite teorico alla compressione dei dati, rappresentando il numero minimo di bit necessari per descrivere un’informazione senza perdite, un principio che l’algoritmo di Huffman realizza con elegante efficacia.
42.5.1 La rilevanza per la ricerca psicologica
Questi concetti trovano un’eco immediata e profonda nella ricerca psicologica. Nell’ambito della modellizzazione cognitiva, l’entropia ci aiuta a quantificare il “lavoro” informazionale richiesto per elaborare stimoli diversi, offrendo una metrica per la complessità dei processi mentali. Lo studio delle emozioni, d’altro canto, beneficia del legame tra probabilità e risposta affettiva: come illustrato dagli studi citati, gli eventi ad alta sorpresa—e quindi ad alta entropia—tendono a innescare reazioni emotive più intense, gettando un ponte tra teoria dell’informazione e neuroscienze affettive. In prospettiva, questi fondamenti ci condurranno direttamente alla valutazione dei modelli psicologici, dove l’entropia costituirà la base per strumenti sofisticati di confronto e selezione basati sulla capacità predittiva.
42.5.2 Verso strumenti più avanzati
L’entropia non rappresenta un punto di arrivo, bensì una solida piattaforma di lancio verso strumenti inferenziali più raffinati. Nel prossimo capitolo incontreremo la divergenza di Kullback-Leibler, che misura direttamente quanto un modello si discosti dalla realtà utilizzando proprio i concetti di entropia che abbiamo assimilato. Questo, a sua volta, ci preparerà all’incontro con l’ELPD (Expected Log Predictive Density), una metrica fondamentale per confrontare modelli bayesiani nella pratica della ricerca.
Comprendere l’entropia significa quindi acquisire una lente interpretativa potente: ci permette di tradurre osservazioni qualitative sulla variabilità del comportamento in misure quantitative rigorose, trasformando l’intuizione in analisi scientifica. È questo salto epistemologico—dal “questo comportamento è variabile” al “l’entropia di questo comportamento è di X bit”—che rende la teoria dell’informazione un alleato indispensabile per la psicologia contemporanea.
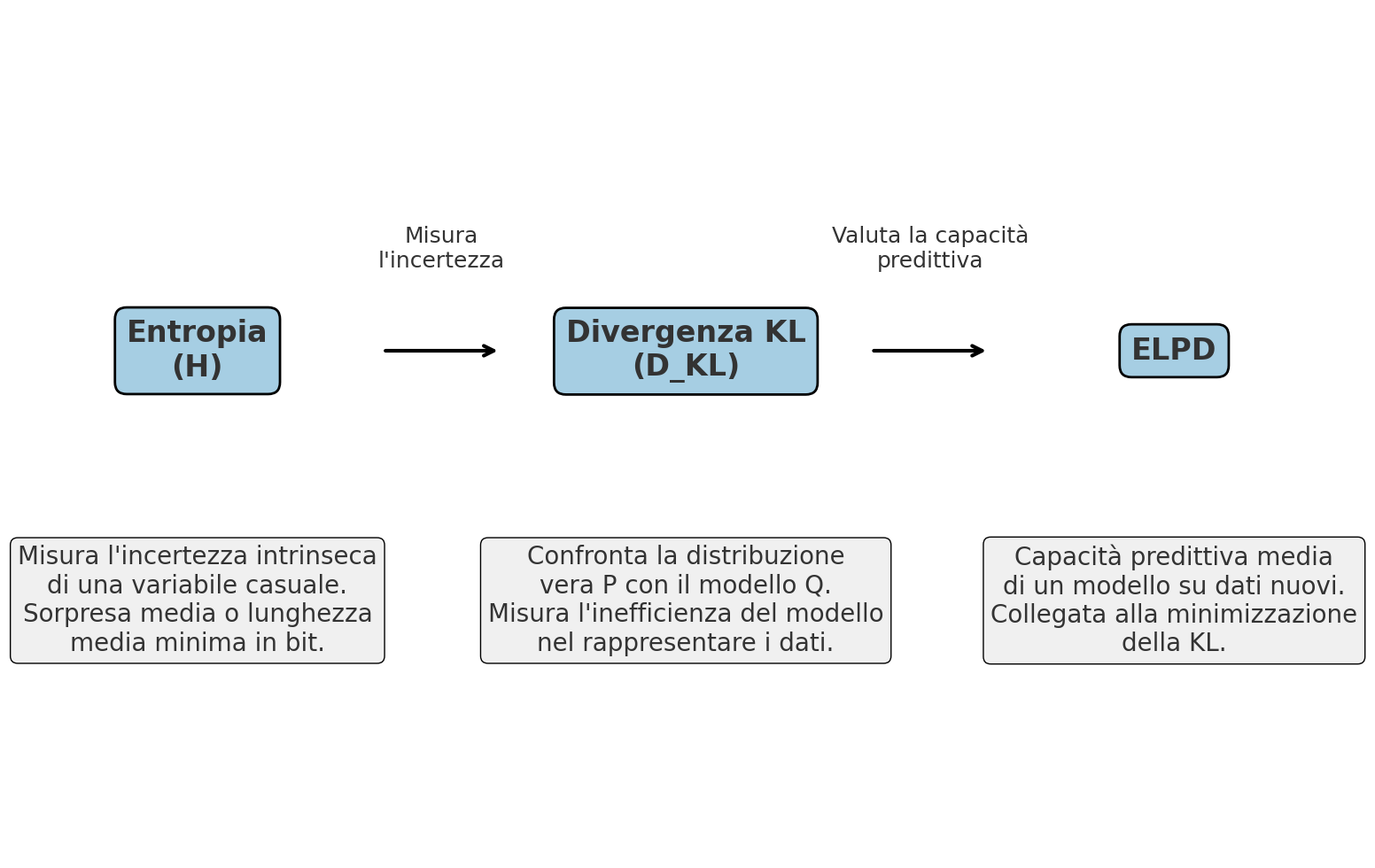
Entropia \(H(X)\)
→ Misura l’incertezza intrinseca di una variabile casuale.
→ Interpretabile come la sorpresa media o la lunghezza media minima (in bit) necessaria per codificare gli esiti di \(X\).
Divergenza di Kullback–Leibler \(D_{KL}(P \parallel Q)\)
→ Confronta due distribuzioni di probabilità \(P\) (la “vera” distribuzione) e \(Q\) (il modello).
→ Misura quanto il modello \(Q\) si discosta da \(P\) in termini di inefficienza nel codificare i dati.
Expected Log Predictive Density (ELPD)
→ Valuta la capacità predittiva di un modello su dati nuovi.
→ Collegata alla minimizzazione della KL tra la distribuzione dei dati e la distribuzione predittiva del modello.
→ Più alto è l’ELPD, migliore è la capacità del modello di rappresentare e prevedere i dati.
Collegamento logico:
Entropia → ci dice quanta incertezza c’è nei dati.
KL → ci dice quanto un modello spreca informazione rispetto a quella incertezza.
ELPD → ci dice quanto bene il modello prevede, riducendo quello spreco.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] tidygraph_1.3.1 ggraph_2.2.2 igraph_2.1.4
#> [4] ragg_1.5.0 tinytable_0.13.0 withr_3.0.2
#> [7] systemfonts_1.2.3 patchwork_1.3.2 ggdist_3.3.3
#> [10] tidybayes_3.0.7 bayesplot_1.14.0 ggplot2_4.0.0
#> [13] reliabilitydiag_0.2.1 priorsense_1.1.1 posterior_1.6.1
#> [16] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [19] brms_2.23.0 Rcpp_1.1.0 sessioninfo_1.2.3
#> [22] conflicted_1.2.0 janitor_2.2.1 matrixStats_1.5.0
#> [25] modelr_0.1.11 tibble_3.3.0 dplyr_1.1.4
#> [28] tidyr_1.3.1 rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 mgcv_1.9-3
#> [10] vctrs_0.6.5 stringr_1.5.2 pkgconfig_2.0.3
#> [13] arrayhelpers_1.1-0 fastmap_1.2.0 backports_1.5.0
#> [16] labeling_0.4.3 rmarkdown_2.30 purrr_1.1.0
#> [19] xfun_0.53 cachem_1.1.0 jsonlite_2.0.0
#> [22] tweenr_2.0.3 broom_1.0.10 parallel_4.5.1
#> [25] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [28] lubridate_1.9.4 estimability_1.5.1 knitr_1.50
#> [31] zoo_1.8-14 Matrix_1.7-4 splines_4.5.1
#> [34] timechange_0.3.0 tidyselect_1.2.1 viridis_0.6.5
#> [37] abind_1.4-8 yaml_2.3.10 codetools_0.2-20
#> [40] curl_7.0.0 pkgbuild_1.4.8 lattice_0.22-7
#> [43] bridgesampling_1.1-2 S7_0.2.0 coda_0.19-4.1
#> [46] evaluate_1.0.5 survival_3.8-3 polyclip_1.10-7
#> [49] RcppParallel_5.1.11-1 pillar_1.11.1 tensorA_0.36.2.1
#> [52] checkmate_2.3.3 stats4_4.5.1 distributional_0.5.0
#> [55] generics_0.1.4 rprojroot_2.1.1 rstantools_2.5.0
#> [58] scales_1.4.0 xtable_1.8-4 glue_1.8.0
#> [61] emmeans_1.11.2-8 tools_4.5.1 graphlayouts_1.2.2
#> [64] mvtnorm_1.3-3 grid_4.5.1 QuickJSR_1.8.1
#> [67] colorspace_2.1-2 nlme_3.1-168 ggforce_0.5.0
#> [70] cli_3.6.5 textshaping_1.0.3 svUnit_1.0.8
#> [73] viridisLite_0.4.2 Brobdingnag_1.2-9 V8_8.0.0
#> [76] gtable_0.3.6 digest_0.6.37 ggrepel_0.9.6
#> [79] TH.data_1.1-4 htmlwidgets_1.6.4 farver_2.1.2
#> [82] memoise_2.0.1 htmltools_0.5.8.1 lifecycle_1.0.4
#> [85] MASS_7.3-65Bibliografia
Per le proprietà dei logaritmi: \(\log(1/x) = -\log(x)\), poiché \(\log(1/x) = \log(1) - \log(x) = 0 - \log(x)\).↩︎