Appendice R — Controllo predittivo a priori
R.1 Esempi di modelli più complessi
Gli esempi del Capitolo 5 si sono concentrati su modelli semplici, in particolare sul caso di una singola proporzione. Estendiamo ora l’analisi a modelli di maggiore complessità. L’obiettivo è illustrare come diverse scelte delle distribuzioni precedenti (prior) per i parametri si traducano in diverse implicazioni predittive per i dati osservabili. Consideriamo tre casi di studio:
- Modello gaussiano (stima dell’intercetta e della varianza dei dati);
- Regressione lineare (scala appropriata per i coefficienti e per la varianza residua);
- Regressione logistica (interpretazione dei coefficienti nella scala logit e loro impatto sulle probabilità sottostanti).
R.1.1 Modello gaussiano semplice
Assumiamo che il meccanismo generativo dei dati segua una distribuzione normale: \(y \sim \mathcal{N}(\mu, \sigma)\).
Domanda cruciale: quali scelte delle distribuzioni precedenti per \(\mu\) e \(\sigma\) producono valori predittivi \(y\) plausibili per la variabile psicologica in esame (ad esempio, punteggi compresi tra 0 e 100)?
S <- 10000
# Scenario A: prior molto larga
mu_A <- rnorm(S, 50, 50) # media plausibile ma molto incerta
sigma_A <- rexp(S, rate = 1/20) # sigma ~ Exp(mean=20), molto larga
yA <- rnorm(S, mu_A, sigma_A)
# Scenario B: prior più informativa
mu_B <- rnorm(S, 50, 10)
sigma_B <- rexp(S, rate = 1/10) # mean=10
yB <- rnorm(S, mu_B, sigma_B)
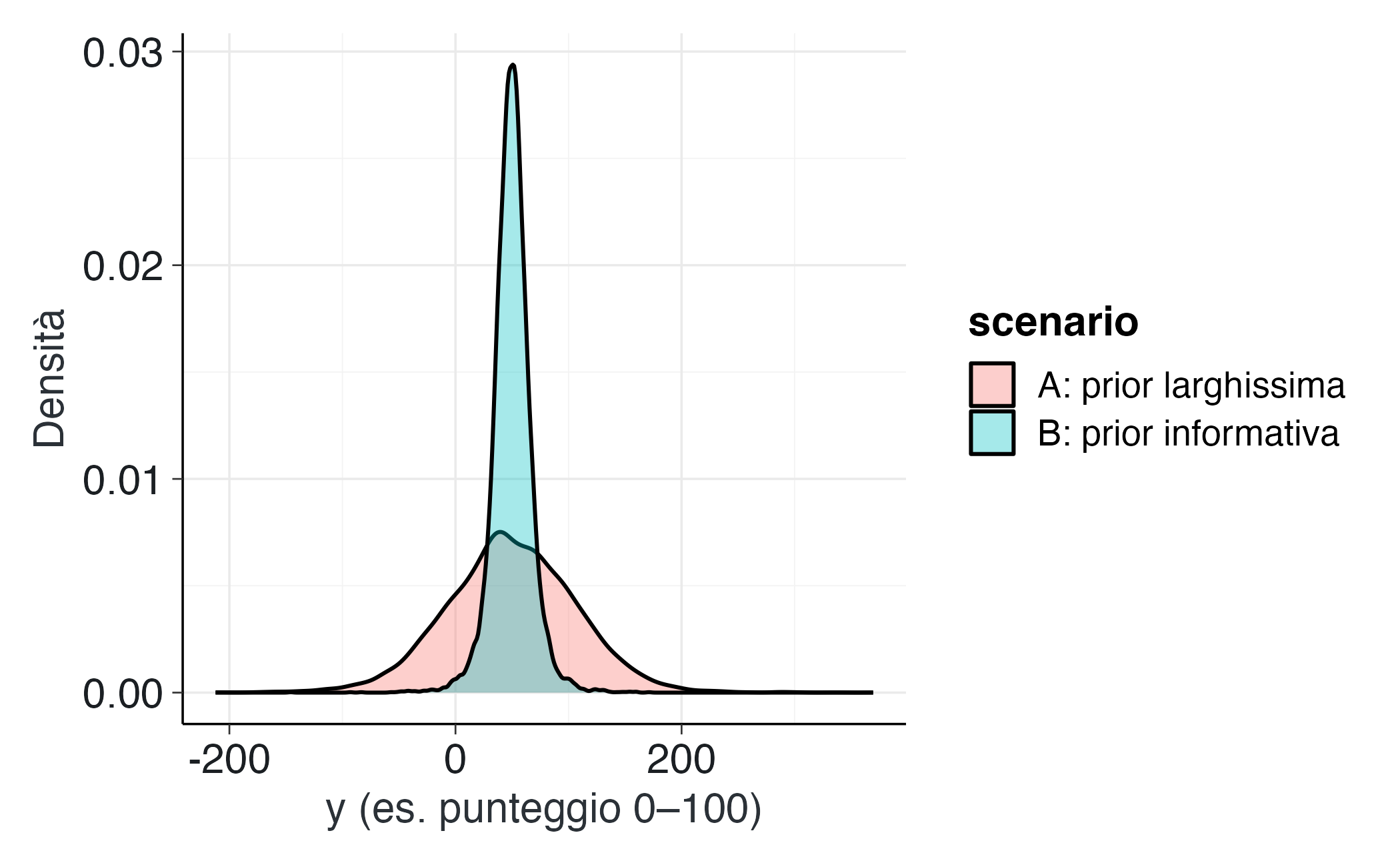
bind_rows(
tibble(y = yA, scenario = "A: prior larghissima"),
tibble(y = yB, scenario = "B: prior informativa")
) |>
ggplot(aes(x = y, fill = scenario)) +
geom_density(alpha = 0.35) +
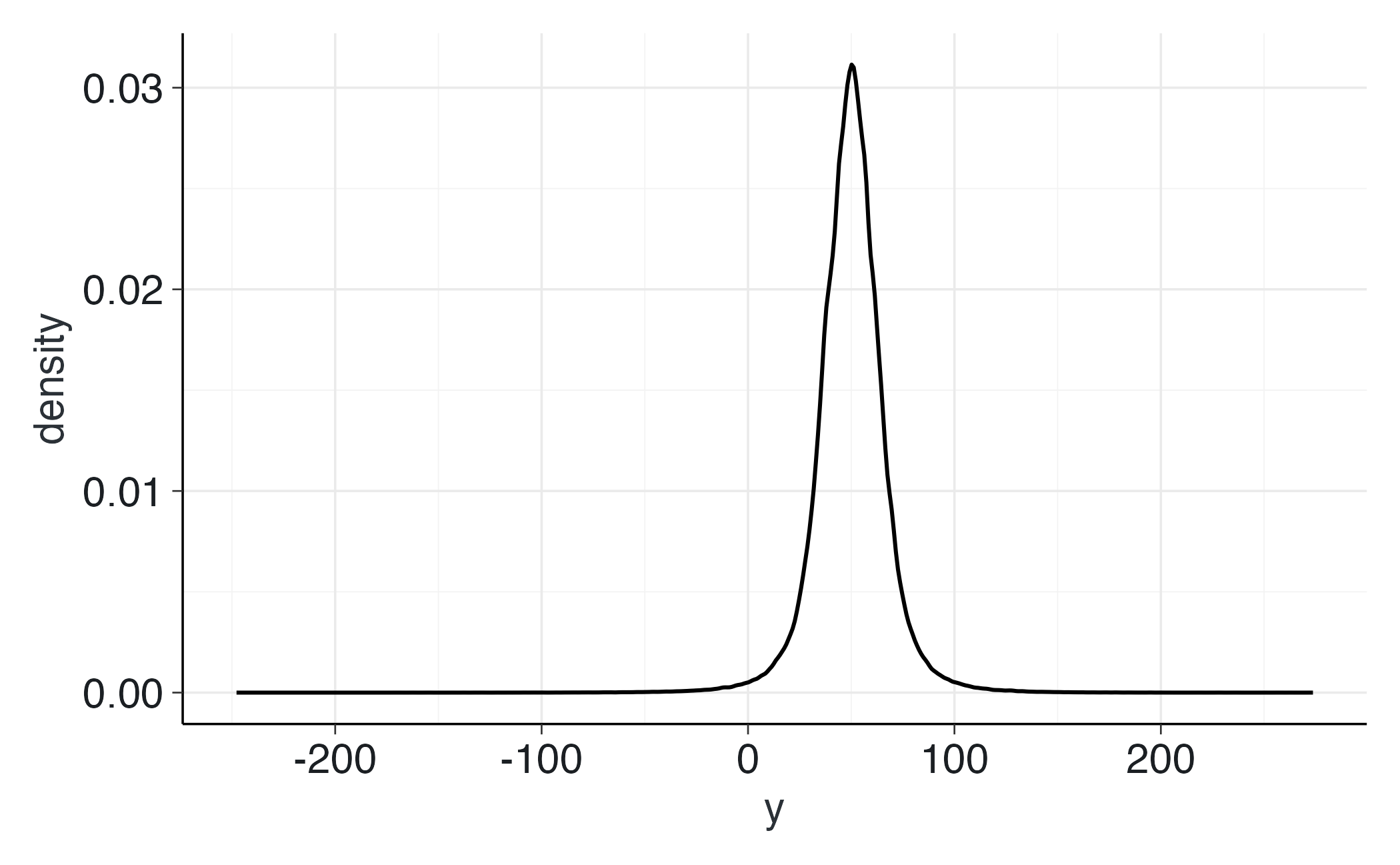
labs(x = "y (es. punteggio 0–100)", y = "Densità")Interpretazione. Se è noto che i punteggi della variabile di interesse sono compresi tra 0 e 100, lo Scenario A potrebbe generare una proporzione eccessiva di valori negativi o superiori a 100, indicando che le distribuzioni precedenti sono troppo poco informative e necessitano di essere ricalibrate (rendendole più informative sia per \(\mu\) che per \(\sigma\)).
Implementazione in Stan: modello solo con prior e generated quantities.
gauss_prior_ppc_stan <- '
data {
int<lower=1> N;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(50, 10);
sigma ~ exponential(1.0/10); // mean 10
}
generated quantities {
vector[N] y_rep;
for (i in 1:N) {
y_rep[i] = normal_rng(mu, sigma);
}
}
'
writeLines(gauss_prior_ppc_stan, "gauss_prior_ppc.stan")mod_gauss <- cmdstan_model("gauss_prior_ppc.stan")fit_gauss <- mod_gauss$sample(
data = list(N = 200),
chains = 4, iter_warmup = 500, iter_sampling = 1000, seed = 123,
refresh = 0
)R.1.2 Regressione lineare
Consideriamo il seguente modello generativo:
\[ y = \alpha + \beta x + \varepsilon, \qquad \varepsilon \sim \mathcal{N}(0,\sigma). \]
R.1.2.1 Importanza della scelta delle distribuzioni precedenti
Nell’ambito della regressione lineare, l’interpretazione del coefficiente \(\beta\) dipende criticamente dalla scala della variabile predittrice \(x\):
- Se \(x\) è standardizzata (media 0, deviazione standard 1), \(\beta\) rappresenta la variazione attesa in \(y\) associata a un incremento di una deviazione standard in \(x\).
- Ad esempio, specificare una distribuzione a priori \(\beta \sim \mathcal{N}(0,1)\) equivale ad assumere che: “effetti di modesta entità sono plausibili, mentre effetti superiori a 3 deviazioni standard sono estremamente rari”.
I controlli predittivi basati sulle distribuzioni a priori (prior predictive checks) consentono di rispondere a due interrogativi fondamentali:
- Le rette di regressione simulate generano valori di \(y\) compatibili con la scala del fenomeno oggetto di studio?
- La dispersione residua intorno alla retta (determinata da \(\sigma\)) è realisticamente plausibile?
Se la risposta a queste domande è negativa, è necessario rivedere le distribuzioni precedenti specificate per \(\alpha\), \(\beta\) e \(\sigma\), o considerare una trasformazione appropriata della variabile \(y\).
R.1.2.2 Scenario C: Distribuzioni a priori eccessivamente diffuse
In questo scenario specifichiamo varianze eccessivamente ampie per \(\alpha\) e \(\beta\). Il risultato: i valori simulati di \(y\) risultano irrealistici (eccessivamente negativi o elevati rispetto alla scala empirica del costrutto).
Interpretazione. Distribuzioni precedenti eccessivamente diffuse per \(\sigma\) e \(\beta\) rendono probabilisticamente plausibili valori di \(y\) privi di senso nel dominio applicativo. Questo non rappresenta un approccio “cauto” o “umile”, ma piuttosto una specificazione incoerente con l’evidenza empirica disponibile.
R.1.2.3 Scenario D: Distribuzioni a priori debolmente informative
In questo scenario adottiamo distribuzioni precedenti centrate su zero ma con varianze moderate:
\(\alpha \sim \mathcal{N}(0,1)\) e \(\beta \sim \mathcal{N}(0,1)\): effetti plausibili ma di entità contenuta \(\sigma \sim \text{Exp}(1/2)\): valore medio atteso di 2, compatibile con la variabilità tipica di punteggi psicologici standardizzati
alpha_D <- rnorm(S, 0, 1)
beta_D <- rnorm(S, 0, 1)
sigma_D <- rexp(S, rate = 1/2) # media ~2
yD <- rnorm(S, alpha_D + beta_D * x, sigma_D)
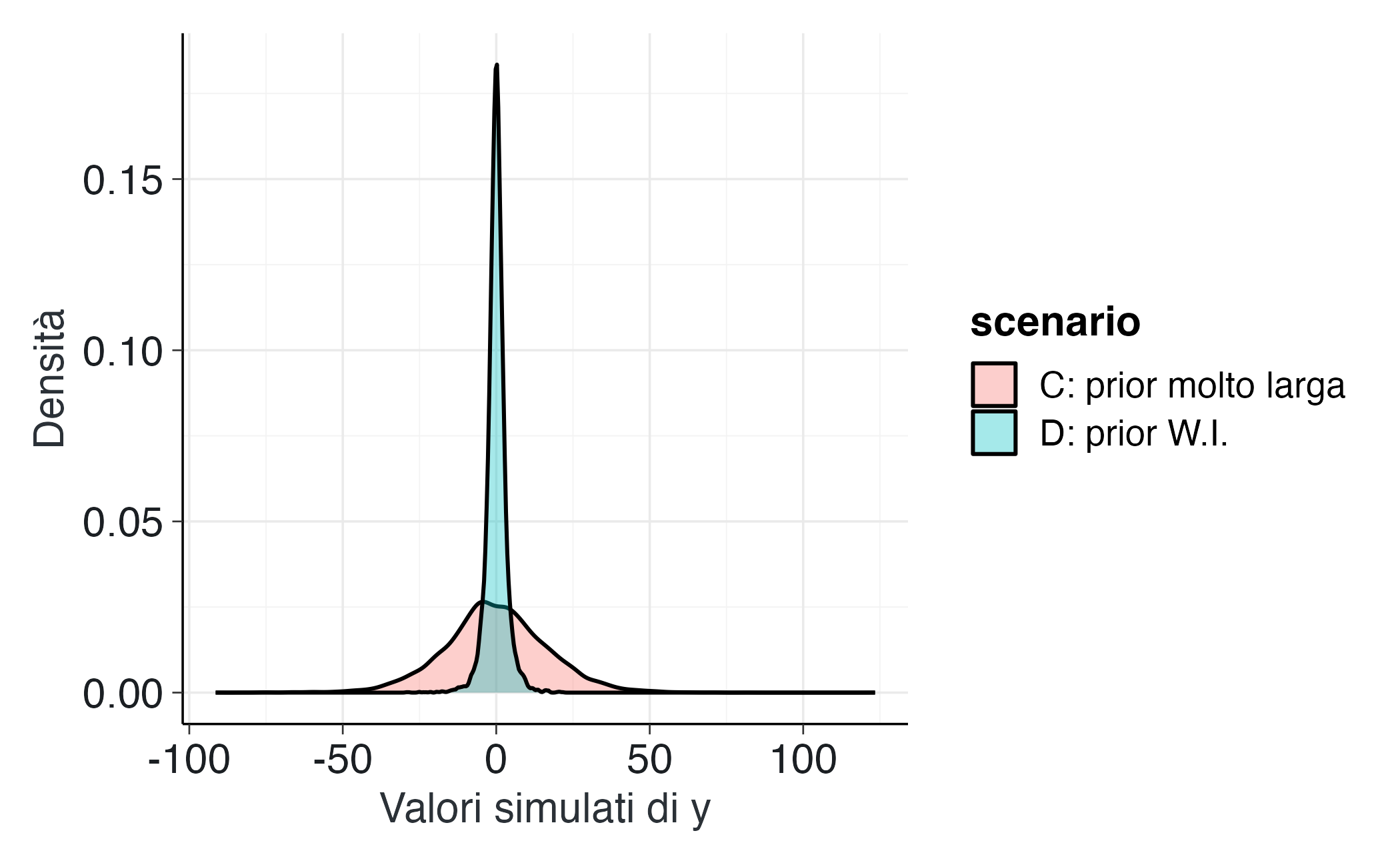
bind_rows(
tibble(y = yC, scenario = "C: prior molto larga"),
tibble(y = yD, scenario = "D: prior W.I.")
) |>
ggplot(aes(x = y, fill = scenario)) +
geom_density(alpha = 0.35) +
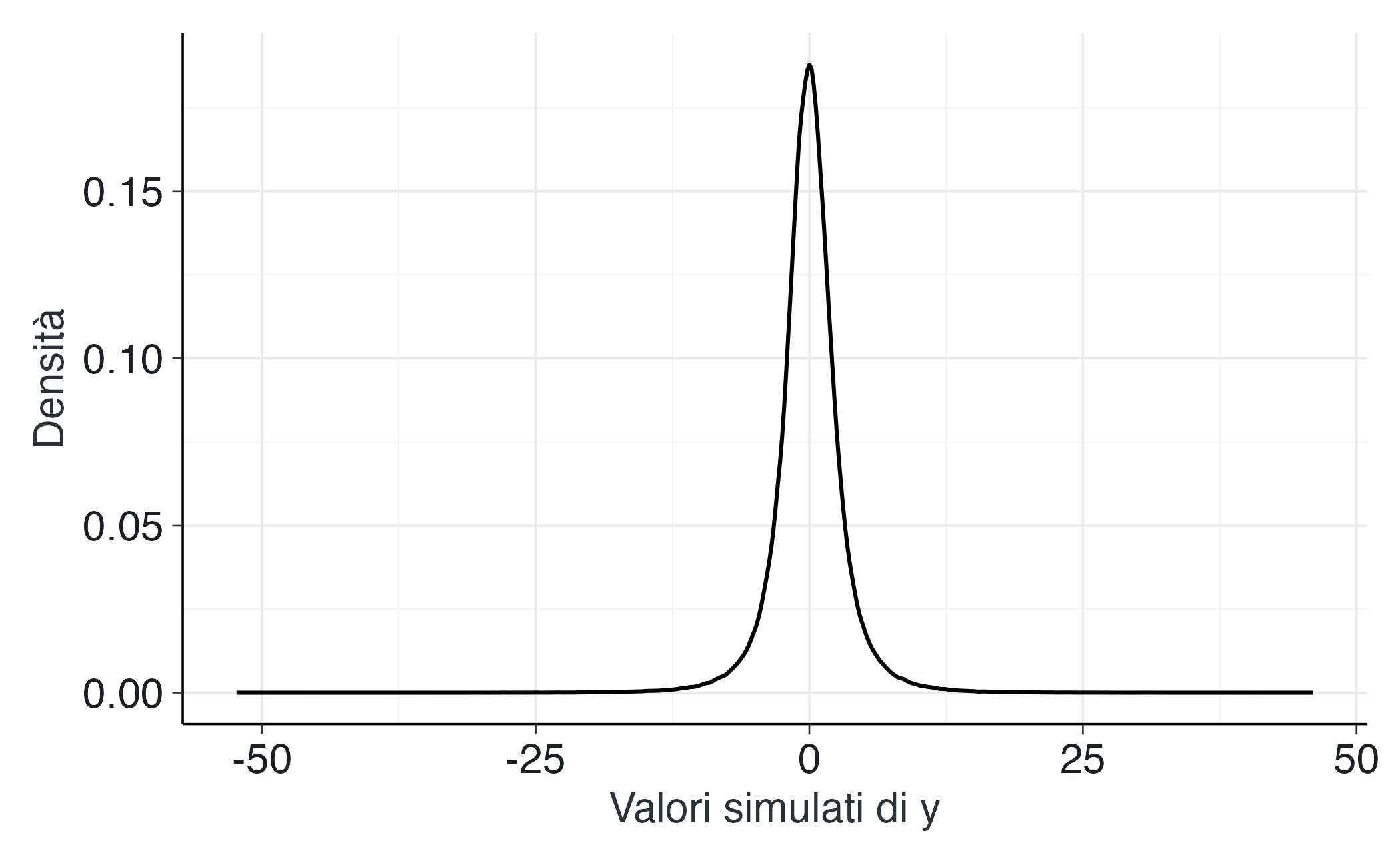
labs(x = "Valori simulati di y", y = "Densità")Interpretazione. Con distribuzioni precedenti debolmente informative, la distribuzione di \(y\) mantiene un’ampiezza plausibile. Al contrario, distribuzioni precedenti eccessivamente diffuse producono una variabilità irrealistica di \(y\).
R.1.2.4 Implementazione in Stan: simulazione esclusiva dalle distribuzioni a priori
Per illustrare esplicitamente il concetto, implementiamo un modello Stan che non incorpora dati osservati ma simula esclusivamente dalle distribuzioni precedenti.
linear_prior_ppc_stan <- '
data {
int<lower=1> N;
vector[N] x;
}
parameters {
real alpha;
real beta;
real<lower=0> sigma;
}
model {
alpha ~ normal(0, 1);
beta ~ normal(0, 1);
sigma ~ exponential(1.0/2); // media 2
}
generated quantities {
vector[N] y_rep;
for (i in 1:N) {
y_rep[i] = normal_rng(alpha + beta * x[i], sigma);
}
}
'
writeLines(linear_prior_ppc_stan, "linear_prior_ppc.stan")Esecuzione della simulazione:
mod_lin <- cmdstan_model("linear_prior_ppc.stan")
x_new <- runif(200, -2, 2)
fit_lin <- mod_lin$sample(
data = list(N = length(x_new), x = x_new),
chains = 4, iter_warmup = 500, iter_sampling = 1000, seed = 123,
refresh = 0
)Visualizzazione della distribuzione predittiva:
R.1.2.5 Conclusioni
- La scala delle distribuzioni precedenti specificate per \(\alpha\), \(\beta\) e \(\sigma\) determina direttamente la distribuzione dei valori simulati di \(y\).
- Se i valori di \(y\) simulati risultano al di fuori del dominio realistico (ad esempio, punteggi negativi o superiori al massimo teorico), le distribuzioni precedenti devono essere ricalibrate.
- L’utilizzo di distribuzioni precedenti debolmente informative (centrate su zero con varianze moderate) produce simulazioni coerenti con il contesto psicologico di riferimento.
R.1.3 Regressione logistica
Nella regressione logistica, il modello per un esito binario è specificato come:
\[ \text{logit}\, P(y=1 \mid x) = \alpha + \beta x . \]
In questo framework, i parametri \(\alpha\) e \(\beta\) operano sulla scala logit, che non è direttamente interpretabile in termini di probabilità. È cruciale ricordare che la funzione logit è caratterizzata da una pendenza accentuata: differenze di 2-3 unità sulla scala logit corrispondono a variazioni estreme nelle probabilità sottostanti (da circa 0.1 a 0.9).
R.1.3.1 Importanza della scelta delle distribuzioni a priori
- Con predittori standardizzati (media 0, deviazione standard 1), una distribuzione a priori \(\beta \sim \mathcal{N}(0,1)\) implica che effetti di moderata entità sono plausibili, mentre probabilità estreme (vicine a 0 o 1) rimangono poco probabili.
- Al contrario, una distribuzione a priori \(\beta \sim \mathcal{N}(0,2.5)\) consente valori sulla scala logit fino a ±5, che corrispondono a probabilità praticamente certe (0 o 1). Questo approccio rischia di incorporare nel modello assunzioni di certezza assoluta prima ancora di osservare i dati.
Il controllo predittivo basato sulle distribuzioni a priori (PPC) permette di verificare se le probabilità implicite generate dalle specifiche scelte parametriche sono coerenti con le aspettative del dominio applicativo.
R.1.3.2 Simulazioni in R
S <- 10000
x <- rnorm(S, 0, 1) # standardizzare è buona pratica
# Scenario E: prior larga
alpha_E <- rnorm(S, 0, 2.5)
beta_E <- rnorm(S, 0, 2.5)
pE <- plogis(alpha_E + beta_E * x)
yE <- rbinom(S, 1, pE)
# Scenario F: prior weakly-informative
alpha_F <- rnorm(S, 0, 1)
beta_F <- rnorm(S, 0, 1)
pF <- plogis(alpha_F + beta_F * x)
yF <- rbinom(S, 1, pF)
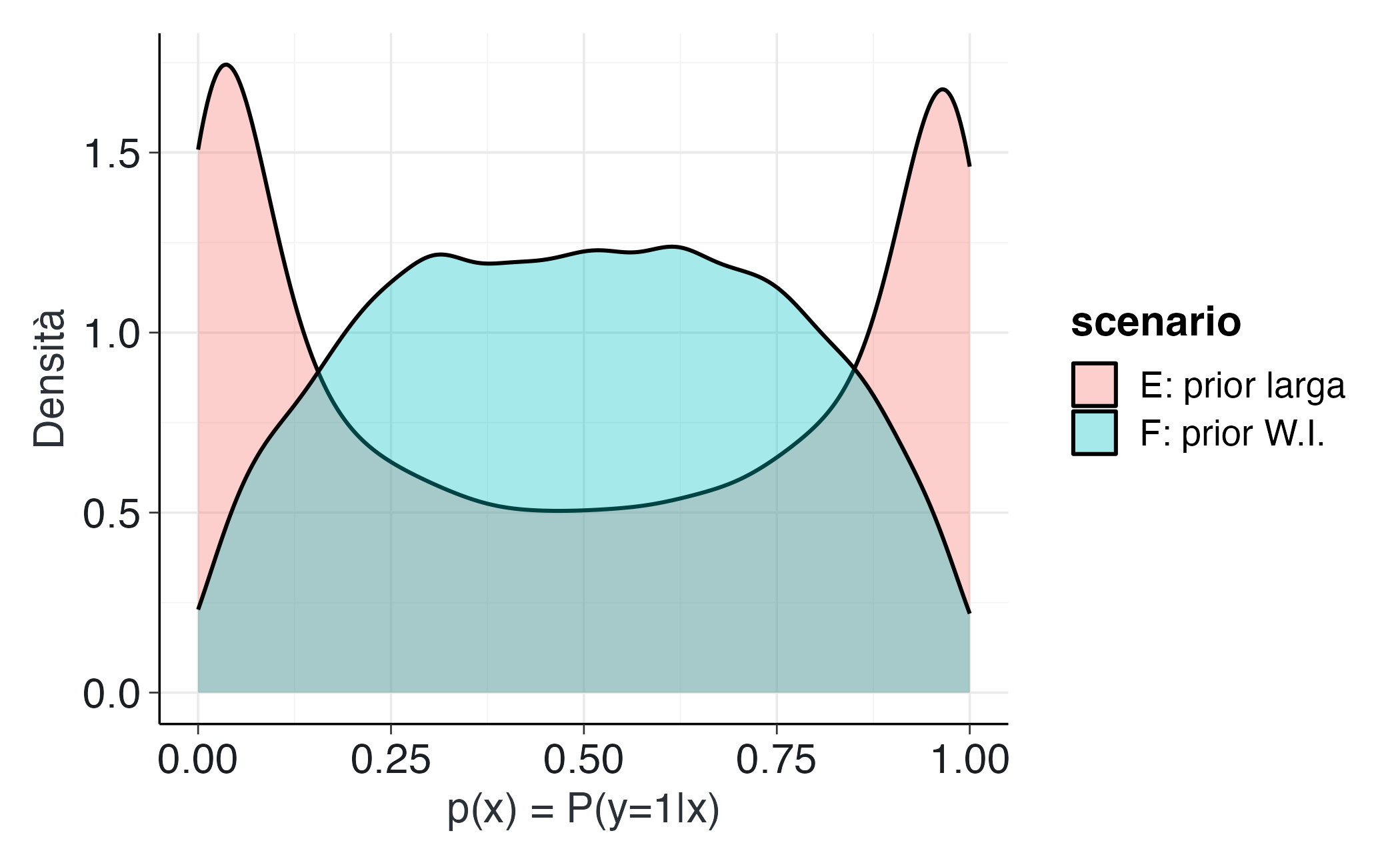
tibble(p = pE, scenario = "E: prior larga") |>
bind_rows(tibble(p = pF, scenario = "F: prior W.I.")) |>
ggplot(aes(x = p, fill = scenario)) +
geom_density(alpha = 0.35) +
labs(x = "p(x) = P(y=1|x)", y = "Densità")Interpretazione.
- Con distribuzioni a priori eccessivamente diffuse (Scenario E), le probabilità implicite sono frequentemente vicine ai valori estremi di 0 o 1. Ciò indica che il modello, in assenza di dati osservati, considera plausibili situazioni di quasi-certezza assoluta.
- Con distribuzioni a priori debolmente informative (Scenario F), le probabilità si distribuiscono in un range più realistico (0.05-0.95), riflettendo appropriatamente l’incertezza caratteristica dei fenomeni psicologici.
Linee guida pratiche
- Con prior standardizzat, l’utilizzo di distribuzioni \(\mathcal{N}(0,1)\) o \(\mathcal{N}(0,1.5)\) per i coefficienti sulla scala logit rappresenta generalmente una scelta robusta: permette sufficiente variabilità senza generare previsioni probabilistiche estreme.
- Distribuzioni a priori eccessivamente diffuse possono produrre modelli “rigidi” che, a priori, assumono comportamenti quasi deterministici, risultando incoerenti con la variabilità tipica dei dati psicologici.
R.1.3.3 Implementazione in Stan: simulazione esclusiva dalle distribuzioni precedenti
Possiamo rendere esplicito il processo mediante un modello Stan che non incorpora dati osservati ma genera esclusivamente previsioni a partire dalle distribuzioni a priori.
logistic_prior_ppc_stan <- '
data {
int<lower=1> N;
vector[N] x;
}
parameters {
real alpha;
real beta;
}
model {
alpha ~ normal(0, 1);
beta ~ normal(0, 1);
}
generated quantities {
vector[N] p;
array[N] int y_rep;
for (i in 1:N) {
p[i] = inv_logit(alpha + beta * x[i]);
y_rep[i] = bernoulli_rng(p[i]);
}
}
'
writeLines(logistic_prior_ppc_stan, "logistic_prior_ppc.stan")Esecuzione del modello:
mod_log <- cmdstan_model("logistic_prior_ppc.stan")
x_new <- rnorm(300)
fit_log <- mod_log$sample(
data = list(N = length(x_new), x = x_new),
chains = 4, iter_warmup = 500, iter_sampling = 1000,
seed = 123, refresh = 0
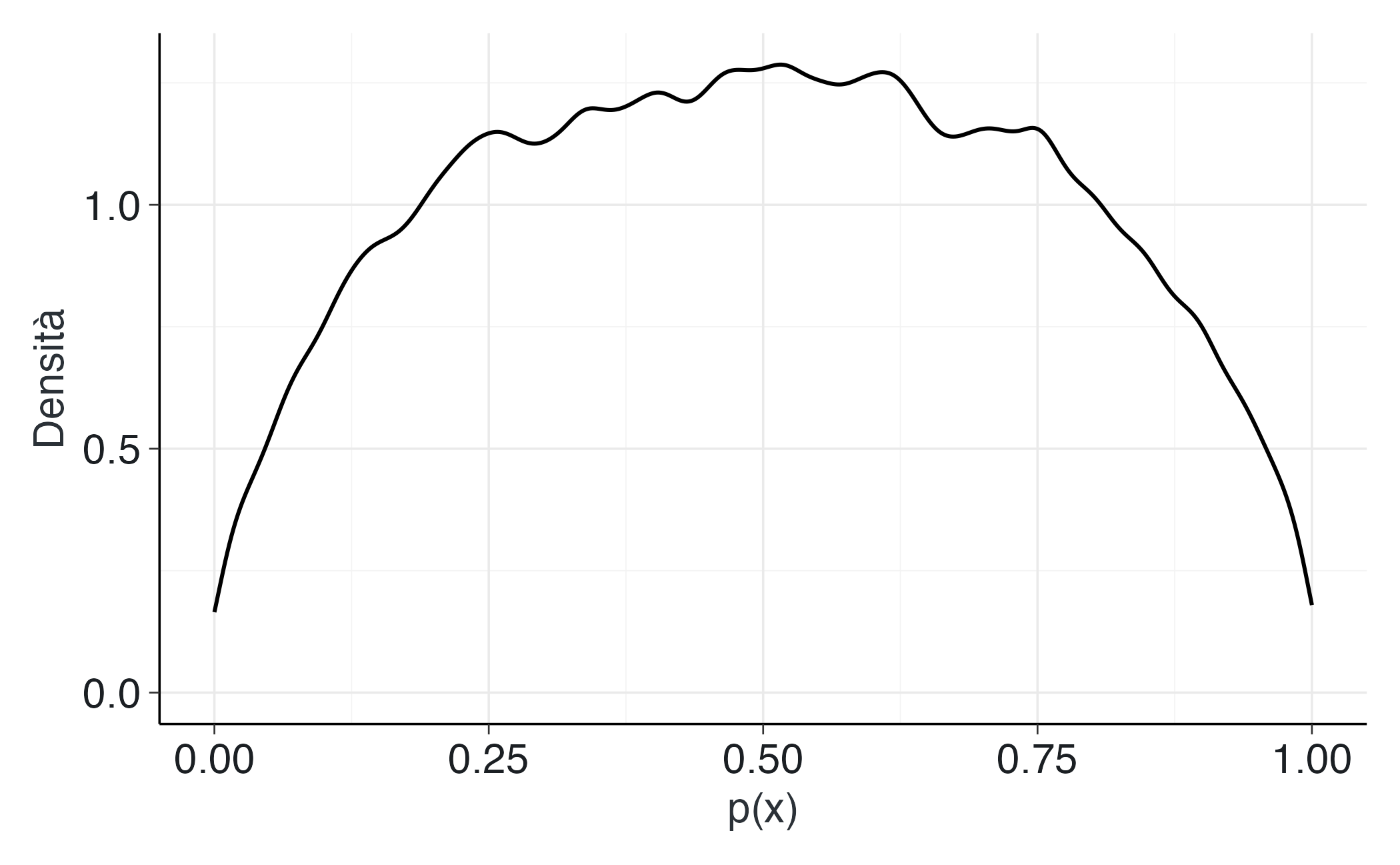
)Visualizzazione delle probabilità implicite:
R.1.3.4 Conclusioni
- Le distribuzioni a priori nella regressione logistica influenzano direttamente la distribuzione delle probabilità implicite generate dal modello.
- Distribuzioni a priori eccessivamente diffuse equivalgono ad assumere, prima di osservare i dati, che siano probabili risposte quasi certe (0 o 1).
- Distribuzioni a priori moderate preservano invece l’incertezza appropriata, riflettendo più fedelmente la realtà dei fenomeni psicologici.
R.2 Linee guida pratiche per la specificazione delle distribuzioni a priori
-
Lavorare sulla scala appropriata
- Quando possibile, standardizzare i predittori (centrati a media 0 e scalati a deviazione standard 1).
- Questo approccio garantisce un’interpretazione uniforme dei coefficienti: una distribuzione Normal(0,1) suggerisce che effetti “moderati” (variazioni di circa una deviazione standard nell’outcome per ogni deviazione standard nel predittore) siano i più plausibili.
-
Coefficienti di regressione (\(\beta\))
- Un punto di partenza solido consiste nell’utilizzare distribuzioni a priori Normal(0, 0.5–2).
- Con \(\beta \sim \mathcal{N}(0,1)\): effetti di piccola e media entità sono considerati plausibili, mentre effetti di grande magnitudine rimangono possibili ma meno probabili.
- Importante: senza standardizzazione dei predittori, la scala di \(\beta\) cambia radicalmente, invalidando queste linee guida.
-
Intercetta (\(\alpha\))
- Per outcome continui (modelli gaussiani), centrare la variabile dipendente \(y\) rende l’intercetta più direttamente interpretabile.
- Per outcome binari (modelli logistici), una Normal(0,1–1.5) implica probabilità a priori tipicamente comprese tra 0.05 e 0.95; una Normal(0,2.5) è significativamente più permissiva, rendendo probabili scenari di quasi-certezza.
-
Parametri di dispersione (\(\sigma\))
- Utilizzare distribuzioni a priori definite solo per valori positivi (Half-Normal, Exponential, Gamma).
- Specificare il parametro di scala dell’Exponential in accordo con l’ordine di grandezza atteso nel dominio applicativo. Ad esempio, per punteggi su scala 0-100, una Exponential(media ≈ 5–10) rappresenta una scelta generalmente ragionevole.
- Verificare sistematicamente mediante simulazioni che la dispersione generata sia coerente con la variabilità attesa nei dati reali.
-
Trasformazioni non lineari (logit, log)
- Evitare di interpretare esclusivamente i coefficienti sulla scala trasformata: convertire sistematicamente nelle scale naturali di interesse.
- Tradurre i coefficienti logit in probabilità implicite e i coefficienti log in tassi attesi.
- Porsi criticamente la domanda: “Queste distribuzioni a priori implicano che i soggetti abbiano probabilità estreme (vicine a 0 o 1) di manifestare il comportamento?”
-
Validazione e trasparenza metodologica
- Eseguire sempre controlli predittivi basati sulle distribuzioni a priori (prior predictive checks): se i dati simulati appaiono “irrealistici” (ad esempio, valori negativi per scale positive o fuori range), le distribuzioni a priori necessitano ri-calibrazione.
- Documentare dettagliatamente il processo di specificazione: quali distribuzioni sono state testate, quali modifiche sono state apportate e le motivazioni sottostanti. Questa trasparenza costituisce un elemento fondamentale del rigore metodologico nell’analisi bayesiana.
brms per i tre casi
Modello gaussiano.
N <- 100
df_g <- tibble(y = rnorm(N, 50, 10)) # placeholder, non usato con "only"
fit_g_prior <- brm(
bf(y ~ 1),
data = df_g,
family = gaussian(),
prior = c(
prior(normal(50, 10), class = "Intercept"),
prior(exponential(0.1), class = "sigma")
# prior(exponential(1.0/10), class = "sigma")
),
sample_prior = "only",
chains = 4, iter = 1000, cores = 4,
backend = "cmdstanr", seed = 123
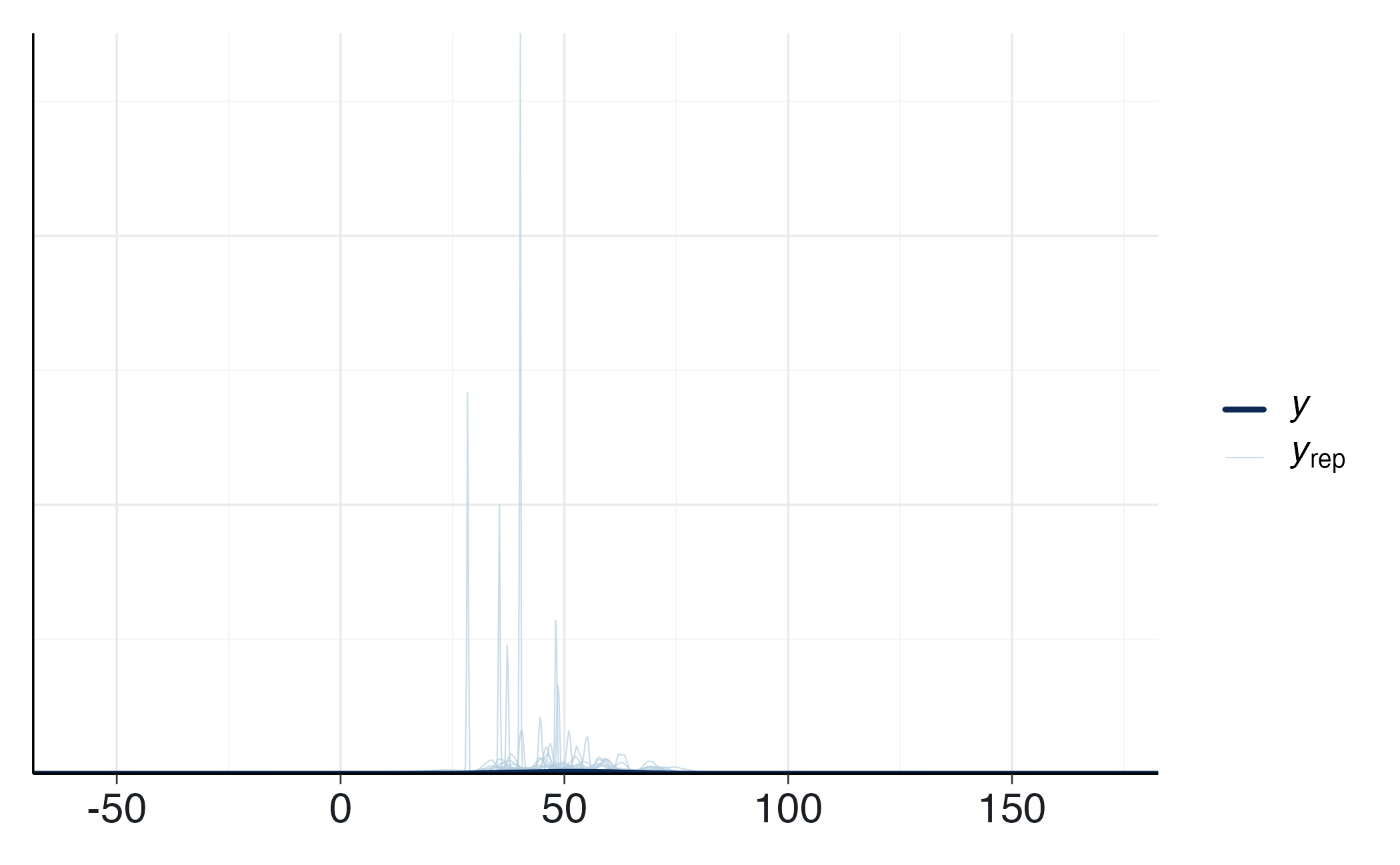
)yrep_g <- posterior_predict(fit_g_prior)
ppc_dens_overlay(y = df_g$y, yrep = yrep_g[1:200, ])Regressione lineare.
fit_l_prior <- brm(
bf(y ~ 1 + x),
data = df_l,
family = gaussian(),
prior = c(
prior(normal(0, 1), class = "Intercept"),
prior(normal(0, 1), class = "b", coef = "x"),
prior(exponential(0.5), class = "sigma") # <-- 0.5 (oppure 1.0/2)
# prior(exponential(1.0/2), class = "sigma") # <-- equivalente
),
sample_prior = "only",
chains = 4, iter = 1000, cores = 4,
backend = "cmdstanr", seed = 123
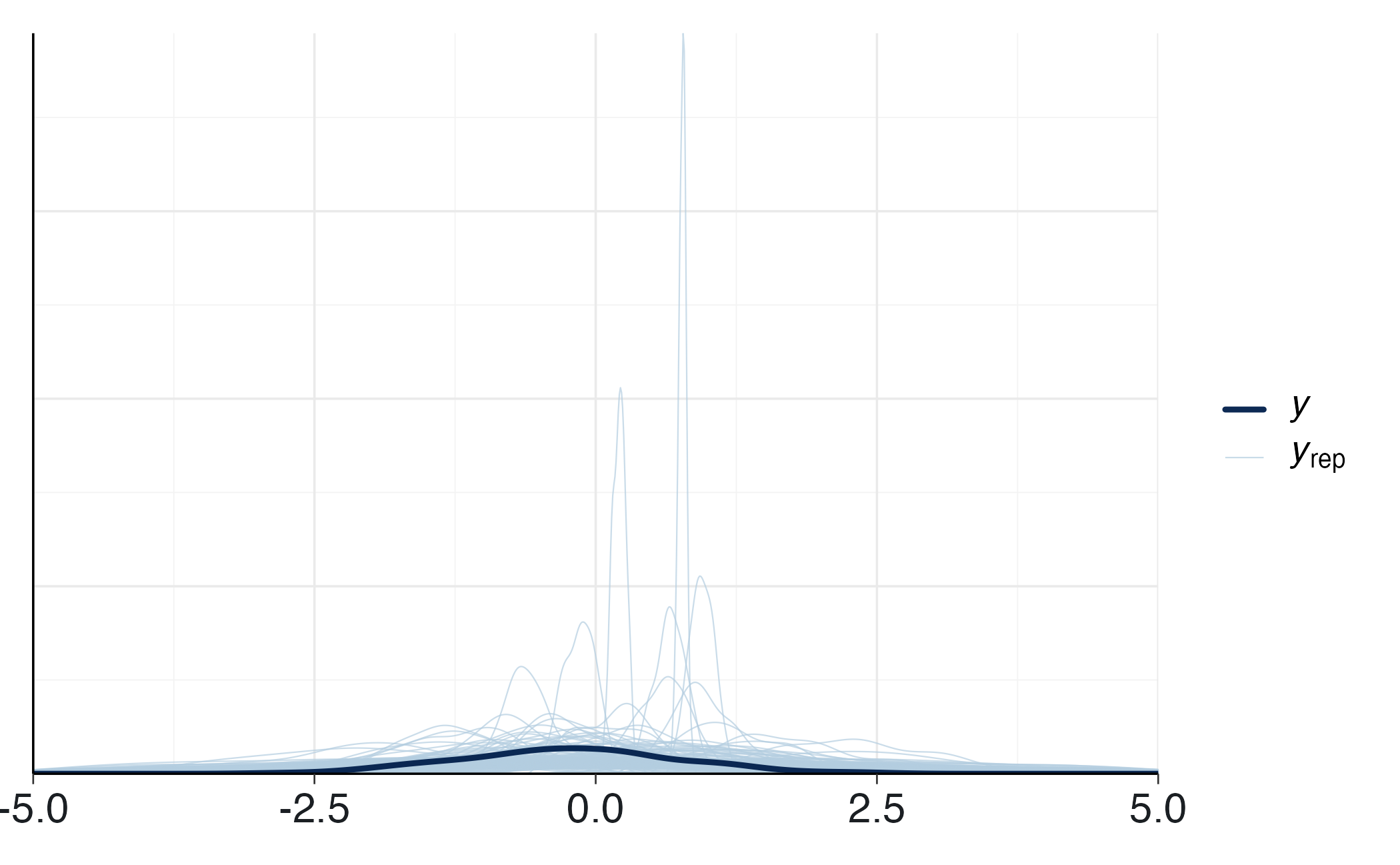
)yrep_l <- posterior_predict(fit_l_prior)
ppc_dens_overlay(y = df_l$y, yrep = yrep_l[1:200, ]) +
xlim(-5, 5)Regressione logistica.
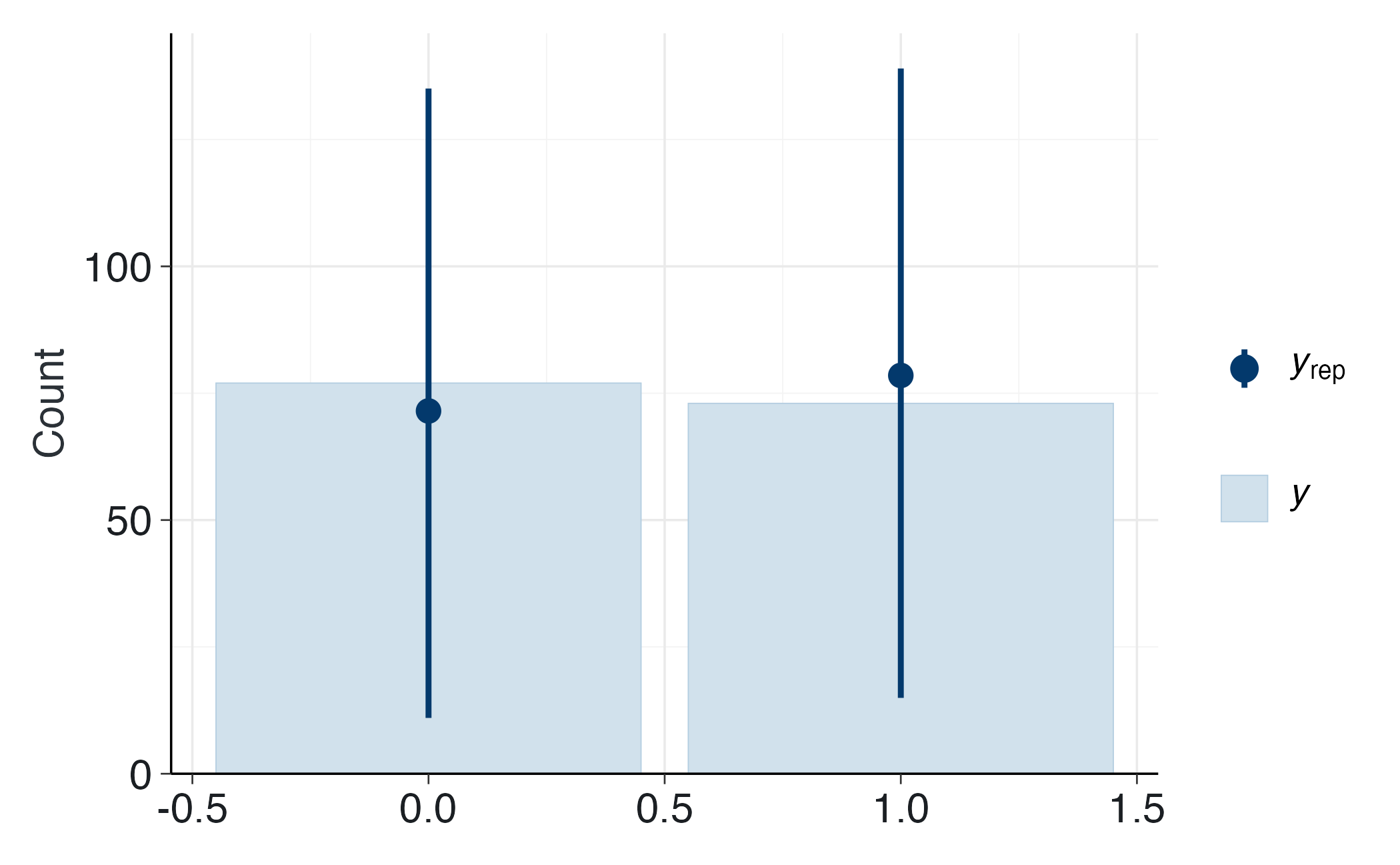
yrep_log <- posterior_predict(fit_log_prior)
ppc_bars(y = df_log$y, yrep = yrep_log[1:200, ])