# Creiamo una griglia di valori per il parametro theta
# Usiamo una sequenza da 0 a 1 con incrementi di 0.1
# Questo ci dà 11 valori possibili: 0.0, 0.1, 0.2, ..., 1.0
theta_griglia <- seq(from = 0, to = 1, by = 0.1)
# Visualizziamo i valori della griglia
theta_griglia
#> [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.01 Quantificare e aggiornare l’incertezza
Introduzione
Nel capitolo 15 del manuale didattico abbiamo esplorato i fondamenti teorici dell’aggiornamento bayesiano, introducendo il concetto di distribuzione di probabilità come strumento per rappresentare l’incertezza e mostrando come il teorema di Bayes consenta di aggiornare in modo coerente le nostre credenze alla luce dei dati. Abbiamo utilizzato l’esempio del globo terrestre per sviluppare un’intuizione visiva del processo di apprendimento bayesiano e abbiamo concluso con un’applicazione concreta nel campo della psicologia: la stima della proporzione di persone che giudicano moralmente accettabile un’azione controversa nel dilemma del carrello ferroviario.
In questo materiale supplementare, mettiamo in pratica questi principi attraverso implementazioni complete in R. L’obiettivo non è semplicemente riprodurre i calcoli presentati nel manuale, ma espandere la comprensione attraverso l’esperienza diretta con il codice. Ogni riga di codice sarà corredata da spiegazioni dettagliate che renderanno trasparente il processo computazionale sottostante.
Il capitolo è suddiviso in tre sezioni principali. Nella prima sezione, implementeremo il metodo basato su griglia, un approccio intuitivo che discretizza lo spazio dei parametri e calcola esplicitamente la distribuzione a posteriori punto per punto. Questo metodo ha un enorme valore pedagogico, in quanto rende visibile ogni passaggio dell’aggiornamento bayesiano. Nella seconda sezione, esploreremo il modello Beta-Binomiale che offre una soluzione analitica elegante per l’aggiornamento continuo. Nella terza sezione, applicheremo questi strumenti a un esercizio pratico sul riconoscimento delle emozioni, consolidando la comprensione attraverso l’applicazione attiva.
1.1 Il dilemma del carrello ferroviario
Il dilemma del carrello ferroviario (Foot, 1978; Thomson, 1976) è uno degli scenari più studiati dalla psicologia morale. La versione classica presenta ai partecipanti una situazione in cui un treno fuori controllo sta per investire cinque persone che verranno inevitabilmente uccise. Il partecipante può deviare il treno su un binario alternativo, salvando le cinque persone ma causando la morte di una persona che si trova su quel binario. La domanda cruciale è: questa azione è moralmente accettabile?
Questo dilemma ha generato decenni di ricerche in psicologia morale, filosofia e neuroscienze cognitive. Le risposte dei partecipanti rivelano il conflitto tra i principi morali deontologici, che vietano di utilizzare una persona come mezzo, e le considerazioni utilitaristiche, che privilegiano il bene maggiore per il maggior numero di persone. La variabilità delle risposte riflette le differenze individuali nei processi di ragionamento morale, nell’influenza delle emozioni sul giudizio e nelle intuizioni etiche di base.
Dal punto di vista dell’inferenza statistica, il nostro obiettivo è stimare la proporzione \(\theta\) della popolazione che giudica moralmente accettabile l’azione di deviare il treno. Ogni partecipante fornisce una risposta binaria: “accettabile” o “non accettabile”. Questi dati possono essere modellati come prove Bernoulliane indipendenti e il conteggio totale delle risposte positive segue una distribuzione binomiale. L’approccio bayesiano ci permette di stimare \(\theta\) integrando le conoscenze pregresse sulla psicologia morale con l’evidenza empirica raccolta nel nostro studio specifico.
Supponiamo di aver reclutato un campione di trenta adulti e di aver osservato che ventidue di essi giudicano moralmente accettabile l’azione. Questi numeri costituiscono la nostra evidenza empirica. La domanda inferenziale è: quale credenza ragionevole possiamo sviluppare riguardo alla proporzione \(\theta\) nella popolazione generale, dati questi risultati campionari?
1.2 Il metodo basato su griglia
Il metodo basato su griglia rappresenta l’approccio più diretto e trasparente per implementare l’aggiornamento bayesiano. La sua logica è molto semplice: dividiamo l’intervallo dei valori possibili per \(\theta\) in un insieme discreto di punti, calcoliamo la plausibilità di ciascun punto combinando prior e verosimiglianza, e normalizziamo per ottenere una distribuzione di probabilità valida.
1.2.1 Costruzione della griglia di valori
Il primo passo consiste nel definire l’insieme dei valori possibili per il parametro \(\theta\). Poiché \(\theta\) rappresenta una proporzione, deve necessariamente cadere nell’intervallo tra 0 e 1. Per rendere il calcolo gestibile, è necessario discretizzare l’intervallo continuo in un numero finito di punti.
La griglia risultante contiene undici valori equidistanti. Questa discretizzazione è sufficientemente fine per scopi didattici, mantenendo comunque i calcoli trasparenti e gestibili. In applicazioni reali, potremmo utilizzare griglie molto più fini, con centinaia o migliaia di punti, per approssimare meglio la distribuzione continua sottostante. Tuttavia, per comprendere il meccanismo fondamentale dell’aggiornamento bayesiano, questa griglia grossolana è perfettamente adeguata e ha il vantaggio di rendere ogni calcolo esplicitamente verificabile.
1.2.2 Specificazione della distribuzione a priori
La distribuzione a priori rappresenta le nostre credenze su \(\theta\) prima di osservare i dati. In un approccio bayesiano, questa componente deve essere specificata esplicitamente, rendendo così trasparenti le assunzioni iniziali. Esistono diverse filosofie riguardo alla scelta del prior. Un prior uniforme, che assegna la stessa probabilità a tutti i valori, rappresenta uno stato di ignoranza totale iniziale. Un prior informativo incorpora invece conoscenze pregresse derivanti dalla letteratura, da studi pilota o da considerazioni teoriche.
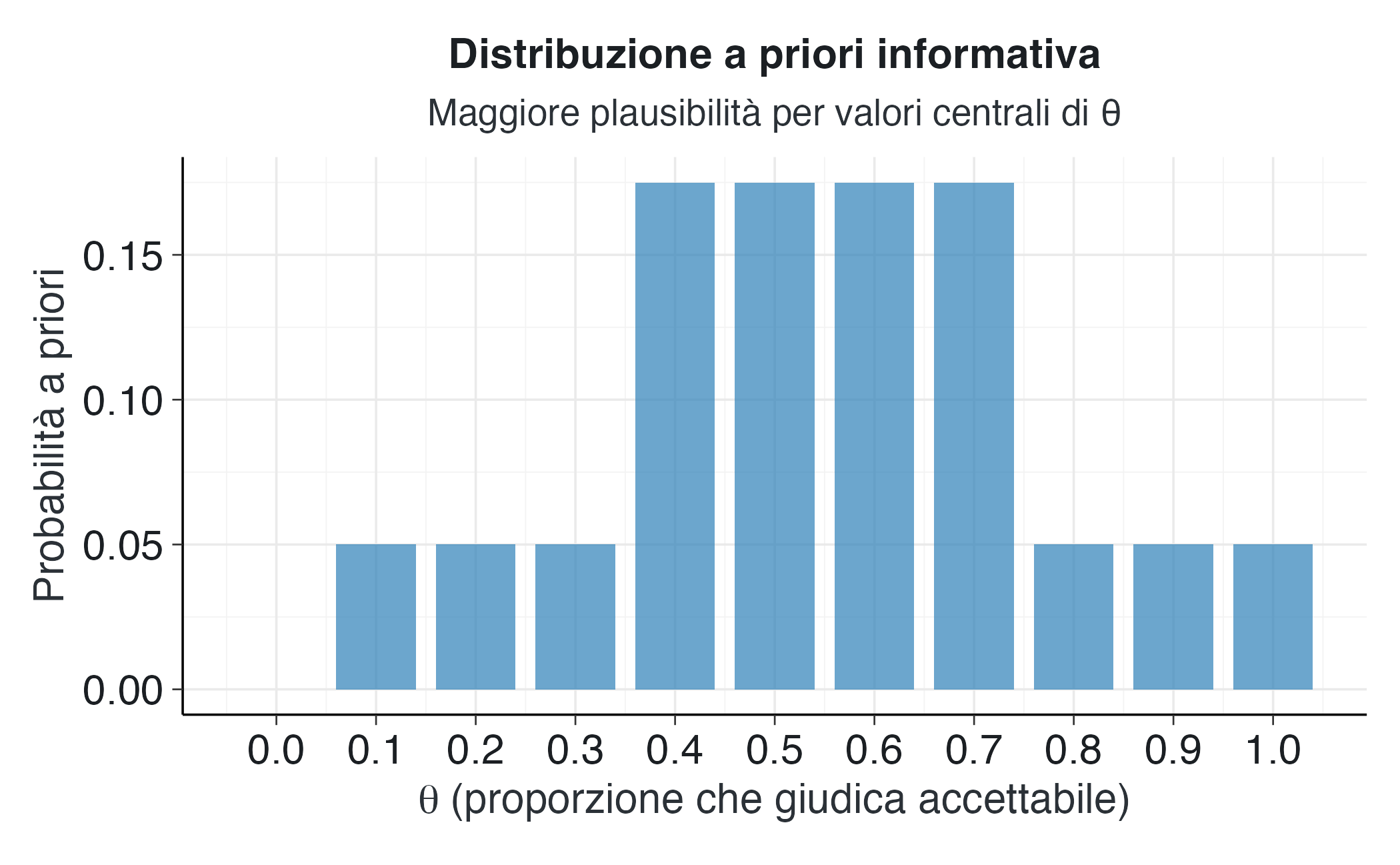
Per questo esempio, adottiamo un prior informativo che riflette una moderata credenza riguardo alla distribuzione di \(\theta\). Questa distribuzione concentra la probabilità sui valori centrali, riflettendo l’aspettativa che le risposte estreme (tutti accettano o tutti rifiutano) siano meno probabili rispetto alle risposte intermedie.
# Definiamo un prior informativo discreto
# Questo vettore contiene le probabilità associate a ciascun valore di theta
# Notiamo che i valori estremi (0 e 1) hanno probabilità zero
# I valori centrali (0.4, 0.5, 0.6, 0.7) hanno probabilità più elevate
prior_informativo <- c(0, 0.05, 0.05, 0.05, 0.175, 0.175, 0.175, 0.175, 0.05, 0.05, 0.05)
# Verifichiamo che le probabilità sommino a uno
# Questa è una proprietà fondamentale di ogni distribuzione di probabilità valida
somma_prior <- sum(prior_informativo)La somma delle probabilità nel nostro prior è 1, il che conferma che abbiamo specificato una distribuzione di probabilità valida. Questa distribuzione assegna una probabilità pari a zero agli estremi, ovvero ai valori di \(\theta\) pari a 0 e a 1, riflettendo la convinzione che sia improbabile che nessuno o tutti accettino l’azione nel dilemma. I valori centrali, compresi tra 0.4 e 0.7, ricevono le probabilità più alte, riflettendo l’aspettativa che le opinioni morali siano distribuite in modo relativamente equilibrato all’interno della popolazione.
# Creiamo una visualizzazione della distribuzione a priori
# Questo grafico mostra chiaramente quali valori di theta consideriamo
# più o meno plausibili prima di osservare i dati
# Organizziamo i dati in un dataframe per facilitare la visualizzazione
dati_prior <- data.frame(
theta = theta_griglia,
probabilita = prior_informativo
)
# Creiamo il grafico a barre
ggplot(dati_prior, aes(x = theta, y = probabilita)) +
# geom_col crea un grafico a barre con larghezza specificata
geom_col(width = 0.08, fill = "#2c7fb8", alpha = 0.7) +
# Personalizziamo le etichette degli assi
labs(
x = expression(theta ~ "(proporzione che giudica accettabile)"),
y = "Probabilità a priori",
title = "Distribuzione a priori informativa",
subtitle = "Maggiore plausibilità per valori centrali di θ"
) +
# Impostiamo i punti di rottura sull'asse x per mostrare tutti i valori
scale_x_continuous(breaks = theta_griglia) Il grafico rivela la struttura della nostra distribuzione a priori. La forma ricorda approssimativamente quella di una distribuzione normale, centrata sui valori intermedi e con code che decrescono verso gli estremi. Questa configurazione riflette una posizione epistemica ragionevole: pur non avendo certezze definitive prima di raccogliere i dati, abbiamo alcune aspettative qualitative basate sulla letteratura e sul buon senso psicologico.
1.2.3 Calcolo della funzione di verosimiglianza
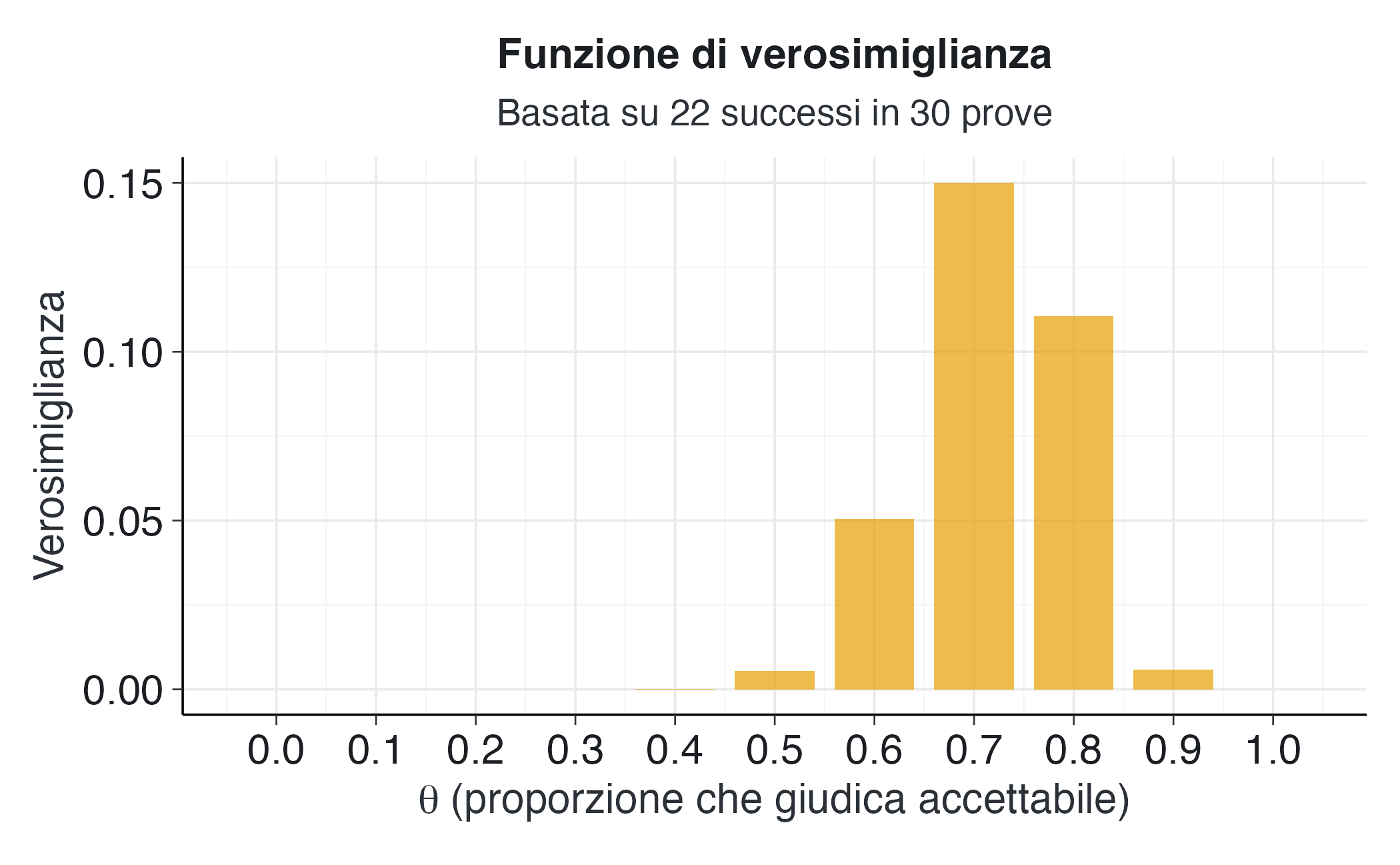
La verosimiglianza quantifica quanto i dati osservati siano compatibili con ciascun possibile valore del parametro. Nel nostro caso, abbiamo osservato ventidue risposte positive su trenta partecipanti. Per ogni valore di \(\theta\) nella griglia, calcoliamo la probabilità di ottenere questo risultato (\(y\) = 22; \(n\) = 30) se quel valore specifico fosse il parametro reale della popolazione.
# Definiamo i dati osservati
successi_osservati <- 22 # numero di risposte "accettabile"
prove_totali <- 30 # numero totale di partecipanti
# Calcoliamo la verosimiglianza per ogni valore di theta nella griglia
# La funzione dbinom calcola la probabilità binomiale
# Argomenti: numero di successi, dimensione del campione, probabilità di successo
verosimiglianza <- dbinom(
x = successi_osservati,
size = prove_totali,
prob = theta_griglia
)
# Visualizziamo i valori di verosimiglianza calcolati
verosimiglianza
#> [1] 0.00e+00 2.52e-16 4.12e-10 1.06e-06 1.73e-04 5.45e-03 5.05e-02 1.50e-01
#> [9] 1.11e-01 5.76e-03 0.00e+00I valori di verosimiglianza mostrano un chiaro andamento. La verosimiglianza è massima per \(\theta\) = 0.7, valore che corrisponde esattamente alla proporzione osservata nel campione (22/30 ≈ 0.73). I valori di \(\theta\) vicini a 0.7 hanno anch’essi una verosimiglianza elevata, mentre i valori molto distanti hanno una verosimiglianza molto bassa o praticamente nulla. Ciò riflette il fatto che i nostri dati sono altamente incompatibili con ipotesi estreme come \(\theta\) = 0.1 o \(\theta\) = 0.9.
# Visualizziamo la funzione di verosimiglianza
# Questo grafico mostra quali valori di theta sono più compatibili
# con i dati che abbiamo osservato
dati_verosimiglianza <- data.frame(
theta = theta_griglia,
verosimiglianza = verosimiglianza
)
ggplot(dati_verosimiglianza, aes(x = theta, y = verosimiglianza)) +
geom_col(width = 0.08, fill = "#E69F00", alpha = 0.7) +
labs(
x = expression(theta ~ "(proporzione che giudica accettabile)"),
y = "Verosimiglianza",
title = "Funzione di verosimiglianza",
subtitle = paste0(
"Basata su ", successi_osservati, " successi in ",
prove_totali, " prove"
)
) +
scale_x_continuous(breaks = theta_griglia) Il picco di verosimiglianza si colloca chiaramente nella regione compresa tra 0.6 e 0.8, con il valore massimo a 0.7. Questo risultato è intuitivo: se dovessimo scegliere un valore di \(\theta\) che massimizza la probabilità dei dati osservati, sceglieremmo un valore prossimo alla proporzione campionaria. Tuttavia, la verosimiglianza da sola non costituisce una stima completa di \(\theta\), in quanto non tiene conto delle nostre conoscenze pregresse né dell’incertezza associata alla stima.
1.2.4 L’aggiornamento bayesiano: combinazione di prior e verosimiglianza
Il cuore dell’inferenza bayesiana risiede nella combinazione della distribuzione a priori con la verosimiglianza per ottenere la distribuzione a posteriori. Matematicamente, questo processo corrisponde alla moltiplicazione punto per punto della distribuzione a priori e della verosimiglianza, seguita da una normalizzazione per garantire che le probabilità sommino a uno.
# Calcoliamo la distribuzione a posteriori non normalizzata
# Questa si ottiene moltiplicando, per ogni valore di theta,
# la probabilità a priori per la verosimiglianza
posteriori_non_normalizzato <- prior_informativo * verosimiglianza
# Visualizziamo i valori non normalizzati
posteriori_non_normalizzato
#> [1] 0.00e+00 1.26e-17 2.06e-11 5.29e-08 3.03e-05 9.54e-04 8.84e-03 2.63e-02
#> [9] 5.53e-03 2.88e-04 0.00e+00I valori non normalizzati riflettono la plausibilità relativa di ciascun valore di \(\theta\) dopo l’osservazione dei dati. Tuttavia, questi numeri non costituiscono ancora una distribuzione di probabilità valida, in quanto la loro somma non è uguale a uno. Il passo finale consiste nel normalizzare questi valori dividendoli per la loro somma totale.
# Calcoliamo il fattore di normalizzazione
# Questo è semplicemente la somma di tutti i valori non normalizzati
fattore_normalizzazione <- sum(posteriori_non_normalizzato)
# Dividiamo ciascun valore per questo fattore per ottenere
# la distribuzione a posteriori normalizzata
posteriori <- posteriori_non_normalizzato / fattore_normalizzazione
# Verifichiamo che la somma sia ora uguale a uno
somma_posteriori <- sum(posteriori)La somma della distribuzione a posteriori è 1, il che conferma che abbiamo ottenuto una distribuzione di probabilità valida. Possiamo ora usare questa distribuzione per fare inferenze su \(\theta\), calcolare statistiche riassuntive e quantificare l’incertezza associata alla nostra stima.
# Visualizziamo la distribuzione a posteriori
dati_posteriori <- data.frame(
theta = theta_griglia,
probabilita = posteriori
)
ggplot(dati_posteriori, aes(x = theta, y = probabilita)) +
geom_col(width = 0.08, fill = "#0072B2", alpha = 0.7) +
labs(
x = expression(theta ~ "(proporzione che giudica accettabile)"),
y = "Probabilità a posteriori",
title = "Distribuzione a posteriori",
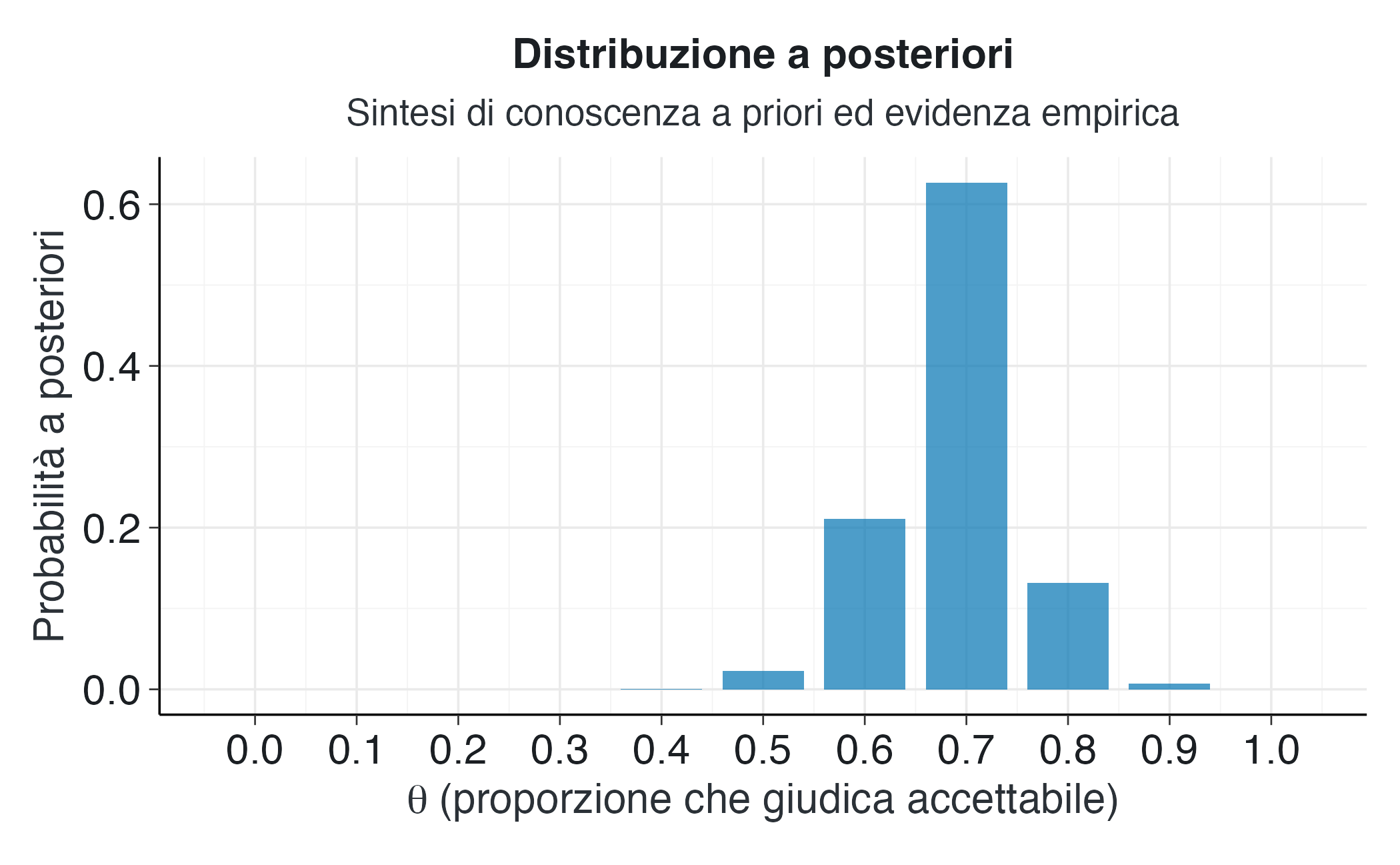
subtitle = "Sintesi di conoscenza a priori ed evidenza empirica"
) +
scale_x_continuous(breaks = theta_griglia) La distribuzione a posteriori mostra una concentrazione di probabilità nella regione tra 0.6 e 0.8, con il massimo a 0.7. Confrontata con la distribuzione a priori, la posteriori è più stretta e spostata verso destra, riflettendo l’influenza dei dati osservati che hanno fornito evidenza di una proporzione relativamente alta di risposte positive.
1.2.5 Statistiche riassuntive della distribuzione a posteriori
Una volta ottenuta la distribuzione a posteriori, è possibile calcolare diverse statistiche che riassumono le nostre credenze aggiornate su \(\theta\). Le tre statistiche più comunemente utilizzate sono la media, la varianza e la moda.
# Calcoliamo la media a posteriori
# Questa è il valore atteso di theta secondo la distribuzione a posteriori
# Si calcola come somma ponderata: ogni valore di theta moltiplicato
# per la sua probabilità a posteriori
media_posteriori <- sum(theta_griglia * posteriori)
# Calcoliamo la varianza a posteriori
# Questa quantifica la dispersione della distribuzione
# e quindi l'incertezza residua su theta
varianza_posteriori <- sum((theta_griglia - media_posteriori)^2 * posteriori)
# La deviazione standard è la radice quadrata della varianza
sd_posteriori <- sqrt(varianza_posteriori)
# Calcoliamo la moda a posteriori
# Questo è il valore di theta con massima probabilità a posteriori
# Viene anche chiamato "stima MAP" (Maximum A Posteriori)
indice_massimo <- which.max(posteriori)
moda_posteriori <- theta_griglia[indice_massimo]La media a posteriori è 0.689, indicando che la nostra migliore stima puntuale di \(\theta\), nel senso del valore atteso, è circa 0.729. La moda a posteriori è 0.7, che rappresenta il singolo valore più plausibile secondo la distribuzione. La deviazione standard è 0.067, quantificando l’incertezza residua sulla stima. Questa deviazione standard è sostanzialmente più piccola di quella che avremmo con un prior uniforme, riflettendo il fatto che il prior informativo ha contribuito a ridurre l’incertezza.
1.2.6 Visualizzazione comparativa dell’aggiornamento bayesiano
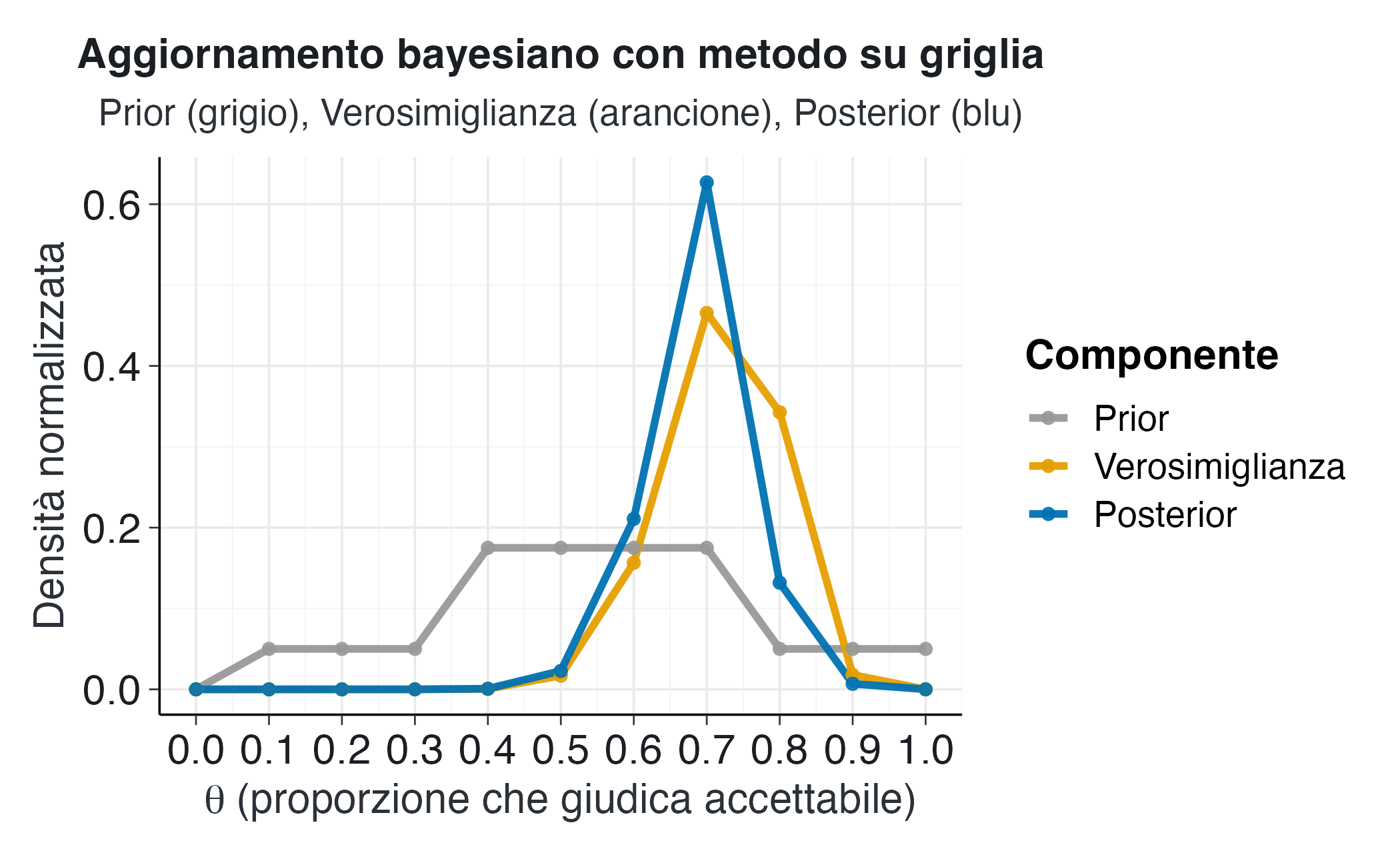
Per apprezzare il processo di aggiornamento bayesiano, è utile visualizzare simultaneamente tutte e tre le componenti: prior, verosimiglianza e posterior. Questa visualizzazione mostra come l’evidenza empirica modifichi le credenze iniziali per produrre quelle aggiornate.
# Prepariamo i dati per la visualizzazione comparativa
# Normalizziamo tutte le distribuzioni per renderle visivamente confrontabili
dati_completi <- data.frame(
theta = rep(theta_griglia, 3),
densita = c(
prior_informativo / sum(prior_informativo),
verosimiglianza / sum(verosimiglianza),
posteriori / sum(posteriori)
),
tipo = rep(
c("Prior", "Verosimiglianza", "Posterior"),
each = length(theta_griglia)
)
)
# Convertiamo il tipo in un fattore ordinato per controllare
# l'ordine di visualizzazione nella legenda
dati_completi$tipo <- factor(
dati_completi$tipo,
levels = c("Prior", "Verosimiglianza", "Posterior")
)
# Creiamo il grafico comparativo usando linee anziché barre
# per enfatizzare la continuità concettuale delle distribuzioni
ggplot(dati_completi, aes(x = theta, y = densita, color = tipo)) +
geom_line(size = 1.3) +
geom_point(size = 2) +
scale_color_manual(
values = c(
"Prior" = "#999999",
"Verosimiglianza" = "#E69F00",
"Posterior" = "#0072B2"
)
) +
labs(
x = expression(theta ~ "(proporzione che giudica accettabile)"),
y = "Densità normalizzata",
title = "Aggiornamento bayesiano con metodo su griglia",
subtitle = "Prior (grigio), Verosimiglianza (arancione), Posterior (blu)",
color = "Componente"
) +
scale_x_continuous(breaks = theta_griglia) Il grafico comparativo rivela diversi aspetti importanti del processo di aggiornamento. La curva grigia del prior mostra una distribuzione relativamente simmetrica centrata sui valori intermedi. La curva arancione della verosimiglianza è fortemente concentrata attorno a 0.7, riflettendo l’evidenza empirica fornita dai ventidue successi su trenta prove. La curva blu del posterior rappresenta un compromesso tra queste due fonti di informazione. La sua posizione è spostata verso destra rispetto al prior, influenzata dall’evidenza forte fornita dai dati, ma mantiene una certa regolarizzazione dovuta al prior che previene stime estreme basate su un campione relativamente piccolo.
1.3 Il modello Beta-Binomiale: soluzione analitica continua
Il metodo basato su griglia fornisce un’approssimazione discreta dell’aggiornamento bayesiano, mentre il modello Beta-Binomiale offre una soluzione analitica esatta per le distribuzioni continue. Il modello beta-binomiale si fonda sulla proprietà di coniugazione tra distribuzione beta e verosimiglianza binomiale.
1.3.1 Fondamenti del modello coniugato
Quando la distribuzione a priori per \(\theta\) è una distribuzione Beta e i dati seguono una distribuzione binomiale, la distribuzione a posteriori è ancora una distribuzione Beta con parametri aggiornati. Questa proprietà semplifica notevolmente i calcoli e fornisce un’interpretazione intuitiva dell’aggiornamento in termini di accumulo di pseudo-osservazioni.
La distribuzione Beta è definita da due parametri, tradizionalmente chiamati \(\alpha\) e \(\beta\). Una distribuzione Beta(\(\alpha\), \(\beta\)) può essere considerata come rappresentante la conoscenza derivante dall’osservazione di \(\alpha\)-1 successi e \(\beta\)-1 insuccessi in un ipotetico studio precedente. Quando si osservano nuovi dati reali, si sommano semplicemente i conteggi osservati a questi pseudo-conteggi.
# Definiamo i parametri della distribuzione a priori Beta
# Scegliamo Beta(2, 2) che rappresenta una credenza moderatamente informativa
# Questa prior è simmetrica e centrata su 0.5
alpha_prior <- 2
beta_prior <- 2
# Calcoliamo la media e la varianza di questa prior
# La media di una Beta(α, β) è α/(α+β)
media_prior_beta <- alpha_prior / (alpha_prior + beta_prior)
# La varianza di una Beta(α, β) è αβ/[(α+β)²(α+β+1)]
varianza_prior_beta <- (alpha_prior * beta_prior) /
((alpha_prior + beta_prior)^2 * (alpha_prior + beta_prior + 1))
sd_prior_beta <- sqrt(varianza_prior_beta)La distribuzione a priori Beta(2, 2) ha media 0.5 e deviazione standard 0.224. Questa distribuzione esprime una credenza iniziale piuttosto vaga, centrata sul valore intermedio di 0.5, ma sufficientemente dispersa da permettere ai dati di influenzare in modo sostanziale la distribuzione a posteriori.
1.3.2 Aggiornamento dei parametri Beta
L’aggiornamento del modello Beta-Binomiale segue una regola estremamente semplice. Se osserviamo \(y\) successi in \(n\) prove, i nuovi parametri della distribuzione a posteriori sono \(\alpha + y\) e \(\beta + (n - y)\). Questo aggiornamento riflette l’idea che stiamo letteralmente aggiungendo i successi osservati ai successi virtuali del prior e gli insuccessi osservati agli insuccessi virtuali del prior.
# Applichiamo la regola di aggiornamento Beta-Binomiale
# I dati sono gli stessi del metodo su griglia: 22 successi su 30 prove
# Calcoliamo il numero di insuccessi
insuccessi_osservati <- prove_totali - successi_osservati
# Aggiorniamo il parametro alpha sommando i successi osservati
alpha_posteriori <- alpha_prior + successi_osservati
# Aggiorniamo il parametro beta sommando gli insuccessi osservati
beta_posteriori <- beta_prior + insuccessi_osservati
# Calcoliamo le statistiche della distribuzione a posteriori
media_posteriori_beta <- alpha_posteriori / (alpha_posteriori + beta_posteriori)
varianza_posteriori_beta <- (alpha_posteriori * beta_posteriori) /
((alpha_posteriori + beta_posteriori)^2 * (alpha_posteriori + beta_posteriori + 1))
sd_posteriori_beta <- sqrt(varianza_posteriori_beta)La distribuzione a posteriori risultante è Beta(24, 10). La media a posteriori è 0.706, molto vicina alla proporzione campionaria osservata di 0.733. La deviazione standard a posteriori è 0.077, sostanzialmente ridotta rispetto al prior, a indicare la riduzione dell’incertezza derivante dall’osservazione di trenta prove.
1.3.3 Visualizzazione dell’aggiornamento continuo
La transizione dal prior al posterior nel modello Beta-Binomiale può essere visualizzata tracciando le curve di densità delle due distribuzioni Beta. Questa visualizzazione mostra come i dati modifichino la forma, la posizione e la dispersione della distribuzione.
# Creiamo una griglia fine di valori per theta
# Usiamo molti più punti rispetto al metodo su griglia
# per ottenere curve lisce e continue
theta_continuo <- seq(from = 0, to = 1, length.out = 500)
# Calcoliamo la densità Beta per il prior e il posterior
# La funzione dbeta calcola la funzione di densità di probabilità
densita_prior_beta <- dbeta(theta_continuo, shape1 = alpha_prior, shape2 = beta_prior)
densita_posteriori_beta <- dbeta(
theta_continuo, shape1 = alpha_posteriori, shape2 = beta_posteriori)
# Organizziamo i dati per la visualizzazione
dati_beta <- data.frame(
theta = rep(theta_continuo, 2),
densita = c(densita_prior_beta, densita_posteriori_beta),
tipo = rep(
c(paste0("Prior Beta(", alpha_prior, ",", beta_prior, ")"),
paste0("Posterior Beta(", alpha_posteriori, ",", beta_posteriori, ")")),
each = length(theta_continuo)
)
)
# Convertiamo in fattore ordinato
dati_beta$tipo <- factor(
dati_beta$tipo,
levels = c(
paste0("Prior Beta(", alpha_prior, ",", beta_prior, ")"),
paste0("Posterior Beta(", alpha_posteriori, ",", beta_posteriori, ")")
)
)
# Creiamo il grafico con linee continue
ggplot(dati_beta, aes(x = theta, y = densita, color = tipo, linetype = tipo)) +
geom_line(size = 1.2) +
scale_color_manual(
values = c(
"#999999", # Grigio per il prior
"#0072B2" # Blu per il posterior
)
) +
scale_linetype_manual(
values = c("dashed", "solid")
) +
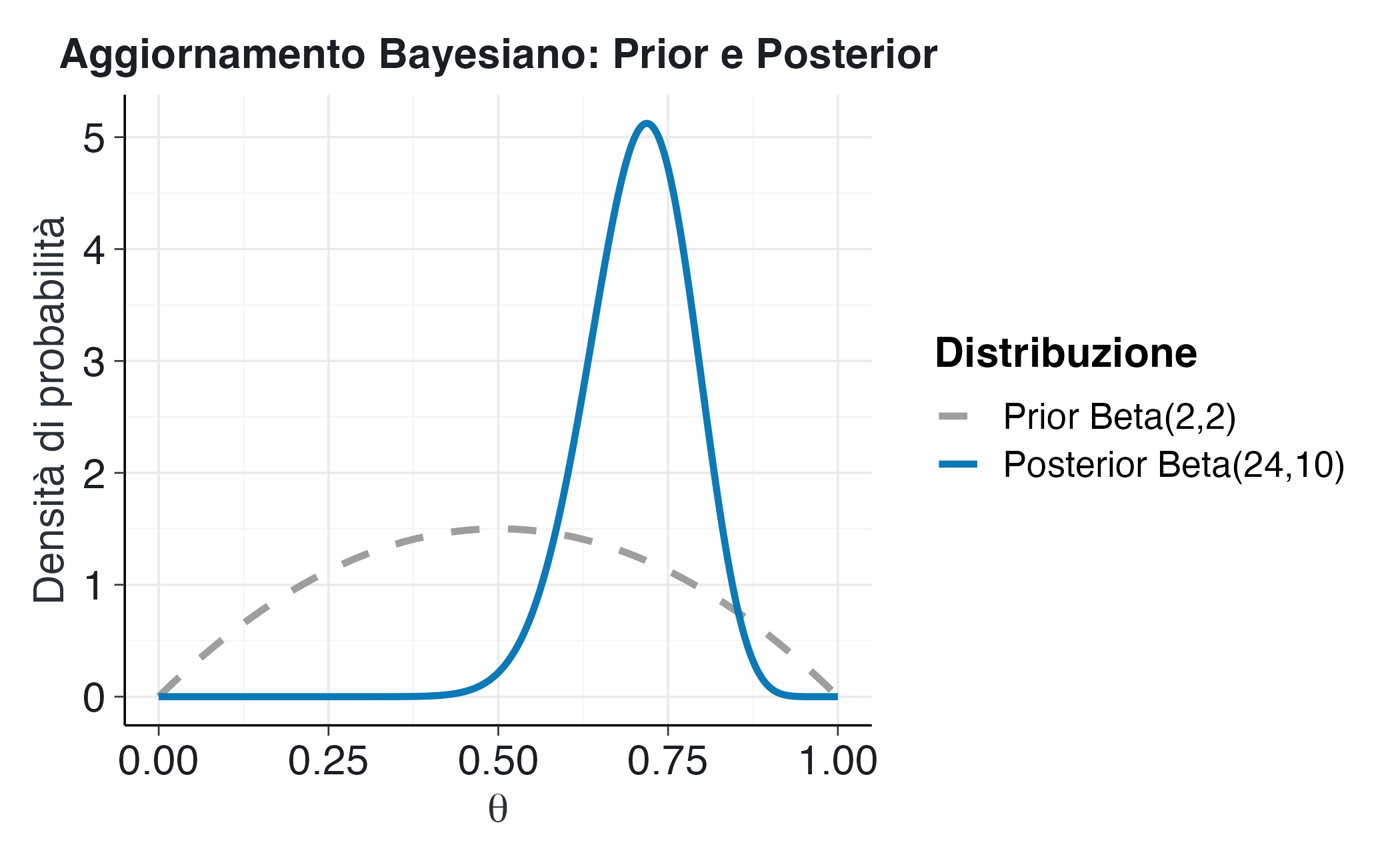
labs(
title = "Aggiornamento Bayesiano: Prior e Posterior",
x = expression(theta),
y = "Densità di probabilità",
color = "Distribuzione",
linetype = "Distribuzione"
)Il grafico mostra chiaramente la trasformazione della distribuzione. La curva tratteggiata grigia del prior Beta(2,2) è relativamente piatta e simmetrica e riflette una conoscenza iniziale vaga, centrata su 0.5. La curva continua blu del posterior Beta(24,10) è più alta, più stretta e spostata verso destra, concentrandosi attorno a 0.7. Questa trasformazione riflette l’apprendimento dai dati: l’osservazione di ventidue successi su trenta prove ha fornito una forte evidenza che il valore di \(\theta\) è probabilmente superiore a 0.5 e l’incertezza si è notevolmente ridotta.
1.3.4 Interpretazione psicologica dei risultati
Tornando al contesto psicologico del dilemma del carrello ferroviario, i risultati della nostra analisi bayesiana forniscono informazioni ricche e sfumate sulla distribuzione delle credenze morali nella popolazione. La media a posteriori di circa 0.71 suggerisce che, alla luce dei dati osservati e delle nostre assunzioni iniziali moderate, è plausibile che circa il 70% della popolazione generale ritenga moralmente accettabile l’azione di deviare il treno.
Tuttavia, la distribuzione a posteriori completa fornisce molto più di una singola stima puntuale. L’intervallo di credibilità al 95% può essere calcolato individuando i percentili 2.5 e 97.5 della distribuzione Beta a posteriori.
# Calcoliamo l'intervallo di credibilità al 95%
# Questo intervallo contiene il 95% della massa di probabilità a posteriori
intervallo_credibilita <- qbeta(
p = c(0.025, 0.975),
shape1 = alpha_posteriori,
shape2 = beta_posteriori
)
limite_inferiore <- intervallo_credibilita[1]
limite_superiore <- intervallo_credibilita[2]L’intervallo di credibilità al 95% si estende da 0.545 a 0.844. Possiamo interpretare questo risultato affermando direttamente che, sulla base dei dati osservati, c’è una probabilità del 95% che la vera proporzione θ nella popolazione sia compresa in questo intervallo. Questa interpretazione diretta e intuitiva rappresenta uno dei vantaggi fondamentali dell’approccio bayesiano rispetto agli intervalli di confidenza frequentisti che, invece, richiedono interpretazioni più contorte e controfattuali.
È anche possibile calcolare le probabilità per ipotesi sostantive specifiche. Per esempio, potremmo chiederci: qual è la probabilità che la maggioranza della popolazione giudichi l’azione accettabile, ovvero che \(\theta\) sia maggiore di 0.5?
# Calcoliamo la probabilità che theta sia maggiore di 0.5
# Questo corrisponde all'area sotto la curva della Beta posteriore
# a destra del valore 0.5
prob_maggioranza <- pbeta(
q = 0.5,
shape1 = alpha_posteriori,
shape2 = beta_posteriori,
lower.tail = FALSE # Vogliamo P(θ > 0.5), non P(θ ≤ 0.5)
)La probabilità che \(\theta\) sia superiore a 0.5 è pari a 0.993, il che indica un livello di certezza pressoché assoluto. Ciò indica che i dati forniscono una prova schiacciante del fatto che la maggior parte della popolazione giudica moralmente accettabile tale azione. Dal punto di vista della psicologia morale, questo risultato suggerisce che, quando si trovano di fronte a questo dilemma, le considerazioni utilitaristiche prevalgono sulle restrizioni deontologiche nella maggior parte delle persone.
1.4 Esercizio guidato: riconoscimento di emozioni facciali
Per consolidare la comprensione dei metodi bayesiani applicati alla stima delle proporzioni, sviluppiamo ora un esercizio completo su un contesto psicologico diverso: il riconoscimento delle emozioni dalle espressioni facciali. Questa competenza fondamentale della cognizione sociale può essere studiata mediante paradigmi sperimentali in cui i partecipanti devono classificare le espressioni emotive presentate visivamente.
1.4.1 Contesto sperimentale e obiettivo di ricerca
Supponiamo di condurre uno studio sulla capacità di riconoscere l’emozione della rabbia dalle espressioni facciali. Un partecipante osserva dieci volti che esprimono rabbia e deve decidere, per ciascuno di essi, se l’emozione espressa è la rabbia o un’altra emozione. Il partecipante risponde correttamente sette volte su dieci. Il nostro obiettivo inferenziale è stimare \(\theta\), ovvero l’accuratezza effettiva del partecipante nel riconoscere la rabbia, tenendo conto sia delle prove fornite da queste dieci prove, sia delle aspettative iniziali basate sulla letteratura.
La letteratura sulla psicologia delle emozioni suggerisce che la rabbia è generalmente riconosciuta con un’accuratezza moderata, solitamente inferiore rispetto a emozioni come la felicità, ma superiore rispetto a emozioni più ambigue. Traduciamo questa conoscenza qualitativa in un prior quantitativo utilizzando una distribuzione Beta(4,6). Questa distribuzione ha una media di 0.4, riflettendo l’aspettativa che l’accuratezza media sia moderata, con una deviazione standard sufficientemente ampia da permettere ai dati di modificare sostanzialmente la credenza.
1.4.2 Implementazione dell’analisi con griglia
Per questo esercizio utilizziamo una griglia molto più fitta rispetto all’esempio del dilemma del carrello ferroviario, con mille punti invece di undici. Questo approccio fornisce un’approssimazione più accurata della distribuzione continua sottostante e consente di calcolare statistiche riassuntive con maggiore precisione.
# Definiamo i dati dell'esperimento sul riconoscimento emotivo
risposte_corrette <- 7
prove_totali_emozioni <- 10
# Creiamo una griglia molto fine per theta
# Usiamo 1000 punti equidistanti tra 0 e 1
theta_fine <- seq(from = 0, to = 1, length.out = 1000)
# Specifichiamo il prior Beta(4, 6)
# Calcoliamo la densità per ogni punto della griglia
prior_emozioni <- dbeta(theta_fine, shape1 = 4, shape2 = 6)
# Calcoliamo la verosimiglianza binomiale
verosimiglianza_emozioni <- dbinom(
x = risposte_corrette,
size = prove_totali_emozioni,
prob = theta_fine
)
# Calcoliamo la distribuzione a posteriori non normalizzata
posteriori_emozioni_non_norm <- prior_emozioni * verosimiglianza_emozioni
# Normalizziamo dividendo per la somma
# Notiamo che con una griglia fine, la somma approssima un integrale
posteriori_emozioni <- posteriori_emozioni_non_norm / sum(posteriori_emozioni_non_norm)La discretizzazione fine permette di ottenere un’approssimazione molto accurata della distribuzione continua. Con mille punti, l’errore di approssimazione è trascurabile ai fini pratici. Questo approccio ibrido combina la trasparenza computazionale del metodo a griglia con l’accuratezza delle soluzioni analitiche continue.
1.4.3 Calcolo delle statistiche riassuntive
Una volta ottenuta la distribuzione a posteriori, calcoliamo le statistiche che descrivono la nostra conoscenza aggiornata sull’accuratezza del partecipante.
# Calcoliamo la media a posteriori
media_posteriori_emozioni <- sum(theta_fine * posteriori_emozioni)
# Calcoliamo la varianza e la deviazione standard a posteriori
varianza_posteriori_emozioni <- sum(
(theta_fine - media_posteriori_emozioni)^2 * posteriori_emozioni
)
sd_posteriori_emozioni <- sqrt(varianza_posteriori_emozioni)
# Identifichiamo la moda (valore con massima probabilità)
indice_moda_emozioni <- which.max(posteriori_emozioni)
moda_posteriori_emozioni <- theta_fine[indice_moda_emozioni]La media a posteriori è 0.55, il che indica che la nostra migliore stima dell’accuratezza è circa il 59%. La moda è 0.556, molto vicina alla media dato che la distribuzione Beta posteriore è approssimativamente simmetrica. La deviazione standard è 0.109, riflettendo un’incertezza moderata dovuta al numero limitato di prove osservate.
Per quantificare l’intervallo di valori plausibili per \(\theta\), calcoliamo un intervallo di credibilità. Utilizziamo un livello del 94% per mostrare che la scelta del livello è arbitraria e dovrebbe essere guidata dalle esigenze specifiche della ricerca piuttosto che da rigide convenzioni.
# Calcoliamo l'intervallo di credibilità al 94%
# Utilizziamo un approccio basato su campionamento dalla distribuzione
# Generiamo un campione casuale ponderato dalla distribuzione a posteriori
set.seed(2025) # Per riproducibilità
n_campioni <- 10000
# Campionamento con sostituzione, ponderato dalle probabilità a posteriori
campione_theta <- sample(
x = theta_fine,
size = n_campioni,
replace = TRUE,
prob = posteriori_emozioni
)
# Calcoliamo i percentili 3% e 97% del campione
# Questi approssimano l'intervallo di credibilità al 94%
percentili <- quantile(campione_theta, probs = c(0.03, 0.97))
limite_inf_94 <- percentili[1]
limite_sup_94 <- percentili[2]L’intervallo di credibilità al 94% si estende approssimativamente da 0.343 a 0.751. Questo intervallo quantifica l’incertezza residua sull’accuratezza effettiva del partecipante. Con solo dieci prove, l’intervallo è relativamente ampio, il che indica che avremmo bisogno di più osservazioni per restringere ulteriormente la stima.
1.4.4 Visualizzazione completa dell’aggiornamento
Ora creiamo una visualizzazione che mostri tutte e tre le componenti dell’inferenza bayesiana per questo esempio.
# Prepariamo i dati per la visualizzazione
# Normalizziamo tutte le distribuzioni per renderle confrontabili
dati_visualizzazione_emozioni <- data.frame(
theta = rep(theta_fine, 3),
densita = c(
prior_emozioni / sum(prior_emozioni),
verosimiglianza_emozioni / sum(verosimiglianza_emozioni),
posteriori_emozioni
),
componente = rep(
c("Prior Beta(4,6)", "Verosimiglianza", "Posterior"),
each = length(theta_fine)
)
)
# Convertiamo in fattore ordinato
dati_visualizzazione_emozioni$componente <- factor(
dati_visualizzazione_emozioni$componente,
levels = c("Prior Beta(4,6)", "Verosimiglianza", "Posterior")
)
# Creiamo il grafico comparativo
ggplot(dati_visualizzazione_emozioni, aes(x = theta, y = densita, color = componente)) +
geom_line(size = 1.2) +
# Aggiungiamo una linea verticale per la media posteriori
geom_vline(
xintercept = media_posteriori_emozioni,
linetype = "dashed",
color = "#0072B2",
size = 0.8
) +
# Aggiungiamo linee verticali per l'intervallo di credibilità
geom_vline(
xintercept = c(limite_inf_94, limite_sup_94),
linetype = "dotted",
color = "#0072B2",
size = 0.6
) +
scale_color_manual(
values = c(
"Prior Beta(4,6)" = "#999999",
"Verosimiglianza" = "#E69F00",
"Posterior" = "#0072B2"
)
) +
labs(
x = expression(theta ~ "(accuratezza nel riconoscimento della rabbia)"),
y = "Densità normalizzata",
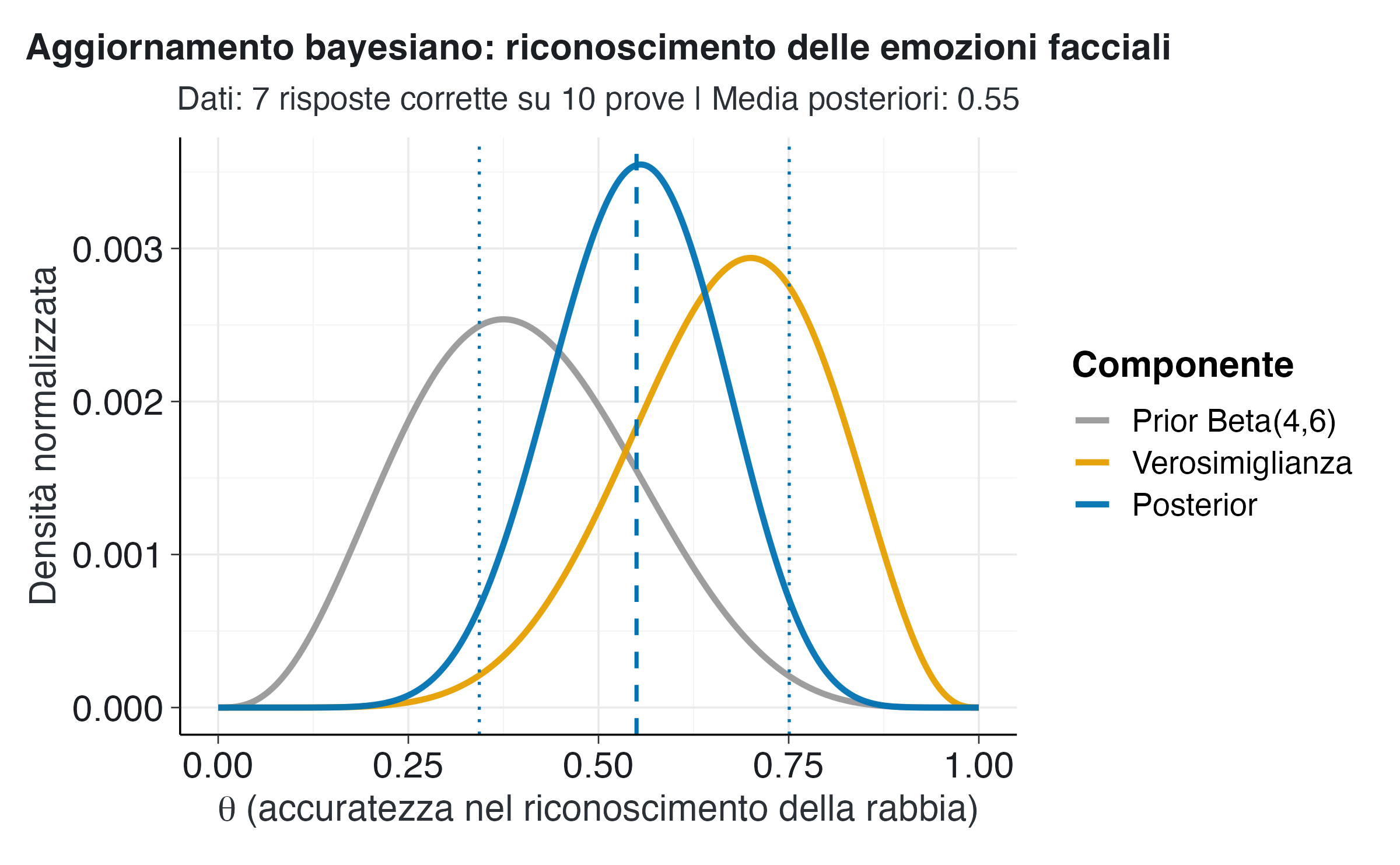
title = "Aggiornamento bayesiano: riconoscimento delle emozioni facciali",
subtitle = paste0(
"Dati: ", risposte_corrette, " risposte corrette su ",
prove_totali_emozioni, " prove | Media posteriori: ",
round(media_posteriori_emozioni, 3)
),
color = "Componente"
) Il grafico mostra la dinamica dell’aggiornamento bayesiano in questo contesto. Il prior Beta(4,6) è centrato su 0.4 e riflette aspettative moderate, basate sulla letteratura. La verosimiglianza mostra un picco più alto attorno a 0.7, corrispondente alla proporzione di sette risposte corrette su dieci osservate. La distribuzione a posteriori rappresenta un compromesso: è spostata verso destra rispetto al prior, riflettendo l’influenza dei dati, ma non coincide completamente con la verosimiglianza, mantenendo l’influenza regolarizzante del prior.
La linea verticale tratteggiata indica la media a posteriori, mentre le linee tratteggiate più sottili delimitano l’intervallo di credibilità al 94%. Questa visualizzazione rende immediatamente evidente sia il valore centrale più plausibile sia l’intervallo di incertezza associato.
1.4.5 Interpretazione psicologica e implicazioni cliniche
Dal punto di vista della psicologia cognitiva, questi risultati suggeriscono che il partecipante mostra un’accuratezza nel riconoscimento della rabbia leggermente superiore alle aspettative iniziali basate sulla popolazione generale. La media posteriore di circa 0.59 indica una competenza moderata, superiore al caso (che sarebbe 0.5 se ci fossero solo due categorie emotive), ma non eccezionale.
L’ampiezza dell’intervallo di credibilità sottolinea la limitatezza di trarre conclusioni basandosi su solo dieci prove. In un contesto di valutazione clinica o educativa, questo risultato suggerirebbe la necessità di ulteriori osservazioni prima di formulare conclusioni definitive sulle competenze del partecipante. L’approccio bayesiano rende esplicita questa limitazione, quantificando l’incertezza residua e evitando interpretazioni eccessivamente fiduciose basate su campioni piccoli.
Se osservassimo dieci prove aggiuntive in una sessione successiva, potremmo aggiornare nuovamente la distribuzione utilizzando il risultato attuale come nuovo prior. Questo processo di aggiornamento sequenziale mostra come l’approccio bayesiano faciliti l’accumulo progressivo di prove, un principio fondamentale per la ricerca cumulativa in psicologia.
Riflessioni conclusive
Questo capitolo ha trasformato i principi bayesiani in applicazioni concrete attraverso due approcci complementari: il metodo a griglia, che garantisce la trasparenza dei calcoli, e il modello Beta-Binomiale coniugato, che assicura l’efficienza analitica. L’implementazione diretta in R ha confermato tre aspetti fondamentali del processo inferenziale bayesiano. In primo luogo, l’aggiornamento delle credenze è deterministico: la combinazione della distribuzione a priori, della funzione di verosimiglianza e dei dati osservati produce in modo univoco la distribuzione a posteriori. In secondo luogo, l’influenza della distribuzione iniziale è perfettamente quantificabile e diminuisce progressivamente con l’aumentare delle osservazioni. Infine, la distribuzione a posteriori fornisce una gamma completa di informazioni inferenziali che superano i limiti delle singole stime puntuali.
Questo tutorial ha utilizzato le funzioni base di R per garantire la trasparenza computazionale, mentre in ambito applicativo si preferisce l’uso di pacchetti specializzati che automatizzano tali processi. Nei prossimi capitoli verranno affrontati modelli di maggiore complessità che richiederanno l’impiego di metodi computazionali avanzati, come il campionamento MCMC. I principi fondamentali di questo capitolo, tuttavia, conservano la loro validità: combinare conoscenza pregressa ed evidenza empirica è la base per ottenere inferenze che quantificano esplicitamente l’incertezza.