9  Analisi bayesiana dell’odds ratio

Introduzione

Questo approfondimento sviluppa ulteriormente il tema dell’inferenza sulle proporzioni, già affrontato nel manuale didattico tramite il modello Beta-Binomiale. In quel contesto, la proprietà della coniugazione aveva permesso di ottenere una soluzione analitica esatta per la distribuzione a posteriori, mentre l’approccio a griglia aveva reso evidente il meccanismo di aggiornamento bayesiano.

Procediamo ora nell’applicazione pratica degli strumenti computazionali, utilizzando Stan per la specificazione dei modelli e il campionamento MCMC. Come passo successivo del nostro percorso, implementeremo un modello focalizzato su una misura di fondamentale importanza per le scienze psicologiche: l’odds ratio.

L’odds ratio è una metrica fondamentale per confrontare la probabilità di un determinato esito tra due gruppi. In psicologia, viene comunemente utilizzato per quantificare, ad esempio, la differenza nella probabilità di successo in un compito sperimentale tra il gruppo sperimentale e il gruppo di controllo o per misurare l’associazione tra variabili categoriali in studi osservazionali.

Questo esempio applicativo persegue un duplice obiettivo didattico. In primo luogo, mostra come implementare in Stan un modello concettualmente noto, confermando che i principi bayesiani (la combinazione di distribuzione a priori, verosimiglianza e dati osservati) restano invariati anche quando si utilizza questo potente strumento computazionale. In secondo luogo, costituisce un’introduzione pratica alla sintassi di Stan e alla gestione dei campionamenti MCMC, gettando le basi per affrontare in seguito modelli statistici più complessi.

Panoramica del capitolo

  • Come si definiscono probabilità, odds e odds ratio.
  • Come si interpreta l’odds ratio in contesti psicologici.
  • Come stimarlo in ottica bayesiana, implementando un modello in Stan.
  • Come presentare i risultati con intervalli di credibilità.
here::here("code", "_common.R") |> 
  source()

if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayesplot, ggplot2, dplyr, tibble)
conflicts_prefer(posterior::ess_bulk)
conflicts_prefer(posterior::ess_tail)

9.1 Il contesto sperimentale

Per introdurre l’analisi bayesiana dell’odds ratio, consideriamo il seguente esperimento. Nella prima metà del Novecento, Karl von Frisch si domandò se le api possedessero la visione dei colori. Per verificarlo, ideò una serie di esperimenti in cui le api potevano associare un colore a una ricompensa. Ispirandoci a una ricostruzione proposta da Hoffmann et al. (2022), possiamo immaginare una versione semplificata del disegno sperimentale:

  • Gruppo sperimentale: api addestrate ad associare un disco blu a una soluzione zuccherina.
  • Gruppo di controllo: api che non ricevono alcun addestramento.

Nella fase di test, la soluzione zuccherina viene rimossa e si registra il numero di volte in cui le api si avvicinano al disco blu (evento critico).

I risultati osservati sono riportati nella tabella seguente:

Gruppo Successi (scelta blu) Totale
Sperimentale 130 200
Controllo 100 200

La domanda di ricerca può essere così formulata: le api addestrate mostrano un odds maggiore di scegliere il disco blu rispetto alle api di controllo?

9.1.1 Dalle probabilità agli odds

La probabilità di successo (scelta del blu) nel gruppo sperimentale è:

\[ p_1 = \frac{130}{200} = 0.65. \]

I corrispondenti odds si calcolano come:

\[ \text{odds}_1 = \frac{p_1}{1-p_1} = \frac{0.65}{0.35} \approx 1.86. \]

Per il gruppo di controllo:

\[ p_2 = \frac{100}{200} = 0.50, \quad \text{odds}_2 = \frac{0.50}{0.50} = 1.00. \]

L’odds ratio (OR) confronta i due odds:

\[ \text{OR} = \frac{\text{odds}_1}{\text{odds}_2} = \frac{1.86}{1.00} \approx 1.86. \]

Interpretazione: le api addestrate presentano odds circa 1.9 volte maggiori di scegliere il disco blu rispetto alle api non addestrate. Notiamo che l’odds ratio confronta due rapporti di probabilità di successo/insuccesso, non le probabilità dirette: per questo un OR di 1.86 non significa che la probabilità di successo sia raddoppiata, ma che il rapporto tra successi e insuccessi è quasi doppio.

Quanto è affidabile questa stima? È a questo punto che l’approccio bayesiano mostra il suo valore: anziché limitarci a una stima puntuale, possiamo ottenere un’intera distribuzione a posteriori per l’OR, che esprime la nostra incertezza dopo aver osservato i dati.

9.1.2 Approccio bayesiano

Nel paradigma frequentista, l’odds ratio è stimato come rapporto tra stime puntuali, e la sua incertezza è descritta da un intervallo di confidenza basato su approssimazioni asintotiche. Nell’approccio bayesiano, invece, otteniamo direttamente la distribuzione a posteriori dell’odds ratio, che rappresenta in modo completo la nostra incertezza. Ciò offre diversi vantaggi interpretativi:

  • Probabilità diretta: possiamo calcolare la probabilità che l’OR sia maggiore di 1;
  • Valutazione di equivalenza: possiamo determinare la probabilità che l’OR ricada in un intervallo di equivalenza pratica (ROPE);
  • Intervalli di credibilità: possiamo ottenere intervalli di credibilità esatti (ETI o HDI) senza ricorrere ad approssimazioni asintotiche.

Questo framework consente non solo una rappresentazione più intuitiva dei risultati, ma permette anche di rispondere direttamente a domande inferenziali in termini probabilistici. Ad esempio: qual è la probabilità che le api addestrate mostrino effettivamente una preferenza maggiore per il blu? O, più formalmente: qual è la probabilità che l’OR sia maggiore di 1?

9.2 Versione binomiale con prior Beta

Per la stima dell’odds ratio un approccio iniziale particolarmente intuitivo consiste nel modellare separatamente le proporzioni di successo nei due gruppi, \(\theta_1\) e \(\theta_2\), utilizzando distribuzioni binomiali con prior Beta. Questo metodo si rivela particolarmente adatto quando i dati sono naturalmente aggregabili in una tabella \(2\times2\). Questa formulazione, in termini di \(\theta_1\) e \(\theta_2\), mantiene una chiara interpretazione psicologica: ciascun parametro rappresenta la propensione a fornire la risposta ‘corretta’ nel rispettivo gruppo.

L’odds ratio viene calcolato come trasformazione delle due probabilità stimate:

\[ \text{OR} = \frac{\theta_1/(1-\theta_1)}{\theta_2/(1-\theta_2)} = \exp\left(\operatorname{logit}(\theta_1) - \operatorname{logit}(\theta_2)\right) \]

Questa formulazione offre una trasparenza didattica immediata: stimiamo separatamente le probabilità di successo nei due gruppi per poi derivare l’effetto di interesse. La scelta di prior Beta(2,2) per entrambi i parametri mantiene coerenza con le impostazioni del capitolo, utilizzando prior debolmente informative.

9.2.1 Implementazione in Stan: modello Beta-Binomiale

stancode_or_beta <- "
data {
  int<lower=0> k1;  // numero di successi nel gruppo sperimentale
  int<lower=1> n1;  // numero totale di prove nel gruppo sperimentale
  int<lower=0> k2;  // numero di successi nel gruppo di controllo
  int<lower=1> n2;  // numero totale di prove nel gruppo di controllo
}
parameters {
  real<lower=0,upper=1> theta1;  // probabilità di successo nel gruppo sperimentale
  real<lower=0,upper=1> theta2;  // probabilità di successo nel gruppo di controllo
}
model {
  // Prior distributions (debolmente informativi, riflettono incertezza iniziale)
  theta1 ~ beta(2, 2);
  theta2 ~ beta(2, 2);
  
  // Likelihood
  k1 ~ binomial(n1, theta1);
  k2 ~ binomial(n2, theta2);
}
generated quantities {
  real logOR = logit(theta1) - logit(theta2);  // log-odds ratio
  real OR = exp(logOR);                        // odds ratio
}
"

Organizziamo i dati nel formato richiesto da Stan:

# Dati aggregati per il modello binomiale
data_list_beta <- list(
  k1 = 130, n1 = 200,  # gruppo sperimentale: 130 successi su 200 prove
  k2 = 100, n2 = 200   # gruppo di controllo: 100 successi su 200 prove
)

9.2.1.1 Compilazione ed esecuzione del modello

stanmod_or_beta <- cmdstanr::cmdstan_model(write_stan_file(stancode_or_beta))

fit_or_beta <- stanmod_or_beta$sample(
  data = data_list_beta,
  iter_warmup = 1000,
  iter_sampling = 4000,
  chains = 4,
  parallel_chains = 4,
  seed = 123,
  refresh = 0
)

9.2.1.2 Diagnostica essenziale

# Indicatori numerici chiave: Rhat ~ 1, ESS adeguati
posterior::summarize_draws(
  fit_or_beta$draws(c("OR")),
  "rhat", "ess_bulk", "ess_tail"
)
#> # A tibble: 1 × 4
#>   variable  rhat ess_bulk ess_tail
#>   <chr>    <dbl>    <dbl>    <dbl>
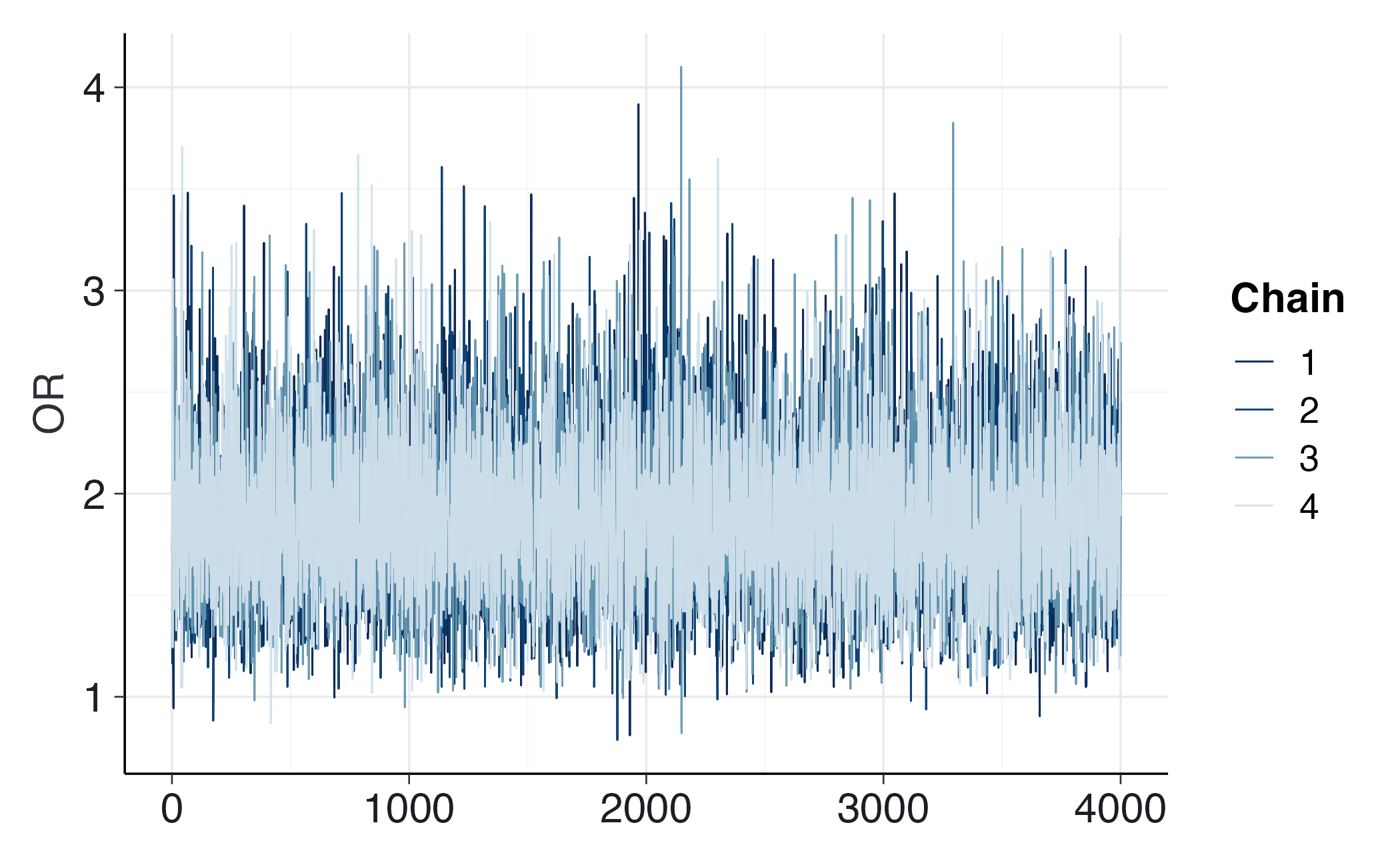
#> 1 OR        1.00   13793.   10545.
# Traceplot di controllo su OR
bayesplot::mcmc_trace(fit_or_beta$draws("OR"))

Se emergono problemi (Rhat > 1.01, ESS basso, divergenze riportate in output), conviene aumentare iter_warmup/iter_sampling, alzare adapt_delta o, in ultima istanza, riconsiderare i prior se sono eccessivamente stretti.

9.2.1.3 Analisi dei risultati

Riassunti posteriori per il modello Beta-Binomiale:

posterior::summarise_draws(
  fit_or_beta$draws(c("theta1", "theta2", "logOR", "OR")),
  mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)
#> # A tibble: 4 × 6
#>   variable  mean     sd `2.5%` `50%` `97.5%`
#>   <chr>    <dbl>  <dbl>  <dbl> <dbl>   <dbl>
#> 1 theta1   0.647 0.0336  0.579 0.648   0.712
#> 2 theta2   0.500 0.0350  0.432 0.500   0.569
#> 3 logOR    0.610 0.204   0.207 0.611   1.00 
#> 4 OR       1.88  0.387   1.23  1.84    2.73

L’output mostra media, deviazione standard, mediana e intervallo di credibilità al 95% per l’odds ratio.

Visualizzazione della distribuzione a posteriori:

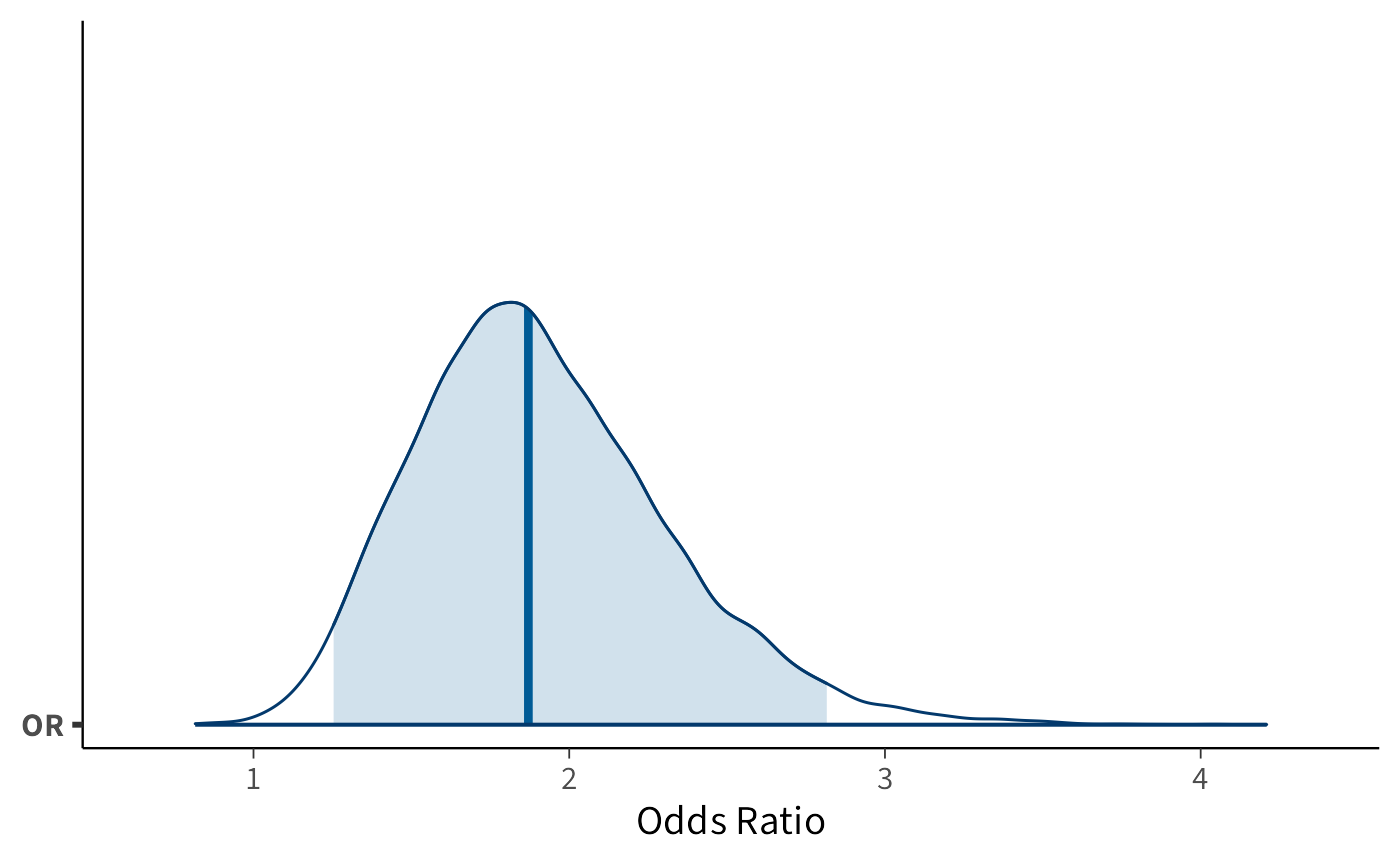
bayesplot::mcmc_areas(fit_or_beta$draws("OR"), prob = 0.95) +
  xlab("Odds Ratio") + ylab("Densità")

Il grafico mostra chiaramente che la distribuzione dell’odds ratio è concentrata su valori superiori a 1, con alta probabilità.

Interpretazione: I risultati forniscono evidenza credibile che l’addestramento aumenta le probabilità che le api scelgano il disco blu rispetto al gruppo di controllo. La distribuzione a posteriori dell’OR è concentrata su valori maggiori di 1, suggerendo che l’effetto è credibilmente diverso dall’assenza di differenza.

9.3 Relazione con la regressione logistica

È anche possibile formulare il problema di ottenere la distribuzione a posteriori dell’OR all’interno del modello della regressione logistica. Modellando la probabilità di successo \(p_i\) mediante un modello logit:

\[ \text{logit}(p_i) = \alpha + \beta \cdot x_i, \] dove \(x_i\) è una variabile indicatrice (0 = gruppo di controllo, 1 = gruppo sperimentale), si ottiene che:

  • \(\exp(\beta)\) corrisponde esattamente all’odds ratio tra il gruppo sperimentale e quello di controllo.

Ciò implica che la stima di un modello di regressione logistica binaria equivale alla stima dell’odds ratio, con il vantaggio di poter estendere agevolmente il modello all’inclusione di ulteriori predittori, covariate o strutture gerarchiche. Questo collegamento è fondamentale: mostra che la regressione logistica non è altro che una generalizzazione del confronto tra due proporzioni, formulata in termini di log-odds.

9.3.1 Versione con modello logistico

I dati vengono rappresentati a livello individuale: ogni ape è codificata come 1 (ha scelto il blu) o 0 (non ha scelto il blu).

# Dati individuali
y <- c(rep(1, 130), rep(0, 70),   # gruppo sperimentale: 130 successi, 70 insuccessi
       rep(1, 100), rep(0, 100))  # gruppo di controllo: 100 successi, 100 insuccessi
x <- c(rep(1, 200), rep(0, 200))  # 1 = sperimentale, 0 = controllo

data_list <- list(N = length(y), y = y, x = x)
glimpse(data_list)
#> List of 3
#>  $ N: int 400
#>  $ y: num [1:400] 1 1 1 1 1 1 1 1 1 1 ...
#>  $ x: num [1:400] 1 1 1 1 1 1 1 1 1 1 ...

9.3.2 Specifica del modello in Stan

stancode_or <- "
data {
  int<lower=1> N;                  // numero totale di osservazioni
  array[N] int<lower=0,upper=1> y; // esito binario (0/1)
  vector[N] x;                     // variabile indicatrice del gruppo (0 = controllo, 1 = sperimentale)
}
parameters {
  real alpha;    // intercetta (log-odds nel gruppo di controllo)
  real beta;     // coefficiente (differenza in log-odds tra gruppo sperimentale e controllo)
}
model {
  // Priors
  alpha ~ normal(0, 5);
  beta  ~ normal(0, 5);
  
  // Likelihood
  y ~ bernoulli_logit(alpha + beta * x);
}
generated quantities {
  real OR = exp(beta);  // odds ratio
}
"

Nel contesto dell’esperimento sulle api, \(\beta\) rappresenta la variazione nei log-odds di scegliere il disco blu dovuta all’addestramento.

9.3.2.1 Compilazione ed esecuzione del modello

stanmod_or <- cmdstanr::cmdstan_model(write_stan_file(stancode_or))

fit_or <- stanmod_or$sample(
  data = data_list,
  iter_warmup = 1000,
  iter_sampling = 4000,
  chains = 4,
  seed = 123,
  refresh = 0
)

9.3.2.2 Interpretazione dei risultati

Riassunto dei parametri di interesse:

print(fit_or$summary(c("alpha", "beta", "OR")), n = Inf)
#> # A tibble: 3 × 10
#>   variable     mean   median    sd   mad     q5   q95  rhat ess_bulk ess_tail
#>   <chr>       <dbl>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 alpha    -0.00366 -0.00355 0.144 0.144 -0.240 0.232  1.00    5153.    6998.
#> 2 beta      0.628    0.626   0.208 0.208  0.288 0.970  1.00    5183.    7043.
#> 3 OR        1.91     1.87    0.403 0.386  1.33  2.64   1.00    5183.    7043.
  • alpha: log-odds di successo nel gruppo di controllo
  • beta: differenza nei log-odds tra gruppo sperimentale e controllo
  • OR: odds ratio (exp(beta))

Distribuzione a posteriori dell’OR:

posterior::summarise_draws(
  fit_or$draws("OR"),
  mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)
#> # A tibble: 1 × 6
#>   variable  mean    sd `2.5%` `50%` `97.5%`
#>   <chr>    <dbl> <dbl>  <dbl> <dbl>   <dbl>
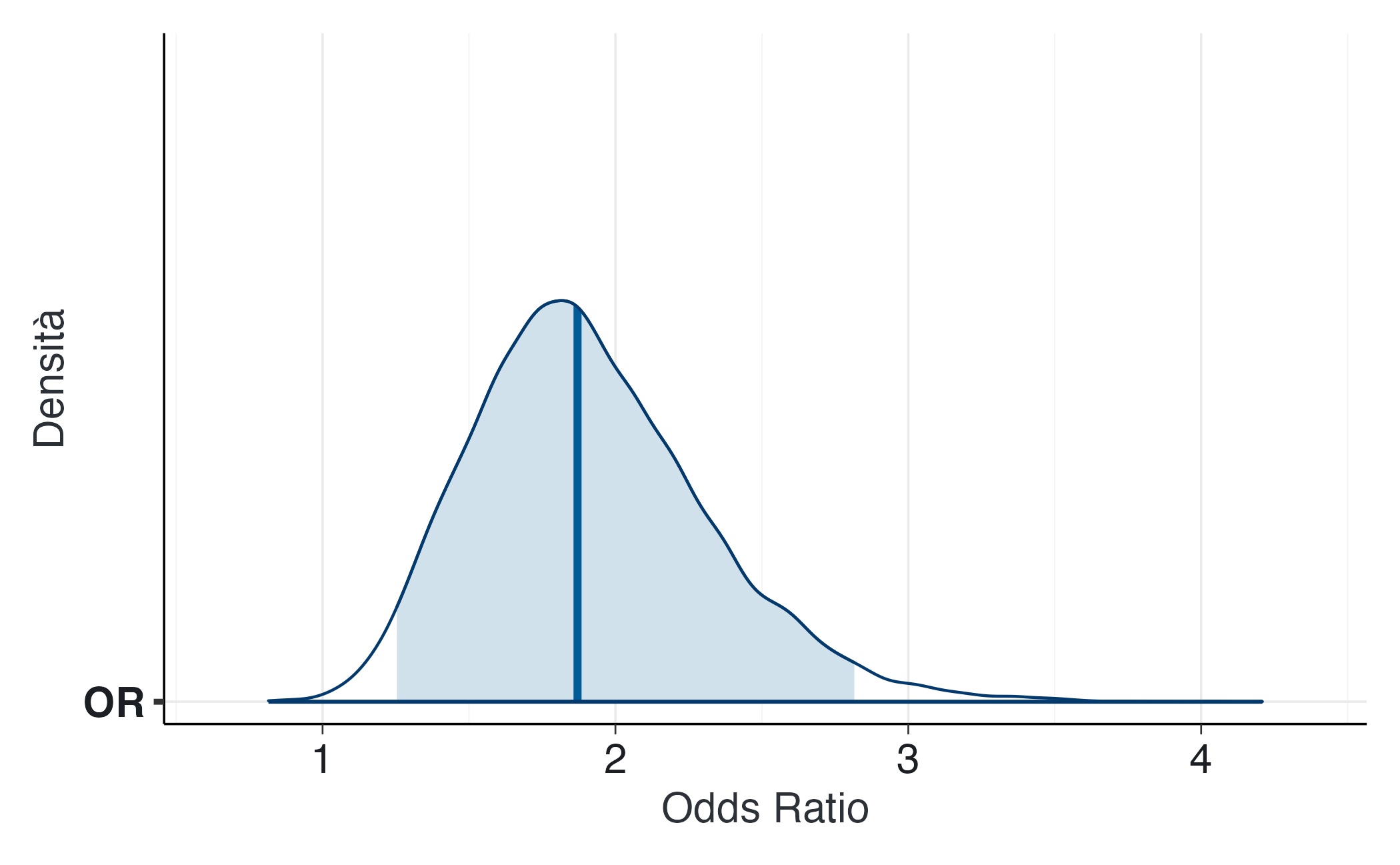
#> 1 OR        1.91 0.403   1.25  1.87    2.82

Visualizzazione della distribuzione a posteriori dell’OR:

bayesplot::mcmc_areas(fit_or$draws("OR"), prob = 0.95) +
  xlab("Odds Ratio") + ylab("Densità")

9.3.2.3 Diagnostica essenziale

# Indicatori numerici chiave: Rhat ~ 1, ESS adeguati
posterior::summarize_draws(
  fit_or$draws(c("alpha","beta","OR")),
  "rhat", "ess_bulk", "ess_tail"
)
#> # A tibble: 3 × 4
#>   variable  rhat ess_bulk ess_tail
#>   <chr>    <dbl>    <dbl>    <dbl>
#> 1 alpha     1.00    5153.    6998.
#> 2 beta      1.00    5183.    7043.
#> 3 OR        1.00    5183.    7043.
# Traceplot di controllo su OR
bayesplot::mcmc_trace(fit_or$draws("OR"))

9.3.2.4 Analisi comparativa dei risultati

Confronto degli intervalli di credibilità tra i due approcci:

summ_logit <- posterior::summarise_draws(
  fit_or$draws("OR"),
  mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)
summ_beta <- posterior::summarise_draws(
  fit_or_beta$draws("OR"),
  mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)

list(Regressione_Logistica = summ_logit, Beta_Binomiale = summ_beta)
#> $Regressione_Logistica
#> # A tibble: 1 × 6
#>   variable  mean    sd `2.5%` `50%` `97.5%`
#>   <chr>    <dbl> <dbl>  <dbl> <dbl>   <dbl>
#> 1 OR        1.91 0.403   1.25  1.87    2.82
#> 
#> $Beta_Binomiale
#> # A tibble: 1 × 6
#>   variable  mean    sd `2.5%` `50%` `97.5%`
#>   <chr>    <dbl> <dbl>  <dbl> <dbl>   <dbl>
#> 1 OR        1.88 0.387   1.23  1.84    2.73

Confronto visivo delle distribuzioni posteriori:

OR_logit <- as.numeric(fit_or$draws("OR"))
OR_beta <- as.numeric(fit_or_beta$draws("OR"))

tibble(
  OR = c(OR_logit, OR_beta),
  Modello = rep(c("Regressione Logistica", "Beta-Binomiale"), 
                c(length(OR_logit), length(OR_beta)))
) |>
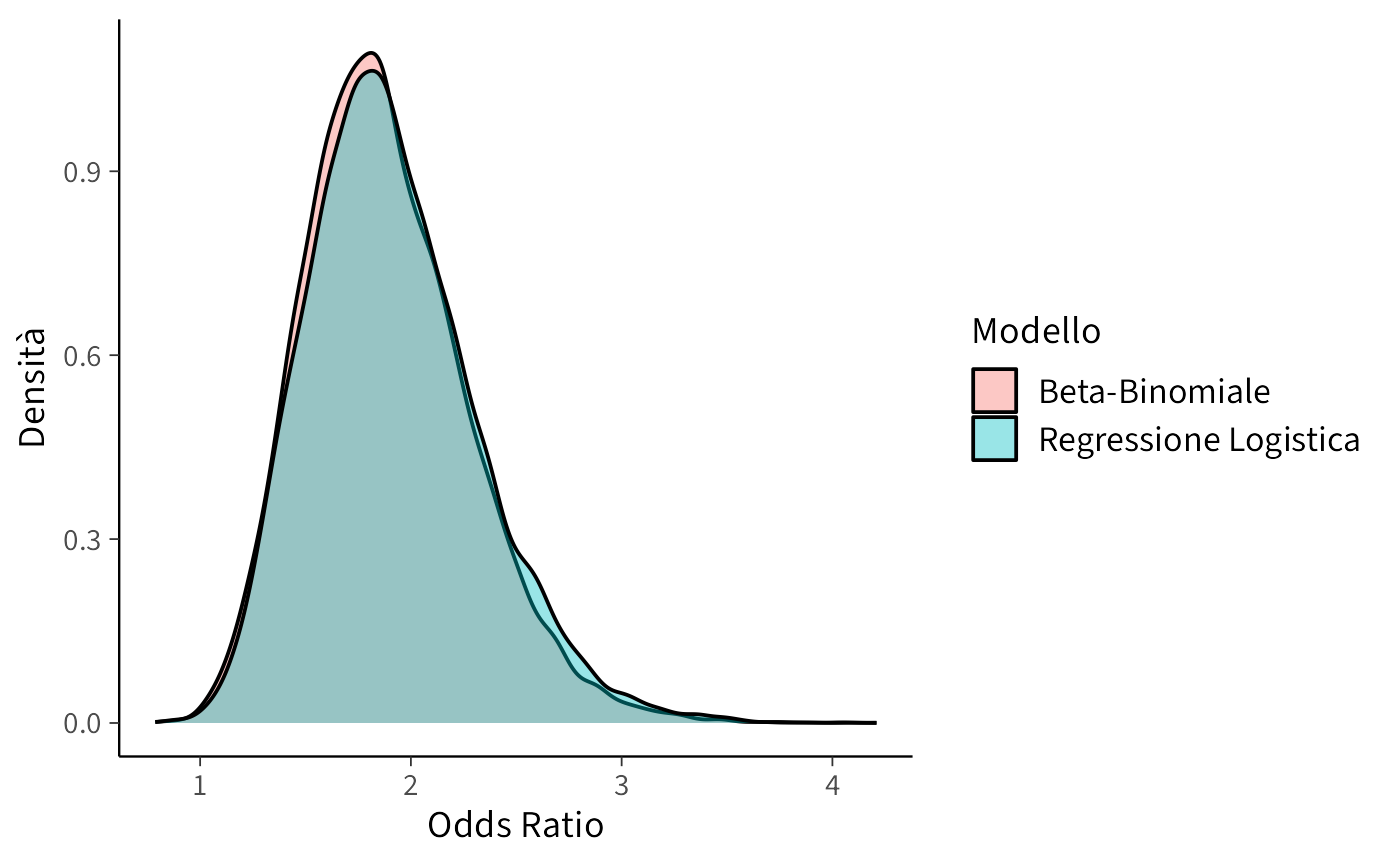
  ggplot(aes(x = OR, fill = Modello)) +
  geom_density(alpha = 0.4) +
  labs(x = "Odds Ratio", y = "Densità")

Le due distribuzioni si sovrappongono quasi completamente, mostrando che le due specificazioni modellano lo stesso effetto con coerenza. Le differenze minime derivano unicamente dalla parametrizzazione (aggregata vs individuale).

Probabilità a posteriori che l’OR sia maggiore di 1:

c(
  Regressione_Logistica = mean(OR_logit > 1),
  Beta_Binomiale = mean(OR_beta > 1)
)
#> Regressione_Logistica        Beta_Binomiale 
#>                 0.999                 0.999

9.4 Considerazioni metodologiche

I due approcci producono risultati sostanzialmente equivalenti, confermando la robustezza delle conclusioni inferenziali. La scelta tra le due specificazioni dipende da considerazioni pratiche e comunicative:

  • Regressione logistica: Ideale per dati individuali e modelli che includono multiple covariate. Offre maggiore flessibilità per estensioni multivariate.

  • Modello Beta-Binomiale: Particolarmente adatto per dati aggregati in tabelle di contingenza. Risulta più intuitivo per comprendere il meccanismo di stima delle proporzioni sottostanti.

Entrambi i modelli arrivano alla stessa conclusione inferenziale: l’addestramento aumenta in modo credibile la probabilità di scelta corretta. La regressione logistica offre una cornice più generale per estendere l’analisi a più predittori, mentre il modello Beta-Binomiale resta la scelta più intuitiva per introdurre il concetto di odds ratio.

Riflessioni conclusive

Questo capitolo ha dimostrato come l’inferenza bayesiana sulle proporzioni, precedentemente affrontata con soluzioni analitiche e metodi a griglia, possa essere efficacemente implementata in Stan. L’esempio dell’odds ratio ha permesso di riconoscere la continuità concettuale dell’approccio bayesiano: sebbene la logica dell’aggiornamento rimanga invariata, Stan ne estende l’applicabilità a una gamma di modelli notevolmente più ampia.

L’analisi condotta ha messo in luce due aspetti particolarmente rilevanti.

In primo luogo, emerge chiaramente la continuità concettuale: Stan non altera i principi fondamentali dell’inferenza bayesiana, ma ne amplia le applicazioni pratiche. Il nucleo del metodo rimane immutato, ovvero il campionamento dalla distribuzione a posteriori per quantificare l’incertezza sui parametri, mentre la potenza computazionale consente di affrontare modelli complessi senza dover ricorrere a soluzioni analiticamente trattabili.

In secondo luogo, l’esempio ha messo in luce il valore pratico di questo approccio. Abbiamo constatato che Stan può trasformarsi in uno strumento di routine per l’analisi dei dati psicologici, anche in contesti modellistici relativamente semplici. In questa prospettiva, l’odds ratio funge da ponte metodologico che consente di sviluppare familiarità con Stan in un ambito concettualmente noto, preparando il terreno per applicazioni più sofisticate, quali i modelli di Poisson o le strutture gerarchiche.

In prospettiva, questo capitolo segna una transizione importante: da questo momento l’inferenza bayesiana cessa di essere confinata a modelli semplici, trasformandosi in una metodologia concretamente praticabile e pienamente riproducibile per l’analisi di qualsiasi tipologia di dato psicologico.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] cmdstanr_0.9.0        ragg_1.5.0            tinytable_0.13.0     
#>  [4] withr_3.0.2           systemfonts_1.3.1     patchwork_1.3.2      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#> [10] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.4            
#> [28] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      ggridges_0.5.7        compiler_4.5.1       
#> [10] reshape2_1.4.4        vctrs_0.6.5           stringr_1.5.2        
#> [13] pkgconfig_2.0.3       arrayhelpers_1.1-0    fastmap_1.2.0        
#> [16] backports_1.5.0       labeling_0.4.3        utf8_1.2.6           
#> [19] rmarkdown_2.30        ps_1.9.1              purrr_1.1.0          
#> [22] xfun_0.53             cachem_1.1.0          jsonlite_2.0.0       
#> [25] broom_1.0.10          parallel_4.5.1        R6_2.6.1             
#> [28] stringi_1.8.7         RColorBrewer_1.1-3    lubridate_1.9.4      
#> [31] estimability_1.5.1    knitr_1.50            zoo_1.8-14           
#> [34] pacman_0.5.1          Matrix_1.7-4          splines_4.5.1        
#> [37] timechange_0.3.0      tidyselect_1.2.1      abind_1.4-8          
#> [40] yaml_2.3.10           codetools_0.2-20      processx_3.8.6       
#> [43] curl_7.0.0            pkgbuild_1.4.8        plyr_1.8.9           
#> [46] lattice_0.22-7        bridgesampling_1.1-2  S7_0.2.0             
#> [49] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [52] RcppParallel_5.1.11-1 pillar_1.11.1         tensorA_0.36.2.1     
#> [55] checkmate_2.3.3       stats4_4.5.1          distributional_0.5.0 
#> [58] generics_0.1.4        rprojroot_2.1.1       rstantools_2.5.0     
#> [61] scales_1.4.0          xtable_1.8-4          glue_1.8.0           
#> [64] emmeans_1.11.2-8      tools_4.5.1           data.table_1.17.8    
#> [67] mvtnorm_1.3-3         grid_4.5.1            QuickJSR_1.8.1       
#> [70] colorspace_2.1-2      nlme_3.1-168          cli_3.6.5            
#> [73] textshaping_1.0.4     svUnit_1.0.8          Brobdingnag_1.2-9    
#> [76] V8_8.0.1              gtable_0.3.6          digest_0.6.37        
#> [79] TH.data_1.1-4         htmlwidgets_1.6.4     farver_2.1.2         
#> [82] memoise_2.0.1         htmltools_0.5.8.1     lifecycle_1.0.4      
#> [85] MASS_7.3-65

Bibliografia

Hoffmann, T., Hofman, A., & Wagenmakers, E.-J. (2022). Bayesian tests of two proportions: A tutorial with R and JASP. Methodology, 18(4), 239–277.