here::here("code", "_common.R") |>
source()
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, brms, bayestestR, insight, dplyr, ggplot2, tibble)
conflicts_prefer(loo::loo)24 Confronto tra le medie di due gruppi
“La domanda non è”è la differenza reale?“, ma piuttosto”quanto è grande la differenza, e di quanto siamo certi?”
– Jeffrey Rouder, Psicologo e Statistico, esperto di statistica bayesiana
Introduzione
Uno dei problemi più ricorrenti nella ricerca psicologica è il confronto tra due gruppi o condizioni. Spesso ci si chiede se chi ha ricevuto un trattamento migliori più di chi non lo ha ricevuto o se un campione clinico differisca da un campione non clinico per quanto riguarda una determinata variabile. In tutte queste situazioni, la domanda davvero utile non riguarda soltanto l’esistenza di una differenza, ma la sua ampiezza e il grado di incertezza con cui possiamo descriverla.
In questo capitolo affronteremo la questione adottando un approccio bayesiano. Immaginiamo una variabile di esito continua, \(y_{ig}\), dove \(i\) indica l’osservazione e \(g\in{0,1}\) l’appartenenza al gruppo. Un modello semplice e naturale assume che i punteggi di ciascun gruppo provengano da una distribuzione normale con la propria media: \(y_{ig}\sim\mathcal N(\mu_g,\sigma)\). La quantità che desideriamo conoscere è la differenza tra le due medie, \(\Delta=\mu_1-\mu_0\), in quanto esprime sinteticamente la variazione attesa passando da un gruppo all’altro.
Lo stesso modello può essere espresso come una regressione lineare con una variabile indicatrice \(x_i\) che vale 0 per il gruppo di riferimento e 1 per il gruppo di confronto: \(y_i\sim \mathcal N(\alpha+\beta x_i,\sigma)\). In questa forma, l’intercetta \(\alpha\) coincide con la media del gruppo di riferimento \((\mu_0)\), mentre il coefficiente \(\beta\) coincide con la differenza tra le medie \((\Delta)\). Quando vogliamo rendere la differenza indipendente dall’unità di misura, consideriamo anche la versione standardizzata \(d=\Delta/\sigma\), che rappresenta una misura di ampiezza dell’effetto.
L’approccio frequentista tradizionale pone l’accento sul calcolo di un p-value rispetto all’ipotesi nulla di uguaglianza tra le medie. L’approccio bayesiano, invece, fornisce un quadro più informativo: produce una distribuzione a posteriori per \(\Delta\), cioè una descrizione probabilistica di quanto riteniamo plausibili i diversi valori della differenza dopo aver osservato i dati. Da questa distribuzione possiamo derivare quantità con interpretazione immediata, come la probabilità che la differenza sia positiva, \(\Pr(\Delta>0\mid\text{dati})\), oppure la probabilità che superi una soglia di rilevanza pratica definita prima dell’analisi, \(\Pr(|\Delta|>\text{SESOI}\mid\text{dati})\). In più, l’inferenza bayesiana rende esplicito il ruolo dell’informazione pregressa tramite le distribuzioni a priori e chiarisce le assunzioni del modello, migliorando la trasparenza e la leggibilità scientifica dell’intero processo.
Il modello di base si fonda su poche ma importanti ipotesi. Le osservazioni devono essere indipendenti, una volta tenuto conto dell’effetto del gruppo; i residui, cioè la parte di variabilità che il modello non spiega, dovrebbero essere approssimativamente normali; la dispersione dei residui, rappresentata da \(\sigma\), è assunta uguale nei due gruppi. Quest’ultima è un’idealizzazione utile per cominciare: più avanti vedremo come rilassarla per gestire varianze diverse tra gruppi.
Nella ricerca applicata non basta stabilire che una differenza esista: occorre chiedersi se quell’ampiezza abbia senso dal punto di vista sostantivo. Per questo è utile definire in anticipo una soglia di rilevanza pratica (SESOI). Se, ad esempio, riteniamo che in un test cognitivo una differenza di 5 punti sia il minimo cambiamento che conti davvero, allora la nostra analisi non si limiterà a valutare se \(\Delta\) sia diverso da zero, ma quantificherà anche la probabilità che \(|\Delta|\) superi tale soglia. Questo semplice accorgimento aiuta a collegare l’inferenza statistica al significato scientifico.
Il percorso del capitolo seguirà un filo logico lineare. Partiremo dalla descrizione del modello per due gruppi e introdurremo alcune varianti più robuste quando la normalità è una semplificazione eccessiva. Discuteremo delle scelte di prior debolmente informative ancorate alla scala di misura della variabile di esito. Una volta stimato il modello, presenteremo le quantità di interesse, ovvero la differenza \(\Delta\) e, quando utile, la versione standardizzata \(d\), insieme alle relative distribuzioni a posteriori e alle probabilità più rilevanti per l’interpretazione. Concluderemo con delle verifiche predittive per valutare l’adeguatezza del modello e, quando necessario, con un breve confronto tra modelli alternativi.
Panoramica del capitolo
In seguito, chiariremo come modellare la differenza tra le medie mediante la regressione lineare bayesiana e vedremo che la variabile indicatrice può essere codificata in modi diversi, tutti equivalenti dal punto di vista sostanziale, ma talvolta più comodi per l’interpretazione o la scelta delle prior. Infine, discuteremo come comunicare i risultati in termini di intervalli di credibilità e previsioni probabilistiche che rispondano a domande sostanziali.
24.1 Il modello a indicatore e le quantità di interesse
Per poter confrontare in modo rigoroso due gruppi, introduciamo un predittore binario \(x_i\), che vale 0 per il gruppo di riferimento e 1 per il gruppo di confronto. Il modello lineare è \(y_i=\alpha+\beta x_i+\varepsilon_i\), con \(\varepsilon_i\sim \mathcal N(0,\sigma)\). In questa formulazione, \(\alpha\) rappresenta la differenza tra le due medie. L’assunzione di omoschedasticità, ovvero di una varianza uguale nei due gruppi, rende il modello particolarmente trasparente al primo incontro.
Le quantità che ci interessano di più sono direttamente ricostruibili dai parametri. La media del gruppo di riferimento è \(\mu_0 = \alpha\), quella del gruppo di confronto è \(\mu_1 = \alpha + \beta\) e la differenza \(\Delta\) coincide con \(\beta\). Il parametro \(\sigma\) descrive la variabilità residua comune, una sorta di “rumore” interno ai gruppi. In alternativa, lo stesso contenuto può essere espresso senza passare dalla forma lineare, specificando semplicemente che \(y_i\) proviene da \(\mathcal{N}(\mu_{x_i},\sigma)\), con \(\mu_{x_i}=\mu_0\) se \(x_i=0\) e \(\mu_{x_i}=\mu_1\) se \(x_i=1\). Questa “forma a medie di cella” non cambia la sostanza, ma rende i parametri ancora più espliciti.
24.2 La codifica centrata dell’indicatore
Talvolta è comodo ricentrare l’indicatore intorno a zero, definendo \(x_c=x-\tfrac12\), in modo che i suoi valori diventino \(-\tfrac12\) e \(+\tfrac12\). La regressione, scritta in termini di \(x_c\), conserva la stessa struttura, ma ne cambia l’interpretazione: l’intercetta \(\alpha_c\) diventa la media complessiva dei due gruppi, ovvero \(\mu_0+\mu_1/2\), mentre il coefficiente della variabile centrata rimane la differenza \(\Delta=\mu_1-\mu_0\). Questo piccolo cambiamento rende spesso più naturale la scelta delle prior, perché consente di esprimere separatamente ciò che si sa sulla media generale e ciò che si ritiene plausibile per l’ampiezza della differenza. Nei modelli più complessi, inoltre, la centratura riduce la correlazione a posteriori tra i parametri e può facilitare la stima.
24.3 Dati di esempio (simulati)
Per rendere riproducibili i blocchi di codice che seguono, generiamo un dataset simulato con due gruppi. La differenza tra le medie è moderata e superiore a una possibile soglia di rilevanza pratica pari a 5 unità; le varianze sono uguali, in linea con il modello di base; le numerosità sono lievemente sbilanciate, come spesso accade nei dati reali.
set.seed(1234)
n0 <- 120 # gruppo di riferimento
n1 <- 90 # gruppo di confronto
mu0 <- 80
mu1 <- 88 # Delta = 8 (> SESOI = 5)
sigma <- 12 # sd comune
x <- c(rep(0, n0), rep(1, n1))
y <- rnorm(n0 + n1, mean = ifelse(x == 0, mu0, mu1), sd = sigma)
df <- tibble(x = x, y = y)
df |>
mutate(group = factor(x, levels = c(0,1), labels = c("G0","G1"))) |>
group_by(group) |>
summarise(n = n(), mean = mean(y), sd = sd(y), .groups = "drop")
#> # A tibble: 2 × 4
#> group n mean sd
#> <fct> <int> <dbl> <dbl>
#> 1 G0 120 78.2 11.4
#> 2 G1 90 89.5 13.0Questa impostazione produce un effetto standardizzato di grandezza approssimativamente pari a \(d\approx 0.67\), sufficiente per illustrare come una stima di \(\Delta\) possa essere interpretata sia in termini di segno e ampiezza, sia in relazione a una soglia di rilevanza.
24.4 Stima con brms
Mostreremo tre parametrizzazioni equivalenti. La prima usa l’indicatore 0/1; la seconda adotta la variabile centrata per interpretare l’intercetta come media complessiva; la terza rinuncia all’intercetta e stima direttamente le due medie di gruppo, cosa utile quando si desidera controllare in modo indipendente le prior su \(\mu_0\) e \(\mu_1\).
24.4.1 Codifica dummy \(x\in{0,1}\)
L’intercetta stima la media del gruppo di riferimento, mentre il coefficiente sull’indicatore stima la differenza tra le due medie. Utilizziamo prior debolmente informative, sufficienti a stabilizzare la stima senza imporre vincoli eccessivi.
Dai campioni a posteriori ricaviamo le medie di gruppo, la differenza \(\Delta\), la deviazione standard residua e l’effetto standardizzato.
draws <- as_draws_df(fit)
post <- draws %>%
transmute(
mu0 = b_Intercept,
mu1 = b_Intercept + b_x,
delta = b_x,
sigma = sigma,
d = delta / sigma
)
posterior::summarise_draws(post[, c("mu0","mu1","delta","d","sigma")])
#> # A tibble: 5 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mu0 78.3 78.3 1.12 1.16 76.4 80.1 1.00 4121. 2971.
#> 2 mu1 89.3 89.3 1.29 1.28 87.2 91.5 1.00 4293. 3248.
#> 3 delta 11.0 11.0 1.67 1.67 8.35 13.8 1.000 4549. 2806.
#> 4 d 0.912 0.910 0.145 0.148 0.677 1.15 1.000 4385. 2898.
#> 5 sigma 12.1 12.1 0.594 0.594 11.2 13.2 1.000 3907. 2814.
SESOI <- 5
c(
P_delta_gt0 = mean(post$delta > 0),
P_delta_gtS = mean(abs(post$delta) > SESOI)
)
#> P_delta_gt0 P_delta_gtS
#> 1 1La lettura delle quantità è diretta: \(\mu_0\) e \(\mu_1\) descrivono i livelli medi dei due gruppi; \(\Delta\) quantifica la differenza; \(d\) la riporta su una scala standardizzata. Le due probabilità a posteriori rispondono rispettivamente alla domanda sul segno della differenza e alla domanda sulla sua rilevanza pratica.
24.4.2 Codifica centrata \(x_c=x-\tfrac12\)
Centrando la variabile, l’intercetta diventa la media complessiva e il coefficiente della variabile centrata rimane la differenza tra le medie. Questa forma è spesso comoda quando si desidera esprimere due priorità distinte sulla media generale e sull’ampiezza dell’effetto.
df <- df %>% mutate(xc = x - 0.5)
fit_c <- brm(
y ~ 1 + xc,
data = df,
family = gaussian(),
prior = c(
prior(normal(0, 10), class = "Intercept"),
prior(normal(0, 10), class = "b"),
prior(student_t(3, 0, 10), class = "sigma")
),
backend = "cmdstanr",
chains = 4, iter = 2000, seed = 123
)
draws_c <- as_draws_df(fit_c)
post_c <- draws_c %>%
transmute(
grand_mean = b_Intercept,
delta = b_xc,
mu0 = b_Intercept - 0.5*b_xc,
mu1 = b_Intercept + 0.5*b_xc,
sigma = sigma,
d = delta / sigma
)
posterior::summarise_draws(post_c[, c("grand_mean","mu0","mu1","delta","d","sigma")])24.4.3 Medie di cella (senza intercetta)
In questa terza variante, i coefficienti del modello coincidono direttamente con le due medie di gruppo. Questa è la parametrizzazione naturale quando si desidera assegnare prior indipendenti su \(\mu_0\) e \(\mu_1\).
df <- df %>% mutate(group = factor(x, levels = c(0,1), labels = c("G0","G1")))
fit_cells <- brm(
y ~ 0 + group,
data = df, family = gaussian(),
prior = c(
prior(normal(0, 10), class = "b", coef = "groupG0"),
prior(normal(0, 10), class = "b", coef = "groupG1"),
prior(student_t(3, 0, 10), class = "sigma")
),
backend = "cmdstanr",
chains = 4, iter = 2000, seed = 123
)
draws_cells <- as_draws_df(fit_cells)
post_cells <- draws_cells %>%
transmute(
mu0 = b_groupG0,
mu1 = b_groupG1,
delta = b_groupG1 - b_groupG0,
sigma = sigma,
d = delta / sigma
)
posterior::summarise_draws(post_cells[, c("mu0","mu1","delta","d","sigma")])Quando il modello viene parametrizzato come “intercetta + differenza”, le prior indipendenti su \(\alpha\) e \(\beta\) generano, per trasformazione lineare, una dipendenza a priori tra \(\mu_0\) e \(\mu_1\). Se l’indipendenza a priori delle due medie è un requisito desiderato, la forma a medie di cella è la più adatta.
Qualunque parametrizzazione si adotti, è opportuno verificare la qualità della stima: valori di \(\widehat R\) prossimi a 1, dimensioni campionarie efficaci adeguate, assenza di divergenze e riscontri favorevoli nei posteriori controlli predittivi. In caso di necessità, i parametri “adapt_delta” e “max_treedepth” possono essere aumentati per stabilizzare l’esplorazione della posteriore.
24.4.4 Interpretare le distribuzioni a posteriori
L’interpretazione ruota sempre attorno a poche quantità chiave. Le medie di gruppo, \(\mu_0\) e \(\mu_1\), descrivono i livelli attesi in ciascun gruppo, la differenza, \(\Delta=\mu_1-\mu_0\), quantifica il contrasto di interesse, mentre l’effetto standardizzato, \(d=\Delta/\sigma\), consente il confronto su una scala priva di unità. Oltre a riportare gli intervalli di credibilità di queste grandezze, l’approccio bayesiano permette di esprimere chiaramente la probabilità che la differenza sia positiva o superi una soglia di rilevanza pratica. Se, per esempio, la distribuzione posteriore di \(\Delta\) ha una media di 4,8, un intervallo di credibilità al 95% pari a [2,1; 7,4] e una probabilità di \(\Delta>0\) pari a 0,99 e di \(\Pr(|\Delta|>5)\) pari a 0,46 con un SESOI pari a 5, potremo concludere che la differenza è verosimilmente positiva, mentre la probabilità che raggiunga la rilevanza pratica prefissata è intermedia: un’informazione preziosa per le decisioni applicative.
24.5 Confronto tra prospettive: frequentista e bayesiana
Le due tradizioni inferenziali rispondono a domande simili con linguaggi diversi. Il frequentismo affida il giudizio a un valore p e a un intervallo di confidenza, concetti legati alla ripetizione ipotetica del campionamento e alla compatibilità dei dati con l’ipotesi nulla. Il bayesismo, invece, descrive direttamente l’incertezza sul parametro di interesse, fornendo una distribuzione a posteriori per \(\Delta\) da cui derivare probabilità con significato immediato: quanto è plausibile che l’effetto sia maggiore di zero o che superi una soglia di rilevanza scelta a priori? Inoltre, l’approccio bayesiano integra senza difficoltà le conoscenze precedenti attraverso le prior e incoraggia a esplicitare le assunzioni del modello, favorendo una rendicontazione più trasparente e strettamente collegata alle domande sostanziali della ricerca.
24.6 Esempio: istruzione materna e QI
Per dare concretezza alle idee esposte finora, analizzeremo un dataset relativo allo studio dello sviluppo cognitivo (Gelman et al., 2021). Per ogni bambino sono disponibili il punteggio di QI (kid_score) e l’indicazione se la madre ha completato la scuola superiore (mom_hs: 0 = non diplomata; 1 = diplomata). La domanda è semplice, ma al tempo stesso paradigmatica: i figli di madri diplomate hanno, in media, un QI diverso dagli altri? Per interpretare i risultati in modo sostanziale, fissiamo anche una soglia di rilevanza pratica pari a 5 punti di QI (SESOI = 5), che in questo contesto può rappresentare il minimo scostamento a cui attribuire un significato concreto.
24.6.1 Esplorazione iniziale dei dati
Come sempre, iniziamo orientandoci nel dataset: importiamo i dati, rendiamo leggibili le etichette e verifichiamo che le due variabili di interesse siano complete. Questo passaggio, per quanto elementare, è essenziale per evitare fraintendimenti successivi.
kidiq <- rio::import(here::here("data", "kidiq.dta"))
kidiq <- kidiq |>
mutate(
mom_hs = factor(mom_hs, levels = c(0, 1),
labels = c("Non diplomata", "Diplomata"))
)
glimpse(kidiq)
#> Rows: 434
#> Columns: 5
#> $ kid_score <dbl> 65, 98, 85, 83, 115, 98, 69, 106, 102, 95, 91, 58, 84, 78, 1…
#> $ mom_hs <fct> Diplomata, Diplomata, Diplomata, Diplomata, Diplomata, Non d…
#> $ mom_iq <dbl> 121.1, 89.4, 115.4, 99.4, 92.7, 107.9, 138.9, 125.1, 81.6, 9…
#> $ mom_work <dbl> 4, 4, 4, 3, 4, 1, 4, 3, 1, 1, 1, 4, 4, 4, 2, 1, 3, 3, 4, 3, …
#> $ mom_age <dbl> 27, 25, 27, 25, 27, 18, 20, 23, 24, 19, 23, 24, 27, 26, 24, …
colSums(is.na(kidiq[, c("kid_score", "mom_hs")]))
#> kid_score mom_hs
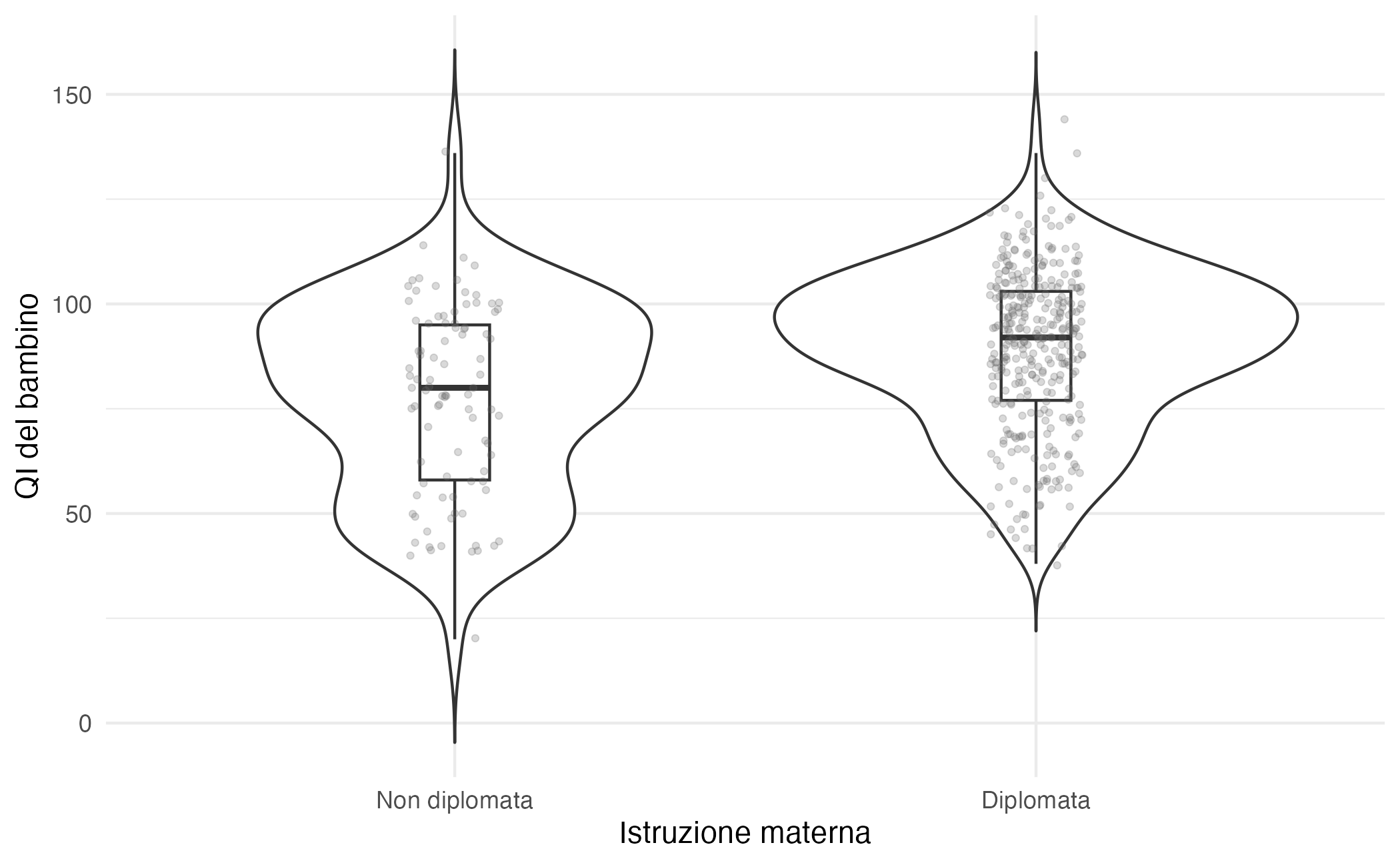
#> 0 0Una volta chiarita la struttura, conviene avere un primo colpo d’occhio su come si distribuiscono i punteggi nei due gruppi. Le statistiche descrittive per gruppo offrono un riassunto compatto (numerosità, media e variabilità), mentre una rappresentazione grafica semplice — ad esempio violini, boxplot e punti jitter — aiuta a percepire l’ampiezza della sovrapposizione tra le distribuzioni.
kidiq |>
group_by(mom_hs) |>
summarise(
n = n(),
media_QI = mean(kid_score, na.rm = TRUE),
sd_QI = sd(kid_score, na.rm = TRUE),
mediana = median(kid_score, na.rm = TRUE),
IQR = IQR(kid_score, na.rm = TRUE)
) |>
ungroup()
#> # A tibble: 2 × 6
#> mom_hs n media_QI sd_QI mediana IQR
#> <fct> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 Non diplomata 93 77.5 22.6 80 37
#> 2 Diplomata 341 89.3 19.0 92 26ggplot(kidiq, aes(x = mom_hs, y = kid_score)) +
geom_violin(trim = FALSE) +
geom_boxplot(width = 0.12, outlier.shape = NA) +
geom_jitter(width = 0.08, alpha = 0.25, size = 1) +
labs(
x = "Istruzione materna",
y = "QI del bambino"
) +
theme_minimal()Queste prime ispezioni suggeriscono che la media del gruppo con madri diplomate sia più alta, ma mostrano anche un’ampia sovrapposizione tra le due distribuzioni. È un quadro tipico nelle scienze psicologiche: un confronto di media può indicare una tendenza, ma non esaurisce l’informazione. Il passo successivo è trasformare questa intuizione in un’analisi inferenziale che quantifichi l’ampiezza della differenza e, soprattutto, l’incertezza che le si accompagna.
24.6.2 Due vie inferenziali a confronto
Possiamo procedere in parallelo lungo due tradizioni. La via frequentista risponde alla domanda se la differenza osservata sia compatibile con la sola variabilità campionaria; la via bayesiana descrive direttamente l’incertezza su \(\Delta\) e consente di calcolare probabilità con interpretazione immediata, ad esempio la probabilità che la differenza sia positiva o che superi la nostra soglia di rilevanza pratica.
24.6.2.1 La lettura frequentista
Come primo riferimento, applichiamo un t-test per campioni indipendenti nella versione con varianze uguali. L’obiettivo è capire se, assumendo che nella popolazione le due medie siano uguali, una differenza grande quanto quella osservata sia rara o meno. Va ricordato che il p-value non è la probabilità che l’ipotesi nulla sia vera, ma una misura della rarità dei dati alla luce di quell’ipotesi.
t.test(
kid_score ~ mom_hs,
data = kidiq,
var.equal = TRUE
)
#>
#> Two Sample t-test
#>
#> data: kid_score by mom_hs
#> t = -5, df = 432, p-value = 0.0000006
#> alternative hypothesis: true difference in means between group Non diplomata and group Diplomata is not equal to 0
#> 95 percent confidence interval:
#> -16.34 -7.21
#> sample estimates:
#> mean in group Non diplomata mean in group Diplomata
#> 77.5 89.3In genere si osserva una media più bassa nel gruppo “Non diplomata” e più alta nel gruppo “Diplomata”, con una differenza nell’ordine di una decina di punti QI. L’intervallo di confidenza fornisce un range di valori compatibili con i dati alla luce del modello frequentista adottato. Nella pratica, quando le varianze e le numerosità tra gruppi sono diverse, la versione di Welch — che in R è il default — risulta più robusta.
24.6.2.2 La lettura bayesiana
Passiamo ora al modello gaussiano in brms, che per semplicità assume varianza comune nei due gruppi. Per ottenere coefficienti interpretabili in modo diretto, fissiamo come riferimento il gruppo “Non diplomata”. In questo modo l’intercetta stima la media del gruppo di riferimento, mentre il coefficiente associato a “Diplomata” stima la differenza tra le due medie.
Dai campioni a posteriori ricaviamo le quantità sostantive. La media del gruppo di riferimento, la media del gruppo con madri diplomate e la loro differenza \(\Delta\) sono direttamente disponibili dai coefficienti del modello; la deviazione standard residua \(\sigma\) quantifica la variabilità non spiegata; l’effetto standardizzato \(d=\Delta/\sigma\) consente di riportare la differenza su una scala priva di unità. Definita la soglia di rilevanza a 5 punti, possiamo infine calcolare la probabilità che la differenza superi il SESOI.
# Ponte tra nomi “umani” e nomi dei draw
term_names <- setdiff(rownames(fixef(fit_1)), "Intercept")
stopifnot(length(term_names) == 1)
b_name <- paste0("b_", term_names)
dr <- as_draws_df(fit_1)
post <- dr %>%
transmute(
mu0 = b_Intercept,
delta = .data[[b_name]],
mu1 = b_Intercept + delta,
sigma = sigma,
d = delta / sigma
)
SESOI <- 5
posterior::summarise_draws(post[, c("mu0","mu1","delta","d","sigma")])
#> # A tibble: 5 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mu0 77.6 77.6 2.03 2.02 74.2 80.9 1.00 3811. 2973.
#> 2 mu1 89.3 89.3 1.06 1.07 87.6 91.1 1.00 3932. 2780.
#> 3 delta 11.7 11.8 2.31 2.31 7.91 15.5 1.000 4155. 3120.
#> 4 d 0.591 0.593 0.118 0.120 0.395 0.783 1.000 4131. 3034.
#> 5 sigma 19.9 19.9 0.702 0.709 18.8 21.1 1.00 3713. 3095.
c(
P_delta_gt0 = mean(post$delta > 0),
P_absDelta_gtS = mean(abs(post$delta) > SESOI)
)
#> P_delta_gt0 P_absDelta_gtS
#> 1.000 0.999La lettura che ne deriva è immediata. Le due medie di gruppo sono stimate con i rispettivi intervalli credibili; la differenza \(\Delta\) esprime l’ampiezza del contrasto, mentre (d) ne offre una versione standardizzata. Le probabilità a posteriori rispondono alle due domande cruciali: quanto è plausibile che la differenza sia positiva e quanto è plausibile che sia anche sufficientemente grande da superare la soglia di rilevanza stabilita a priori.
24.7 Approfondimenti bayesiani
Stimare una differenza non basta: occorre interrogarsi sulla qualità del modello. La prospettiva bayesiana offre strumenti particolarmente naturali per farlo, mettendo a confronto i dati osservati con quelli che il modello sarebbe in grado di generare e valutando, quando necessario, specificazioni alternative.
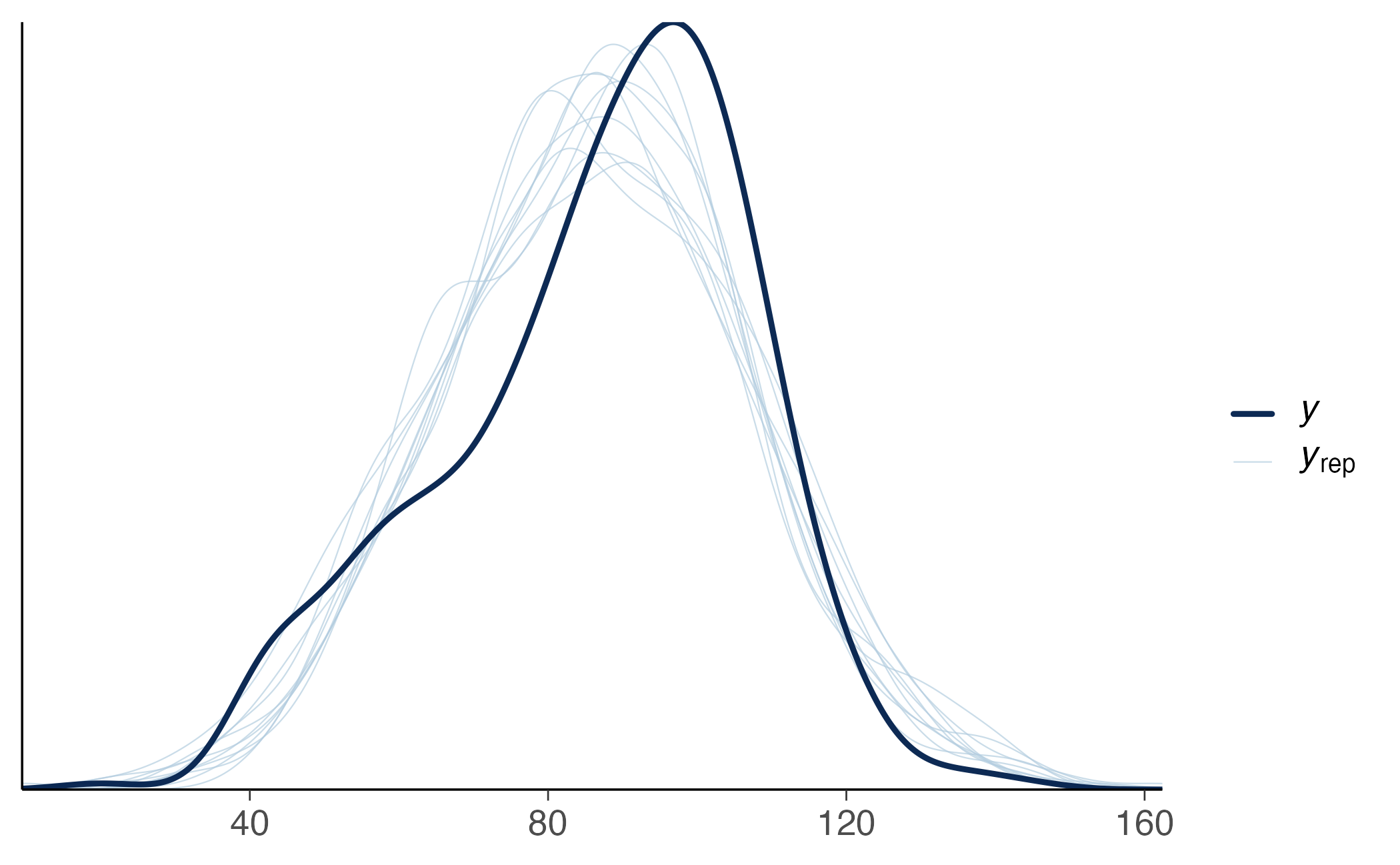
24.7.1 Verifica predittiva a posteriori
Il primo controllo consiste nel chiedersi se il modello sa rigenerare dati simili a quelli che abbiamo osservato. Le posterior predictive checks fanno esattamente questo: simulano nuovi dati dalle posteriori e li confrontano con i dati reali. Se le distribuzioni simulata e osservata divergono in modo sistematico — ad esempio perché il modello sottostima le code o non cattura una leggera asimmetria — è un segnale che la specificazione può essere raffinata.
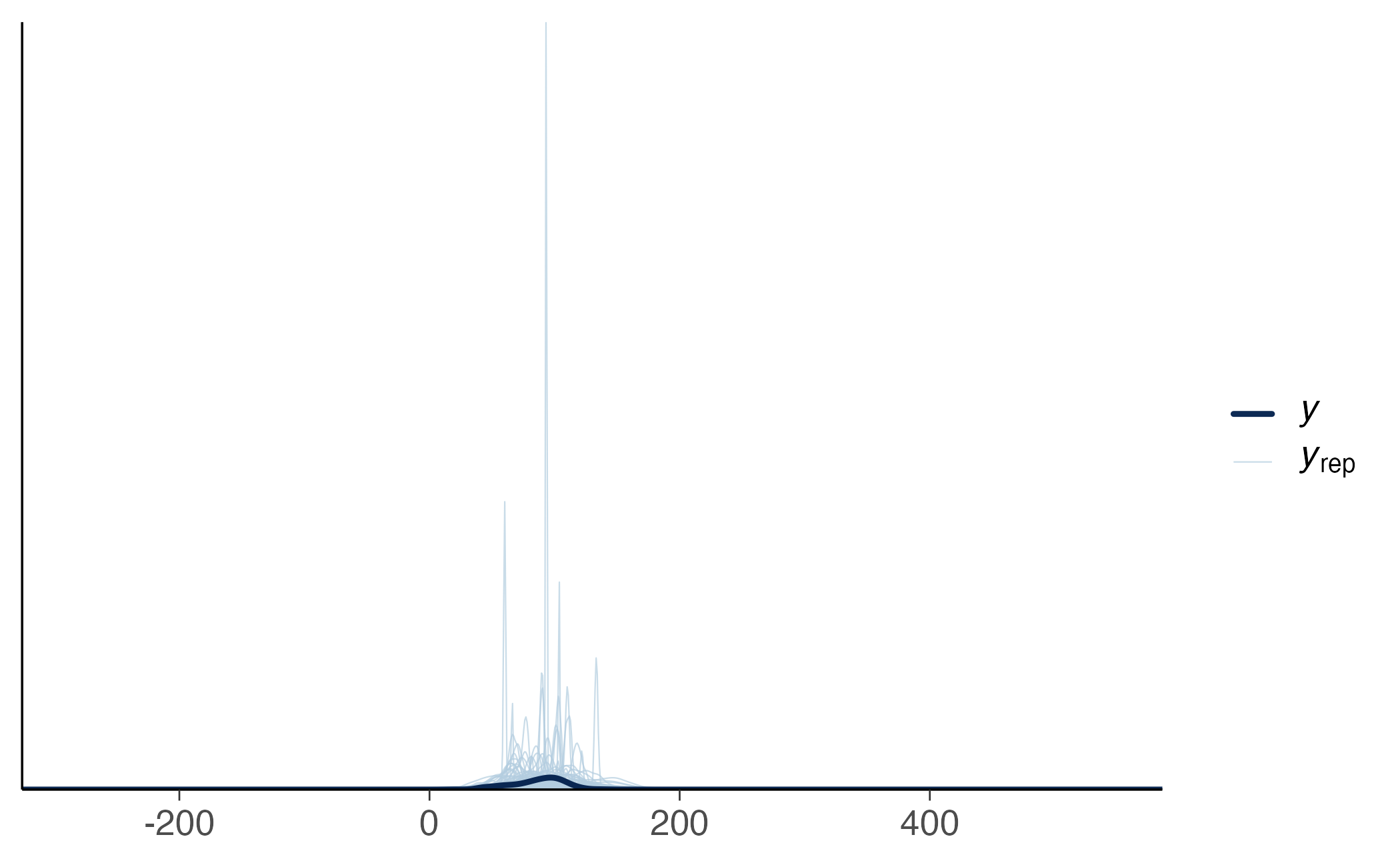
24.7.2 Verifica predittiva a priori
È altrettanto istruttivo chiedersi se le prior che abbiamo scelto, prese di per sé, producano dati plausibili. Con sample_prior = "only" il modello ignora i dati reali e simula direttamente dai prior. Se i punteggi simulati finiscono spesso in regioni irrealistiche — ad esempio QI troppo estremi — conviene riallineare le prior alla conoscenza di dominio.
pri <- c(
prior(normal(90, 20), class = "Intercept"),
prior(normal(0, 15), class = "b"),
prior(student_t(3, 0, 20), class = "sigma")
)
fit_prior <- brm(
kid_score ~ mom_hs,
data = kidiq,
family = gaussian(),
prior = pri,
sample_prior = "only",
backend = "cmdstanr",
chains = 2, iter = 1000, seed = 123
)24.7.3 Varianti del modello e scelta predittiva
Quando le verifiche evidenziano limitazioni, si possono considerare varianti mirate. La t di Student gestisce meglio la presenza di code pesanti o outlier; un modello eteroscedastico consente varianze diverse nei due gruppi; una skew-normal può accomodare una lieve asimmetria. La scelta non è meramente estetica: modelli diversi implicano assunzioni diverse sul meccanismo che ha generato i dati e possono cambiare, talora di poco, le stime delle quantità sostantive.
fit_t <- brm(kid_score ~ mom_hs, family = student(), data = kidiq,
backend = "cmdstanr", chains = 4, iter = 2000, seed = 123)
fit_het <- brm(bf(kid_score ~ mom_hs, sigma ~ mom_hs),
family = gaussian(), data = kidiq,
backend = "cmdstanr", chains = 4, iter = 2000, seed = 123)
fit_sn <- brm(kid_score ~ mom_hs, family = skew_normal(), data = kidiq,
backend = "cmdstanr", chains = 4, iter = 2000, seed = 123)Per orientare la scelta finale, è utile confrontare i modelli sul piano predittivo tramite PSIS–LOO ed ELPD. Un valore di ELPD più alto indica, a parità d’informazione, una migliore capacità di predire dati nuovi e simili a quelli osservati. Quando le differenze sono dell’ordine del loro errore standard, il vantaggio è modesto e conviene privilegiare il modello più semplice che superi le verifiche predittive; valori di Pareto (k) persistentemente elevati invitano a considerare procedure come il reloo o una validazione incrociata k-fold.
loo_fit1 <- loo(fit_1)
loo_fit_t <- loo(fit_t)
loo_fit_het<- loo(fit_het)
loo_fit_sn <- loo(fit_sn)
loo_compare(loo_fit1, loo_fit_t, loo_fit_het, loo_fit_sn)
#> elpd_diff se_diff
#> fit_sn 0.0 0.0
#> fit_het -6.0 5.9
#> fit_1 -7.4 5.3
#> fit_t -8.8 5.5Nelle applicazioni su kidiq si osserva spesso un lieve vantaggio di specificazioni che catturano meglio leggere deviazioni dalla normalità (ad esempio una skew-normal), ma le differenze predittive sono in genere contenute. In queste circostanze, la decisione si appoggia a tre pilastri: compatibilità predittiva (LOO/ELPD), esito delle posterior predictive checks e stabilità delle quantità sostantive — come \(\Delta\), \(\Pr(\Delta>0)\) e \(\Pr(|\Delta|>\text{SESOI})\) — al variare di assunzioni ragionevoli. Quando queste grandezze restano stabili tra modelli vicini, la scelta finale può legittimamente cadere sulla specificazione più semplice e più comunicabile.
Prima di interpretare i risultati, è opportuno verificare che la stima sia affidabile: \(\widehat R\) vicino a 1, dimensione campionaria efficace adeguata e assenza di divergenze. Eventuali difficoltà possono essere mitigate aumentando adapt_delta e max_treedepth o, se necessario, semplificando la parametrizzazione.
24.7.4 Una sintesi interpretativa
Il valore aggiunto dell’analisi bayesiana non sta nel sostituire un test con un altro, ma nel produrre una descrizione completa dell’incertezza sulle quantità che contano. Nel nostro esempio, la stima della differenza tra le medie è accompagnata da una distribuzione a posteriori dalla quale derivano due informazioni decisive: la plausibilità del segno dell’effetto e la plausibilità che l’effetto sia anche rilevante in senso sostantivo, rispetto alla soglia stabilita prima di guardare i dati. È esattamente questo passaggio — dall’astrazione della significatività statistica alla concretezza della rilevanza pratica — che rende l’inferenza più utile per prendere decisioni informate nella ricerca psicologica.
Riflessioni conclusive
In questo capitolo abbiamo riletto il confronto tra due gruppi con gli strumenti dell’inferenza bayesiana, mostrando come il problema possa essere formulato sia come differenza tra le medie di due distribuzioni normali, \(\Delta=\mu_1-\mu_0\), sia come un semplice modello di regressione con variabile indicatrice. Le due prospettive sono equivalenti sul piano matematico e, soprattutto, conducono alla stessa idea centrale: ciò che conta non è un verdetto sì/no sull’esistenza di una differenza, bensì una descrizione calibrata della sua ampiezza e dell’incertezza che l’accompagna. Questa descrizione è fornita dalla distribuzione a posteriori di \(\Delta\), che consente di rispondere a domande sostantive in linguaggio probabilistico: quanto è plausibile che la differenza sia positiva? quanto è plausibile che superi una soglia di rilevanza stabilita prima dell’analisi?
Il passaggio dalla logica della significatività a quella della rilevanza pratica è, a ben vedere, il guadagno principale. La soglia SESOI scandisce il confine fra differenze che, pur esistendo, non cambiano le conclusioni sostantive, e differenze che invece contano nel contesto applicativo. Allo stesso tempo, l’approccio bayesiano rende trasparente il ruolo dell’informazione pregressa attraverso le prior e invita a esplicitare le assunzioni del modello. Quando l’ipotesi di normalità o di varianza comune è troppo restrittiva, abbiamo visto come sia naturale introdurre varianti più robuste — ad esempio una t di Student per gestire code pesanti, un modello eteroscedastico per varianze diverse o una skew-normal per leggere asimmetrie — e valutare in che misura le nostre conclusioni su \(\Delta\) rimangano stabili. Le verifiche predittive a posteriori, affiancate al confronto predittivo tramite LOO/ELPD, offrono una bussola pratica per bilanciare adeguatezza descrittiva e parsimonia.
Dal punto di vista della comunicazione dei risultati, la buona pratica è ormai chiara: presentare \(\mu_0\) e \(\mu_1\) con i rispettivi intervalli credibili, riportare \(\Delta\) e, quando utile, l’effetto standardizzato \(d=\Delta/\sigma\), accompagnando queste quantità con le probabilità a posteriori più direttamente interpretabili \((\Pr(\Delta>0)\) e \(\Pr(|\Delta|>\text{SESOI}))\). Quando differenze predittive fra modelli sono piccole, la coerenza di queste grandezze attraverso specificazioni ragionevoli diventa l’argomento decisivo per la scelta del modello: se le conclusioni sostantive non cambiano, è legittimo preferire la formulazione più semplice e più comunicabile.
Il confronto tra due gruppi, così riformulato, non è un punto di arrivo ma un punto di partenza. Gli stessi principi — centralità della quantità di interesse, esplicitazione delle assunzioni, uso di prior debolmente informative ma sensibili al contesto, verifica predittiva e attenzione alla rilevanza pratica — si estendono naturalmente a scenari più complessi, con covariate, gerarchie e dipendenze nel tempo. Nel capitolo successivo riprenderemo il filo introducendo la nozione di grandezza dell’effetto in modo sistematico: collegheremo la differenza tra medie alla variabilità dei dati, discuteremo il ruolo della standardizzazione e mostreremo come integrare la prospettiva della SESOI in un quadro coerente di valutazione dell’importanza scientifica degli effetti.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] insight_1.4.2 bayestestR_0.17.0 cmdstanr_0.9.0
#> [4] ragg_1.5.0 tinytable_0.13.0 withr_3.0.2
#> [7] systemfonts_1.3.1 patchwork_1.3.2 ggdist_3.3.3
#> [10] tidybayes_3.0.7 bayesplot_1.14.0 ggplot2_4.0.0
#> [13] reliabilitydiag_0.2.1 priorsense_1.1.1 posterior_1.6.1
#> [16] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [19] brms_2.23.0 Rcpp_1.1.0 sessioninfo_1.2.3
#> [22] conflicted_1.2.0 janitor_2.2.1 matrixStats_1.5.0
#> [25] modelr_0.1.11 tibble_3.3.0 dplyr_1.1.4
#> [28] tidyr_1.3.1 rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-29
#> [7] snakecase_0.11.1 compiler_4.5.1 reshape2_1.4.4
#> [10] vctrs_0.6.5 stringr_1.5.2 pkgconfig_2.0.3
#> [13] arrayhelpers_1.1-0 fastmap_1.2.0 backports_1.5.0
#> [16] labeling_0.4.3 utf8_1.2.6 rmarkdown_2.30
#> [19] tzdb_0.5.0 haven_2.5.5 ps_1.9.1
#> [22] purrr_1.1.0 xfun_0.53 cachem_1.1.0
#> [25] jsonlite_2.0.0 broom_1.0.10 parallel_4.5.1
#> [28] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [31] lubridate_1.9.4 estimability_1.5.1 knitr_1.50
#> [34] zoo_1.8-14 R.utils_2.13.0 pacman_0.5.1
#> [37] readr_2.1.5 Matrix_1.7-4 splines_4.5.1
#> [40] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [43] yaml_2.3.10 codetools_0.2-20 processx_3.8.6
#> [46] curl_7.0.0 pkgbuild_1.4.8 plyr_1.8.9
#> [49] lattice_0.22-7 bridgesampling_1.1-2 S7_0.2.0
#> [52] coda_0.19-4.1 evaluate_1.0.5 survival_3.8-3
#> [55] RcppParallel_5.1.11-1 pillar_1.11.1 tensorA_0.36.2.1
#> [58] checkmate_2.3.3 stats4_4.5.1 distributional_0.5.0
#> [61] generics_0.1.4 rprojroot_2.1.1 hms_1.1.4
#> [64] rstantools_2.5.0 scales_1.4.0 xtable_1.8-4
#> [67] glue_1.8.0 emmeans_1.11.2-8 tools_4.5.1
#> [70] data.table_1.17.8 forcats_1.0.1 mvtnorm_1.3-3
#> [73] grid_4.5.1 QuickJSR_1.8.1 colorspace_2.1-2
#> [76] nlme_3.1-168 cli_3.6.5 textshaping_1.0.4
#> [79] svUnit_1.0.8 Brobdingnag_1.2-9 V8_8.0.1
#> [82] gtable_0.3.6 R.methodsS3_1.8.2 digest_0.6.37
#> [85] TH.data_1.1-4 htmlwidgets_1.6.4 farver_2.1.2
#> [88] R.oo_1.27.1 memoise_2.0.1 htmltools_0.5.8.1
#> [91] lifecycle_1.0.4 MASS_7.3-65