18  Confrontare due medie

Nel manuale didattico, il confronto tra due medie viene presentato nell’ambito della regressione lineare con un predittore dicotomico (0 = controllo, 1 = intervento). In quella sede si mostra che la differenza tra le medie di gruppo coincida con il coefficiente del predittore, e come l’incertezza su tale differenza corrisponda alla varianza stimata del coefficiente stesso.

In questo capitolo affronteremo lo stesso problema, ma ma adottando un’ottica generativa-bayesiana mediante Stan. approccio ci consentirà di: (i) rendere esplicite le assunzioni stocastiche sottostanti il processo generativo dei dati, (ii) specificare prior debolmente informative, coerenti con una variabile standardizzata, (iii) stimare congiuntamente la differenza tra le medie e la differenza tra le varianze, e (iv) scegliere tra modelli sulla base della loro capacità predittiva, utilizzando l’ELPD calcolato con PSIS-LOO.

Panoramica del capitolo

  • Comprendere il problema del confronto tra due medie in un’ottica bayesiana.
  • Motivare la standardizzazione dei dati e la scelta di prior debolmente informative.
  • Implementare in Stan un modello con varianza comune e uno con varianze distinte.
  • Valutare la capacità predittiva dei modelli attraverso PSIS-LOO.
  • Interpretare la distribuzione a posteriori della differenza tra le medie e le verifiche predittive.
  • Comprendere i limiti degli effetti medi di gruppo e la necessità dell’analisi idiografica.
  • Applicare il ragionamento bayesiano alla valutazione del cambiamento individuale.
  • Anticipare il ruolo dei modelli multilivello nell’integrare analisi di gruppo e individuali.
here::here("code", "_common.R") |> 
  source()

if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayesplot, ggplot2, dplyr, tibble, forcats)
conflicts_prefer(posterior::ess_bulk)
conflicts_prefer(posterior::ess_tail)

18.1 Una descrizione completa della nostra credenza sulla differenza tra medie

Per illustrare l’uso di Stan in un confronto tra due gruppi, consideriamo uno studio sul punteggio medio settimanale di affetto negativo condotto su un gruppo sperimentale che segue un training di mindfulness e su un gruppo di controllo. In questo contesto, la domanda di ricerca non si limita a verificare l’esistenza di un effetto, ma mira a quantificarlo in modo completo, determinando di quanto i gruppi differiscano e valutando quanta incertezza circondi questa stima. La nostra prospettiva consiste quindi nel stimare l’intera distribuzione a posteriori della differenza tra le medie, al fine di ottenere affermazioni probabilistiche direttamente applicabili alla pratica psicologica.

Un aspetto cruciale, spesso trascurato, è la variabilità. Il training potrebbe infatti ridurre l’affetto negativo medio, ma al tempo stesso aumentare l’eterogeneità delle risposte individuali. In tal caso, la differenza tra le deviazioni standard dei due gruppi ha un’importanza paragonabile a quella delle medie. L’inferenza bayesiana permette di stimare entrambe le quantità insieme alla loro incertezza in modo naturale.

Per stabilizzare le stime e semplificare la scelta delle prior, standardizziamo la variabile di esito sull’intero campione (media 0, deviazione standard 1). Lavoreremo con due modelli complementari: uno che assume varianze comuni e uno che ammette varianze distinte. In entrambi i casi, useremo prior normali centrate su zero per le medie e prior esponenziali per le deviazioni standard, in coerenza con la scala standardizzata.

L’obiettivo non è stabilire quale modello sia “vero”, ma quale predica meglio i nuovi dati simili ai nostri, bilanciando adeguatezza descrittiva e parsimonia. Confronteremo i due modelli utilizzando l’ELPD (Expected Log Predictive Density), stimata tramite PSIS-LOO. Il cuore dell’analisi rimane comunque la distribuzione a posteriori della differenza tra le medie, su cui calcoleremo intervalli di credibilità e probabilità a posteriori per scenari di interesse sostanziale (ad esempio, la probabilità che la differenza sia inferiore a 0,2 SD, soglia considerata clinicamente rilevante). Quando l’obiettivo è valutare l’assenza di un effetto praticamente significativo, useremo una ROPE (Region of Practical Equivalence) attorno allo zero per quantificare la plausibilità di effetti trascurabili.

Obiettivo dell’approfondimento in Stan. Rispetto a una trattazione standard tramite regressione lineare, questo capitolo mira a:

  1. mostrare l’equivalenza concettuale tra il problema della “differenza tra medie” e la stima di un coefficiente di regressione, implementandola in un modello generativo esplicito;
  2. fornire un workflow completo in Stan, dalla specificazione del modello e delle prior alla diagnostica MCMC e alla Predictive Posterior Check (PPC), per passare da semplici stime puntuali a distribuzioni posteriori pienamente interpretabili;
  3. introdurre il confronto predittivo tra modelli (tramite ELPD/PSIS-LOO) come criterio operativo per scegliere tra un modello a varianza comune e uno a varianze distinte;
  4. integrare la lettura sostanziale con strumenti come la ROPE e, se necessario, estensioni robuste (ad esempio, l’uso di una likelihood t di Student per gestire dati con code pesanti o outlier).

In sintesi, utilizzeremo Stan per stimare e confrontare due modelli semplici, mantenendo il focus sulle conclusioni sostanziali: di quanto il training modifica l’affetto negativo medio, quanto sia plausibile un effetto trascurabile e come cambi l’eterogeneità delle risposte tra i partecipanti.

18.2 Codice R

Simuliamo i dati di un piccolo studio psicologico: Gruppo A = controllo, Gruppo B = training mindfulness.

set.seed(123)  # per rendere i risultati riproducibili

n_A <- 80   # numero partecipanti controllo
n_B <- 90   # numero partecipanti training

# Medie "vere" dei gruppi (in SD standardizzate)
true_mean_A <- 0.2   # controllo con affetto negativo leggermente più alto
true_mean_B <- -0.3   # training mindfulness riduce affetto negativo

# Deviazioni standard "vere"
true_sd_A <- 1.0
true_sd_B <- 1.0   # prova a cambiare in 1.4 per simulare varianze diverse

# Creiamo un data frame con le osservazioni
df <- tibble(
  score  = c(rnorm(n_A, true_mean_A, true_sd_A),
             rnorm(n_B, true_mean_B, true_sd_B)),
  group  = factor(c(rep("Controllo", n_A), rep("Mindfulness", n_B)))
)

# Standardizziamo la variabile di esito
df <- df %>%
  mutate(
    score_std = (score - mean(score)) / sd(score),
    g = as.integer(group)   # Stan richiede indici numerici dei gruppi
  )

# Prepariamo la lista di dati per Stan
stan_data <- list(
  N = nrow(df),             # numero totale osservazioni
  J = 2L,                   # numero di gruppi
  y = df$score_std,         # variabile risposta standardizzata
  g = df$g                  # indice di gruppo
)

glimpse(stan_data)
#> List of 4
#>  $ N: int 170
#>  $ J: int 2
#>  $ y: num [1:170] -0.3016 0.0317 1.8369 0.3352 0.3945 ...
#>  $ g: int [1:170] 1 1 1 1 1 1 1 1 1 1 ...

In questo esempio, la variabile score rappresenta il livello di affetto negativo. Abbiamo simulato un piccolo effetto del training: il gruppo mindfulness, in media, ottiene punteggi più bassi (indicando dunque un minore affetto negativo) rispetto al gruppo di controllo. Standardizzando questa variabile, ovvero trasformando i punteggi grezzi in unità di deviazione standard, lavoriamo su una scala adimensionale che facilita la scelta delle prior e rende immediatamente confrontabili le stime.

18.2.1 Differenza di medie e ROPE

Prima ancora di stimare i modelli in Stan, possiamo calcolare la differenza empirica tra le medie dei gruppi e confrontarla con una regione di equivalenza pratica (ROPE). Questo confronto preliminare introduce un cambiamento fondamentale di prospettiva.

Ad esempio, possiamo stabilire che differenze inferiori a 0.1 deviazioni standard (SD) siano irrilevanti dal punto di vista psicologico nel nostro contesto applicativo. Mentre un test \(t\) di Student si limita a rispondere alla domanda “La differenza è diversa da zero?”, l’analisi con la ROPE ci permette di affrontare la domanda sostanziale: “L’effetto osservato è praticamente rilevante o trascurabile?”.

# Differenza empirica tra le medie
mean_diff <- mean(df$score_std[df$group == "Mindfulness"]) -
             mean(df$score_std[df$group == "Controllo"])

mean_diff
#> [1] -0.535

# Definiamo una ROPE di ±0.1 SD
rope_lower <- -0.1
rope_upper <-  0.1

cat("Differenza osservata =", round(mean_diff, 3), 
    " | ROPE = [", rope_lower, ",", rope_upper, "]\n")
#> Differenza osservata = -0.535  | ROPE = [ -0.1 , 0.1 ]

Naturalmente, la vera potenza del metodo bayesiano emergerà quando stimeremo la distribuzione a posteriori della differenza di medie. Questa stima ci permetterà di calcolare direttamente la probabilità a posteriori che il vero effetto si collochi all’interno o all’esterno della ROPE, ottenendo un’informazione più ricca e interpretabile rispetto al semplice valore-\(p\).

18.3 Modello a varianza comune

L’assunzione fondamentale è che i due gruppi abbiano la stessa dispersione attorno alle loro medie, condividendo una singola deviazione standard comune. Questa scelta costituisce spesso una buona approssimazione iniziale, riduce i parametri da stimare e favorisce la stabilità delle stime con campioni di dimensione limitata. Il fulcro dell’analisi rimane la differenza tra le medie: se il training di mindfulness è efficace nel ridurre l’affetto negativo, la media del gruppo sperimentale risulterà più bassa e la differenza Mindfulness – Controllo sarà quindi negativa, espressa in unità di deviazione standard.

# Salviamo il modello Stan con varianza comune
stan_equal_var <- "
data {
  int<lower=1> N;                      // numero di osservazioni
  int<lower=2> J;                      // numero di gruppi (qui: 2)
  vector[N] y;                         // esito standardizzato
  array[N] int<lower=1, upper=J> g;    // indice di gruppo per ogni osservazione
}
parameters {
  vector[J] mu;                        // medie dei due gruppi
  real<lower=0> sigma;                 // deviazione standard comune
}
model {
  // Priors debolmente informative, coerenti con y standardizzata
  mu    ~ normal(0, 1.5);
  sigma ~ exponential(1);

  // Likelihood: ogni y appartiene al suo gruppo g[i]
  for (i in 1:N)
    y[i] ~ normal(mu[g[i]], sigma);
}
generated quantities {
  vector[N] log_lik;                   // log-verosimiglianze per PSIS-LOO
  vector[N] y_rep;                     // repliche per posterior predictive checks
  real diff_mu;                        // differenza tra le medie (Gruppo 2 - Gruppo 1)

  // calcolo log_lik e repliche
  for (i in 1:N) {
    log_lik[i] = normal_lpdf(y[i] | mu[g[i]], sigma);
    y_rep[i]   = normal_rng(mu[g[i]], sigma);
  }

  // differenza di interesse sostantivo:
  // attenzione: per coerenza didattica, assumiamo g=1 -> Controllo, g=2 -> Mindfulness
  diff_mu = mu[2] - mu[1];
}
"
mod_eq <- cmdstanr::cmdstan_model(write_stan_file(stan_equal_var))

Eseguiamo il campionaento dalla distribuzione a posteriori:

fit_eq <- mod_eq$sample(
  data = stan_data,                    # creato nella sezione precedente
  seed = 2025,
  chains = 4, parallel_chains = 4,
  iter_warmup = 1000, iter_sampling = 1000,
  refresh = 0
)

Dopo l’esecuzione del campionatore, esaminiamo rapidamente i principali diagnostici. Se il valore R-hat è vicino a 1 e le dimensioni efficaci del campione (effective sample sizes) sono adeguate, possiamo procedere con sicurezza all’interpretazione dei risultati. Per garantire continuità didattica tra specificazione del modello e analisi, estraiamo e utilizziamo direttamente le quantità calcolate nel blocco generated quantities.

# Differenza tra medie: estraiamo il vettore 'diff_mu'
diff_draws <- fit_eq$draws(variables = "diff_mu", format = "draws_matrix")

# Riassunto compatto della posteriore: media, sd e intervallo di credibilità al 95%
q025 <- function(x) posterior::quantile2(x, probs = 0.025)
q975 <- function(x) posterior::quantile2(x, probs = 0.975)

posterior::summarize_draws(diff_draws, mean, sd, q025, q975)
#> # A tibble: 1 × 5
#>   variable   mean    sd   q2.5  q97.5
#>   <chr>     <dbl> <dbl>  <dbl>  <dbl>
#> 1 diff_mu  -0.536 0.148 -0.817 -0.243

L’oggetto diff_mu rappresenta la quantità principale di principale interesse della nostra analisi. Un suo valore negativo indica che, in media, il gruppo Mindfulness presenta un livello di affetto negativo inferiore rispetto al gruppo di controllo.

Per tradurre direttamente questo risultato statistico in un’interpretazione dal punto di vista psicologico, calcoliamo la probabilità a posteriori che la differenza effettiva tra i gruppi superi una soglia di rilevanza clinica. A titolo esemplificativo, definiamo un intervallo di effetti clinicamente irrilevanti pari a $$0,1 deviazioni standard. La scelta di questa soglia critica non è di natura statistica, ma scientifica: adattarla al contesto specifico della ricerca è parte integrante della responsabilità dello sperimentatore.

# Calcolo ROPE: probabilità a posteriori dentro/fuori la regione
rope_lower <- -0.1
rope_upper <-  0.1

diff_vec <- as.numeric(diff_draws[, "diff_mu"])
p_in_rope  <- mean(diff_vec > rope_lower & diff_vec < rope_upper)
p_below    <- mean(diff_vec < rope_lower)
p_above    <- mean(diff_vec > rope_upper)

tibble(
  `P(diff in ROPE)`  = p_in_rope,
  `P(diff < lower)`  = p_below,
  `P(diff > upper)`  = p_above
)
#> # A tibble: 1 × 3
#>   `P(diff in ROPE)` `P(diff < lower)` `P(diff > upper)`
#>               <dbl>             <dbl>             <dbl>
#> 1            0.0025             0.998                 0

Queste probabilità rivelano ciò che un semplice t-test non può offrire: non ci dicono solo se la differenza sia statisticamente diversa da zero, ma ci permettono anche di classificarla come trascurabile, peggiorativa o migliorativa rispetto a una soglia di rilevanza pratica predeterminata. In un report didattico completo, queste stime probabilistiche dovrebbero sempre essere sempre accompagnate da un confronto predittivo tra modelli e da una verifica grafica della coerenza del modello con i dati osservati.

A questo punto, abbiamo tutti gli elementi per interpretare in modo sostanziale il modello a varianza comune: la distribuzione a posteriori della differenza tra le medie con il relativo intervallo di credibilità, la probabilità a posteriori che quantifica direttamente la plausibilità di effetti clinicamente rilevanti o trascurabili e la verifica predittiva che conferma la capacità del modello di riprodurre dati verosimili.

Il passo successivo consiste nel verificare se l’assunzione di omogeneità delle varianze sia appropriata, e introduce il modello a varianze distinte. Utilizzeremo l’indice PSIS-LOO per confrontare i due modelli e valutare se il maggiore dettaglio parametrico garantisca un effettivo e stabile miglioramento nella loro capacità di predire nuovi dati. Se il confronto non evidenzierà un vantaggio predittivo, potremo concludere che il modello a varianza comune più parsimonioso è sufficiente, senza compromettere la validità delle nostre conclusioni sostanziali.

18.4 Modello a varianze distinte

In questa specificazione si rilassa l’ipotesi di omogeneità, ammettendo che i due gruppi possano presentare un diverso grado di dispersione attorno alle rispettive medie. Ciò consente di modellare, ad esempio, uno scenario in cui il training di mindfulness riduca in media l’affetto negativo, ma produca al contempo risposte più eterogenee tra i partecipanti rispetto al gruppo di controllo. Pertanto, stimiamo in modo congiunto e indipendente le medie (\(\mu_1,\mu_2\)) e le deviazioni standard (\(\sigma_1,\sigma_2\)) di ciascun gruppo.

Anche in questo caso, poiché i dati sono standardizzati, le prior di riferimento restano coerenti con la scala adottata: utilizziamo prior normali \(\text{Normal}(0, 1.5)\) per le medie e prior esponenziali \(\text{Exponential}(1)\) per le deviazioni standard. Tale parametrizzazione, debolmente informativa, garantisce che le stime siano dominate dall’evidenza dei dati.

# Modello Stan: varianze distinte
stan_unequal_var <- "
data {
  int<lower=1> N;                      // numero di osservazioni
  int<lower=2> J;                      // numero di gruppi (qui: 2)
  vector[N] y;                         // esito standardizzato
  array[N] int<lower=1, upper=J> g;    // indice di gruppo
}
parameters {
  vector[J] mu;                        // medie per gruppo
  vector<lower=0>[J] sigma;            // sd specifica di gruppo
}
model {
  // Priors debolmente informative
  mu    ~ normal(0, 1.5);
  sigma ~ exponential(1);

  // Likelihood con sd per gruppo
  for (i in 1:N)
    y[i] ~ normal(mu[g[i]], sigma[g[i]]);
}
generated quantities {
  vector[N] log_lik;                   // per PSIS-LOO
  vector[N] y_rep;                     // posterior predictive checks
  real diff_mu;                        // mu[2] - mu[1], Mindfulness - Controllo
  real diff_sigma;                     // sigma[2] - sigma[1]

  for (i in 1:N) {
    log_lik[i] = normal_lpdf(y[i] | mu[g[i]], sigma[g[i]]);
    y_rep[i]   = normal_rng(mu[g[i]], sigma[g[i]]);
  }

  diff_mu    = mu[2]    - mu[1];
  diff_sigma = sigma[2] - sigma[1];
}
"

Compilazione:

mod_neq <- cmdstanr::cmdstan_model(write_stan_file(stan_unequal_var))

Campionamento:

fit_neq <- mod_neq$sample(
  data = stan_data, 
  seed = 2025,
  chains = 4, parallel_chains = 4,
  iter_warmup = 1000, iter_sampling = 1000,
  refresh = 0
)
#> Running MCMC with 4 parallel chains...
#> Chain 1 finished in 0.1 seconds.
#> Chain 2 finished in 0.1 seconds.
#> Chain 3 finished in 0.1 seconds.
#> Chain 4 finished in 0.1 seconds.
#> 
#> All 4 chains finished successfully.
#> Mean chain execution time: 0.1 seconds.
#> Total execution time: 0.3 seconds.

18.4.1 Lettura sostantiva dei parametri

Come nel modello precedente, la quantità principale è diff_mu = mu[2] - mu[1], che rappresenta la differenza delle medie tra il gruppo Mindfulness e quello di controllo. Tuttavia, questo modello ci fornisce anche una seconda informazione cruciale: diff_sigma = sigma[2] - sigma[1], che stima la differenza tra le deviazioni standard dei due gruppi.

Questo parametro aggiuntivo ci permette di valutare se, oltre a un eventuale effetto sulla media, il training di mindfulness modifichi anche l’eterogeneità delle risposte dei partecipanti. Ad esempio, un valore positivo di diff_sigma indicherebbe una maggiore variabilità nel gruppo sperimentale, suggerendo che l’intervento potrebbe influenzare gli individui in modo più differenziato rispetto alla condizione di controllo.

# Estraiamo le quantità principali
neq_draws_mu     <- fit_neq$draws(variables = c("mu[1]", "mu[2]", "diff_mu"), format = "draws_matrix")
neq_draws_sigma  <- fit_neq$draws(variables = c("sigma[1]", "sigma[2]", "diff_sigma"), format = "draws_matrix")

q025 <- function(x) posterior::quantile2(x, probs = 0.025)
q975 <- function(x) posterior::quantile2(x, probs = 0.975)

# Riassunti posteriori
posterior::summarize_draws(neq_draws_mu,    mean, sd, q025, q975)
#> # A tibble: 3 × 5
#>   variable   mean    sd    q2.5   q97.5
#>   <chr>     <dbl> <dbl>   <dbl>   <dbl>
#> 1 mu[1]     0.282 0.102  0.0821  0.483 
#> 2 mu[2]    -0.254 0.108 -0.461  -0.0414
#> 3 diff_mu  -0.536 0.148 -0.826  -0.249
posterior::summarize_draws(neq_draws_sigma, mean, sd, q025, q975)
#> # A tibble: 3 × 5
#>   variable     mean     sd   q2.5 q97.5
#>   <chr>       <dbl>  <dbl>  <dbl> <dbl>
#> 1 sigma[1]   0.940  0.0762  0.804 1.10 
#> 2 sigma[2]   1.00   0.0759  0.871 1.17 
#> 3 diff_sigma 0.0629 0.107  -0.144 0.274

Se diff_mu è negativo, significa che il gruppo mindfulness mostra in media un affetto negativo inferiore rispetto al gruppo di controllo. Se il valore di diff_sigma è positivo, il gruppo mindfulness risulta più eterogeneo; se è negativo, risulta più omogeneo.

Quest’ultimo aspetto, che riguarda la variabilità, è solitamente trascurato dal tradizionale test \(t\) di Student, ma è di rilevanza scientifica sostanziale: un intervento può infatti alterare non solo la tendenza centrale dei dati, ma anche la dispersione delle risposte individuali attorno a tale tendenza.

Per mantenere una continuità metodologica con l’analisi precedente, applichiamo anche qui il concetto di ROPE alla differenza delle medie. Lo scopo è spostare l’attenzione dalla semplice significatività statistica a una valutazione pratica: l’entità dell’effetto osservato è clinicamente o teoricamente trascurabile?

# ROPE su diff_mu (stessa soglia di prima)
rope_lower <- -0.1
rope_upper <-  0.1

diff_mu_vec <- as.numeric(neq_draws_mu[, "diff_mu"])
p_in_rope_neq <- mean(diff_mu_vec > rope_lower & diff_mu_vec < rope_upper)
p_below_neq   <- mean(diff_mu_vec < rope_lower)
p_above_neq   <- mean(diff_mu_vec > rope_upper)

tibble(
  Model = "Varianze distinte",
  `P(diff in ROPE)` = p_in_rope_neq,
  `P(diff < lower)` = p_below_neq,
  `P(diff > upper)` = p_above_neq
)
#> # A tibble: 1 × 4
#>   Model             `P(diff in ROPE)` `P(diff < lower)` `P(diff > upper)`
#>   <chr>                         <dbl>             <dbl>             <dbl>
#> 1 Varianze distinte            0.0005             1.000                 0

18.4.2 Confronto predittivo con PSIS-LOO

Ora procediamo al confronto tra il modello a varianza comune (fit_eq) e il modello a varianze distinte (fit_neq) utilizzando l’Expected Log Predictive Density (ELPD) stimata via PSIS-LOO. Ricordiamo che, in questa metrica, valori più alti indicano una migliore capacità predittiva.

Oltre alla differenza di ELPD, esaminiamo attentamente i diagnostici Pareto-k. Valori superiori a 0.7 segnalano potenziali osservazioni influenti che possono inficiare l’affidabilità del confronto e richiedono un’analisi specifica.

La decisione finale segue un criterio pragmatico:

  • se il vantaggio predittivo del modello più complesso (fit_neq) è marginale e incerto, si privilegia il principio più parsimonioso, mantenendo il modello a varianza comune;
  • se il vantaggio è netto, stabile e supportato da diagnostici solidi, si giustifica l’adozione del modello a varianze distinte, accettandone la maggiore complessità parametrale.
# LOO per entrambi i modelli
loo_eq  <- fit_eq$loo()
loo_neq <- fit_neq$loo()

print(loo_eq)
#> 
#> Computed from 4000 by 170 log-likelihood matrix.
#> 
#>          Estimate   SE
#> elpd_loo   -237.5  9.8
#> p_loo         3.1  0.5
#> looic       474.9 19.5
#> ------
#> MCSE of elpd_loo is 0.0.
#> MCSE and ESS estimates assume MCMC draws (r_eff in [0.8, 1.1]).
#> 
#> All Pareto k estimates are good (k < 0.7).
#> See help('pareto-k-diagnostic') for details.
print(loo_neq)
#> 
#> Computed from 4000 by 170 log-likelihood matrix.
#> 
#>          Estimate   SE
#> elpd_loo   -238.3  9.8
#> p_loo         4.1  0.8
#> looic       476.6 19.6
#> ------
#> MCSE of elpd_loo is 0.0.
#> MCSE and ESS estimates assume MCMC draws (r_eff in [1.0, 1.3]).
#> 
#> All Pareto k estimates are good (k < 0.7).
#> See help('pareto-k-diagnostic') for details.
# Confronto
comp <- loo::loo_compare(list(equal_var = loo_eq, unequal_var = loo_neq))
comp_df <- as.data.frame(comp)
comp_df
#>             elpd_diff se_diff elpd_loo se_elpd_loo p_loo se_p_loo looic
#> equal_var       0.000    0.00     -237        9.76  3.05    0.539   475
#> unequal_var    -0.856    0.61     -238        9.81  4.06    0.780   477
#>             se_looic
#> equal_var       19.5
#> unequal_var     19.6

Per una decisione didatticamente “manuale”, possiamo usare una regola semplice: se |ΔELPD| < 2 × SE(Δ), consideriamo i modelli sostanzialmente equivalenti; in tal caso scegliamo il modello più semplice.

# Piccolo helper decisionale
delta_elpd <- comp_df$elpd_diff[1]     # per la riga in cima
se_delta   <- comp_df$se_diff[1]

decision <- if (abs(delta_elpd) < 2 * se_delta) {
  "Modelli predittivamente equivalenti: preferire la varianza comune per parsimonia."
} else if (delta_elpd > 0) {
  "Il modello a varianze distinte offre un vantaggio predittivo credibile: preferirlo."
} else {
  "Il modello a varianza comune è migliore: preferirlo."
}

tibble(Delta_ELPD = delta_elpd, SE_Delta = se_delta, Decisione = decision)
#> # A tibble: 1 × 3
#>   Delta_ELPD SE_Delta Decisione                                           
#>        <dbl>    <dbl> <chr>                                               
#> 1          0        0 Il modello a varianza comune è migliore: preferirlo.

18.4.3 Verifiche predittive a posteriori

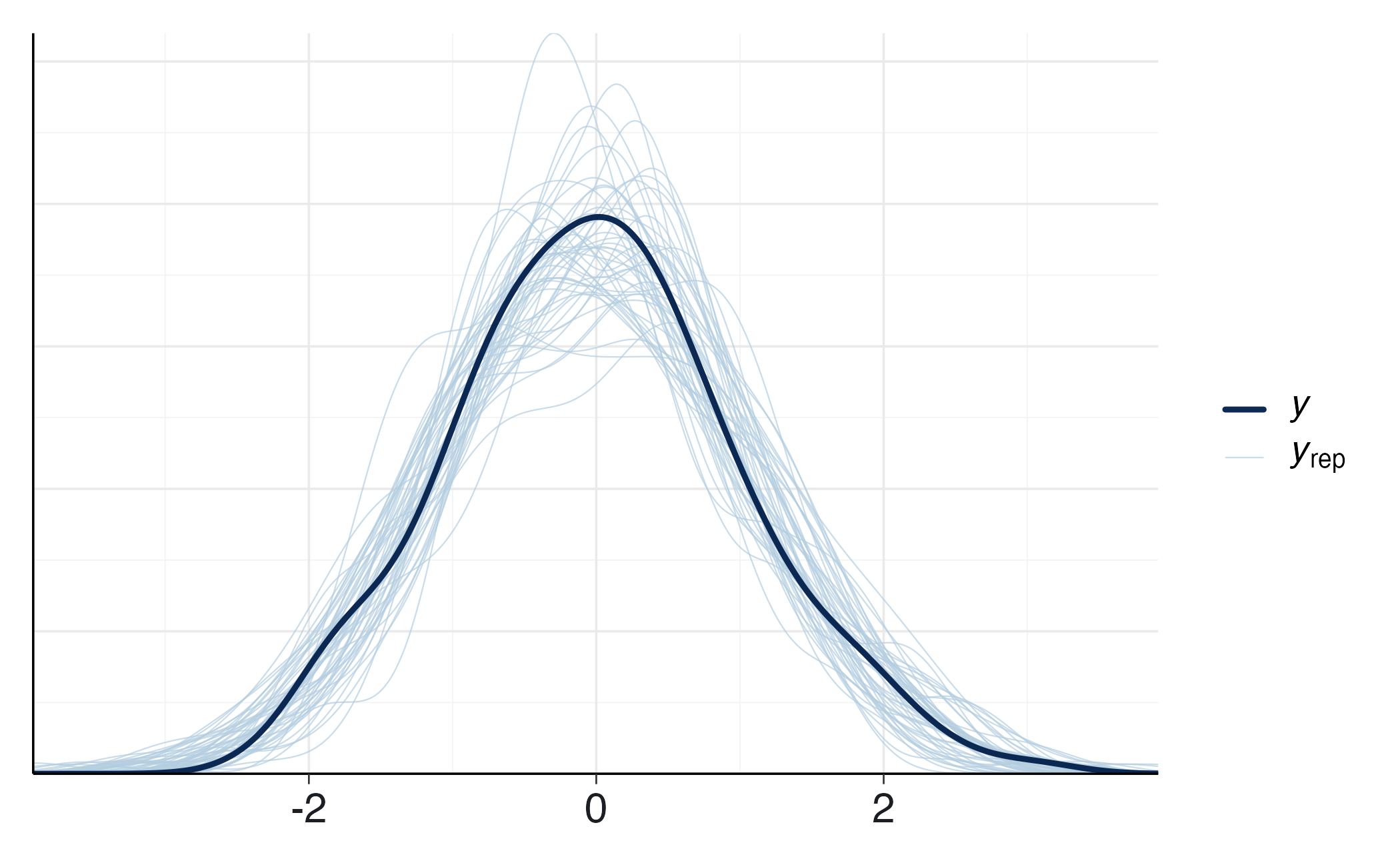
Verifichiamo la capacità dei due modelli di riprodurre le caratteristiche chiave della distribuzione osservata, in particolare la forma e la dispersione dei dati nei due gruppi. Se entrambi i modelli superano questa verifica senza mostrare discrepanze sostanziali, il criterio decisivo per la scelta sarà il confronto predittivo basato sull’ELPD. Se invece uno dei modelli evidenzia inadeguatezze sistematiche (ad esempio, sottostimando la variabilità in uno dei gruppi), questo costituisce un segnale di primaria importanza, che suggerisce di preferire il modello alternativo a prescindere dalle differenze di ELPD, in quanto la sua rappresentazione del processo generativo risulta fondamentalmente carente.

# Equal variance
yrep_eq <- fit_eq$draws("y_rep", format = "matrix")
bayesplot::ppc_dens_overlay(y = stan_data$y, yrep = yrep_eq[1:50, ])

# Unequal variances
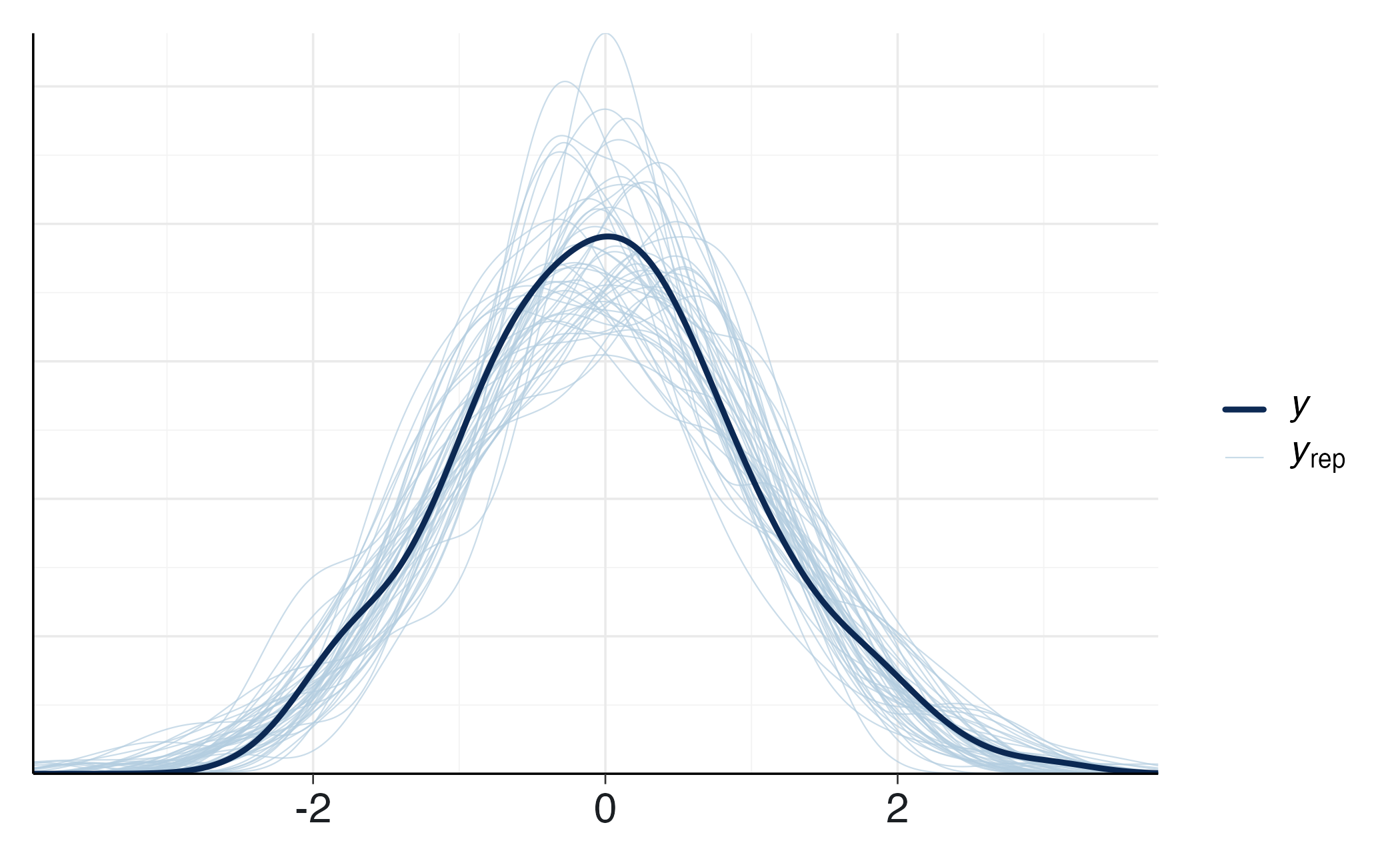
yrep_neq <- fit_neq$draws("y_rep", format = "matrix")
bayesplot::ppc_dens_overlay(y = stan_data$y, yrep = yrep_neq[1:50, ])

18.5 Cosa impariamo

  1. Differenza tra le medie. La posteriore di diff_mu dice di quanto il training modifica l’affetto negativo medio, con intervallo di credibilità; la ROPE ci dice se l’effetto è praticamente trascurabile o rilevante. Questo è un vantaggio diretto rispetto al t-test, che non fornisce probabilità di “effetto rilevante” né gestisce l’equivalenza pratica in modo naturale.

  2. Differenza tra varianze. La posteriore di diff_sigma chiarisce se l’intervento modifica l’eterogeneità delle risposte: informazione spesso ignorata, ma importante in psicologia applicata.

  3. Capacità predittiva. Il confronto PSIS-LOO ci guida nella scelta del livello di complessità. Se ΔELPD è piccolo e incerto, preferiamo la parsimonia (varianza comune); se il vantaggio è stabile e sostanziale, ha senso adottare il modello con varianze distinte.

18.6 Dall’effetto medio al cambiamento individuale: un cambio di prospettiva

18.6.1 Il limite fondamentale delle medie di gruppo

L’analisi presentata finora risponde a una domanda importante: in media, il gruppo che ha seguito il training di mindfulness mostra un affetto negativo inferiore rispetto al gruppo di controllo? Tuttavia, questa domanda, per quanto centrale nella ricerca sperimentale, può risultare insufficiente, e talvolta persino fuorviante, quando l’obiettivo è comprendere l’efficacia di un intervento nella pratica clinica.

Il problema è che l’effetto medio di gruppo può mascherare un’enorme eterogeneità nelle risposte individuali. Consideriamo uno scenario concreto: supponiamo che il nostro training di mindfulness produca una riduzione media dell’affetto negativo pari a 0.5 deviazioni standard, ovvero un effetto di dimensione medio-grande secondo le convenzioni di Cohen. Questo risultato potrebbe derivare da situazioni molto diverse:

  • scenario A: tutti i partecipanti migliorano in modo simile, con riduzioni individuali comprese tra 0.4 e 0.6 SD;
  • scenario B: metà dei partecipanti mostra miglioramenti sostanziali (circa 1.0 SD), mentre l’altra metà non mostra alcun cambiamento o addirittura peggiora leggermente;
  • scenario C: la maggior parte dei partecipanti mostra cambiamenti minimi, ma alcuni “super-responder” mostrano miglioramenti drammatici che spingono la media verso l’alto.

In tutti e tre gli scenari, l’effetto medio di gruppo sarebbe identico. Tuttavia, le implicazioni cliniche sarebbero radicalmente diverse. Nel primo scenario, potremmo raccomandare l’intervento con fiducia a qualsiasi paziente. Nel secondo scenario, dovremmo chiederci quali caratteristiche distinguono i responder dai non-responder. Nel terzo scenario, l’intervento potrebbe rivelarsi inefficace per la maggior parte delle persone e la media positiva sarebbe solo il risultato di pochi casi eccezionali.

18.6.2 La fallacia ecologica e i suoi rischi

Nella letteratura metodologica questo problema prende il nome di fallacia ecologica (o ecological fallacy). Si tratta dell’errore logico di inferire caratteristiche individuali a partire da dati aggregati. In termini formali, il fatto che \(\mathbb{E}[Y \mid \text{gruppo} = \text{trattamento}] < \mathbb{E}[Y \mid \text{gruppo} = \text{controllo}]\) non implica che per ogni individuo \(i\) nel gruppo di trattamento valga \(Y_i^{\text{post}} < Y_i^{\text{pre}}\).

La psicologia clinica è particolarmente vulnerabile a questa fallacia, in quanto si occupa di individui e non di gruppi. Quando uno psicologo clinico deve decidere se raccomandare un determinato trattamento a un paziente specifico, la domanda rilevante non è “Il trattamento funziona in media?” ma “Il trattamento funzionerà per questa persona?”. Allo stesso modo, quando si valuta l’efficacia di un percorso terapeutico già concluso, la domanda da porsi è: “Questo paziente ha effettivamente beneficiato dell’intervento, o il cambiamento osservato è compatibile con la semplice variabilità dell’errore di misurazione?”.

18.6.3 Perché l’analisi idiografica è essenziale

L’approccio idiografico, termine derivato dal greco ἴδιος (proprio, privato, particolare), si concentra sull’individuo come unità di analisi primaria, in contrasto con l’approccio nomotetico che cerca leggi generali applicabili a popolazioni.1 In psicologia, questa distinzione ha una lunga storia che risale almeno a Gordon Allport, e assume particolare rilevanza nell’era della medicina personalizzata e degli interventi evidence-based.

L’analisi idiografica del cambiamento individuale risponde a domande cruciali dal punto di vista della psicologia clinica: il paziente è migliorato in modo clinicamente rilevante? Il cambiamento osservato supera ciò che ci si potrebbe aspettare dalla sola imprecisione dello strumento di misurazione? Qual è la probabilità che il cambiamento sia sostanziale piuttosto che trascurabile?

Queste domande non possono trovare risposta nelle statistiche aggregate di gruppo. Richiedono un framework inferenziale che operi a livello del singolo individuo e che incorpori esplicitamente l’incertezza della misurazione, in modo da poter fare affermazioni probabilistiche sul cambiamento vero (latente) a partire da quello osservato.

18.6.4 Le sfide dell’inferenza a livello del singolo individuo

L’analisi a livello individuale presenta però notevoli sfide metodologiche. La più importante è la scarsità di informazioni: mentre l’analisi a livello di gruppo può contare su decine o centinaia di osservazioni, l’analisi del caso singolo si basa tipicamente su due soli punti temporali (prima e dopo l’intervento). Questa asimmetria ha importanti conseguenze.

In primo luogo, l’incertezza è necessariamente maggiore. Con soli due punteggi per persona, la stima del cambiamento individuale è fortemente influenzata dall’errore di misurazione. Un miglioramento osservato di 5 punti potrebbe riflettere un vero miglioramento di 5 punti, ma potrebbe anche essere compatibile con un miglioramento reale di 10 punti mascherato da un errore di misurazione di segno negativo o con l’assenza di un miglioramento reale in presenza di un errore di misurazione di segno positivo di 5 punti.

In secondo luogo, la distribuzione a posteriori sarà più ampia. Mentre la distribuzione a posteriori della differenza tra le medie dei gruppi, basata su molte osservazioni, può essere relativamente stretta e precisa, la distribuzione a posteriori del cambiamento individuale, basata su soli due punti, sarà inevitabilmente più dispersa. Questo non è un difetto dell’analisi bayesiana, ma una corretta rappresentazione dell’incertezza epistemica: con pochi dati siamo più incerti.

In terzo luogo, le conclusioni saranno più sfumate. Raramente potremo affermare con assoluta certezza che un individuo sia migliorato o peggiorato. Piuttosto, dovremo ragionare in termini probabilistici, ad esempio: “La probabilità di un miglioramento clinicamente rilevante è del 72%” o “C’è una probabilità del 15% che il cambiamento osservato sia dovuto solo all’errore di misurazione”.

18.6.5 Verso un’integrazione delle due prospettive: l’anticipazione dei modelli multilivello

Le difficoltà dell’analisi idiografica “pura”, ovvero condotta separatamente per ciascun individuo, possono essere in parte superate attraverso i modelli multilivello (o gerarchici), che saranno trattati nei capitoli successivi. In questi modelli, le stime individuali non vengono calcolate in isolamento, ma sono informate anche dai dati dell’intero campione, grazie a un meccanismo di condivisione statistica dell’informazione.

In un modello multilivello, i cambiamenti individuali sono concepiti come realizzazioni di una distribuzione comune a livello di popolazione. Questo impianto conduce a un fenomeno noto come shrinkage (o regolarizzazione), per cui le stime individuali vengono “tirate” verso la media di gruppo in misura proporzionale alla loro incertezza. Gli individui con dati più rumorosi o con osservazioni estreme sono soggetti a una maggiore regolarizzazione, mentre quelli con dati più informativi mantengono stime più vicine ai valori osservati.

Questo approccio presenta due vantaggi. Da un lato, le stime individuali sono più stabili e meno sensibili all’errore casuale; dall’altro, il modello fornisce simultaneamente una stima dell’effetto medio di gruppo, coerente con una prospettiva nomotetica, e stime dei cambiamenti individuali, coerenti con una prospettiva idiografica. I due livelli di analisi non sono più considerati come alternativi, ma sono integrati all’interno di un unico framework concettuale e statistico.

Nel presente capitolo, tuttavia, adotteremo un approccio più semplice che non richiede la specifica esplicita di un modello multilivello completo. Questo approccio, basato sulla teoria classica dei test, fornisce un’introduzione accessibile all’inferenza bayesiana sul cambiamento individuale e fornisce una base concettuale per le successive estensioni di tipo gerarchico.

18.7 L’analisi del cambiamento individuale

18.7.1 Il modello di misurazione del cambiamento

L’obiettivo è stimare il cambiamento vero di un individuo a partire dalla differenza osservata tra due somministrazioni dello stesso test, tipicamente in un disegno pre–post intervento. Indichiamo con \[ D = X_{\text{post}} - X_{\text{pre}} \] la differenza osservata per un dato individuo. È importante chiarire che \(D\) rappresenta un’informazione direttamente osservabile, mentre il cambiamento psicologico di interesse teorico è il cambiamento vero, che indichiamo con \(\Delta\). Quest’ultimo non è osservabile direttamente ed è inevitabilmente contaminato dall’errore di misurazione associato alle singole osservazioni.

Il problema centrale consiste quindi nel distinguere tra \(D\) e \(\Delta\). Poiché ogni misura psicometrica è affetta da errore, non possiamo assumere che \(D = \Delta\). La questione inferenziale fondamentale diventa allora la seguente: dato un valore osservato di \(D\), quali conclusioni possiamo trarre in merito al valore plausibile di \(\Delta\)?

18.7.2 La quantificazione dell’errore di misura

Il quadro concettuale di riferimento per la formalizzazione dell’incertezza di misura è fornito dalla Teoria Classica dei Test (TCT) (Lord & Novick, 2008). In tale prospettiva, ogni punteggio osservato \(X\) viene scomposto in una componente vera \(T\) e in una componente di errore casuale \(E\), secondo la relazione: \[ X = T + E . \] L’affidabilità del test (\(r_{xx}\)) è definita come il rapporto tra la varianza del punteggio vero e la varianza del punteggio osservato: \[ r_{xx} = \frac{\mathrm{Var}(T)}{\mathrm{Var}(X)} . \] Da questa definizione segue immediatamente che la varianza dell’errore di misura è \[ \mathrm{Var}(E) = \mathrm{Var}(X)(1 - r_{xx}) , \] e che lo Standard Error of Measurement (SEM) è dato da \[ \mathrm{SEM} = SD_X \sqrt{1 - r_{xx}} , \] dove \(SD_X\) indica la deviazione standard campionaria dei punteggi osservati.

Per quanto riguarda la varianza della differenza tra due misurazioni, consideriamo il caso più semplice, in cui gli errori associati alle misure pre e post siano indipendenti e caratterizzati dalla medesima deviazione standard, pari al SEM del test. In queste condizioni, la varianza della differenza \[ D = X_{\text{post}} - X_{\text{pre}} \] è pari alla somma delle varianze degli errori di misura: \[ \mathrm{Var}(D) = \mathrm{Var}(E_{\text{post}}) + \mathrm{Var}(E_{\text{pre}}) = \mathrm{SEM}^2 + \mathrm{SEM}^2 = 2\,\mathrm{SEM}^2 . \] Ne consegue che la deviazione standard associata alla differenza osservata è \[ \mathrm{SE}_{\mathrm{diff}} = \sqrt{2}\,\mathrm{SEM} . \]

Questo risultato ha una conseguenza rilevante sul piano interpretativo: l’incertezza associata a un punteggio di cambiamento è maggiore di quella relativa a una singola misurazione. Nel calcolo della differenza tra due punteggi, infatti, l’errore di misura non si annulla, ma si somma, riflettendo l’incertezza presente in entrambe le misurazioni.

18.7.3 Il modello bayesiano per il cambiamento individuale

Il modello probabilistico che mette in relazione la differenza osservata \(D\) con il cambiamento vero \(\Delta\) si basa su una funzione di verosimiglianza di tipo normale: \[ D \mid \Delta \sim \mathcal{N}\!\left(\Delta, \mathrm{SE}_{\mathrm{diff}}^{,2}\right). \] Questa specificazione formalizza l’idea che, a parità di cambiamento vero \(\Delta\), le differenze osservate si distribuiscano normalmente attorno a \(\Delta\), con una dispersione determinata esclusivamente dall’errore di misurazione associato al punteggio di cambiamento.

Il modello viene completato specificando una distribuzione a priori per \(\Delta\). In assenza di informazioni specifiche, assumiamo una distribuzione normale centrata sull’assenza di cambiamento: \[ \Delta \sim \mathcal{N}(0, \sigma_0^2), \] dove \(\sigma_0^2\) rappresenta la varianza a priori. Il centramento della prior sullo zero riflette un’assunzione deliberatamente conservativa: in mancanza di evidenze preliminari, miglioramenti e peggioramenti di piccola entità sono considerati ugualmente plausibili. Il parametro \(\sigma_0\) definisce invece la scala dei cambiamenti ritenuti verosimili a priori.

È importante sottolineare che questa scelta della distribuzione a priori non è neutra, ma intenzionalmente prudente. In contesti applicativi in cui esistono solide ragioni teoriche o empiriche per attendersi un effetto positivo dell’intervento, potrebbe essere appropriato adottare una prior moderatamente spostata verso valori positivi di \(\Delta\). Tuttavia, una prior centrata sullo zero costituisce una scelta metodologicamente produente, in quanto evita di introdurre un’informazione favorevole all’ipotesi di efficacia che non sia giustificata dai dati.

18.7.4 L’inferenza e la sua interpretazione clinica

La combinazione di una distribuzione a priori normale e di una verosimiglianza normale conduce a una distribuzione a posteriori anch’essa normale per il cambiamento vero \(\Delta\), i cui parametri sono dati da: \[ \sigma_{\text{post}}^2 = \left( \frac{1}{\sigma_0^2} + \frac{1}{\mathrm{SE}_{\mathrm{diff}}^2} \right)^{-1}, \qquad \mu_{\text{post}} = \sigma_{\text{post}}^2 \cdot \frac{D}{\mathrm{SE}_{\mathrm{diff}}^2}. \]

Queste espressioni rendono esplicito il meccanismo di regolarizzazione (shrinkage) caratteristico dell’inferenza bayesiana. In termini intuitivi, la media a posteriori \(\mu_{\text{post}}\) può essere interpretata come una media ponderata tra il dato osservato \(D\) e il centro della distribuzione a priori (zero), in cui i pesi sono determinati dalle rispettive precisioni (ovvero dagli inversi delle varianze).

In termini intuitivi:

  • se l’errore di misura è piccolo rispetto alla varianza a priori (\(\mathrm{SE}_{\mathrm{diff}}^2 \ll \sigma_0^2\)), l’informazione empirica è altamente affidabile e la stima a posteriori risulta prossima al valore osservato \(D\);
  • se l’errore di misura è grande rispetto alla varianza a priori (\(\mathrm{SE}_{\mathrm{diff}}^2 \gg \sigma_0^2\)), l’informazione empirica è debole e la stima a posteriori viene fortemente “attratta” verso zero, dando luogo a uno shrinkage marcato.

Questo comportamento è esattamente quello desiderabile in un contesto applicativo: quando i dati sono informativi, il modello li valorizza; quando sono rumorosi, l’inferenza diventa più prudente e si affida maggiormente alle assunzioni a priori.

Un ulteriore vantaggio dell’approccio bayesiano è che la distribuzione a posteriori consente di formulare risposte dirette a quesiti clinicamente rilevanti, sotto forma di probabilità facilmente interpretabili:

  • probabilità di cambiamento trascurabile: \[ P(-\rho < \Delta < \rho \mid D), \] ovvero la massa della distribuzione a posteriori contenuta nell’intervallo di equivalenza pratica, dove \(\rho\) definisce la soglia di irrilevanza clinica;

  • probabilità di miglioramento clinicamente rilevante: \[ P(\Delta < -\tau \mid D), \] corrispondente all’area della coda sinistra oltre la soglia clinica \(\tau > 0\) (assumendo, come nel caso dell’affetto negativo, che valori più bassi indichino un miglioramento);

  • probabilità di peggioramento clinicamente rilevante: \[ P(\Delta > \tau \mid D), \] ovvero l’area della coda destra oltre la soglia \(\tau\).

Queste quantità forniscono un quadro inferenziale ricco e direttamente utilizzabile in ambito clinico, che supera il tradizionale esito dicotomico (“cambiamento affidabile sì/no”) associato al Reliable Change Index (Jacobson & Truax, 1992), restituendo invece una rappresentazione probabilistica del cambiamento individuale.

18.7.5 Implementazione

L’implementazione che segue può essere letta come una generalizzazione bayesiana del Reliable Change Index (RCI) di Jacobson & Truax (1992). Nel RCI classico, un cambiamento viene considerato clinicamente rilevante solo se soddisfa due criteri distinti:

  1. significatività statistica, ossia un cambiamento sufficientemente grande da eccedere l’errore di misurazione;
  2. rilevanza pratica o clinica, ossia il superamento di una soglia che distingua cambiamenti sostanziali da variazioni di entità trascurabile.

Nel modello bayesiano questi due criteri non vengono più valutati tramite regole dicotomiche, ma sono tradotti in termini probabilistici. In particolare:

  • l’errore di misurazione è incorporato nella verosimiglianza attraverso \(\mathrm{SE}_{\mathrm{diff}}\);
  • la trascurabilità pratica è formalizzata mediante una ROPE (Region of Practical Equivalence), centrata su zero;
  • la rilevanza clinica è definita tramite una soglia \(\tau_{\text{clin}}\), espressa in unità di deviazione standard.

Nel codice che segue, utilizziamo a titolo illustrativo:

  • una ROPE di ampiezza ±0.10 SD, coerente con quanto discusso nei capitoli precedenti;
  • una soglia clinica \(\tau_{\text{clin}} = 0.30\) SD, un valore che rappresenta una convenzione metodologica consolidata per indicare un cambiamento di entità moderata. È importante sottolineare che tale soglia non è universale, ma deve essere giustificata in base al costrutto, allo strumento e al contesto clinico.
# ------------------------------------------------------------
# RCI bayesiano (versione semplice, chiusa-forma)
# ------------------------------------------------------------
# Likelihood:  D = post - pre  ~ Normal(Delta, SEdiff^2)
# Prior:       Delta ~ Normal(0, prior_sd_delta^2)
# Posterior:   Delta | D ~ Normal(m_post, s_post^2)
# ------------------------------------------------------------

rci_bayes <- function(pre, post,
                      test_sd, reliability,
                      rope_width = 0.10,   # ROPE ±0.10 SD (coerente con capitolo)
                      tau_clin   = 0.30,   # soglia clinica 0.30 SD (esempio)
                      prior_sd_delta = 0.60) {
  # 1) Differenza osservata
  D <- post - pre
  
  # 2) SEM e SE della differenza
  #    SEM = SD * sqrt(1 - reliability)
  SEM    <- test_sd * sqrt(max(0, 1 - reliability))
  SEdiff <- sqrt(SEM^2 + SEM^2)  # ipotesi: stessa metrica/affidabilità a pre e post
  
  # 3) Prior e posteriori (Normale–Normale)
  s0 <- prior_sd_delta
  s  <- SEdiff
  
  s2_post <- 1 / (1/s0^2 + 1/s^2)
  s_post  <- sqrt(s2_post)
  m_post  <- (s2_post / s^2) * D
  
  # 4) Probabilità di interesse
  p_in_rope   <- pnorm( rope_width, mean = m_post, sd = s_post) -
                 pnorm(-rope_width, mean = m_post, sd = s_post)
  p_gt_tau    <- 1 - pnorm(tau_clin,  mean = m_post, sd = s_post)
  p_lt_neg_tau<- pnorm(-tau_clin,     mean = m_post, sd = s_post)
  
  list(
    observed_diff   = D,
    SEM             = SEM,
    SEdiff          = SEdiff,
    prior_sd_delta  = s0,
    post_mean       = m_post,
    post_sd         = s_post,
    rope            = c(-rope_width, rope_width),
    tau_clin        = tau_clin,
    probs = c(
      P_in_ROPE         = p_in_rope,
      P_diff_gt_tau     = p_gt_tau,
      P_diff_lt_neg_tau = p_lt_neg_tau
    )
  )
}

18.7.6 Esempio numerico

Applichiamo il modello a un soggetto del gruppo sperimentale dello studio sull’intervento di mindfulness. I punteggi, espressi in deviazioni standard rispetto alla media normativa, sono: pre = 0.40, post = 0.05. Ciò corrisponde a una riduzione osservata dell’affetto negativo pari a 0.35 SD.

Assumiamo un’affidabilità del test pari a 0.85, un valore tipico per questionari psicometrici ben costruiti, e utilizziamo la deviazione standard campionaria dell’intero dataset come metrica di riferimento.

# 'df' proviene dalle sezioni precedenti del capitolo (score in SD naturali)
test_sd <- sd(df$score)

res_demo <- rci_bayes(
  pre  = 0.40,
  post = 0.05,
  test_sd     = test_sd,
  reliability = 0.85,
  rope_width  = 0.10,  # ROPE ±0.10 SD (trascurabile)
  tau_clin    = 0.30,  # soglia clinica 0.30 SD (rilevante)
  prior_sd_delta = 0.60
)

cat(sprintf(
  "\nRCI bayesiano (soggetto esempio)\n---------------------------------\nDiff. osservata (post-pre): %.3f\nSEM: %.3f | SE diff: %.3f\nPosterior Delta ~ Normal(%.3f, %.3f^2)\nROPE: [%.2f, %.2f] | tau_clin: ±%.2f\nP(Delta in ROPE)      = %.3f\nP(Delta >  tau_clin)  = %.3f\nP(Delta < -tau_clin)  = %.3f\n",
  res_demo$observed_diff, res_demo$SEM, res_demo$SEdiff,
  res_demo$post_mean, res_demo$post_sd,
  res_demo$rope[1], res_demo$rope[2], res_demo$tau_clin,
  res_demo$probs["P_in_ROPE"], res_demo$probs["P_diff_gt_tau"], res_demo$probs["P_diff_lt_neg_tau"]
))
#> 
#> RCI bayesiano (soggetto esempio)
#> ---------------------------------
#> Diff. osservata (post-pre): -0.350
#> SEM: 0.384 | SE diff: 0.543
#> Posterior Delta ~ Normal(-0.192, 0.403^2)
#> ROPE: [-0.10, 0.10] | tau_clin: ±0.30
#> P(Delta in ROPE)      = 0.175
#> P(Delta >  tau_clin)  = 0.111
#> P(Delta < -tau_clin)  = 0.395

18.7.7 Interpretazione dei risultati

I risultati dell’analisi bayesiana delineano un profilo di cambiamento probabilistico che supera la logica dicotomica tipica dell’RCI tradizionale. Analizziamo i principali elementi.

Il soggetto mostra una riduzione osservata dell’affetto negativo pari a \[ D = -0.350 \text{ SD}. \] Tenendo conto dell’errore di misurazione e dell’informazione a priori, la stima bayesiana del cambiamento vero risulta pari a \[ \mu_{\text{post}} = -0.192 \text{ SD}. \] La differenza tra \(D\) e \(\mu_{\text{post}}\) riflette l’effetto di regolarizzazione (shrinkage): il cambiamento osservato viene ridimensionato verso lo zero, poiché parte di esso potrebbe essere attribuibile all’errore di misurazione.

La deviazione standard a posteriori (\(\sigma_{\text{post}} = 0.301\)) quantifica l’incertezza residua sul vero valore di \(\Delta\). Da essa si può ricavare un intervallo di credibilità al 95% approssimativamente pari a \[ [-0.78,\; +0.40]. \] L’intervallo include lo zero, ma è chiaramente sbilanciato verso valori negativi, coerenti con un miglioramento.

Le probabilità derivate dalla distribuzione a posteriori permettono una lettura clinicamente informata:

  • \(P(\text{cambiamento trascurabile})\) = 0.175. La probabilità che il vero cambiamento rientri in una regione di irrilevanza pratica è relativamente bassa.

  • \(P(\text{peggioramento clinicamente rilevante})\) = 0.111. La probabilità di un peggioramento sostanziale è contenuta.

  • \(P(\text{miglioramento clinicamente rilevante})\) = 0.395. Questa è la probabilità più elevata tra quelle considerate, suggerendo che l’ipotesi di un miglioramento clinicamente rilevante è quella maggiormente supportata dai dati.

Si noti che la somma di queste probabilità non è 1, poiché esiste uno spazio di esiti intermedi (ad esempio, cambiamenti piccoli ma clinicamente ambigui) che non vengono catturati né dalla definizione di ROPE né dal superamento della soglia clinica.

18.7.8 Confronto concettuale con l’RCI classico

L’RCI tradizionale produce un giudizio binario, classificando il cambiamento come semplicemente “affidabile e clinicamente significativo” oppure no. L’approccio bayesiano qui proposto non sostituisce i due criteri fondamentali, ma li trasforma da constatazioni categoriche in stime probabilistiche informate dai dati:

  • Affidabilità del cambiamento: non più un “sì/no” sull’attraversamento di una soglia di errore, ma una probabilità che la variazione osservata superi l’incertezza di misurazione.

  • Rilevanza clinica: non più un giudizio basato su una soglia fissa, ma una probabilità che il cambiamento ecceda una soglia clinicamente sostanziale.

Mentre l’RCI classico confronta un singolo punteggio di differenza con un intervallo di errore statico, il metodo bayesiano quantifica l’incertezza posteriore attorno alla stima del cambiamento vero, confrontandola direttamente con le regioni di interesse (ROPE e soglia clinica).

Cosa comunicare al clinico? Una possibile sintesi è la seguente:

Il paziente mostra segnali coerenti con un miglioramento dell’affetto negativo. La probabilità che tale miglioramento sia clinicamente rilevante è di circa il 40%, mentre la probabilità di un peggioramento rilevante è inferiore al 12%. Sebbene non si possa escludere un contributo dell’errore di misurazione, l’evidenza complessiva è più compatibile con un effetto benefico dell’intervento che con un effetto nullo o negativo.

Questa formulazione restituisce l’incertezza in modo esplicito, senza rinunciare alla rilevanza decisionale, e rappresenta uno dei principali vantaggi dell’approccio bayesiano al cambiamento individuale.

18.7.9 Considerazioni metodologiche

La versione del modello presentata in questo capitolo è intenzionalmente minimale e risponde a finalità eminentemente didattiche. In contesti di ricerca o di pratica clinica più avanzati, sono possibili, e spesso auspicabili, diverse estensioni che ne aumentano il realismo e la flessibilità inferenziale.

Incertezza sull’affidabilità. Nel modello illustrato, l’affidabilità del test (\(r = 0.85\)) è considerata un valore noto e privo di incertezza. In realtà, l’affidabilità è essa stessa una stima campionaria e, in quanto tale, soggetta a variabilità. Un’estensione naturale consiste nel modellare \(r\) come un parametro aleatorio dotato di una propria distribuzione a priori, consentendo di propagare l’incertezza sull’affidabilità attraverso l’intero processo inferenziale.

Robustezza agli outlier. L’assunzione di normalità degli errori di misura può risultare inadeguata in presenza di osservazioni anomale o di distribuzioni a code pesanti. In tali situazioni, la sostituzione della distribuzione normale con una distribuzione \(t\) di Student nella funzione di verosimiglianza consente di ottenere inferenze più robuste, riducendo l’influenza indebita degli outlier sulle stime del cambiamento.

Distribuzioni a priori informative. La distribuzione a priori \(\mathcal{N}(0, 0.6^2)\) utilizzata negli esempi precedenti è volutamente debole e conservativa. In contesti applicativi in cui siano disponibili evidenze cumulative — ad esempio meta-analisi sugli effetti medi di un determinato intervento — è possibile specificare prior più informative, in grado di incorporare in modo esplicito la conoscenza pregressa e migliorare l’efficienza inferenziale.

Estensione gerarchica. Il limite principale dell’approccio presentato è che ciascun individuo viene analizzato in modo indipendente dagli altri. Come anticipato, i modelli multilivello (o gerarchici) permettono di analizzare simultaneamente tutti gli individui, assumendo che i cambiamenti individuali derivino da una distribuzione comune stimata dai dati. Questo meccanismo di pooling parziale produce stime individuali più stabili e meno rumorose, preservando al contempo la stima dell’effetto medio di gruppo.

Questa estensione rappresenta il collegamento naturale tra l’analisi di gruppo discussa nella prima parte del capitolo e l’analisi idiografica sviluppata in questa sezione. Nei modelli multilivello, i livelli nomotetico e idiografico non sono più considerati come alternativi o separati, ma sono integrati all’interno di un unico framework inferenziale coerente. L’approfondimento di questi modelli sarà oggetto dei capitoli successivi.

Riflessioni conclusive

L’analisi sviluppata in questo capitolo mette in luce i principali punti di forza dell’approccio bayesiano applicato al confronto tra gruppi e, più in generale, alla valutazione del cambiamento psicologico. La quantità centrale dell’inferenza non è più un singolo indice riassuntivo né un valore-\(p\), bensì l’intera distribuzione a posteriori delle differenze di interesse. È questa distribuzione a costituire l’oggetto sostantivo dell’interpretazione: nel nostro esempio, essa descrive non solo di quanto il gruppo sottoposto all’intervento di mindfulness differisca in media dal gruppo di controllo, ma anche con quale grado di incertezza ciascun valore della differenza sia plausibile. In questo modo, l’inferenza si libera dal verdetto dicotomico “c’è/non c’è una differenza” per assumere la forma di un ragionamento continuo basato su gradazioni di plausibilità.

Un ulteriore vantaggio dell’approccio bayesiano riguarda la possibilità di valutare direttamente la rilevanza pratica degli effetti stimati. L’introduzione di una Region Of Practical Equivalence (ROPE) permette di distinguere tra differenze che, pur essendo statisticamente distinguibili da zero, sono trascurabili dal punto di vista psicologico, e differenze che invece raggiungono un’entità potenzialmente rilevante per la pratica clinica. Questo approccio permette di rispondere a domande sostanziali, quali: “Qual è la probabilità che l’effetto osservato sia, non soltanto diverso da zero, ma anche sufficientemente grande da essere clinicamente rilevante?”.

Il confronto tra modelli con varianza comune e modelli con varianze distinte ha inoltre messo in evidenza che le assunzioni statistiche devono essere valutate in termini predittivi, piuttosto che essere accettate o rifiutate in modo automatico. Attraverso il criterio ELPD stimato con PSIS-LOO, abbiamo verificato se la maggiore complessità del modello con varianze distinte si traducesse effettivamente in una migliore capacità di predire dati simili a quelli osservati. Quando il guadagno predittivo risulta marginale, il principio di parsimonia suggerisce di preferire il modello più semplice; quando invece il miglioramento è sostanziale, la complessità aggiuntiva risulta giustificata. Questo modo di procedere è più trasparente e metodologicamente coerente rispetto a molte alternative frequentiste, in cui le decisioni modellistiche sono spesso delegate a test di difficile interpretazione sostanziale per le domande della ricerca.

Il passaggio all’analisi idiografica ha consentito di estendere il ragionamento bayesiano dal livello di gruppo a quello individuale. È emerso come l’effetto medio, pur informativo, possa mascherare una notevole eterogeneità nelle risposte individuali e come la fallacia ecologica rappresenti un rischio concreto quando si traggono conclusioni cliniche a partire da statistiche aggregate. L’analisi bayesiana del cambiamento individuale, anche nella sua formulazione semplificata, fornisce un quadro concettuale e operativo per quantificare la probabilità che un singolo paziente abbia effettivamente tratto beneficio dall’intervento, distinguendo tra cambiamenti trascurabili, clinicamente rilevanti e compatibili con il solo errore di misurazione.

Le difficoltà tipiche dell’analisi idiografica, quali la scarsità di dati a livello individuale, l’elevata incertezza e la necessità di conclusioni non dicotomiche, non rappresentano dei limiti per l’approccio bayesiano, ma piuttosto una rappresentazione onesta della complessità del fenomeno studiato. L’inferenza bayesiana non elimina queste difficoltà, ma le rende esplicite e gestibili mediante un linguaggio probabilistico. Il percorso verso stime individuali più precise passa naturalmente attraverso i modelli multilivello, che consentono di integrare in modo coerente l’informazione proveniente dal livello di gruppo e da quello individuale.

In sintesi, l’approccio bayesiano invita a ripensare il significato stesso dell’inferenza statistica: non come un meccanismo per accettare o rifiutare un’ipotesi nulla, ma come uno strumento per descrivere la plausibilità di diversi scenari e collegarli al significato psicologico dei dati. Questo vale tanto per le differenze tra gruppi quanto per i cambiamenti nei singoli individui. In tal senso, l’approccio bayesiano allinea la statistica alle domande rilevanti per la psicologia, senza limitarsi a stabilire se un effetto esista, ma esplorando la sua entità, quantificando l’incertezza, valutandone la rilevanza clinica e stimandone la probabilità di beneficio per il singolo paziente. È in questa capacità di produrre inferenze interpretabili dal punto di vista sostanziale che risiede il principale valore aggiunto dell’approccio bayesiano.

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.1
#> 
#> Matrix products: default
#> BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] forcats_1.0.1         cmdstanr_0.8.0        ragg_1.5.0           
#>  [4] tinytable_0.15.1      withr_3.0.2           systemfonts_1.3.1    
#>  [7] patchwork_1.3.2       ggdist_3.3.3          tidybayes_3.0.7      
#> [10] bayesplot_1.14.0      ggplot2_4.0.1         reliabilitydiag_0.2.1
#> [13] priorsense_1.2.0      posterior_1.6.1       loo_2.8.0            
#> [16] rstan_2.32.7          StanHeaders_2.32.10   brms_2.23.0          
#> [19] Rcpp_1.1.0            sessioninfo_1.2.3     conflicted_1.2.0     
#> [22] janitor_2.2.1         matrixStats_1.5.0     modelr_0.1.11        
#> [25] tibble_3.3.0          dplyr_1.1.4           tidyr_1.3.1          
#> [28] rio_1.2.4             here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-29      
#>  [7] snakecase_0.11.1      compiler_4.5.2        reshape2_1.4.5       
#> [10] vctrs_0.6.5           stringr_1.6.0         pkgconfig_2.0.3      
#> [13] arrayhelpers_1.1-0    fastmap_1.2.0         backports_1.5.0      
#> [16] labeling_0.4.3        utf8_1.2.6            rmarkdown_2.30       
#> [19] ps_1.9.1              purrr_1.2.0           xfun_0.54            
#> [22] cachem_1.1.0          jsonlite_2.0.0        broom_1.0.11         
#> [25] parallel_4.5.2        R6_2.6.1              stringi_1.8.7        
#> [28] RColorBrewer_1.1-3    lubridate_1.9.4       estimability_1.5.1   
#> [31] knitr_1.50            zoo_1.8-14            pacman_0.5.1         
#> [34] Matrix_1.7-4          splines_4.5.2         timechange_0.3.0     
#> [37] tidyselect_1.2.1      abind_1.4-8           yaml_2.3.12          
#> [40] codetools_0.2-20      processx_3.8.6        curl_7.0.0           
#> [43] pkgbuild_1.4.8        plyr_1.8.9            lattice_0.22-7       
#> [46] bridgesampling_1.2-1  S7_0.2.1              coda_0.19-4.1        
#> [49] evaluate_1.0.5        survival_3.8-3        RcppParallel_5.1.11-1
#> [52] pillar_1.11.1         tensorA_0.36.2.1      checkmate_2.3.3      
#> [55] stats4_4.5.2          distributional_0.5.0  generics_0.1.4       
#> [58] rprojroot_2.1.1       rstantools_2.5.0      scales_1.4.0         
#> [61] xtable_1.8-4          glue_1.8.0            emmeans_2.0.0        
#> [64] tools_4.5.2           data.table_1.17.8     mvtnorm_1.3-3        
#> [67] grid_4.5.2            QuickJSR_1.8.1        colorspace_2.1-2     
#> [70] nlme_3.1-168          cli_3.6.5             textshaping_1.0.4    
#> [73] svUnit_1.0.8          Brobdingnag_1.2-9     V8_8.0.1             
#> [76] gtable_0.3.6          digest_0.6.39         TH.data_1.1-5        
#> [79] htmlwidgets_1.6.4     farver_2.1.2          memoise_2.0.1        
#> [82] htmltools_0.5.9       lifecycle_1.0.4       MASS_7.3-65

Bibliografia

Jacobson, N. S., & Truax, P. (1992). Clinical Significance: A Statistical Approach to Defining Meaningful Change in Psychotherapy Research. In A. E. Kazdin (A c. Di), Methodological Issues & Strategies in Clinical Research (pp. 631–648). American Psychological Association. https://doi.org/10.1037/10109-042
Lord, F. M., & Novick, M. R. (2008). Statistical theories of mental test scores. IAP.

  1. I concetti di “nomotetico” e “idiografico” furono introdotti dal filosofo neokantiano Wilhelm Windelband per distinguere due orientamenti fondamentali della conoscenza scientifica. Secondo Windelband, l’attività scientifica può legittimamente avvalersi di entrambi gli approcci, in quanto rappresentano prospettive complementari sull’oggetto di studio. L’approccio nomotetico, riconducibile a quella che Kant descriveva come una tendenza alla generalizzazione, è tipico delle scienze naturali e mira alla formulazione di leggi generali capaci di spiegare classi di fenomeni in termini universali. L’approccio idiografico, invece, si fonda sulla tendenza kantiana alla specificazione ed è caratteristico delle scienze umane: esso è orientato alla comprensione di eventi singolari, contingenti e irripetibili, spesso connessi a dimensioni storiche, culturali o soggettive.↩︎