5 Controllo predittivo a priori
Introduzione
Questo materiale costituisce un approfondimento del capitolo 18 del manuale didattico, focalizzandosi sulle procedure per la validazione delle assunzioni a priori.
L’inferenza bayesiana integra sistematicamente due fonti di informazione: le conoscenze preliminari (formalizzate attraverso distribuzioni a priori) e l’evidenza empirica (rappresentata dalla funzione di verosimiglianza). Questo bilanciamento tra assunzioni iniziali e dati osservati costituisce il fondamento epistemologico del ragionamento statistico bayesiano. Ma sorge una questione metodologica fondamentale: come possiamo valutare l’adeguatezza delle distribuzioni a priori prima di osservare i dati?
A questo interrogativo rispondono le verifiche predittive a priori [prior predictive checks; Gelman et al. (2020)]. Il principio è tanto potente quanto intuitivo: se i prior codificano le nostre credenze preliminari, possiamo utilizzarli per generare dati simulati e verificare se questi risultati siano plausibili. Quando le simulazioni producono sistematicamente valori impossibili, ordini di grandezza irrealistici o pattern inverosimili, abbiamo un chiaro segnale che qualcosa non funziona nella specifica iniziale del modello.
- Comprendere il quadro teorico della verifica predittiva a priori.
- Capire perché è essenziale per una modellazione statisticamente coerente.
- Imparare ad applicarla in pratica attraverso esempi concreti.
5.1 La distribuzione predittiva a priori: definizione e importanza
5.1.1 Significato intuitivo
La distribuzione predittiva a priori rappresenta l’insieme delle previsioni generate dal modello prima che vengano osservati i dati reali. In altre parole, essa formalizza quali dati ci si aspetta di osservare sulla base delle sole assunzioni iniziali, tenendo conto dell’incertezza sui parametri.
Questa distribuzione è cruciale perché:
- identifica previsioni irrealistiche o impossibili;
- verifica la coerenza tra credenze iniziali e conoscenza del dominio;
- identifica previsioni irrealistiche o impossibili;
- esplicita le conseguenze empiriche delle scelte di modellazione.
Prima di raccogliere dati reali, la distribuzione predittiva a priori ti dice: “Ecco il tipo di dati che il tuo modello considera plausibili”. Se quei dati simulati non hanno senso, il problema è nel modello, non nei dati (che non hai ancora visto)!
5.1.2 Definizione formale
Matematicamente, la distribuzione predittiva a priori si ottiene integrando la verosimiglianza dei dati futuri rispetto alla distribuzione a priori dei parametri:
\[ p(\tilde{y}) = \int p(\tilde{y} \mid \theta) \, p(\theta) \, d\theta, \tag{5.1}\] dove:
- \(\tilde{y}\) rappresenta un’osservazione futura (o un insieme di osservazioni) non ancora rilevata;
- \(\theta\) è il vettore dei parametri del modello;
- \(p(\theta)\) è la distribuzione a priori che esprime l’incertezza iniziale su \(\theta\);
- \(p(\tilde{y} \mid \theta)\) è la verosimiglianza che specifica come i dati dipendono dai parametri.
Cosa fa questa formula? Calcola una media ponderata: per ogni possibile valore dei parametri \(\theta\), genera una previsione per \(\tilde{y}\); poi combina tutte queste previsioni pesandole con la loro plausibilità a priori \(p(\theta)\).
Il risultato cattura due fonti di incertezza:
- la variabilità intrinseca del processo che genera i dati;
- l’incertezza epistemica sui valori veri dei parametri.
5.1.3 Intuizione con un esperimento mentale
Per comprendere l’Equazione 5.1, è utile pensare alla distribuzione predittiva a priori come una media ponderata di distribuzioni predittive, dove i pesi provengono dalle nostre credenze iniziali.
Esempio concreto: il modello beta-binomiale.
Immaginiamo di voler prevedere quanti studenti risponderanno correttamente a un test di 10 domande. Il parametro \(\theta\) rappresenta la probabilità di risposta corretta. Procediamo così:
Consideriamo vari valori plausibili di \(\theta\): ad esempio, 0, 0.1, 0.2, …, 0.9, 1.0.
-
Per ciascun valore \(\theta_j\), generiamo una previsione: \[ p(\tilde y \mid \theta_j) = \binom{10}{\tilde y} (\theta_j)^{\tilde y} (1 - \theta_j)^{10 - \tilde y}. \]
Questa è la distribuzione binomiale che dice: “Se la vera probabilità fosse \(\theta_j\), ecco quanti successi mi aspetterei”.
-
Pesiamo ogni previsione in base a quanto è plausibile \(\theta_j\) secondo il nostro prior \(p(\theta_j)\):
- se il prior concentra massa su \(\theta \approx 0.7\) → le previsioni con \(\theta \approx 0.7\) peseranno molto;
- se il prior assegna probabilità quasi zero a \(\theta \approx 0.1\) → quelle previsioni contribuiranno poco.
Combiniamo tutto sommando le probabilità pesate per ogni possibile esito \(\tilde y = k\).
La distribuzione predittiva a priori NON è una singola previsione per un valore fisso di \(\theta\). È una media di tutte le possibili previsioni, pesata dalle nostre credenze iniziali su \(\theta\).
5.1.4 Confronto: prior vs posterior
La struttura matematica è identica per le distribuzioni predittive a priori e a posteriori. I pesi, però, cambiano radicalmente.
| Distribuzione | Pesi utilizzati | Cosa riflette |
|---|---|---|
| Predittiva a priori | \(p(\theta)\) | Solo credenze iniziali |
| Predittiva a posteriori | \(p(\theta \mid y)\) | Credenze aggiornate dai dati |
Conseguenze pratiche:
- Prior vago → distribuzione predittiva a priori dispersa, con code pesanti.
- Prior informativo → distribuzione predittiva a priori concentrata sugli esiti coerenti con la nostra conoscenza preliminare.
Confrontiamo due specificazioni a priori per \(p \sim \text{Beta}(\alpha, \beta)\):
Scenario 1: Prior poco informativo \(\text{Beta}(2,2)\)
- \(\mathbb{E}[p] = 0.5\), ma con molta incertezza.
- Distribuzione predittiva a priori: massa distribuita su tutti i possibili risultati da 0 a 10.
- I risultati estremi (0/10 o 10/10) hanno probabilità non trascurabile.
Scenario 2: Prior informativo \(\text{Beta}(10,3)\)
- \(\mathbb{E}[p] \approx 0.77\), con varianza ridotta.
- Distribuzione predittiva a priori: massa concentrata su 6-9 successi.
- I risultati estremi diventano estremamente improbabili.
5.1.5 Perché è cruciale per la modellazione
La distribuzione predittiva a priori è il primo e più importante controllo di coerenza di un modello bayesiano.
Verifica compatibilità con il dominio: rende espliciti i dati che il modello considera plausibili prima dell’osservazione, rivelando eventuali incongruenze tra i priors formali e la conoscenza sostanziale.
Previene errori grossolani: un prior che assegna una massa significativa a parametri impossibili (ad esempio, probabilità negative o varianze infinite) produrrà predizioni irrealistiche.
Facilita la comunicazione: trasforma assunzioni astratte in previsioni concrete e verificabili.
Migliora la specificazione: permette di apportare aggiustamenti iterativi al modello prima di impegnare tempo nell’analisi.
Non confondere “prior non informativo” con “prior ragionevole”. Un prior uniforme su \((-\infty, +\infty)\) può sembrare “neutrale”, ma spesso porta a previsioni assurde. La verifica predittiva a priori lo rivelerebbe immediatamente.
5.2 Il processo di verifica predittiva a priori
5.2.1 Workflow generale
Il processo di prior predictive check segue questi passaggi:
- specificare le distribuzioni a priori dei parametri;
- simulare campioni dal prior \(\theta^{(s)} \sim p(\theta)\) per \(s = 1, \ldots, S\);
- generare dati predetti: per ogni \(\theta^{(s)}\), campionare \(\tilde{y}^{(s)} \sim p(y \mid \theta^{(s)})\);
- valutare la plausibilità dell’insieme \(\{\tilde{y}^{(s)}\}\) rispetto alla conoscenza del dominio;
- iterare se necessario, rivedere i prior e ripetere il processo.
Non stiamo cercando il prior “perfetto” che predica esattamente i dati reali (che non abbiamo ancora visto!). Stiamo solo verificando che il modello non produca previsioni assurde.
5.2.2 Criteri di valutazione
Quando esaminiamo i dati simulati, ci poniamo le seguenti domande.
Supporto dei dati:
- I valori simulati rispettano i vincoli del problema?
- Ci sono valori impossibili, come conteggi negativi o proporzioni superiori a 1?
Ordini di grandezza:
- Gli ordini di grandezza sono coerenti con le aspettative basate sulla conoscenza del dominio?
- I valori rientrano nell’intervallo atteso, basato sulla conoscenza del dominio?
- Per esempio, nel caso dei tempi di reazione, simulare 0.001 secondi o 1000 secondi indica un problema.
Pattern di variabilità:
- La dispersione simulata è realistica?
- Un prior troppo vago può generare una variabilità implausibilmente alta.
Concentrazione della massa:
- Dove si concentra la maggior parte delle simulazioni?
- Esempio: nel contesto dell’efficacia di un intervento psicologico, simulare tassi di miglioramento del 10-20% quando la letteratura consolidata riporta effetti nell’ordine del 60-70% rivela un’incoerenza sostanziale tra le aspettative formalizzate nel prior e l’evidenza empirica disponibile.
Se mostrassi i dati simulati a un collega esperto del settore (senza dirgli che si tratta di dati simulati), li troverebbe plausibili? Se la risposta è “assolutamente no”, i prior necessitano di una revisione.
5.2.3 Quando rivedere i prior
Segnali di allarme che richiedono revisione.
- Violazioni dei vincoli fisici: simulazioni che producono valori impossibili.
- Estremi irrealistici: >5-10% delle simulazioni in regioni note per essere estremamente rare.
- Disallineamento con la letteratura: predizioni sistematicamente lontane da quanto riportato in studi precedenti.
- Incertezza eccessiva: simulazioni che coprono l’intero spazio parametrico senza concentrazione.
Come rivedere:
- aggiungere vincoli se il modello permette valori impossibili;
- stringere i prior se troppo vaghi (ma senza sovraspecificare);
- aggiungere vincoli se il modello permette valori impossibili;
- incorporare informazioni dalla letteratura;
- utilizzare prior gerarchici, se appropriato.
Rivedere i prior basandosi su simulazioni a priori è legittimo e raccomandato. Rivederli dopo aver visto i dati reali per “migliorare il fit” è metodologicamente scorretto (P-hacking bayesiano).
5.3 Simulazione predittiva a priori in R
5.3.1 Approccio manuale con il modello beta-binomiale
Consideriamo un esempio concreto: un test di 10 domande somministrato a degli studenti. Vogliamo modellare il numero di risposte corrette.
Modello:
- \(y_i \sim \text{Binomial}(10, p)\) per studente \(i\);
- \(p \sim \text{Beta}(\alpha, \beta)\).
Scenario di ricerca: sappiamo da studi precedenti che gli studenti tendono a rispondere correttamente al 70-80% delle domande. Usiamo la distribuzione \(\text{Beta}(10, 3)\) che ha una media approssimativamente pari a 0.77.
set.seed(42)
n_sim <- 10000 # numero di simulazioni
n_items <- 10 # domande nel test
alpha_prior <- 10 # parametri Beta
beta_prior <- 3
# Passo 1: simula parametri dal prior
p_sim <- rbeta(n_sim, alpha_prior, beta_prior)
# Passo 2: per ogni p simulato, genera dati
y_sim <- rbinom(n_sim, size = n_items, prob = p_sim)
# Visualizza la distribuzione predittiva a priori
tibble(y_sim = y_sim) |>
ggplot(aes(x = y_sim)) +
geom_histogram(
aes(y = after_stat(density)),
bins = 11,
fill = modern_palette$blue,
color = modern_palette$white,
alpha = 0.8
) +
scale_x_continuous(breaks = 0:10) +
labs(
x = "Numero di risposte corrette (su 10)",
y = "Densità",
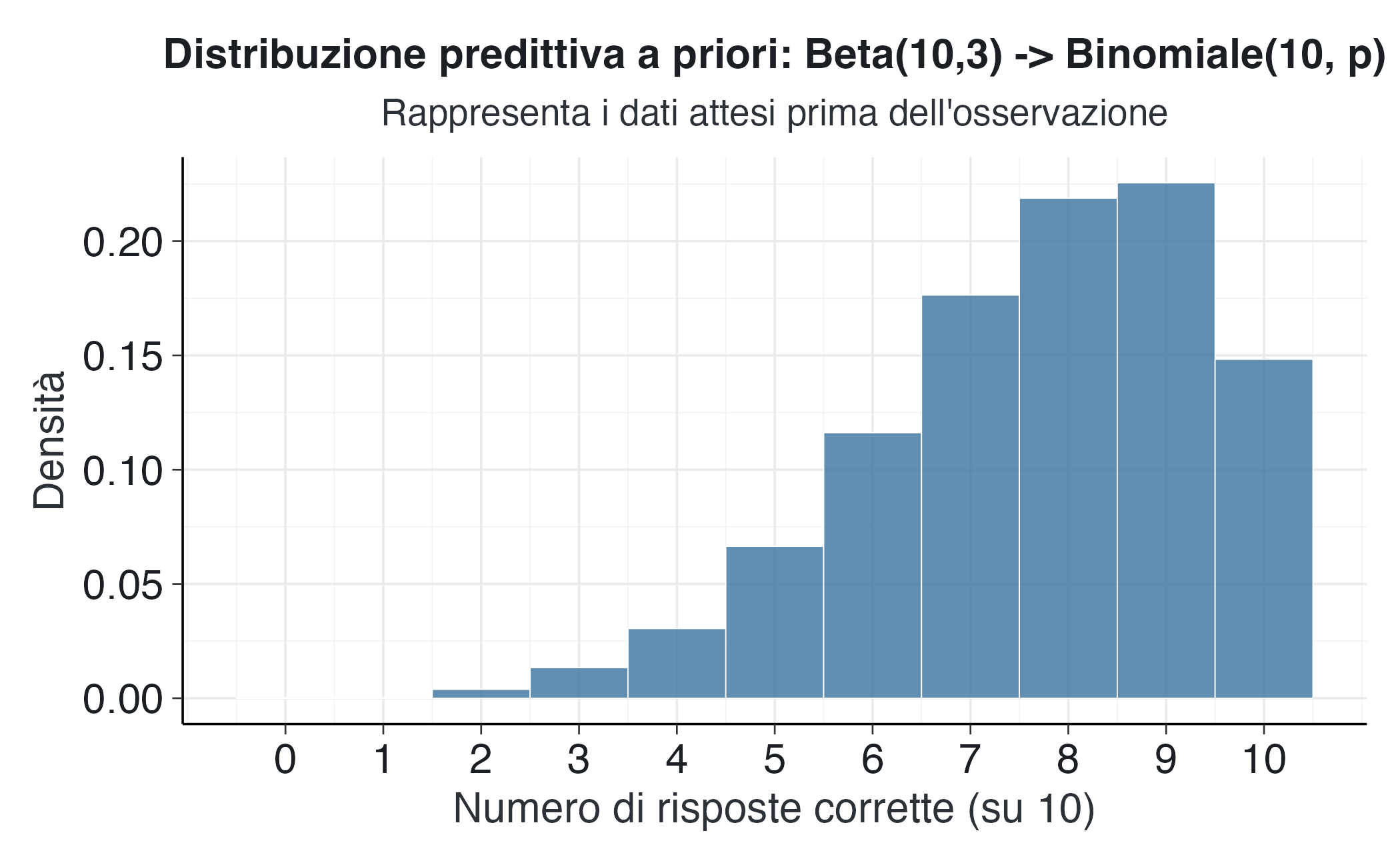
title = "Distribuzione predittiva a priori: Beta(10,3) -> Binomiale(10, p)",
subtitle = "Rappresenta i dati attesi prima dell'osservazione"
)Interpretazione:
- la maggior parte delle simulazioni prevede tra 6 e 9 risposte corrette;
- questo è coerente con l’aspettativa di accuratezza ~70-80%;
- valori estremi (0-2 o 10) sono rari, come ci si aspetterebbe.
Prova a cambiare i parametri a \(\text{Beta}(2, 2)\) (prior uniforme). Cosa succede alla distribuzione predittiva? È ancora plausibile per il nostro scenario?
5.3.2 Confronto tra specificazioni alternative
Confrontiamo tre scelte di prior per comprendere l’impatto sulla predittiva.
# Simulazioni per tre prior differenti
simulate_prior_predictive <- function(alpha, beta, n_sim = 10000, n_items = 10) {
p_sim <- rbeta(n_sim, alpha, beta)
y_sim <- rbinom(n_sim, size = n_items, prob = p_sim)
return(y_sim)
}
# Prior 1: Molto vago - Beta(1,1) = Uniforme(0,1)
y_vague <- simulate_prior_predictive(1, 1)
# Prior 2: Debolmente informativo - Beta(2,2)
y_weak <- simulate_prior_predictive(2, 2)
# Prior 3: Informativo - Beta(10,3)
y_informative <- simulate_prior_predictive(10, 3)
# Combina per visualizzazione
prior_comparison <- tibble(
y = c(y_vague, y_weak, y_informative),
prior = rep(
c("Beta(1,1):\nUniforme", "Beta(2,2):\nDebole", "Beta(10,3):\nInformativo"),
each = 10000
)
)
prior_comparison |>
ggplot(aes(x = y, fill = prior)) +
geom_histogram(
aes(y = after_stat(density)),
bins = 11,
position = "identity",
alpha = 0.6
) +
facet_wrap(~prior, nrow = 1) +
scale_x_continuous(breaks = 0:10) +
labs(
x = "Numero di risposte corrette",
y = "Densità",
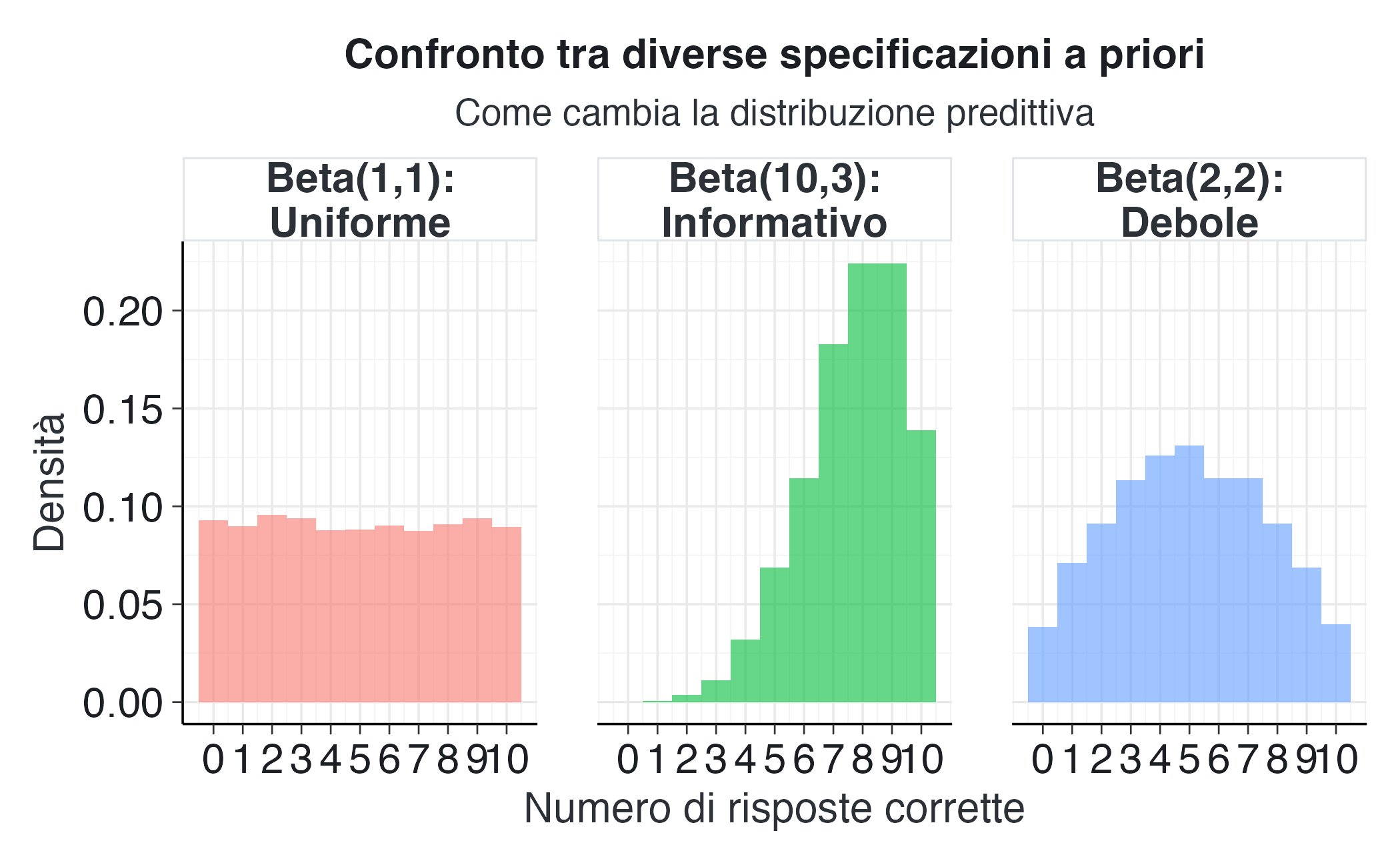
title = "Confronto tra diverse specificazioni a priori",
subtitle = "Come cambia la distribuzione predittiva"
) +
theme(legend.position = "none") Osservazioni:
- Beta(1,1) - Uniforme:
- ogni valore compreso tra 0 e 10 è quasi equiprobabile;
- implica che non sappiamo letteralmente nulla;
- è troppo vago se abbiamo conoscenze sul dominio.
- Beta(2,2) - Debole:
- leggera preferenza per i valori centrali (4-6);
- è ancora abbastanza disperso;
- ragionevole se abbiamo poche informazioni preliminari.
- Beta(10,3) - Informativo:
- forte concentrazione su 6-9 risposte corrette;
- coerente con un’aspettativa di accuratezza del 70-80%;
- appropriato quando abbiamo una conoscenza robusta.
Non esiste una scelta “migliore” in assoluto. La scelta dipende dalla conoscenza disponibile:
- Poche informazioni: prior più vago (ma non completamente piatto).
- Letteratura consolidata: prior informativo.
- Incertezza su aspetti specifici: prior gerarchico (argomento avanzato).
5.3.3 Verifica formale della plausibilità
Possiamo quantificare alcune proprietà delle simulazioni.
# Calcola statistiche descrittive per il prior informativo
summary_stats <- tibble(y = y_informative) |>
summarise(
media = mean(y),
mediana = median(y),
dev_std = sd(y),
q05 = quantile(y, 0.05),
q95 = quantile(y, 0.95),
prob_estremi = mean(y <= 2 | y >= 10)
)
summary_stats |>
knitr::kable(
digits = 2,
caption = "Statistiche della distribuzione predittiva: Beta(10,3)"
)| media | mediana | dev_std | q05 | q95 | prob_estremi |
|---|---|---|---|---|---|
| 7.68 | 8 | 1.7 | 5 | 10 | 0.14 |
Checklist di validazione:
✓ Media ~7.7: coerente con l’aspettativa teorica (\(\mathbb{E}[p] \times 10 \approx 0.77 \times 10\)).
✓ Intervallo credibile 90% (Q05-Q95): dovrebbe coprire il range realistico.
✓ Probabilità di estremi (<3 o >9): dovrebbe essere bassa se non ci si aspetta valori estremi.
5.4 Implementazione in Stan
Per analisi più complesse, Stan fornisce un framework robusto per le verifiche predittive.
5.4.1 Modello Stan completo
binom_prior_ppc_stan <- '
data {
int<lower=1> N; // numero di unità di osservazione (studenti)
int<lower=1> n_items; // numero di item per studente
}
parameters {
real<lower=0, upper=1> p; // probabilità di successo globale
}
model {
p ~ beta(10, 3); // distribuzione a priori esatta
// Nessuna verosimiglianza: campionamento esclusivamente dalle distribuzioni a priori
}
generated quantities {
array[N] int y_rep; // dati replicati
for (i in 1:N) {
y_rep[i] = binomial_rng(n_items, p);
}
}
'Struttura del modello:
-
Blocco
data: dichiara le dimensioni del problema (numero studenti, domande). -
Blocco
parameters: definisce \(p\) con supporto \([0,1]\). -
Blocco
model: specifica il prior \(p \sim \text{Beta}(10,3)\). -
Blocco
generated quantities: simula dati dalla distribuzione predittiva.
Vantaggi di Stan:
- Sampling efficiente anche per prior complessi.
- Facile incorporare gerarchie e correlazioni.
- Controllo automatico di diagnostiche di convergenza.
5.4.2 Compilazione ed esecuzione
mod <- cmdstan_model(
write_stan_file(binom_prior_ppc_stan),
compile = TRUE
)n_studenti <- 50
n_item <- 10
fit_beta <- mod$sample(
data = list(N = n_studenti, n_items = n_item),
chains = 4, iter_warmup = 500, iter_sampling = 1000,
seed = 123, refresh = 0
)Processo di simulazione in tre fasi:
Campionamento dai prior: il campionatore estrae valori del parametro \(p\) dalla distribuzione a priori specificata \(\text{Beta}(10, 3)\), generando così l’insieme dei valori plausibili del parametro prima di osservare i dati.
Propagazione probabilistica: per ogni valore campionato \(p^{(s)}\), il modello propaga l’incertezza attraverso la distribuzione predittiva \(\text{Binomial}(n = 10, p = p^{(s)})\), che formalizza il meccanismo di generazione dei dati.
Generazione di dati replicati: ogni campione \(y_{\text{rep}}^{(s)}\) rappresenta un possibile insieme di dati che il modello considera plausibile sotto le attuali assunzioni a priori, permettendo così una valutazione empirica della loro ragionevolezza.
Questa sequenza opera esclusivamente a livello delle distribuzioni a priori, senza essere influenzata dai dati osservati, e costituisce quindi una verifica puramente pre-osservativa del modello specificato.
5.4.3 Visualizzazione dei risultati
# Estrai e visualizza le simulazioni
draws_mat <- fit_beta$draws("y_rep", format = "draws_matrix")
y_rep_vec <- as.vector(as.matrix(draws_mat))
tibble(y = y_rep_vec) |>
ggplot(aes(x = y)) +
geom_histogram(
aes(y = after_stat(density)),
bins = 11,
fill = modern_palette$grey5,
color = modern_palette$white,
linewidth = 0.2,
alpha = 0.85
) +
scale_x_continuous(breaks = 0:10) +
labs(
x = "Numero di risposte corrette su 10",
y = "Densità",
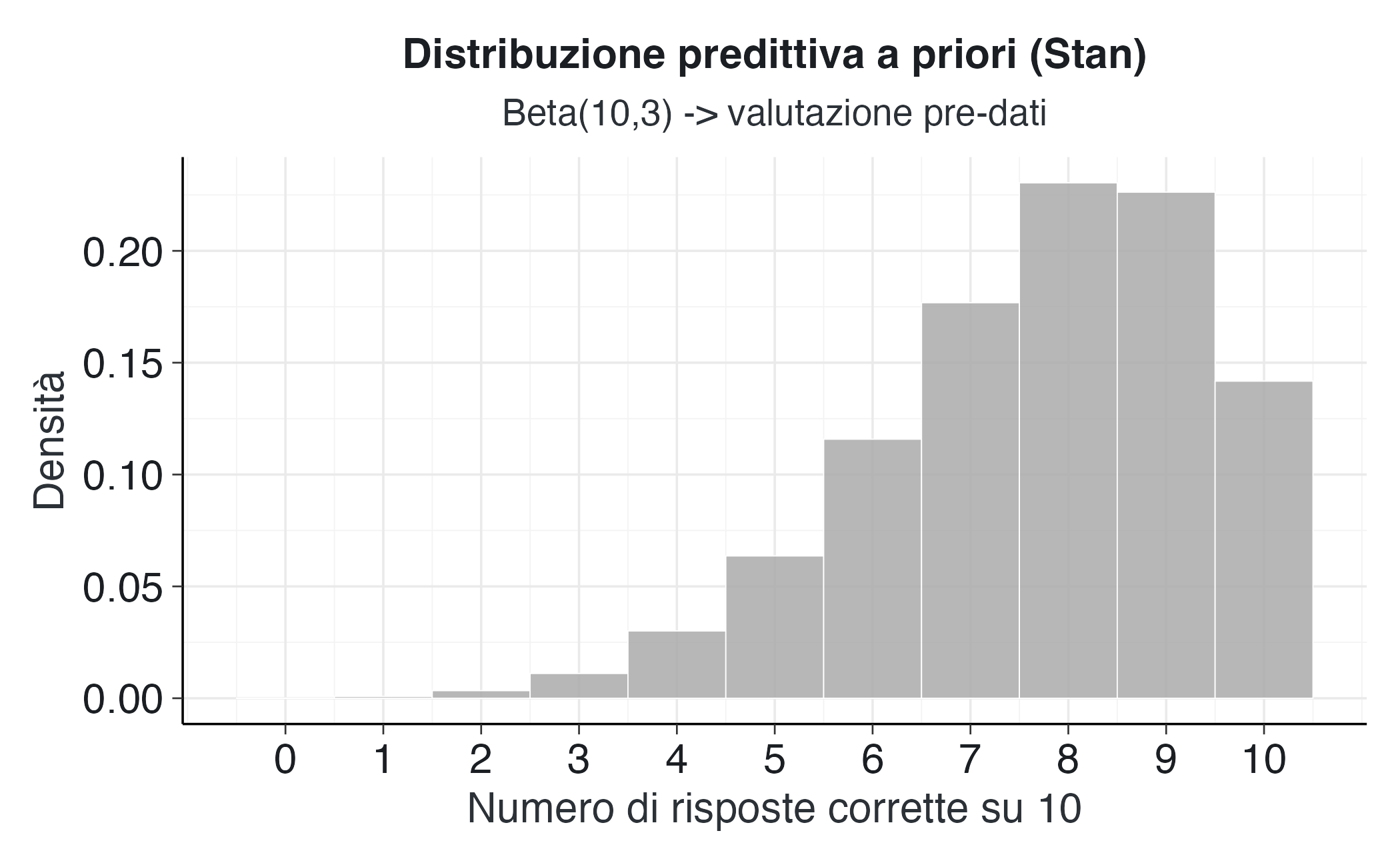
title = "Distribuzione predittiva a priori (Stan)",
subtitle = "Beta(10,3) -> valutazione pre-dati"
)Visualizzazione:
# Usa bayesplot
vars <- paste0("y_rep[", 1:n_studenti, "]")
yrep_mat <- posterior::as_draws_matrix(fit_beta$draws(variables = vars))
p <- bayesplot::ppc_bars(
y = rep(0, n_studenti), # placeholder (non abbiamo dati reali)
yrep = as.matrix(yrep_mat)[1:200, ]
) +
labs(
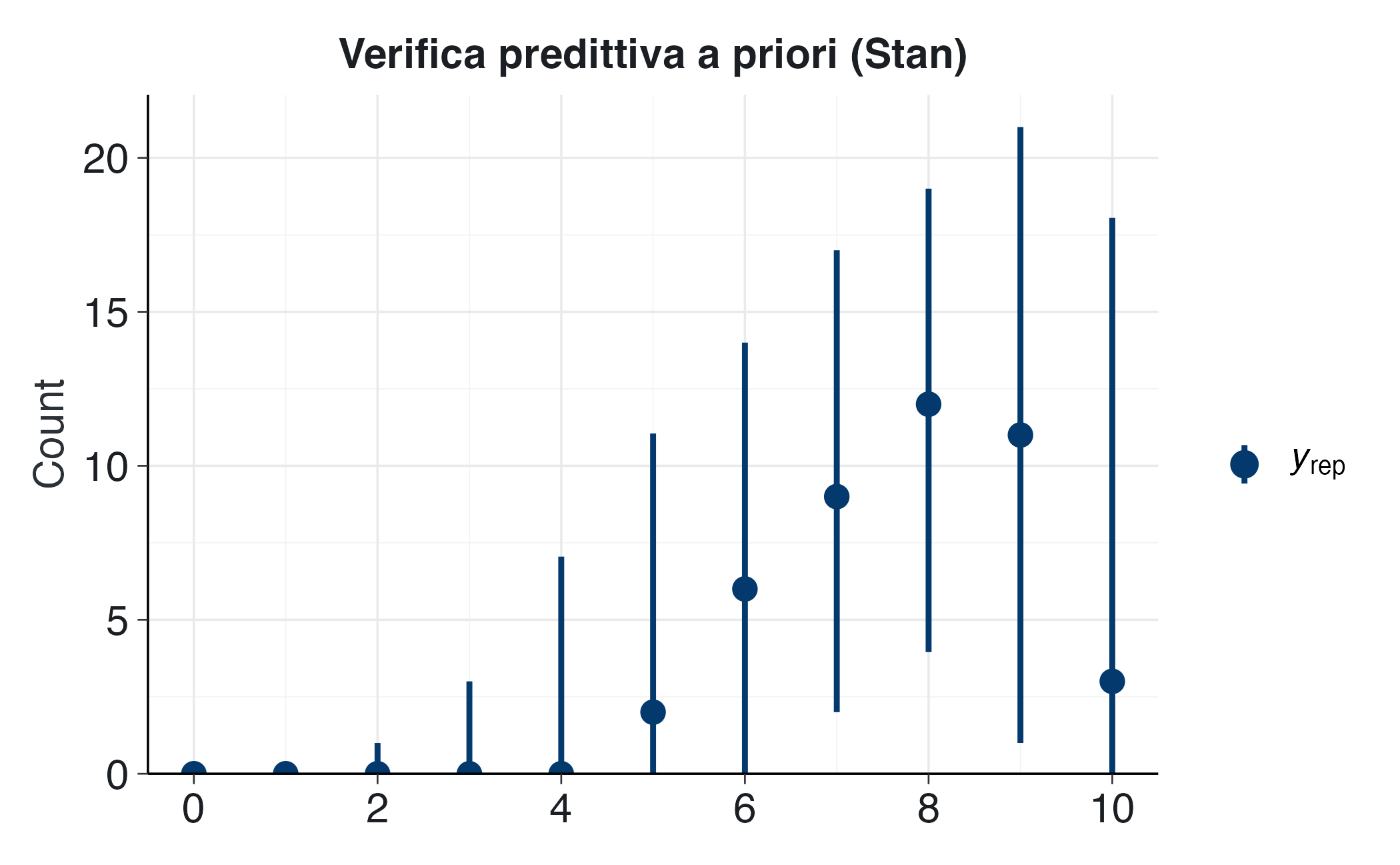
title = "Verifica predittiva a priori (Stan)",
# subtitle = "Distribuzione attesa per ciascuno studente"
)
# Il primo layer (rimosso) è la barra dei dati fittizi osservati
p$layers <- p$layers[-1]
p5.4.4 Rilevanza metodologica
- Trasparenza: l’implementazione diretta in Stan rende esplicite le implicazioni delle nostre scelte a priori.
- Prevenzione degli errori: consente di identificare criticità nella specificazione del modello prima di impegnare risorse nella raccolta e analisi dei dati osservati.
- Apprendimento concettuale: favorisce una comprensione più profonda del nesso tra distribuzioni a priori e distribuzioni predittive.
La verifica predittiva a priori funge da “test di coerenza sostantiva” per le nostre assunzioni iniziali. Se i dati simulati risultano sistematicamente implausibili, la criticità non risiede nei dati reali — che non sono ancora stati osservati — bensì nella specificazione del modello bayesiano, la quale richiede una revisione critica.
Riflessioni conclusive
Il controllo predittivo a priori trasforma le assunzioni iniziali da entità astratte in ipotesi empiricamente verificabili. Questo approccio consente una valutazione ante hoc di plausibilità, prima della raccolta dei dati, migliorando così gli standard di trasparenza nella ricerca empirica.
La distribuzione predittiva a priori è una media ponderata delle previsioni del modello, dove i pesi riflettono le credenze iniziali codificate nei prior.
Distribuzioni a priori apparentemente plausibili sulla scala dei parametri possono generare previsioni empiricamente incoerenti una volta proiettate sulla scala osservabile dei dati, il che sottolinea la necessità di una validazione sistematica delle implicazioni predittive delle assunzioni iniziali.
Il flusso di lavoro iterativo si articola in una sequenza ciclica che prevede la specifica delle distribuzioni a priori, la simulazione dei dati attesi, la valutazione della loro plausibilità sostanziale e, se necessario, la revisione critica delle assunzioni iniziali. Questa procedura conserva la propria integrità metodologica solo se implementata in fase pre-osservativa, preservando l’indipendenza tra le assunzioni iniziali e l’evidenza empirica. Gli strumenti pratici forniti da R e Stan rendono questo processo accessibile e riproducibile.
I prossimi approfondimenti estenderanno questo framework ai controlli predittivi a posteriori, completando così l’architettura di una modellazione bayesiana coerente, rigorosa e trasparente. Per un’esplorazione più approfondita che coinvolga modelli di complessità crescente, si rimanda all’Appendice R.
Un modello bayesiano ben specificato deve superare due verifiche complementari: il controllo predittivo a priori, che valuta se il modello genera dati plausibili prima dell’osservazione, e il controllo predittivo a posteriori, che verifica quanto bene il modello riproduca i dati effettivamente osservati. Trascurare la prima verifica significa costruire l’edificio inferenziale su fondamenta traballanti, compromettendo la solidità dell’intera analisi.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] cmdstanr_0.9.0 ragg_1.5.0 tinytable_0.13.0
#> [4] withr_3.0.2 systemfonts_1.3.1 patchwork_1.3.2
#> [7] ggdist_3.3.3 tidybayes_3.0.7 bayesplot_1.14.0
#> [10] ggplot2_4.0.0 reliabilitydiag_0.2.1 priorsense_1.1.1
#> [13] posterior_1.6.1 loo_2.8.0 rstan_2.32.7
#> [16] StanHeaders_2.32.10 brms_2.23.0 Rcpp_1.1.0
#> [19] sessioninfo_1.2.3 conflicted_1.2.0 janitor_2.2.1
#> [22] matrixStats_1.5.0 modelr_0.1.11 tibble_3.3.0
#> [25] dplyr_1.1.4 tidyr_1.3.1 rio_1.2.4
#> [28] here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 reshape2_1.4.4
#> [10] vctrs_0.6.5 stringr_1.5.2 pkgconfig_2.0.3
#> [13] arrayhelpers_1.1-0 fastmap_1.2.0 backports_1.5.0
#> [16] labeling_0.4.3 rmarkdown_2.30 ps_1.9.1
#> [19] purrr_1.1.0 xfun_0.53 cachem_1.1.0
#> [22] jsonlite_2.0.0 broom_1.0.10 parallel_4.5.1
#> [25] R6_2.6.1 stringi_1.8.7 RColorBrewer_1.1-3
#> [28] lubridate_1.9.4 estimability_1.5.1 knitr_1.50
#> [31] zoo_1.8-14 Matrix_1.7-4 splines_4.5.1
#> [34] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [37] yaml_2.3.10 codetools_0.2-20 curl_7.0.0
#> [40] processx_3.8.6 pkgbuild_1.4.8 plyr_1.8.9
#> [43] lattice_0.22-7 bridgesampling_1.1-2 S7_0.2.0
#> [46] coda_0.19-4.1 evaluate_1.0.5 survival_3.8-3
#> [49] RcppParallel_5.1.11-1 pillar_1.11.1 tensorA_0.36.2.1
#> [52] checkmate_2.3.3 stats4_4.5.1 distributional_0.5.0
#> [55] generics_0.1.4 rprojroot_2.1.1 rstantools_2.5.0
#> [58] scales_1.4.0 xtable_1.8-4 glue_1.8.0
#> [61] emmeans_1.11.2-8 tools_4.5.1 data.table_1.17.8
#> [64] mvtnorm_1.3-3 grid_4.5.1 QuickJSR_1.8.1
#> [67] colorspace_2.1-2 nlme_3.1-168 cli_3.6.5
#> [70] textshaping_1.0.4 svUnit_1.0.8 Brobdingnag_1.2-9
#> [73] V8_8.0.1 gtable_0.3.6 digest_0.6.37
#> [76] TH.data_1.1-4 htmlwidgets_1.6.4 farver_2.1.2
#> [79] memoise_2.0.1 htmltools_0.5.8.1 lifecycle_1.0.4
#> [82] MASS_7.3-65