29  La grandezza dell’effetto: valutare la rilevanza pratica

“Il valore di P non misura l’importanza di un risultato. Per l’importanza, guardate all’entità dell’effetto.”

– Jacob Cohen, Statistician and psychologist

Introduzione

Nei capitoli precedenti abbiamo visto come formulare il problema dell’inferenza su una media e come estenderlo al confronto tra due gruppi. Questi passaggi ci hanno permesso di comprendere che la domanda scientifica non è semplicemente se esista una differenza, ma quanto grande essa sia e con quale grado di incertezza.

È qui che entra in gioco il concetto di grandezza dell’effetto. Nella ricerca psicologica non basta dimostrare che due gruppi differiscono: occorre valutare se la differenza osservata abbia una rilevanza pratica o teorica. Un effetto può essere statisticamente distinto da zero, ma così piccolo da non avere alcuna importanza sostantiva; al contrario, un effetto di ampiezza moderata o grande può essere cruciale anche se stimato con incertezza.

In questo capitolo discuteremo come quantificare la grandezza di un effetto sia in termini assoluti (\(\Delta\), la differenza tra medie) sia in termini standardizzati (\(d = \Delta/\sigma\)), che permettono il confronto tra studi e misure diverse. L’approccio bayesiano ci offre un vantaggio importante: la possibilità di esprimere la nostra incertezza sulla grandezza dell’effetto attraverso una distribuzione a posteriori e di calcolare probabilità direttamente interpretabili, ad esempio la probabilità che l’effetto superi una soglia di rilevanza pratica (ROPE o SESOI).

La grandezza dell’effetto rappresenta quindi un ponte tra la statistica e la sostanza psicologica: ci aiuta a passare da un risultato numerico alla valutazione della sua importanza per la teoria, la pratica clinica o l’intervento applicativo.

Panoramica del capitolo

  • Che cosa misuriamo quando parliamo di “grandezza dell’effetto”.
  • Come stimarlo con modelli bayesiani in brms.
  • Come comunicarlo con intervalli e predizioni.
  • Leggere “Bayesian estimation supersedes the t test” (Kruschke, 2013).
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, brms, bayestestR, insight)

29.1 Perché stimare la grandezza dell’effetto

La grandezza dell’effetto fornisce un ponte tra analisi statistica e interpretazione sostanziale dei dati. Essa consente di rispondere a domande come:

  • Quanto è marcata la differenza osservata?
  • L’effetto ha un impatto concreto nella vita reale o nelle applicazioni cliniche?
  • La variazione osservata è sufficiente a giustificare interventi, cambiamenti o nuove ipotesi teoriche?

L’American Psychological Association (APA) raccomanda di riportare sempre una misura di grandezza dell’effetto, in quanto essa fornisce un’informazione critica che va oltre la mera dicotomia “effetto presente / effetto assente”.

29.2 Standardizzare le differenze: il d di Cohen

Nel confronto tra due gruppi, una delle misure più comuni di grandezza dell’effetto è il d di Cohen, che esprime la differenza tra due medie in unità di deviazione standard:

\[ d = \frac{\mu_1 - \mu_2}{\sigma}, \]

dove:

  • \(\mu_1\) e \(\mu_2\) sono le medie dei due gruppi,
  • \(\sigma\) è una stima comune della deviazione standard.

L’interpretazione di d è indipendente dalle unità di misura originali, il che la rende particolarmente utile per confrontare risultati provenienti da diversi studi o contesti.

29.3 Il d di Cohen in un’ottica bayesiana

Nell’approccio bayesiano non ci limitiamo a stimare un singolo valore di d. L’idea è diversa: costruiamo una distribuzione a posteriori di valori plausibili per la grandezza dell’effetto. Questa distribuzione si ottiene combinando i campioni posteriori della differenza tra gruppi con quelli della deviazione standard residua. In questo modo, invece di una stima unica, otteniamo un quadro completo delle incertezze ancora presenti dopo aver osservato i dati.

29.3.1 Esempio pratico con brms

Riprendiamo il modello già stimato nel capitolo precedente:

kidiq <- rio::import(here::here("data", "kidiq.dta"))

fit_1 <- brm(
  kid_score ~ mom_hs, 
  data = kidiq, 
  backend = "cmdstanr",
  silent = 0
)

Dai campioni posteriori estraiamo sia la stima della differenza tra i gruppi (b_mom_hs) sia la stima della deviazione standard residua (sigma). Dividendo i due otteniamo i campioni della distribuzione di Cohen’s d:

post <- as_draws_df(fit_1)
d_samples <- post$b_mom_hs / post$sigma

29.3.2 Visualizzare la distribuzione di d

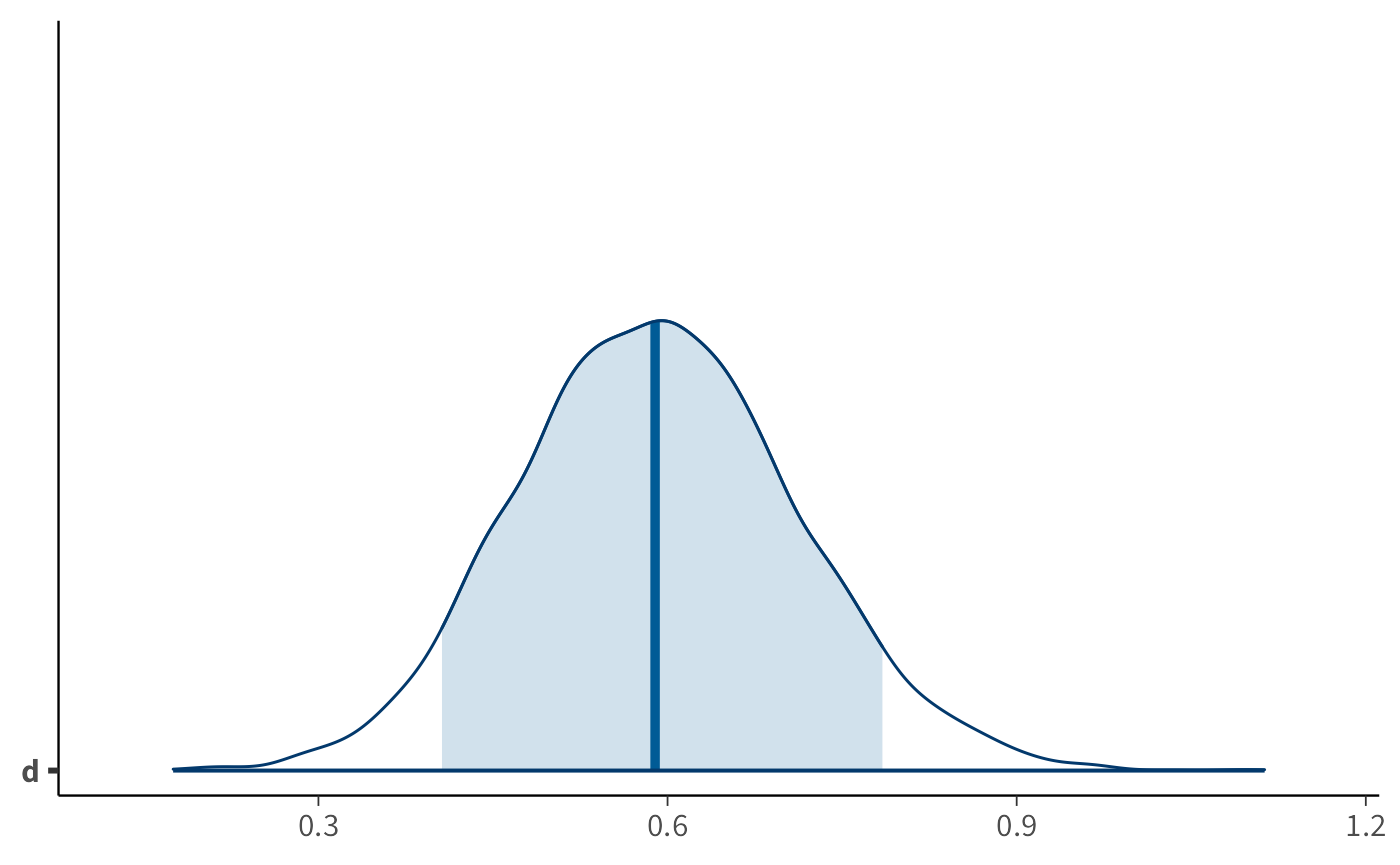
La distribuzione a posteriori di d si può esplorare graficamente. Ad esempio:

mcmc_areas(as_draws_df(tibble(d = d_samples)), pars = "d", prob = 0.89)

Il grafico mostra l’intero intervallo di valori plausibili per la grandezza dell’effetto, mettendo in evidenza la regione che contiene l’89% degli esiti più credibili. È una rappresentazione diretta dell’incertezza che rimane anche dopo aver osservato i dati.

29.3.3 Statistiche riassuntive

Per sintetizzare numericamente i risultati si può usare la funzione describe_posterior():

bayestestR::describe_posterior(d_samples, ci = 0.89)
#> Summary of Posterior Distribution
#> 
#> Parameter | Median |       89% CI |   pd |          ROPE | % in ROPE
#> --------------------------------------------------------------------
#> Posterior |   0.59 | [0.41, 0.78] | 100% | [-0.10, 0.10] |        0%

Questa funzione restituisce la stima centrale (media o mediana), l’intervallo di credibilità, e la probabilità che la grandezza dell’effetto superi o resti al di sotto di valori soglia rilevanti.

29.3.4 Interpretare la grandezza dell’effetto

Nella tradizione frequentista è comune adottare la classificazione proposta da Cohen:

Valore di d Interpretazione convenzionale
≈ 0.2 Effetto piccolo
≈ 0.5 Effetto medio
≥ 0.8 Effetto grande

Queste soglie sono utili come orientamento, ma rischiano di essere applicate in modo meccanico. L’approccio bayesiano offre un vantaggio importante: consente di trasformare queste soglie in domande probabilistiche. Possiamo chiederci, ad esempio, qual è la probabilità che d sia almeno pari a 0.5, oppure la probabilità che resti al di sotto di 0.2. Con i campioni posteriori queste domande trovano risposta diretta:

mean(d_samples > 0.5)  # Probabilità che l'effetto sia almeno medio
#> [1] 0.78
mean(d_samples > 0.8)  # Probabilità che l'effetto sia grande
#> [1] 0.0435
mean(d_samples < 0.2)  # Probabilità che l'effetto sia trascurabile
#> [1] 0.00025

In questo modo non abbiamo un giudizio binario (grande/piccolo), ma una descrizione più sfumata e realistica.

29.3.5 La soglia di rilevanza pratica

In applicazioni concrete non è sufficiente stabilire che l’effetto sia diverso da zero: è necessario valutare se supera una soglia di rilevanza pratica (minimum effect of interest, o ROPE — region of practical equivalence).

Supponiamo, per esempio, che uno psicologo clinico ritenga irrilevante qualsiasi effetto inferiore a d = 0.3. In questo caso, la domanda da porsi è: qual è la probabilità che l’effetto osservato sia superiore a 0.3? La risposta si ottiene immediatamente dai campioni posteriori:

mean(d_samples > 0.3)
#> [1] 0.994

Questo numero esprime in modo diretto la probabilità che la differenza osservata abbia una rilevanza clinica concreta, spostando l’attenzione da soglie arbitrarie a valutazioni fondate sulle esigenze specifiche del contesto.

Riflessioni conclusive

In questo capitolo abbiamo visto come la differenza tra due gruppi non debba essere valutata solo in termini di esistenza, ma anche di ampiezza e di rilevanza pratica. L’approccio bayesiano ci permette di quantificare questa ampiezza attraverso la distribuzione a posteriori dell’effetto, fornendo una rappresentazione trasparente dell’incertezza e consentendo di calcolare probabilità direttamente interpretabili: la probabilità che l’effetto sia positivo, che superi una soglia di rilevanza pratica, o che ricada in una regione di equivalenza.

Questa prospettiva sposta l’attenzione dal verdetto dicotomico tipico dell’approccio frequentista alla valutazione sfumata e continua della plausibilità dei diversi scenari. In altre parole, non ci limitiamo più a dire se un effetto “c’è o non c’è”, ma cerchiamo di capire quanto sia importante in rapporto alle nostre domande scientifiche e applicative.

La grandezza dell’effetto rappresenta dunque un punto di incontro tra la statistica e la psicologia: ci ricorda che i numeri hanno senso solo se inseriti in un contesto teorico e pratico, e che l’obiettivo ultimo dell’analisi non è solo descrivere i dati, ma trarne indicazioni utili per la comprensione dei fenomeni.

Il passo successivo è conseguente: se l’interesse è valutare effetti di una certa ampiezza, diventa cruciale chiedersi quanti dati servono per stimarli con un’incertezza accettabile. Nel prossimo capitolo affronteremo quindi il tema della pianificazione della dimensione campionaria, mostrando come il quadro bayesiano possa guidare scelte di ricerca più consapevoli ed efficienti.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] insight_1.4.2         bayestestR_0.17.0     cmdstanr_0.9.0       
#>  [4] pillar_1.11.1         tinytable_0.13.0      patchwork_1.3.2      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#> [10] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [28] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      ggridges_0.5.7        compiler_4.5.1       
#> [10] reshape2_1.4.4        systemfonts_1.2.3     vctrs_0.6.5          
#> [13] stringr_1.5.2         pkgconfig_2.0.3       arrayhelpers_1.1-0   
#> [16] fastmap_1.2.0         backports_1.5.0       labeling_0.4.3       
#> [19] rmarkdown_2.29        tzdb_0.5.0            haven_2.5.5          
#> [22] ps_1.9.1              ragg_1.5.0            purrr_1.1.0          
#> [25] xfun_0.53             cachem_1.1.0          jsonlite_2.0.0       
#> [28] broom_1.0.10          parallel_4.5.1        R6_2.6.1             
#> [31] stringi_1.8.7         RColorBrewer_1.1-3    lubridate_1.9.4      
#> [34] estimability_1.5.1    knitr_1.50            zoo_1.8-14           
#> [37] R.utils_2.13.0        pacman_0.5.1          readr_2.1.5          
#> [40] Matrix_1.7-4          splines_4.5.1         timechange_0.3.0     
#> [43] tidyselect_1.2.1      abind_1.4-8           yaml_2.3.10          
#> [46] codetools_0.2-20      curl_7.0.0            processx_3.8.6       
#> [49] pkgbuild_1.4.8        plyr_1.8.9            lattice_0.22-7       
#> [52] withr_3.0.2           bridgesampling_1.1-2  S7_0.2.0             
#> [55] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [58] RcppParallel_5.1.11-1 tensorA_0.36.2.1      checkmate_2.3.3      
#> [61] stats4_4.5.1          distributional_0.5.0  generics_0.1.4       
#> [64] rprojroot_2.1.1       hms_1.1.3             rstantools_2.5.0     
#> [67] scales_1.4.0          xtable_1.8-4          glue_1.8.0           
#> [70] emmeans_1.11.2-8      tools_4.5.1           data.table_1.17.8    
#> [73] forcats_1.0.0         mvtnorm_1.3-3         grid_4.5.1           
#> [76] QuickJSR_1.8.0        datawizard_1.2.0      colorspace_2.1-1     
#> [79] nlme_3.1-168          cli_3.6.5             textshaping_1.0.3    
#> [82] svUnit_1.0.8          Brobdingnag_1.2-9     V8_7.0.0             
#> [85] gtable_0.3.6          R.methodsS3_1.8.2     digest_0.6.37        
#> [88] TH.data_1.1-4         htmlwidgets_1.6.4     farver_2.1.2         
#> [91] R.oo_1.27.1           memoise_2.0.1         htmltools_0.5.8.1    
#> [94] lifecycle_1.0.4       MASS_7.3-65

Bibliografia

Kruschke, J. K. (2013). Bayesian estimation supersedes the t test. Journal of Experimental Psychology: General, 142(2), 573–603.