2  Famiglie coniugate classiche

Introduzione

Questo materiale costituisce un approfondimento del capitolo 16 del manuale didattico, dedicato allo studio delle famiglie coniugate nell’inferenza bayesiana.

Una famiglia coniugata rappresenta una particolare combinazione matematica nella quale una distribuzione a priori e una funzione di verosimiglianza sono scelte in modo tale che la distribuzione a posteriori risultante appartenga alla stessa famiglia della distribuzione a priori. Questa proprietà non è solo un’eleganza matematica, ma offre vantaggi concreti per l’analisi e l’interpretazione dei risultati.

La proprietà fondamentale della coniugazione è che l’aggiornamento bayesiano avviene attraverso formule matematiche esplicite, senza necessità di algoritmi computazionali complessi. Quando utilizziamo una coppia coniugata, è sufficiente aggiornare i parametri della distribuzione secondo regole ben definite. Nel modello Beta-Binomiale, per esempio, basta sommare i successi osservati al parametro \(\alpha\) e gli insuccessi al parametro \(\beta\). Questa semplicità permette di concentrarsi sull’interpretazione sostantiva dei risultati piuttosto che sugli aspetti tecnici del calcolo.

I parametri delle distribuzioni coniugate possiedono significati concreti e intuitivi. Nel caso della distribuzione Beta, i parametri \(\alpha\) e \(\beta\) possono essere interpretati come “osservazioni virtuali” o “pseudo-conteggi” che rappresentano la nostra conoscenza preliminare. Quando aggiorniamo la distribuzione con dati reali, stiamo letteralmente sommando le nostre osservazioni virtuali a quelle empiriche. Questa interpretazione rende trasparente il processo di apprendimento bayesiano e facilita la comunicazione dei risultati.

Un ulteriore vantaggio pratico delle famiglie coniugate riguarda la possibilità di aggiornamento sequenziale. Quando nuovi dati diventano disponibili nel tempo, possiamo aggiornare i parametri in modo iterativo senza dover riprocessare l’intero dataset. La distribuzione a posteriori ottenuta da un primo blocco di dati diventa la distribuzione a priori per l’analisi del blocco successivo. Questo approccio si rivela particolarmente utile nella pratica clinica, dove il monitoraggio dei pazienti avviene nel tempo e le valutazioni devono essere aggiornate continuamente.

2.1 Panoramica delle principali coppie coniugate

Prima di entrare nei dettagli implementativi, presentiamo una sintesi delle principali coppie coniugate che utilizzeremo negli esempi. Ogni riga della tabella mostra come una particolare distribuzione per i dati si combina con una specifica distribuzione a priori per produrre una distribuzione a posteriori della stessa famiglia del prior.

Modello dati	Parametro	Prior coniugata	Posterior
Binomiale\((n,\theta)\)	\(\theta \in [0,1]\)	Beta\((\alpha,\beta)\)	Beta\((\alpha+y, \beta+n-y)\)
Poisson\((\theta)\)	\(\theta > 0\)	Gamma\((a,b)\)	Gamma\((a+\sum y_i, b+n)\)
Esponenziale\((\theta)\)	\(\theta > 0\)	Gamma\((a,b)\)	Gamma\((a+n, b+\sum y_i)\)
Normale\((\mu,\sigma^2)\)	\(\mu \in \mathbb{R}\)	\(\mathcal{N}(\mu_0,\tau_0^2)\)	\(\mathcal{N}(\mu_n,\tau_n^2)\)

Osserviamo alcuni pattern ricorrenti in queste formule di aggiornamento. Nel modello Beta-Binomiale, i parametri della distribuzione a posteriori si ottengono sommando semplicemente i conteggi osservati ai parametri del prior. Nel modello Gamma-Poisson, la forma della distribuzione aumenta del numero totale di eventi osservati, mentre il parametro di scala aumenta del numero di intervalli temporali. Il modello Normale-Normale presenta invece una struttura più complessa, basata sulla combinazione ponderata delle precisioni.

2.2 Funzioni per l’aggiornamento bayesiano

Implementiamo ora quattro funzioni che automatizzano il calcolo dell’aggiornamento bayesiano per i modelli coniugati più comuni. Ciascuna funzione accetta come input i parametri del prior e i dati osservati, restituendo i parametri della distribuzione a posteriori. Il codice è volutamente esplicito e commentato per facilitare la comprensione del processo di calcolo.

2.2.1 Beta-Binomiale: proporzioni e percentuali

Il modello Beta-Binomiale è appropriato quando vogliamo fare inferenza su una proporzione o percentuale incognita. Tipici esempi includono la stima dell’accuratezza in un compito di riconoscimento, la proporzione di pazienti che rispondono a un trattamento, o la percentuale di comportamenti desiderati in un contesto educativo.

beta_binomiale_aggiorna <- function(successi, prove, alpha_prior, beta_prior) {
  # Questa funzione implementa l'aggiornamento bayesiano per il modello Beta-Binomiale
  #
  # ARGOMENTI:
  #   successi: numero di "successi" osservati (es. risposte corrette)
  #   prove: numero totale di prove o tentativi
  #   alpha_prior: parametro alpha della distribuzione Beta a priori
  #   beta_prior: parametro beta della distribuzione Beta a priori
  #
  # VALORE RESTITUITO:
  #   Una lista contenente i due parametri della distribuzione a posteriori
  
  # L'aggiornamento bayesiano consiste nel sommare i conteggi osservati
  # ai parametri del prior. Questo riflette l'accumulo di evidenza.
  
  # Al parametro alpha (che rappresenta i "successi virtuali" nel prior)
  # sommiamo i successi realmente osservati
  alpha_posteriori <- alpha_prior + successi
  
  # Al parametro beta (che rappresenta gli "insuccessi virtuali" nel prior)
  # sommiamo gli insuccessi osservati, calcolati come (prove - successi)
  insuccessi <- prove - successi
  beta_posteriori <- beta_prior + insuccessi
  
  # Restituiamo i parametri aggiornati in una lista nominata
  # per facilitarne l'accesso successivo
  risultato <- list(
    alpha_post = alpha_posteriori,
    beta_post = beta_posteriori
  )
  
  return(risultato)
}

La logica dell’aggiornamento è particolarmente intuitiva nel caso Beta-Binomiale. I parametri α e β della distribuzione Beta possono essere pensati come conteggi virtuali di successi e insuccessi derivanti da esperienze o conoscenze pregresse. Quando osserviamo nuovi dati, aggiungiamo semplicemente i conteggi reali a quelli virtuali. Se avevamo un prior Beta(2,2) e osserviamo 7 successi su 10 prove, il posterior diventa Beta(2+7, 2+3) = Beta(9,5).

2.2.2 Normale-Normale: medie e misure continue

Il modello Normale-Normale si applica quando vogliamo stimare la media di una variabile continua, assumendo che la varianza sia nota. Questo modello è frequente in psicometria e neuropsicologia, dove molte misure standardizzate hanno varianza nota per costruzione.

normale_normale_aggiorna <- function(media_campionaria, numerosita, 
                                     sigma_noto, mu_prior, tau_prior) {
  # Questa funzione implementa l'aggiornamento bayesiano per il modello Normale-Normale
  # quando la varianza dei dati è nota
  #
  # ARGOMENTI:
  #   media_campionaria: la media calcolata sui dati osservati
  #   numerosita: il numero di osservazioni nel campione
  #   sigma_noto: la deviazione standard (nota) dei dati
  #   mu_prior: la media della distribuzione a priori
  #   tau_prior: la deviazione standard della distribuzione a priori
  #
  # VALORE RESTITUITO:
  #   Una lista con media e deviazione standard della distribuzione a posteriori
  
  # Nel modello Normale-Normale, lavoriamo con le "precisioni" anziché le varianze
  # La precisione è definita come 1/varianza e misura quanto siamo certi di una stima
  
  # Calcoliamo la precisione della nostra conoscenza a priori
  # Più piccola è tau_prior, più alta è la precisione, più siamo certi
  precisione_prior <- 1 / (tau_prior^2)
  
  # Calcoliamo la precisione fornita dai dati osservati
  # Dipende sia dalla varianza dei dati sia dalla numerosità campionaria
  # Più osservazioni abbiamo, più precisa è la nostra stima
  precisione_dati <- numerosita / (sigma_noto^2)
  
  # La precisione a posteriori è la SOMMA delle due precisioni
  # Questo è un principio fondamentale: l'informazione si accumula additivamente
  precisione_posteriori <- precisione_prior + precisione_dati
  
  # La varianza a posteriori è l'inverso della precisione
  varianza_posteriori <- 1 / precisione_posteriori
  
  # La deviazione standard a posteriori è la radice della varianza
  sd_posteriori <- sqrt(varianza_posteriori)
  
  # La media a posteriori è una media ponderata tra il prior e i dati
  # I pesi sono proporzionali alle rispettive precisioni
  # Fonti più precise hanno maggiore influenza sulla stima finale
  mu_posteriori <- varianza_posteriori * (
    mu_prior * precisione_prior + media_campionaria * precisione_dati
  )
  
  # Restituiamo i parametri della distribuzione a posteriori
  risultato <- list(
    mu_post = mu_posteriori,
    sd_post = sd_posteriori
  )
  
  return(risultato)
}

La caratteristica distintiva del modello Normale-Normale è che l’informazione viene misurata in termini di precisione. Questo concetto merita attenzione perché rappresenta un modo diverso di pensare all’incertezza. Una varianza piccola corrisponde a un’alta precisione, indicando che siamo molto certi del nostro valore. Quando combiniamo informazioni da diverse fonti, le precisioni si sommano in modo diretto e semplice.

2.2.3 Gamma-Poisson: conteggi di eventi

Il modello Gamma-Poisson è appropriato quando analizziamo il conteggio di eventi che si verificano in intervalli di tempo o spazio fissi. Esempi tipici includono il numero di episodi sintomatici per settimana, il numero di errori in un compito cognitivo, o la frequenza di comportamenti target in sessioni di osservazione.

gamma_poisson_aggiorna <- function(conteggi_osservati, a_prior, b_prior) {
  # Questa funzione implementa l'aggiornamento bayesiano per il modello Gamma-Poisson
  # utilizzato per stimare il tasso di eventi rari
  #
  # ARGOMENTI:
  #   conteggi_osservati: vettore con i conteggi in ciascun intervallo temporale
  #   a_prior: parametro di forma della distribuzione Gamma a priori
  #   b_prior: parametro di scala della distribuzione Gamma a priori
  #
  # VALORE RESTITUITO:
  #   Una lista con i parametri aggiornati della distribuzione Gamma
  
  # Calcoliamo il numero totale di eventi osservati
  # sommando tutti i conteggi nei diversi intervalli temporali
  eventi_totali <- sum(conteggi_osservati)
  
  # Contiamo quanti intervalli temporali abbiamo osservato
  # Questo corrisponde alla lunghezza del vettore dei conteggi
  numero_intervalli <- length(conteggi_osservati)
  
  # Nel modello Gamma-Poisson, il parametro di forma (a) rappresenta
  # il numero di eventi. L'aggiornamento consiste nel sommare
  # gli eventi osservati agli eventi "virtuali" del prior
  a_posteriori <- a_prior + eventi_totali
  
  # Il parametro di scala (b) rappresenta il numero di intervalli
  # temporali osservati. Sommiamo gli intervalli reali a quelli virtuali
  b_posteriori <- b_prior + numero_intervalli
  
  # Restituiamo i parametri aggiornati
  risultato <- list(
    a_post = a_posteriori,
    b_post = b_posteriori
  )
  
  return(risultato)
}

L’interpretazione dei parametri nel modello Gamma-Poisson può essere compresa pensando a uno studio preliminare ipotetico. Se il nostro prior è Gamma(2,4), possiamo immaginare di aver osservato virtualmente 2 eventi in 4 intervalli temporali, suggerendo un tasso di 0.5 eventi per intervallo. Quando osserviamo poi 4 nuovi eventi in 4 settimane reali, il posterior diventa Gamma(6,8), riflettendo un’esperienza complessiva di 6 eventi in 8 settimane.

2.2.4 Gamma-Esponenziale: tempi tra eventi

Il modello Gamma-Esponenziale viene utilizzato quando siamo interessati ai tempi di attesa tra eventi consecutivi. È complementare al modello Gamma-Poisson: mentre quest’ultimo analizza quanti eventi si verificano in un tempo fisso, il Gamma-Esponenziale analizza quanto tempo intercorre tra gli eventi.

gamma_esponenziale_aggiorna <- function(tempi_osservati, a_prior, b_prior) {
  # Questa funzione implementa l'aggiornamento bayesiano per il modello Gamma-Esponenziale
  # utilizzato per stimare il tasso di occorrenza quando osserviamo i tempi tra eventi
  #
  # ARGOMENTI:
  #   tempi_osservati: vettore con i tempi di attesa tra eventi consecutivi
  #   a_prior: parametro di forma della distribuzione Gamma a priori
  #   b_prior: parametro di scala della distribuzione Gamma a priori
  #
  # VALORE RESTITUITO:
  #   Una lista con i parametri aggiornati della distribuzione Gamma
  
  # Sommiamo tutti i tempi di attesa osservati per ottenere
  # il tempo totale trascorso durante l'osservazione
  tempo_totale <- sum(tempi_osservati)
  
  # Contiamo quanti intervalli temporali abbiamo osservato
  # Questo corrisponde al numero di transizioni tra eventi
  numero_intervalli <- length(tempi_osservati)
  
  # Nel modello Gamma-Esponenziale, il parametro di forma rappresenta
  # il numero di intervalli osservati. Sommiamo i nuovi intervalli
  # a quelli "virtuali" del prior
  a_posteriori <- a_prior + numero_intervalli
  
  # Il parametro di scala rappresenta il tempo totale osservato
  # Sommiamo il tempo reale al tempo "virtuale" del prior
  b_posteriori <- b_prior + tempo_totale
  
  # Restituiamo i parametri aggiornati
  risultato <- list(
    a_post = a_posteriori,
    b_post = b_posteriori
  )
  
  return(risultato)
}

La distinzione tra Gamma-Poisson e Gamma-Esponenziale si comprende meglio considerando la natura dei dati. Nel primo caso osserviamo “quanti eventi in ciascun periodo”, nel secondo “quanto tempo tra eventi consecutivi”. Le formule di aggiornamento riflettono questa differenza: nel Poisson sommiamo i conteggi, nell’Esponenziale sommiamo i tempi.

2.3 Il modello beta-binomiale: lo studio sull’obbedienza di Milgram

L’esperimento condotto da Milgram (1963) rimane uno degli studi più controversi e influenti nella storia della psicologia sociale. Il suo paradigma sperimentale — progettato per indagare i meccanismi dell’obbedienza all’autorità — prevedeva che i partecipanti somministrassero quelle che percepivano come scosse elettriche di intensità crescente a un’altra persona. Sebbene in realtà le scosse fossero simulate e il destinatario fosse un collaboratore dello sperimentatore, i partecipanti agivano nella ferma convinzione di infliggere un dolore reale. I risultati furono sorprendenti: ventisei partecipanti su quaranta (pari al 65%) proseguirono fino al livello massimo dello strumento, contrassegnato dalla dicitura «Pericolo: scossa grave».

Da un punto di vista statistico, il dato empirico solleva un fondamentale quesito inferenziale: quanto è generalizzabile il fenomeno osservato? Quale proporzione della popolazione generale mostrerebbe un analogo livello di obbedienza in condizioni sperimentali simili? Per rispondere a questa domanda utilizziamo l’inferenza bayesiana, che ci permette di quantificare l’incertezza associata a questa stima e di valutare esplicitamente quanto i dati modifichino le nostre credenze iniziali.

2.3.1 Specificazione del prior: formalizzare lo scetticismo iniziale

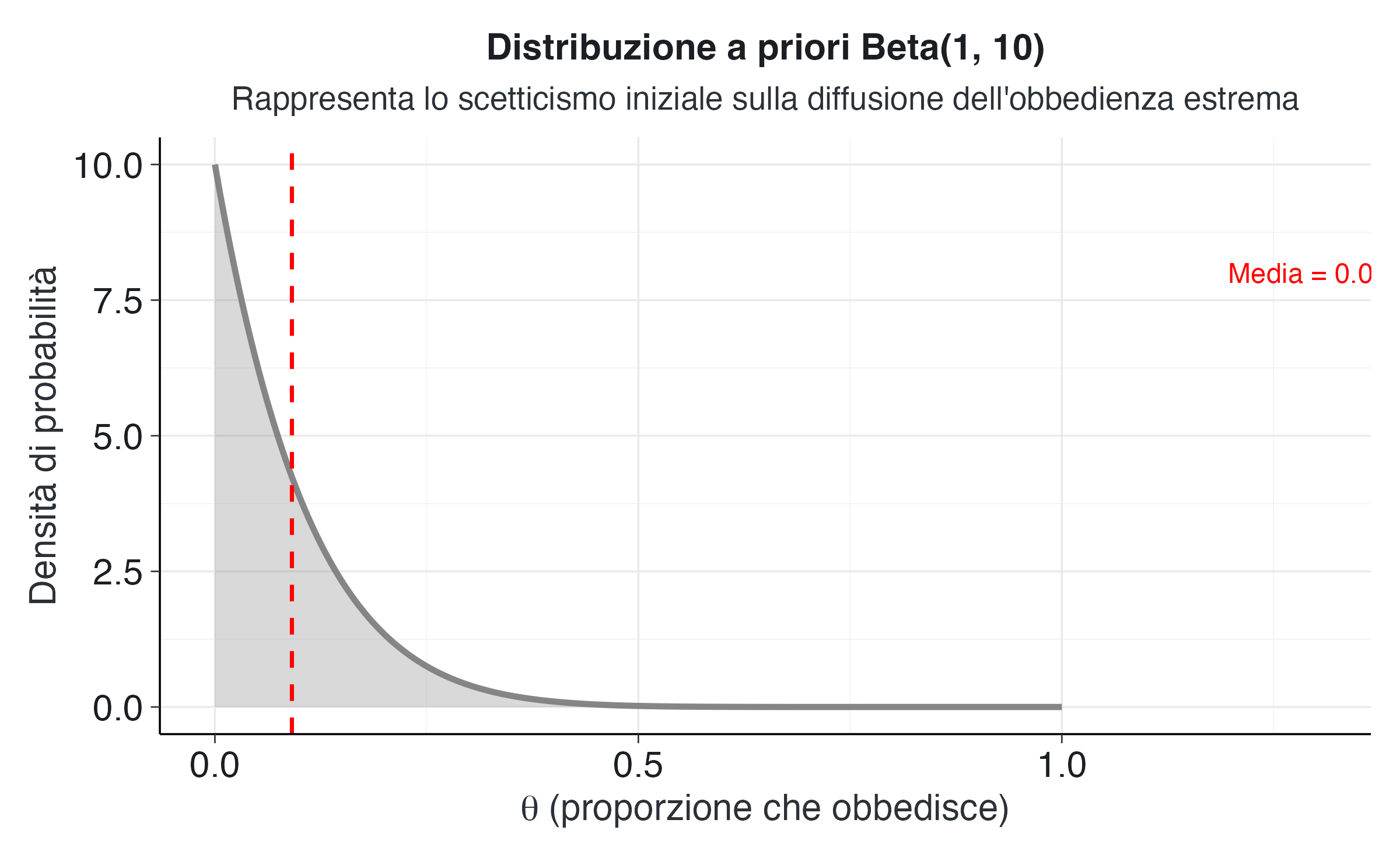
Prima di esaminare i dati di Milgram, è legittimo chiedersi: quale proporzione di persone ci si aspetterebbe che, ragionevolmente, arrivi a obbedire fino al limite estremo nell’esperimento? Per esprimere scetticismo riguardo alla diffusione dell’obbedienza estrema, adottiamo come distribuzione a priori una Beta(1,10).

# Definiamo i parametri della distribuzione a priori
alpha_prior <- 1
beta_prior <- 10

# La media di una distribuzione Beta(alpha, beta) è alpha/(alpha + beta)
media_prior <- alpha_prior / (alpha_prior + beta_prior)

# Creiamo una sequenza di possibili valori del parametro theta
# che rappresenta la proporzione di obbedienza nella popolazione
theta_valori <- seq(from = 0, to = 1, length.out = 500)

# Calcoliamo la densità di probabilità per ciascun valore di theta
# usando la funzione dbeta() che implementa la distribuzione Beta
densita_prior <- dbeta(theta_valori, shape1 = alpha_prior, shape2 = beta_prior)

# Organizziamo i dati in un dataframe per facilitare la visualizzazione
dati_prior <- data.frame(
  theta = theta_valori,
  densita = densita_prior
)

Come mostrato nella figura precedente, la distribuzione Beta(1,10) ha una media di 0.091, ovvero circa il 9%. Questo valore riflette l’aspettativa iniziale che solo una piccola frazione della popolazione proseguirebbe fino all’estremo. I parametri scelti corrispondono a un esperimento pilota ipotetico in cui solo un partecipante su undici manifesta un’obbedienza estrema, da cui emerge una proporzione di 1/11 ≈ 0.09.

# Creiamo la visualizzazione della distribuzione a priori
ggplot(dati_prior, aes(x = theta, y = densita)) +
  # Linea principale che mostra la forma della distribuzione
  geom_line(color = "#7f7f7f", size = 1.2) +
  # Area sottostante la curva per enfatizzare la densità di probabilità
  geom_area(fill = "#7f7f7f", alpha = 0.3) +
  # Linea verticale che indica la media della distribuzione
  geom_vline(xintercept = media_prior, linetype = "dashed", color = "red", size = 0.8) +
  # Annotazione testuale che riporta il valore della media
  annotate("text", x = 1.3, y = max(densita_prior) * 0.8,
           label = paste("Media =", round(media_prior, 3)),
           color = "red", size = 4) +
  # Etichette degli assi e titolo
  labs(
    title = "Distribuzione a priori Beta(1, 10)",
    subtitle = "Rappresenta lo scetticismo iniziale sulla diffusione dell'obbedienza estrema",
    x = expression(theta ~ "(proporzione che obbedisce)"),
    y = "Densità di probabilità"
  ) 

Il grafico mostra come la distribuzione a priori concentri la maggior parte della massa di probabilità su valori bassi di \(\theta\). La forma decrescente della curva esprime l’idea che proporzioni più alte di obbedienza siano considerate, in partenza, poco plausibili.

2.3.2 L’aggiornamento bayesiano: integrare evidenza e credenze

Aggiorniamo ora le nostre credenze sulla base dei dati empirici di Milgram. L’inferenza bayesiana procede applicando la regola di aggiornamento che abbiamo definito in precedenza, sommando semplicemente i conteggi osservati ai parametri del prior.

# Dati osservati nell'esperimento di Milgram
successi_osservati <- 26  # partecipanti che hanno obbedito completamente
prove_totali <- 40         # numero totale di partecipanti

# Applichiamo la funzione di aggiornamento bayesiano
parametri_posteriori <- beta_binomiale_aggiorna(
  successi = successi_osservati,
  prove = prove_totali,
  alpha_prior = alpha_prior,
  beta_prior = beta_prior
)

# Estraiamo i parametri aggiornati dalla lista restituita
alpha_post <- parametri_posteriori$alpha_post
beta_post <- parametri_posteriori$beta_post

# Calcoliamo la media della distribuzione a posteriori
media_post <- alpha_post / (alpha_post + beta_post)

I parametri della distribuzione a posteriori sono Alpha = 27 e Beta = 24. Questi valori riflettono l’accumulo di esperienza: i 26 successi osservati si sono sommati al singolo successo virtuale del prior (1 + 26 = 27), mentre i 14 insuccessi osservati si sono sommati ai 10 insuccessi virtuali (10 + 14 = 24). La media della distribuzione a posteriori è 0.529, ovvero circa il 53%, un valore considerevolmente più alto della media a priori del 9%.

2.3.3 Visualizzazione dell’aggiornamento: dalle credenze iniziali alla sintesi finale

Per comprendere pienamente il meccanismo dell’aggiornamento bayesiano, è utile visualizzare simultaneamente tre componenti: la distribuzione a priori, la funzione di verosimiglianza e la distribuzione a posteriori. Ciascuna di queste curve fornisce informazioni complementari sul processo inferenziale.

# Prepariamo i dati per la visualizzazione di tutte e tre le curve

# Distribuzione a priori (già calcolata)
prior_densita <- dbeta(theta_valori, alpha_prior, beta_prior)

# Funzione di verosimiglianza
# Indica quanto i dati sono compatibili con ciascun valore di theta
likelihood_raw <- dbinom(
  x = successi_osservati, 
  size = prove_totali, 
  prob = theta_valori
)

# Distribuzione a posteriori
posterior_densita <- dbeta(theta_valori, alpha_post, beta_post)

# La verosimiglianza non è una densità di probabilità, quindi la scaliamo
# per renderla visivamente confrontabile con prior e posterior
likelihood_scaled <- likelihood_raw / max(likelihood_raw) * max(posterior_densita)

# Creiamo un dataframe "lungo" per ggplot2 con tutte e tre le distribuzioni
dati_complete <- data.frame(
  theta = rep(theta_valori, 3),
  densita = c(prior_densita, likelihood_scaled, posterior_densita),
  tipo = rep(
    c("Prior", "Verosimiglianza", "Posterior"), 
    each = length(theta_valori)
  )
)

# Convertiamo 'tipo' in un fattore ordinato per controllare la legenda
dati_complete$tipo <- factor(
  dati_complete$tipo,
  levels = c("Prior", "Verosimiglianza", "Posterior")
)

# Creiamo il grafico che mostra l'intero processo di aggiornamento
ggplot(dati_complete, aes(x = theta, y = densita, color = tipo)) +
  geom_line(size = 1.3) +
  # Assegniamo colori distinti a ciascuna curva
  scale_color_manual(
    values = c(
      "Prior" = "#7f7f7f",
      "Verosimiglianza" = "#E69F00",
      "Posterior" = "#1f78b4"
    )
  ) +
  labs(
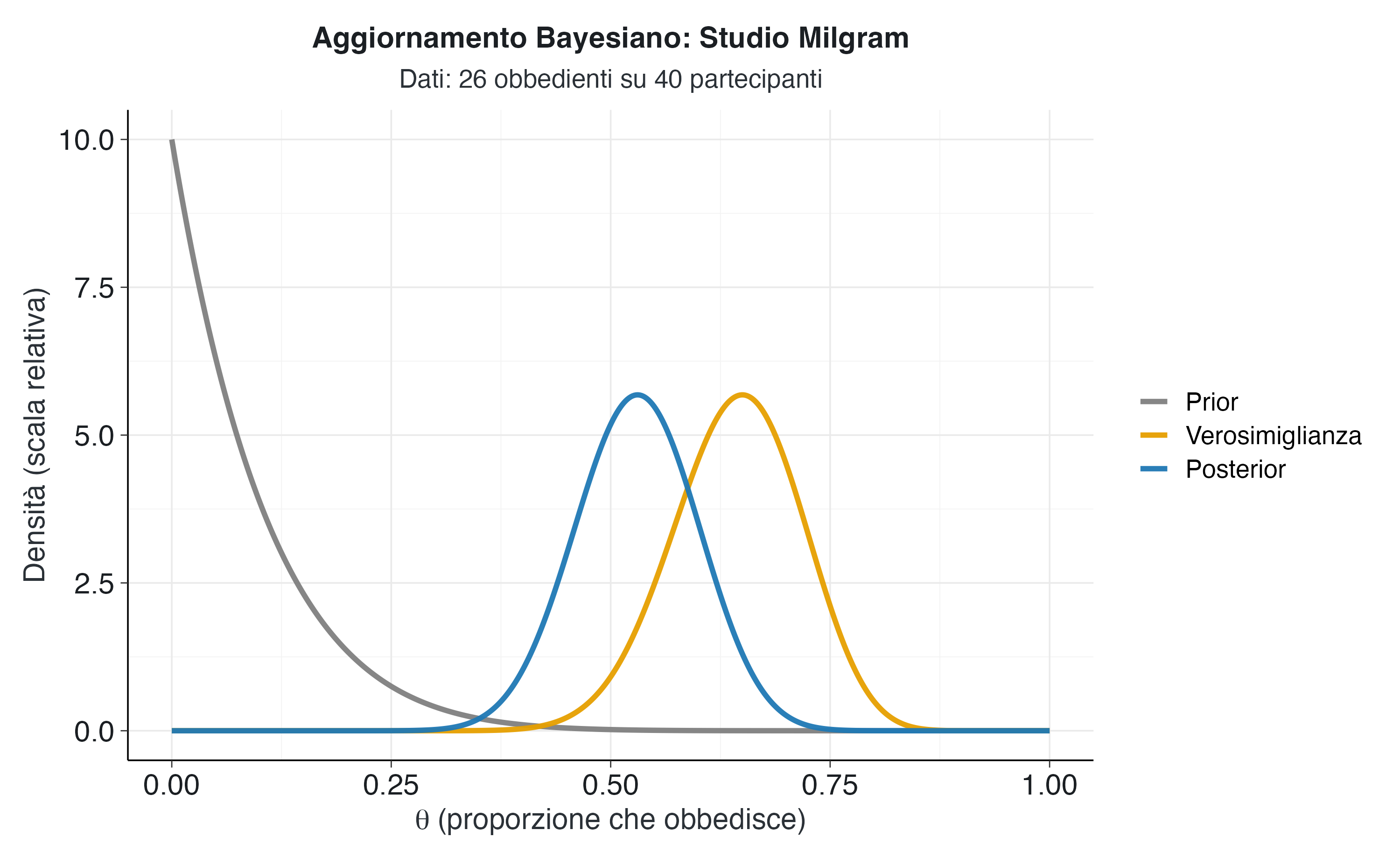
    title = "Aggiornamento Bayesiano: Studio Milgram",
    subtitle = paste0(
      "Dati: ", successi_osservati, " obbedienti su ", 
      prove_totali, " partecipanti"
    ),
    x = expression(theta ~ "(proporzione che obbedisce)"),
    y = "Densità (scala relativa)",
    color = NULL
  ) 

Il grafico seguente esemplifica il meccanismo dell’inferenza bayesiana. La curva grigia rappresenta le credenze a priori, concentrate sui valori più bassi di \(\theta\). A questa si contrappone la verosimiglianza (curva arancione), che riflette l’informazione campionaria con un picco netto in corrispondenza della proporzione osservata (26/40 = 0.65).

La distribuzione a posteriori (curva blu) sintetizza queste due fonti di informazione, posizionandosi in un punto di equilibrio tra il prior e i dati. La sua collocazione, spostata verso la verosimiglianza ma non sovrapposta ad essa, evidenzia l’effetto regolarizzante del prior: questo modera la stima puramente empirica, incorporando nel risultato finale il nostro scetticismo iniziale.

2.3.4 Quantificazione dell’incertezza e inferenza probabilistica

Uno dei vantaggi fondamentali dell’approccio bayesiano è la possibilità di formulare direttamente affermazioni probabilistiche sui parametri di interesse. Possiamo calcolare diverse quantità che riassumono la distribuzione a posteriori e rispondono a domande specifiche di interesse sostantivo.

# Calcoliamo statistiche riassuntive della distribuzione a posteriori

# Media: valore atteso della proporzione
media_posteriori <- alpha_post / (alpha_post + beta_post)

# Moda: valore più plausibile (quando alpha, beta > 1)
moda_posteriori <- (alpha_post - 1) / (alpha_post + beta_post - 2)

# Varianza e deviazione standard: misure di incertezza
varianza_posteriori <- (alpha_post * beta_post) / 
  ((alpha_post + beta_post)^2 * (alpha_post + beta_post + 1))
sd_posteriori <- sqrt(varianza_posteriori)

# Probabilità che theta superi 0.5 (la maggioranza obbedisce)
prob_maggioranza <- pbeta(
  q = 0.5, 
  shape1 = alpha_post, 
  shape2 = beta_post, 
  lower.tail = FALSE
)

# Intervallo di credibilità al 95% (HDI)
# Rappresenta la regione più densa che contiene il 95% della probabilità
intervallo_credibilita_95 <- HDInterval::hdi(
  qbeta, 
  credMass = 0.95, 
  shape1 = alpha_post, 
  shape2 = beta_post
)

La media della distribuzione a posteriori è 0.529, che rappresenta la nostra migliore stima puntuale della proporzione \(\theta\). La moda, pari a 0.531, indica il valore singolo più plausibile secondo la distribuzione a posteriori. La deviazione standard di 0.069 quantifica l’incertezza residua sulla stima, corrispondente a circa 6.9 punti percentuali.

Un risultato di particolare interesse concerne la probabilità che più della metà della popolazione manifesti obbedienza estrema in condizioni analoghe. Tale probabilità è pari a 0.664 (circa il 66.4%). Questo valore fornisce una misura diretta dell’evidenza a favore dell’ipotesi che l’obbedienza estrema sia un fenomeno maggioritario nella popolazione.

L’intervallo di credibilità al 95% si estende da 0.394 a 0.664. A differenza degli intervalli di confidenza frequentisti, possiamo interpretare questo intervallo in modo diretto e intuitivo: esiste una probabilità del 95% che la vera proporzione \(\theta\) sia contenuta in questo intervallo, data l’evidenza osservata e le nostre assunzioni iniziali. In termini percentuali, siamo 95% certi che tra il 39.4% e il 66.4% della popolazione mostrerebbe obbedienza estrema nelle condizioni sperimentali di Milgram.

2.3.5 Distribuzione predittiva a posteriori: proiezioni per studi futuri

L’approccio bayesiano consente di formulare previsioni probabilistiche per osservazioni future. Supponendo di replicare l’esperimento con un nuovo campione di 40 partecipanti, ci potremmo chiedere: quale numero di soggetti è prevedibile che mostri un’obbedienza estrema? Non possiamo rispondere a questa domanda con una stima puntuale. È necessaria invece una distribuzione di probabilità che incorpori due fonti di incertezza:

1. l’incertezza sul parametro \(\theta\), rappresentata dalla distribuzione a posteriori,
2. la variabilità campionaria intrinseca al processo binomiale.

Anche se conoscessimo il vero valore di \(\theta\), il numero di soggetti che mostrano un’obbedienza estrema in un campione futuro di quaranta varierebbe secondo la distribuzione binomiale. Ma, d’altro canto, non conosciamo \(\theta\) in maniera precisa, ma disponiamo solo della sua distribuzione a posteriori. La distribuzione predittiva a posteriori integra queste due fonti di intertezza.

Nel caso del modello Beta-Binomiale, la distribuzione predittiva ha una forma analitica chiusa nota come distribuzione Beta-Binomiale. Questa distribuzione fornisce le probabilità per ciascun possibile esito futuro integrando le due fonti di incertezza descritte in precedenza.

# Impostiamo i parametri per la previsione
dimensione_nuovo_studio <- 40

# Generiamo tutti i possibili esiti in un nuovo studio
# da 0 partecipanti obbedienti fino a tutti i 40
possibili_esiti <- 0:dimensione_nuovo_studio

# Definiamo la funzione che calcola la distribuzione Beta-Binomiale
# Questa formula combina l'incertezza su theta con la variabilità binomiale
calcola_beta_binomiale <- function(k, m, alpha, beta) {
  # k: numero di successi predetto
  # m: dimensione del campione futuro
  # alpha, beta: parametri della distribuzione a posteriori
  
  # La formula utilizza la funzione beta di Eulero
  # choose(m, k) rappresenta il coefficiente binomiale
  probabilita <- choose(m, k) * 
    beta(alpha + k, beta + m - k) / 
    beta(alpha, beta)
  
  return(probabilita)
}

# Calcoliamo la probabilità per ciascun possibile esito
probabilita_predittive <- calcola_beta_binomiale(
  k = possibili_esiti,
  m = dimensione_nuovo_studio,
  alpha = alpha_post,
  beta = beta_post
)

# Calcoliamo il valore atteso (media) della distribuzione predittiva
esito_medio_predetto <- sum(possibili_esiti * probabilita_predittive)

# Identifichiamo l'esito più probabile (moda)
esito_modale <- possibili_esiti[which.max(probabilita_predittive)]

# Creiamo un dataframe per la visualizzazione
dati_predittivi <- data.frame(
  numero_obbedienti = possibili_esiti,
  probabilita = probabilita_predittive
)

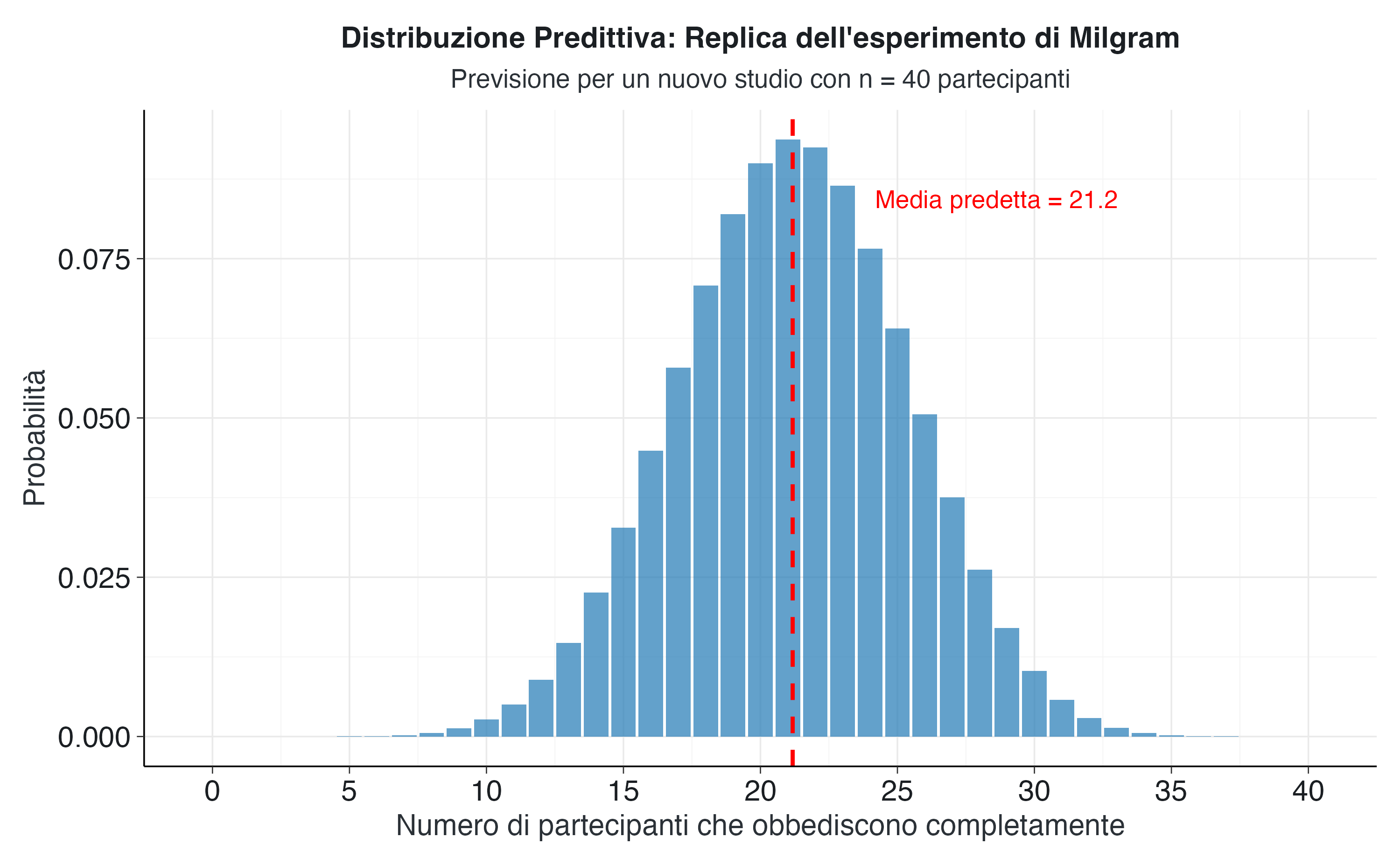
Il valore medio predetto è 21.2 partecipanti che mostrano un’obbiedienza estrama, mentre l’esito più probabile (moda) è 21 partecipanti. Questi valori riflettono la nostra migliore previsione basata sull’evidenza accumulata, ma la distribuzione completa ci fornisce informazioni molto più ricche sulle possibilità future.

# Creiamo la visualizzazione della distribuzione predittiva
ggplot(dati_predittivi, aes(x = numero_obbedienti, y = probabilita)) +
  # Grafico a barre che mostra la probabilità di ciascun esito
  geom_col(fill = "#1f78b4", alpha = 0.7, width = 0.9) +
  # Linea verticale che indica il valore medio predetto
  geom_vline(
    xintercept = esito_medio_predetto, 
    color = "red", 
    linetype = "dashed", 
    size = 1
  ) +
  # Annotazione testuale per il valore medio
  annotate(
    "text", 
    x = esito_medio_predetto + 3, 
    y = max(probabilita_predittive) * 0.9,
    label = paste("Media predetta =", round(esito_medio_predetto, 1)),
    color = "red", 
    size = 4.5,
    hjust = 0
  ) +
  labs(
    title = "Distribuzione Predittiva: Replica dell'esperimento di Milgram",
    subtitle = paste0("Previsione per un nuovo studio con n = ", dimensione_nuovo_studio, " partecipanti"),
    x = "Numero di partecipanti che obbediscono completamente",
    y = "Probabilità"
  ) +
  scale_x_continuous(breaks = seq(0, 40, by = 5)) 

La distribuzione predittiva, approssimativamente normale e centrata attorno a 21 partecipanti, combina l’incertezza sul parametro \(\theta\) e la variabilità campionaria. Presenta una lieve asimmetria, ereditata dalla forma non perfettamente simmetrica della distribuzione a posteriori di \(\theta\).

2.3.6 Quantificazione dell’incertezza predittiva

Per comprendere meglio le implicazioni pratiche di questa distribuzione, calcoliamo alcuni intervalli e probabilità di interesse. Questi valori aiutano a definire aspettative realistiche per gli studi futuri e a identificare quali risultati potrebbero essere considerati sorprendenti alla luce delle evidenze disponibili.

# Calcoliamo la distribuzione cumulativa
probabilita_cumulativa <- cumsum(probabilita_predittive)

# Determiniamo l'intervallo di predizione al 90%
# Cerchiamo i valori che racchiudono il 90% centrale della distribuzione
indice_inferiore <- which(probabilita_cumulativa >= 0.05)[1]
indice_superiore <- which(probabilita_cumulativa >= 0.95)[1]

limite_inf_90 <- possibili_esiti[indice_inferiore]
limite_sup_90 <- possibili_esiti[indice_superiore]

# Calcoliamo probabilità per esiti estremi
# Risultato "sorprendentemente basso" (meno di 15 obbedienti)
prob_molto_basso <- sum(probabilita_predittive[1:16])  # k = 0-15

# Risultato "sorprendentemente alto" (più di 30 obbedienti)
prob_molto_alto <- sum(probabilita_predittive[32:41])  # k = 30-40

# Calcoliamo la deviazione standard predittiva
varianza_predittiva <- sum((possibili_esiti - esito_medio_predetto)^2 * probabilita_predittive)
sd_predittiva <- sqrt(varianza_predittiva)

L’intervallo di predizione al 90% va da 14 a 28 partecipanti estremamente obbedienti. Ciò significa che, in una replica dell’esperimento, il numero atteso di persone estremamente obbedienti ricadrebbe in questo intervallo con una probabilità del 90%. Valori inferiori a 14 o superiori a 28 risulterebbero quindi insoliti e richiederebbero un approfondimento.

La probabilità di osservare un tasso di obbedienza “notevolmente basso” (inferiore a 15 partecipanti) è pari a 0.089 (circa 8.9%), e quantifica quanto un simile risultato si discosterebbe dalle evidenze disponibili. Allo stesso modo, la probabilità di un risultato “notevolmente alto” (oltre 30 partecipanti estremamente obbedienti) è pari a 0.011 (circa 1.1%).

La deviazione standard della distribuzione predittiva è di 4.18 partecipanti, sensibilmente maggiore di quella della distribuzione a posteriori di \(\theta\) (2.8 partecipanti). Questa differenza evidenzia come la variabilità predittiva incorpori sia l’incertezza sul parametro, sia la variabilità campionaria intrinseca, presente anche conoscendo il parametro con esattezza.

2.3.7 Implicazioni metodologiche ed etiche

La distribuzione predittiva a posteriori fornisce un fondamento quantitativo per diverse decisioni metodologiche ed etiche nella pianificazione di studi futuri. L’analisi rivela che esiste un’elevata probabilità di replicare livelli sostanziali di obbedienza estrema, con implicazioni importanti per la protezione dei partecipanti.

Dal punto di vista della pianificazione sperimentale, la distribuzione predittiva può guidare la determinazione della dimensione campionaria ottimale. Se l’obiettivo di una replica fosse stimare \(\theta\) con una precisione maggiore, potremmo utilizzare la distribuzione predittiva per calcolare quanto la nostra incertezza diminuirebbe con campioni di diverse dimensioni.

Le considerazioni etiche assumono particolare rilevanza alla luce dei risultati predittivi. La probabilità di osservare nuovamente alti livelli di obbedienza estrema sottolinea l’importanza di rigorosi protocolli di debriefing e di supporto psicologico post-sperimentale. I partecipanti che scoprono di aver obbedito a comandi potenzialmente dannosi potrebbero sperimentare qualche forma di disagio psicologico. La distribuzione predittiva quantifica l’aspettativa che una proporzione considerevole dei partecipanti possa trovarsi in questa situazione, il che rende necessario un attento bilanciamento tra il valore scientifico della replica e il benessere dei partecipanti.

Un aspetto metodologicamente rilevante riguarda la validazione del modello. Se i risultati effettivamente osservati ricadessero nelle code estreme della distribuzione predittiva, ciò suggerirebbe la necessità di rivedere il modello o le assunzioni su cui si basa. Una discrepanza sistematica tra previsioni e osservazioni potrebbe indicare l’influenza di variabili contestuali non considerate nel modello originale, come le differenze culturali, temporali o metodologiche. La distribuzione predittiva, quindi, non fornisce solo uno strumento per la pianificazione, ma anche un criterio per la validazione e il potenziale affinamento delle teorie psicologiche.

2.3.8 Aggiornamento sequenziale: l’apprendimento continuo

Un ultimo vantaggio dell’approccio bayesiano, particolarmente rilevante nel contesto della distribuzione predittiva, riguarda la possibilità di aggiornamento sequenziale. Se conducessimo una replica e osservassimo, ad esempio, che 19 partecipanti su 40 sono obbedienti, potremmo utilizzare la distribuzione a posteriori attuale come nuovo prior e aggiornare nuovamente le nostre credenze. La distribuzione a posteriori risultante rifletterebbe l’evidenza combinata di entrambi gli studi e fornirebbe una stima più precisa di θ e una distribuzione predittiva più informativa per eventuali studi futuri.

# Simuliamo un aggiornamento sequenziale con dati ipotetici da una replica
successi_replica <- 19
prove_replica <- 40

# La distribuzione a posteriori attuale diventa il nuovo prior
parametri_aggiornati <- beta_binomiale_aggiorna(
  successi = successi_replica,
  prove = prove_replica,
  alpha_prior = alpha_post,  # Il posterior attuale diventa il prior
  beta_prior = beta_post
)

alpha_post_aggiornato <- parametri_aggiornati$alpha_post
beta_post_aggiornato <- parametri_aggiornati$beta_post

# Nuova media dopo l'aggiornamento sequenziale
media_post_aggiornata <- alpha_post_aggiornato / 
  (alpha_post_aggiornato + beta_post_aggiornato)

# Nuova deviazione standard
varianza_post_aggiornata <- (alpha_post_aggiornato * beta_post_aggiornato) / 
  ((alpha_post_aggiornato + beta_post_aggiornato)^2 * 
   (alpha_post_aggiornato + beta_post_aggiornato + 1))
sd_post_aggiornata <- sqrt(varianza_post_aggiornata)

Se osservassimo 19 obbedienti in una replica con 40 partecipanti, la distribuzione a posteriori aggiornata avrebbe parametri Alpha = 46 e Beta = 45. La media si aggiornerebbe a 0.505, con una deviazione standard ridotta a 0.052. Notiamo che l’incertezza diminuisce man mano che si accumula l’evidenza: la deviazione standard dopo due studi è inferiore a quella basata su un solo studio. Ciò riflette il principio fondamentale secondo cui l’incertezza diminuisce con l’accumulo di dati.

Questo meccanismo di aggiornamento sequenziale rappresenta una formalizzazione del processo di apprendimento scientifico, in cui la conoscenza si accumula progressivamente attraverso studi successivi. Ogni nuovo studio non invalida i precedenti, ma si integra con essi, producendo stime sempre più precise e affidabili dei fenomeni di interesse.

2.4 Il modello Gamma-Poisson: la valutazione clinica degli attacchi di panico

Nel trattamento cognitivo-comportamentale del disturbo di panico, il monitoraggio della frequenza degli attacchi rappresenta un indicatore cruciale dell’efficacia della terapia. La registrazione sistematica dei sintomi permette di superare le distorsioni percettive tipiche del disturbo e di ottenere dati affidabili per valutare i progressi. I pazienti tendono infatti a sovrastimare la frequenza degli episodi nelle fasi acute e a sottovalutare i miglioramenti graduali. Un monitoraggio quantitativo offre dunque un riferimento oggettivo a supporto della valutazione clinica e del dialogo terapeutico.

Si consideri il caso di un paziente monitorato per quattro settimane consecutive nell’ambito di un protocollo terapeutico. Il registro settimanale mostra una riduzione progressiva: due attacchi nella prima settimana, uno nella seconda, nessuno nella terza e un episodio nella quarta, per un totale di quattro attacchi nel mese. Questo andamento suggerisce un miglioramento complessivo, sebbene con una certa variabilità. Per ottenere inferenze più robuste e previsioni più accurate, è tuttavia opportuno adottare un modello probabilistico che quantifichi l’incertezza e consenta aggiornamenti continui.

2.4.1 Fondamenti del modello Gamma-Poisson

Gli attacchi di panico possono essere modellati come eventi rari che si verificano in intervalli temporali definiti. La distribuzione di Poisson fornisce una rappresentazione naturale per questo tipo di fenomeni, basandosi su tre assunzioni fondamentali: gli eventi sono indipendenti l’uno dall’altro, si verificano con un tasso medio costante nel tempo e la probabilità di osservare due o più eventi nello stesso istante è trascurabile.

Nel nostro contesto clinico, l’indicatore centrale per valutare l’andamento del trattamento è il parametro \(\theta\), che rappresenta il tasso medio settimanale di attacchi di panico. Valori elevati di \(\theta\) corrispondono a una sintomatologia più frequente, mentre valori ridotti segnalano un miglior controllo dei sintomi.

L’incertezza su \(\theta\) è particolarmente elevata nelle fasi iniziali del trattamento, quando i dati osservativi sono limitati. L’approccio bayesiano affronta questa incertezza assegnando a \(\theta\) una distribuzione di probabilità a priori, che viene aggiornata alla luce dei nuovi dati. L’utilizzo di una distribuzione Gamma come prior per il parametro \(\theta\) in un modello di Poisson sfrutta il meccanismo delle famiglie coniugate, che garantisce una forma analitica chiusa per la distribuzione a posteriori.

2.4.2 Configurazione del modello e scelta del prior

Per iniziare l’analisi, dobbiamo specificare una distribuzione a priori che rifletta la nostra conoscenza preliminare sul tasso di attacchi del paziente. In assenza di informazioni dettagliate da una fase di assessment prolungata, adottiamo un prior debolmente informativo Gamma(1,1).

# Dati clinici osservati nell'arco di quattro settimane
attacchi_settimanali <- c(2, 1, 0, 1)

# Parametri della distribuzione a priori Gamma(1, 1)
a_prior <- 1
b_prior <- 1

# Calcoliamo alcune caratteristiche del prior per comprenderne le implicazioni
media_prior <- a_prior / b_prior
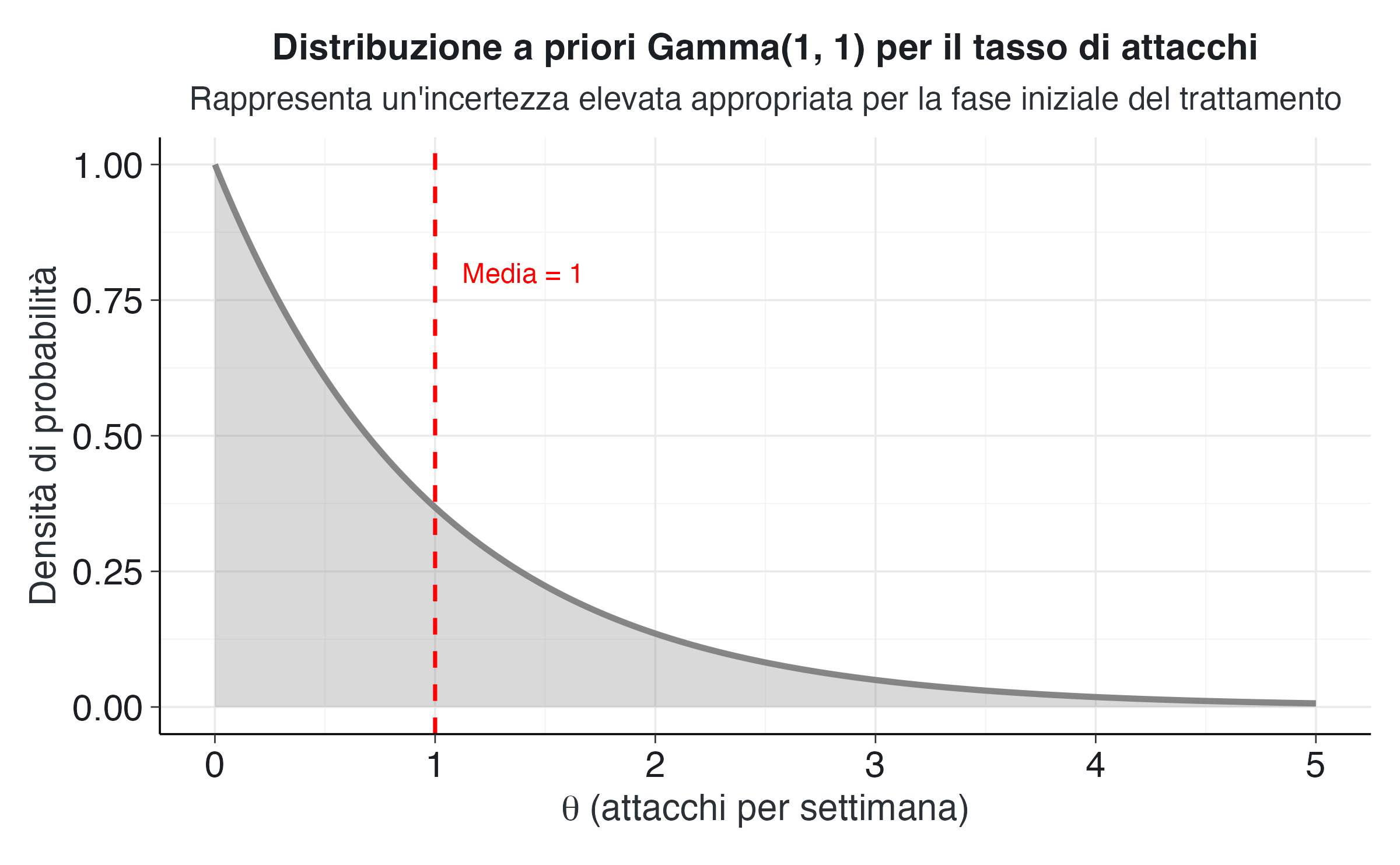
sd_prior <- sqrt(a_prior) / b_prior

La distribuzione Gamma(1,1) presenta una media di 1 attacchi settimanali e una deviazione standard di 1. Questa scelta riflette un’incertezza sostanziale: la distribuzione assegna probabilità comparabili a un’ampia gamma di valori di \(\theta\), da tassi molto bassi a valori elevati.

I parametri (1,1) hanno un’interpretazione intuitiva: corrispondono a un’osservazione virtuale di un singolo attacco in una settimana. Questa configurazione risulta appropriata in contesti caratterizzati da effettiva scarsità di informazioni preliminari, come durante il primo colloquio clinico o in assenza di dati anamnestici sufficientemente dettagliati.

# Creiamo una sequenza di possibili valori del tasso theta
theta_valori <- seq(from = 0, to = 5, length.out = 500)

# Calcoliamo la densità della distribuzione a priori
densita_prior <- dgamma(theta_valori, shape = a_prior, rate = b_prior)

# Organizziamo i dati per la visualizzazione
dati_prior <- data.frame(
  theta = theta_valori,
  densita = densita_prior
)

# Visualizziamo la distribuzione a priori
ggplot(dati_prior, aes(x = theta, y = densita)) +
  geom_line(color = "#7f7f7f", size = 1.2) +
  geom_area(fill = "#7f7f7f", alpha = 0.3) +
  geom_vline(xintercept = media_prior, linetype = "dashed", color = "red", size = 0.8) +
  annotate("text", x = media_prior + 0.4, y = max(densita_prior) * 0.8,
           label = paste("Media =", round(media_prior, 2)),
           color = "red", size = 4) +
  labs(
    title = "Distribuzione a priori Gamma(1, 1) per il tasso di attacchi",
    subtitle = "Rappresenta un'incertezza elevata appropriata per la fase iniziale del trattamento",
    x = expression(theta ~ "(attacchi per settimana)"),
    y = "Densità di probabilità"
  ) 

Il grafico mostra la forma caratteristica della distribuzione Gamma con i parametri specificati. Questa configurazione riflette un’aspettativa clinicamente plausibile per il paziente preso in considerazione: sebbene statisticamente sia più probabile osservare tassi moderati o contenuti, il modello rimane sufficientemente flessibile da adattarsi a scenari con frequenze più elevate, qualora i dati lo indichino.

2.4.3 L’aggiornamento bayesiano e la distribuzione a posteriori

Procediamo ora ad aggiornare le nostre credenze integrando le osservazioni cliniche delle quattro settimane considerate.

# Applichiamo la funzione di aggiornamento bayesiano
parametri_posteriori <- gamma_poisson_aggiorna(
  conteggi_osservati = attacchi_settimanali,
  a_prior = a_prior,
  b_prior = b_prior
)

# Estraiamo i parametri aggiornati
a_post <- parametri_posteriori$a_post
b_post <- parametri_posteriori$b_post

# Calcoliamo statistiche riassuntive della distribuzione a posteriori
tasso_medio_post <- a_post / b_post
sd_post <- sqrt(a_post) / b_post

# Calcoliamo anche un intervallo di credibilità al 95%
intervallo_credibilita_95 <- qgamma(
  p = c(0.025, 0.975),
  shape = a_post,
  rate = b_post
)

La distribuzione a posteriori risultante è Gamma(5, 5). Questi parametri aggiornati incorporano l’intera esperienza disponibile: i quattro attacchi osservati si sono sommati al singolo evento virtuale del prior (1 + 4 = 5), mentre le quattro settimane di osservazione si sono sommate all’unica settimana virtuale (1 + 4 = 5). Il tasso medio stimato è ora 1 attacchi per settimana, con una deviazione standard di 0.447.

L’intervallo di credibilità al 95% per il tasso di attacchi si estende da 0.325 a 2.048 attacchi per settimana. Possiamo interpretare questo intervallo affermando direttamente che, alla luce dei dati osservati e delle nostre assunzioni iniziali, c’è una probabilità del 95% che il vero tasso medio di attacchi del paziente sia compreso in questo intervallo. Notiamo che l’intervallo è relativamente ampio: ciò riflette il fatto che quattro settimane di osservazione forniscono informazioni limitate e mantengono un’elevata incertezza sulla stima del parametro.

# Prepariamo i dati per visualizzare prior, likelihood e posterior

# Densità del prior (già calcolata)
prior_densita <- dgamma(theta_valori, shape = a_prior, rate = b_prior)

# Per la verosimiglianza nel modello Poisson, calcoliamo la probabilità
# dei dati osservati per ogni possibile valore di theta
# La verosimiglianza totale è il prodotto delle singole verosimiglianze
calcola_likelihood_poisson <- function(theta, conteggi, n_periodi) {
  # Per ogni settimana, calcoliamo la probabilità di quel conteggio
  likelihood <- 1
  for (k in conteggi) {
    likelihood <- likelihood * dpois(k, lambda = theta)
  }
  return(likelihood)
}

likelihood_raw <- sapply(theta_valori, function(t) {
  calcola_likelihood_poisson(t, attacchi_settimanali, length(attacchi_settimanali))
})

# Densità del posterior
posterior_densita <- dgamma(theta_valori, shape = a_post, rate = b_post)

# Scaliamo la verosimiglianza per renderla visivamente confrontabile
likelihood_scaled <- likelihood_raw / max(likelihood_raw) * max(posterior_densita)

# Creiamo un dataframe per la visualizzazione
dati_complete <- data.frame(
  theta = rep(theta_valori, 3),
  densita = c(prior_densita, likelihood_scaled, posterior_densita),
  tipo = rep(
    c("Prior", "Verosimiglianza", "Posterior"),
    each = length(theta_valori)
  )
)

dati_complete$tipo <- factor(
  dati_complete$tipo,
  levels = c("Prior", "Verosimiglianza", "Posterior")
)

# Creiamo il grafico dell'aggiornamento bayesiano
ggplot(dati_complete, aes(x = theta, y = densita, color = tipo)) +
  geom_line(size = 1.3) +
  scale_color_manual(
    values = c(
      "Prior" = "#7f7f7f",
      "Verosimiglianza" = "#E69F00",
      "Posterior" = "#1f78b4"
    )
  ) +
  labs(
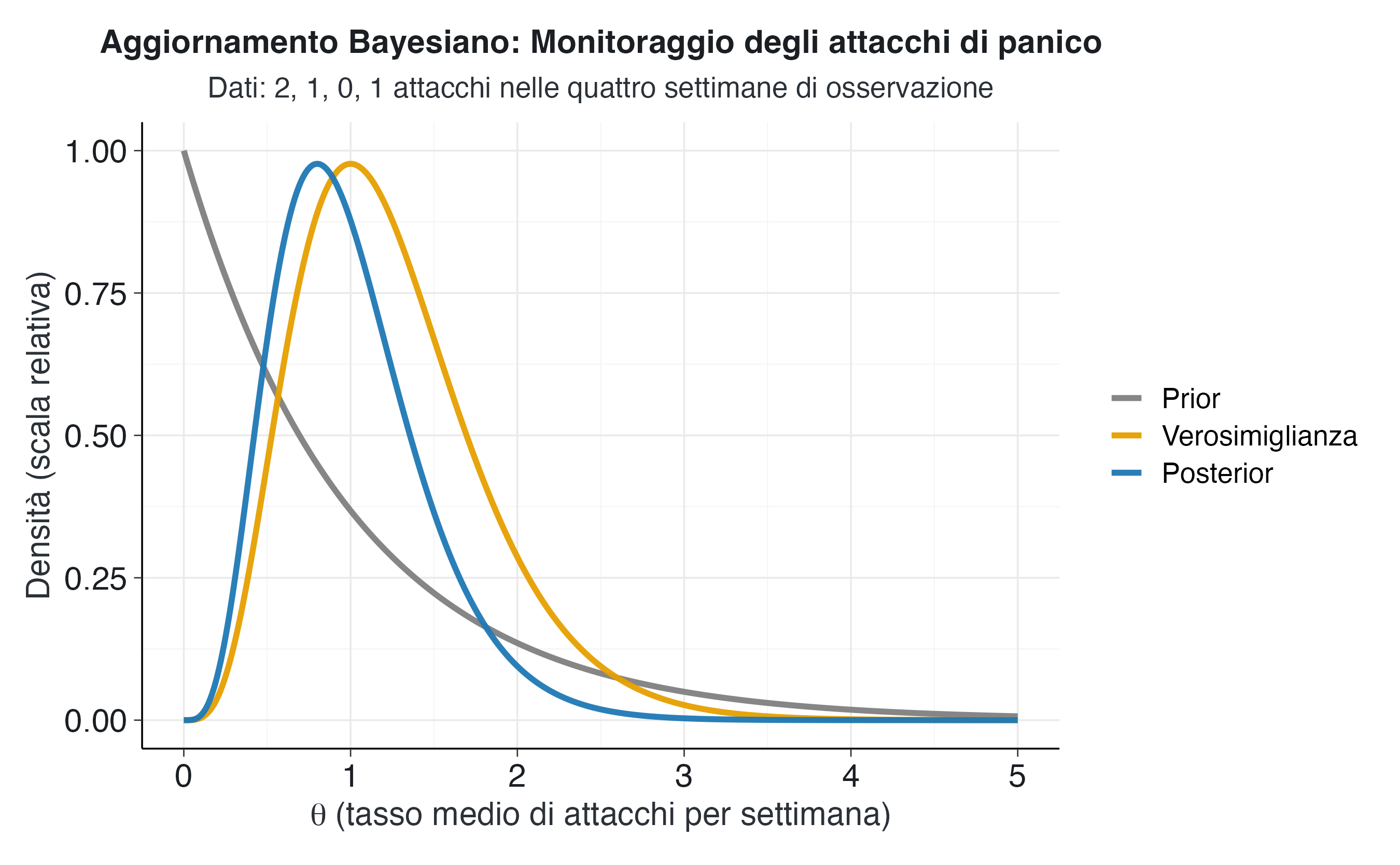
    title = "Aggiornamento Bayesiano: Monitoraggio degli attacchi di panico",
    subtitle = "Dati: 2, 1, 0, 1 attacchi nelle quattro settimane di osservazione",
    x = expression(theta ~ "(tasso medio di attacchi per settimana)"),
    y = "Densità (scala relativa)",
    color = NULL
  ) 

Il grafico illustra il processo di aggiornamento bayesiano nel monitoraggio clinico. La distribuzione a priori (in grigio) riflette l’incertezza iniziale, mentre la verosimiglianza (in arancione) presenta un picco corrispondente al tasso empirico osservato (1,0 attacchi a settimana, corrispondenti a 4 episodi in 4 settimane). La distribuzione a posteriori (blu) sintetizza queste due fonti di informazione.

La sovrapposizione tra verosimiglianza e posterior è dovuta alla scarsa informatività del prior: i dati osservati hanno quindi determinato l’aggiornamento in modo pressoché completo.

2.4.4 Valutazione rispetto a criteri di efficacia terapeutica

Per tradurre questi risultati in valutazioni clinicamente rilevanti, è utile definire criteri espliciti di efficacia terapeutica. Supponiamo che il trattamento sia considerato efficace se riduce il tasso medio di attacchi al di sotto di 0.5 episodi per settimana. Questa soglia corrisponde grossomodo a non più di due attacchi al mese, un livello che molti clinici considererebbero indicativo di un buon controllo sintomatologico.

# Definiamo la soglia di efficacia clinica
soglia_efficacia <- 0.5

# Calcoliamo la probabilità che il tasso sia inferiore alla soglia
probabilita_sotto_soglia <- pgamma(
  q = soglia_efficacia,
  shape = a_post,
  rate = b_post
)

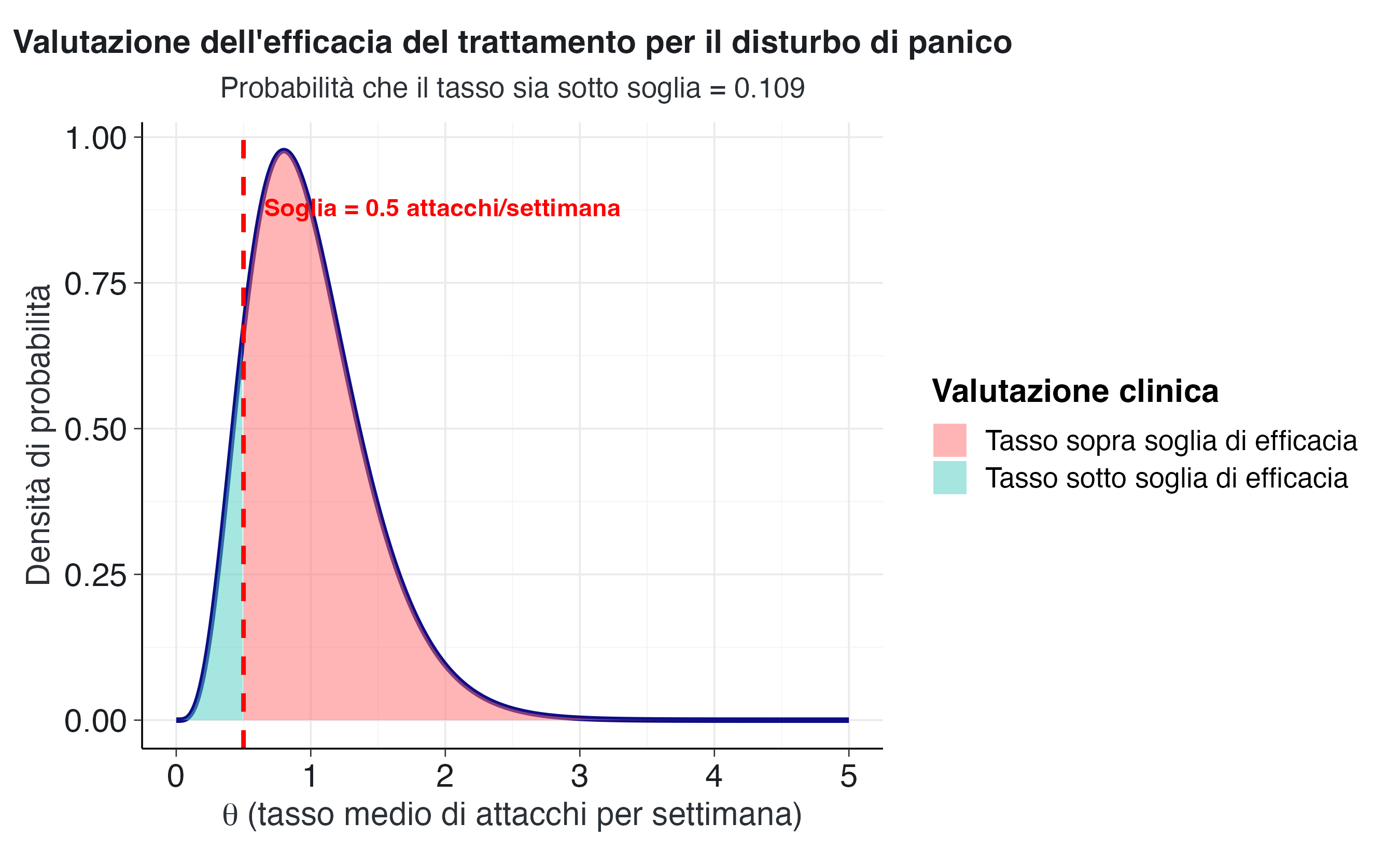
La probabilità che il tasso effettivo di attacchi sia inferiore a 0.5 episodi settimanali è 0.109 (circa 10.9%). Questo valore indica che esistono scarse evidenze a sostegno del raggiungimento dell’obiettivo terapeutico. In termini pratici, su 100 scenari plausibili per questo paziente, solo in circa 11 di essi il tasso effettivo di attacchi risulterebbe inferiore alla soglia desiderata.

# Creiamo una visualizzazione che evidenzia le regioni di efficacia

# Identifichiamo quali valori cadono sopra o sotto la soglia
dati_decisione <- data.frame(
  theta = theta_valori,
  densita = posterior_densita,
  regione = ifelse(
    theta_valori < soglia_efficacia,
    "Tasso sotto soglia di efficacia",
    "Tasso sopra soglia di efficacia"
  )
)

ggplot(dati_decisione, aes(x = theta, y = densita)) +
  geom_line(color = "navy", size = 1.2) +
  geom_area(aes(fill = regione), alpha = 0.5) +
  geom_vline(
    xintercept = soglia_efficacia,
    linetype = "dashed",
    color = "red",
    size = 1
  ) +
  annotate(
    "text",
    x = soglia_efficacia + 0.15,
    y = max(posterior_densita) * 0.9,
    label = paste0("Soglia = ", soglia_efficacia, " attacchi/settimana"),
    color = "red",
    size = 4,
    fontface = "bold",
    hjust = 0
  ) +
  scale_fill_manual(
    values = c(
      "Tasso sotto soglia di efficacia" = "#4ECDC4",
      "Tasso sopra soglia di efficacia" = "#FF6B6B"
    )
  ) +
  labs(
    title = "Valutazione dell'efficacia del trattamento per il disturbo di panico",
    subtitle = paste0(
      "Probabilità che il tasso sia sotto soglia = ",
      round(probabilita_sotto_soglia, 3)
    ),
    x = expression(theta ~ "(tasso medio di attacchi per settimana)"),
    y = "Densità di probabilità",
    fill = "Valutazione clinica"
  ) 

Il grafico visualizza la distribuzione di probabilità del tasso di attacchi in relazione alla soglia di efficacia. L’area verde (10.9%) rappresenta i valori per i quali il trattamento sarebbe considerato efficace, mentre l’area rossa (89.1%) indica valori superiori alla soglia desiderata. La netta prevalenza dell’area rossa conferma che, allo stato attuale, non possiamo considerare il trattamento pienamente efficace secondo il criterio stabilito.

2.4.5 Raccomandazioni cliniche basate sull’evidenza

Sulla base di questa analisi quantitativa, possiamo formulare raccomandazioni cliniche esplicite e graduate in funzione della forza dell’evidenza. L’approccio bayesiano permette di evitare decisioni dicotomiche rigide, favorendo invece una valutazione sfumata che riflette l’incertezza reale della situazione clinica.

# Formuliamo raccomandazioni basate su soglie probabilistiche graduate
if (probabilita_sotto_soglia > 0.8) {
  raccomandazione <- "Il trattamento mostra evidenza forte di efficacia. La strategia attuale dovrebbe essere mantenuta per consolidare i risultati ottenuti. Si raccomanda di continuare il monitoraggio per confermare la stabilità del miglioramento nel tempo."
} else if (probabilita_sotto_soglia > 0.5) {
  raccomandazione <- "Il trattamento mostra progressi significativi ma l'obiettivo di remissione non è ancora chiaramente raggiunto. Si raccomanda di continuare il protocollo attuale con monitoraggio ravvicinato per almeno altre quattro settimane. Se il pattern di miglioramento si conferma, la probabilità di efficacia aumenterà con l'accumulo di evidenza."
} else if (probabilita_sotto_soglia > 0.3) {
  raccomandazione <- "Il trattamento mostra una tendenza positiva ma il tasso di attacchi rimane sopra la soglia target. Si raccomanda di intensificare il supporto nelle fasce orarie o situazioni identificate come ad alto rischio. Potrebbe essere utile integrare tecniche di gestione acuta dell'ansia o rivedere l'aderenza agli esercizi di esposizione."
} else {
  raccomandazione <- "L'evidenza attuale non supporta l'efficacia del protocollo corrente. Si raccomanda una rivalutazione approfondita dell'intervento e la considerazione di strategie alternative, come l'integrazione di farmacoterapia, l'intensificazione della frequenza delle sedute, o l'esplorazione di fattori di mantenimento non precedentemente identificati."
}

Nel caso specifico del nostro paziente, con una probabilità del 10.9% di avere un tasso sotto soglia, la raccomandazione appropriata è la seguente.

L’evidenza attuale non supporta l’efficacia del protocollo corrente. Si raccomanda una rivalutazione approfondita dell’intervento e la considerazione di strategie alternative, come l’integrazione di farmacoterapia, l’intensificazione della frequenza delle sedute, o l’esplorazione di fattori di mantenimento non precedentemente identificati.

2.4.6 Previsioni per la settimana successiva: la distribuzione predittiva

Uno degli aspetti più utili dell’analisi bayesiana nel contesto clinico è la possibilità di formulare previsioni esplicite per il futuro prossimo. Queste non si limitano a estrapolare i dati osservati, ma integrano sistematicamente due fonti di incertezza: quella sul parametro soggiacente e quella intrinseca alla variabilità sintomatologica.

Queste previsioni si basano sulla distribuzione predittiva a posteriori, che nel modello Gamma-Poisson si ottiene integrando l’incertezza residua sul tasso medio \(\theta\). Formalmente:

\[ p(y_{n+1} \mid \mathbf{y}) = \int p(y_{n+1} \mid \theta), p(\theta \mid \mathbf{y}), d\theta, \] dove

• \(p(\theta \mid \mathbf{y}) = \mathrm{Gamma}(\theta \mid a_{\text{post}}, b_{\text{post}})\) è la distribuzione a posteriori del tasso di occorrenza,
• \(p(y_{n+1} \mid \theta) = \mathrm{Poisson}(y_{n+1} \mid \theta)\) è la verosimiglianza per nuove osservazioni.

L’integrazione di queste due componenti ammette una soluzione analitica: la distribuzione predittiva a posteriori segue una distribuzione Binomiale Negativa:

\[ p(y_{n+1} \mid \mathbf{y}) = \mathrm{NegBin}\!\left(y_{n+1} \mid r = a_{\text{post}},\, p = \frac{b_{\text{post}}}{b_{\text{post}} + 1}\right). \]

# La distribuzione predittiva per il modello Gamma-Poisson è una Binomiale Negativa
# Calcoliamo i parametri di questa distribuzione

# I parametri della Binomiale Negativa sono:
# r (size) = a_post
# p (prob) = b_post / (b_post + 1)
r_pred <- a_post
p_pred <- b_post / (b_post + 1)

# Generiamo possibili valori per il numero di attacchi nella prossima settimana
possibili_attacchi <- 0:10

# Calcoliamo la probabilità di ciascun esito
probabilita_predittive <- dnbinom(
  x = possibili_attacchi,
  size = r_pred,
  prob = p_pred
)

# Calcoliamo il numero atteso di attacchi
attacchi_attesi <- sum(possibili_attacchi * probabilita_predittive)

# Calcoliamo probabilità cumulative per intervalli di interesse
prob_zero_attacchi <- probabilita_predittive[1]
prob_massimo_uno <- sum(probabilita_predittive[1:2])
prob_tre_o_piu <- sum(probabilita_predittive[4:length(probabilita_predittive)])

# Creiamo un dataframe per la visualizzazione
dati_predittivi <- data.frame(
  numero_attacchi = possibili_attacchi,
  probabilita = probabilita_predittive
)

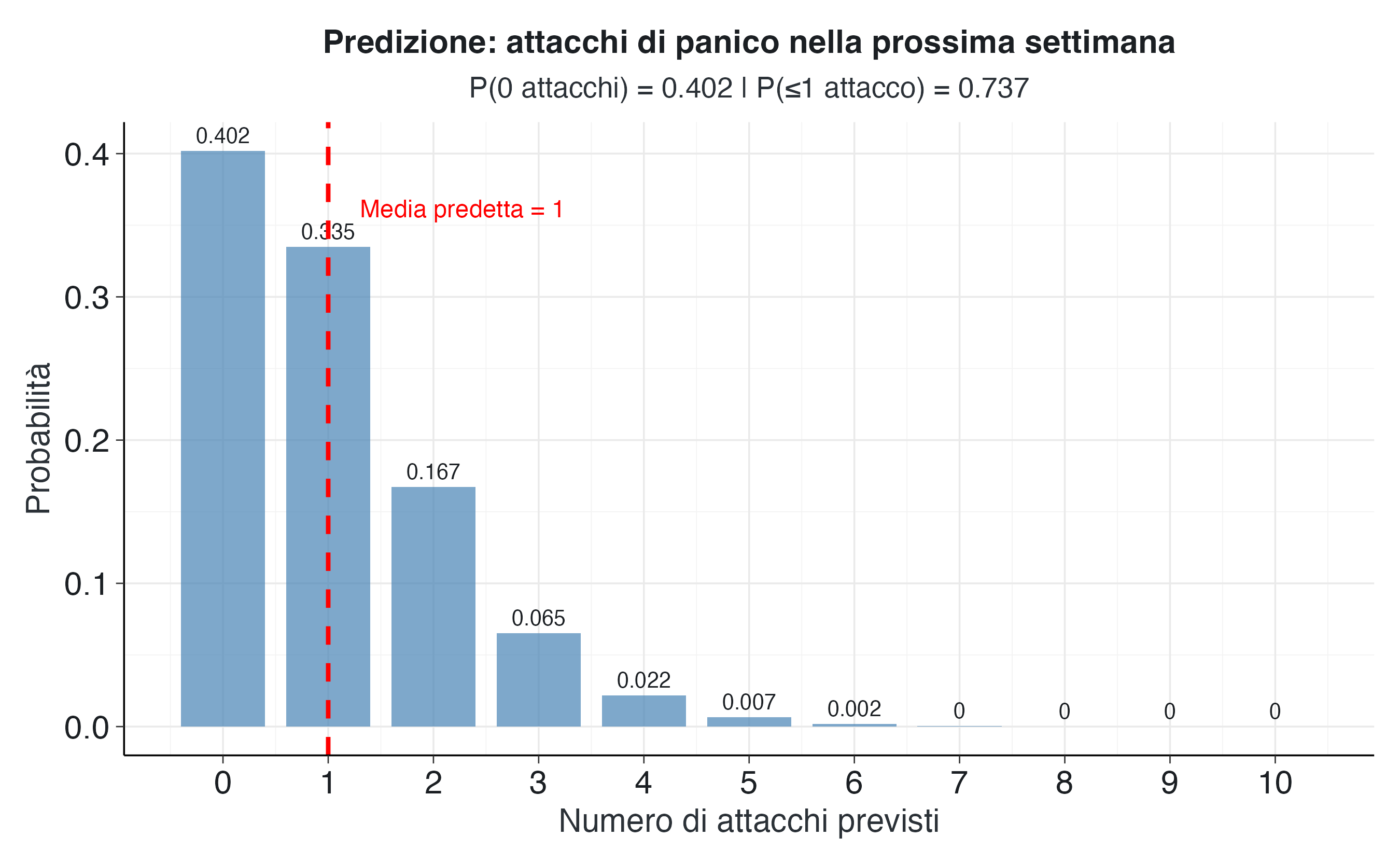
Per la prossima settimana, il numero atteso di attacchi è 1, in linea con il tasso medio stimato. La distribuzione predittiva offre tuttavia un quadro più articolato. La probabilità di non osservare alcun attacco nella settimana successiva è pari a 0.402, circa il 40.2%. La probabilità di osservare al massimo un attacco è pari a 0.737, ovvero circa il 73.7%. Al contrario, la probabilità di osservare tre o più attacchi è pari a 0.096, circa il 9.6%.

# Creiamo la visualizzazione della distribuzione predittiva
ggplot(dati_predittivi, aes(x = numero_attacchi, y = probabilita)) +
  geom_col(fill = "steelblue", alpha = 0.7, width = 0.8) +
  geom_text(
    aes(label = round(probabilita, 3)),
    vjust = -0.5,
    size = 3.5
  ) +
  geom_vline(
    xintercept = attacchi_attesi,
    color = "red",
    linetype = "dashed",
    size = 1
  ) +
  annotate(
    "text",
    x = attacchi_attesi + 0.3,
    y = max(probabilita_predittive) * 0.9,
    label = paste("Media predetta =", round(attacchi_attesi, 2)),
    color = "red",
    size = 4,
    hjust = 0
  ) +
  labs(
    title = "Predizione: attacchi di panico nella prossima settimana",
    subtitle = paste0(
      "P(0 attacchi) = ", round(prob_zero_attacchi, 3),
      " | P(≤1 attacco) = ", round(prob_massimo_uno, 3)
    ),
    x = "Numero di attacchi previsti",
    y = "Probabilità"
  ) +
  scale_x_continuous(breaks = possibili_attacchi) 

Queste previsioni probabilistiche possono essere utilizzate in diversi modi nella pratica clinica. Innanzitutto, aiutano a costruire aspettative realistiche nel paziente, riducendo l’ansia anticipatoria che deriva dall’incertezza sul futuro. Possiamo comunicare al paziente che, sebbene ci aspettiamo circa un attacco nella settimana successiva, c’è una buona probabilità (circa il 40.2%) di non averne affatto. Questo tipo di comunicazione trasparente e quantitativa può ridurre la tendenza del paziente alla catastrofizzazione di eventuali ricadute.

In secondo luogo, le previsioni forniscono un riferimento per valutare l’evoluzione sintomatologica. Se nella settimana successiva il paziente non dovesse sperimentare attacchi, questo risultato cadrebbe nel 40.2% più probabile delle possibilità, confermando il pattern di miglioramento. Al contrario, se si verificassero tre o più attacchi (probabilità del 9.6%), questo suggerirebbe un peggioramento che merita attenzione clinica immediata.

2.4.7 Comunicazione terapeutica evidence-based

La traduzione dei risultati in un linguaggio accessibile rappresenta un elemento fondamentale per l’alleanza terapeutica. L’approccio bayesiano, grazie alla sua capacità di quantificare l’incertezza ed esprimere probabilità esplicite, si rivela particolarmente adatto a una comunicazione trasparente e fondata sui dati.

Un esempio di comunicazione efficace potrebbe essere formulato nel modo seguente: “Sulla base dei dati delle ultime quattro settimane, abbiamo osservato un miglioramento complessivo nella frequenza dei suoi attacchi di panico. In media, stiamo osservando circa un attacco a settimana, rispetto ai due della prima settimana. Per la prossima settimana, ci aspettiamo in media circa un episodio, ma c’è una probabilità concreta, pari a circa il 40.2%, che lei non abbia alcun attacco. Questo è un segnale incoraggiante del fatto che le strategie che stiamo applicando stanno cominciando a produrre effetti positivi.”

Questa formulazione evita sia un eccessivo ottimismo sia un ingiustificato pessimismo. Riconosce esplicitamente il miglioramento osservato, quantifica le aspettative in modo realistico e sottolinea la possibilità di ulteriori progressi. Inoltre, comunicare basandosi sulle probabilità aiuta il paziente a sviluppare una tolleranza più adeguata all’incertezza, una competenza psicologica fondamentale per chi soffre di disturbi d’ansia.

2.4.8 Aggiornamento continuo e apprendimento progressivo

Un altro vantaggio dell’approccio bayesiano nel monitoraggio clinico è la possibilità di aggiornamento sequenziale, man mano che nuovi dati diventano disponibili. La distribuzione a posteriori ottenuta dopo quattro settimane può essere utilizzata come prior per l’analisi della quinta settimana e così via. Questo meccanismo formalizza il processo naturale di apprendimento clinico, in cui le valutazioni si affinano progressivamente con l’accumulo di esperienza.

# Simuliamo un aggiornamento sequenziale con dati ipotetici dalla quinta settimana
# Supponiamo di osservare 0 attacchi nella quinta settimana
attacchi_settimana_5 <- 0

# La distribuzione a posteriori attuale diventa il nuovo prior
parametri_aggiornati <- gamma_poisson_aggiorna(
  conteggi_osservati = attacchi_settimana_5,
  a_prior = a_post,  # Il posterior attuale diventa il prior
  b_prior = b_post
)

a_post_aggiornato <- parametri_aggiornati$a_post
b_post_aggiornato <- parametri_aggiornati$b_post

# Nuova stima del tasso dopo l'aggiornamento
tasso_aggiornato <- a_post_aggiornato / b_post_aggiornato
sd_aggiornato <- sqrt(a_post_aggiornato) / b_post_aggiornato

# Nuova probabilità di essere sotto soglia
prob_sotto_soglia_aggiornata <- pgamma(
  q = soglia_efficacia,
  shape = a_post_aggiornato,
  rate = b_post_aggiornato
)

Se nella quinta settimana il paziente non dovesse sperimentare alcun attacco, la distribuzione a posteriori si aggiornerà a Gamma(5, 6). Il tasso medio stimato scenderebbe a 0.833 attacchi per settimana, con una deviazione standard ridotta a 0.373. La probabilità di essere sotto la soglia di efficacia aumenterebbe a 0.185, ovvero circa il 18.5%. Questo miglioramento nella valutazione riflette sia la riduzione del tasso stimato, sia la maggiore certezza derivante dall’osservazione di cinque settimane anziché di quattro.

Questo meccanismo di aggiornamento continuo consente al clinico di adattare le valutazioni e le decisioni terapeutiche in modo flessibile e basato sull’evidenza. Ogni settimana fornisce nuove informazioni che si integrano con quelle precedenti, producendo stime sempre più precise e affidabili. L’incertezza diminuisce progressivamente con l’estensione del periodo di osservazione, consentendo decisioni terapeutiche sempre più sicure.

In conclusione, il modello Gamma-Poisson fornisce un quadro rigoroso ma accessibile per il monitoraggio quantitativo dei sintomi in psicologia clinica. La sua applicazione al disturbo di panico mostra come l’inferenza bayesiana possa supportare la pratica basata sull’evidenza, fornendo strumenti concreti per valutare l’efficacia terapeutica, formulare previsioni informate e comunicare in modo trasparente con i pazienti.

2.5 Modello esponenziale-gamma per il monitoraggio dei tempi tra episodi comportamentali

Nel contesto educativo, il monitoraggio dei comportamenti dirompenti è una componente essenziale per valutare l’efficacia degli interventi comportamentali. Mentre l’approccio tradizionale si concentra spesso sul conteggio degli episodi problematici in intervalli di tempo prestabiliti, un’alternativa complementare consiste nel misurare l’intervallo di tempo tra un episodio e il successivo. Questo approccio temporale è particolarmente rilevante quando l’obiettivo dell’intervento è quello di aumentare la durata dei periodi di comportamento adeguato, allungando progressivamente gli intervalli liberi da episodi problematici.

Consideriamo il caso di un bambino in età scolare che manifesta comportamenti dirompenti durante le attività didattiche. Viene implementato un intervento educativo basato sul rinforzo positivo e sulle strategie di autoregolazione con l’obiettivo di ridurre la frequenza di questi episodi. Durante una settimana di osservazione intensiva, sono stati registrati i seguenti intervalli temporali tra episodi consecutivi: 0.5, 1.2, 0.8 e 2.4 ore. Questi dati costituiscono la base empirica per stimare l’efficacia dell’intervento e formulare previsioni sul comportamento futuro.

2.5.1 Fondamenti del modello esponenziale e differenze con il modello di Poisson

La distribuzione esponenziale fornisce il modello probabilistico naturale per i tempi di attesa tra eventi che si verificano secondo un processo di Poisson. Mentre il modello di Poisson descrive il numero di eventi che si verificano in un intervallo di tempo fisso, la distribuzione esponenziale descrive il tempo che intercorre tra un evento e il successivo. Questa dualità matematica riflette due modi complementari di osservare lo stesso fenomeno sottostante.

Se gli episodi comportamentali si verificano con un tasso costante, espresso in eventi per ora, pari a \(\theta\), allora il tempo \(T\) che intercorre tra un episodio e il successivo segue una distribuzione esponenziale con parametro \(\theta\). Il valore atteso di questo tempo è 1/\(\theta\), una quantità di immediata interpretazione comportamentale. Per esempio, se il tasso è di 0.5 episodi per ora, il tempo medio tra un episodio e l’altro è di 2 ore (1/0.5). Un obiettivo educativo tipico consiste nell’aumentare questo tempo medio, corrispondentemente riducendo il tasso \(\theta\).

La distribuzione Gamma si conferma come il prior coniugato anche per il modello esponenziale, consentendo un aggiornamento bayesiano esprimibile in forma analitica chiusa. Tuttavia, è fondamentale comprendere che i dati presentano una struttura diversa rispetto al caso della distribuzione di Poisson. Nel modello Gamma-Poisson si osservano i conteggi degli eventi in intervalli fissi, mentre nel modello Gamma-Esponenziale si osservano le durate temporali tra gli eventi. Le formule di aggiornamento riflettono questa differenza fondamentale nella natura delle osservazioni.

2.5.2 Configurazione del modello e interpretazione del prior

Per iniziare l’analisi, specifichiamo una distribuzione a priori che esprima la nostra conoscenza preliminare sul tasso di episodi comportamentali. In assenza di dati storici dettagliati sul bambino, adottiamo un prior debole Gamma(1,1) che riflette un’ampia incertezza appropriata per la fase iniziale dell’intervento.

# Dati osservati: intervalli temporali tra episodi consecutivi (in ore)
intervalli_temporali <- c(0.5, 1.2, 0.8, 2.4)

# Parametri della distribuzione a priori Gamma(1, 1)
a_prior <- 1
b_prior <- 1

# Calcoliamo alcune caratteristiche del prior per comprenderne le implicazioni
# Nel modello esponenziale, il tasso medio è a/b
tasso_prior <- a_prior / b_prior
# Il tempo medio tra eventi è l'inverso del tasso
tempo_medio_prior <- 1 / tasso_prior

# Intervallo di credibilità al 95% per il tasso a priori
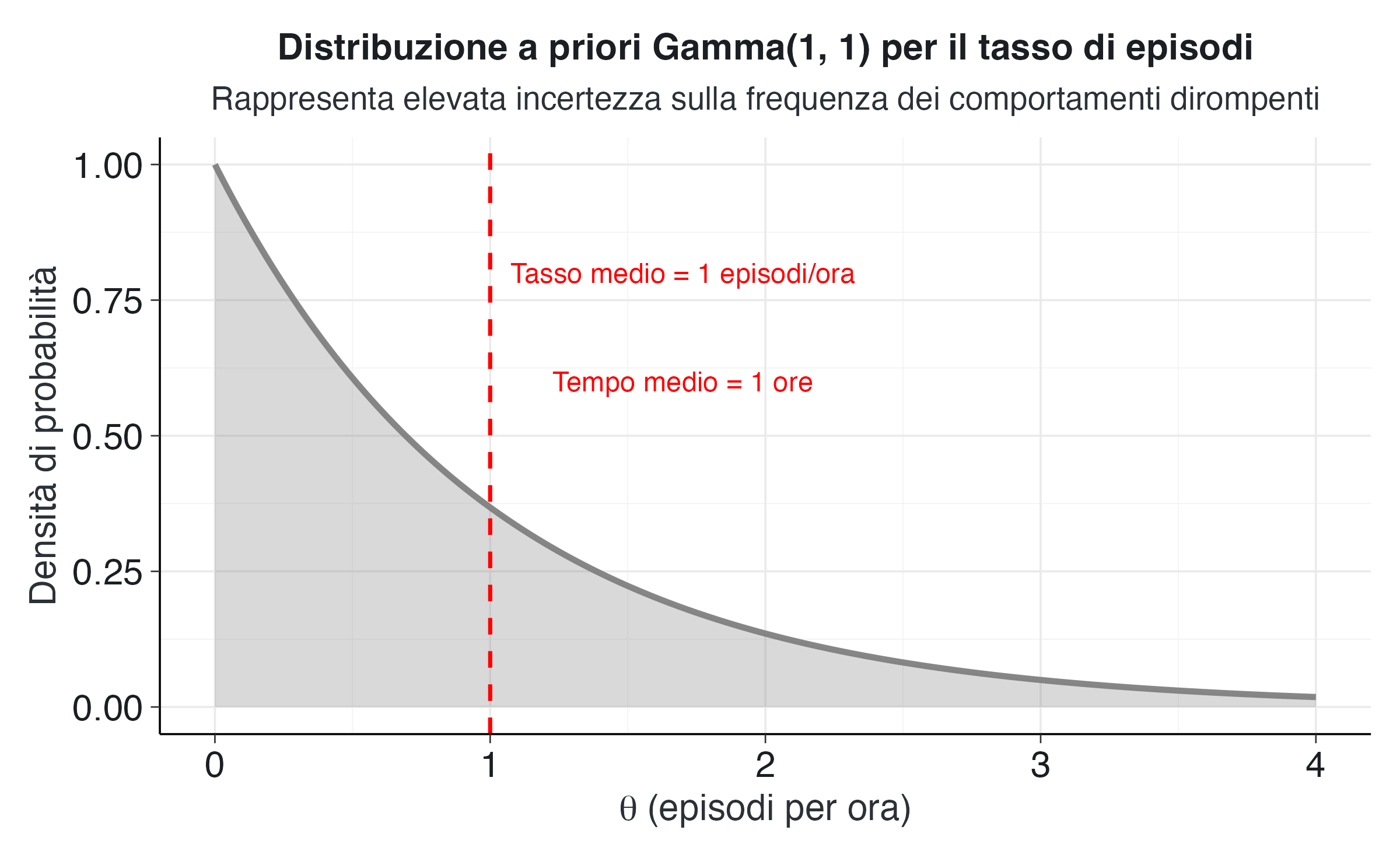
intervallo_tasso_prior <- qgamma(c(0.025, 0.975), shape = a_prior, rate = b_prior)

La distribuzione Gamma(1,1) per il tasso \(\theta\) corrisponde a un tempo medio atteso tra gli episodi pari a 1 ore. In questo contesto, l’interpretazione dei parametri è la seguente: il parametro di forma \(a = 1\) indica che disponiamo dell’equivalente di un’unica osservazione preliminare, mentre il parametro di scala \(b = 1\) (ora) rappresenta la durata totale di tale osservazione. In pratica, questo prior equivale a un’unica osservazione virtuale di un singolo episodio avvenuto dopo un’ora di monitoraggio.

L’intervallo di credibilità al 95% per il tasso a priori si estende da 0.025 a 3.689 episodi per ora. Questo intervallo molto ampio riflette l’elevata incertezza iniziale. In termini di tempo medio tra episodi, questo corrisponde a un intervallo da 0.27 a 39.5 ore, una gamma che copre situazioni molto diverse dal punto di vista educativo.

# Creiamo una sequenza di possibili valori del tasso theta
theta_valori <- seq(from = 0, to = 4, length.out = 500)

# Calcoliamo la densità della distribuzione a priori
densita_prior <- dgamma(theta_valori, shape = a_prior, rate = b_prior)

# Organizziamo i dati per la visualizzazione
dati_prior <- data.frame(
  theta = theta_valori,
  densita = densita_prior
)

# Visualizziamo la distribuzione a priori
ggplot(dati_prior, aes(x = theta, y = densita)) +
  geom_line(color = "#7f7f7f", size = 1.2) +
  geom_area(fill = "#7f7f7f", alpha = 0.3) +
  geom_vline(xintercept = tasso_prior, linetype = "dashed", color = "red", size = 0.8) +
  annotate("text", x = tasso_prior + 0.7, y = max(densita_prior) * 0.8,
           label = paste("Tasso medio =", round(tasso_prior, 2), "episodi/ora"),
           color = "red", size = 4) +
  annotate("text", x = tasso_prior + 0.7, y = max(densita_prior) * 0.6,
           label = paste("Tempo medio =", round(tempo_medio_prior, 2), "ore"),
           color = "red", size = 4) +
  labs(
    title = "Distribuzione a priori Gamma(1, 1) per il tasso di episodi",
    subtitle = "Rappresenta elevata incertezza sulla frequenza dei comportamenti dirompenti",
    x = expression(theta ~ "(episodi per ora)"),
    y = "Densità di probabilità"
  ) 

Il grafico mostra la forma caratteristica della distribuzione Gamma(1,1). Questa forma esprime una preferenza debole per tassi moderati o bassi, pur rimanendo sufficientemente vaga da permettere ai dati di dominare l’aggiornamento bayesiano.

2.5.3 Statistiche descrittive e prime osservazioni

Prima di procedere con l’aggiornamento bayesiano, è utile esaminare le caratteristiche empiriche dei dati osservati. Queste statistiche descrittive forniscono un’intuizione preliminare sui pattern comportamentali e suggeriscono cosa possiamo aspettarci dalla distribuzione a posteriori.

# Calcoliamo statistiche descrittive dei tempi osservati
numero_intervalli <- length(intervalli_temporali)
tempo_totale <- sum(intervalli_temporali)
tempo_medio_osservato <- mean(intervalli_temporali)
tempo_minimo <- min(intervalli_temporali)
tempo_massimo <- max(intervalli_temporali)

# Il tasso empirico è l'inverso del tempo medio
tasso_empirico <- 1 / tempo_medio_osservato

Nei dati osservati abbiamo registrato 4 intervalli temporali per un totale di 4.9 ore. Il tempo medio tra episodi è pari a circa 1.23 ore, corrispondente a un tasso empirico di circa 0.816 episodi all’ora. La variabilità è considerevole: l’intervallo più breve è stato di 0.5 ore, mentre il più lungo ha raggiunto 2.4 ore. Questa variabilità riflette la natura stocastica del comportamento e sottolinea l’importanza di utilizzare un modello probabilistico che tenga conto dell’incertezza.

L’osservazione di un intervallo particolarmente lungo (2.4 ore) è incoraggiante dal punto di vista educativo, in quanto suggerisce che il bambino è in grado di mantenere comportamenti adeguati per periodi prolungati. Tuttavia, la presenza di intervalli brevi indica che il controllo comportamentale non è ancora stabile. L’obiettivo dell’intervento è aumentare sia la media che la consistenza dei tempi tra gli episodi.

2.5.4 L’aggiornamento bayesiano nel modello esponenziale

Procediamo ora ad aggiornare le nostre credenze integrando i dati osservati, applicando la funzione di aggiornamento bayesiano al modello Gamma-Esponenziale.

# Applichiamo la funzione di aggiornamento bayesiano
parametri_posteriori <- gamma_esponenziale_aggiorna(
  tempi_osservati = intervalli_temporali,
  a_prior = a_prior,
  b_prior = b_prior
)

# Estraiamo i parametri aggiornati
a_post <- parametri_posteriori$a_post
b_post <- parametri_posteriori$b_post

# Calcoliamo statistiche riassuntive della distribuzione a posteriori
tasso_medio_post <- a_post / b_post
sd_tasso_post <- sqrt(a_post) / b_post

# Per il tempo medio tra episodi, dobbiamo campionare dalla distribuzione
# del tasso e poi trasformare in tempi (T = 1/theta)
set.seed(123)
n_campioni <- 10000
campioni_tasso <- rgamma(n_campioni, shape = a_post, rate = b_post)
campioni_tempo <- 1 / campioni_tasso

# Statistiche del tempo medio tra episodi
tempo_medio_post <- mean(campioni_tempo)
sd_tempo_post <- sd(campioni_tempo)
intervallo_tempo_95 <- quantile(campioni_tempo, probs = c(0.025, 0.975))

# Intervallo di credibilità per il tasso
intervallo_tasso_95 <- qgamma(c(0.025, 0.975), shape = a_post, rate = b_post)

La distribuzione a posteriori risultante è Gamma(5, 5.9). Questi parametri aggiornati riflettono l’accumulo di esperienza osservativa: i 4 intervalli osservati si sono sommati al singolo intervallo virtuale del prior (1 + 4 = 5), mentre le 4.9 ore totali osservate si sono sommate all’ora virtuale del prior (1 + 4.9 = 5.9).

Il tasso medio stimato è ora pari a 0.847 episodi all’ora, con una deviazione standard di 0.379. Questi valori sono molto vicini alle stime empiriche e riflettono il fatto che il prior debole ha avuto un’influenza minima sui dati osservati. L’intervallo di credibilità al 95% per il tasso si estende da 0.275 a 1.736 episodi per ora.

Dal punto di vista educativo, è più intuitivo ragionare in termini di tempo medio tra gli episodi piuttosto che in termini di tasso. Il tempo medio stimato tra gli episodi è di 1.48 ore, con una deviazione standard di 0.85 ore. L’intervallo di credibilità al 95% per il tempo medio si estende da 0.59 ore a 3.61 ore. Possiamo interpretare questo risultato affermando che, sulla base delle osservazioni effettuate, siamo certi al 95% che il tempo medio effettivo tra gli episodi del bambino sia compreso in questo intervallo.

# Prepariamo i dati per visualizzare prior, likelihood e posterior

# Densità del prior (già calcolata)
prior_densita <- dgamma(theta_valori, shape = a_prior, rate = b_prior)

# Per la verosimiglianza nel modello esponenziale, calcoliamo la probabilità
# dei dati osservati per ogni possibile valore di theta
# La verosimiglianza per ciascun tempo è theta * exp(-theta * t)
calcola_likelihood_esponenziale <- function(theta, tempi) {
  # Per ogni tempo osservato, calcoliamo la densità esponenziale
  likelihood <- 1
  for (t in tempi) {
    likelihood <- likelihood * dexp(t, rate = theta)
  }
  return(likelihood)
}

likelihood_raw <- sapply(theta_valori, function(t) {
  calcola_likelihood_esponenziale(t, intervalli_temporali)
})

# Densità del posterior
posterior_densita <- dgamma(theta_valori, shape = a_post, rate = b_post)

# Scaliamo la verosimiglianza per renderla visivamente confrontabile
likelihood_scaled <- likelihood_raw / max(likelihood_raw) * max(posterior_densita)

# Creiamo un dataframe per la visualizzazione
dati_complete <- data.frame(
  theta = rep(theta_valori, 3),
  densita = c(prior_densita, likelihood_scaled, posterior_densita),
  tipo = rep(
    c("Prior", "Verosimiglianza", "Posterior"),
    each = length(theta_valori)
  )
)

dati_complete$tipo <- factor(
  dati_complete$tipo,
  levels = c("Prior", "Verosimiglianza", "Posterior")
)

# Creiamo il grafico dell'aggiornamento bayesiano
ggplot(dati_complete, aes(x = theta, y = densita, color = tipo)) +
  geom_line(size = 1.3) +
  scale_color_manual(
    values = c(
      "Prior" = "#7f7f7f",
      "Verosimiglianza" = "#E69F00",
      "Posterior" = "#1f78b4"
    )
  ) +
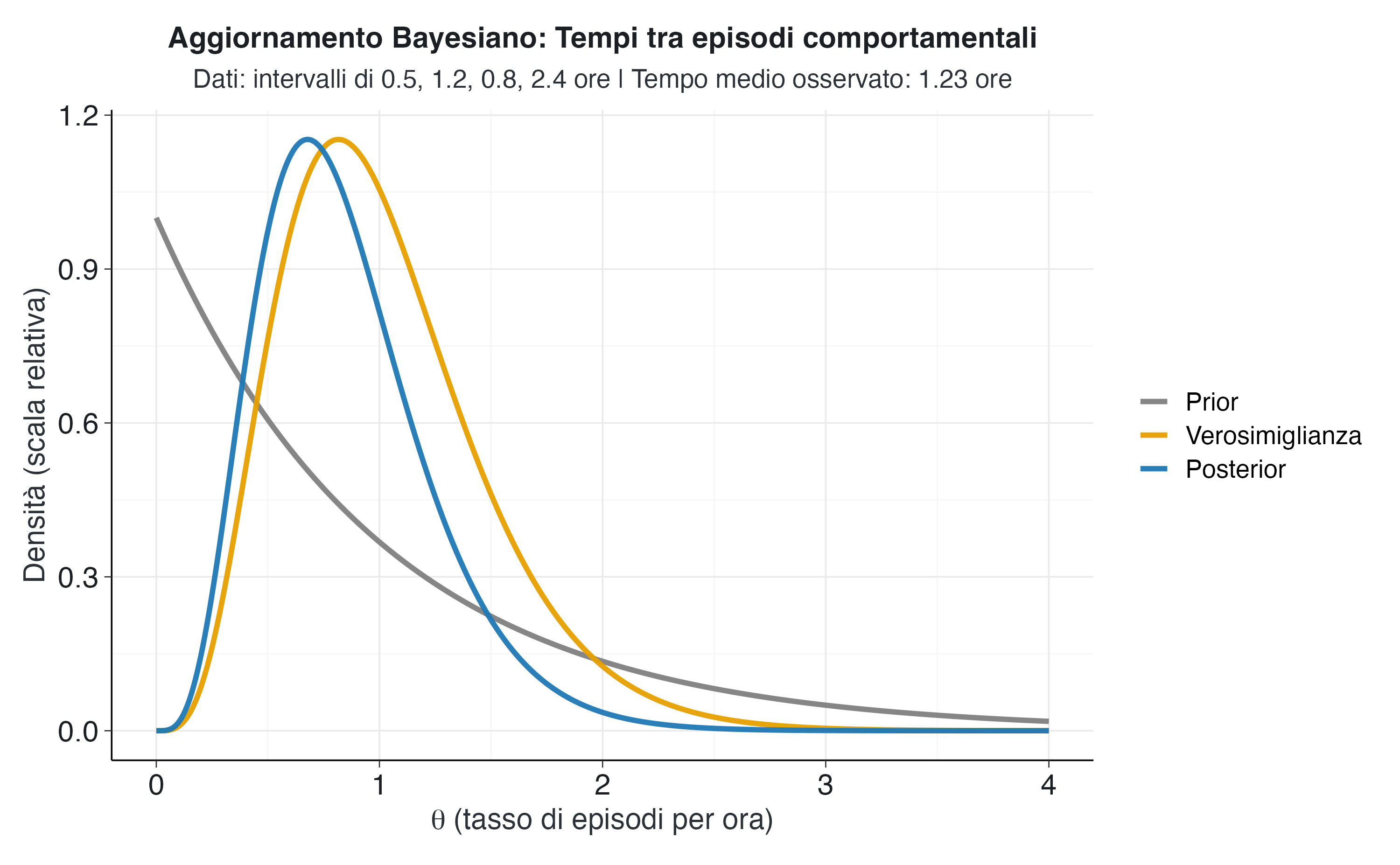
  labs(
    title = "Aggiornamento Bayesiano: Tempi tra episodi comportamentali",
    subtitle = paste0(
      "Dati: intervalli di ", paste(intervalli_temporali, collapse = ", "),
      " ore | Tempo medio osservato: ", round(tempo_medio_osservato, 2), " ore"
    ),
    x = expression(theta ~ "(tasso di episodi per ora)"),
    y = "Densità (scala relativa)",
    color = NULL
  ) 

Il grafico dell’aggiornamento bayesiano rivela la dinamica dell’apprendimento dai dati nel modello esponenziale. La curva grigia del prior esprime l’incertezza iniziale sul tasso di episodi. La curva arancione della verosimiglianza mostra dove si concentra l’evidenza fornita dai dati osservati, con un picco attorno al tasso empirico di circa 0.82 episodi per ora (corrispondente al tempo medio osservato di 1.23 ore). La curva blu del posterior rappresenta la sintesi ottimale di queste informazioni e si posiziona essenzialmente dove indica la verosimiglianza, dato che il prior era molto debole.

2.5.5 Valutazione rispetto agli obiettivi educativi

Per tradurre questi risultati in termini di efficacia educativa, è necessario definire criteri espliciti di successo dell’intervento. Supponiamo che l’obiettivo educativo sia quello di estendere il tempo medio tra gli episodi a più di due ore. Questo obiettivo corrisponde a un tasso inferiore a 0.5 episodi per ora e rappresenta un livello di autoregolazione che permetterebbe al bambino di partecipare proficuamente alle attività didattiche per periodi prolungati.

# Definiamo l'obiettivo in termini di tempo minimo tra episodi
tempo_target <- 2  # ore

# Questo corrisponde a un tasso massimo di:
tasso_target <- 1 / tempo_target

# Calcoliamo la probabilità che il tasso sia inferiore al target
# (equivalente a: tempo medio maggiore del target)
probabilita_sotto_tasso_target <- pgamma(
  q = tasso_target,
  shape = a_post,
  rate = b_post
)

# Calcoliamo anche direttamente la proporzione di campioni
# del tempo medio che superano il target
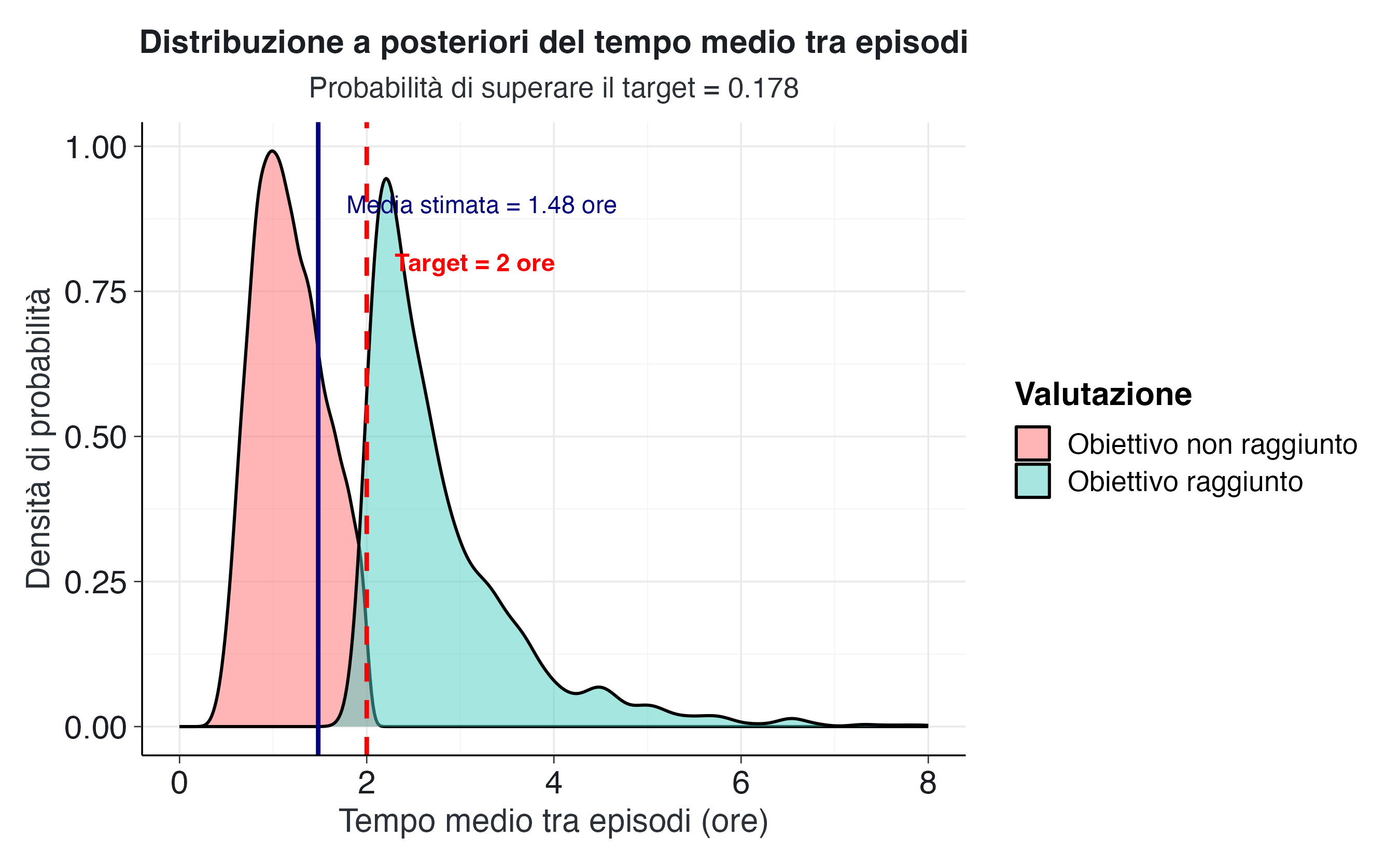
proporzione_sopra_target_tempo <- mean(campioni_tempo > tempo_target)

La probabilità che il tasso effettivo di episodi sia inferiore a 0.5 episodi per ora (equivalente a un tempo medio superiore a 2 ore) è 0.176, ovvero circa il 17.6%. Utilizzando i campioni dalla distribuzione del tempo medio, otteniamo una stima molto simile: circa il 17.8% della distribuzione a posteriori corrisponde a tempi medi superiori al target.

Questo valore indica che l’evidenza attuale non fornisce un forte supporto al raggiungimento dell’obiettivo educativo. Sebbene il tempo medio osservato di 1.23 ore sia vicino al target di 2 ore, l’incertezza associata alla stima (derivante dalla limitata dimensione del campione e dalla variabilità osservata) implica che non possiamo essere ragionevolmente certi che il tempo medio effettivo superi la soglia desiderata.

# Creiamo una visualizzazione che mostra la distribuzione del tempo medio
# in relazione all'obiettivo educativo

# Creiamo un dataframe con i campioni del tempo medio
dati_tempo_posterior <- data.frame(
  tempo_medio = campioni_tempo
)

# Identifichiamo quali campioni soddisfano l'obiettivo
dati_tempo_posterior$regione <- ifelse(
  dati_tempo_posterior$tempo_medio >= tempo_target,
  "Obiettivo raggiunto",
  "Obiettivo non raggiunto"
)

# Creiamo il grafico della distribuzione del tempo medio
ggplot(dati_tempo_posterior, aes(x = tempo_medio)) +
  geom_density(aes(fill = regione), alpha = 0.5) +
  geom_vline(
    xintercept = tempo_target,
    linetype = "dashed",
    color = "red",
    size = 1
  ) +
  geom_vline(
    xintercept = tempo_medio_post,
    linetype = "solid",
    color = "navy",
    size = 1
  ) +
  annotate(
    "text",
    x = tempo_target + 0.3,
    y = 0.8,
    label = paste0("Target = ", tempo_target, " ore"),
    color = "red",
    size = 4,
    fontface = "bold",
    hjust = 0
  ) +
  annotate(
    "text",
    x = tempo_medio_post + 0.3,
    y = 0.9,
    label = paste0("Media stimata = ", round(tempo_medio_post, 2), " ore"),
    color = "navy",
    size = 4,
    hjust = 0
  ) +
  scale_fill_manual(
    values = c(
      "Obiettivo raggiunto" = "#4ECDC4",
      "Obiettivo non raggiunto" = "#FF6B6B"
    )
  ) +
  xlim(0, 8) +
  labs(
    title = "Distribuzione a posteriori del tempo medio tra episodi",
    subtitle = paste0(
      "Probabilità di superare il target = ",
      round(proporzione_sopra_target_tempo, 3)
    ),
    x = "Tempo medio tra episodi (ore)",
    y = "Densità di probabilità",
    fill = "Valutazione"
  ) 

Il grafico visualizza la distribuzione della nostra incertezza sul tempo medio tra gli episodi in relazione all’obiettivo educativo di 2 ore. L’area verde rappresenta i valori del tempo medio per i quali l’obiettivo sarebbe considerato raggiunto, mentre l’area rossa corrisponde a valori inferiori al target. La distribuzione si sovrappone a entrambe le regioni, con una leggera prevalenza nell’area rossa, evidenziando come i dati osservati non forniscano ancora un supporto convincente per affermare il raggiungimento dell’obiettivo terapeutico.

La linea verticale blu continua indica la media a posteriori del tempo medio (1.48 ore), che si avvicina al target, ma rimane leggermente al di sotto di esso. Ciò suggerisce che, sebbene il bambino stia facendo progressi apprezzabili, l’obiettivo educativo completo non è ancora stato raggiunto con sufficiente certezza.

2.5.6 Strategie decisionali graduate basate sull’evidenza

Sulla base di questa analisi quantitativa, possiamo formulare raccomandazioni educative graduali che riflettano la forza delle prove disponibili e l’incertezza residua.

# Formuliamo raccomandazioni basate su soglie probabilistiche graduate
if (proporzione_sopra_target_tempo > 0.80) {
  raccomandazione <- "Il comportamento del bambino mostra evidenza forte di miglioramento con tempi medi tra episodi che superano stabilmente il target educativo. Si raccomanda di mantenere le strategie attuali per consolidare i risultati e di iniziare gradualmente a ridurre il livello di supporto esterno (fading), promuovendo l'autonomia e l'autoregolazione spontanea."
} else if (proporzione_sopra_target_tempo > 0.50) {
  raccomandazione <- "Il bambino mostra progressi significativi con una tendenza positiva verso il raggiungimento dell'obiettivo. Si raccomanda di continuare l'intervento attuale con monitoraggio ravvicinato per almeno altre due settimane. L'analisi bayesiana suggerisce che con l'accumulo di ulteriore evidenza positiva, la certezza del raggiungimento dell'obiettivo aumenterà considerevolmente."
} else if (proporzione_sopra_target_tempo > 0.30) {
  raccomandazione <- "Il bambino mostra una tendenza positiva ma l'obiettivo educativo non è ancora chiaramente raggiunto. Si raccomanda di intensificare il supporto nelle situazioni identificate come ad alto rischio. Potrebbe essere utile analizzare gli antecedenti degli episodi con intervalli particolarmente brevi per identificare fattori scatenanti specifici e sviluppare strategie preventive mirate."
} else {
  raccomandazione <- "L'evidenza attuale non supporta il raggiungimento dell'obiettivo educativo. Si raccomanda una rivalutazione approfondita dell'intervento. Considerare l'analisi funzionale del comportamento per identificare possibili funzioni non precedentemente riconosciute, la revisione dei rinforzi utilizzati per verificarne l'effettiva motivazione, e l'eventuale integrazione con strategie aggiuntive come l'insegnamento di abilità di coping alternative."
}

Nel caso specifico del nostro bambino, con una probabilità del 17.8% di avere un tempo medio superiore al target, la raccomandazione appropriata è la seguente: L’evidenza attuale non supporta il raggiungimento dell’obiettivo educativo. Si raccomanda una rivalutazione approfondita dell’intervento. Considerare l’analisi funzionale del comportamento per identificare possibili funzioni non precedentemente riconosciute, la revisione dei rinforzi utilizzati per verificarne l’effettiva motivazione, e l’eventuale integrazione con strategie aggiuntive come l’insegnamento di abilità di coping alternative.

Questa valutazione riconosce i progressi osservati, in particolare la presenza di intervalli lunghi come quello di 2.4 ore, ma mantiene una necessaria cautela dovuta alla variabilità comportamentale ancora presente e alla breve finestra di osservazione. L’approccio bayesiano consente di evitare conclusioni affrettate, favorendo decisioni educative informate che bilanciano l’ottimismo pedagogico con il rigore valutativo.

2.5.7 Distribuzione predittiva: anticipare il prossimo intervallo

Un’applicazione particolarmente utile dell’analisi bayesiana nel contesto educativo riguarda la formulazione di previsioni esplicite per gli intervalli futuri. Tali previsioni possono guidare la pianificazione delle attività, l’allocazione delle risorse di supporto, e la comunicazione con gli insegnanti e i genitori.

La distribuzione predittiva per il prossimo intervallo temporale tra episodi integra due fonti di incertezza: l’incertezza sul valore effettivo del tasso \(\theta\) e la variabilità intrinseca dei tempi di attesa, anche in presenza di un valore noto di \(\theta\). Per calcolare questa distribuzione, è possibile utilizzare un approccio basato sul campionamento.

# Generiamo previsioni per il prossimo intervallo temporale
# Campionamento dalla distribuzione predittiva:
# 1. Campioniamo un valore di theta dalla distribuzione a posteriori
# 2. Per quel valore di theta, campioniamo un tempo dalla distribuzione esponenziale

set.seed(456)
n_predizioni <- 10000

# Campionamento dal posterior per theta
theta_campionato <- rgamma(n_predizioni, shape = a_post, rate = b_post)

# Per ogni theta campionato, generiamo un tempo futuro
tempi_predetti <- rexp(n_predizioni, rate = theta_campionato)

# Calcoliamo statistiche della distribuzione predittiva
tempo_predetto_medio <- mean(tempi_predetti)
tempo_predetto_mediano <- median(tempi_predetti)
sd_predittiva <- sd(tempi_predetti)

# Calcoliamo alcune probabilità di interesse pratico
prob_intervallo_lungo <- mean(tempi_predetti > 2)
prob_intervallo_breve <- mean(tempi_predetti < 0.5)
prob_intervallo_moderato <- mean(tempi_predetti >= 0.5 & tempi_predetti <= 2)

# Intervallo di predizione al 90%
intervallo_predittivo_90 <- quantile(tempi_predetti, probs = c(0.05, 0.95))

Per il prossimo intervallo tra episodi, il tempo medio predetto è 1.47 ore, con una mediana di 0.89 ore. La mediana è generalmente più appropriata della media per distribuzioni asimmetriche come quella esponenziale. La deviazione standard della distribuzione predittiva è 1.92 ore, il che indica una considerevole variabilità nelle possibili realizzazioni future.

La probabilità che il prossimo intervallo superi le 2 ore (il nostro obiettivo educativo) è pari a 0.233, circa il 23.3%. La probabilità di un intervallo molto breve (meno di 0.5 ore) è 0.335, circa il 33.5%. La probabilità di un intervallo moderato tra 0.5 e 2 ore è pari a 0.432, circa il 43.2%. L’intervallo di predizione al 90% si estende da 0.06 ore a 4.76 ore.

# Creiamo una visualizzazione della distribuzione predittiva

# Per una visualizzazione più chiara, limitiamo il range
dati_predittivi <- data.frame(
  tempo_predetto = tempi_predetti[tempi_predetti <= 6]  # Limitiamo a 6 ore per chiarezza
)

ggplot(dati_predittivi, aes(x = tempo_predetto)) +
  geom_histogram(aes(y = ..density..), bins = 50, fill = "steelblue", alpha = 0.7) +
  geom_density(color = "navy", size = 1.2) +
  geom_vline(
    xintercept = tempo_predetto_mediano,
    color = "red",
    linetype = "dashed",
    size = 1
  ) +
  geom_vline(
    xintercept = tempo_target,
    color = "darkgreen",
    linetype = "dashed",
    size = 1
  ) +
  annotate(
    "text",
    x = tempo_predetto_mediano + 0.1,
    y = 0.5,
    label = paste("Mediana =", round(tempo_predetto_mediano, 2), "ore"),
    color = "red",
    size = 4,
    hjust = 0
  ) +
  annotate(
    "text",
    x = tempo_target + 0.1,
    y = 0.4,
    label = paste("Target =", tempo_target, "ore"),
    color = "darkgreen",
    size = 4,
    hjust = 0
  ) +
  labs(
    title = "Distribuzione predittiva: prossimo intervallo tra episodi",
    subtitle = paste0(
      "P(tempo > 2 ore) = ", round(prob_intervallo_lungo, 3),
      " | P(tempo < 0.5 ore) = ", round(prob_intervallo_breve, 3)
    ),
    x = "Durata predetta del prossimo intervallo (ore)",
    y = "Densità di probabilità"
  ) 

Il grafico mostra la distribuzione predittiva del prossimo intervallo temporale tra gli episodi. La forma della distribuzione è tipica delle distribuzioni esponenziali: una densità decrescente che assegna una maggiore probabilità ai tempi brevi, ma che mantiene anche una coda lunga che permette di considerare intervalli molto lunghi. La mediana predetta (linea rossa tratteggiata) si colloca leggermente al di sotto del target di 2 ore (linea verde tratteggiata), in linea con la probabilità del 23.3% di superare il target.

2.5.8 Implicazioni operative per la gestione educativa

Queste previsioni probabilistiche hanno diverse applicazioni pratiche nella gestione quotidiana del comportamento in classe. La probabilità del 33.5% di un intervallo molto breve (inferiore a 30 minuti) suggerisce la necessità di mantenere alta l’attenzione durante le transizioni tra le attività e nei momenti più strutturati della giornata, quando il rischio di episodi ravvicinati è più alto.

Al contrario, la probabilità del 23.3% di un intervallo lungo (oltre 2 ore) indica che ci sono buone possibilità di mantenere un comportamento adeguato per periodi prolungati. Ciò suggerisce l’opportunità di pianificare attività più complesse che richiedono una concentrazione prolungata, da svolgere quando le condizioni sono favorevoli. L’insegnante può utilizzare queste informazioni per bilanciare i compiti impegnativi con i momenti di recupero, ottimizzando così l’esperienza di apprendimento del bambino.

L’intervallo di predizione al 90%, che si estende da 0.06 a 4.76 ore, fornisce un intervallo realistico di aspettative. Se il prossimo intervallo dovesse cadere al di fuori di questo intervallo, in particolare se risultasse molto più breve del limite inferiore, ciò segnalerebbe la necessità di un’analisi immediata degli antecedenti e delle conseguenze per identificare eventuali fattori scatenanti non previsti.

2.5.9 Comunicazione con il team educativo e i genitori

La traduzione di questi risultati quantitativi in un linguaggio accessibile agli insegnanti e ai genitori è un aspetto cruciale per un intervento educativo efficace. L’approccio bayesiano, con la sua enfasi sulle probabilità esplicite e sulla quantificazione dell’incertezza, facilita una comunicazione trasparente basata sull’evidenza.

Un esempio di comunicazione efficace con il team educativo potrebbe essere formulato nel modo seguente: “Durante l’ultima settimana di monitoraggio intensivo, abbiamo osservato quattro episodi di comportamento dirompente, con intervalli tra gli episodi variabili tra 30 minuti e 2 ore e mezza. Il tempo medio tra gli episodi è attualmente di circa 1.5 ore. Questo rappresenta un miglioramento rispetto alla fase iniziale dell’intervento, ma non abbiamo ancora raggiunto con certezza il nostro obiettivo di 2 ore. Nelle prossime settimane, ci aspettiamo che gli intervalli siano tipicamente compresi tra i 0.1 minuti e le 4.8 ore. C’è una probabilità del 23% circa che il bambino mantenga il controllo comportamentale per più di 2 ore consecutive, ma anche una probabilità del 34% di episodi ravvicinati. Ciò significa che il progresso è in atto ma la consistenza deve ancora essere consolidata.”

Questa formulazione evita un ottimismo ingiustificato o una valutazione eccessivamente pessimistica. Riconosce i progressi evidenti, quantifica realisticamente le aspettative, sottolinea le aree che necessitano ancora di attenzione e fornisce al team informazioni concrete per la pianificazione delle attività quotidiane. La comunicazione basata sulle probabilità aiuta tutti gli stakeholder a sviluppare aspettative adeguate e a interpretare correttamente la variabilità comportamentale naturale.

2.5.10 Monitoraggio longitudinale e aggiornamento sequenziale

Come nel caso del disturbo di panico, un vantaggio fondamentale dell’approccio bayesiano nel contesto educativo è la possibilità di aggiornare le stime in modo sequenziale man mano che si accumulano nuove osservazioni. Questo meccanismo formalizza il processo naturale di apprendimento dall’esperienza e consente di adattare gli interventi in modo dinamico, basandosi sull’evidenza emergente.

# Simuliamo un aggiornamento sequenziale con dati ipotetici dalla settimana successiva
# Supponiamo di osservare i seguenti nuovi intervalli: 1.5, 2.8, 1.9 ore
nuovi_intervalli <- c(1.5, 2.8, 1.9)

# La distribuzione a posteriori attuale diventa il nuovo prior
parametri_aggiornati <- gamma_esponenziale_aggiorna(
  tempi_osservati = nuovi_intervalli,
  a_prior = a_post,  # Il posterior attuale diventa il prior
  b_prior = b_post
)

a_post_aggiornato <- parametri_aggiornati$a_post
b_post_aggiornato <- parametri_aggiornati$b_post

# Nuova stima del tasso dopo l'aggiornamento
tasso_aggiornato <- a_post_aggiornato / b_post_aggiornato

# Campionamento per stimare il tempo medio aggiornato
campioni_tasso_aggiornato <- rgamma(10000, shape = a_post_aggiornato, rate = b_post_aggiornato)
campioni_tempo_aggiornato <- 1 / campioni_tasso_aggiornato
tempo_medio_aggiornato <- mean(campioni_tempo_aggiornato)
sd_tempo_aggiornato <- sd(campioni_tempo_aggiornato)

# Nuova probabilità di superare il target
prob_sopra_target_aggiornata <- mean(campioni_tempo_aggiornato > tempo_target)

Se nella settimana successiva si osservassero tre nuovi intervalli di 1.5, 2.8 e 1.9 ore, la distribuzione a posteriori si aggiornerà a Gamma(8, 12.1). Il tempo medio stimato aumenterebbe a 1.75 ore, con una deviazione standard ridotta a 0.72 ore. La probabilità di superare il target di 2 ore aumenterebbe a 0.275, circa il 27.5%.

Questo miglioramento nella valutazione riflette sia l’aumento del tempo medio osservato (i nuovi intervalli includono un valore particolarmente alto di 2.8 ore), sia la maggiore certezza derivante dall’osservazione di sette intervalli totali anziché quattro. L’accumulo progressivo di evidenze consente di ottenere stime sempre più precise e affidabili, che supportano decisioni educative sempre più sicure riguardo alla modifica, al mantenimento o all’intensificazione dell’intervento.

# Confrontiamo le due distribuzioni posteriori

# Creiamo campioni per entrambe le distribuzioni
campioni_tempo_iniziale <- campioni_tempo
campioni_tempo_dopo <- campioni_tempo_aggiornato

# Organizziamo i dati per la visualizzazione comparativa
dati_confronto <- data.frame(
  tempo = c(campioni_tempo_iniziale[campioni_tempo_iniziale <= 8],
            campioni_tempo_dopo[campioni_tempo_dopo <= 8]),
  fase = rep(
    c("Dopo prima settimana (4 intervalli)", 
      "Dopo due settimane (7 intervalli)"),
    c(sum(campioni_tempo_iniziale <= 8), sum(campioni_tempo_dopo <= 8))
  )
)

ggplot(dati_confronto, aes(x = tempo, fill = fase)) +
  geom_density(alpha = 0.5) +
  geom_vline(xintercept = tempo_target, linetype = "dashed", color = "red", size = 1) +
  scale_fill_manual(
    values = c(
      "Dopo prima settimana (4 intervalli)" = "#E69F00",
      "Dopo due settimane (7 intervalli)" = "#1f78b4"
    )
  ) +
  annotate(
    "text",
    x = tempo_target + 0.3,
    y = 0.6,
    label = paste("Target =", tempo_target, "ore"),
    color = "red",
    size = 4,
    hjust = 0
  ) +
  labs(
    title = "Evoluzione della distribuzione a posteriori con l'accumulo di evidenza",
    subtitle = paste0(
      "Probabilità di superare target: ",
      round(proporzione_sopra_target_tempo, 3), " -> ",
      round(prob_sopra_target_aggiornata, 3)
    ),
    x = "Tempo medio tra episodi (ore)",
    y = "Densità di probabilità",
    fill = "Fase di monitoraggio"
  ) 

Il grafico comparativo mostra chiaramente come la distribuzione a posteriori cambi con l’accumulo di evidenza. La distribuzione dopo la seconda settimana (curva blu) è sia più spostata verso destra sia più concentrata rispetto a quella della prima settimana (curva arancione). Ciò riflette sia il miglioramento del comportamento osservato, sia la riduzione dell’incertezza dovuta all’aumento della quantità di dati. La massa di probabilità oltre la linea del target di 2 ore aumenta visibilmente, indicando una crescente fiducia nel raggiungimento dell’obiettivo educativo.

In conclusione, il modello Gamma-Esponenziale fornisce un framework analitico rigoroso e flessibile per il monitoraggio dei tempi tra gli episodi comportamentali nel contesto educativo. La sua applicazione complementa il modello Gamma-Poisson, offrendo una prospettiva temporale che risulta spesso più intuitiva per insegnanti e genitori. L’enfasi sui tempi di attesa tra gli episodi piuttosto che sui conteggi allinea l’analisi quantitativa con l’esperienza soggettiva di chi gestisce quotidianamente il comportamento, facilitando la comunicazione e la pianificazione educativa basata sull’evidenza.

Riflessioni conclusive

I modelli coniugati che abbiamo esaminato, ovvero Beta-Binomiale, Normale-Normale, Gamma-Poisson e Gamma-Esponenziale, ci hanno permesso di osservare da vicino i meccanismi dell’aggiornamento bayesiano. La proprietà di coniugazione, che mantiene inalterata la forma della distribuzione durante l’aggiornamento, ha reso evidente il processo attraverso cui le credenze iniziali si integrano con l’evidenza empirica.

La trasparenza matematica di queste famiglie di distribuzioni ha mostrato chiaramente i principi fondamentali del ragionamento bayesiano. Nel modello Beta-Binomiale, abbiamo osservato come l’aggiornamento avvenga tramite la semplice somma dei conteggi osservati. Nel caso Normale-Normale, abbiamo osservato come le precisioni si combinino in modo additivo. I modelli Gamma-Poisson e Gamma-Esponenziale hanno offerto prospettive complementari sullo stesso fenomeno sottostante. Questa semplicità di calcolo ha un notevole valore didattico, in quanto permette di concentrarsi sui concetti fondamentali in modo diretto.

Tuttavia, è importante riconoscere che i modelli coniugati rappresentano un caso particolare piuttosto che la norma nell’analisi dei dati psicologici. La maggior parte dei fenomeni che studiamo presenta una complessità che va oltre le assunzioni semplificatrici di queste famiglie di modelli. Le variabili psicologiche, infatti, spesso presentano asimmetrie, correlazioni e strutture di dipendenza che i modelli coniugati non sono in grado di cogliere in modo adeguato. La scelta delle distribuzioni a priori dovrebbe essere guidata dalla sostanza teorica piuttosto che dalla convenienza computazionale.

I progressi nei metodi computazionali, in particolare lo sviluppo delle tecniche di campionamento MCMC, hanno superato questi limiti, consentendo l’inferenza bayesiana per modelli di complessità arbitraria. Questi metodi consentono di utilizzare distribuzioni a priori non coniugate, di costruire strutture gerarchiche complesse e di incorporare forme di dipendenza tra le variabili più articolate. I principi fondamentali appresi dallo studio dei modelli coniugati rimangono comunque validi anche in questi contesti più generali e forniscono l’intuizione necessaria per interpretare correttamente i risultati di analisi computazionalmente più complesse.

I modelli coniugati rappresentano quindi un collegamento essenziale tra i principi teorici del ragionamento bayesiano e la pratica dell’analisi dei dati. La loro comprensione fornisce le basi per affrontare modelli più complessi, mantenendo come criterio fondamentale l’adeguatezza delle scelte modellistiche rispetto alle domande di ricerca e alle caratteristiche dei dati.

Bibliografia

Milgram, S. (1963). Behavioral study of obedience. The Journal of Abnormal and Social Psychology, 67(4), 371–378.