here::here("code", "_common.R") |>
source()
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, insight)8 Stan: concetti di base
Introduzione
L’algoritmo di Metropolis, analizzato nel capitolo 17 del manuale didattico, costituisce il fondamento concettuale del campionamento MCMC. Queste basi teoriche trovano oggi piena realizzazione pratica in Stan, l’ambiente di programmazione probabilistica divenuto riferimento standard per la modellazione bayesiana avanzata
Stan è un linguaggio di programmazione probabilistica specializzato nell’espressione dichiarativa di modelli bayesiani e nell’inferenza tramite algoritmi avanzati. La sua implementazione dell’Hamiltonian Monte Carlo (HMC) e, in particolare, dell’algoritmo NUTS (No-U-Turn Sampler) garantisce un’efficienza esplorativa notevolmente superiore rispetto ai campionatori Metropolis elementari, pur mantenendo la coerenza con i principi inferenziali che abbiamo già acquisito. Il passaggio a Stan rappresenta quindi l’evoluzione naturale del nostro percorso di apprendimento.
Il vantaggio operativo per la ricerca psicologica è notevole: modelli gerarchici, processi di apprendimento iterativo e strutture dinamiche – tradizionalmente complessi da implementare con codice personalizzato – diventano accessibili attraverso una sintassi dichiarativa intuitiva. Questa caratteristica permette ai ricercatori di concentrarsi sulla formalizzazione teorica piuttosto che sui dettagli computazionali.
Obiettivi del capitolo
In questo capitolo padroneggeremo gli elementi costitutivi di Stan con un approccio progressivo:
- Anatomia del codice: struttura fondamentale e componenti essenziali.
-
Implementazione diretta: modelli semplici attraverso l’interfaccia
cmdstanr. - Diagnostica integrata: interpretazione dei risultati e verifica della convergenza.
- Validazione predittiva: verifiche a priori e a posteriori.
L’obiettivo finale è sviluppare la capacità di tradurre costrutti psicologici in modelli generativi espliciti, conducendo analisi che unisca rigore statistico a significato sostantivo.
8.1 Programmazione probabilistica con Stan
I programmi Stan seguono una struttura modulare organizzata in blocchi dedicati, ciascuno con una funzione specifica nel processo di modellazione (Nicenboim et al., 2025):
-
data- dichiara i dati osservati dello studio (punteggi test, risposte partecipanti, etc.); -
parameters- definisce i parametri incogniti da stimare (medi, coefficienti, varianze); -
model- specifica il modello probabilistico, collegando parametri e dati attraverso distribuzioni a priori e funzione di verosimiglianza; -
generated quantities- calcola quantità derivate (previsioni, indicatori diagnostici, trasformazioni parametriche).
Questa architettura blocchi rende il codice intuitivo e trasparente: il flusso computazionale rispecchia direttamente il ragionamento statistico sottostante. Si parte dai dati osservati, si definiscono le incognite, si formalizzano le relazioni probabilistiche, e si derivano output interpretativi.
La stessa struttura si applica coerentemente a tutta la famiglia dei modelli bayesiani - dai modelli lineari di base alle architetture gerarchiche più sofisticate - offrendo un framework unificato per tradurre tradurre il ragionamento statistico in calcolo computazionale.
8.1.1 L’ecosistema Stan in R
L’interfaccia cmdstanr integra Stan in R attraverso un flusso di lavoro strutturato:
-
Specificazione – scrittura del modello in un file
.stan. - Compilazione – traduzione in codice eseguibile ottimizzato.
- Preparazione dati – organizzazione dei dati in lista R.
-
Campionamento – esecuzione dell’inferenza con
sample(). -
Analisi – esplorazione risultati con
posteriorebayesplot.
Questa sequenza chiara rende l’intero processo trasparente e riproducibile, permettendo di concentrarsi sulla sostanza del modello piuttosto che sui dettagli implementativi.
8.1.2 Sistema di tipizzazione in Stan
Stan adotta un sistema di tipizzazione statica: ogni variabile deve essere dichiarata specificandone il tipo e, quando rilevante, i vincoli sul suo dominio di valori.
I tipi fondamentali includono:
-
int– numeri interi (es. conteggi, numero di osservazioni); -
real– numeri reali (es. medie, parametri continui); -
vector– array numerici (es. predittori, coefficienti).
Vincoli come <lower=0> – delimitano il range ammissibile (es. deviazioni standard positive).
La dichiarazione esplicita dei tipi assolve a tre funzioni essenziali: fornisce un controllo degli errori che previene incongruenze (come una probabilità > 1), aumenta l’efficienza computazionale ottimizzando gli algoritmi sulla base della struttura dei dati e funge infine da documentazione automatica, rendendo trasparenti le assunzioni del modello direttamente nel codice.
8.2 Modello Beta–Binomiale in Stan
Come primo esempio concreto, implementiamo in Stan un modello per la stima della probabilità di successo \(\theta\) in una sequenza di prove bernoulliane, utilizzando un prior Beta. Il modello beta-binomiale ammette una soluzione analitica esatta e, in linea di principio, non richiederebbe il campionamento MCMC. In questo contesto didattico, la sua utilità risiede proprio nel confronto tra i risultati di Stan e il benchmark teorico noto, che ci permette di validare l’output dell’algoritmo contro una soluzione certa.
8.2.1 Scenario applicativo: un dado forse truccato
Immaginiamo di lanciare un dado 1000 volte. Registriamo ogni 6 come successo (valore 1) e gli altri risultati come insuccesso (valore 0). Un dado equilibrato avrebbe probabilità di successo \(\theta = 1/6 \approx 0.167\). Ma noi non assumiamo che il dado sia equo: vogliamo che siano i dati a dirci qual è il valore più plausibile di \(\theta\).
In R, possiamo simulare i dati in questo modo:
set.seed(123)
n <- 1000
dice_df <- tibble(res = sample(1:6, size = n, replace = TRUE))
y <- as.integer(dice_df$res == 6) # 1 per “6”, 0 altrimenti
mean(y) # Frequenza osservata di "6"
#> [1] 0.1648.2.2 Formalizzazione del modello
Il modello si basa su due componenti essenziali:
- Verosimiglianza – ogni risultato \(y_i\) è una prova di Bernoulli indipendente: \[ y_i \sim \text{Bernoulli}(\theta). \]
- Prior – assumiamo come iniziale una distribuzione uniforme su [0,1]: \[ \theta \sim \text{Beta}(1,1). \]1
Questa struttura equivale a un modello Beta-Binomiale: il conteggio totale dei successi \(k = \sum_{i=1}^N y_i\) segue infatti \[ k \sim \text{Binomiale}(N, \theta). \]
8.2.3 Implementazione Bernoulliana vettoriale
Il modo più naturale di implementare il modello in Stan è specificare che ogni osservazione \(y_i\) proviene da una distribuzione Bernoulli con parametro \(\theta\). Grazie alla sintassi vettoriale di Stan, questa relazione può essere espressa in modo compatto, applicando il modello a tutte le osservazioni simultaneamente con una singola istruzione.
stancode <- "
data {
int<lower=1> N; // Numero di osservazioni
array[N] int<lower=0, upper=1> y; // Esiti binari (0/1)
}
parameters {
real<lower=0, upper=1> theta; // Probabilità di successo
}
model {
theta ~ beta(1, 1); // Prior uniforme
y ~ bernoulli(theta); // Verosimiglianza vettorializzata
}
"Questa formulazione riflette la logica modulare di Stan:
- il blocco
datariceve i dati osservati; - il blocco
parametersdichiara i parametri da stimare; - il blocco
modeldescrive la struttura probabilistica del modello.
8.2.4 Scelta tra array e vector in Stan
In Stan, la selezione tra array e vector dipende dalla natura matematica delle variabili:
-
array[N] int– per dati discreti (valori interi), come risposte binarie (0, 1) o conteggi; -
vector[N]– per dati continui (valori reali), come misurazioni o punteggi.
Nel nostro scenario, i risultati Bernoulli sono per definizione discreti, pertanto vanno dichiarati come array[N] int. L’uso di vector[N] causerebbe un errore di compilazione, poiché i vettori accettano esclusivamente valori reali.
Questa distinzione tipologica funziona da controllo di coerenza integrato, prevenendo incongruenze logiche nella specificazione del modello.
8.2.5 Implementazione binomiale: la via della sufficienza statistica
L’approccio Bernoulliano, sebbene concettualmente chiaro, presenta inefficienze computazionali. Nel nostro modello, tutta l’informazione rilevante nei dati è contenuta nel numero totale di successi — una statistica sufficiente per \(\theta\). Possiamo quindi sostituire le \(N\) osservazioni Bernoulliane con una singola osservazione Binomiale, semplificando notevolmente il calcolo senza perdere informazioni.
stancode <- "
data {
int<lower=1> N; // Numero di prove
array[N] int<lower=0, upper=1> y; // Sequenza di esiti
}
transformed data {
int<lower=0, upper=N> k = sum(y); // Successi totali (statistica sufficiente)
}
parameters {
real<lower=0, upper=1> theta; // Probabilità di successo
}
model {
theta ~ beta(1, 1); // Prior uniforme
k ~ binomial(N, theta); // Verosimiglianza compatta
}
"Questa versione compatta produce inferenze identiche, ma con un carico computazionale ridotto: Stan calcola direttamente la probabilità di osservare \(k\) successi su \(N\) prove, anziché elaborare ciascun dato singolarmente.
Il modello rimane così statisticamente equivalente ma computazionalmente più efficiente.
8.2.6 In sintesi
| Versione | Descrizione | Vantaggio principale |
|---|---|---|
| Bernoulliana vettoriale | Modello esplicito per ogni osservazione | Più intuitiva e trasparente |
| Binomiale compatta | Modello basato sulla statistica sufficiente (k) | Più efficiente nel calcolo |
Ottimo testo — chiaro, completo e ben organizzato. Per renderlo più didattico e adatto a studenti di psicologia (magari non abituati al linguaggio computazionale), conviene:
- alleggerire il tono tecnico e rendere più espliciti i collegamenti concettuali tra teoria e codice;
- introdurre brevi frasi di transizione che aiutino a “leggere” i blocchi di codice come parte del ragionamento inferenziale;
- semplificare alcune formulazioni (“target”, “benchmark analitico”) mantenendo rigore e precisione.
8.2.6.1 Verifica mediante soluzione analitica
Nel modello Beta–Binomiale, la coniugazione tra prior e verosimiglianza consente di ottenere una soluzione analitica esatta, che rappresenta un utile punto di riferimento per verificare i risultati ottenuti tramite campionamento MCMC.
Le stime ottenute con il campionamento MCMC dovrebbero avvicinarsi a questi valori, con differenze dovute esclusivamente alla variabilità Monte Carlo.
8.2.7 Workflow operativo: dalla compilazione all’analisi
L’intero processo in Stan segue una sequenza logica ben definita, che può essere vista come un vero e proprio workflow inferenziale.
1. Compilazione del modello
mod <- cmdstan_model(
write_stan_file(stancode),
compile = TRUE
)La compilazione traduce il modello Stan in un programma eseguibile ottimizzato, che può essere riutilizzato per analizzare dataset diversi senza doverlo ricompilare ogni volta.
2. Preparazione dei dati
I nomi e le strutture delle variabili devono corrispondere esattamente a quelli dichiarati nel blocco data del modello Stan, altrimenti l’esecuzione produrrà un errore.
3. Campionamento MCMC
fit1 <- mod$sample(
data = stan_data,
iter_warmup = 1000, # Fase di adattamento (burn-in)
iter_sampling = 2000, # Campioni usati per l’inferenza
chains = 4, # Catene indipendenti
parallel_chains = 4, # Esecuzione parallela
seed = 4790,
refresh = 0
)In questa fase, Stan esegue il campionamento MCMC per esplorare la distribuzione a posteriori di \(\theta\). Ogni catena parte da un punto iniziale diverso e, dopo la fase di adattamento, genera campioni dalla stessa distribuzione.
8.2.8 Analisi dei risultati
Statistiche descrittive
fit1$summary(variables = "theta")
#> # A tibble: 1 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 theta 0.164 0.164 0.0117 0.0119 0.145 0.184 1.00 2443. 3636.Restituisce le principali statistiche riassuntive (media, deviazione standard, quantili).
Diagnostiche di convergenza
draws <- fit1$draws(variables = "theta", format = "draws_matrix")
posterior::summarise_draws(
draws,
mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975)), rhat, ess_bulk, ess_tail
)
#> # A tibble: 1 × 9
#> variable mean sd `2.5%` `50%` `97.5%` rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
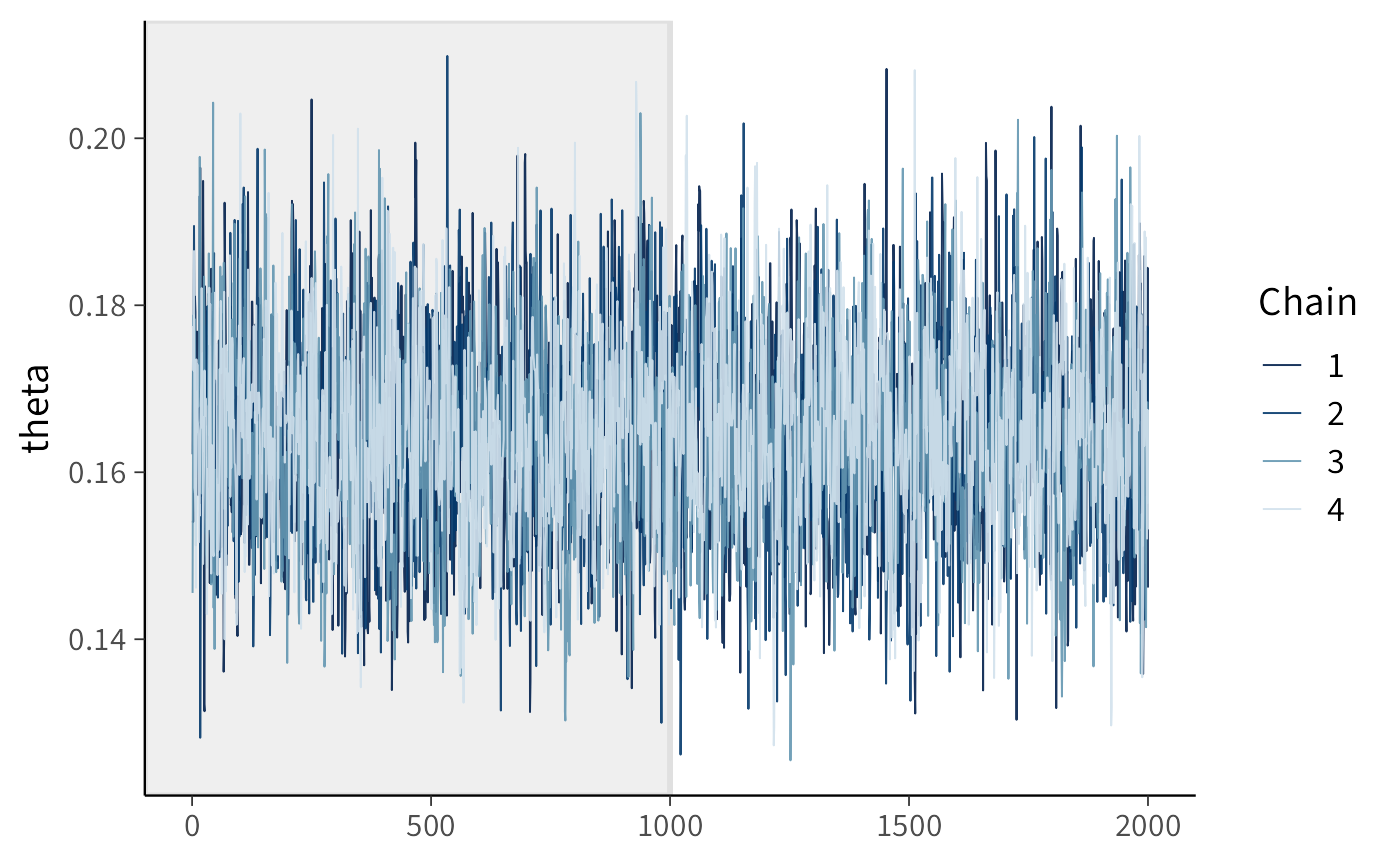
#> 1 theta 0.164 0.0117 0.142 0.164 0.188 1.00 2443. 3636.Valori di \(\hat{R} \approx 1.0\) e Effective Sample Size (ESS) elevati indicano che le catene sono ben mescolate e che il campionamento ha raggiunto la convergenza verso la distribuzione a posteriori.
Validazione grafica
bayesplot::mcmc_trace(fit1$draws("theta"), n_warmup = 1000)Il traceplot mostra l’andamento delle catene nel tempo. Catene sovrapposte e senza trend sistematici sono il segnale visivo di una buona convergenza.
8.2.9 Sintesi interpretativa
L’approccio bayesiano consente di andare oltre la semplice stima puntuale, offrendo una rappresentazione completa dell’incertezza. La distribuzione a posteriori di \(\theta\) non fornisce un valore singolo, ma un insieme coerente di valori plausibili, ciascuno ponderato in base alla probabilità che sia vero, alla luce dei dati e delle conoscenze pregresse. In questo modo, l’inferenza non si limita a descrivere ciò che è più probabile, ma mostra anche quanto possiamo essere certi delle nostre conclusioni. Inoltre, il quadro bayesiano integra naturalmente strumenti diagnostici per valutare la qualità delle stime e fornisce una base rigorosa per formulare previsioni e decisioni coerenti con il grado di incertezza stimato.
8.2.10 Distribuzione predittiva a posteriori
Stimare i parametri del modello è solo il primo passo dell’inferenza bayesiana. L’obiettivo finale è valutare cosa il modello prevede: quanti successi potremmo aspettarci se ripetessimo l’esperimento in condizioni simili?
La distribuzione predittiva a posteriori formalizza questa idea combinando la variabilità del processo, descritta dalla verosimiglianza, con l’incertezza sui parametri, descritta dalla distribuzione a posteriori. In altre parole, tiene conto sia del caso sia di ciò che non sappiamo con certezza sul parametro.
Per nuovi dati \(\tilde{y}\) la distribuzione predittiva si ottiene integrando su tutti i possibili valori di \(\theta\):
\[ p(\tilde{y} \mid y) = \int p(\tilde{y} \mid \theta) p(\theta \mid y) d\theta. \] Questa espressione rappresenta la “media ponderata” di tutte le possibili previsioni condizionate su \(\theta\), ponderate dalla loro plausibilità a posteriori.
8.2.10.1 Implementazione mediante campionamento
In pratica, l’integrale precedente si calcola per approssimazione Monte Carlo, sfruttando direttamente i campioni MCMC già ottenuti. Il procedimento è semplice:
- campionamento parametrico: estraiamo molti valori \(\theta^{(s)}\) dalla distribuzione a posteriori;
- simulazione predittiva: per ciascun \(\theta^{(s)}\), generiamo un possibile numero di successi futuri \(\tilde{y}^{(s)} \sim \text{Binomiale}(n_{\text{new}}, \theta^{(s)})\).
# Numero di prove nel nuovo esperimento
n_new <- 1000
# Campioni posteriori di theta
posterior_theta <- as.numeric(fit1$draws("theta", format = "matrix"))
# Simulazione della distribuzione predittiva
yrep_count <- rbinom(
n = length(posterior_theta),
size = n_new,
prob = posterior_theta
)8.2.10.2 Analisi dei risultati predittivi
# Statistiche riassuntive
mean_pred <- mean(yrep_count)
ci_pred <- quantile(yrep_count, c(0.025, 0.5, 0.975)) |> as.numeric()
c(Media = mean_pred,
"Mediana" = ci_pred[2],
"2.5%" = ci_pred[1],
"97.5%" = ci_pred[3])
#> Media Mediana 2.5% 97.5%
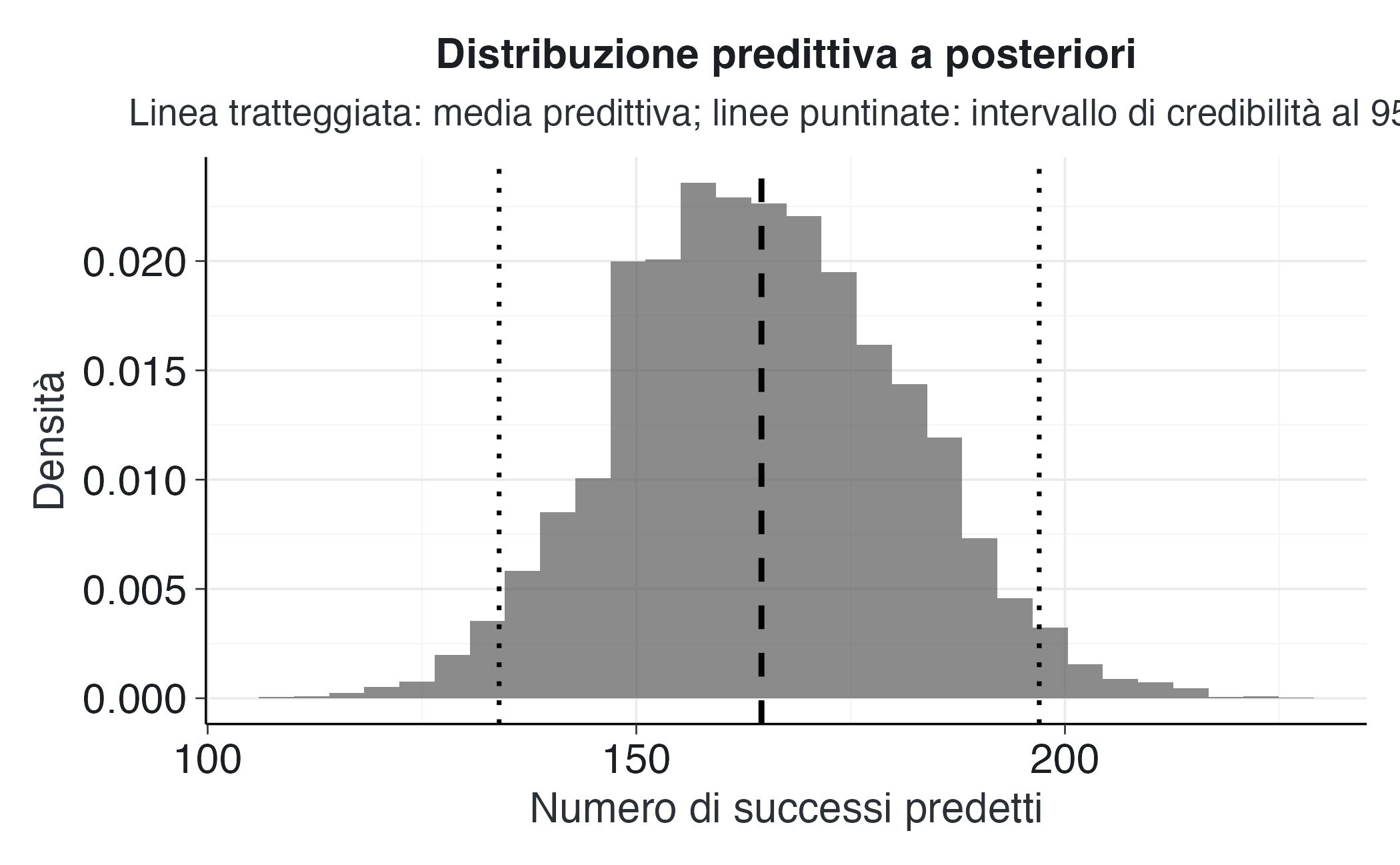
#> 165 164 134 197La media e i quantili della distribuzione predittiva riassumono le previsioni del modello: la media indica il numero di successi “atteso”, mentre i limiti dell’intervallo di credibilità esprimono il grado di incertezza.
8.2.10.3 Visualizzazione della distribuzione predittiva
tibble(Successi = yrep_count) |>
ggplot(aes(x = Successi)) +
geom_histogram(aes(y = after_stat(density)), bins = 30, alpha = 0.7) +
geom_vline(xintercept = mean_pred, linetype = "dashed", linewidth = 1) +
geom_vline(xintercept = ci_pred[c(1,3)], linetype = "dotted", linewidth = 0.8) +
labs(
x = "Numero di successi predetti",
y = "Densità",
title = "Distribuzione predittiva a posteriori",
subtitle = "Linea tratteggiata: media predittiva; linee puntinate: intervallo di credibilità al 95%"
)Il grafico mostra la distribuzione dei possibili numeri di successi futuri: le linee verticali indicano la media predittiva e l’intervallo di credibilità al 95%.
8.2.10.4 Analisi dei risultati predittivi con bayesplot
Un modo alternativo — e spesso più elegante — per ottenere la distribuzione predittiva consiste nel lasciare che sia Stan a generare i dati simulati durante il campionamento, sfruttando il blocco generated quantities. In questo modo l’intera procedura inferenziale (stima + previsione) rimane all’interno dello stesso modello.
1. Estensione del modello Stan
Nel blocco generated quantities si può aggiungere la generazione di un nuovo numero di successi predetti \(\tilde{y}\):
stancode_pred <- "
data {
int<lower=1> N; // Numero di prove osservate
array[N] int<lower=0, upper=1> y; // Esiti osservati
int<lower=1> N_new; // Numero di prove future
}
transformed data {
int<lower=0, upper=N> k = sum(y); // Successi osservati
}
parameters {
real<lower=0, upper=1> theta; // Probabilità di successo
}
model {
theta ~ beta(1, 1); // Prior uniforme
k ~ binomial(N, theta); // Verosimiglianza
}
generated quantities {
int yrep; // Successi predetti
yrep = binomial_rng(N_new, theta); // Simulazione predittiva
}
"Questo semplice blocco aggiunge, per ogni campione MCMC, una replica simulata del numero di successi futuri yrep.
2. Esecuzione del modello con Stan
# Preparazione dei dati per Stan
stan_data_pred <- list(
N = length(y),
y = y,
N_new = 1000
)
# Compilazione e campionamento
mod_pred <- cmdstan_model(write_stan_file(stancode_pred))
fit_pred <- mod_pred$sample(
data = stan_data_pred,
iter_warmup = 1000,
iter_sampling = 2000,
chains = 4,
parallel_chains = 4,
seed = 4790,
refresh = 0
)Ora ogni iterazione MCMC restituisce, oltre a theta, anche una simulazione predittiva yrep.
3. Estrazione e analisi della distribuzione predittiva
# Estrazione delle repliche predittive
yrep_stan <- fit_pred$draws("yrep", format = "matrix")
# Statistiche riassuntive
posterior::summarise_draws(
yrep_stan,
mean, sd, ~quantile(.x, c(0.025, 0.5, 0.975))
)
#> # A tibble: 1 × 6
#> variable mean sd `2.5%` `50%` `97.5%`
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 yrep 165. 16.4 133 165 197I risultati coincidono (entro l’errore Monte Carlo) con quelli ottenuti manualmente tramite rbinom().
4. Visualizzazione con bayesplot
bayesplot::mcmc_hist(
yrep_stan,
binwidth = 5,
color = "white"
) +
vline_at(mean_pred, linetype = "dashed", linewidth = 1) +
vline_at(ci_pred[c(1,3)], linetype = "dotted", linewidth = 0.8) +
labs(
title = "Distribuzione predittiva a posteriori (da Stan)",
subtitle = "Linea tratteggiata: media predittiva; linee puntinate: intervallo di credibilità al 95%",
x = "Numero di successi predetti",
y = "Densità"
)Il grafico risultante è del tutto analogo a quello prodotto con ggplot2, ma qui la distribuzione predittiva proviene direttamente dal modello Stan, senza ulteriori passaggi in R.
5. Interpretazione
Questo approccio offre due vantaggi principali:
- l’intero processo di inferenza e previsione rimane internamente coerente, poiché le simulazioni sono basate sugli stessi campioni posteriori usati per stimare \(\theta\);
- i risultati possono essere facilmente confrontati o riutilizzati in altre analisi bayesiane (posterior predictive checks, confronti modello–dati, ecc.).
In sintesi: sia l’approccio manuale (con rbinom()) sia quello integrato in Stan producono la stessa distribuzione predittiva. Tuttavia, includere la simulazione nel blocco generated quantities è la pratica più elegante e riproducibile, perché mantiene l’intera catena logica — dati, stima, previsione — all’interno del modello stesso.
8.2.10.5 Interpretazione sostantiva
La distribuzione predittiva rappresenta una previsione pienamente bayesiana: non si limita a usare un valore puntuale di \(\theta\), ma incorpora l’intera incertezza sul parametro.
- Scenario equo: se il dado è equilibrato (\(\theta = 1/6 \approx 0.167\)), il numero atteso di successi in 1000 lanci sarebbe circa 167.
- Scenario osservato: la distribuzione predittiva si centra intorno a \(n_{\text{new}} \times \mathbb{E}[\theta \mid y]\), riflettendo ciò che abbiamo appreso dai dati.
- Decisione inferenziale: uno scostamento sistematico da questo scenario equo suggerirebbe che il dado non è bilanciato.
In sintesi, la distribuzione predittiva a posteriori propaga l’incertezza in modo coerente: dai parametri stimati alle osservazioni future. Questo approccio fornisce previsioni più realistiche e complete rispetto a una semplice stima puntuale.
8.3 Dati continui: stima della media con varianza nota
Un problema di base nelle scienze psicologiche è stimare la media di popolazione di una variabile continua. Per fissare le idee, pensiamo ai punteggi a un test di intelligenza (QI). Per concentrarci sull’idea chiave, assumiamo nota la deviazione standard della popolazione, \(\sigma = 15\). È un’ipotesi rara nella pratica, ma didatticamente utile: in questo modo l’unico parametro incognito è la media \(\mu\). La semplificazione aiuta a confrontare con chiarezza approccio classico e bayesiano.
8.3.1 Generazione dei dati simulati
Supponiamo di raccogliere i punteggi di \(n = 30\) partecipanti, ipotizzando che il valore vero della media nella popolazione sia \(\mu = 105\):
8.3.2 Specificazione del modello bayesiano
8.3.2.1 Verosimiglianza (componente probabilistica)
Assumiamo osservazioni indipendenti, ciascuna con distribuzione Normale di media \(\mu\) e deviazione standard \(\sigma\) nota:
\[ y_i \sim \mathcal{N}(\mu, \sigma), \quad \text{per } i = 1, \dots, n. \]
8.3.2.2 Conoscenza a priori
Poniamo un prior normale su \(\mu\), centrato su \(\mu_0=100\) e con deviazione standard \(\tau=30\):
\[ \mu \sim \mathcal{N}(\mu_0, \tau). \]
Un \(\tau\) ampio riflette grande incertezza iniziale, lasciando che i dati “spostino” la distribuzione a posteriori in modo sostanziale.
8.3.3 Implementazione in Stan
Il modello bayesiano viene implementato nel seguente codice Stan:
stancode_norm <- "
data {
int<lower=1> N; // numerosità campionaria
vector[N] y; // vettore delle osservazioni
real<lower=0> sigma; // deviazione standard nota
real mu0; // media della distribuzione prior
real<lower=0> tau; // deviazione standard del prior
}
parameters {
real mu; // parametro di interesse: media della popolazione
}
model {
// Distribuzione prior
mu ~ normal(mu0, tau);
// Funzione di verosimiglianza
y ~ normal(mu, sigma);
}
"8.3.4 Preparazione dei dati e campionamento MCMC
I dati devono essere organizzati in una lista compatibile con la specifica del blocco data:
Procediamo quindi con la compilazione del modello e il campionamento mediante algoritmo MCMC:
mod2 <- cmdstanr::cmdstan_model(write_stan_file(stancode_norm), compile = TRUE)
fit2 <- mod2$sample(
data = stan_data2,
iter_warmup = 1000, # iterazioni di burn-in
iter_sampling = 4000, # iterazioni per campionamento
chains = 4, # numero di catene
parallel_chains = 4, # catene parallele
seed = 4790, # seme per riproducibilità
refresh = 0 # output silenziato
)8.3.5 Analisi dei risultati
8.3.5.1 Sintesi numerica della distribuzione a posteriori
I risultati del campionamento MCMC possono essere sintetizzati come segue:
print(fit2$summary(variables = "mu"), n = Inf)
#> # A tibble: 1 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mu 104. 104. 2.72 2.74 99.8 109. 1.00 5500. 7540.Alternativamente, utilizzando il pacchetto posterior:
draws2 <- fit2$draws(variables = "mu", format = "draws_matrix")
posterior::summarise_draws(
draws2,
mean,
sd,
~quantile(.x, c(0.025, 0.5, 0.975)),
rhat,
ess_bulk,
ess_tail
)
#> # A tibble: 1 × 9
#> variable mean sd `2.5%` `50%` `97.5%` rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mu 104. 2.72 98.9 104. 110. 1.00 5500. 7540.8.3.6 Diagnostica della convergenza e interpretazione
- \(\hat R \approx 1\) → catene ben mescolate e convergenti.
- ESS alto → campioni efficaci, stime stabili.
- Media a posteriori → stima puntuale bayesiana di \(\mu\).
- Intervallo di credibilità 95% → incertezza residua sulla media (qui non enorme, dato \(n=30\), ma ancora informativa).
In sintesi: l’approccio bayesiano fornisce l’intera posterior di \(\mu\), non solo una media. All’aumentare di \(n\), l’intervallo di credibilità si restringe: l’informazione dei dati domina sul prior.
8.3.7 Verifica analitica della coniugatezza
Con \(\sigma^2\) nota e prior normale su \(\mu\), la posterior è ancora normale (coniugatezza). In forma chiusa:
\[ \begin{aligned} \text{Var}(\mu \mid \mathbf{y}) &= \left(\frac{n}{\sigma^2} + \frac{1}{\tau^2}\right)^{-1}, \\ \mathbb{E}[\mu \mid \mathbf{y}] &= \text{Var}(\mu \mid \mathbf{y}) \cdot \left(\frac{n\bar{y}}{\sigma^2} + \frac{\mu_0}{\tau^2}\right). \end{aligned} \]
Applichiamo le formule ai nostri dati simulati:
# Calcolo delle quantità necessarie
ybar <- mean(y_cont)
tau2 <- 30^2
sigma2 <- sigma^2
# Varianza e deviazione standard a posteriori
post_var <- 1 / (n / sigma2 + 1 / tau2)
post_sd <- sqrt(post_var)
# Media a posteriori
post_mean <- post_var * (n * ybar / sigma2 + 100 / tau2)
# Risultati
c(post_mean_closed = post_mean, post_sd_closed = post_sd)
#> post_mean_closed post_sd_closed
#> 104.26 2.73Confrontiamo tali risultati con le stime MCMC.
Estraiamo i campioni della catena MCMC per il parametro \(\mu\):
mu_draws <- as.numeric(draws2[, "mu"])Calcoliamo media e deviazione standard:
I valori coincidono entro il rumore Monte Carlo, validando sia il modello sia l’implementazione.
8.3.8 Visualizzazione dei risultati
Un punto di partenza fondamentale è l’analisi dell’istogramma dei campioni MCMC:
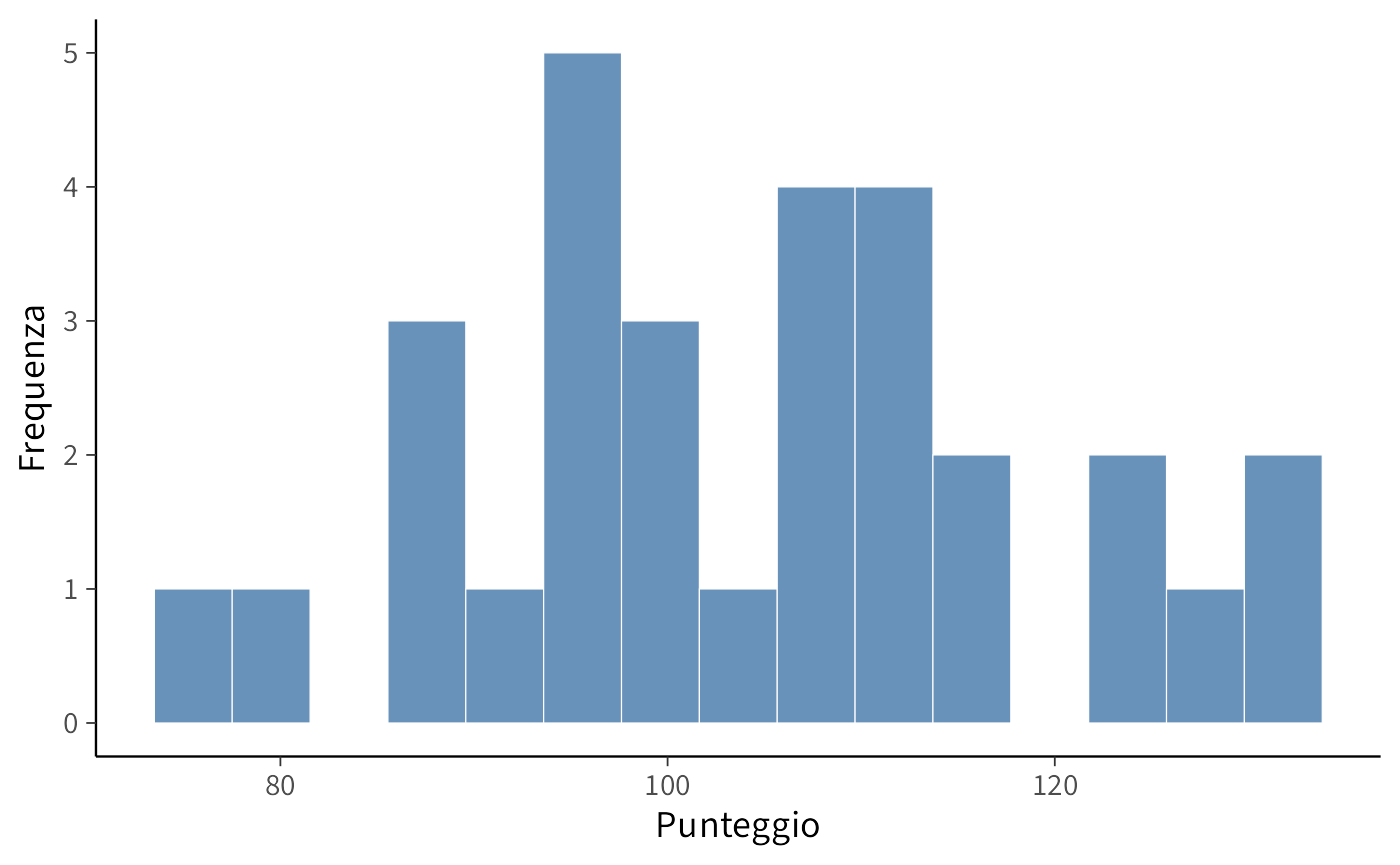
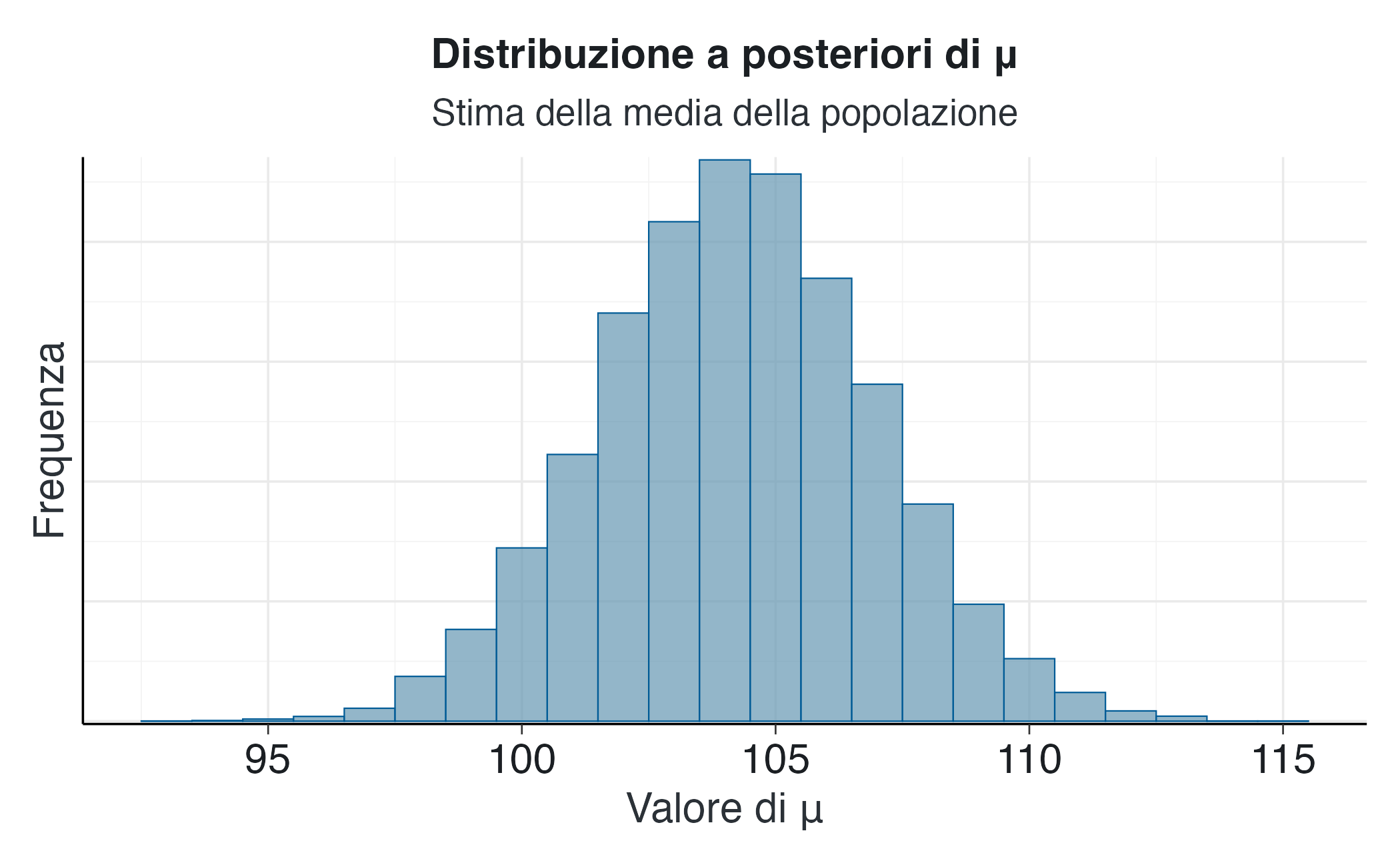
bayesplot::mcmc_hist(fit2$draws("mu"),
binwidth = 1,
fill = "steelblue",
alpha = 0.7) +
labs(title = "Distribuzione a posteriori di μ",
subtitle = "Stima della media della popolazione",
x = "Valore di μ",
y = "Frequenza")Questa visualizzazione non si limita a mostrare una singola stima puntuale (come la media campionaria), ma rappresenta l’intera distribuzione a posteriori del parametro \(\mu\). Questa distribuzione quantifica l’incertezza residua sulla stima, sintetizzando in modo coerente l’informazione a priori (la nostra conoscenza iniziale) con l’evidenza empirica fornita dai dati osservati. La sua forma e la sua dispersione ci consentono di valutare l’intero spettro di valori plausibili per \(\mu\) e le rispettive probabilità.
8.3.8.1 Traiettorie delle catene
Per valutare la convergenza delle catene MCMC, è utile esaminare le traiettorie di campionamento:
bayesplot::mcmc_trace(fit2$draws("mu"),
alpha = 0.7) +
labs(title = "Traiettorie delle catene MCMC per μ",
x = "Iterazione",
y = "Valore di μ") 8.3.8.2 Densità delle catene
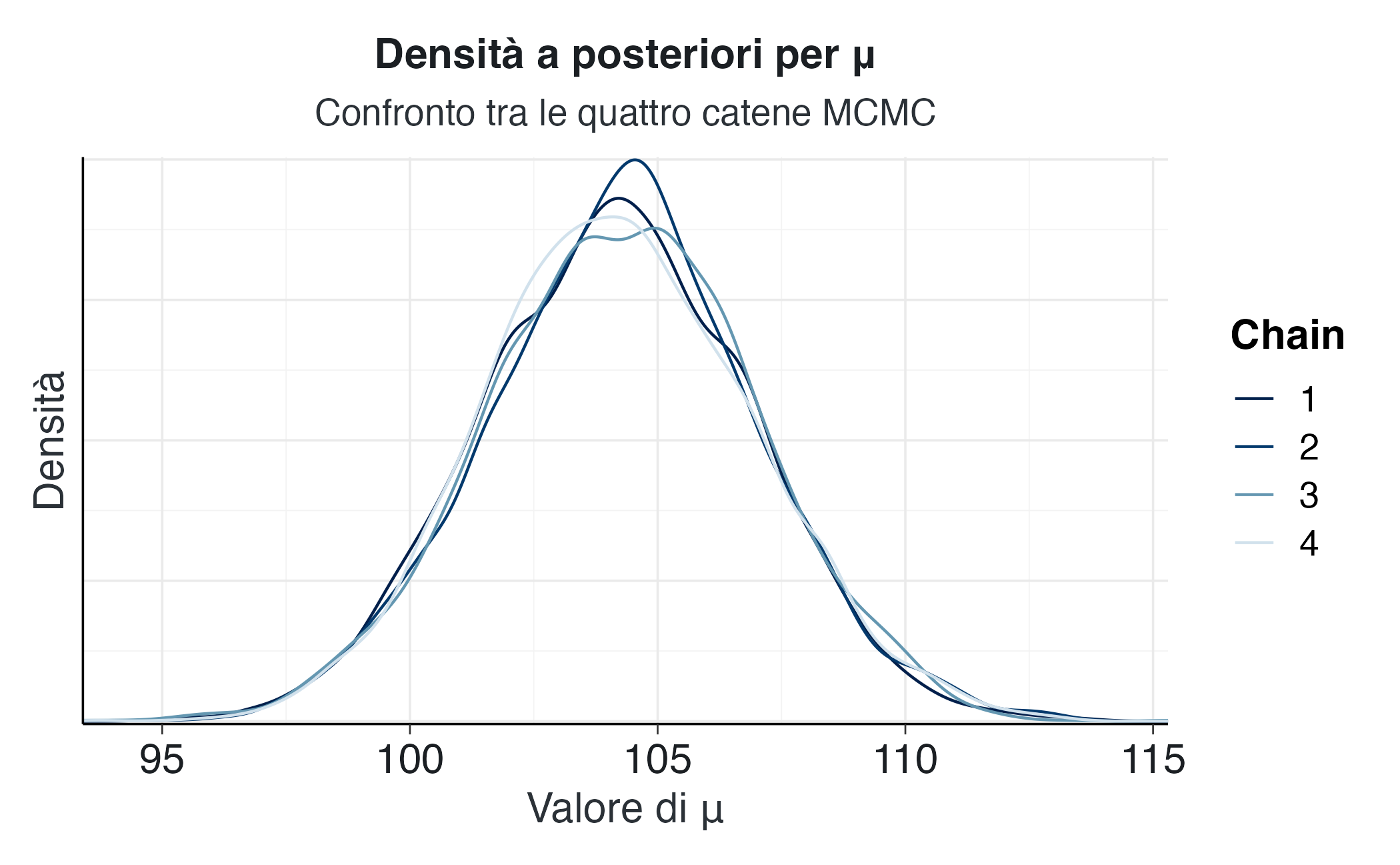
La sovrapposizione delle densità delle diverse catene fornisce un’ulteriore verifica della stabilità del campionamento:
bayesplot::mcmc_dens_overlay(fit2$draws("mu")) +
labs(title = "Densità a posteriori per μ",
subtitle = "Confronto tra le quattro catene MCMC",
x = "Valore di μ",
y = "Densità")Tracce ben mescolate e densità sovrapposte indicano una buona convergenza.
8.3.8.3 Interpretazione metodologica
Questo esempio implementa un test bayesiano per la media in un contesto parametrico (deviazione standard nota, prior normale non informativo). A differenza dell’approccio frequentista, che produce stime puntuali e intervalli di confidenza, l’output di questo approccio è l’intera distribuzione di probabilità a posteriori per il parametro \(\mu\).
Il vantaggio è notevole: la distribuzione a posteriori costituisce di per sé uno strumento inferenziale completo. Quantifica in modo trasparente tutta l’incertezza residua sul parametro, sintetizza coerentemente la conoscenza iniziale e l’evidenza empirica e può essere utilizzata direttamente per la propagazione dell’incertezza in previsioni e processi decisionali, supportando così scelte robuste in condizioni di incertezza.
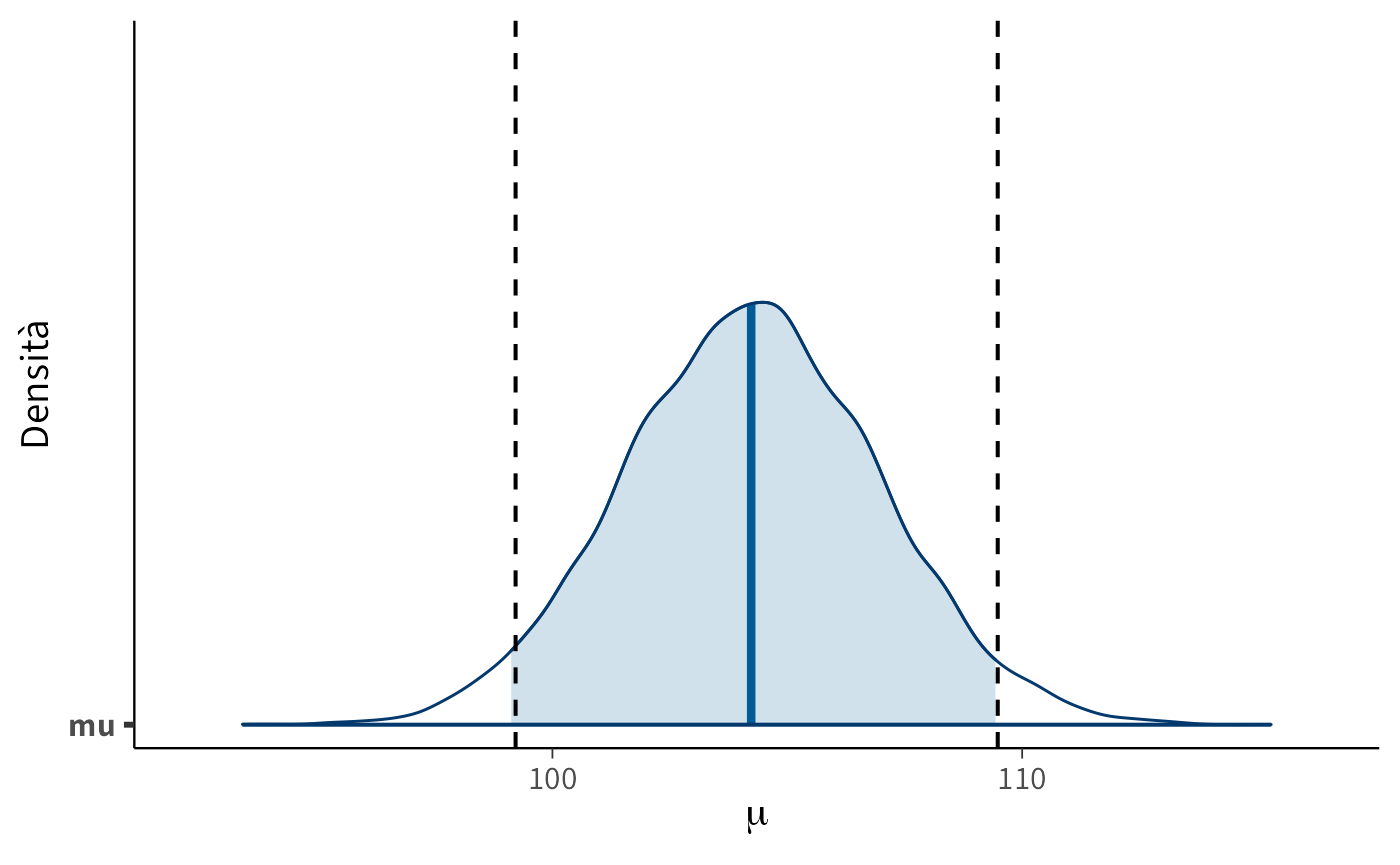
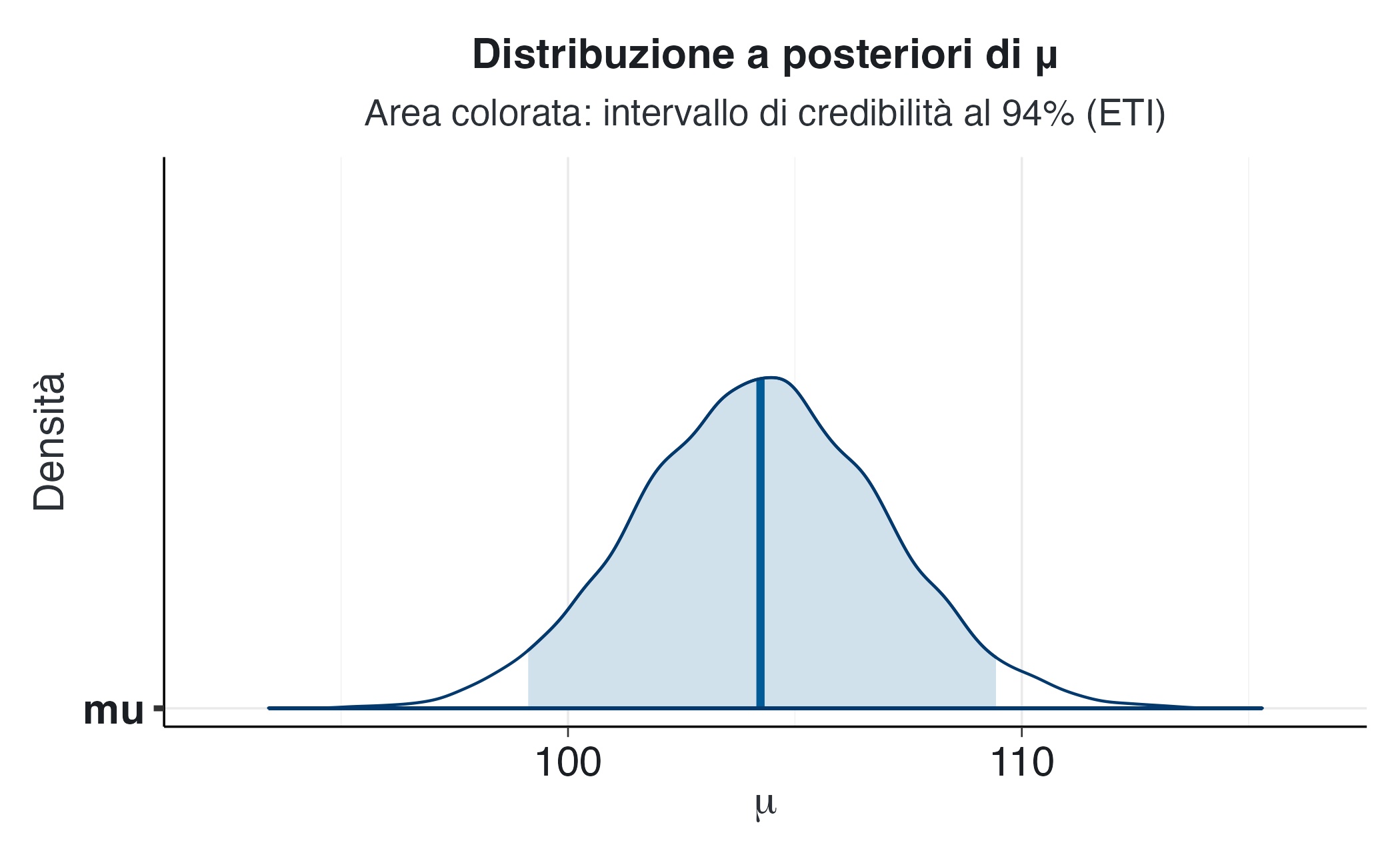
8.3.9 Intervalli di credibilità nell’inferenza bayesiana
La distribuzione a posteriori può essere sintetizzata tramite intervalli di credibilità, che individuano le regioni di valori più plausibili per un parametro dati il modello e i dati osservati. Dire che l’intervallo di credibilità al 94% per \(\mu\) è [101, 110] significa che, condizionatamente ai dati e al modello, la probabilità che \(\mu\) si trovi in quell’intervallo è pari a 0.94. Questa interpretazione è immediatamente probabilistica, a differenza dell’intervallo di confidenza frequentista che si riferisce alla frequenza di copertura in ipotetiche ripetizioni dell’esperimento.
Due definizioni sono comunemente utilizzate. L’Equal-Tailed Interval (ETI) lascia uguale probabilità nelle due code della distribuzione (ad esempio 3% + 3% in un intervallo al 94%). È stabile e facilmente interpretabile, ma può includere zone a bassa densità in distribuzioni asimmetriche. L’Highest Density Interval (HDI), invece, è l’intervallo più breve che contiene la probabilità specificata, concentrandosi sulle regioni più credibili. Rappresenta meglio le distribuzioni asimmetriche, anche se non è invariante rispetto alle trasformazioni monotone. Nei casi simmetrici, come una distribuzione normale, ETI e HDI coincidono.
In R, il calcolo dell’ETI e dell’HDI può essere realizzato come segue:
mu_samples <- as.numeric(fit2$draws("mu"))
# Equal-Tailed Interval (ETI) al 94%
eti_94 <- quantile(mu_samples, probs = c(0.03, 0.97))
eti_94
#> 3% 97%
#> 99.1 109.4
# Highest Density Interval (HDI) al 94%
hdi_vals <- bayestestR::hdi(mu_samples, ci = 0.94)
hdi_vals
#> 94% HDI: [99.22, 109.48]La visualizzazione grafica facilita la comunicazione dei risultati e mostra chiaramente la relazione tra la stima centrale e l’incertezza. Con la funzione bayesplot::mcmc_areas() è possibile rappresentare la distribuzione a posteriori evidenziando l’intervallo di credibilità:
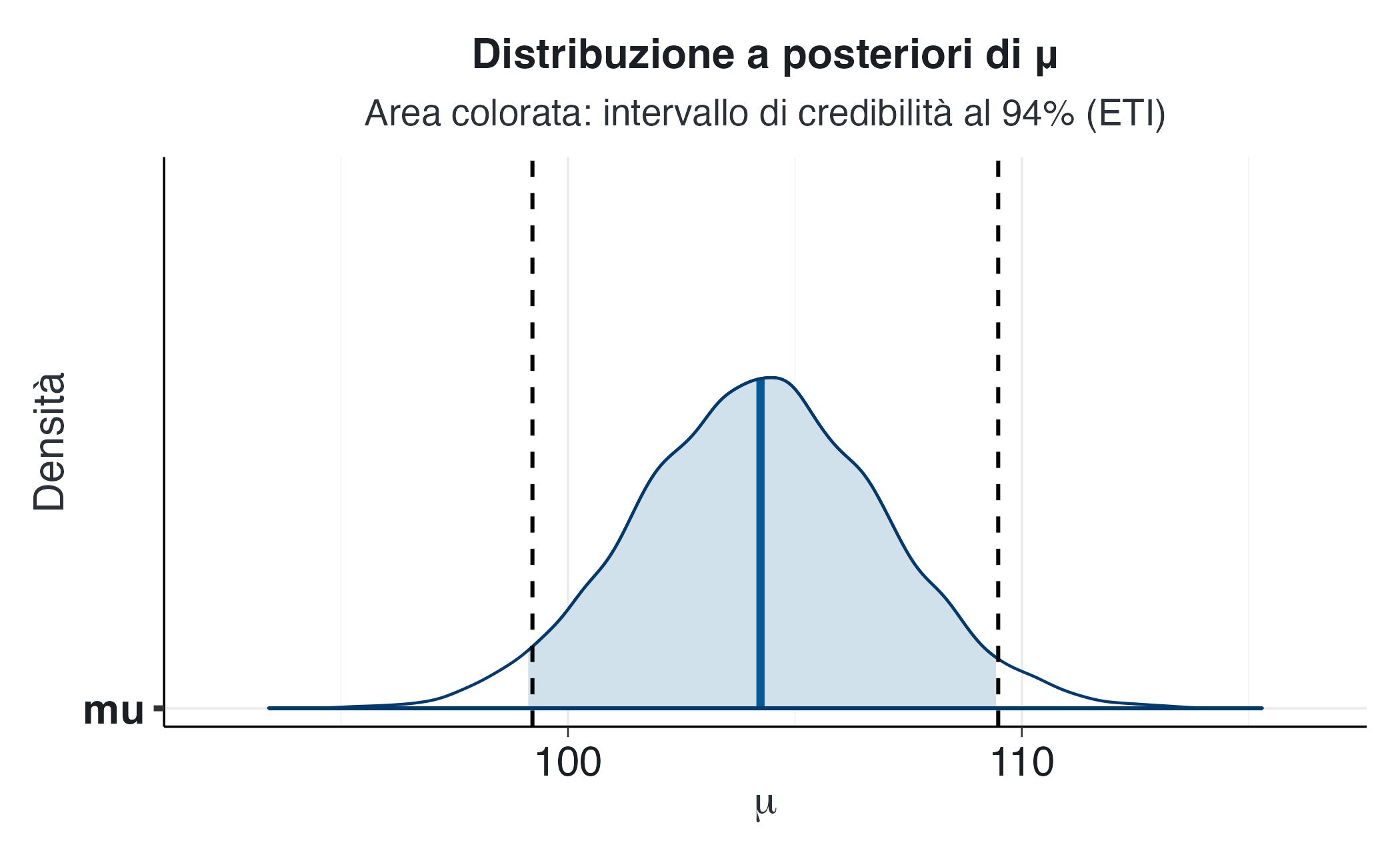
p <- bayesplot::mcmc_areas(fit2$draws("mu"), prob = 0.94, point_est = "mean") +
labs(x = expression(mu), y = "Densità",
title = "Distribuzione a posteriori di μ",
subtitle = "Area colorata: intervallo di credibilità al 94% (ETI)")
pPer confrontare visivamente ETI e HDI, è utile sovrapporre le linee verticali corrispondenti ai limiti dell’HDI:
hdi_lower <- hdi_vals$CI_low
hdi_upper <- hdi_vals$CI_high
p + geom_vline(xintercept = c(hdi_lower, hdi_upper),
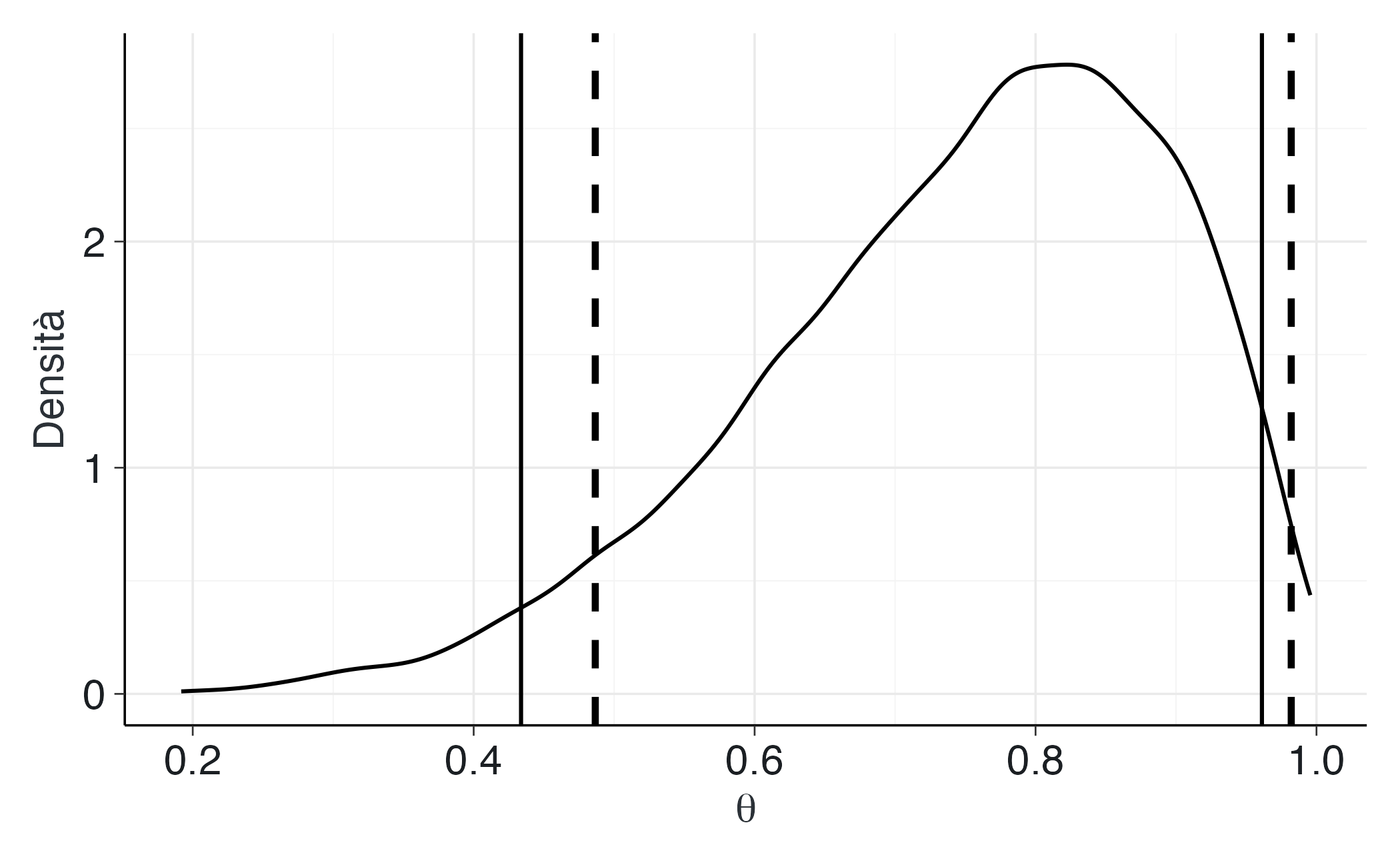
linetype = "dashed")Nel caso di distribuzioni simmetriche, le linee tratteggiate dell’HDI coincidono con i bordi dell’area colorata dell’ETI. Con distribuzioni asimmetriche, come la Beta(6, 2), le differenze diventano evidenti:
set.seed(123)
theta_draws <- rbeta(5000, shape1 = 6, shape2 = 2)
eti_beta <- bayestestR::eti(theta_draws, ci = 0.94)
hdi_beta <- bayestestR::hdi(theta_draws, ci = 0.94)
ggplot(data.frame(theta = theta_draws), aes(x = theta)) +
geom_density() +
geom_vline(xintercept = c(eti_beta$CI_low, eti_beta$CI_high), linewidth = 0.7) +
geom_vline(xintercept = c(hdi_beta$CI_low, hdi_beta$CI_high),
linewidth = 1.2, linetype = "dashed") +
labs(x = expression(theta), y = "Densità")In questo esempio, l’HDI risulta più concentrato nella regione ad alta densità, mentre l’ETI si estende verso la coda meno informativa.
La scelta del livello di probabilità (89%, 94%, 95%) è convenzionale: McElreath (2020) suggerisce il 94%, Kruschke (2014) l’89%, mentre molti autori mantengono il 95% per continuità con la tradizione frequentista. L’importante è essere coerenti e specificare chiaramente sia il livello che il tipo di intervallo utilizzato. In presenza di distribuzioni asimmetriche, mostrare entrambi gli intervalli può offrire una rappresentazione più completa della distribuzione a posteriori.
8.4 Test di ipotesi in prospettiva bayesiana
L’approccio bayesiano permette di formulare domande direttamente rilevanti per la pratica clinica o decisionale, come:
“Qual è la probabilità che la media superi una soglia clinicamente rilevante?”
A differenza dell’approccio frequentista, che si limita a un esito dicotomico di rifiuto o non rifiuto dell’ipotesi nulla, il metodo bayesiano fornisce una misura continua della plausibilità delle ipotesi, rendendo l’incertezza esplicita e interpretabile.
8.4.1 Probabilità a posteriori sopra una soglia
Nel modello normale a varianza nota, possiamo chiedere quale sia la probabilità che la media di popolazione superi 110:
\[ P(\mu > 110 \mid y). \]
Questa probabilità si calcola direttamente dai campioni MCMC della distribuzione a posteriori di \(\mu\):
mu_draws <- as.numeric(fit2$draws("mu"))
p_gt_110 <- mean(mu_draws > 110)
p_gt_110
#> [1] 0.0193Il valore ottenuto rappresenta la probabilità, condizionatamente a dati e modello, che \(\mu\) superi 110 — una stima graduata della forza dell’evidenza. Lo stesso risultato si può verificare analiticamente, sfruttando la coniugatezza del modello normale-normale:
Le piccole differenze tra i due valori dipendono dal rumore Monte Carlo.
8.4.2 Decisione pratica e ROPE
L’inferenza diventa realmente utile quando si traduce in una decisione. Una regola semplice consiste nell’agire come se \(\mu > 110\) solo se \(P(\mu > 110 \mid y)\) supera una soglia \(p^*\), scelta in base al bilancio tra rischi e benefici dell’azione. Con \(p^* = 0.90\), ad esempio, si decide di intervenire solo se la probabilità supera il 90%. In ambito clinico o educativo, questo significa rendere trasparente il legame tra evidenza statistica e conseguenze pratiche, calibrando la decisione sulla gravità del rischio o sul costo dell’errore.
Spesso, tuttavia, la domanda non riguarda un valore esatto ma un’area di equivalenza pratica. La ROPE (Region of Practical Equivalence) definisce un intervallo entro il quale differenze da una soglia di riferimento sono considerate clinicamente irrilevanti. Ad esempio:
\[ \text{ROPE} = [108, 112]. \]
In tal caso ci si chiede se \(\mu\) ricada entro questo intervallo, cioè se la differenza rispetto a 110 sia trascurabile per le implicazioni reali del problema.
8.4.3 Calcolo e interpretazione
A partire dai campioni MCMC, possiamo stimare la probabilità che \(\mu\) cada al di sotto, all’interno o al di sopra della ROPE:
La stessa stima può essere ottenuta in forma chiusa quando la distribuzione a posteriori è normale:
P_below_cf <- pnorm(rope[1], mean = post_mean, sd = post_sd)
P_in_cf <- pnorm(rope[2], mean = post_mean, sd = post_sd) -
pnorm(rope[1], mean = post_mean, sd = post_sd)
P_above_cf <- 1 - pnorm(rope[2], mean = post_mean, sd = post_sd)
c(P_below_cf = P_below_cf, P_in_cf = P_in_cf, P_above_cf = P_above_cf)
#> P_below_cf P_in_cf P_above_cf
#> 0.91498 0.08275 0.00226Se la probabilità che \(\mu\) ricada all’interno della ROPE è elevata, possiamo concludere che la media è praticamente equivalente alla soglia di riferimento. Se invece la probabilità si concentra al di sopra o al di sotto, si ottiene evidenza di una differenza rilevante. Nei casi ambigui, in cui le tre aree hanno probabilità simili, la risposta è di incertezza: si può decidere di raccogliere ulteriori dati o ridefinire la ROPE in base alla sensibilità clinica richiesta.
8.4.4 Esempio di report
Con ROPE = \([108,112]\), si ottiene: \(P(\mu < 108) = 0.92\), \(P(108 \leq \mu \leq 112) = 0.08\), \(P(\mu > 112) = 0.003\). Questi risultati indicano che la media \(\mu\) è con alta probabilità inferiore al valore di riferimento 110, in senso praticamente rilevante.
In un contesto applicativo, tale risultato può suggerire che il gruppo osservato presenta una prestazione inferiore rispetto alla norma, giustificando un intervento o un monitoraggio aggiuntivo.
8.5 Verifica predittiva: prior e posterior
Dopo la verifica della qualità del campionamento, è necessario controllare se il modello produce dati plausibili. Questa analisi, detta predictive checking, si articola in due fasi: il prior predictive check (prima dei dati) e il posterior predictive check (dopo l’aggiornamento con i dati).
8.5.1 Prior Predictive Check
Serve a valutare se le assunzioni a priori generano valori realistici rispetto al contesto. Nel modello
\[ y_i \mid \mu \sim \mathcal{N}(\mu, \sigma), \qquad \mu \sim \mathcal{N}(\mu_0, \tau). \]
la distribuzione predittiva a priori per \(y_i\) è \(y_i \sim \mathcal{N}(\mu_0, \sqrt{\sigma^2 + \tau^2})\). Se questa produce punteggi di QI troppo estremi o improbabili, il prior è inappropriato.
8.5.1.1 Implementazione in Stan
Per eseguire un prior predictive check possiamo utilizzare lo stesso modello Stan destinato all’inferenza, con una piccola modifica. Introduciamo una variabile booleana compute_likelihood che decide se attivare o meno la riga y ~ normal(mu, sigma);. In questo modo possiamo “spegnere” la verosimiglianza e simulare esclusivamente dal prior. Inoltre, nel blocco generated quantities generiamo delle repliche \(y_{\text{rep}}\) da confrontare con i dati osservati.
stancode_norm_ppc <- "
data {
int<lower=0> N;
vector[N] y; // usato solo se compute_likelihood=1
real<lower=0> sigma; // sd nota
real mu0; // media del prior su mu
real<lower=0> mu_prior_sd; // sd del prior
int<lower=0, upper=1> compute_likelihood; // 1 = attiva likelihood
}
parameters {
real mu;
}
model {
mu ~ normal(mu0, mu_prior_sd);
if (compute_likelihood == 1) {
y ~ normal(mu, sigma);
}
}
generated quantities {
vector[N] y_rep;
vector[N] log_lik;
for (n in 1:N) {
y_rep[n] = normal_rng(mu, sigma);
log_lik[n] = normal_lpdf(y[n] | mu, sigma);
}
}
"
stanmod_ppc <- cmdstan_model(write_stan_file(stancode_norm_ppc), compile = TRUE)Per un controllo puro del prior impostiamo compute_likelihood = 0:
N_ppc <- length(y_cont)
stan_data_prior <- list(
N = N_ppc,
y = rep(0, N_ppc), # placeholder, ignorato se compute_likelihood=0
sigma = sigma,
mu0 = 100,
mu_prior_sd = 30,
compute_likelihood = 0
)
fit_prior <- stanmod_ppc$sample(
data = stan_data_prior,
iter_warmup = 500,
iter_sampling = 2000,
chains = 4,
parallel_chains = 4,
seed = 4790,
refresh = 500
)Dopo il campionamento estraiamo le repliche \(y_{\text{rep}}\):
# Estrazione delle repliche
yrep_mat_prior <- posterior::as_draws_matrix(fit_prior$draws("y_rep"))
# Selezione delle colonne y_rep[1],...,y_rep[N]
yrep_mat_prior <- as.matrix(
yrep_mat_prior[, paste0("y_rep[", 1:N_ppc, "]")]
)Possiamo ora confrontare i dati osservati con alcune repliche simulate:
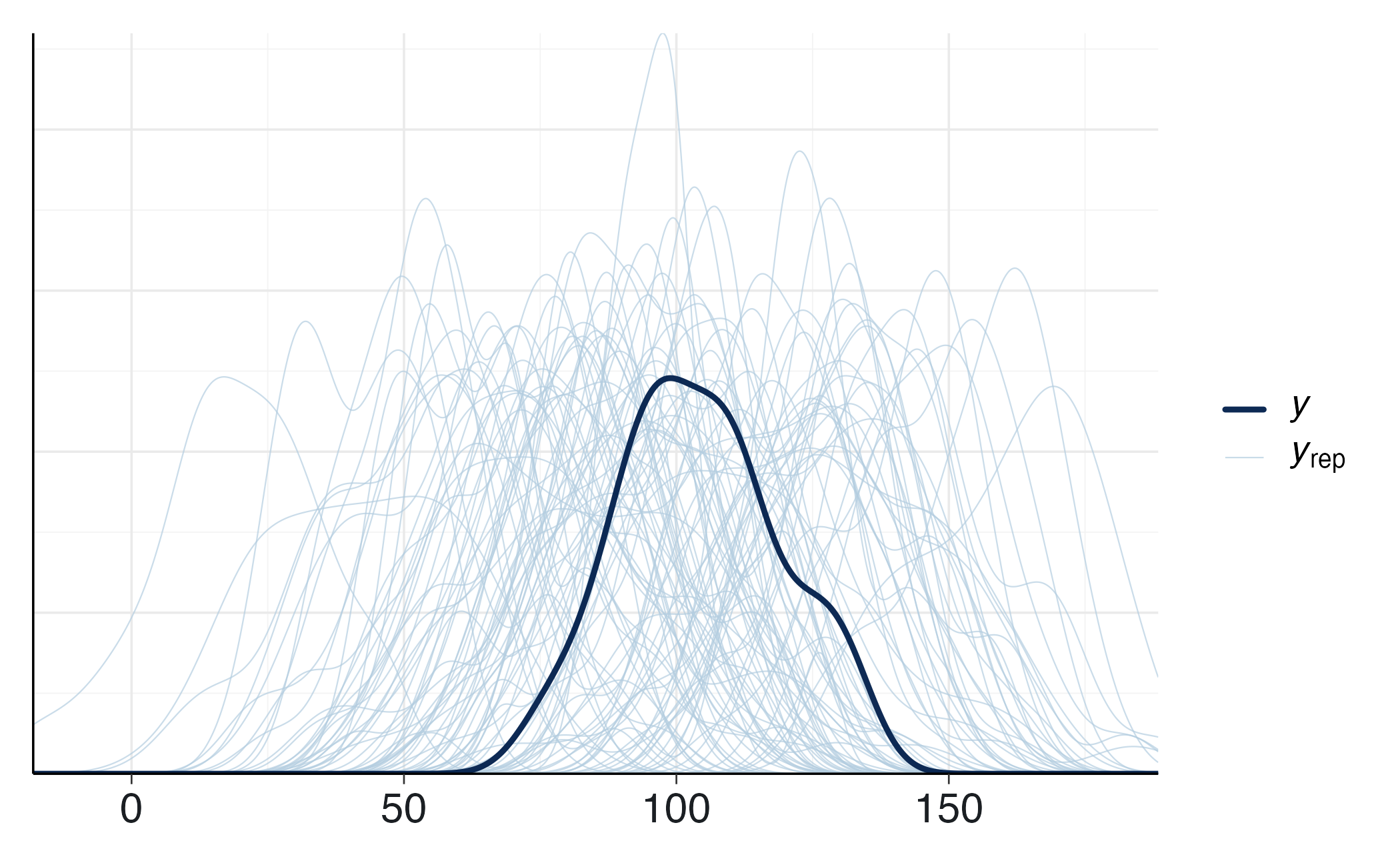
idx <- sample(seq_len(nrow(yrep_mat_prior)), 100)
bayesplot::ppc_dens_overlay(
y = y_cont,
yrep = yrep_mat_prior[idx, , drop = FALSE]
) Se le repliche simulate coprono la distribuzione empirica, il prior è coerente con la conoscenza di base. In caso contrario, occorre rivedere media e deviazione standard del prior.
8.5.2 Posterior Predictive Check
Dopo l’aggiornamento con i dati, il posterior predictive check valuta se il modello riproduce con realismo l’evidenza empirica. Stan genera repliche \(y_{\text{rep}}\) nel blocco generated quantities, che possiamo confrontare con i dati osservati.
Eseguiamo il campionamento:
fit_post <- stanmod_ppc$sample(
data = stan_data_post,
iter_warmup = 1000,
iter_sampling = 10000,
chains = 4,
parallel_chains = 4,
seed = 4790,
refresh = 1000
)Una volta estratte le repliche, possiamo confrontarle con i dati reali:
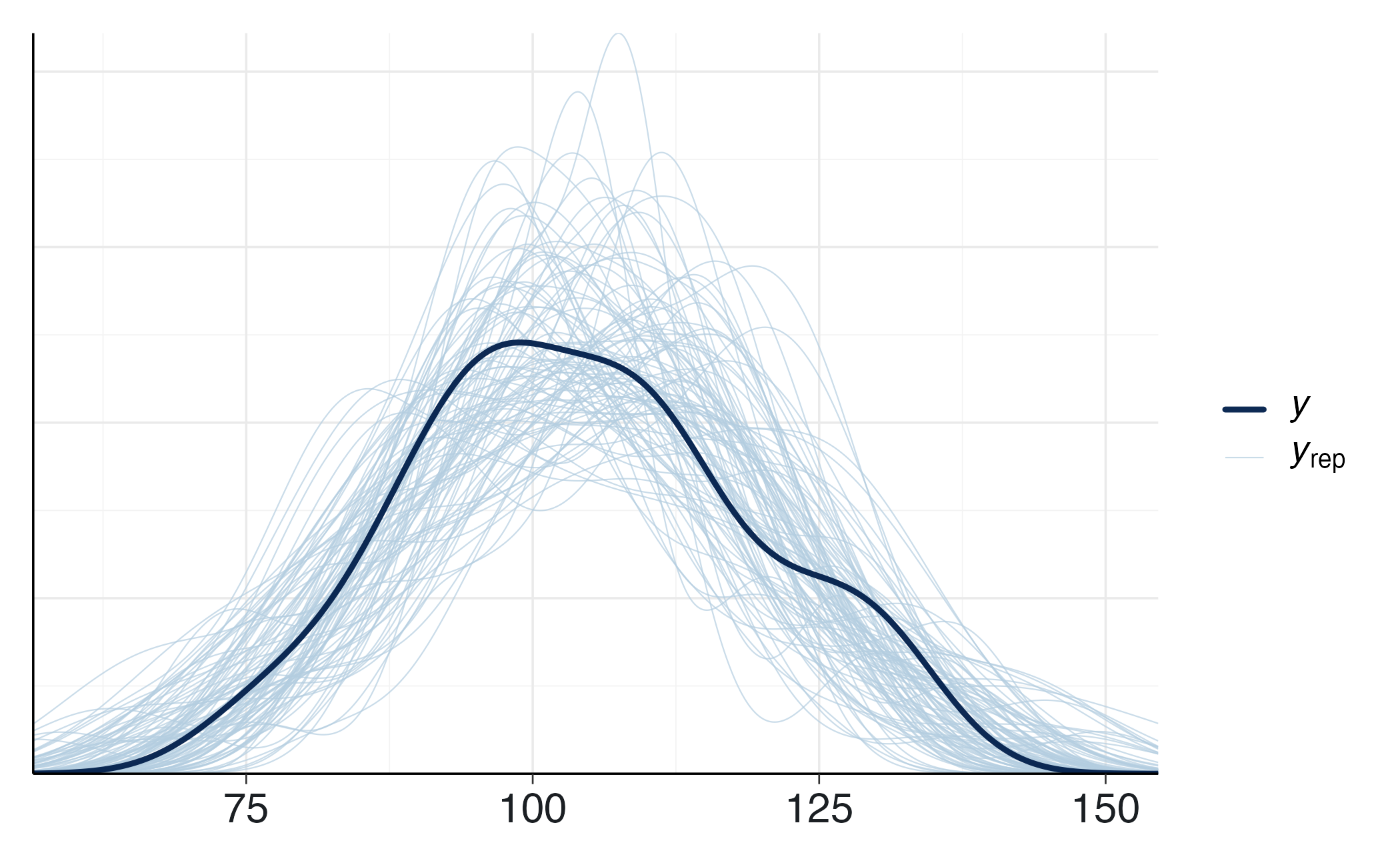
y_rep <- fit_post$draws("y_rep", format = "matrix")
ppc_dens_overlay(y = stan_data_post$y, yrep = y_rep[1:100, ])Se le distribuzioni simulate coincidono con quella osservata, il modello descrive adeguatamente il fenomeno. Scostamenti sistematici — ad esempio repliche troppo concentrate o troppo disperse — indicano che la struttura del modello o i priors richiedono revisione.
Nel nostro esempio, la sovrapposizione tra dati reali e repliche simulate suggerisce una buona aderenza: la media simulata coincide con quella osservata e la variabilità è realistica. Ciò conferma che il modello normale con prior specificato è adeguato a rappresentare i punteggi di QI.
In generale, i controlli predittivi forniscono un riscontro concreto sulla plausibilità sostantiva del modello, mostrando se le assunzioni statistiche producono previsioni coerenti con la realtà psicologica o clinica studiata.
Riflessioni conclusive
Stan rappresenta il punto di approdo naturale del percorso seguito fin qui. Dopo aver introdotto la logica dell’inferenza bayesiana con algoritmi semplici come Metropolis e aver visto come i linguaggi probabilistici abbiano reso più accessibile questa logica, Stan ci mette ora a disposizione uno strumento capace di tradurre queste idee in pratica su modelli reali e complessi.
Il suo valore non risiede soltanto nella potenza computazionale, ma soprattutto nella possibilità di spostare l’attenzione dal calcolo all’idea scientifica. Con Stan possiamo formulare ipotesi psicologiche in termini formali, esplicitarne le assunzioni e sottoporle a verifica empirica in modo trasparente e riproducibile. Il ricercatore non è più costretto a concentrarsi sui dettagli algoritmici, ma può dedicarsi a ciò che conta davvero: la sostanza teorica del modello e la sua capacità di descrivere i dati.
Nei prossimi capitoli, l’uso di Stan verrà introdotto progressivamente, attraverso esempi sempre più complessi, a partire da applicazioni semplici fino ad arrivare a modelli più articolati. L’obiettivo non è solo acquisire familiarità con la sintassi, ma soprattutto interiorizzare un modo di pensare: il pensiero bayesiano, che libera il ricercatore dal vincolo delle domande statistiche standardizzate e gli permette di costruire risposte formali alle sue specifiche domande di ricerca.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] insight_1.4.2 cmdstanr_0.9.0 ragg_1.5.0
#> [4] tinytable_0.13.0 withr_3.0.2 systemfonts_1.3.1
#> [7] patchwork_1.3.2 ggdist_3.3.3 tidybayes_3.0.7
#> [10] bayesplot_1.14.0 ggplot2_4.0.0 reliabilitydiag_0.2.1
#> [13] priorsense_1.1.1 posterior_1.6.1 loo_2.8.0
#> [16] rstan_2.32.7 StanHeaders_2.32.10 brms_2.23.0
#> [19] Rcpp_1.1.0 sessioninfo_1.2.3 conflicted_1.2.0
#> [22] janitor_2.2.1 matrixStats_1.5.0 modelr_0.1.11
#> [25] tibble_3.3.0 dplyr_1.1.4 tidyr_1.3.1
#> [28] rio_1.2.4 here_1.0.2
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.4 multcomp_1.4-28
#> [7] snakecase_0.11.1 ggridges_0.5.7 compiler_4.5.1
#> [10] reshape2_1.4.4 vctrs_0.6.5 stringr_1.5.2
#> [13] pkgconfig_2.0.3 arrayhelpers_1.1-0 fastmap_1.2.0
#> [16] backports_1.5.0 labeling_0.4.3 utf8_1.2.6
#> [19] rmarkdown_2.30 ps_1.9.1 purrr_1.1.0
#> [22] xfun_0.53 cachem_1.1.0 jsonlite_2.0.0
#> [25] broom_1.0.10 parallel_4.5.1 R6_2.6.1
#> [28] stringi_1.8.7 RColorBrewer_1.1-3 lubridate_1.9.4
#> [31] estimability_1.5.1 knitr_1.50 zoo_1.8-14
#> [34] pacman_0.5.1 Matrix_1.7-4 splines_4.5.1
#> [37] timechange_0.3.0 tidyselect_1.2.1 abind_1.4-8
#> [40] yaml_2.3.10 codetools_0.2-20 processx_3.8.6
#> [43] curl_7.0.0 pkgbuild_1.4.8 plyr_1.8.9
#> [46] lattice_0.22-7 bayestestR_0.17.0 bridgesampling_1.1-2
#> [49] S7_0.2.0 coda_0.19-4.1 evaluate_1.0.5
#> [52] survival_3.8-3 RcppParallel_5.1.11-1 pillar_1.11.1
#> [55] tensorA_0.36.2.1 checkmate_2.3.3 stats4_4.5.1
#> [58] distributional_0.5.0 generics_0.1.4 rprojroot_2.1.1
#> [61] rstantools_2.5.0 scales_1.4.0 xtable_1.8-4
#> [64] glue_1.8.0 emmeans_1.11.2-8 tools_4.5.1
#> [67] data.table_1.17.8 mvtnorm_1.3-3 grid_4.5.1
#> [70] QuickJSR_1.8.1 colorspace_2.1-2 nlme_3.1-168
#> [73] cli_3.6.5 textshaping_1.0.4 svUnit_1.0.8
#> [76] Brobdingnag_1.2-9 V8_8.0.1 gtable_0.3.6
#> [79] digest_0.6.37 TH.data_1.1-4 htmlwidgets_1.6.4
#> [82] farver_2.1.2 memoise_2.0.1 htmltools_0.5.8.1
#> [85] lifecycle_1.0.4 MASS_7.3-65Bibliografia
In Stan, un parametro vincolato in [0,1] senza prior esplicita riceve automaticamente una prior uniforme.↩︎