here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, cmdstanr, tidybayes, loo, patchwork)63 Regressione lineare in Stan
Introduzione
Stan permette di costruire modelli di regressione che vanno dalla semplice regressione lineare ai modelli lineari generalizzati multilivello.
63.1 Il caso più semplice: regressione lineare con un predittore
Consideriamo il caso di una regressione lineare molto semplice, con un solo predittore, un’intercetta (\(\alpha\)), un coefficiente di pendenza (\(\beta\)) e un termine di errore normalmente distribuito con deviazione standard \(\sigma\). Nella notazione standard della regressione, il modello è:
\[ y_n = \alpha + \beta \, x_n + \varepsilon_n, \quad \varepsilon_n \sim \mathcal{N}(0, \sigma) . \]
In Stan, la forma più compatta di questo modello si scrive così:
data {
int<lower=0> N; // numero di osservazioni
vector[N] x; // predittore
vector[N] y; // variabile risposta
}
parameters {
real alpha; // intercetta
real beta; // coefficiente di pendenza
real<lower=0> sigma; // deviazione standard dell’errore
}
model {
y ~ normal(alpha + beta * x, sigma);
}In questo modello:
- N è il numero di osservazioni;
- per ogni osservazione abbiamo un valore di x (predittore) e un valore di y (variabile risposta);
- alpha è l’intercetta e beta la pendenza;
- sigma rappresenta la deviazione standard del termine di errore, che si assume distribuito normalmente.
Le variabili alpha e beta hanno un prior improprio (cioè non specificato esplicitamente), mentre sigma è vincolato ad assumere valori non negativi.
63.1.1 Notazione matriciale e vettorializzazione
La riga:
y ~ normal(alpha + beta * x, sigma);è vettorializzata, cioè calcola la probabilità di tutte le osservazioni in un’unica istruzione. È equivalente a scrivere:
for (n in 1:N) {
y[n] ~ normal(alpha + beta * x[n], sigma);
}La forma vettorializzata è più compatta e molto più veloce da eseguire. In Stan, quando un argomento di una distribuzione è un vettore, anche gli altri argomenti possono esserlo (purché abbiano la stessa dimensione) oppure possono essere scalari (in tal caso vengono “riciclati” per tutte le osservazioni).
Ora estendiamo il ragionamento al caso in cui i predittori siano più di uno, così da introdurre il concetto di effetto parziale.
63.2 Il modello di regressione multipla in notazione matriciale
Quando abbiamo più predittori per ciascuna osservazione, possiamo scrivere il modello di regressione in forma vettoriale/matriciale (Caudek & Luccio, 2001).
In forma compatta, il modello è:
\[ \mathbf{y} = \mathbf{X} \, \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]
dove:
- \(\mathbf{y}\) è un vettore colonna di dimensione \(N \times 1\), che contiene la variabile risposta per le \(N\) osservazioni;
- \(\mathbf{X}\) è una matrice \(N \times K\), dove ogni riga corrisponde a un’osservazione e ogni colonna a un predittore (la prima colonna, se presente, è di 1 e serve per l’intercetta);
- \(\boldsymbol{\beta}\) è un vettore colonna di dimensione \(K \times 1\), che contiene i coefficienti del modello (inclusa l’intercetta se la colonna di 1 è presente in \(\mathbf{X}\));
- \(\boldsymbol{\varepsilon}\) è un vettore \(N \times 1\) di errori casuali, che assumiamo distribuiti come \(\mathcal{N}(0, \sigma^2)\).
| Notazione matematica | Significato | Oggetto in Stan | Dichiarazione Stan |
|---|---|---|---|
| \(\mathbf{y}\) | Vettore colonna degli esiti (variabile risposta) | y |
vector[N] y; |
| \(\mathbf{X}\) | Matrice dei predittori (N osservazioni × K predittori) | x |
matrix[N, K] x; |
| \(\boldsymbol{\beta}\) | Vettore colonna dei coefficienti di regressione | beta |
vector[K] beta; |
| \(\beta_0\) | Intercetta | alpha |
real alpha; |
| \(\sigma\) | Deviazione standard dell’errore | sigma |
real<lower=0> sigma; |
| \(\hat{\mathbf{y}} = \mathbf{X} \boldsymbol{\beta} + \beta_0\) | Vettore delle predizioni lineari | x * beta + alpha |
Espressione all’interno del modello Stan |
| \(\boldsymbol{\varepsilon}\) | Vettore degli errori casuali | — | Implicito nella distribuzione normal(..., sigma)
|
63.2.1 Sviluppo riga per riga
Scrivendo esplicitamente il contenuto della moltiplicazione \(\mathbf{X} \, \boldsymbol{\beta}\), otteniamo:
\[ \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & x_{12} & \dots & x_{1,K-1} \\ 1 & x_{21} & x_{22} & \dots & x_{2,K-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{N1} & x_{N2} & \dots & x_{N,K-1} \end{bmatrix} \begin{bmatrix} \beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{K-1} \end{bmatrix} + \begin{bmatrix} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{N} \end{bmatrix} \]
63.2.2 Interpretazione
- Ogni riga della matrice \(\mathbf{X}\) contiene i valori dei predittori per una singola osservazione.
- La stessa colonna di \(\boldsymbol{\beta}\) (cioè lo stesso coefficiente) si applica a tutte le righe, moltiplicando il rispettivo valore del predittore.
- Il termine \(\beta_0\) è l’intercetta: è costante e si applica a tutte le osservazioni.
- La moltiplicazione \(\mathbf{X} \, \boldsymbol{\beta}\) produce un vettore \(N \times 1\) di valori previsti (\(\hat{y}\)), uno per ogni osservazione.
- Gli errori \(\boldsymbol{\varepsilon}\) rappresentano la differenza tra il valore osservato \(y_i\) e il valore previsto \(\hat{y}_i\).
63.2.3 Esempio numerico
Se \(N=3\) e \(K=3\) (intercetta + 2 predittori), abbiamo:
\[ \underbrace{\begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \end{bmatrix}}_{\mathbf{y}} = \underbrace{\begin{bmatrix} 1 & x_{11} & x_{12} \\ 1 & x_{21} & x_{22} \\ 1 & x_{31} & x_{32} \end{bmatrix}}_{\mathbf{X}} \underbrace{\begin{bmatrix} \beta_{0} \\ \beta_{1} \\ \beta_{2} \end{bmatrix}}_{\boldsymbol{\beta}} + \underbrace{\begin{bmatrix} \varepsilon_{1} \\ \varepsilon_{2} \\ \varepsilon_{3} \end{bmatrix}}_{\boldsymbol{\varepsilon}} \]
Il che equivale a:
\[ \begin{cases} y_{1} = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + \varepsilon_{1} \\ y_{2} = \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + \varepsilon_{2} \\ y_{3} = \beta_0 + \beta_1 x_{31} + \beta_2 x_{32} + \varepsilon_{3} \end{cases} \]
63.2.4 Interpretazione dei coefficienti parziali di regressione
In un modello di regressione multipla ogni coefficiente \(\beta_j\) rappresenta l’effetto parziale del predittore \(x_j\) sulla variabile risposta \(y\), tenendo costanti (cioè controllando per) gli altri predittori inclusi nel modello.
- Effetto parziale: \(\beta_j\) indica di quanto ci si attende che cambi \(y\) in media se \(x_j\) aumenta di una unità, mentre tutti gli altri predittori del modello restano invariati.
- Unità di misura: l’interpretazione è sempre nella scala originale di \(y\) e \(x_j\) (se non abbiamo standardizzato).
- Segno: positivo se, a parità degli altri predittori, un aumento di \(x_j\) è associato a un aumento di \(y\); negativo se associato a una diminuzione.
63.2.4.1 Differenza con la regressione bivariata
Se stimiamo un modello bivariato (cioè con un solo predittore per volta), il coefficiente di regressione di \(x_j\) rappresenta l’associazione totale tra \(x_j\) e \(y\), senza tenere conto di altri fattori. Questo può essere fuorviante quando i predittori sono correlati tra loro e/o esiste un predittore \(x_k\) che spiega parte della stessa varianza di \(y\) che spiega \(x_j\).
In questi casi:
- Modello bivariato: il coefficiente di \(x_j\) include anche l’effetto “indiretto” dovuto alla sua correlazione con altri predittori.
- Modello multiplo: il coefficiente di \(x_j\) è “depurato” dagli effetti degli altri predittori, cioè riflette l’associazione residua unica di \(x_j\) con \(y\).
63.2.4.2 Esempio numerico
Immaginiamo di voler prevedere punteggi di ansia (\(y\)) a partire da:
- stress percepito (\(x_1\), scala 0–10),
- ore di sonno (\(x_2\), scala 0–10).
Se \(x_1\) e \(x_2\) sono correlati (chi dorme poco tende anche a percepire più stress), allora:
- Nel modello bivariato \(y \sim x_1\), il coefficiente di \(x_1\) cattura sia l’effetto diretto dello stress sia quello indiretto dovuto al fatto che più stress → meno sonno → più ansia.
- Nel modello di regressione multipla \(y \sim x_1 + x_2\), il coefficiente di \(x_1\) misura solo la variazione di ansia associata a un aumento di stress a parità di ore di sonno.
In sintesi:
- i coefficienti bivariati misurano l’associazione totale tra predittore e risposta,
- i coefficienti parziali misurano l’associazione unica (al netto degli altri predittori),
- la differenza tra i due diventa rilevante quando i predittori sono correlati.
63.2.5 Regressione con più predittori in Stan
Con più predittori, anche in Stan possiamo usare la notazione matriciale:
data {
int<lower=0> N; // numero di osservazioni
int<lower=0> K; // numero di predittori
matrix[N, K] x; // matrice dei predittori
vector[N] y; // variabile risposta
}
parameters {
real alpha; // intercetta
vector[K] beta; // coefficienti di regressione
real<lower=0> sigma; // deviazione standard dell’errore
}
model {
y ~ normal(x * beta + alpha, sigma);
}Qui:
-
xè una matrice N × K di predittori; -
betaè un vettore con K coefficienti; -
x * betaproduce un vettore di N valori predetti; - aggiungendo
alphaotteniamo la previsione completa per ogni osservazione.
Anche in questo caso la forma vettorializzata è equivalente a:
for (n in 1:N) {
y[n] ~ normal(x[n] * beta + alpha, sigma);
}63.2.6 Intercetta come colonna della matrice dei predittori
Se preferiamo non dichiarare un parametro separato per l’intercetta (alpha), possiamo inserire una colonna di 1 come prima colonna della matrice x. In questo caso il primo elemento di beta (beta[1]) fungerà da intercetta.
Se però vogliamo assegnare un prior diverso all’intercetta rispetto agli altri coefficienti, è meglio dichiarare alpha come parametro separato. Questo è anche leggermente più efficiente, ma la differenza di velocità è trascurabile: la scelta va fatta per chiarezza del codice.
63.2.7 Esempio numerico
Per fare un esempio concreto, ipotizziamo che l’esito \(y\) sia un punteggio di distress su scala 0–100. I due predittori sono:
- \(x_1\): affetto negativo istantaneo su scala 0–10 (più alto = più negativo);
- \(x_2\): ore di sonno nell’ultima notte su scala 0–10.
Per rendere l’esempio realistico, supponiamo che:
- a parità di altre condizioni, aumentare l’affetto negativo di 1 punto (su 0–10) faccia crescere il distress di qualche punto (effetto positivo);
- dormire di più riduca il distress (effetto negativo);
- il livello medio di distress a affetto negativo medio e sonno medio sia moderato.
1) Simulazione dei dati.
set.seed(123)
N <- 200
# Predittori su scala "naturale"
x1 <- pmin(pmax(rnorm(N, mean = 5, sd = 2), 0), 10) # Affetto negativo (0-10)
x2 <- pmin(pmax(rnorm(N, mean = 7, sd = 1.5), 0), 10) # Ore di sonno (0-10)
# Veri parametri (sconosciuti allo stimatore)
alpha_true <- 20 # baseline di distress a x1=5, x2=7 circa
beta1_true <- 4 # +4 punti distress per +1 punto di affetto negativo
beta2_true <- -3 # -3 punti distress per +1 ora di sonno
sigma_true <- 8 # rumore/residuo (DS)
# Generazione dell'esito
y <- alpha_true + beta1_true * x1 + beta2_true * x2 + rnorm(N, 0, sigma_true)
# Controllo rapide statistiche
summary(data.frame(y, x1, x2))
#> y x1 x2
#> Min. :-11.9 Min. : 0.382 Min. : 3.30
#> 1st Qu.: 10.6 1st Qu.: 3.748 1st Qu.: 6.11
#> Median : 20.2 Median : 4.883 Median : 7.03
#> Mean : 19.0 Mean : 4.975 Mean : 7.05
#> 3rd Qu.: 27.1 3rd Qu.: 6.137 3rd Qu.: 8.07
#> Max. : 59.6 Max. :10.000 Max. :10.002) Modello Stan.
Lavoriamo senza standardizzare le variabili. Questo ci consente di specificare prior direttamente interpretabili nelle unità psicologiche originali, evitando di dover ricondurre mentalmente i coefficienti a scale standardizzate.
stancode <- "
data {
int<lower=1> N;
vector[N] x1; // affetto negativo (0-10)
vector[N] x2; // ore di sonno (0-10)
vector[N] y; // distress (0-100)
}
parameters {
real alpha; // intercetta (baseline distress)
vector[2] beta; // beta[1]=effetto x1, beta[2]=effetto x2
real<lower=0> sigma; // DS dell'errore
}
model {
// PRIORS informativi ma prudenti (scala grezza)
alpha ~ normal(20, 20); // baseline tipica, DS ampia
beta[1] ~ normal(4, 2); // NA: aumento atteso +4 distress per +1 punto
beta[2] ~ normal(-3, 2); // Sonno: riduzione attesa -3 distress per +1 ora
sigma ~ student_t(4, 0, 10); // Rumore: DS ~5-15, tolleranza outlier
// LIKELIHOOD vettorializzato
y ~ normal(alpha + beta[1] * x1 + beta[2] * x2, sigma);
}
generated quantities {
vector[N] y_rep; // repliche per PPC
for (n in 1:N)
y_rep[n] = normal_rng(alpha + beta[1]*x1[n] + beta[2]*x2[n], sigma);
}
"3) Compilazione del modello.
stanmod <- cmdstan_model(
write_stan_file(stancode),
compile = TRUE
)4) Dati di input per Stan.
data_list <- list(N = N, x1 = x1, x2 = x2, y = y)5) Campionamento.
fit <- stanmod$sample(
data = data_list,
seed = 2025,
chains = 4, parallel_chains = 4,
iter_warmup = 1000, iter_sampling = 2000
)6) Confronto tra parametri veri e stime a posteriori.
post_sum <- fit$summary(variables = c("alpha", "beta[1]", "beta[2]", "sigma"))
post_sum
#> # A tibble: 4 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 alpha 22.87 22.86 3.01 2.97 17.94 27.85 1.00 3261.06 3703.23
#> 2 beta[1] 3.85 3.85 0.29 0.29 3.37 4.33 1.00 4837.34 4324.04
#> 3 beta[2] -3.26 -3.26 0.37 0.36 -3.88 -2.66 1.00 3952.02 4078.60
#> 4 sigma 7.78 7.76 0.40 0.39 7.15 8.47 1.00 5233.37 4444.49
true_vals <- data.frame(
parameter = c("alpha", "beta[1]", "beta[2]", "sigma"),
true = c(20, 4, -3, 8)
)
true_vals
#> parameter true
#> 1 alpha 20
#> 2 beta[1] 4
#> 3 beta[2] -3
#> 4 sigma 8Interpretazione: Se i posterior mean per beta[1] e beta[2] risultano vicini a 4 e -3, e gli intervalli di credibilità li includono, il modello sta recuperando bene i valori simulati. Lavorare su scala grezza rende i coefficienti subito leggibili:
-
beta[1]: “+1 punto di NA → +4 punti di distress”, -
beta[2]: “+1 ora di sonno → −3 punti di distress”.
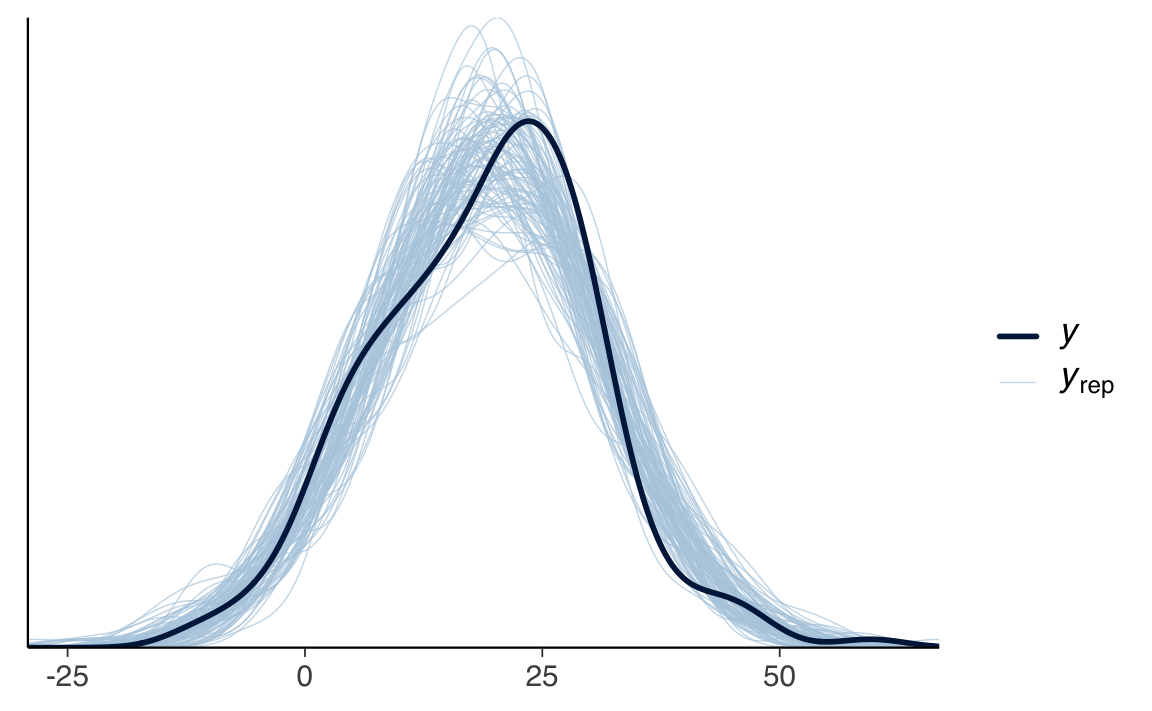
7) Controllo predittivo posteriore.
y_rep_mat <- posterior::as_draws_matrix(fit$draws("y_rep"))
bayesplot::ppc_dens_overlay(data_list$y, y_rep_mat[1:100, ])Se le curve replicate si sovrappongono bene alla distribuzione osservata di \(y\), il modello ha una buona calibrazione predittiva.
Riflessioni conclusive
In questo capitolo abbiamo visto come esprimere la regressione lineare in Stan, partendo dal caso con un solo predittore fino ad arrivare al modello multiplo in notazione matriciale. Abbiamo introdotto la distinzione tra coefficiente bivariato e coefficiente parziale, chiarendo perché in un contesto con predittori correlati il secondo fornisca un’informazione più precisa e interpretativamente solida.
Dal punto di vista pratico, abbiamo:
- simulato dati psicologici plausibili su scala grezza, evitando la standardizzazione per mantenere l’interpretazione diretta dei coefficienti;
- discusso la scelta di prior informativi ma prudenziali derivati da conoscenze precedenti, illustrando il legame tra teoria psicologica e specificazione del modello;
- eseguito il modello in Stan via CmdStanR, verificando la capacità di recuperare i parametri simulati;
- effettuato un controllo predittivo posteriore per confrontare distribuzioni osservate e replicate.
Questo approccio ha permesso di vedere l’intero flusso di lavoro: dalla formulazione teorica del modello alla sua implementazione computazionale, fino alla valutazione della bontà di adattamento.
Informazioni sull’Ambiente di Sviluppo
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] cmdstanr_0.9.0 pillar_1.11.0 tinytable_0.11.0
#> [4] conflicted_1.2.0 patchwork_1.3.1 ggdist_3.3.3
#> [7] tidybayes_3.0.7 bayesplot_1.13.0 ggplot2_3.5.2
#> [10] reliabilitydiag_0.2.1 priorsense_1.1.0 posterior_1.6.1
#> [13] loo_2.8.0 rstan_2.32.7 StanHeaders_2.32.10
#> [16] brms_2.22.0 Rcpp_1.1.0 janitor_2.2.1
#> [19] matrixStats_1.5.0 modelr_0.1.11 tibble_3.3.0
#> [22] dplyr_1.1.4 tidyr_1.3.1 rio_1.2.3
#> [25] here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] svUnit_1.0.6 tidyselect_1.2.1 farver_2.1.2
#> [4] fastmap_1.2.0 TH.data_1.1-3 tensorA_0.36.2.1
#> [7] pacman_0.5.1 digest_0.6.37 estimability_1.5.1
#> [10] timechange_0.3.0 lifecycle_1.0.4 processx_3.8.6
#> [13] survival_3.8-3 magrittr_2.0.3 compiler_4.5.1
#> [16] rlang_1.1.6 tools_4.5.1 utf8_1.2.6
#> [19] yaml_2.3.10 data.table_1.17.8 knitr_1.50
#> [22] labeling_0.4.3 bridgesampling_1.1-2 htmlwidgets_1.6.4
#> [25] pkgbuild_1.4.8 curl_6.4.0 plyr_1.8.9
#> [28] RColorBrewer_1.1-3 multcomp_1.4-28 abind_1.4-8
#> [31] withr_3.0.2 purrr_1.1.0 grid_4.5.1
#> [34] stats4_4.5.1 xtable_1.8-4 colorspace_2.1-1
#> [37] inline_0.3.21 emmeans_1.11.2 scales_1.4.0
#> [40] MASS_7.3-65 cli_3.6.5 mvtnorm_1.3-3
#> [43] rmarkdown_2.29 generics_0.1.4 RcppParallel_5.1.10
#> [46] reshape2_1.4.4 cachem_1.1.0 stringr_1.5.1
#> [49] splines_4.5.1 parallel_4.5.1 vctrs_0.6.5
#> [52] V8_6.0.5 Matrix_1.7-3 sandwich_3.1-1
#> [55] jsonlite_2.0.0 arrayhelpers_1.1-0 glue_1.8.0
#> [58] ps_1.9.1 codetools_0.2-20 distributional_0.5.0
#> [61] lubridate_1.9.4 stringi_1.8.7 gtable_0.3.6
#> [64] QuickJSR_1.8.0 htmltools_0.5.8.1 Brobdingnag_1.2-9
#> [67] R6_2.6.1 rprojroot_2.1.0 evaluate_1.0.4
#> [70] lattice_0.22-7 backports_1.5.0 memoise_2.0.1
#> [73] broom_1.0.9 snakecase_0.11.1 rstantools_2.4.0
#> [76] coda_0.19-4.1 gridExtra_2.3 nlme_3.1-168
#> [79] checkmate_2.3.2 xfun_0.52 zoo_1.8-14
#> [82] pkgconfig_2.0.3