67  La grandezza dell’effetto: valutare la rilevanza pratica

“Il valore di P non misura l’importanza di un risultato. Per l’importanza, guardate all’entità dell’effetto.”

– Jacob Cohen, Statistician and psychologist

Introduzione

Nel capitolo precedente abbiamo esaminato la differenza nei punteggi di QI tra bambini nati da madri con e senza diploma di scuola superiore. L’analisi bayesiana ci ha permesso di ottenere una distribuzione a posteriori per questa differenza, da cui derivano inferenze probabilistiche ricche e sfumate. Ma un interrogativo cruciale rimane aperto: questa differenza è importante?

In psicologia, come in molte scienze applicate, non è sufficiente stabilire che un effetto esiste: bisogna valutare se l’effetto ha una magnitudine sufficiente da avere rilevanza teorica, clinica o sociale. È in questa prospettiva che si introduce il concetto di grandezza dell’effetto (effect size), una misura quantitativa dell’intensità di un risultato.

Panoramica del capitolo

  • Che cosa misuriamo quando parliamo di “grandezza dell’effetto”.
  • Come stimarlo con modelli bayesiani in brms.
  • Come comunicarlo con intervalli e predizioni.
  • Leggere “Bayesian estimation supersedes the t test” (Kruschke, 2013).
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, brms, bayestestR, insight)

67.1 Perché stimare la grandezza dell’effetto

La grandezza dell’effetto fornisce un ponte tra analisi statistica e interpretazione sostanziale dei dati. Essa consente di rispondere a domande come:

  • Quanto è marcata la differenza osservata?
  • L’effetto ha un impatto concreto nella vita reale o nelle applicazioni cliniche?
  • La variazione osservata è sufficiente a giustificare interventi, cambiamenti o nuove ipotesi teoriche?

L’American Psychological Association (APA) raccomanda di riportare sempre una misura di grandezza dell’effetto, in quanto essa fornisce un’informazione critica che va oltre la mera dicotomia “effetto presente / effetto assente”.

67.2 Standardizzare le differenze: il Cohen’s d

Nel confronto tra due gruppi, una delle misure più comuni di grandezza dell’effetto è il Cohen’s d**, che esprime la differenza tra due medie in unità di deviazione standard:

\[ d = \frac{\mu_1 - \mu_2}{\sigma}, \]

dove:

  • \(\mu_1\) e \(\mu_2\) sono le medie dei due gruppi,
  • \(\sigma\) è una stima comune della deviazione standard.

L’interpretazione di d è indipendente dalle unità di misura originali, il che la rende particolarmente utile per confrontare risultati provenienti da diversi studi o contesti.

67.3 Il Cohen’s d in ottica bayesiana

Nell’approccio bayesiano, non calcoliamo un unico valore di d, ma una distribuzione a posteriori di valori plausibili per d, ottenuta combinando:

  • i campioni posteriori della differenza tra gruppi,
  • i campioni posteriori della deviazione standard residua.

67.3.1 Esempio pratico con brms

A partire dal modello stimato nel capitolo precedente:

kidiq <- rio::import(here::here("data", "kidiq.dta"))

fit_1 <- brm(
  kid_score ~ mom_hs, 
  data = kidiq, 
  backend = "cmdstanr",
  silent = 0
)

Otteniamo i campioni posteriori:

post <- as_draws_df(fit_1)
d_samples <- post$b_mom_hs / post$sigma

67.3.1.1 Visualizzazione della distribuzione di d 

mcmc_areas(as_draws_df(tibble(d = d_samples)), pars = "d", prob = 0.89) +
  labs(
    title = "Distribuzione a posteriori di Cohen's d",
    subtitle = "Stima bayesiana della grandezza dell’effetto"
  )

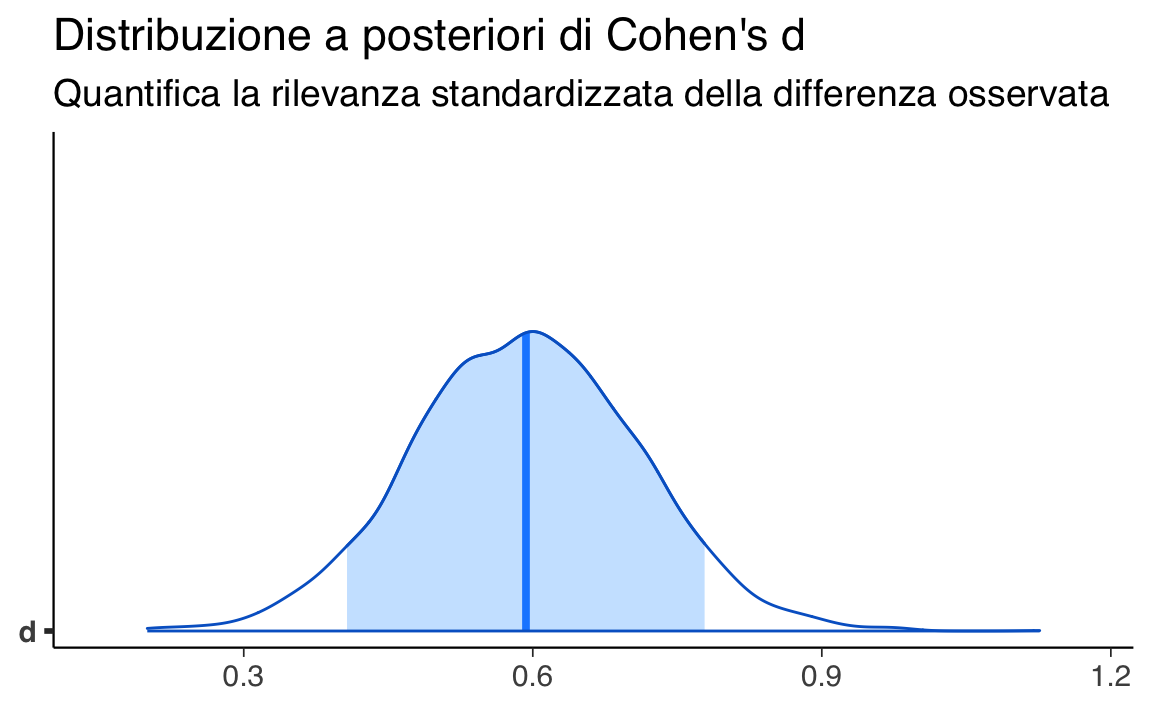
Questa distribuzione esprime l’incertezza residua sulla grandezza dell’effetto, dopo aver osservato i dati, ed è il punto di partenza per una valutazione più completa.

67.3.1.2 Statistiche riassuntive

bayestestR::describe_posterior(d_samples, ci = 0.89)
#> Summary of Posterior Distribution
#> 
#> Parameter | Median |       89% CI |   pd |          ROPE | % in ROPE
#> --------------------------------------------------------------------
#> Posterior |   0.59 | [0.41, 0.78] | 100% | [-0.10, 0.10] |        0%

Questa funzione fornisce:

  • la stima centrale (media o mediana) di d,
  • l’intervallo di credibilità,
  • la probabilità che d sia maggiore o minore di soglie rilevanti.

67.3.1.3 Interpretare la grandezza dell’effetto: da soglie fisse a giudizi probabilistici

In ambito frequentista, la seguente classificazione è comunemente usata:

Valore di d Interpretazione convenzionale
≈ 0.2 Effetto piccolo
≈ 0.5 Effetto medio
≥ 0.8 Effetto grande

Queste soglie hanno valore euristico, ma non vanno applicate meccanicamente. Nell’approccio bayesiano possiamo invece porre domande più informative, del tipo:

  • Qual è la probabilità che l’effetto superi 0.5 (soglia di effetto medio)?
  • Qual è la probabilità che sia minore di 0.2 (effetto trascurabile)?
  • Qual è l’intervallo entro cui cade il 89% degli effetti più credibili?

Queste domande trovano risposta diretta nei dati posteriori:

mean(d_samples > 0.5)  # Probabilità che l'effetto sia almeno medio
#> [1] 0.7873
mean(d_samples > 0.8)  # Probabilità che l'effetto sia grande
#> [1] 0.037
mean(d_samples < 0.2)  # Probabilità che l'effetto sia trascurabile
#> [1] 0.00025

67.3.1.4 La soglia di rilevanza pratica

In contesti applicativi, non basta sapere che l’effetto è diverso da zero: bisogna chiedersi se supera una soglia minima di rilevanza (minimum effect of interest, o region of practical equivalence).

Ad esempio, se uno psicologo clinico ritiene che un effetto inferiore a d = 0.3 sia irrilevante dal punto di vista terapeutico, può valutare:

mean(d_samples > 0.3)
#> [1] 0.9938

Questa quantità risponde alla domanda: qual è la probabilità che l’effetto sia rilevante nella pratica clinica?

Riflessioni conclusive

Le linee guida dell’American Psychological Association (APA) sottolineano l’importanza di riportare sistematicamente le stime della dimensione dell’effetto (effect size) nella comunicazione dei risultati della ricerca. Questa raccomandazione nasce dalla consapevolezza che la mera verifica di ipotesi, spesso concentrata su un valore di probabilità, fornisce un’informazione limitata. La stima dell’effect size, al contrario, consente di quantificare la magnitudine di un fenomeno, offrendo una base più solida per valutarne la rilevanza teorica o applicativa. L’identificazione di un effetto statisticamente rilevante rappresenta dunque solo un primo passo; la sua reale interpretazione scientifica richiede una comprensione approfondita della sua entità.

Nell’ambito della statistica frequentista, la dimensione dell’effetto viene tipicamente comunicata attraverso una stima puntuale corredata da un intervallo di confidenza. Quest’ultimo descrive la variabilità attesa della stima in un’ipotetica sequenza di replicazioni dello studio. Sebbene utile, questa rappresentazione può incoraggiare, anche involontariamente, un’interpretazione dicotomica dei risultati, dove l’attenzione si concentra esclusivamente sul superamento di una soglia di significatività.

L’inferenza bayesiana propone una prospettiva alternativa, trattando la dimensione dell’effetto non come un parametro fisso ma come una variabile aleatoria. La sua incertezza viene rappresentata attraverso una distribuzione di probabilità a posteriori, che sintetizza l’evidenza proveniente dai dati osservati e dalle conoscenze preliminari, formalizzate in una distribuzione a priori. Questo quadro concettuale permette di formulare affermazioni probabilistiche dirette sull’effect size, come calcolare la probabilità che esso superi una determinata soglia di rilevanza clinica o teorica. L’incertezza viene così rappresentata in modo continuo e sfumato, evitando categorizzazioni rigide.

Questo approccio si adatta particolarmente bene all’indagine dei processi psicologici, caratterizzati da un’elevata complessità e variabilità. L’obiettivo dell’analisi bayesiana non è quello di giungere a una conclusione definitiva, ma di aggiornare in modo coerente e trasparente il grado di plausibilità associato a diverse ipotesi. In questo contesto, la stima della dimensione dell’effetto assume un ruolo centrale, diventando uno strumento inferenziale per valutare la credibilità e l’importanza pratica dei risultati ottenuti.

Adottare una prospettiva bayesiana significa quindi abbracciare un paradigma inferenziale che privilegia la valutazione probabilistica e contestualizzata rispetto alla decisione dicotomica. Questo passaggio favorisce una comunicazione scientifica più ricca e meno ambigua, contribuendo a una psicologia maggiormente riflessiva, trasparente e focalizzata sul significato sostanziale dei propri risultati.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] insight_1.3.1         bayestestR_0.16.1     cmdstanr_0.9.0       
#>  [4] pillar_1.11.0         tinytable_0.11.0      patchwork_1.3.1      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.13.0     
#> [10] ggplot2_3.5.2         reliabilitydiag_0.2.1 priorsense_1.1.0     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.22.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [28] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3        inline_0.3.21        sandwich_3.1-1      
#>  [4] rlang_1.1.6          magrittr_2.0.3       multcomp_1.4-28     
#>  [7] snakecase_0.11.1     ggridges_0.5.6       compiler_4.5.1      
#> [10] reshape2_1.4.4       systemfonts_1.2.3    vctrs_0.6.5         
#> [13] stringr_1.5.1        pkgconfig_2.0.3      arrayhelpers_1.1-0  
#> [16] fastmap_1.2.0        backports_1.5.0      labeling_0.4.3      
#> [19] rmarkdown_2.29       tzdb_0.5.0           haven_2.5.5         
#> [22] ps_1.9.1             ragg_1.4.0           purrr_1.1.0         
#> [25] xfun_0.52            cachem_1.1.0         jsonlite_2.0.0      
#> [28] broom_1.0.9          parallel_4.5.1       R6_2.6.1            
#> [31] stringi_1.8.7        RColorBrewer_1.1-3   lubridate_1.9.4     
#> [34] estimability_1.5.1   knitr_1.50           zoo_1.8-14          
#> [37] R.utils_2.13.0       pacman_0.5.1         readr_2.1.5         
#> [40] Matrix_1.7-3         splines_4.5.1        timechange_0.3.0    
#> [43] tidyselect_1.2.1     abind_1.4-8          yaml_2.3.10         
#> [46] codetools_0.2-20     curl_6.4.0           processx_3.8.6      
#> [49] pkgbuild_1.4.8       plyr_1.8.9           lattice_0.22-7      
#> [52] withr_3.0.2          bridgesampling_1.1-2 coda_0.19-4.1       
#> [55] evaluate_1.0.4       survival_3.8-3       RcppParallel_5.1.10 
#> [58] tensorA_0.36.2.1     checkmate_2.3.2      stats4_4.5.1        
#> [61] distributional_0.5.0 generics_0.1.4       rprojroot_2.1.0     
#> [64] hms_1.1.3            rstantools_2.4.0     scales_1.4.0        
#> [67] xtable_1.8-4         glue_1.8.0           emmeans_1.11.2      
#> [70] tools_4.5.1          data.table_1.17.8    forcats_1.0.0       
#> [73] mvtnorm_1.3-3        grid_4.5.1           QuickJSR_1.8.0      
#> [76] datawizard_1.2.0     colorspace_2.1-1     nlme_3.1-168        
#> [79] cli_3.6.5            textshaping_1.0.1    svUnit_1.0.6        
#> [82] Brobdingnag_1.2-9    V8_6.0.5             gtable_0.3.6        
#> [85] R.methodsS3_1.8.2    digest_0.6.37        TH.data_1.1-3       
#> [88] htmlwidgets_1.6.4    farver_2.1.2         R.oo_1.27.1         
#> [91] memoise_2.0.1        htmltools_0.5.8.1    lifecycle_1.0.4     
#> [94] MASS_7.3-65

Bibliografia

Kruschke, J. K. (2013). Bayesian estimation supersedes the t test. Journal of Experimental Psychology: General, 142(2), 573–603.