here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(mice)46 Distribuzioni coniugate (2)
“The great advantage of conjugate families is that they make Bayesian updating almost automatic.”
– Dennis V. Lindley, Bayesian Statistics: A Review (1972)
Introduzione
Nel capitolo precedente abbiamo esplorato il modello Beta-Binomiale, un esempio paradigmatico di coniugazione nel contesto dei dati discreti. Ora, ci addentriamo nel dominio continuo con il modello Normale-Normale. Grazie alla sua eleganza analitica e alla sua trattabilità, questo modello rappresenta uno strumento cardine nell’inferenza bayesiana.
Consideriamo di avere \(n\) osservazioni \(y_1, \dots, y_n\) che assumiamo essere indipendenti e identicamente distribuite (iid) secondo una distribuzione Normale (o Gaussiana) con media \(\mu\) e varianza \(\sigma^2\), ossia \(y_i \stackrel{\text{iid}}{\sim} \mathcal{N}(\mu, \sigma^2)\). Nell’approccio bayesiano, esprimiamo le nostre conoscenze preliminari su \(\mu\) (e, se necessario, su \(\sigma^2\)) attraverso una distribuzione a priori, tipicamente anch’essa Gaussiana. La magia di questo modello risiede nella coniugazione: se la distribuzione a priori è Normale e la verosimiglianza è Normale, anche la distribuzione a posteriori per \(\mu\) sarà Normale.
L’inferenza bayesiana è un processo iterativo di apprendimento che combina in modo sistematico:
- Convinzioni Iniziali (Distribuzione a Priori): Definiamo una distribuzione a priori per il parametro di nostro interesse, in questo caso la media \(\mu\). Questa riflette la nostra incertezza o conoscenza su \(\mu\) prima di osservare i dati.
- Evidenza Empirica (Funzione di Verosimiglianza): Osserviamo i dati e costruiamo la funzione di verosimiglianza, che ci dice quanto sono probabili i dati osservati per diversi valori possibili di \(\mu\).
- Aggiornamento della Conoscenza (Distribuzione a Posteriori): Applichiamo il teorema di Bayes per combinare la prior e la verosimiglianza. Il risultato è la distribuzione a posteriori, che rappresenta la nostra conoscenza aggiornata su \(\mu\) dopo aver considerato i dati.
Un beneficio chiave di questo approccio è la progressiva riduzione dell’incertezza. All’aumentare del numero di osservazioni, la varianza della distribuzione a posteriori tende a diminuire, fornendo una stima sempre più precisa (cioè con un intervallo di plausibilità più ristretto) per \(\mu\).
In questo capitolo, ci concentreremo sulle famiglie coniugate (per approfondimenti, si veda Capitolo 45), con un focus specifico sul modello Normale-Normale. Vedremo come, partendo da una prior Normale e una verosimiglianza Normale, la distribuzione a posteriori per la media \(\mu\) risulti anch’essa Normale, semplificando notevolmente i calcoli.
Panoramica del capitolo
- introdurre il modello Normale-Normale come esempio di famiglia coniugata;
- mostrare come combinare prior e verosimiglianza per ottenere la distribuzione a posteriori;
- calcolare media e varianza a posteriori in forma chiusa;
- interpretare il ruolo relativo di prior e dati nell’aggiornamento bayesiano;
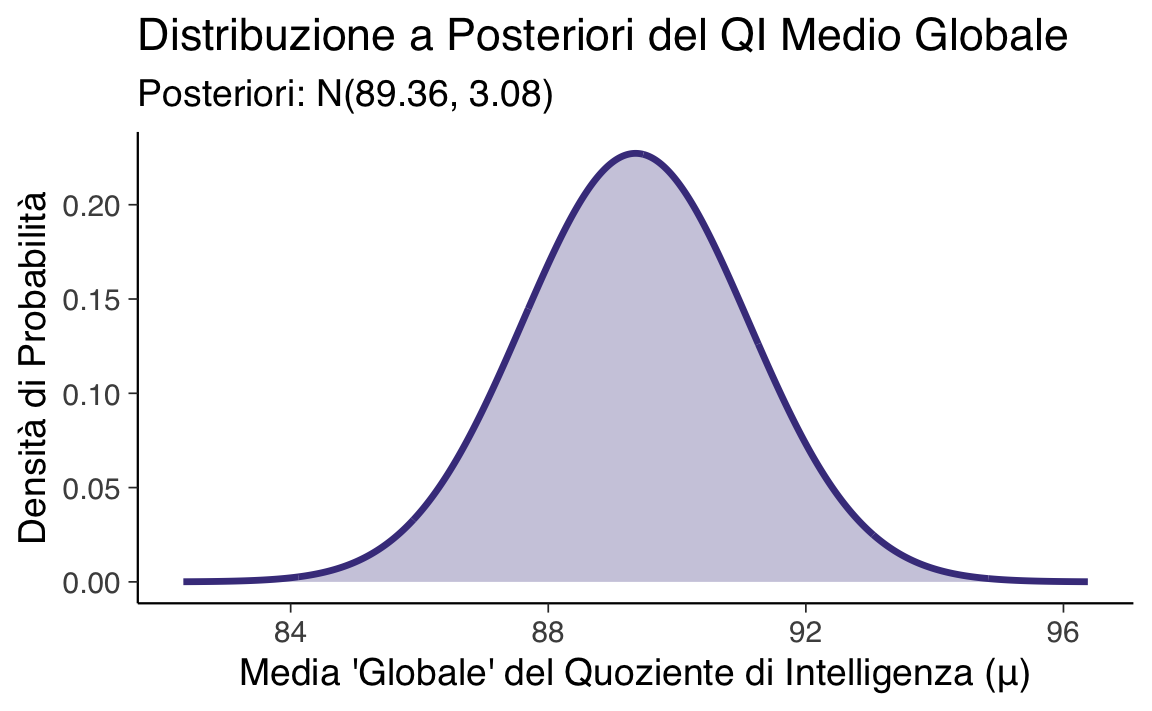
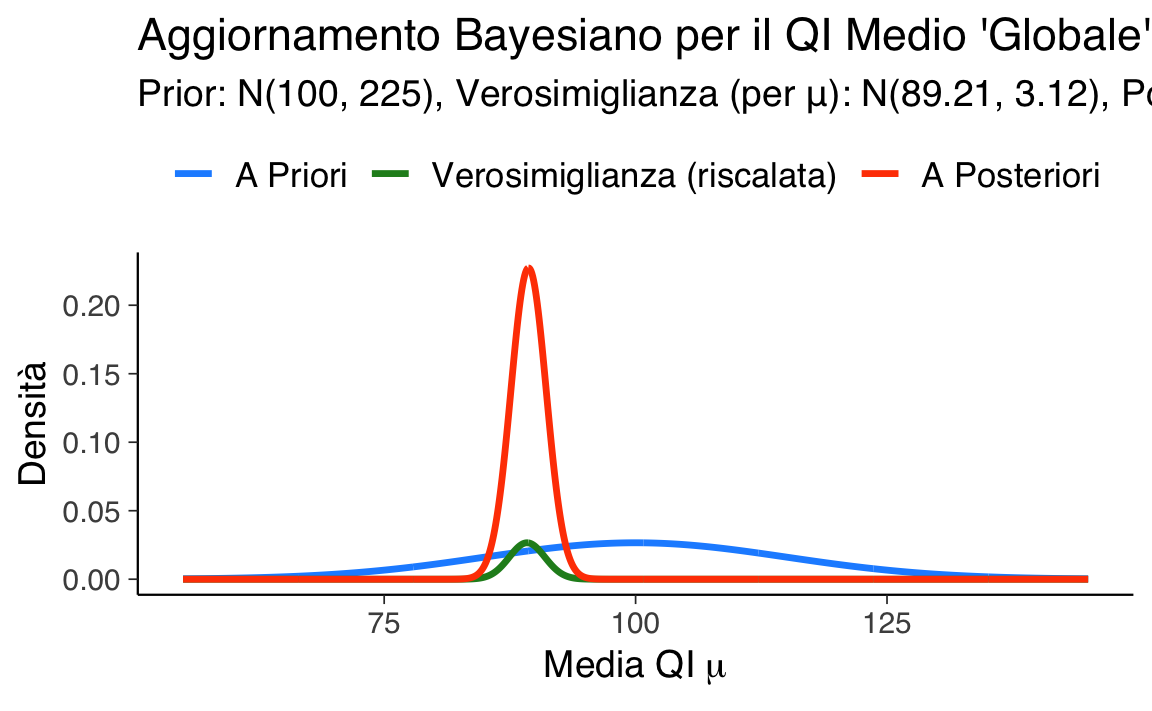
- applicare il modello a casi concreti (tempi di reazione, punteggi di QI).
46.1 Perché Scegliere una Distribuzione Normale?
La scelta di una distribuzione a priori (e di una verosimiglianza) Normale offre numerosi vantaggi, sia dal punto di vista teorico che pratico:
Simmetria e Adattabilità: La caratteristica forma “a campana” e simmetrica della distribuzione Normale ben si adatta a descrivere molti fenomeni naturali, psicologici e cognitivi, come i tempi di reazione, i punteggi di abilità, o gli errori di misurazione. Questa simmetria facilita l’interpretazione della media \(\mu\) come misura di tendenza centrale e della varianza \(\sigma^2\) come misura della dispersione o incertezza.
Efficienza Parametrica: Nel modello Normale-Normale con varianza nota, l’incertezza sulla media \(\mu\) nella distribuzione a priori è descritta dal singolo parametro \(\sigma_0^2\) (la varianza della prior). Analogamente, la variabilità dei dati è descritta da \(\sigma^2\). Questa parsimonia parametrica semplifica sia la fase di modellizzazione sia la comunicazione dei risultati.
Convergenza con l’Inferenza Classica: Per campioni di dati sufficientemente ampi, le stime bayesiane ottenute con il modello Normale tendono a convergere verso quelle dell’inferenza frequentista. Questa proprietà, legata al teorema di Bernstein-von Mises, è talvolta indicata come calibrazione asintotica e fa sì che il modello Normale-Normale possa agire da ponte tra i due paradigmi inferenziali.
Semplicità Computazionale: Le operazioni matematiche tra distribuzioni Normali (come il prodotto richiesto dal teorema di Bayes) risultano in un’altra distribuzione Normale. Questo permette di ottenere soluzioni analitiche in forma chiusa per i parametri della distribuzione a posteriori, evitando la necessità di ricorrere a metodi di approssimazione numerica complessi, come le simulazioni Monte Carlo Markov Chain (MCMC), almeno nei casi più semplici.
In sintesi: se le nostre conoscenze preliminari suggeriscono una distribuzione unimodale e simmetrica per il parametro di interesse, o se ci aspettiamo che la distribuzione a posteriori abbia tali caratteristiche (cosa spesso favorita dal Teorema del Limite Centrale quando si ha un campione ampio), la distribuzione Normale rappresenta una scelta robusta, elegante e computazionalmente vantaggiosa per condurre un’inferenza rigorosa.
46.2 Inferenza Bayesiana per la Media di una Popolazione Normale (Varianza Nota)
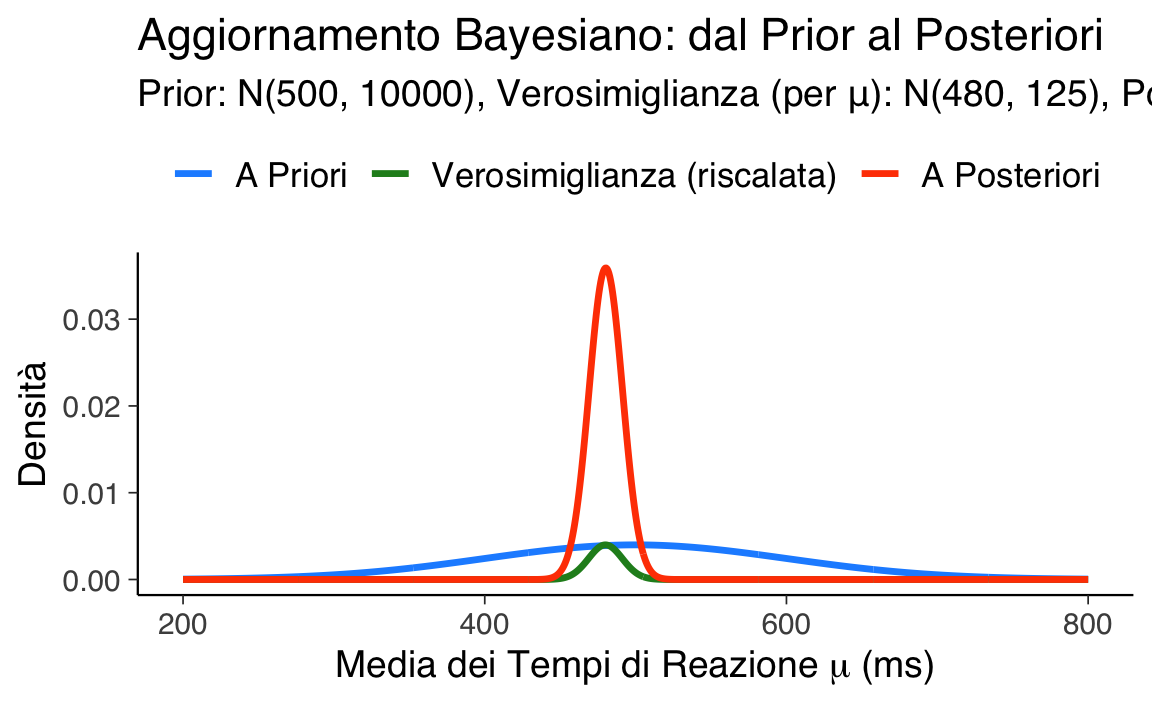
Immaginiamo di voler stimare il tempo medio di reazione \(\mu\) (in millisecondi, ms) di una popolazione di studenti impegnati in un compito Stroop. Supponiamo di aver raccolto i tempi di reazione \(y_1, \dots, y_n\) da un campione di \(n\) studenti. Assumiamo che questi dati provengano da una distribuzione Normale \(y_i \sim \mathcal{N}(\mu, \sigma^2)\) e, per semplificare inizialmente il modello, assumiamo che la varianza \(\sigma^2\) della popolazione sia nota (ad esempio, da studi precedenti o dalla natura standardizzata del compito). Sia \(\sigma = 50\) ms la deviazione standard nota.
46.2.1 I Tre Passi Fondamentali dell’Inferenza Bayesiana
Il processo di inferenza bayesiana si articola nei seguenti passaggi chiave:
| Passo | Significato Intuitivo | Formalizzazione Matematica (Modello Normale-Normale) |
|---|---|---|
| A. Distribuzione a Priori | Le nostre convinzioni iniziali sulla media \(\mu\). | \(\mu \sim \mathcal{N}(\mu_0, \sigma_0^2)\) |
| B. Verosimiglianza dei Dati | L’informazione su \(\mu\) contenuta nei dati osservati. | \(y_i \stackrel{\text{iid}}{\sim} \mathcal{N}(\mu, \sigma^2)\) |
| C. Distribuzione a Posteriori | Le nostre convinzioni aggiornate su \(\mu\) dopo i dati. | \(\mu \mid \mathbf{y} \sim \mathcal{N}(\mu_p, \sigma_p^2)\) |
Quando la varianza \(\sigma^2\) dei dati è nota e la prior per \(\mu\) è Normale, la distribuzione Normale è coniugata per la media \(\mu\). Ciò significa che la distribuzione a posteriori per \(\mu\) sarà anch’essa Normale, mantenendo la stessa forma funzionale attraverso l’aggiornamento bayesiano.
46.2.2 Distribuzione A priori
\(\mu \sim \mathcal{N}(\mu_0,\sigma_0^2)\): descrive dove crediamo sia \(\mu\) e quanta incertezza abbiamo, una varianza grande significa poca informazione.
46.2.3 Verosimiglianza
\[ p(y\mid\mu,\sigma)=\prod_{i=1}^{n}\frac{1}{\sigma\sqrt{2\pi}} \exp\!\Bigl[-\tfrac{(y_i-\mu)^2}{2\sigma^2}\Bigr]. \]
46.2.4 Teorema di Bayes
Il teorema di Bayes combina prior e verosimiglianza attraverso un prodotto ponderato:
\[ p(\mu\mid y)=\frac{p(y\mid\mu)\,p(\mu)}{p(y)} \;\; \propto\;\; \underbrace{\mathcal{N}(\mu_0,\sigma_0^2)}_{\text{prior}} \; \times \; \underbrace{\mathcal{N}(\bar y,\sigma^2/n)}_{\text{verosimiglianza}} . \]
Il prodotto di due distribuzioni gaussiane è una distribuzione gaussiana: basta aggiornare media e varianza.
46.2.5 Media a posteriori
\[ \mu_p=\frac{\tfrac{1}{\sigma_0^2}\,\mu_0 + \tfrac{n}{\sigma^2}\,\bar y} {\tfrac{1}{\sigma_0^2} + \tfrac{n}{\sigma^2}}, \qquad \bar y=\frac{1}{n}\sum_{i=1}^{n}y_i. \tag{46.1}\]
\(\mu_0\): l’idea iniziale.
\(\sigma_0^2\): la fiducia in quell’idea.
\(\bar y\): ciò che dicono i dati.
\(n/\sigma^2\): la quantità di informazione empirica, aumenta con più casi e diminuisce con misure rumorose.
-
Interpretazione: Il peso relativo di prior e dati dipende dalla loro credibilità:
- La prior è influente se ha alta precisione, ovvero 1/\(\sigma_0^2\) è grande, o se ci sono pochi dati, \(n\) piccolo.
- I dati sono dominanti se la prior ha bassa precisione o se c’è un ampio campione.
46.2.6 Varianza a posteriori
\[ \sigma_p^2=\frac{1}{\tfrac{1}{\sigma_0^2}+\tfrac{n}{\sigma^2}}. \tag{46.2}\]
- Proprietà Chiave: \(\sigma_p^2 \le \min(\sigma_0^2, \sigma^2/n)\). L’incertezza diminuisce monotonicamente all’aumentare di \(n\).
Esercizio 1.
Supponiamo di voler stimare il tempo medio di reazione \(\mu\) (in millisecondi) di un gruppo di studenti a un compito Stroop. Dalla letteratura o da esperienze precedenti, assumiamo che la deviazione standard dei tempi di reazione per questo tipo di compito sia \(\sigma = 50\) ms.
Definiamo la nostra distribuzione a priori per \(\mu\) basandoci su una nostra conoscenza preliminare o un’ipotesi plausibile. Ad esempio, potremmo ipotizzare che il tempo medio sia attorno ai 500 ms, con una certa incertezza: * Media a priori: \(\mu_0 = 500\) ms * Deviazione standard a priori: \(\sigma_0 = 100\) ms (quindi varianza a priori \(\sigma_0^2 = 100^2 = 10000\))
Successivamente, raccogliamo i dati da \(n=20\) studenti e osserviamo una media campionaria dei tempi di reazione \(\bar{y} = 480\) ms.
Riepilogo dei parametri:
| Simbolo | Descrizione | Valore |
|---|---|---|
| \(\mu_0\) | Media a priori | 500 ms |
| \(\sigma_0\) | Dev. std. a priori | 100 ms |
| \(\sigma_0^2\) | Varianza a priori | 10000 ms² |
| \(\sigma\) | Dev. std. dei dati (nota) | 50 ms |
| \(\sigma^2\) | Varianza dei dati (nota) | 2500 ms² |
| \(n\) | Numero di osservazioni | 20 |
| \(\bar{y}\) | Media campionaria osservata | 480 ms |
1. Calcolo delle Precisioni (Pesi):
- Precisione a priori: \(w_0 = \frac{1}{\sigma_0^2} = \frac{1}{100^2} = \frac{1}{10000} = 0.0001\)
- Precisione dei dati: \(w_{\text{dati}} = \frac{n}{\sigma^2} = \frac{20}{50^2} = \frac{20}{2500} = 0.008\)
2. Calcolo della Media a Posteriori (\(\mu_n\)): \[ \mu_n = \frac{w_0 \mu_0 + w_{\text{dati}} \bar{y}}{w_0 + w_{\text{dati}}} = \frac{0.0001 \times 500 + 0.008 \times 480}{0.0001 + 0.008} = \frac{0.05 + 3.84}{0.0081} = \frac{3.89}{0.0081} \approx 480.247 \text{ ms} \]
3. Calcolo della Varianza a Posteriori (\(\sigma_n^2\)): \[ \sigma_n^2 = \frac{1}{w_0 + w_{\text{dati}}} = \frac{1}{0.0001 + 0.008} = \frac{1}{0.0081} \approx 123.457 \text{ ms}^2 \] La deviazione standard a posteriori è \(\sigma_n = \sqrt{\sigma_n^2} \approx \sqrt{123.457} \approx 11.11 \text{ ms}\).
Risultato e Interpretazione: Siamo partiti da una stima a priori di \(\mu \approx 500 \pm 100\) ms. Dopo aver osservato 20 tempi di reazione con una media di 480 ms (e sapendo che \(\sigma=50\) ms), la nostra stima aggiornata per la media dei tempi di reazione è \(\mu_n \approx 480.25 \pm 11.11\) ms. Notiamo che la media a posteriori (480.25 ms) è molto più vicina alla media campionaria (480 ms) che alla media a priori (500 ms). Questo perché la precisione dei dati (0.008) è significativamente maggiore della precisione a priori (0.0001). Inoltre, la nostra incertezza si è drasticamente ridotta: la deviazione standard è passata da 100 ms a circa 11 ms dopo sole 20 osservazioni. Questo illustra il potere dell’aggiornamento bayesiano nel raffinare le nostre stime e ridurre l’incertezza.
# ---- Parametri dell'esempio -------------------------------------------
mu0 <- 500 # Media a priori
sigma0 <- 100 # Deviazione standard a priori
sigma <- 50 # Deviazione standard nota dei dati
n <- 20 # Dimensione del campione
ybar <- 480 # Media campionaria osservata
# ---- Calcolo dei parametri a posteriori -------------------------------
# Precisioni
prec_prior <- 1 / sigma0^2
prec_data <- n / sigma^2
# Parametri posteriori
sigma_p2 <- 1 / (prec_prior + prec_data) # Varianza a posteriori
sigma_p <- sqrt(sigma_p2) # Deviazione standard a posteriori
mu_p <- (mu0 * prec_prior + ybar * prec_data) / (prec_prior + prec_data) # Media a posteriori
# ---- Griglia di valori per il parametro mu -----------------------------
# Definiamo un range che copra bene tutte e tre le distribuzioni
min_mu <- min(mu0 - 3*sigma0, ybar - 3*sigma/sqrt(n), mu_p - 3*sigma_p)
max_mu <- max(mu0 + 3*sigma0, ybar + 3*sigma/sqrt(n), mu_p + 3*sigma_p)
mu_grid <- seq(min_mu, max_mu, length.out = 1000)
# ---- Calcolo delle densità delle tre curve -----------------------------
prior_dens <- dnorm(mu_grid, mean = mu0, sd = sigma0) # Densità a priori
post_dens <- dnorm(mu_grid, mean = mu_p, sd = sigma_p) # Densità a posteriori
# Verosimiglianza (standardizzata per mu, basata sulla media campionaria)
# La sd per la verosimiglianza di mu è sigma/sqrt(n)
lik_dens_raw <- dnorm(mu_grid, mean = ybar, sd = sigma / sqrt(n))
# Riscaliamo la verosimiglianza per renderla graficamente confrontabile con la prior
# Questo è solo per visualizzazione, la verosimiglianza non è una densità per mu in senso stretto
lik_dens_scaled <- lik_dens_raw * (max(prior_dens) / max(lik_dens_raw))
# ---- Preparazione dati in formato "lungo" per ggplot2 ------------------
df <- data.frame(
mu = mu_grid,
Prior = prior_dens,
Likelihood_scaled = lik_dens_scaled, # Usiamo quella riscalata
Posterior = post_dens
)
df_long <- pivot_longer(df, -mu, names_to = "Distribuzione", values_to = "Densita")
df_long$Distribuzione <- factor(df_long$Distribuzione,
levels = c("Prior", "Likelihood_scaled", "Posterior"),
labels = c("A Priori", "Verosimiglianza (riscalata)", "A Posteriori"))
# ---- Grafico delle distribuzioni ---------------------------------------
ggplot(df_long, aes(x = mu, y = Densita, colour = Distribuzione)) +
geom_line(linewidth = 1.2) +
labs(
x = expression(paste("Media dei Tempi di Reazione ", mu, " (ms)")),
y = "Densità",
title = "Aggiornamento Bayesiano: dal Prior al Posteriori",
subtitle = paste0("Prior: N(", mu0, ", ", sigma0^2, "), ",
"Verosimiglianza (per μ): N(", ybar, ", ", round((sigma^2/n),2), "), ",
"Posteriori: N(", round(mu_p,2), ", ", round(sigma_p2,2), ")")
) +
scale_color_manual(values = c("A Priori" = "dodgerblue",
"Verosimiglianza (riscalata)" = "forestgreen",
"A Posteriori" = "orangered")) +
theme(legend.title = element_blank(), legend.position = "top")
Il grafico Figura 46.1 illustra chiaramente come la distribuzione a posteriori sia “spostata” verso la verosimiglianza (che è più informativa della prior in questo caso) e come la sua varianza sia notevolmente ridotta rispetto a entrambe.
Messaggi chiave sull’inferenza con varianza nota
- Dialogo Costruttivo: L’inferenza bayesiana è un processo dinamico di dialogo tra le nostre ipotesi iniziali (prior) e l’evidenza empirica (dati/verosimiglianza).
- Calcoli Trasparenti: Con la varianza della popolazione \(\sigma^2\) nota, i calcoli per la media e la varianza a posteriori sono diretti e possono essere eseguiti analiticamente (anche “a mano” per esempi semplici).
- Riduzione Garantita dell’Incertezza: Dopo aver osservato i dati, l’incertezza sul parametro (misurata dalla varianza a posteriori) non può che diminuire o, al limite, rimanere uguale (caso teorico di dati non informativi), rispetto alla varianza a priori.
- Peso dell’Evidenza: Con pochi dati o dati molto “rumorosi” (alta \(\sigma^2\)), la distribuzione a priori esercita un’influenza maggiore sulla stima finale. Con molti dati o dati molto precisi (bassa \(\sigma^2\)), l’informazione proveniente dai dati tende a dominare, e l’influenza della prior sulla stima a posteriori diminuisce.
- Applicabilità Vasta: Lo schema concettuale e matematico del modello Normale-Normale si applica a una vasta gamma di problemi in diverse discipline, inclusa la psicologia sperimentale (es. tempi di reazione, punteggi a test, ampiezze di segnali EEG), l’ingegneria, l’economia, e molte altre aree dove si misurano quantità continue. :::
Esercizio 2.
I test standard di Quoziente Intellettivo (QI) sono generalmente calibrati per avere una media di 100 e una deviazione standard di 15 nella popolazione di riferimento. Tuttavia, sono state sollevate questioni riguardo a possibili bias culturali che potrebbero favorire alcuni gruppi rispetto ad altri. Un’ulteriore complicazione sorge quando i punteggi QI vengono aggregati a livello nazionale, poiché le medie nazionali possono mascherare eterogeneità intra-paese significative.
Questo esempio, ispirato da Gill (2015) (che discute i dati di Lynn e Vanhanen, 2001), analizza i dati di QI medio riportati per 80 nazioni. L’obiettivo è stimare un QI medio “globale” \(\mu\) utilizzando un approccio bayesiano Normale-Normale, e riflettere criticamente sul risultato.
Assumiamo una deviazione standard nota \(\sigma = 15\) per i punteggi QI (questa è una semplificazione, poiché la variabilità delle medie nazionali potrebbe essere diversa dalla variabilità individuale).
I dati di QI medio per \(n=80\) nazioni sono forniti di seguito:
| Paese | IQ | Paese | IQ | Paese | IQ | Paese | IQ |
|---|---|---|---|---|---|---|---|
| Argentina | 96 | Australia | 98 | Austria | 102 | Barbados | 78 |
| Belgium | 100 | Brazil | 87 | Bulgaria | 93 | Canada | 97 |
| China | 100 | Congo (Br.) | 73 | Congo (Zr.) | 65 | Croatia | 90 |
| Cuba | 85 | Czech Repub. | 97 | Denmark | 98 | Ecuador | 80 |
| Egypt | 83 | Eq. Guinea | 59 | Ethiopia | 63 | Fiji | 84 |
| Finland | 97 | France | 98 | Germany | 102 | Ghana | 71 |
| Greece | 92 | Guatemala | 79 | Guinea | 66 | Hong Kong | 107 |
| Hungary | 99 | India | 81 | Indonesia | 89 | Iran | 84 |
| Iraq | 87 | Ireland | 93 | Israel | 94 | Italy | 102 |
| Jamaica | 72 | Japan | 105 | Kenya | 72 | Korea (S.) | 106 |
| Lebanon | 86 | Malaysia | 92 | Marshall I. | 84 | Mexico | 87 |
| Morocco | 85 | Nepal | 78 | Netherlands | 102 | New Zealand | 100 |
| Nigeria | 67 | Norway | 98 | Peru | 90 | Philippines | 86 |
| Poland | 99 | Portugal | 95 | Puerto Rico | 84 | Qatar | 78 |
| Romania | 94 | Russia | 96 | Samoa | 87 | Sierra Leone | 64 |
| Singapore | 103 | Slovakia | 96 | Slovenia | 95 | South Africa | 72 |
| Spain | 97 | Sudan | 72 | Suriname | 89 | Sweden | 101 |
| Switzerland | 101 | Taiwan | 104 | Tanzania | 72 | Thailand | 91 |
| Tonga | 87 | Turkey | 90 | Uganda | 73 | U.K. | 100 |
| U.S. | 98 | Uruguay | 96 | Zambia | 77 | Zimbabwe | 66 |
Impostazione del Modello Bayesiano:
- Prior per \(\mu\): Stabiliamo una prior basata sulla standardizzazione tipica dei test QI:
- \(\mu_0 = 100\) (media a priori)
- \(\sigma_0 = 15\) (deviazione standard a priori, che riflette una certa incertezza sulla media globale, o la stessa scala della \(\sigma\) individuale). Quindi, \(\mu \sim \mathcal{N}(100, 15^2)\).
- Verosimiglianza: Ogni QI nazionale \(y_i\) è considerato come un’osservazione della media “vera” \(\mu\) con varianza \(\sigma^2 = 15^2\). La media campionaria dei QI nazionali sarà \(\bar{y}\).
(Nota: Questa è una semplificazione. Idealmente, ogni \(y_i\) è già una media, e dovremmo considerare la sua precisione \(N_i/\sigma^2\) se \(N_i\) fosse la dimensione del campione per quella nazione. Qui, trattiamo ogni media nazionale come un singolo dato \(y_i\) proveniente da \(\mathcal{N}(\mu, \sigma^2)\)).
Implementiamo le informazioni necessarie in R.
# Dati IQ delle 80 nazioni (valori aggregati per paese)
iq <- c(
96, 100, 100, 85, 83, 97, 92, 99, 87, 72, 86, 85, 67, 99, 94, 103, 97, 101,
87, 98, 87, 73, 97, 59, 98, 79, 81, 93, 105, 92, 78, 98, 95, 96, 72, 104,
90, 96, 98, 102, 78, 90, 63, 84, 84, 107, 86, 102, 106, 94, 102, 72, 101,
89, 72, 101, 91, 100, 100, 66, 107, 86, 78, 84, 78, 64, 72, 101, 91, 100,
67, 86
) # Dati da Lynn e Vanhanen (2001) come presentati in Gill (2015)
# Numero di osservazioni (nazioni)
n <- length(iq)
# Media campionaria dei QI nazionali
y_bar <- mean(iq)
# Deviazione standard assunta nota (per la "popolazione" da cui provengono le medie nazionali)
sigma <- 15
# Parametri a priori
mu_0 <- 100 # Media a priori
sigma_0 <- 15 # Dev. std. a priori
cat(paste("Numero di nazioni (n):", n))
#> Numero di nazioni (n): 72
cat(paste("\nMedia campionaria dei QI nazionali (y_bar):", round(y_bar, 2)))
#>
#> Media campionaria dei QI nazionali (y_bar): 89.21Calcolo dei parametri a posteriori:
Utilizziamo le formule derivate precedentemente:
\[\mu_n = \frac{\frac{1}{\sigma_0^2}\mu_0 + \frac{n}{\sigma^2}\bar{y}}{\frac {1}{\sigma_0^2} + \frac{n}{\sigma^2}} \]
\[ \sigma_n^2 = \frac{1}{\frac {1}{\sigma_0^2}+ \frac{n}{\sigma^2}} \]
# Precisioni
prec_prior_iq <- 1 / sigma_0^2
prec_data_iq <- n / sigma^2
# Parametri posteriori
mu_p_iq <- (mu_0 * prec_prior_iq + y_bar * prec_data_iq) / (prec_prior_iq + prec_data_iq)
sigma_p_sq_iq <- 1 / (prec_prior_iq + prec_data_iq)
sigma_p_iq <- sqrt(sigma_p_sq_iq)
cat(paste("Media a posteriori (mu_n):", round(mu_p_iq, 2)))
#> Media a posteriori (mu_n): 89.36
cat(paste("\nVarianza a posteriori (sigma_n^2):", round(sigma_p_sq_iq, 2)))
#>
#> Varianza a posteriori (sigma_n^2): 3.08
cat(paste("\nDeviazione standard a posteriori (sigma_n):", round(sigma_p_iq, 2)))
#>
#> Deviazione standard a posteriori (sigma_n): 1.76Generiamo una rappresentazione grafica della distribuzione a posteriori della media del IQ sulla base dei dati osservati, avendo assunto mu_0 = 100 e sigma_0 = 15 per la distribuzione a priori.
# Definizione dei valori sull'asse x per il grafico della posteriori
x_qi <- seq(mu_p_iq - 4 * sigma_p_iq, mu_p_iq + 4 * sigma_p_iq, length.out = 1000)
# Calcolo della densità di probabilità per la posteriori
pdf_qi <- dnorm(x_qi, mean = mu_p_iq, sd = sigma_p_iq)
# Creazione del grafico
ggplot(data.frame(x = x_qi, pdf = pdf_qi), aes(x = x, y = pdf)) +
geom_line(color = "darkslateblue", linewidth = 1.2) +
geom_area(fill = "darkslateblue", alpha = 0.3) +
labs(
x = "Media 'Globale' del Quoziente di Intelligenza (μ)",
y = "Densità di Probabilità",
title = "Distribuzione a Posteriori del QI Medio Globale",
subtitle = paste0("Posteriori: N(", round(mu_p_iq, 2), ", ", round(sigma_p_sq_iq, 2), ")")
) +
theme(legend.position = "none")
Per completezza, visualizziamo anche prior, likelihood e posterior:
mu_grid_iq <- seq(min(mu_0 - 3 * sigma_0, y_bar - 3 * sigma / sqrt(n), mu_p_iq - 3 * sigma_p_iq),
max(mu_0 + 3 * sigma_0, y_bar + 3 * sigma / sqrt(n), mu_p_iq + 3 * sigma_p_iq),
length.out = 1000
)
prior_dens_iq <- dnorm(mu_grid_iq, mean = mu_0, sd = sigma_0)
lik_dens_raw_iq <- dnorm(mu_grid_iq, mean = y_bar, sd = sigma / sqrt(n)) # SD della media campionaria
lik_dens_scaled_iq <- lik_dens_raw_iq * (max(prior_dens_iq) / max(lik_dens_raw_iq, na.rm = TRUE)) # Scalata
post_dens_iq <- dnorm(mu_grid_iq, mean = mu_p_iq, sd = sigma_p_iq)
df_iq <- data.frame(
mu = mu_grid_iq,
Prior = prior_dens_iq,
Likelihood_scaled = lik_dens_scaled_iq,
Posterior = post_dens_iq
)
df_long_iq <- pivot_longer(df_iq, -mu, names_to = "Distribuzione", values_to = "Densita")
df_long_iq$Distribuzione <- factor(df_long_iq$Distribuzione,
levels = c("Prior", "Likelihood_scaled", "Posterior"),
labels = c("A Priori", "Verosimiglianza (riscalata)", "A Posteriori")
)
ggplot(df_long_iq, aes(x = mu, y = Densita, colour = Distribuzione)) +
geom_line(linewidth = 1.2) +
labs(
x = expression(paste("Media QI ", mu)),
y = "Densità",
title = "Aggiornamento Bayesiano per il QI Medio 'Globale'",
subtitle = paste0(
"Prior: N(", mu_0, ", ", sigma_0^2, "), ",
"Verosimiglianza (per μ): N(", round(y_bar, 2), ", ", round((sigma^2 / n), 2), "), ",
"Posteriori: N(", round(mu_p_iq, 2), ", ", round(sigma_p_sq_iq, 2), ")"
)
) +
scale_color_manual(values = c(
"A Priori" = "dodgerblue",
"Verosimiglianza (riscalata)" = "forestgreen",
"A Posteriori" = "orangered"
)) +
theme(legend.title = element_blank(), legend.position = "top")
Discussione critica dei risultati
L’analisi bayesiana ha prodotto una media a posteriori per il QI “globale” di \(\mu_n \approx 89.36\), con una deviazione standard a posteriori molto piccola (\(\sigma_n \approx 1.66\)). Questo valore è notevolmente inferiore alla media standard di 100.
Tuttavia, è cruciale interpretare questo risultato con estrema cautela, considerando diversi fattori limitanti e criticità:
- Effetto di Aggregazione (Ecological Fallacy): La media a posteriori è calcolata aggregando i dati QI medi di 80 nazioni. Questa media aggregata potrebbe non riflettere accuratamente la distribuzione del QI a livello individuale all’interno delle singole nazioni, né la vera distribuzione “globale” se si potessero testare tutti gli individui. Le differenze significative tra le nazioni (in termini di medie, varianze, e contesti socio-culturali) vengono “appiattite” in un unico valore, potenzialmente mascherando eterogeneità importanti.
- Dati Non Ponderati: L’analisi tratta ogni nazione come un’singola osservazione, indipendentemente dalla sua popolazione. Nazioni con popolazioni molto diverse contribuiscono allo stesso modo alla stima della media \(\bar{y}\). Una media ponderata per la popolazione potrebbe fornire un quadro diverso, sebbene anch’esso soggetto a critiche.
- Contesto e Fattori Concomitanti: La deviazione dalla media standard di 100 potrebbe riflettere non solo (o non principalmente) differenze “reali” nell’intelligenza media, ma anche enormi disparità nei contesti sanitari, educativi, socio-economici e politici in cui i test sono stati (eventualmente) somministrati o i dati raccolti. Fattori come l’accesso all’istruzione di qualità, la nutrizione, la salute pubblica, e l’esposizione a stimoli cognitivi variano drasticamente tra le nazioni e possono influenzare significativamente i punteggi medi.
- Bias Culturale dei Test: I test del QI sono stati storicamente sviluppati e standardizzati in contesti culturali specifici (principalmente occidentali, industrializzati). La loro applicabilità e validità cross-culturale è oggetto di un acceso dibattito. È possibile che i test stessi presentino bias culturali che portano a sottostimare le capacità cognitive in contesti culturali diversi da quello di origine, influenzando così le medie nazionali riportate.
- Qualità e Origine dei Dati: I dati originali di Lynn e Vanhanen sono stati oggetto di numerose critiche metodologiche riguardanti la raccolta, la comparabilità e la qualità dei punteggi QI tra diverse nazioni. Utilizzare questi dati senza un esame approfondito delle loro limitazioni può portare a conclusioni fuorvianti.
- Assunzione di \(\sigma\) Nota e Uguale: L’assunzione che \(\sigma=15\) sia la deviazione standard rilevante per le medie nazionali è una forte semplificazione. La variabilità tra le medie nazionali potrebbe essere diversa dalla variabilità individuale all’interno di una popolazione di riferimento.
In conclusione, sebbene il modello Normale-Normale fornisca una stima quantitativa (\(\mu_n \approx 89.36\)), le profonde questioni metodologiche, concettuali ed etiche legate ai dati sul QI internazionale rendono problematica un’interpretazione diretta di questo valore come “vera” media globale dell’intelligenza. Questo esempio serve più come illustrazione meccanica dell’aggiornamento bayesiano che come un’affermazione sostanziale sul QI globale. Un’analisi seria richiederebbe modelli gerarchici più complessi, una discussione approfondita della validità dei dati e una considerazione attenta dei fattori contestuali.
Riflessioni conclusive
In questo capitolo, abbiamo esplorato il meccanismo dell’aggiornamento bayesiano attraverso l’applicazione del modello Normale-Normale, specificamente nel caso in cui la varianza \(\sigma^2\) della popolazione da cui provengono i dati sia considerata nota.
Il processo inizia con la definizione di una distribuzione a priori per la media incognita \(\mu\). Questa prior, \(\mu \sim \mathcal{N}(\mu_0, \sigma_0^2)\), quantifica le nostre conoscenze o ipotesi iniziali su \(\mu\) attraverso la sua media \(\mu_0\) e la sua varianza \(\sigma_0^2\).
Successivamente, acquisiamo nuovi dati \(y_1, \dots, y_n\), che assumiamo essere campionati da una distribuzione Normale \(\mathcal{N}(\mu, \sigma^2)\). L’informazione contenuta nei dati viene sintetizzata dalla media campionaria \(\bar{y}\) e dalla dimensione del campione \(n\), che, insieme alla varianza nota \(\sigma^2\), determinano la forma della funzione di verosimiglianza (proporzionale a \(\mathcal{N}(\bar{y}, \sigma^2/n)\) come funzione di \(\mu\)).
Applicando il Teorema di Bayes, combiniamo la prior e la verosimiglianza. Grazie alla proprietà di coniugatezza tra la distribuzione Normale (per la prior) e la verosimiglianza Normale (per i dati), la distribuzione a posteriori per \(\mu\) risulta anch’essa Normale: \(\mu \mid \mathbf{y} \sim \mathcal{N}(\mu_n, \sigma_n^2)\).
La media a posteriori \(\mu_n\) è una media ponderata della media a priori \(\mu_0\) e della media campionaria \(\bar{y}\). I pesi sono determinati dalle rispettive precisioni (il reciproco delle varianze):
\[ \mu_n = \frac{\left(\frac{1}{\sigma_0^2}\right)\mu_0 + \left(\frac{n}{\sigma^2}\right)\bar{y}}{\frac{1}{\sigma_0^2} + \frac{n}{\sigma^2}} \]
La varianza a posteriori \(\sigma_n^2\) è calcolata in modo che la sua precisione sia la somma delle precisioni della prior e dei dati:
\[ \frac{1}{\sigma_n^2} = \frac{1}{\sigma_0^2} + \frac{n}{\sigma^2} \quad \implies \quad \sigma_n^2 = \left(\frac{1}{\sigma_0^2} + \frac{n}{\sigma^2}\right)^{-1} \]
Un aspetto fondamentale è che la varianza a posteriori \(\sigma_n^2\) è sempre minore o uguale sia a \(\sigma_0^2\) sia a \(\sigma^2/n\), indicando che l’incorporazione dei dati porta a una riduzione (o al più, a nessuna variazione) dell’incertezza su \(\mu\).
In sintesi, il modello Normale-Normale con varianza nota offre un quadro analiticamente trattabile e intuitivo per l’aggiornamento bayesiano. La coniugatezza semplifica i calcoli, permettendo di concentrarsi sull’interpretazione di come le credenze iniziali vengono modificate dall’evidenza empirica. Sebbene l’assunzione di varianza nota sia una semplificazione, questo modello getta le basi per comprendere modelli più complessi in cui anche la varianza è incognita e stimata.
Bibliografia
Gill, J. (2015). Bayesian methods: A social and behavioral sciences approach (3rd Edition). Chapman; Hall/CRC.
Johnson, A. A., Ott, M., & Dogucu, M. (2022). Bayes Rules! An Introduction to Bayesian Modeling with R. CRC Press.