here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(HistData)60 La regressione verso la media
“The mean filial regression towards mediocrity was directly proportional to the parental deviation from it.”
– Francis Galton, Regression Towards Mediocrity in Hereditary Stature, Journal of the Anthropological Institute 15, 1886, pp. 246–263.
Introduzione
Il concetto di regressione verso la media fu introdotto da Francis Galton studiando la trasmissione ereditaria dell’altezza. Egli osservò che i figli di padri molto alti tendevano sì ad essere sopra la media, ma meno dei loro padri; allo stesso modo, i figli di padri molto bassi risultavano meno estremi dei padri. Questo “ritorno parziale verso il centro” della distribuzione è il fenomeno che oggi chiamiamo regressione verso la media.
Perché accade? Un’altezza eccezionale può essere il risultato della combinazione di fattori genetici, ambientali e casuali. I figli ereditano solo una parte di tali fattori e, con l’aggiunta di nuove influenze, la loro altezza tende ad avvicinarsi alla media della popolazione. Non significa che un figlio di un padre altissimo diventi basso: resta sopra la media, ma meno estremo.
Il cuore statistico del fenomeno è la correlazione imperfetta tra le due variabili (altezza del padre e del figlio). Se la correlazione fosse 1, i valori estremi si replicherebbero perfettamente. Ma, quando \(\rho < 1\), i valori attesi dei figli sono più vicini alla media rispetto a quelli dei padri. Galton stimò una correlazione attorno a 0.5: dunque, gran parte ma non tutta l’estremità del tratto paterno si trasmette al figlio.
Panoramica del capitolo
- Origine storica e intuizione del fenomeno (Galton).
- Regressione e correlazione: forme standardizzate e non standardizzate.
- Visualizzazione della RTM tramite retta di regressione.
- RTM ≠ causalità: errori di misura e artefatti di selezione.
60.0.1 I dati di Galton
Esaminiamo il fenomeno della regressione verso la media usando i dati di Galton. Nel pacchetto HistData di R sono disponibili i dati originali raccolti da Galton, che includono informazioni sull’altezza di padri, madri, figli maschi e femmine. Per semplificare l’analisi, possiamo creare un dataset che include solo l’altezza del padre e l’altezza di un figlio maschio scelto casualmente da ogni famiglia:
Questo dataset contiene due colonne: father (altezza del padre) e son (altezza del figlio maschio). Calcolando la media e la deviazione standard delle altezze dei padri e dei figli, otteniamo:
I risultati mostrano che, in media, i padri e i figli hanno altezze simili, anche se le distribuzioni non sono identiche. Un grafico di dispersione (scatterplot) evidenzia una chiara tendenza: padri più alti tendono ad avere figli più alti:
galton_heights |>
ggplot(aes(father, son)) +
geom_point(alpha = 0.5)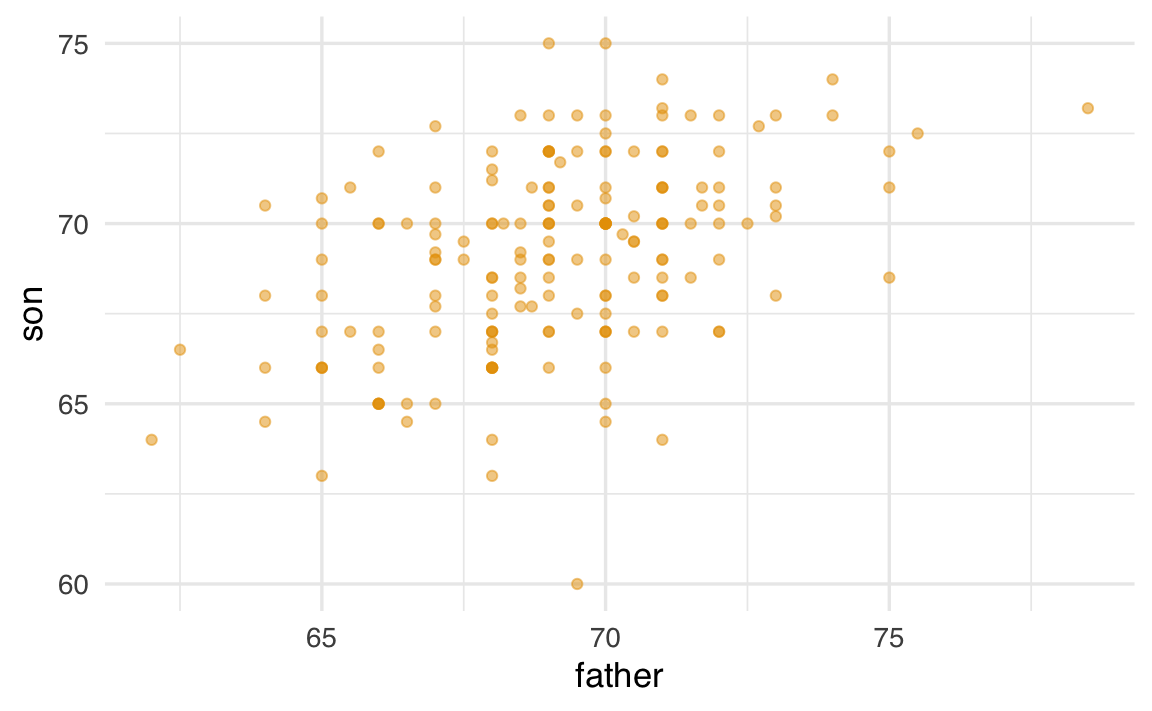
60.0.2 Il coefficiente di correlazione
La forza e la direzione dell’associazione lineare tra le due variabili sono misurate dal coefficiente di correlazione di Pearson, definito come:
\[ \rho = \frac{1}{n}\sum_{i=1}^n \left(\frac{x_i - \mu_x}{\sigma_x}\right) \left(\frac{y_i - \mu_y}{\sigma_y}\right). \]
dove \(\mu_X, \mu_Y\) sono le medie e \(\sigma_X, \sigma_Y\) le deviazioni standard delle rispettive popolazioni. La sua stima campionaria, \(r\), è calcolata in R come:
galton_heights |>
summarize(r = cor(father, son)) |>
pull(r)
#> [1] 0.4434Un coefficiente di 0.5 indica un’associazione lineare positiva di moderata intensità, implicando che l’altezza paterna spiega solo parzialmente la variabilità dell’altezza dei figli.
60.0.3 L’aspettativa condizionata e l’emergenza del fenomeno di regressione
Un obiettivo inferenziale comune è la stima del valore atteso dell’altezza del figlio (\(Y\)), condizionata a un specifico valore dell’altezza del padre (\(X = x_0\)), formalmente \(\mathbb{E}(Y \mid X = x_0)\).
Un approccio intuitivo è stratificare i dati e calcolare la media campionaria del sottogruppo. Ad esempio, per \(X = 72\) pollici:
Tale stima risulta sistematicamente più vicina alla media generale di \(Y\) di quanto \(x_0\) non lo sia alla media di \(X\). Questo fenomeno è noto come regressione verso la media.
60.1 Visualizzare del fenomeno attraverso la stratificazione
Il fenomeno è generalizzabile visualizzando la media condizionata \(\mathbb{E}(Y \mid X = x)\) per diversi valori di \(x\), ottenuti tramite stratificazione:
galton_heights |>
mutate(father_strata = factor(round(father))) |>
group_by(father_strata) |>
summarize(avg_son = mean(son)) |>
ggplot(aes(x = father_strata, y = avg_son)) +
geom_point()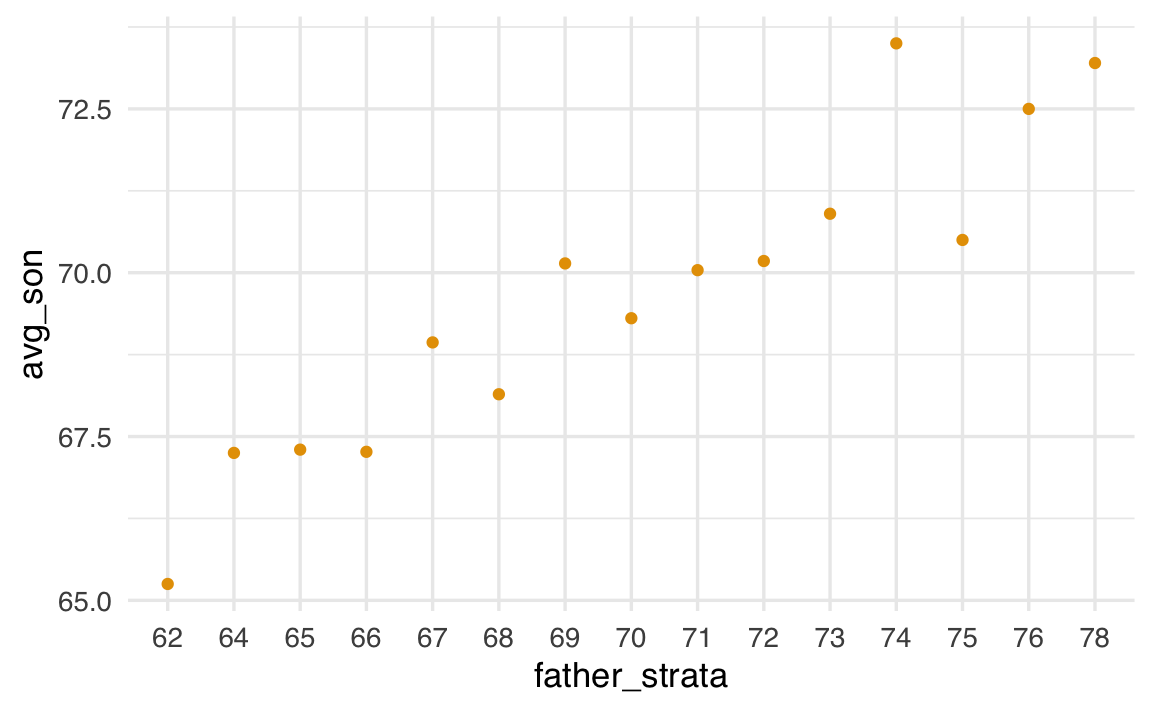
La nube di punti delle medie condizionate presenta una pendenza positiva ma inferiore a 45°, dimostrando visivamente la regressione verso la media.
60.2 Modello di regressione lineare e interpretazione dei parametri
Il modello statistico che formalizza questa relazione è la regressione lineare semplice:
\[ Y = \beta_0 + \beta_1 X + \varepsilon , \]
dove \(\epsilon\) è un termine di errore stocastico con media zero.
Gli stimatori dei minimi quadrati ordinari (OLS) per i parametri \(\beta_0\) (intercetta) e \(\beta_1\) (pendenza) sono:
\[ \hat{\beta}_1 = r \frac{s_Y}{s_X}, \quad \hat{\beta}_0 = \bar{Y} - \hat{\beta}_1\bar{X} \]
dove \(s_X\), \(s_Y\) sono le deviazioni standard campionarie e \(\bar{X}\), \(\bar{Y}\) le medie campionarie.
L’applicazione del modello ai dati di Galton fornisce:
La pendenza stimata \(\hat{\beta}_1 = 0.454\) conferma che per ogni pollice in più del padre, l’altezza attesa del figlio aumenta di circa 0.454 pollici, un valore inferiore a 1 che è consistente con la regressione verso la media.
60.2.0.1 Standardizzazione
Standardizzando le variabili (\(Z_X = (X - \bar{X})/s_X\), \(Z_Y = (Y - \bar{Y})/s_Y\)), il modello di regressione assume la forma
\[ Z_Y = \rho\, Z_X + \varepsilon. \]
Vediamo come si arriva a questo risultato. Consideriamo il modello lineare semplice
\[ Y = \beta_0 + \beta_1 X + \varepsilon, \qquad \mathbb{E}[\varepsilon] = 0, \qquad \mathrm{Cov}(X,\varepsilon) = 0. \]
Dalle equazioni normali dei minimi quadrati otteniamo, a livello di popolazione:
\[ \beta_1 = \frac{\mathrm{Cov}(X,Y)}{\mathrm{Var}(X)}, \qquad \beta_0 = \mu_Y - \beta_1 \mu_X. \]
Scrivendo la covarianza come \(\mathrm{Cov}(X,Y) = \rho \sigma_X \sigma_Y\), segue che
\[ \beta_1 = \rho \,\frac{\sigma_Y}{\sigma_X}. \]
Se ora standardizziamo \(X\) e \(Y\), entrambe le deviazioni standard valgono 1, quindi la pendenza diventa
\[ \beta_1^* = \rho. \]
Inoltre, poiché le variabili standardizzate hanno media zero, anche l’intercetta scompare.
In conclusione, la regressione di \(Z_Y\) su \(Z_X\) ha sempre intercetta pari a 0 e coefficiente angolare pari alla correlazione \(\rho\).
Infatti, nei dati campionari:
La pendenza è \(0.4434\), numericamente uguale alla correlazione \(r\) calcolata in precedenza (a meno di errori di arrotondamento). Poiché \(|\rho| < 1\), la previsione per un valore standardizzato \(z_x\) sarà \(\hat{z}_y = \rho z_x\), che è sempre, in valore assoluto, minore di \(z_x\). Questo spiega matematicamente il perché un valore estremo di \(X\) porta a una previsione per \(Y\) che è meno estrema, ossia più vicina alla sua media standardizzata (zero).
In sintesi, la correlazione imperfetta (\(\rho < 1\)) è la ragione principale per cui un valore estremo di \(X\) (ad esempio, un padre molto alto) porta a un valore \(\hat{Y}\) che è sì superiore (o inferiore) alla media, ma meno estremo del padre. Questo “ritorno verso il centro” è ciò che chiamiamo regressione verso la media.
Riflessioni conclusive
La regressione verso la media è un fenomeno statistico che si verifica inevitabilmente quando due misurazioni della stessa variabile presentano una correlazione imperfetta (0 < \(\rho\) < 1). In tali condizioni, i valori estremi osservati nella prima misurazione (\(X\)) sono associati, nella seconda misurazione (\(Y\)), a valori che si discostano meno dalla media della distribuzione.
Dal punto di vista matematico, il valore atteso condizionato del punteggio standardizzato \(Z_Y\), dato il punteggio \(Z_X = z\), è: \(\mathbb{E}[Z_Y \mid Z_X = z] = \rho z\). Ne consegue che la retta di regressione dei punteggi standardizzati ha una pendenza pari a \(\rho\), inferiore a 1, riflettendo il caratteristico richiamo dei valori verso la media.
La causa fondamentale di questo fenomeno risiede nell’affidabilità non perfetta delle misurazioni psicologiche. L’errore di misura e la componente di variabilità casuale fanno sì che parte dell’estremità osservata in \(X\) sia attribuibile a fluttuazioni transitorie piuttosto che a differenze individuali stabili. Di conseguenza, l’entità della regressione verso la media è inversamente proporzionale all’affidabilità dello strumento di misura: minore è l’affidabilità, maggiore sarà l’effetto.
Le implicazioni pratiche di questo artefatto statistico sono notevoli. In contesti pre-post privi di gruppo di controllo, un apparente miglioramento dei soggetti con punteggi iniziali bassi, così come un peggioramento di quelli con punteggi iniziali alti, può essere interamente attribuibile alla regressione verso la media, in assenza di qualsiasi effetto reale dell’intervento.
Pertanto, per isolare e correggere tale artefatto, è indispensabile adottare disegni di ricerca appropriati, quali l’inclusione di un gruppo di controllo randomizzato, e tecniche analitiche specifiche. Queste includono:
- modelli di regressione che controllano il punteggio di base (ANCOVA);
- modelli gerarchici o ad equazioni strutturali in grado di tenere esplicitamente conto dell’errore di misura.
- procedure di correzione basate sulla stima dell’affidabilità della misura.
L’impiego di tali metodologie consente di distinguere i cambiamenti genuini dagli artefatti statistici, evitando interpretazioni erronee degli effetti osservati. Questi accorgimenti permettono di evitare di attribuire erroneamente a un intervento o a un predittore ciò che in realtà è un artefatto statistico.
Bibliografia
Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK: