19  Indicatori di tendenza centrale e variabilità

“La tendenza centrale senza una misura di variabilità è spesso di utilità limitata.”

– Jacob Cohen, Statistical Power Analysis for the Behavioral Sciences (1988)

Introduzione

La visualizzazione grafica dei dati rappresenta il pilastro fondamentale di ogni analisi quantitativa. Grazie alle rappresentazioni grafiche adeguate, è possibile individuare importanti caratteristiche di una distribuzione, quali la simmetria o l’asimmetria, nonché la presenza di una o più mode. Successivamente, al fine di descrivere sinteticamente le principali caratteristiche dei dati, si rende necessario l’utilizzo di specifici indici numerici. In questo capitolo, verranno presentati i principali indicatori della statistica descrittiva.

Panoramica del capitolo

  • Tendenza centrale: Scelta della misura (media, mediana, moda) in base al tipo di dati e alla presenza di valori anomali.
  • Variabilità: Interpretazione di range, varianza, deviazione standard e IQR per quantificare la dispersione dei dati attorno al valore centrale
  • Leggere “Most Psychological Researchers Assume Their Samples Are Ergodic: Evidence From a Year of Articles in Three Major Journals” (Speelman et al., 2024).
  • Studiare l’Appendice F.
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(tidyr, viridis, vcd)

19.1 Indici di tendenza centrale

Gli indici di tendenza centrale sono misure statistiche che cercano di rappresentare un valore tipico o centrale all’interno di un insieme di dati. Sono utilizzati per ottenere una comprensione immediata della distribuzione dei dati senza dover analizzare l’intero insieme. Gli indici di tendenza centrale sono fondamentali nell’analisi statistica, in quanto forniscono una sintesi semplice e comprensibile delle caratteristiche principali di un insieme di dati. I principali indici di tendenza centrale sono:

  1. Media: La media è la somma di tutti i valori divisa per il numero totale di valori. È spesso utilizzata come misura generale di tendenza centrale, ma è sensibile agli estremi (valori molto alti o molto bassi).
  2. Mediana: La mediana è il valore che divide l’insieme di dati in due parti uguali. A differenza della media, non è influenzata da valori estremi ed è quindi più robusta in presenza di outlier.
  3. Moda: La moda è il valore che appare più frequentemente in un insieme di dati. In alcuni casi, può non essere presente o esserci più di una moda.

La scelta dell’indice di tendenza centrale appropriato dipende dalla natura dei dati e dall’obiettivo dell’analisi. Ad esempio, la mediana potrebbe essere preferita alla media se l’insieme di dati contiene valori anomali che potrebbero distorcere la rappresentazione centrale. La conoscenza e l’applicazione corretta di questi indici possono fornire una preziosa intuizione sulle caratteristiche centrali di una distribuzione di dati.

19.1.1 Moda

La moda (\(\text{Mo}\)) rappresenta il valore della variabile che compare con maggiore frequenza in una distribuzione. In altre parole, è il valore più ricorrente nei dati.

  • Nelle distribuzioni unimodali, esiste una sola moda, che coincide con il valore centrale della distribuzione più frequente.
  • Tuttavia, in alcune distribuzioni, possono emergere più di una moda, rendendole multimodali. In questi casi, la moda perde il suo significato di indicatore unico di tendenza centrale, poiché la presenza di più valori con frequenze elevate rende difficile individuare un singolo punto di riferimento.

19.1.2 Mediana

La mediana (\(\tilde{x}\)) corrisponde al valore che divide il campione in due metà: il 50% dei dati è inferiore o uguale alla mediana e il restante 50% è superiore o uguale. A differenza della media, la mediana è meno influenzata dai valori estremi, rendendola una misura particolarmente robusta in presenza di dati asimmetrici o outlier.

19.1.3 Media

La media aritmetica di un insieme di valori rappresenta il punto centrale o il baricentro della distribuzione dei dati. È calcolata come la somma di tutti i valori divisa per il numero totale di valori, ed è espressa dalla formula:

\[ \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i, \tag{19.1}\]

dove \(x_i\) rappresenta i valori nell’insieme, \(n\) è il numero totale di valori, e \(\sum\) indica la sommatoria.

19.1.3.1 Calcolo della media con R

Per calcolare la media di un piccolo numero di valori in R, possiamo utilizzare la somma di questi valori e dividerla per il numero totale di elementi. Consideriamo ad esempio i valori 12, 44, 21, 62, 24:

(12 + 44 + 21 + 62 + 24) / 5
#> [1] 32.6

ovvero

x <- c(12, 44, 21, 62, 24)
mean(x)
#> [1] 32.6

19.1.3.2 Media spuntata

La media spuntata, indicata come \(\bar{x}_t\) o trimmed mean, è un metodo di calcolo della media che prevede l’eliminazione di una determinata percentuale di dati estremi prima di effettuare la media aritmetica. Solitamente, viene eliminato il 10% dei dati, ovvero il 5% all’inizio e alla fine della distribuzione. Per ottenere la media spuntata, i dati vengono ordinati in modo crescente, \(x_1 \leq x_2 \leq x_3 \leq \dots \leq x_n\), e quindi viene eliminato il primo 5% e l’ultimo 5% dei dati nella sequenza ordinata. Infine, la media spuntata è calcolata come la media aritmetica dei dati rimanenti. Questo approccio è utile quando ci sono valori anomali o quando la distribuzione è asimmetrica e la media aritmetica non rappresenta adeguatamente la tendenza centrale dei dati.

Per illustrare la media spuntata, utilizzeremo i dati del Progetto Natsal, contenuti nel file sexual-partners.csv.

Negli anni ’80, con la crescente preoccupazione per l’AIDS, le autorità sanitarie del Regno Unito si resero conto della mancanza di dati affidabili sui comportamenti sessuali della popolazione. In particolare, vi erano dubbi sulla frequenza con cui le persone cambiavano partner, sul numero di partner simultanei e sulle pratiche sessuali adottate. Questa conoscenza era essenziale per prevedere la diffusione delle malattie sessualmente trasmissibili nella società e per pianificare adeguatamente i servizi sanitari. Tuttavia, si faceva ancora riferimento ai dati raccolti da Alfred Kinsey negli Stati Uniti negli anni ’40, che non tenevano conto della rappresentatività del campione.

A partire dalla fine degli anni ’80, vennero dunque avviati nel Regno Unito e negli Stati Uniti ampi e rigorosi studi sui comportamenti sessuali, nonostante una forte opposizione in alcuni ambienti. Nel Regno Unito, il governo guidato da Margaret Thatcher ritirò il proprio sostegno a un’importante indagine sui comportamenti sessuali all’ultimo momento. Fortunatamente, i ricercatori riuscirono a ottenere finanziamenti da enti benefici, dando vita al National Sexual Attitudes and Lifestyles Survey (Natsal). Da allora, questa indagine viene condotta ogni dieci anni, a partire dal 1990. La terza rilevazione, denominata Natsal-3, è stata effettuata intorno al 2010.

Poniamoci il problema di descrivere la tendenza centrale con la media spuntata per i dati contenuti nel file sexual-partners.csv, separatamente per maschi e femmine. Il dataset fornisce la distribuzione del numero totale dichiarato di partner sessuali di sesso opposto nella vita per uomini e donne di età compresa tra 35 e 44 anni. I dati provengono dal sondaggio Natsal-3 e corrispondono a un totale di 796 uomini e 1193 donne.

Procediamo all’importazione dei dati per iniziare l’analisi.

sexual_partners <- rio::import(here::here("data", "sexual-partners.csv"))

Esaminiamo alcune righe prese a caso dal data frame sexual_partners:

sexual_partners[sample(1:nrow(sexual_partners), size = 10, replace = FALSE), ]
#>      Gender NumPartners
#> 561     Man          15
#> 321     Man           6
#> 1177  Woman           3
#> 1098  Woman           2
#> 1252  Woman           4
#> 1170  Woman           3
#> 634     Man          21
#> 49      Man           1
#> 1152  Woman           3
#> 1327  Woman           5

La colonna Gender riporta il genere del rispondente e la colonna NumPartners il numero di partner sessuali di sesso opposto dichiarati.

Calcoliamo la media spuntata per gli uomini:

sex_partners_men <- sexual_partners[sexual_partners$Gender == "Man", "NumPartners"]
mean(sex_partners_men, trim = 0.10, na.rm = TRUE)
#> [1] 10.6

Calcoliamo la media spuntata per le donne:

sex_partners_women <- sexual_partners[sexual_partners$Gender == "Woman", "NumPartners"]
mean(sex_partners_women, trim = 0.10, na.rm = TRUE)
#> [1] 6.013

19.1.3.3 Proprietà della media

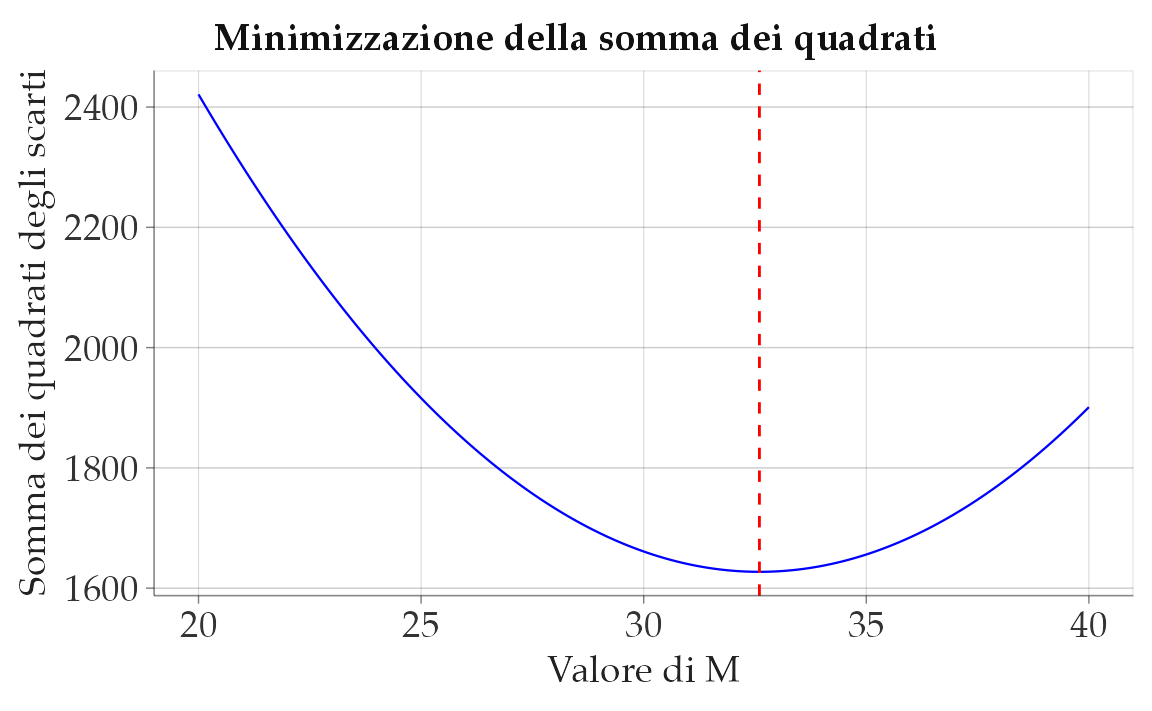
Una proprietà fondamentale della media è che la somma degli scarti di ciascun valore dalla media è zero:

\[ \sum_{i=1}^n (x_i - \bar{x}) = 0.\notag \tag{19.2}\]

Infatti,

\[ \begin{aligned} \sum_{i=1}^n (x_i - \bar{x}) &= \sum_i x_i - \sum_i \bar{x}\notag\\ &= \sum_i x_i - n \bar{x}\notag\\ &= \sum_i x_i - \sum_i x_i = 0.\notag \end{aligned} \]

Questa proprietà implica che i dati sono equamente distribuiti intorno alla media.

In R abbiamo:

sum(x - mean(x))
#> [1] -7.105e-15

Quando in un terminale viene visualizzato un numero come -7.105e-15 in notazione scientifica, esso corrisponde a \(-7.105 \cdot 10^{-15}\), che è effettivamente zero nel contesto dei calcoli numerici.

Questa approssimazione è una conseguenza diretta della precisione finita dei calcolatori. I sistemi digitali, infatti, rappresentano i numeri reali attraverso una codifica in virgola mobile (floating point), che comporta inevitabili errori di arrotondamento. La ragione risiede nell’impossibilità di memorizzare numeri reali con precisione assoluta.

Lo standard IEEE 754 a doppia precisione (64 bit), ampiamente utilizzato, suddivide la memoria in tre componenti:

  • 1 bit per il segno (positivo/negativo),
  • 11 bit per l’esponente (intervallo di scala),
  • 52 bit per la mantissa (o significando), che definisce le cifre significative.

Grazie a questa struttura, è possibile rappresentare numeri con una precisione di circa 15-17 cifre decimali. Tuttavia, qualsiasi valore non esprimibile in formato binario entro questi limiti subisce un troncamento o un arrotondamento, generando piccole discrepanze rispetto al risultato teorico.

19.1.3.4 La media come centro di gravità dell’istogramma

La media aritmetica può essere interpretata come il centro di gravità o il punto di equilibrio della distribuzione dei dati. In termini fisici, il centro di gravità è il punto in cui la massa di un sistema è equilibrata o concentrata.

In termini statistici, possiamo considerare la media come il punto in cui la distribuzione dei dati è in equilibrio. Ogni valore dell’insieme di dati può essere visto come un punto materiale con una massa proporzionale al suo valore. Se immaginiamo questi punti disposti su una linea, con valori più grandi a destra e più piccoli a sinistra, la media corrisponderà esattamente al punto in cui la distribuzione sarebbe in equilibrio.

Il metodo dei minimi quadrati afferma che la posizione della media minimizza la somma dei quadrati delle distanze dai dati. Matematicamente, ciò significa che la somma dei quadrati degli scarti tra ciascun valore osservato e la media è minima. Questo principio è alla base dell’analisi statistica della regressione e conferma il ruolo della media come centro di gravità della distribuzione dei dati.

Simulazione. Utilizziamo una simulazione per verificare questo principio, calcolando la somma dei quadrati degli scarti per diversi valori e visualizzando il risultato con ggplot2.

# Definizione dell'intervallo di valori da testare
nrep <- 10000
M <- seq(20, 40, length.out = nrep)
res <- rep(NA, nrep)

# Calcolo della somma dei quadrati degli scarti per ciascun valore di M
for (i in 1:nrep) {
  res[i] = sum((x - M[i])^2)
}

# Identificazione del valore minimo
min_index <- which.min(res)
min_M <- M[min_index]

# Creazione del dataframe per ggplot
df <- data.frame(M, res)

df |> 
  ggplot(aes(x = M, y = res)) +
  geom_line(color = "blue") +
  geom_vline(xintercept = min_M, linetype = "dashed", color = "red") +
  labs(
    title = "Minimizzazione della somma dei quadrati",
    x = "Valore di M",
    y = "Somma dei quadrati degli scarti"
  )

Stampiamo il minimo:

min_M
#> [1] 32.6

Confronto con la media:

mean(x)
#> [1] 32.6

Osserviamo che il valore di M che minimizza la somma dei quadrati degli scarti coincide con la media dei dati, confermando il principio dei minimi quadrati.

19.1.3.5 Le proporzioni sono medie

Se una collezione consiste solo di uni e zeri, allora la somma della collezione è il numero di uni in essa, e la media della collezione è la proporzione di uni.

zero_one <- c(1, 1, 1, 0)
result <- mean(zero_one)
result
#> [1] 0.75

È possibile sostituire 1 con il valore booleano True e 0 con False:

mean(c(TRUE, TRUE, TRUE, FALSE))
#> [1] 0.75

19.1.3.6 Limiti della media aritmetica

La media aritmetica, tuttavia, ha alcune limitazioni: non sempre è l’indice più adeguato per descrivere accuratamente la tendenza centrale della distribuzione, specialmente quando si verificano asimmetrie o valori anomali (outlier). In queste situazioni, è più indicato utilizzare la mediana o la media spuntata (come spiegheremo successivamente).

Gli indici di tendenza centrale – moda, mediana e media – assumono significati molto diversi quando la distribuzione dei dati è asimmetrica. Per esempio, consideriamo i dati del Progetto Natsal (sexual-partners.csv), che riportano il numero di partner sessuali di sesso opposto dichiarati da uomini e donne (35–44 anni).

  1. Esplorazione dei dati.

Estraggo dieci righe a caso:

sexual_partners[sample(1:nrow(sexual_partners), 10), ]
#>      Gender NumPartners
#> 24      Man           1
#> 1863  Woman          16
#> 356     Man           7
#> 1625  Woman           8
#> 165     Man           3
#> 622     Man          20
#> 1556  Woman           7
#> 410     Man           8
#> 1906  Woman          20
#> 1903  Woman          20

Il dataset contiene due colonne principali:

  • Gender: genere del rispondente,
  • NumPartners: numero di partner sessuali dichiarati.

Vediamo quanti soggetti ci sono in ciascun gruppo:

sexual_partners |> 
  group_by(Gender) |> 
  summarise(count = n())
#> # A tibble: 2 × 2
#>   Gender count
#>   <chr>  <int>
#> 1 Man      796
#> 2 Woman   1193

Il numero massimo riportato è molto alto (oltre 500), ma per chiarezza limitiamo l’analisi a valori ≤ 50:

sexual_partners |> 
  group_by(Gender) |> 
  summarise(maximum = max(NumPartners))
#> # A tibble: 2 × 2
#>   Gender maximum
#>   <chr>    <int>
#> 1 Man        501
#> 2 Woman      550
  1. Visualizzazione.

Calcoliamo e rappresentiamo la distribuzione dei partner (≤50) separatamente per genere:

sexual_partners_truncated <- sexual_partners |> 
  filter(NumPartners <= 50)

percentage_data <- sexual_partners_truncated %>%
  group_by(Gender, NumPartners) %>%
  summarise(Count = n(), .groups = "drop") %>%
  group_by(Gender) %>%
  mutate(Percentage = Count / sum(Count) * 100)

y_max <- max(percentage_data$Percentage)

gender_labels <- c("Man" = "Uomini 35–44", "Woman" = "Donne 35–44")

percentage_data |>
  ggplot(aes(NumPartners, Percentage, fill = Gender)) +
  geom_col(position = "dodge", color = "black") +
  facet_wrap(~Gender, labeller = labeller(Gender = gender_labels)) +
  scale_y_continuous(limits = c(0, y_max)) +
  labs(x = "Numero di partner sessuali dichiarati", y = "Percentuale") +
  theme(legend.position = "none")

La distribuzione risulta altamente asimmetrica positiva: molti soggetti dichiarano pochi partner, pochi soggetti valori molto alti.

  1. Indici di tendenza centrale.

Calcoliamo media, mediana e moda per ciascun genere:

get_mode <- function(x) {
  tbl <- table(x)
  as.numeric(names(tbl)[which.max(tbl)])
}

sexual_partners_truncated |> 
  group_by(Gender) |> 
  summarise(
    media   = mean(NumPartners, na.rm = TRUE),
    mediana = median(NumPartners, na.rm = TRUE),
    moda    = get_mode(NumPartners)
  )
#> # A tibble: 2 × 4
#>   Gender media mediana  moda
#>   <chr>  <dbl>   <dbl> <dbl>
#> 1 Man    11.4        7     1
#> 2 Woman   7.51       5     1
  1. Interpretazione.
  • Media: più alta di mediana e moda → influenzata dalla coda lunga a destra.
  • Mediana: valore centrale, meno influenzata da estremi → misura più robusta.
  • Moda: valore più frequente (1 partner), ma spesso poco rappresentativa in distribuzioni molto sparse.
  1. Conclusioni pratiche.
  • In distribuzioni asimmetriche, la mediana è in genere l’indice di tendenza centrale più affidabile.
  • È utile riportare anche media e moda per evidenziare le differenze.
  • La descrizione numerica va sempre accompagnata da una visualizzazione grafica (istogrammi, boxplot) per cogliere l’asimmetria e i valori estremi.
  • Una descrizione completa richiede anche misure di dispersione, che vedremo nella sezione successiva.

19.1.3.7 La media come rappresentazione della psicologia umana: un’arma a doppio taglio?

La media è uno degli strumenti statistici più semplici e intuitivi che i ricercatori utilizzano per sintetizzare i dati. È un indice di tendenza centrale familiare e intuitivo: se chiediamo a un gruppo di persone la loro età e calcoliamo la media, otteniamo un valore che sintetizza in un’unica cifra l’informazione disponibile. Ma cosa significa, in realtà, “riassumere” i dati con la media? E soprattutto, questa operazione ha senso quando si studiano i processi psicologici e il comportamento umano?

In molte discipline scientifiche, il concetto di media è utile perché descrive fenomeni che tendono a essere stabili e uniformi. Per esempio, se misuriamo l’altezza di un gruppo di persone, possiamo aspettarci che la distribuzione sia approssimativamente normale e che la media offra una stima ragionevole di un valore tipico. Tuttavia, la mente umana e i processi psicologici non funzionano come il sistema cardiovascolare o i muscoli. Ogni persona ha esperienze uniche che plasmano le sue risposte, i suoi pensieri e le sue emozioni.

Un problema centrale, sollevato da Speelman & McGann (2013), riguarda l’implicita assunzione che ci sia un vero valore sottostante ai processi psicologici che possiamo stimare attraverso la media, come se il comportamento umano fosse determinato da meccanismi identici in ogni individuo, con le differenze attribuibili solo a “rumore” sperimentale. Questo approccio, tipico della psicologia sperimentale tradizionale, assume che testare un gruppo di persone e mediare i loro risultati ci permetta di rivelare la struttura comune della mente umana. Ma questa assunzione è davvero giustificata?

19.1.3.8 La fallacia ergodica e l’illusione dell’universalità

Un errore metodologico frequente nella psicologia è la cosiddetta fallacia ergodica, ovvero l’errata convinzione che le caratteristiche medie di un gruppo possano essere automaticamente applicate ai singoli individui che lo compongono (Speelman et al., 2024). Questo equivoco nasce dall’idea che la media descriva un valore “tipico” valido per tutti, senza considerare le differenze individuali o le variazioni nel tempo.

Immaginiamo di studiare la felicità di un gruppo di persone nel corso di una settimana e di calcolare la media dei loro punteggi di benessere giornalieri. Se lunedì una persona ha un punteggio di 2 (molto infelice), mercoledì 5 (moderatamente felice) e sabato 8 (molto felice), il suo punteggio medio sarà 5. Tuttavia, questo valore intermedio non rappresenta in alcun modo la realtà soggettiva vissuta da quella persona nei singoli giorni. Lo stesso problema si pone quando si usano le medie per descrivere abilità cognitive, tratti di personalità o stati emotivi: la media può nascondere fluttuazioni e differenze individuali fondamentali per comprendere la psicologia umana.

Il rischio, come sottolineato da Molden & Dweck (2006), è che il nostro desiderio di trovare universalità nei processi cognitivi ci porti a enfatizzare somiglianze tra le persone, ignorando le variazioni individuali che possono essere altrettanto, se non più, informative. Per esempio, due studenti con lo stesso punteggio medio in un test di memoria potrebbero aver ottenuto quel risultato in modi completamente diversi: uno potrebbe aver avuto prestazioni costantemente nella media, mentre l’altro potrebbe aver avuto picchi di eccellenza alternati a difficoltà estreme.

19.1.3.9 La media: uno strumento da usare con cautela

Questi problemi non significano che la media sia inutile in psicologia. È un indicatore potente e spesso informativo, ma deve essere interpretato con cautela. In particolare, non può essere usata per fare inferenze sui singoli individui senza considerare altre misure, come la varianza e la deviazione standard, che ci dicono quanto i dati siano dispersi intorno alla media.

In psicologia, comprendere la variabilità è tanto importante quanto individuare una tendenza centrale. Se vogliamo davvero capire il comportamento umano, dobbiamo chiederci non solo qual è il valore medio? ma anche quanto variano i dati? e cosa ci dice questa variabilità sulle differenze individuali? Nella prossima sezione, esamineremo questi concetti e vedremo come la varianza e la deviazione standard ci aiutano a catturare le differenze che la media, da sola, non può rivelare.

La selezione della misura di tendenza centrale più adeguata è un aspetto fondamentale dell’analisi statistica. Tale scelta deve basarsi sulla natura dei dati a disposizione, sulla loro distribuzione e sulla potenziale presenza di valori anomali o asimmetrie. Comprendere le caratteristiche distintive di ciascun indicatore è cruciale per una rappresentazione corretta e significativa dell’informazione.

La Moda trova la sua principale applicazione nei dati di tipo categoriale o nominale, dove rappresenta l’unica misura di tendenza centrale calcolabile. La sua utilità è massima nelle distribuzioni unimodali, ovvero quelle in cui un unico valore emerge con frequenza predominante. Al contrario, in presenza di distribuzioni multimodali, caratterizzate da più picchi di frequenza, la moda perde di significatività, poiché l’identificazione di un singolo valore rappresentativo diventa impossibile. Nei dati continui, infine, la moda può spesso non essere definita o risultare poco informativa.

La Media Aritmetica è l’indicatore più comune e fornisce una stima eccellente della tendenza centrale per distribuzioni simmetriche e prive di valori anomali. Tuttavia, la media presenta una critica debolezza: la sua estrema sensibilità ai valori estremi. In distribuzioni asimmetriche o contaminata da outlier, la media subisce uno spostamento marcato verso la coda della distribuzione, finendo per non rappresentare più fedelmente la maggior parte dei dati.

La Media Spuntata si propone come una valida alternativa alla media tradizionale quando si sospetta la presenza di valori anomali. Questo indicatore, calcolato escludendo una certa percentuale dei valori più estremi (ad esempio, il 5% per ogni coda), offre un compromesso vantaggioso. Rispetto alla media, è molto più robusta agli outlier; rispetto alla mediana, tiene conto di un maggior numero di osservazioni, preservando parte dell’informazione contenuta nei dati.

La Mediana, essendo definita come il valore centrale di una distribuzione ordinata, possiede una robustezza intrinseca ai valori anomali. La sua natura posizionale fa sì che essa non venga influenzata dall’entità numerica dei dati, ma solo dal loro rango. Questo la rende la misura d’elezione per distribuzioni fortemente asimmetriche o con outlier. Inoltre, è l’indicatore preferibile per i dati ordinali, dove le distanze tra le categorie non sono definite numericamente.

Linee guida per una scelta consapevole.

Per distribuzioni simmetriche e unimodali, la media aritmetica costituisce generalmente la scelta ottimale, in quanto ne coglie appieno il centro. Quando si affrontano distribuzioni asimmetriche o dataset contenenti valori anomali, la mediana è da preferire per la sua innata resistenza a tali distorsioni. La media spuntata rappresenta un’ottima opzione quando si desidera attenuare l’impatto di pochi outlier senza rinunciare completamente all’informazione che forniscono. Per i dati categoriali (nominali), la moda è l’unica misura applicabile, a patto che la distribuzione sia unimodale. In scenari complessi come le distribuzioni multimodali, nessuna singola misura è sufficiente a descrivere la tendenza centrale. In questi casi, è indispensabile affiancare agli indicatori statistici una visualizzazione grafica (ad esempio un istogramma) e una descrizione analitica dei diversi picchi presenti.

In sintesi, non esiste una misura migliore in assoluto. La media è potente per dati simmetrici, la mediana è lo strumento robusto per proteggersi dalle distorsioni, la media spuntata è un utile compromesso e la moda è essenziale per i dati categoriali. La scelta deve sempre essere guidata da una attenta valutazione preliminare della distribuzione dei dati.

19.2 La variabilità nei dati psicologici

Nei fenomeni psicologici e comportamentali, la variabilità è una caratteristica intrinseca. Ad esempio, se misuriamo il livello di stress percepito da una persona più volte nella stessa giornata, è raro osservare lo stesso valore anche utilizzando strumenti identici. Allo stesso modo, un questionario standardizzato sull’autostima somministrato a un gruppo di studenti universitari restituirà punteggi differenti per ciascun partecipante. Anche registrando i tempi di reazione in un compito cognitivo, noteremo fluttuazioni sia tra individui diversi sia nelle prestazioni dello stesso individuo in prove ripetute.

Questa dispersione sistematica non è un “rumore” da ignorare, ma un elemento informativo cruciale. L’analisi statistica in psicologia ha infatti uno scopo duplice: da un lato, quantificare la variabilità; dall’altro, identificarne le origini. Differenze individuali, contesto ambientale, errori di misurazione o interazioni tra fattori sono solo alcune delle possibili fonti che contribuiscono alla variazione osservata.

In questa sezione esploreremo:

  1. La scomposizione della variabilità in componenti spiegate (attribuibili a fattori noti, come un intervento sperimentale) e non spiegate (legate a elementi casuali o non controllati).
  2. Strumenti per descriverla, sia attraverso rappresentazioni grafiche (boxplot, istogrammi) sia mediante indici numerici (differenza interquartile, varianza, deviazione standard).

Comprendere la variabilità non è un esercizio tecnico, ma un passo fondamentale per interpretare fenomeni complessi come le differenze di personalità, le oscillazioni emotive o l’efficacia di una terapia. Ogni modello psicologico, infatti, deve fare i conti con questa dimensione dinamica e multideterminata dei dati.

19.2.1 Quantili

Accanto alle misure di tendenza centrale, i quantili descrivono la posizione relativa di un’osservazione in una distribuzione. Se media, mediana e moda individuano un valore “tipico”, i quantili rispondono invece a una domanda diversa: qual è il valore al di sotto del quale si colloca una determinata proporzione dei dati?

19.2.1.1 Definizione

Il quantile di ordine \(p\) (\(0 < p < 1\)) è il valore \(q_p = x_{(k)}\), dove \(x_{(k)}\) rappresenta il \(k\)-esimo elemento dei dati ordinati in senso crescente e \(k = \lceil p \cdot n \rceil\), con \(n\) numero totale di osservazioni e \(\lceil \cdot \rceil\) funzione di arrotondamento per eccesso. Questo è il cosiddetto quantile non interpolato. Quando \(p \cdot n\) non è intero, si ricorre di norma all’interpolazione lineare tra due osservazioni consecutive: è il metodo implementato nei principali software statistici.

Per chiarire, consideriamo i dati ordinati \({15, 20, 23, 25, 28, 30, 35, 40, 45, 50}\). Il 30° percentile (\(p=0.3\)) si calcola come \(k = \lceil 0.3 \cdot 10 \rceil = 3\), dunque \(q_{0.3} = 23\).

19.2.1.2 Percentili e quartili

Un caso particolare sono i percentili, che suddividono la distribuzione in cento parti uguali. Il 25° percentile (o primo quartile \(Q_1\)) lascia al di sotto di sé un quarto dei dati, il 50° percentile corrisponde alla mediana e il 75° percentile (terzo quartile \(Q_3\)) delimita i tre quarti inferiori della distribuzione.

19.2.1.3 Esempio applicativo

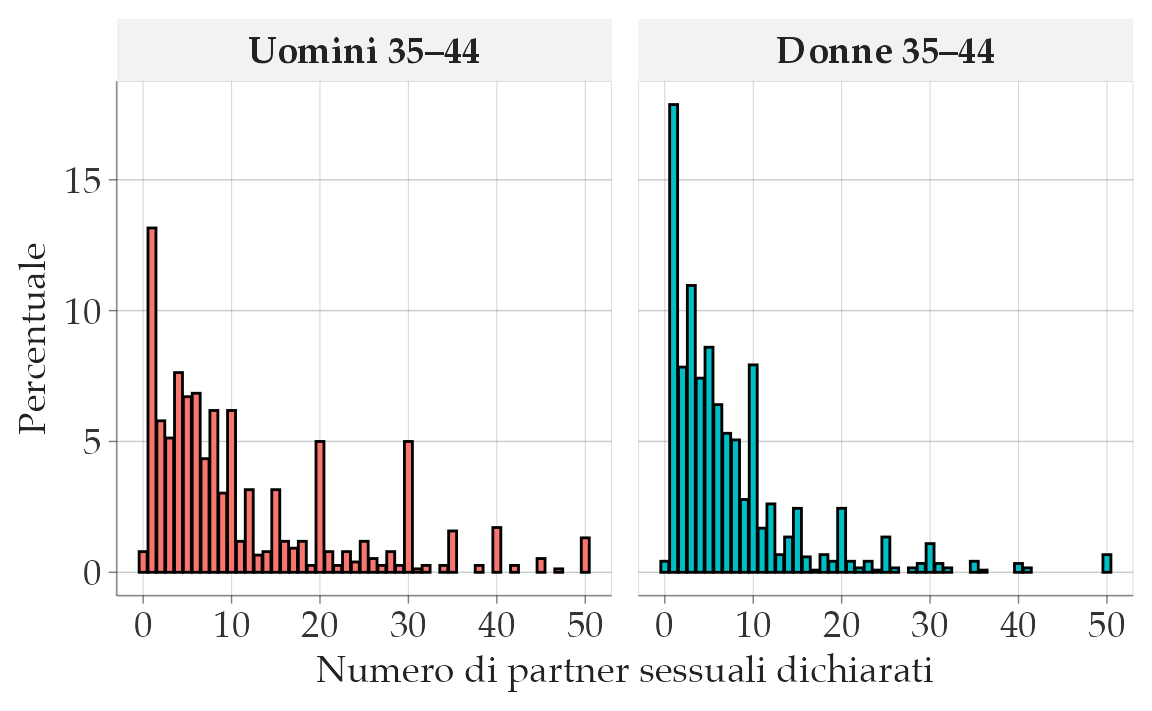
Per illustrare l’uso dei quantili, consideriamo la variabile NumPartners, distinta per genere. Calcoliamo il 10° e il 90° percentile.

# Quantili per gli uomini
quantile(
  sexual_partners[sexual_partners$Gender == "Man", "NumPartners"], 
  probs = c(0.1, 0.9)
  )
#>  10%  90% 
#>  1.0 34.5

# Quantili per le donne
quantile(
  sexual_partners[sexual_partners$Gender == "Woman", "NumPartners"], 
  probs = c(0.1, 0.9)
  )
#> 10% 90% 
#>   1  18

I risultati mostrano che, tra gli uomini, il 10% ha dichiarato al massimo un partner, mentre il 10% con i valori più elevati supera i 34 partner. Tra le donne, il 10° percentile coincide ancora con un partner, ma il 90° percentile non va oltre 18.

Questa differenza indica che le distribuzioni dei due gruppi condividono una base simile (molti individui con pochi partner) ma divergono nella coda superiore: negli uomini, pochi soggetti con valori estremi spingono la distribuzione verso destra, generando una maggiore asimmetria positiva.

19.2.1.4 Misure di dispersione basate sui quantili

I quantili possono essere utilizzati anche per costruire indici di variabilità che non fanno ipotesi sulla forma della distribuzione. La misura più semplice è l’intervallo di variazione, pari alla differenza tra valore massimo e minimo. Questo indice è immediato da calcolare, ma dipende esclusivamente dagli estremi e risulta quindi molto sensibile agli outlier.

x <- c(12, 18, 20, 22, 25, 28, 30, 35)
range(x)
#> [1] 12 35
diff(range(x))
#> [1] 23

Nell’esempio l’intervallo è 23, valore che descrive l’ampiezza complessiva dei dati ma non la loro distribuzione interna.

Un indicatore più robusto è la differenza interquartile (IQR), che misura la distanza fra il terzo e il primo quartile, racchiudendo così il 50% centrale dei dati.

IQR(x)
#> [1] 9

Se in un gruppo di studenti i quartili sono \(Q_1 = 25\) e \(Q_3 = 40\), l’IQR è pari a 15: significa che metà dei punteggi si colloca in un intervallo di 15 unità. Questo indice riduce l’influenza dei valori estremi, anche se non rappresenta l’intera dispersione della distribuzione.

In sintesi, l’intervallo di variazione e l’IQR offrono due prospettive complementari: il primo fornisce un’idea immediata dell’ampiezza totale dei dati, il secondo descrive la variabilità tipica della parte centrale della distribuzione. Entrambi hanno limiti che rendono necessario affiancarli a misure più complete, come la varianza e la deviazione standard, di cui parleremo nella sezione successiva.

19.2.2 La varianza

La varianza è una delle misure di dispersione più utilizzate in statistica perché tiene conto di tutte le osservazioni e descrive quanto i valori si discostano dalla loro media. Formalmente, se abbiamo \(n\) osservazioni \(x_1, x_2, \dots, x_n\) e indichiamo con \(\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i\) la loro media, la varianza (in versione descrittiva) si calcola così:

\[ S^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2. \tag{19.3}\]

In altre parole, per trovare la varianza:

  1. calcoliamo la media di tutti i valori (\(\bar{x}\)),
  2. sottraiamo la media a ciascun valore, ottenendo così lo scarto \((x_i - \bar{x})\),
  3. eleviamo ogni scarto al quadrato, per rendere positivi i valori ed enfatizzare gli scostamenti più grandi,
  4. infine, facciamo la media di questi quadrati.

Maggiore è la varianza, maggiore è la variabilità (o dispersione) dei dati rispetto alla media. Al contrario, una varianza prossima allo zero indica che le osservazioni sono molto vicine tra loro e quasi coincidenti con la media.

Nota su popolazione e campione. Spesso, nell’analisi di dati campionari, la varianza viene calcolata usando \(\frac{1}{n-1}\) al denominatore al posto di \(\frac{1}{n}\). In questo modo otteniamo una stima corretta (non distorta) della varianza della popolazione. Nel contesto della formula sopra riportata, invece, stiamo calcolando la varianza descrittiva (o popolazione completa).

Immaginiamo di aver misurato il numero di ore di studio giornaliere di un piccolo gruppo di partecipanti a un esperimento di psicologia. I dati raccolti sono:

\[ x = \{3,\, 1,\, 4,\, 2\}. \]

Passo 1: Calcolo della media

\[ \bar{x} = \frac{3 + 1 + 4 + 2}{4} = \frac{10}{4} = 2.5. \]

Passo 2: Scarti dalla media

  • Per il primo valore (\(x_1 = 3\)): \(3 - 2.5 = 0.5\)
  • Per il secondo valore (\(x_2 = 1\)): \(1 - 2.5 = -1.5\)
  • Per il terzo valore (\(x_3 = 4\)): \(4 - 2.5 = 1.5\)
  • Per il quarto valore (\(x_4 = 2\)): \(2 - 2.5 = -0.5\)

Passo 3: Quadrati degli scarti

  • \((0.5)^2 = 0.25\)
  • \((-1.5)^2 = 2.25\)
  • \((1.5)^2 = 2.25\)
  • \((-0.5)^2 = 0.25\)

Passo 4: Calcolo della varianza

Facciamo la media di questi valori:

\[ S^2 = \frac{0.25 + 2.25 + 2.25 + 0.25}{4} = \frac{5}{4} = 1.25. \]

Dunque la varianza è 1.25.

19.2.2.1 Interpretazione

Nel caso dell’esempio precedente relativo alle ore di studio giornaliere, una varianza pari a 1.25 indica che le ore di studio giornaliere si discostano, in media, di 1.25 unità quadrate dalla media di 2.5 ore. Per comprendere meglio l’ordine di grandezza di questa dispersione, solitamente si fa riferimento alla deviazione standard, che è la radice quadrata della varianza. In questo caso, \(\sqrt{1.25} \approx 1.12\) ore.

  • Se la varianza (o la deviazione standard) fosse stata molto più grande, avremmo dedotto che gli studenti del campione presentano abitudini di studio molto diverse.
  • Al contrario, se la varianza fosse prossima a 0, significherebbe che quasi tutti studiano un numero di ore molto simile a 2.5.

19.2.2.2 Calcolo in R

Se volessimo effettuare in R i calcoli relativi all’esempio sulle ore di studio, potremmo fare così:

# Dati
x <- c(3, 1, 4, 2)

# Calcolo manuale della media
media_x <- mean(x)

# Calcolo manuale della varianza secondo la formula descrittiva
varianza_descr <- mean((x - media_x)^2)
varianza_descr
#> [1] 1.25
# [1] 1.25

# Calcolo della varianza con la funzione var() di R
# (Attenzione: per default var() usa n-1 al denominatore)
varianza_campionaria <- var(x)
varianza_campionaria
#> [1] 1.667
# [1] 1.666667

Osserviamo che var(x) dà un valore di circa 1.67 perché R, di default, calcola la varianza campionaria (con \(n-1\) al denominatore). Se vogliamo la varianza descrittiva (come nella formula con \(n\) al denominatore), usiamo la nostra varianza_descr.

In sintesi, la varianza fornisce un modo per quantificare quanto siano diverse tra loro le osservazioni. Nel caso dell’esempio sulle ore di studio, abbiamo visto che i valori, pur non essendo tutti identici, non mostrano una dispersione eccessiva (la varianza è 1.25). Se i comportamenti di studio fossero estremamente diversificati (per esempio, se qualcuno studiasse 0 ore al giorno e qualcun altro 10), la varianza sarebbe molto più elevata, indicando una marcata eterogeneità nel campione.

19.2.2.3 Stima della varianza della popolazione

Si noti il denominatore della formula della varianza. Nell’Equazione 19.3, ho utilizzato \(n\) come denominatore (l’ampiezza campionaria, ovvero il numero di osservazioni nel campione). In questo modo, otteniamo la varianza come statistica descrittiva del campione. Tuttavia, è possibile utilizzare \(n-1\) come denominatore alternativo:

\[ s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2 . \tag{19.4}\]

In questo secondo caso, otteniamo la varianza come stimatore della varianza della popolazione. Si può dimostrare che l’Equazione 19.4 fornisce una stima corretta (ovvero, non distorta) della varianza della popolazione da cui abbiamo ottenuto il campione, mentre l’Equazione 19.3 fornisce (in media) una stima troppo piccola della varianza della popolazione. Si presti attenzione alla notazione: \(S^2\) rappresenta la varianza come statistica descrittiva, mentre \(s^2\) rappresenta la varianza come stimatore.

Per illustrare questo punto, svolgiamo una simulazione. Consideriamo la distribuzione dei punteggi del quoziente di intelligenza (QI). I valori del QI seguono una particolare distribuzione chiamata distribuzione normale (v. Capitolo 20), con media 100 e deviazione standard 15. La forma di questa distribuzione è illustrata nella figura seguente.

# Define parameters
x <- seq(100 - 4 * 15, 100 + 4 * 15, by = 0.001)
mu <- 100
sigma <- 15

# Compute the PDF
pdf <- dnorm(x, mean = mu, sd = sigma)

# Plot using ggplot2
data <- tibble(x = x, pdf = pdf)
ggplot(data, aes(x = x, y = pdf)) +
  geom_line() +
  labs(
    x = "QI", 
    y = "Densità", 
    title = "Distribuzione del QI nella popolazione"
  )

Supponiamo di estrarre un campione casuale di 4 osservazioni dalla popolazione del quoziente di intelligenza – in altre parole, supponiamo di misurare il quoziente di intelligenza di 4 persone prese a caso dalla popolazione.

set.seed(123) 
x <- rnorm(4, mean = 100, sd = 15)
print(x)
#> [1]  91.59  96.55 123.38 101.06

Calcoliamo la varianza usando \(n\) al denominatore. Si noti che la vera varianza del quoziente di intelligenza è \(15^2\) = 225.

var(x)
#> [1] 196.9

Consideriamo ora 10 campioni casuali del QI, ciascuno di ampiezza 4.

mu <- 100
sigma <- 15
size <- 4
niter <- 10
random_samples <- list()

set.seed(123) 

for (i in 1:niter) {
  one_sample <- rnorm(size, mean = mu, sd = sigma)
  random_samples[[i]] <- one_sample
}

Il primo campione è

random_samples[1]
#> [[1]]
#> [1]  91.59  96.55 123.38 101.06

Il decimo campione è

random_samples[10]
#> [[1]]
#> [1] 108.31  99.07  95.41  94.29

Stampiamo i valori di tutti i 10 campioni.

rs <- do.call(rbind, random_samples)
rs
#>         [,1]   [,2]   [,3]   [,4]
#>  [1,]  91.59  96.55 123.38 101.06
#>  [2,] 101.94 125.73 106.91  81.02
#>  [3,]  89.70  93.32 118.36 105.40
#>  [4,] 106.01 101.66  91.66 126.80
#>  [5,] 107.47  70.50 110.52  92.91
#>  [6,]  83.98  96.73  84.61  89.07
#>  [7,]  90.62  74.70 112.57 102.30
#>  [8,]  82.93 118.81 106.40  95.57
#>  [9,] 113.43 113.17 112.32 110.33
#> [10,] 108.31  99.07  95.41  94.29

Per ciascun campione (ovvero, per ciascuna riga della matrice precedente), calcoliamo la varianza usando la formula con \(n\) al denominatore. Otteniamo così 10 stime della varianza della popolazione del QI.

x_var <- apply(rs, 1, var)  # Applica la funzione var su ciascuna riga
print(x_var)
#>  [1] 196.940 337.536 168.547 218.684 333.476  34.520 264.378 234.081   1.971
#> [10]  40.468

Notiamo due cose:

  • le stime sono molto diverse tra loro; questo fenomeno è noto con il nome di variabilità campionaria;
  • in media le stime sono troppo piccole.

Per aumentare la sicurezza riguardo al secondo punto menzionato in precedenza, ripeteremo la simulazione utilizzando un numero di iterazioni maggiore.

mu <- 100
sigma <- 15
size <- 4
niter <- 10000
random_samples <- list()

set.seed(123) # Replace 123 with your desired seed for reproducibility

for (i in 1:niter) {
  one_sample <- rnorm(size, mean = mu, sd = sigma)
  random_samples[[i]] <- one_sample
}

rs <- do.call(rbind, random_samples)
x_var <- apply(rs, 1, var) * (size - 1) / size  # Adjust for population variance (ddof = 0)

Esaminiamo la distribuzione dei valori ottenuti.

# Create a data frame for plotting
data <- data.frame(x_var = x_var)

# Plot the histogram using ggplot2
ggplot(data, aes(x = x_var)) +
  geom_histogram(fill = "lightblue", bins = 30, color = "black") +
  scale_x_continuous(limits = c(0, 1500)) +
  scale_y_continuous(limits = c(0, 2250)) +
  labs(
    x = "Varianza", 
    y = "Frequenza", 
    title = "Varianza del QI in campioni di n = 4"
  )

La stima più verosimile della varianza del QI è dato dalla media di questa distribuzione.

mean(x_var)
#> [1] 168.9

Si noti che il nostro spospetto è stato confermato: il valore medio della stima della varianza ottenuta con l’Equazione 19.3 è troppo piccolo rispetto al valore corretto di \(15^2 = 225\).

Ripetiamo ora la simulazione usando la formula della varianza con \(n-1\) al denominatore.

set.seed(123) 

mu <- 100
sigma <- 15
size <- 4
niter <- 10000
random_samples <- list()

for (i in 1:niter) {
  one_sample <- rnorm(size, mean = mu, sd = sigma)
  random_samples[[i]] <- one_sample
}

rs <- do.call(rbind, random_samples)
x_var <- apply(rs, 1, var)  # ddof = 1 is default for var in R

Esaminiamo la distribuzione dei valori ottenuti.

# Create a data frame for plotting
data <- data.frame(x_var = x_var)

# Plot the histogram using ggplot2
ggplot(data, aes(x = x_var)) +
  geom_histogram(fill = "lightblue", bins = 30, color = "black") +
  scale_x_continuous(limits = c(0, 1500)) +
  scale_y_continuous(limits = c(0, 2250)) +
  labs(
    x = "Varianza Corretta", 
    y = "Frequenza", 
    title = "Varianza corretta del QI in campioni di n = 4"
  )

Nel secondo caso, se utilizziamo \(n-1\) come denominatore per calcolare la stima della varianza, il valore atteso di questa stima è molto vicino al valore corretto di 225. Se il numero di campioni fosse infinito, i due valori sarebbero identici.

mean(x_var)
#> [1] 225.2

In conclusione, le due formule della varianza hanno scopi diversi.

  • La formula della varianza con \(n\) al denominatore viene utilizzata come statistica descrittiva per descrivere la variabilità di un particolare campione di osservazioni.
  • D’altro canto, la formula della varianza con \(n-1\) al denominatore viene utilizzata come stimatore per ottenere la migliore stima della varianza della popolazione da cui quel campione è stato estratto.

19.2.3 Deviazione standard

Per interpretare la varianza in modo più intuitivo, si può calcolare la deviazione standard (o scarto quadratico medio o scarto tipo) prendendo la radice quadrata della varianza. La deviazione standard è espressa nell’unità di misura originaria dei dati, a differenza della varianza che è espressa nel quadrato dell’unità di misura dei dati. La deviazione standard fornisce una misura della dispersione dei dati attorno alla media, rendendo più facile la comprensione della variabilità dei dati.

La deviazione standard (o scarto quadratico medio, o scarto tipo) è definita come:

\[ s^2 = \sqrt{(n-1)^{-1} \sum_{i=1}^n (x_i - \bar{x})^2}. \tag{19.5}\]

Quando tutte le osservazioni sono uguali, \(s = 0\), altrimenti \(s > 0\).

Il termine standard deviation è stato introdotto in statistica da Pearson nel 1894 assieme alla lettera greca \(\sigma\) che lo rappresenta. Il termine italiano “deviazione standard” ne è la traduzione più utilizzata nel linguaggio comune; il termine dell’Ente Nazionale Italiano di Unificazione è tuttavia “scarto tipo”, definito come la radice quadrata positiva della varianza.

La deviazione standard \(s\) dovrebbe essere utilizzata solo quando la media è una misura appropriata per descrivere il centro della distribuzione, ad esempio nel caso di distribuzioni simmetriche. Tuttavia, è importante tener conto che, come la media \(\bar{x}\), anche la deviazione standard è fortemente influenzata dalla presenza di dati anomali, ovvero pochi valori che si discostano notevolmente dalla media rispetto agli altri dati della distribuzione. In presenza di dati anomali, la deviazione standard può risultare ingannevole e non rappresentare accuratamente la variabilità complessiva della distribuzione. Pertanto, è fondamentale considerare attentamente il contesto e le caratteristiche dei dati prima di utilizzare la deviazione standard come misura di dispersione. In alcune situazioni, potrebbe essere più appropriato ricorrere a misure di dispersione robuste o ad altre statistiche descrittive per caratterizzare la variabilità dei dati in modo più accurato e affidabile.

19.2.3.1 Interpretazione

La deviazione standard misura la dispersione dei dati rispetto alla media aritmetica. In termini semplici, indica quanto, in media, ciascun valore osservato si discosta dalla media del campione. Anche se è simile allo scarto semplice medio campionario (la media dei valori assoluti degli scarti rispetto alla media), la deviazione standard utilizza lo scarto quadratico medio e produce un valore leggermente diverso.

Esempio 19.1 Per verificare l’interpretazione della deviazione standard, utilizziamo i punteggi relativi alle ore di studio di un piccolo numero di studenti.

x <- c(3, 1, 4, 2)

std_x <- sqrt(var(x) * 3 / 4)
std_x
#> [1] 1.118

La deviazione standard calcolata è 1.12. Questo valore ci dice che, in media, ciascun punteggio si discosta di circa 1.12 ore dalla media aritmetica delle ore di studio di questo gruppo di studenti.

  • Valore più alto: indica maggiore dispersione dei dati intorno alla media.
  • Valore più basso: i dati sono più concentrati vicino alla media.

Se calcoliamo anche lo scarto semplice medio campionario per confronto, otteniamo:

mean(abs(x - mean(x)))
#> [1] 1

I due valori (deviazione standard e scarto semplice medio) sono simili ma non identici, a causa delle diverse definizioni matematiche.

19.2.4 Varianza spiegata e non spiegata

La varianza, come abbiamo visto, misura quanto i dati si disperdono attorno alla media. Un concetto fondamentale nei modelli statistici lineari è la distinzione tra varianza spiegata e varianza non spiegata, che ci permette di valutare quanto bene un modello teorico riesca a chiarire la variabilità osservata nei dati.

19.2.4.1 Decomposizione della varianza

Quando osserviamo un fenomeno (ad esempio i risultati di un test), troviamo inevitabilmente differenze tra individui. Queste differenze possono essere suddivise in due componenti principali:

  • varianza spiegata: la parte di variabilità che può essere attribuita a fattori identificati e misurabili;
  • varianza non spiegata: la parte rimanente di variabilità che non è chiarita dai fattori considerati.

Formalmente, questa decomposizione può essere espressa come:

\[ \sum_{i=1}^{n}(Y_i - \bar{Y})^2 = \sum_{i=1}^{n}(\hat{Y}_i - \bar{Y})^2 + \sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2 , \]

dove:

  • \(Y_i\) sono i dati osservati,
  • \(\bar{Y}\) è la media dei dati osservati,
  • \(\hat{Y}_i\) sono i valori attesi (previsti) dal modello teorico.

Intuitivamente:

  • la varianza totale (lato sinistro della formula) rappresenta la dispersione complessiva dei dati attorno alla loro media;
  • la varianza spiegata (primo termine a destra) indica quanto bene i valori previsti dal modello descrivono il comportamento dei dati;
  • la varianza non spiegata (secondo termine a destra) riflette ciò che il modello non riesce a prevedere.

Supponiamo di analizzare i punteggi di un esame universitario di “Psicometria” ottenuti da 200 studenti. La nostra teoria indica che i punteggi dipendano da:

  1. Ore settimanali dedicate allo studio;
  2. Presenza o assenza di “paura della matematica” (math anxiety) (Barroso et al., 2021).

Nello specifico, ipotizziamo:

  • una relazione positiva tra ore di studio e punteggio ottenuto;
  • una riduzione del 30% del punteggio per chi presenta paura della matematica rispetto agli altri studenti, a parità di ore di studio.

Ecco la simulazione in R:

set.seed(123)

# Simuliamo i dati per 200 studenti
n <- 200
ore_studio <- runif(n, min = 2, max = 15) |> round()
paura_mat <- rbinom(n, 1, prob = 0.3)

k <- 2  # Ogni ora di studio corrisponde a circa 2 punti

# Calcoliamo i punteggi attesi, limitati a 30 punti massimo
punteggio_atteso <- ore_studio * k * ifelse(paura_mat == 1, 0.7, 1) |> round()
punteggio_atteso <- ifelse(punteggio_atteso > 30, 30, punteggio_atteso)

# Generiamo punteggi reali aggiungendo casualità (tra 0 e 30 punti)
punteggio_reale <- (punteggio_atteso + rnorm(n, mean = 0, sd = 3)) |> round()
punteggio_reale <- pmin(pmax(punteggio_reale, 0), 30)

# Creiamo il dataset finale
data <- data.frame(ore_studio, paura_mat, punteggio_atteso, punteggio_reale)
head(data)
#>   ore_studio paura_mat punteggio_atteso punteggio_reale
#> 1          6         0               12              19
#> 2         12         1               24              28
#> 3          7         0               14              13
#> 4         13         0               26              28
#> 5         14         0               28              27
#> 6          3         1                6               5

Calcoliamo ora la decomposizione della varianza usando le formule indicate:

# Media dei punteggi reali
media_reale <- mean(data$punteggio_reale)

# Calcolo delle componenti della varianza
varianza_totale <- mean((data$punteggio_reale - media_reale)^2)
varianza_spiegata <- mean((data$punteggio_atteso - media_reale)^2)
varianza_non_spiegata <- mean((data$punteggio_reale - data$punteggio_atteso)^2)

# Risultati
c(varianza_totale, varianza_spiegata, varianza_non_spiegata)
#> [1] 60.37 51.65  8.29

Interpretazione dei risultati:

  • la varianza totale indica quanto in generale i punteggi differiscono tra loro,
  • la varianza spiegata rappresenta quanto della variabilità totale può essere attribuita ai fattori teorici (ore di studio e paura della matematica),
  • la varianza non spiegata evidenzia la variabilità residua che il modello non riesce a cogliere.

La proporzione di varianza spiegata è data dal rapporto:

prop_spiegata <- varianza_spiegata / varianza_totale
prop_spiegata
#> [1] 0.8555

Questa proporzione è sempre compresa tra 0 e 1:

  • valori vicini a 1 indicano che il modello è efficace nel descrivere i dati;
  • valori vicini a 0 suggeriscono che il modello non cattura adeguatamente la realtà osservata.

Questa decomposizione della varianza è uno strumento cruciale per valutare l’efficacia delle teorie e dei modelli statistici. Approfondiremo ulteriormente questi aspetti nel capitolo dedicato ai modelli di regressione (v. Capitolo 59).

19.2.5 Deviazione mediana assoluta

La deviazione mediana assoluta (MAD) è una misura robusta di dispersione basata sulla mediana. È definita come la mediana dei valori assoluti delle deviazioni dei dati rispetto alla mediana:

\[ \text{MAD} = \text{median} \left( |X_i - \text{median}(X)| \right) \tag{19.6}\]

La MAD è particolarmente utile per analizzare dati contenenti outlier o distribuzioni asimmetriche, poiché è meno influenzata dai valori estremi rispetto alla deviazione standard.

19.2.5.1 Relazione tra MAD e deviazione standard in una distribuzione normale

Quando i dati seguono una distribuzione normale (gaussiana), esiste una relazione approssimativa tra MAD e deviazione standard. La MAD può essere convertita in una stima della deviazione standard moltiplicandola per una costante di 1.4826:

\[ \sigma \approx k \times \text{MAD}, \]

dove:

  • \(\sigma\) è la deviazione standard,
  • MAD è la Mediana della Deviazione Assoluta,
  • \(k\) è una costante che, per una distribuzione normale, è tipicamente presa come circa 1.4826.

Questa costante deriva dalla proprietà della distribuzione normale, in cui circa il 50% dei valori si trova entro 0.6745 deviazioni standard dalla media.

La formula completa per convertire la MAD in una stima della deviazione standard in una distribuzione normale è:

\[ \sigma \approx 1.4826 \times \text{MAD} \]

Questa relazione è utile per stimare la deviazione standard in modo più robusto, specialmente quando si sospetta la presenza di outlier o si ha a che fare con campioni piccoli. Di conseguenza, molti software restituiscono il valore MAD moltiplicato per questa costante per fornire un’indicazione più intuitiva della variabilità dei dati. Tuttavia, è importante notare che questa relazione si mantiene accurata solo per le distribuzioni che sono effettivamente normali. In presenza di distribuzioni fortemente asimmetriche o con elevati outlier, la deviazione standard e la MAD possono fornire indicazioni molto diverse sulla variabilità dei dati.

Per verificare questo principio, usiamo un campione di dati simulati dalla distribuzione del QI:

qi <- rnorm(200, 100, 15)
1.4826 * median(abs(qi - median(qi)), na.rm = TRUE)
#> [1] 14.06

Otteniamo un valore che è simile alla deviazione standard calcolata con:

sqrt(
  var(qi) * (length(qi) - 1) / length(qi)
)
#> [1] 14.44

Ciò conferma la relazione tra MAD e deviazione standard in distribuzioni gaussiane.

Se invece usiamo dei dati non normali, l’approssimazione non è buona:

set.seed(123) 
y <- rchisq(200, 1)
1.4826 * median(abs(y - median(y)))
#> [1] 0.4743
sqrt(
  var(y) * (length(y) - 1) / length(y)
)
#> [1] 1.412

19.2.5.2 Quando usare deviazione standard e MAD

  • Deviazione standard: È la misura più appropriata per dati normalmente distribuiti e situazioni in cui l’obiettivo è descrivere la dispersione dei dati rispetto alla media. Tuttavia, è sensibile ai valori anomali (outlier).

  • Deviazione mediana assoluta: È ideale quando i dati sono non normali, asimmetrici o contengono outlier. La MAD è più robusta poiché utilizza la mediana anziché la media e non è influenzata da valori estremi.

19.2.6 Indici di variabilità relativi

A volte può essere necessario confrontare la variabilità di grandezze incommensurabili, ovvero di caratteri misurati con differenti unità di misura. In queste situazioni, le misure di variabilità descritte in precedenza diventano inadeguate poiché dipendono dall’unità di misura utilizzata. Per superare questo problema, si ricorre a specifici numeri adimensionali chiamati indici relativi di variabilità.

Il più importante di questi indici è il coefficiente di variazione (\(C_v\)), definito come il rapporto tra la deviazione standard (\(\sigma\)) e la media dei dati (\(\bar{x}\)):

\[ C_v = \frac{\sigma}{\bar{x}}. \tag{19.7}\]

Il coefficiente di variazione è un numero puro e permette di confrontare la variabilità di distribuzioni con unità di misura diverse.

Un altro indice relativo di variabilità è la differenza interquartile rapportata a uno dei tre quartili (primo quartile, terzo quartile o mediana). Questo indice è definito come:

\[ \frac{x_{0.75} - x_{0.25}}{x_{0.25}}, \qquad \frac{x_{0.75} - x_{0.25}}{x_{0.75}}, \qquad \frac{x_{0.75} - x_{0.25}}{x_{0.50}}. \]

Questi indici relativi di variabilità forniscono una misura adimensionale della dispersione dei dati, rendendo possibile il confronto tra grandezze con diverse unità di misura e facilitando l’analisi delle differenze di variabilità tra i dati.

Riflessioni conclusive

Le statistiche descrittive forniscono strumenti essenziali per sintetizzare e comprendere i dati raccolti in psicologia e nelle scienze sociali. Le misure di tendenza centrale, come la media, la mediana e la moda, ci permettono di individuare un valore tipico o rappresentativo di una distribuzione, facilitando la sintesi e l’interpretazione generale dei dati raccolti. Parallelamente, gli indici di dispersione, come la deviazione standard, la varianza e l’intervallo interquartile, offrono informazioni cruciali sulla variabilità, mostrandoci quanto i singoli dati siano vicini o distanti da questa tendenza centrale.

Tuttavia, è fondamentale riflettere attentamente sulle implicazioni teoriche e metodologiche che accompagnano l’uso di queste misure. In particolare, è importante considerare il rischio della fallacia ergodica, ovvero l’errata convinzione che i risultati ottenuti da medie e statistiche aggregate possano automaticamente applicarsi ai singoli individui. Nella pratica psicologica, infatti, ogni persona è caratterizzata da una notevole variabilità intra- e inter-individuale, che spesso non può essere adeguatamente rappresentata da semplici indicatori aggregati.

Le statistiche descrittive rappresentano quindi un primo e fondamentale passo nella comprensione dei dati psicologici, ma devono essere integrate da analisi più approfondite e attente alle differenze individuali. L’uso critico e consapevole di questi strumenti statistici ci consente di evitare generalizzazioni eccessive, fornendo una visione più accurata e realistica dei fenomeni psicologici e comportamentali che studiamo.

Esercizi

Parte 1: Domande Teoriche

  1. Definizione e comprensione dei concetti

    • Spiega la differenza tra media, mediana e moda.
    • In quali situazioni la mediana fornisce una misura della tendenza centrale migliore rispetto alla media?
    • Perché la media è sensibile ai valori estremi?
    • Quali sono i vantaggi della deviazione mediana assoluta (MAD) rispetto alla deviazione standard?

  2. Interpretazione della variabilità

    • Spiega il concetto di varianza e la sua interpretazione.
    • Qual è la differenza tra varianza e deviazione standard?
    • Descrivi in quali casi l’utilizzo del coefficiente di variazione è più appropriato rispetto alla deviazione standard.
    • Quali sono i limiti della moda come indice di tendenza centrale?

Parte 2: Calcoli Manuali

  1. Calcolo della media, mediana e moda

    • Considera i seguenti punteggi totali della SWLS che sono stati raccolti in un campione di studenti. Calcola manualmente:

      • La media
      • La mediana
      • La moda
      • Il range

  2. Calcolo della varianza e della deviazione standard

    • Usando gli stessi dati dell’esercizio precedente, calcola:
      • La varianza
      • La deviazione standard
      • La deviazione mediana assoluta (MAD)

Parte 3: Esercizi con R

  1. Analisi descrittiva con R

    • Carica il dataset swls_scores.csv contenente i punteggi SWLS degli studenti.
    • Calcola media, mediana e moda utilizzando R.
    • Calcola la varianza e la deviazione standard utilizzando le funzioni appropriate in R.

    Codice suggerito:

    library(tidyverse)
library(rio)

# Caricamento del dataset
df <- import("swls_scores.csv")

# Calcolo delle statistiche descrittive
mean(df$swls_total)
median(df$swls_total)

# Moda (funzione personalizzata)
get_mode <- function(x) {
  tbl <- table(x)
  as.numeric(names(tbl)[which.max(tbl)])
}
get_mode(df$swls_total)

# Varianza e deviazione standard
var(df$swls_total)
sd(df$swls_total)

# Deviazione mediana assoluta
mad(df$swls_total)

  2. Visualizzazione della distribuzione dei dati

    • Crea un istogramma dei punteggi totali della SWLS.
    • Aggiungi una linea verticale che rappresenti la media e una che rappresenti la mediana.

    Codice suggerito:

    ggplot(df, aes(x = swls_total)) +
  geom_histogram(binwidth = 2, fill = "blue", alpha = 0.5, color = "black") +
  geom_vline(aes(xintercept = mean(swls_total)), color = "red", linetype = "dashed", size = 1) +
  geom_vline(aes(xintercept = median(swls_total)), color = "green", linetype = "dotted", size = 1) +
  labs(title = "Distribuzione dei punteggi SWLS", x = "Punteggio SWLS", y = "Frequenza")

Parte 4: Domande di Comprensione

  1. Analisi concettuale

    • Perché la media aritmetica può essere considerata il “baricentro” della distribuzione dei dati?
    • Se aggiungiamo un valore estremo al dataset, quale delle misure di tendenza centrale subirà il maggior impatto?
    • In quali situazioni la varianza campionaria è preferibile rispetto alla varianza della popolazione?
    • Qual è la relazione tra la deviazione standard e la varianza?
    • Fornisci un’interpretazione intuitiva della deviazione standard.
    • Discuti le differenze e le somiglianze tra la deviazione standard e MAD. Usa queste informazioni per ridescrivere in maniera intuitiva il significato di deviazione standard.

Poniamo che i valori SWLS siano [ 18, 22, 26, 19, 24, 30, 26, 22, 18, 28, 21 ].

  1. Media: \[ \bar{x} = \frac{18 + 22 + 26 + 19 + 24 + 30 + 26 + 22 + 18 + 28 + 21}{11} = 23.36 \]

  2. Mediana: Ordinando i dati: [ 18, 18, 19, 21, 22, 22, 24, 26, 26, 28, 30 ] La mediana è il valore centrale: \(22\)

  3. Moda: Il valore più frequente è 22 (appare due volte).

  4. Varianza: \[ s^2 = \frac{\sum (x_i - \bar{x})^2}{n-1} = 13.96 \]

  5. Deviazione Standard: \[ s = \sqrt{13.96} = 3.73 \]

  6. MAD: \[ \text{MAD} = \text{mediana}(|X_i - \text{mediana}(X)|) = 4 \]

Soluzioni con R

I risultati eseguendo il codice R:

  • Media: 23.36
  • Mediana: 22
  • Moda: 22
  • Varianza: 13.96
  • Deviazione standard: 3.73
  • MAD: 4

Soluzioni alle Domande di Comprensione

  1. La media è il baricentro poiché minimizza la somma degli scarti quadrati.
  2. La media è più influenzata dai valori estremi rispetto alla mediana.
  3. La varianza campionaria corregge la sottostima della varianza popolazionale.
  4. La deviazione standard è la radice quadrata della varianza, consentendo un’interpretazione del risultato sulla scala dei dati grezzi.
  5. La deviazione standard è simile, ma non identica, al valore medio degli scarti assoluti tra ciascun valore della distribuzione e la media. In altre parole, rappresenta la “distanza tipica” media tra le osservazioni e il valore medio della distribuzione.
  6. La deviazione standard e il MAD (Median Absolute Deviation, o scarto medio assoluto) sono entrambi misure di variabilità che descrivono quanto i valori in un insieme di dati si discostino dal centro della distribuzione. Tuttavia, presentano alcune importanti differenze e somiglianze.

Somiglianze

  • Entrambe le misure quantificano la dispersione dei dati attorno a un punto centrale.
  • Sia la deviazione standard che il MAD utilizzano lo scarto (la differenza tra ciascun valore e un punto centrale) per calcolare la variabilità.

Differenze

  • Punto centrale usato: La deviazione standard si basa sulla media aritmetica, mentre il MAD si basa sulla mediana.
  • Trattamento degli scarti: Nella deviazione standard, gli scarti vengono elevati al quadrato prima di essere mediati, quindi la radice quadrata viene applicata al risultato finale. Questo processo penalizza maggiormente gli scarti più grandi, rendendo la deviazione standard più sensibile agli outlier. Il MAD, invece, considera semplicemente il valore assoluto degli scarti, rendendolo meno influenzato dagli estremi.
  • Sensibilità agli outlier: Poiché la deviazione standard dipende dai quadrati degli scarti, è più sensibile alle osservazioni estreme (outlier). Il MAD, essendo basato sulla mediana, è una misura più robusta e resiste meglio alla presenza di valori anomali.

Ridescrizione Intuitiva della Deviazione Standard

  • La deviazione standard può essere vista come una misura della “dispersione tipica” dei dati attorno alla media, ma con un’enfasi particolare sugli scarti più grandi. Immagina di prendere ogni valore del dataset, calcolarne la distanza dalla media, amplificare queste distanze attraverso il quadrato, poi trovare una sorta di “distanza media” ponderata. Questo processo dà maggiore peso agli scarti più grandi, fornendo così una visione della variabilità che tiene conto sia delle fluttuazioni ordinarie sia di eventuali valori estremi. In sintesi, mentre il MAD offre una visione più resistente e diretta della variabilità centrata sulla mediana, la deviazione standard fornisce una misura più dettagliata e sensibile alla forma complessiva della distribuzione, inclusi i suoi possibili outliers.
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] grid      stats     graphics  grDevices utils     datasets  methods  
#> [8] base     
#> 
#> other attached packages:
#>  [1] vcd_1.4-13            viridis_0.6.5         viridisLite_0.4.2    
#>  [4] pillar_1.11.0         tinytable_0.11.0      patchwork_1.3.1      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.13.0     
#> [10] ggplot2_3.5.2         reliabilitydiag_0.2.1 priorsense_1.1.0     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.22.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [28] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3        inline_0.3.21        sandwich_3.1-1      
#>  [4] rlang_1.1.6          magrittr_2.0.3       multcomp_1.4-28     
#>  [7] snakecase_0.11.1     compiler_4.5.1       systemfonts_1.2.3   
#> [10] vctrs_0.6.5          stringr_1.5.1        pkgconfig_2.0.3     
#> [13] arrayhelpers_1.1-0   fastmap_1.2.0        backports_1.5.0     
#> [16] labeling_0.4.3       utf8_1.2.6           rmarkdown_2.29      
#> [19] ragg_1.4.0           purrr_1.1.0          xfun_0.52           
#> [22] cachem_1.1.0         jsonlite_2.0.0       broom_1.0.9         
#> [25] parallel_4.5.1       R6_2.6.1             stringi_1.8.7       
#> [28] RColorBrewer_1.1-3   lmtest_0.9-40        lubridate_1.9.4     
#> [31] estimability_1.5.1   knitr_1.50           zoo_1.8-14          
#> [34] R.utils_2.13.0       pacman_0.5.1         Matrix_1.7-3        
#> [37] splines_4.5.1        timechange_0.3.0     tidyselect_1.2.1    
#> [40] abind_1.4-8          codetools_0.2-20     curl_6.4.0          
#> [43] pkgbuild_1.4.8       lattice_0.22-7       withr_3.0.2         
#> [46] bridgesampling_1.1-2 coda_0.19-4.1        evaluate_1.0.4      
#> [49] survival_3.8-3       RcppParallel_5.1.10  tensorA_0.36.2.1    
#> [52] checkmate_2.3.2      stats4_4.5.1         distributional_0.5.0
#> [55] generics_0.1.4       rprojroot_2.1.0      rstantools_2.4.0    
#> [58] scales_1.4.0         xtable_1.8-4         glue_1.8.0          
#> [61] emmeans_1.11.2       tools_4.5.1          data.table_1.17.8   
#> [64] mvtnorm_1.3-3        QuickJSR_1.8.0       colorspace_2.1-1    
#> [67] nlme_3.1-168         cli_3.6.5            textshaping_1.0.1   
#> [70] svUnit_1.0.6         Brobdingnag_1.2-9    V8_6.0.5            
#> [73] gtable_0.3.6         R.methodsS3_1.8.2    digest_0.6.37       
#> [76] TH.data_1.1-3        htmlwidgets_1.6.4    farver_2.1.2        
#> [79] R.oo_1.27.1          memoise_2.0.1        htmltools_0.5.8.1   
#> [82] lifecycle_1.0.4      MASS_7.3-65

Bibliografia

Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A., & Daucourt, M. C. (2021). A meta-analysis of the relation between math anxiety and math achievement. Psychological Bulletin, 147(2), 134–168.
Molden, D. C., & Dweck, C. S. (2006). Finding" meaning" in psychology: a lay theories approach to self-regulation, social perception, and social development. American Psychologist, 61(3), 192–203.
Speelman, C. P., & McGann, M. (2013). How mean is the mean? Frontiers in Psychology, 4, 451.
Speelman, C. P., Parker, L., Rapley, B. J., & McGann, M. (2024). Most Psychological Researchers Assume Their Samples Are Ergodic: Evidence From a Year of Articles in Three Major Journals. Collabra: Psychology, 10(1).