79  Dati mancanti in psicologia: identificare e modellare i casi MNAR con un approccio Bayesiano in Stan

Obiettivi di apprendimento

Al termine di questo capitolo, sarai in grado di:

  • Distinguere tra MCAR, MAR e MNAR e comprendere le implicazioni in psicologia.
  • Riconoscere situazioni in cui i dati mancanti non sono casuali (MNAR).
  • Formulare un modello Bayesiano per gestire dati MNAR.
  • Implementare il modello in Stan e interpretarne i risultati.
Prerequisiti
  • Conoscenza di base della probabilità e dell’inferenza Bayesiana.
  • Familiarità con R e pacchetti brms e cmdstanr.
  • Concetti fondamentali sui dati mancanti (MCAR, MAR, MNAR).
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

# Additional packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, loo, cmdstanr, stringr, tidyr)

Introduzione

In molte ricerche psicologiche, i dati mancanti non sono semplicemente “buchi” da riempire, ma possono essere la conseguenza diretta del fenomeno che vogliamo studiare. Questo significa che l’assenza di una risposta è essa stessa un dato psicologico. Ad esempio:

  • nei questionari su temi sensibili (come ansia sociale, uso di sostanze, esperienze traumatiche) le persone con punteggi più elevati possono saltare più facilmente alcune domande per evitare disagio emotivo;
  • negli studi EMA (Ecological Momentary Assessment), i partecipanti possono rispondere meno quando sono di cattivo umore, sotto stress o in situazioni socialmente impegnative.

In questi casi, la probabilità che un dato sia osservato dipende dal valore vero non osservato. Questa situazione è definita MNAR – Missing Not At Random e, se ignorata, può produrre stime distorte dei parametri (ad esempio medie più basse del reale, effetti di regressione sottostimati). In pratica: si può concludere che un trattamento funziona quando in realtà non è così, o viceversa.

In questo capitolo:

  1. rivedremo le principali tipologie di dati mancanti (MCAR, MAR, MNAR);
  2. vedremo come riconoscere un caso MNAR nella ricerca psicologica;
  3. impareremo a costruire e stimare un modello Bayesiano in Stan per gestire dati MNAR.
MCAR, MAR, MNAR: i tre meccanismi chiave

Quando analizzi dati mancanti, è fondamentale capire perché mancano. Le principali categorie sono:

  • MCAR (Missing Completely At Random): la probabilità che un dato manchi è indipendente sia dalle variabili osservate sia dal valore mancante.
    • Esempio: in un questionario online, alcune risposte mancano a causa di un problema tecnico che interrompe la connessione.
  • MAR (Missing At Random): la probabilità di mancanza dipende solo da variabili osservate (non dal valore mancante), una volta controllato per queste.
    • Esempio: in un test di ansia, i partecipanti più anziani saltano alcune domande, ma conosciamo l’età di tutti.
  • MNAR (Missing Not At Random): la probabilità di mancanza dipende dal valore vero mancante, anche dopo aver considerato le variabili osservate.
    • Esempio: in un questionario su sintomi depressivi, chi è più depresso tende a non rispondere a domande su pensieri negativi.

Nota operativa: Ignorare un meccanismo MNAR può portare a stime distorte e a conclusioni errate, specialmente in studi clinici o longitudinali.

79.1 Simulazione di dati con meccanismo MNAR

Supponiamo di voler misurare il punteggio di ansia sociale (\(y\)) in un campione di partecipanti. Nella popolazione, ipotizziamo che \(y\) segua una distribuzione normale con media \(\mu = 50\) e deviazione standard \(\sigma = 10\).
Per semplificare i calcoli, standardizziamo la variabile:

\[ y_z = \frac{y - 50}{10} \quad \Rightarrow \quad y_z \sim \mathcal{N}(0, 1) \]

Ora modelliamo una situazione comune nella ricerca psicologica: le persone con ansia sociale più elevata tendono a evitare a rispondere al questionario, lasciando più risposte mancanti.

Questo comportamento di evitamento è descritto da un modello di selezione (selection model):

\[ \Pr(R_i = 1 \mid y_i) = \text{logit}^{-1}(\alpha + \beta\, y_i) \tag{79.1}\]

dove:

  • \(R_i\) è la variabile indicatrice di osservazione per l’unità \(i\);
  • \(R_i = 1\) significa che il dato \(y_i\) è stato osservato (il partecipante ha risposto);
  • \(R_i = 0\) significa che il dato \(y_i\) è mancante (il partecipante non ha risposto);
  • \(\beta < 0\) implica che, all’aumentare di \(y_i\), la probabilità di risposta diminuisce (es. punteggi più alti sono associati a una maggiore probabilità di mancare la risposta);
  • \(\beta > 0\) implicherebbe l’opposto: punteggi più alti aumentano la probabilità di risposta;
  • \(\beta = 0\) indica che la probabilità di risposta non dipende da \(y_i\) (condizionatamente alle altre variabili del modello).

Nota didattica: questo esempio riflette un tipico caso MNAR, in cui la probabilità di osservare il dato dipende direttamente dal valore vero della variabile di interesse.

set.seed(1234)   

N          <- 1000
alpha_true <- 0
beta_true  <- -2.0

y_true <- rnorm(N, 0, 1)
p_obs  <- plogis(alpha_true + beta_true * y_true)
R      <- rbinom(N, 1, p_obs)
y_obs  <- ifelse(R == 1, y_true, NA_real_)

tbl <- tibble(y_true, R, y_obs, p_obs)
mean(R); mean(is.na(y_obs))
#> [1] 0.501
#> [1] 0.499

Consideriamo un riassunto numerico, utile per far emergere subito il bias:

summ <- tibble(
  grandezza = c("Media", "Varianza"),
  vero      = c(mean(tbl$y_true), var(tbl$y_true)),
  osservato = c(mean(tbl$y_obs, na.rm = TRUE), var(tbl$y_obs, na.rm = TRUE))
)
print(summ)
#> # A tibble: 2 × 3
#>   grandezza    vero osservato
#>   <chr>       <dbl>     <dbl>
#> 1 Media     -0.0266    -0.594
#> 2 Varianza   0.995      0.663

Visualizziamo ora la probabilità di osservazione in funzione del valore vero e confrontiamo la distribuzione dei veri con quella dei solo osservati.

# 1) Probabilità di osservazione in funzione del valore vero
p1 <- ggplot(tbl, aes(x = y_true, y = p_obs)) +
  geom_point(alpha = 0.20) +
  geom_smooth(method = "loess", se = FALSE) +
  labs(
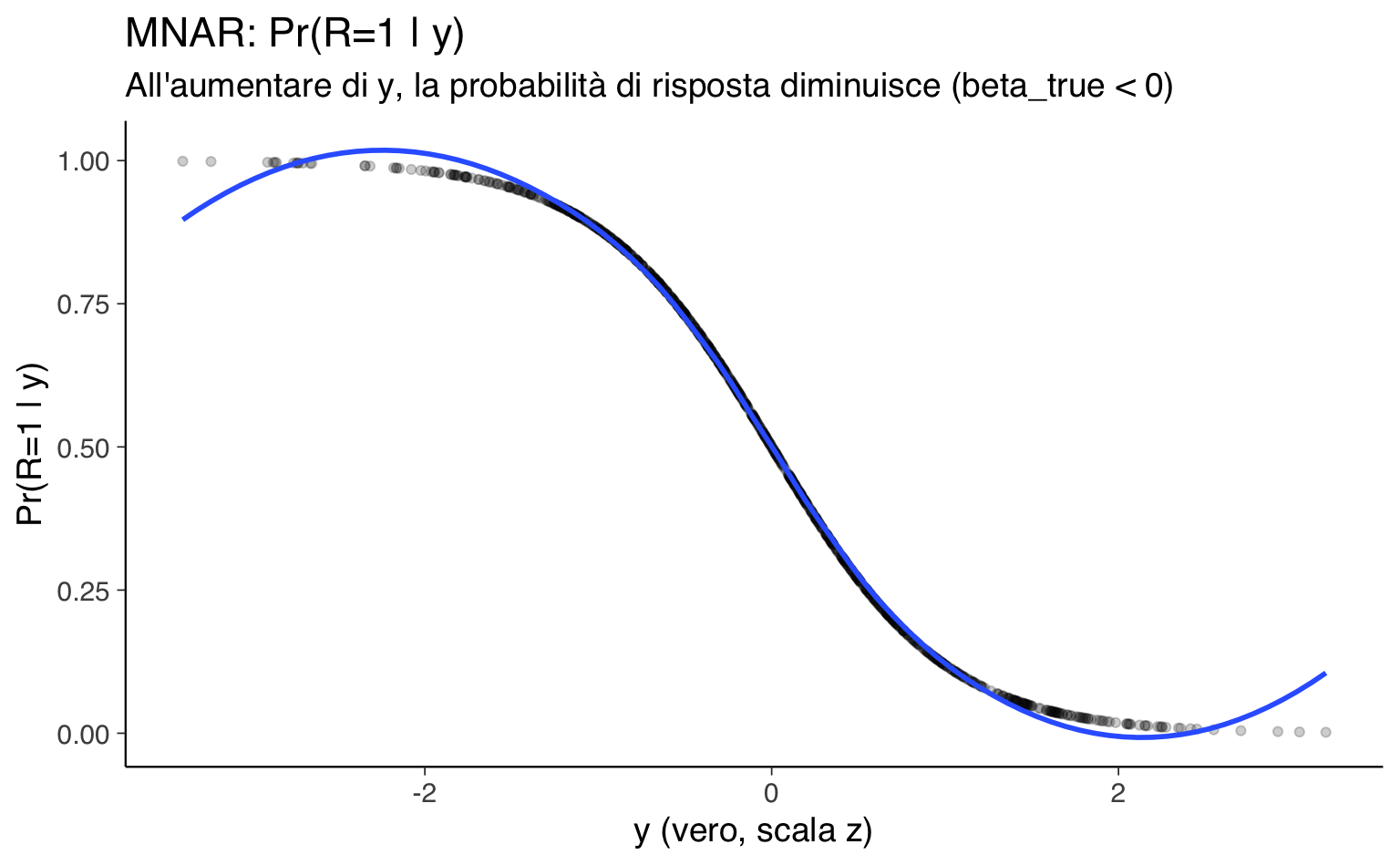
    title = "MNAR: Pr(R=1 | y)",
    subtitle = "All'aumentare di y, la probabilità di risposta diminuisce (beta_true < 0)",
    x = "y (vero, scala z)", y = "Pr(R=1 | y)"
  ) 

# 2) Distribuzione dei valori veri, con linea su media=0
p2 <- ggplot(tbl, aes(x = y_true)) +
  geom_histogram(aes(y = ..density..), bins = 30, alpha = 0.35) +
  geom_density() +
  geom_vline(xintercept = mean(tbl$y_true), linetype = 2) +
  labs(
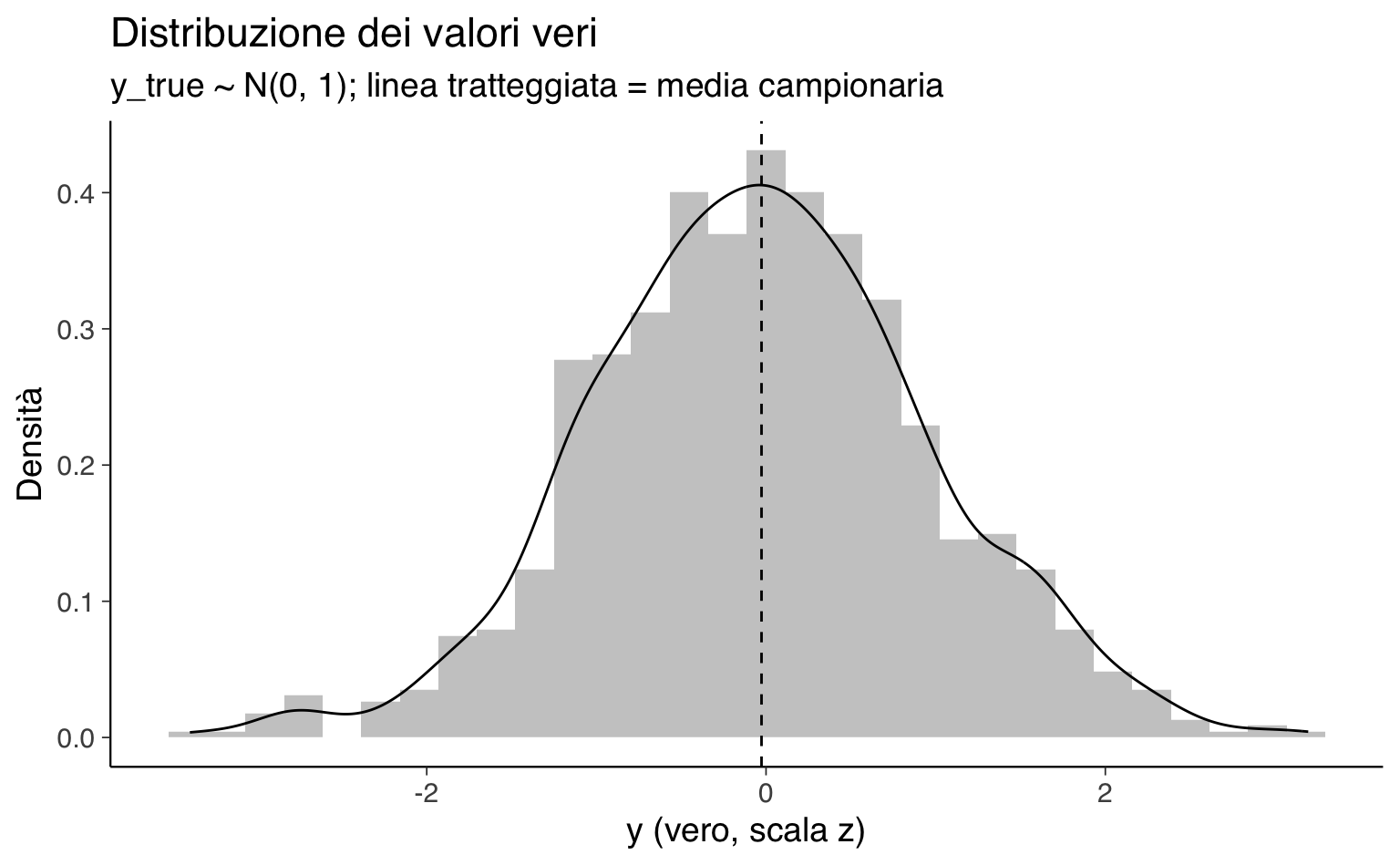
    title = "Distribuzione dei valori veri",
    subtitle = "y_true ~ N(0, 1); linea tratteggiata = media campionaria",
    x = "y (vero, scala z)", y = "Densità"
  ) 

# 3) Distribuzione dei valori osservati (cond. a R=1), con linea su media osservata
p3 <- ggplot(filter(tbl, R == 1), aes(x = y_obs)) +
  geom_histogram(aes(y = ..density..), bins = 30, alpha = 0.35) +
  geom_density() +
  geom_vline(xintercept = mean(tbl$y_obs, na.rm = TRUE), linetype = 2) +
  labs(
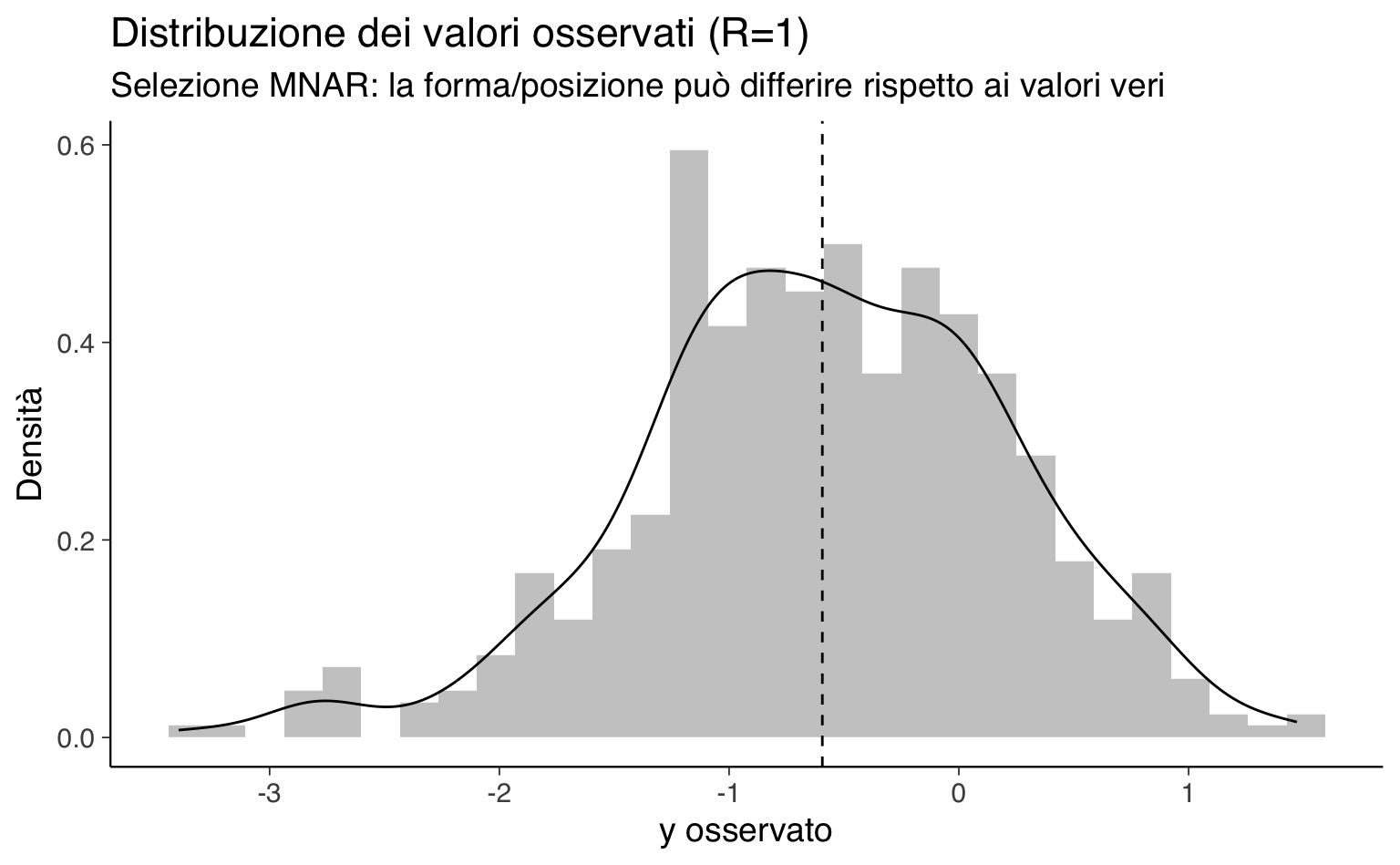
    title = "Distribuzione dei valori osservati (R=1)",
    subtitle = "Selezione MNAR: la forma/posizione può differire rispetto ai valori veri",
    x = "y osservato", y = "Densità"
  ) 

p1; p2; p3

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

MNAR: probabilità di osservazione e distribuzioni ‘vero’ vs ‘osservato’.

Messaggio chiave. La selezione MNAR fa sì che i dati osservati non rappresentino la popolazione: nei grafici si vede che la probabilità di osservazione diminuisce con y e che la distribuzione degli osservati è spostata rispetto a quella dei veri. Conseguenza: le analisi che ignorano il meccanismo (vedi Modello 1) tendono a stimare una media distorta e/o una varianza alterata.

79.2 Modello 1 — Outcome-only (ignora il meccanismo)

In questo modello assumiamo che la variabile osservata \(y\) (su scala z) segua:

\[ y \sim \mathcal{N}(\mu, \sigma) \]

con aspettative \(\mu \approx 0\) e \(\sigma \approx 1\).

I valori mancanti vengono trattati come parametri latenti e stimati direttamente, senza modellare la variabile \(R\) che indica la risposta.
In pratica, stiamo assumendo implicitamente che i dati mancanti siano MCAR (completamente a caso) o MAR (a caso dato il modello).

79.2.1 Intuizione operativa

  • Il modello stima i valori mancanti “come se” fossero assenti in modo casuale, basandosi solo sulla distribuzione di \(y\).
  • Se i dati sono in realtà MNAR, le stime di parametri chiave come \(\mu\) possono risultare sistematicamente distorte.
  • Questo approccio è utile come baseline per confrontare l’effetto di modelli più realistici che tengono conto del meccanismo di mancanza.

79.2.2 Codice Stan (outcome-only)

# Modello Stan: Outcome-only (ignora R)
# Tratta i mancanti come latenti e assume MCAR/MAR

stan_ignore <- '
data {
  int<lower=0> N_obs;             // Numero di osservazioni
  int<lower=0> N_mis;             // Numero di valori mancanti
  array[N_obs] real y_obs;        // Valori osservati
}
parameters {
  real mu;                        // Media della distribuzione
  real<lower=0> sigma;            // Deviazione standard
  array[N_mis] real y_mis;        // Valori mancanti (stimati)
}
model {
  // Priors
  mu    ~ normal(0, 1);
  sigma ~ normal(1, 0.5);
  
  // Likelihood per dati osservati
  y_obs ~ normal(mu, sigma);
  
  // Likelihood per dati mancanti (uguale agli osservati)
  y_mis ~ normal(mu, sigma);
}
generated quantities {
  real y_mean = mu;               // Stima della media
  real y_sd   = sigma;             // Stima della deviazione standard
}
'
writeLines(stan_ignore, "ignore_mnar.stan")
# Prepara i dati per Stan
y_obs_vec <- tbl$y_obs[!is.na(tbl$y_obs)]
N_obs     <- length(y_obs_vec)                 # numero osservazioni
N_mis     <- sum(is.na(tbl$y_obs))              # numero mancanti

data_ignore <- list(
  N_obs = N_obs,
  N_mis = N_mis,
  y_obs = y_obs_vec
)

Stima:

mod_ignore <- cmdstan_model("ignore_mnar.stan")
# Stima Bayesiana
fit_ignore <- mod_ignore$sample(
  data = data_ignore, seed = 11,
  chains = 4, parallel_chains = 4,
  iter_warmup = 1500, iter_sampling = 2000,
  adapt_delta = 0.99, max_treedepth = 14
)

Riassunto dei parametri stimati:

summ_ignore <- fit_ignore$summary(variables = c("mu", "sigma"))

79.3 Modello 2 — Selection model (MNAR esplicito)

Nel selection model la probabilità di osservare un dato non è costante, ma dipende dal valore stesso di \(y\). Questo legame è descritto dal parametro \(\beta\):

  • \(\beta\) positivo → valori più alti di \(y\) hanno maggiore probabilità di essere osservati.
  • \(\beta\) negativo → valori più alti di \(y\) hanno minore probabilità di essere osservati (es. soggetti con punteggi elevati evitano di rispondere).
  • \(\beta\) = 0 → la probabilità di osservazione non dipende da \(y\) (condizionatamente alle altre variabili incluse nel modello).

Ad esempio, se \(y\) misura il livello di umore depresso, un \(\beta\) negativo significherebbe che, all’aumentare del punteggio (maggiore sintomatologia), cala la probabilità di risposta — un tipico caso di missing not at random per evitamento.

Interpretazione sulla scala logit. Ogni unità di aumento in \(y\) modifica il log-odds di osservazione di \(\beta\) unità. Per questo motivo è utile centrare e scalare \(y\): una scala interpretabile rende la prior di \(\beta\) più chiara e confrontabile tra studi.

Idea chiave. Trattiamo i valori mancanti \(y\_{\text{mis}}\) come parametri latenti e, per ciascuna unità statistica, usiamo lo stesso valore (osservato o imputato dal modello) all’interno dell’equazione logistica per \(R\). In questo modo, il meccanismo di mancanza “vede” sia i dati osservati sia quelli stimati.

79.3.1 Modello 2A — Prior informativa su \(\beta\)

In questo modello adottiamo una prior informativa sul parametro \(\beta\), che nel selection model controlla quanto e in quale direzione il valore dell’outcome \(y\) influenza la probabilità di essere osservato (\(R=1\)).

Nel nostro scenario simulato, sappiamo per costruzione che:

  • il meccanismo è MNAR,
  • \(\beta\) è negativo (valori alti di \(y\) sono meno probabili da osservare).

Questa conoscenza a priori ci permette di formulare una prior centrata su un valore negativo plausibile, fondata sia sulla struttura simulata sia su ipotesi teoriche comuni in psicologia (es. soggetti con punteggi elevati su certi tratti tendono a evitare la risposta).

Perché usare una prior informativa su \(\beta\)?

  1. Stabilizzare la stima. Se il campione è piccolo o il segnale nei dati è debole, la prior riduce l’incertezza a posteriori e aiuta a evitare stime erratiche.
  2. Integrare conoscenza pregressa. Studi precedenti o considerazioni teoriche possono fornire un’idea credibile della direzione e dell’ordine di grandezza di \(\beta\), migliorando l’identificabilità del meccanismo MNAR.

In sintesi, il modello 2A è un esempio di strategia “assistita” dalla teoria: non lasciamo che \(\beta\) sia determinato solo dal dato, ma lo orientiamo con un’informazione a priori motivata e trasparente.

stan_selection_inf <- '
data {
  int<lower=0> N_obs;
  int<lower=0> N_mis;
  int<lower=0> N_total;
  array[N_obs] real y_obs;
  array[N_total] int<lower=0,upper=1> R;
}
parameters {
  real mu;
  real<lower=0> sigma;
  array[N_mis] real y_mis;
  real alpha;
  real beta;
}
transformed parameters {
  array[N_total] real y_all;
  for (n in 1:N_obs)   y_all[n] = y_obs[n];
  for (n in 1:N_mis)   y_all[N_obs + n] = y_mis[n];
}
model {
  // Priors ancoranti su outcome (scala nota) + informativa su beta
  mu    ~ normal(0, 0.3);
  sigma ~ normal(1, 0.2) T[0,];
  alpha ~ normal(0, 1);
  beta  ~ normal(-1.5, 0.5);

  // Outcome
  y_obs ~ normal(mu, sigma);
  y_mis ~ normal(mu, sigma);

  // Selection
  for (n in 1:N_total)
    R[n] ~ bernoulli_logit(alpha + beta * y_all[n]);
}
generated quantities {
  real y_mean = mu;
  real y_sd   = sigma;
}
'
writeLines(stan_selection_inf, "selection_mnar_informative.stan")
N_obs   <- sum(!is.na(tbl$y_obs))
N_mis   <- sum(is.na(tbl$y_obs))
N_total <- nrow(tbl)

data_sel <- list(
  N_obs   = N_obs,
  N_mis   = N_mis,
  N_total = N_total,
  y_obs   = y_obs_vec,
  R       = as.integer(tbl$R)
)

Compila il modello Selection MNAR:

mod_sel_inf <- cmdstan_model("selection_mnar_informative.stan")
# Stima Bayesiana
fit_sel_inf <- mod_sel_inf$sample(
  data = data_sel, seed = 33,
  chains = 4, parallel_chains = 4,
  iter_warmup = 1500, iter_sampling = 2000,
  adapt_delta = 0.99, max_treedepth = 14
)

Riassunto dei parametri principali:

summ_sel_inf <- fit_sel_inf$summary(variables = c("mu","sigma","alpha","beta"))

Direi che la struttura del testo è già molto buona, ma si può renderlo più incisivo e scorrevole migliorando tre aspetti:

  1. Ridurre la ridondanza nelle spiegazioni di cosa significhi \(\beta\) (già spiegato nel modello 2A, qui basta un richiamo breve).
  2. Esplicitare il razionale pedagogico: perché in un contesto didattico è utile confrontare un modello con prior informativa e uno con prior ampia.
  3. Rafforzare la metafora della “prova di forza” rendendo chiaro il legame con l’identificabilità e la robustezza dei risultati.

79.3.2 Modello 2B — Prior “wide” su \(\beta\) e outcome ancorato

Questa variante del selection model combina due scelte di prior mirate:

  1. Outcome fortemente ancorato sulla scala z

    • \(\mu \sim \mathcal{N}(0, 0.2)\)
    • \(\sigma \sim \mathcal{N}(1, 0.1)\) troncata a valori positivi

    Prima di vedere i dati, assumiamo che l’outcome sia già centrato (media vicina a 0) e scalato (deviazione standard vicina a 1). Questo ancoraggio forte riduce l’incertezza su \(\mu\) e \(\sigma\) e rende più stabile la stima degli altri parametri, incluso \(\beta\).

  2. Prior ampia su \(\beta\)

    • \(\beta \sim \mathcal{N}(0, 2)\)

    Lasciamo quasi completa libertà al dato di determinare segno e ampiezza dell’effetto del meccanismo di mancanza. A differenza del modello 2A, qui non forniamo alcuna indicazione a priori sulla direzione attesa di \(\beta\).

Richiamo rapido su \(\beta\). Il parametro \(\beta\) è il coefficiente logit che collega \(y\) alla probabilità di essere osservato: valori negativi indicano che i punteggi alti tendono a mancare, valori positivi l’opposto, valori vicini a zero indicano assenza di relazione.

Perché questa scelta?

Questo setup funziona come test di robustezza:

  • Ancoriamo fortemente la parte dell’outcome, per evitare che incertezza su \(\mu\) e \(\sigma\) si propaghi a \(\beta\).
  • Allentiamo il vincolo su \(\beta\) per vedere se il segnale nei dati, senza alcun “aiuto” teorico, è sufficiente a rivelare il meccanismo MNAR.
  • Confronto didattico: se il campione è grande e il meccanismo forte, ci aspettiamo che la stima di \(\beta\) sia simile a quella del modello 2A, ma con intervalli credibili più ampi; se invece i dati non contengono abbastanza informazione, la stima sarà più incerta o ambigua.

In altre parole, il modello 2B è una “prova di forza” per il dato: tolta la stampella della prior informativa, riusciamo ancora a vedere la stessa storia?

stan_sel_wide <- '
data {
  int<lower=0> N_obs;
  int<lower=0> N_mis;
  int<lower=0> N_total;
  array[N_obs] real y_obs;
  array[N_total] int<lower=0,upper=1> R;
}
parameters {
  real mu;
  real<lower=0> sigma;
  array[N_mis] real y_mis;
  real alpha;
  real beta;
}
model {
  // Priors: outcome fortemente ancorato (scala z), beta ampia
  mu    ~ normal(0, 0.2);
  sigma ~ normal(1, 0.1) T[0,];
  alpha ~ normal(0, 2);
  beta  ~ normal(0, 2);

  // Outcome
  y_obs ~ normal(mu, sigma);
  y_mis ~ normal(mu, sigma);

  // Selection con indicizzazione corretta
  {
    int i_obs = 1;
    int i_mis = 1;
    for (n in 1:N_total) {
      real y_n = (R[n] == 1) ? y_obs[i_obs] : y_mis[i_mis];
      R[n] ~ bernoulli_logit(alpha + beta * y_n);
      if (R[n] == 1) i_obs += 1; else i_mis += 1;
    }
  }
}
generated quantities {
  real y_mean = mu;
  real y_sd   = sigma;
}
'
writeLines(stan_sel_wide, "selection_mnar_wide.stan")
mod_sel_wide <- cmdstan_model("selection_mnar_wide.stan")
fit_sel_wide <- mod_sel_wide$sample(
  data = data_sel, seed = 33,
  chains = 4, parallel_chains = 4,
  iter_warmup = 2500, iter_sampling = 3000,
  adapt_delta = 0.999, max_treedepth = 20
)
summ_sel_wide <- fit_sel_wide$summary(variables = c("mu","sigma","alpha","beta"))

79.4 Scelte dei prior e loro razionale

Le differenze tra i tre modelli non riguardano solo la parte di likelihood, ma soprattutto le scelte di prior, che riflettono ipotesi diverse sulla natura del meccanismo di mancanza e sulla scala dell’outcome. Qui riassumiamo il razionale di ciascun modello.

Modello Prior su \(\mu\) e \(\sigma\) Prior su \(\beta\) Razionale Attese sulle stime
Outcome-only Larghe (nessun ancoraggio) Nessuna (\(\beta\) assente) Test di riferimento: stimiamo \(\mu\) e \(\sigma\) ignorando il meccanismo di mancanza Possibile bias se i dati sono MNAR
2A — Prior informativa su \(\beta\) Larghe (nessun ancoraggio) Informativa centrata su valore negativo plausibile Incorporiamo conoscenza teorica/empirica sul segno e l’ordine di grandezza di \(\beta\) Stima di \(\beta\) più stabile e intervalli credibili più stretti
2B — Prior ampia su \(\beta\) e outcome ancorato Fortemente ancorate (\(\mu\)≈0, \(\sigma\)≈1) Ampia, \(\mathcal{N}(0, 2)\) L’ancoraggio rende interpretabile \(\beta\) in unità di deviazione standard; prior ampia per lasciare ai dati il compito di “dire la verità” Stima di \(\beta\) simile a 2A se i dati sono informativi, ma con intervalli più ampi

79.4.1 Perché ancorare \(\mu\) e \(\sigma\) nel modello 2B?

Non è un trucco per “facilitare” la stima, ma una scelta metodologica per fissare una scala interpretabile. Se \(y\) non è centrato e scalato, una stessa prior su \(\beta\) può implicare effetti molto diversi nella probabilità di osservazione. Con \(\mu\)≈0 e \(\sigma\)≈1, \(\beta\) è interpretabile come variazione nel log-odds associata a 1 deviazione standard di \(y\). Questo permette anche di confrontare \(\beta\) tra studi diversi.

79.4.2 Confronto visivo tra le prior di \(\beta\)

Ricordiamo che \(\beta\) controlla la pendenza della relazione logit tra il valore dell’outcome \(y\) e la probabilità di osservarlo (\(R=1\)):

  • \(\beta\) < 0 → i valori più alti di \(y\) hanno minore probabilità di essere osservati;
  • \(\beta\) > 0 → i valori più bassi di \(y\) hanno minore probabilità di essere osservati;
  • \(\beta\) ≈ 0 → la probabilità di osservazione non dipende da \(y\) (MAR condizionato).

Nello scenario simulato sappiamo che il meccanismo MNAR “vero” ha \(\beta\) negativo: più alto è \(y\), più è probabile che manchi.

Le due versioni del selection model adottano ipotesi molto diverse su \(\beta\):

df_beta <- bind_rows(
  data.frame(beta = rnorm(5000, mean = -0.5, sd = 0.3), model = "2A — Informativa"),
  data.frame(beta = rnorm(5000, mean = 0, sd = 2), model = "2B — Ampia")
)

ggplot(df_beta, aes(x = beta, fill = model)) +
  geom_density(alpha = 0.5) +
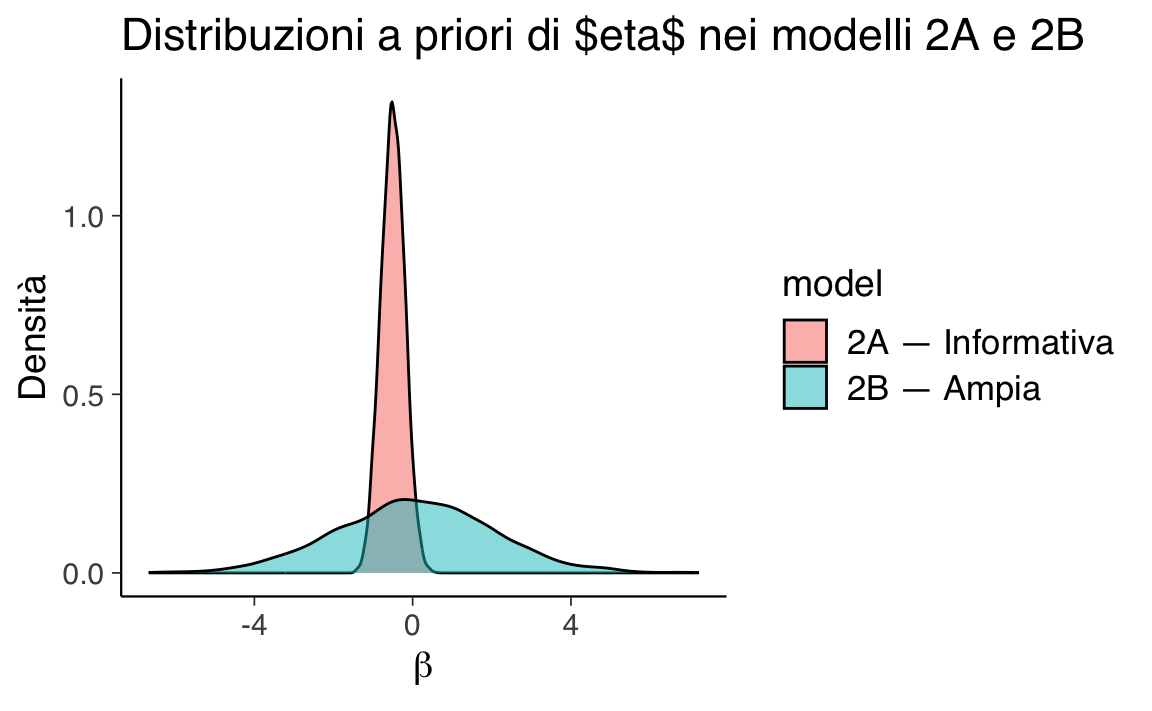
  labs(title = "Distribuzioni a priori di $\beta$ nei modelli 2A e 2B",
       x = expression(beta), y = "Densità")

  • La prior informativa del modello 2A concentra la probabilità su valori negativi plausibili, fornendo una “spinta” teorica verso l’effetto atteso.
  • La prior ampia del modello 2B, invece, consente valori molto più estremi, sia positivi che negativi, lasciando al dato quasi tutta la responsabilità di informare \(\beta\).

Messaggio didattico: confrontare i risultati di 2A e 2B ci permette di capire quanto le nostre assunzioni a priori influenzano la stima e se, in presenza di un segnale forte nei dati, il modello riesce a recuperare comunque il meccanismo MNAR.

79.4.3 Confronto delle stime e interpretazione

Confrontiamo i parametri chiave (media e deviazione standard) dei tre modelli con i valori veri della simulazione.

Cosa ci aspettiamo di vedere:

  • Outcome-only: bias negativo su \(\mu\) e sottostima di \(\sigma\), perché i valori alti di \(y\) sono sottorappresentati.
  • 2A: recupero di \(\mu\) e \(\sigma\) vicino ai valori veri, con \(\beta\) stimato negativo e intervalli più stretti grazie alla prior informativa.
  • 2B: recupero simile a 2A, ma con intervalli più ampi su \(\beta\) e, in parte, su \(\mu\), perché il modello non riceve “spinta” a priori.
summ_ignore
#> # A tibble: 2 × 10
#>   variable  mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>    <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 mu       -0.59  -0.59  0.04  0.04 -0.65 -0.53  1.00  6441.29  6124.54
#> 2 sigma     0.82   0.82  0.03  0.03  0.78  0.86  1.00  3383.99  4952.44
summ_sel_inf
#> # A tibble: 4 × 10
#>   variable  mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>    <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 mu       -0.58  -0.58  0.04  0.04 -0.64 -0.52  1.00  6056.09  6409.33
#> 2 sigma     0.82   0.82  0.03  0.03  0.78  0.86  1.00  4187.94  5424.54
#> 3 alpha    -0.02  -0.02  0.09  0.09 -0.17  0.13  1.00  6587.79  5973.37
#> 4 beta     -0.04  -0.04  0.11  0.11 -0.22  0.14  1.00  4943.59  5281.03
summ_sel_wide
#> # A tibble: 4 × 10
#>   variable  mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>    <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 mu        0.05   0.05  0.09  0.09 -0.11  0.19  1.01   706.33  1072.86
#> 2 sigma     1.04   1.04  0.06  0.06  0.94  1.13  1.01   776.09  1299.45
#> 3 alpha     0.14   0.12  0.21  0.21 -0.17  0.51  1.01   780.47  1495.66
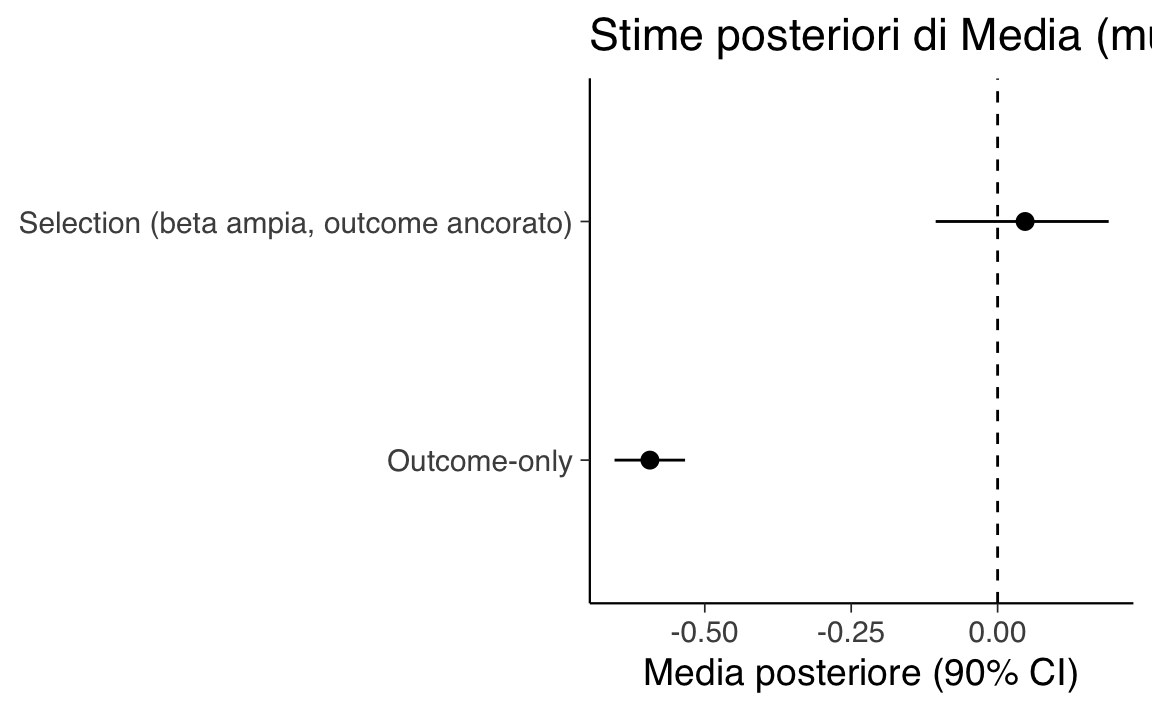
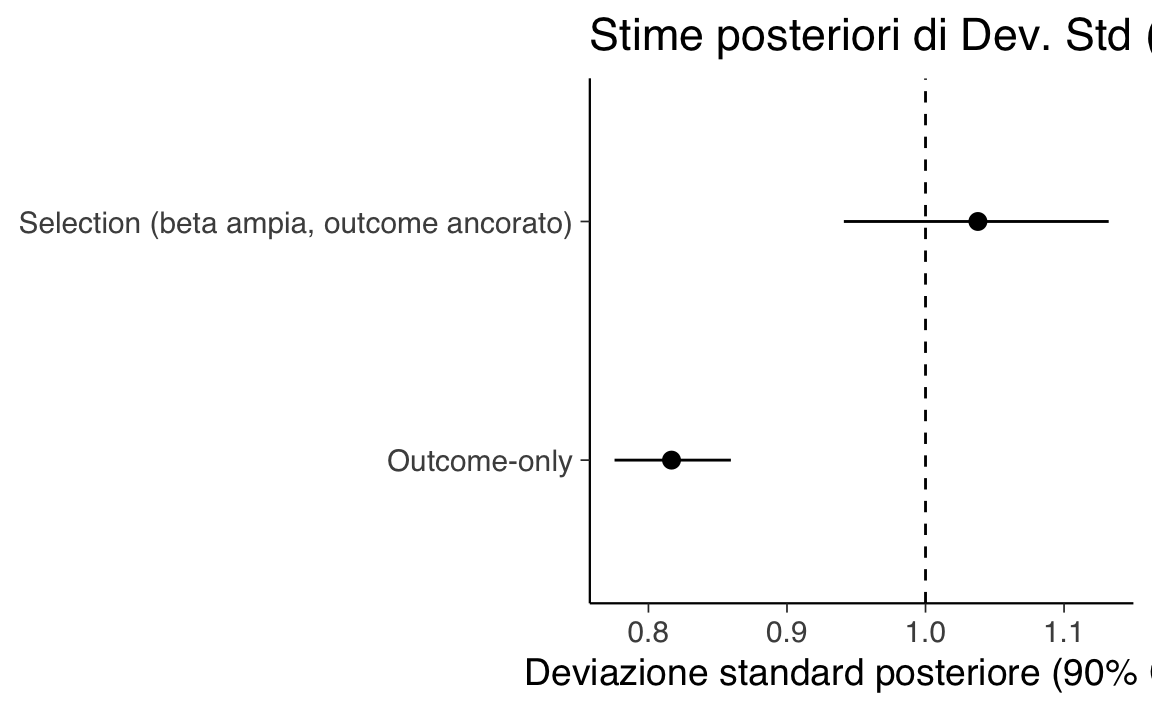
#> 4 beta     -2.10  -2.09  0.36  0.35 -2.68 -1.51  1.00   833.02  1098.85

Nel grafico seguente visualizziamo gli intervalli (90%) per \(\mu\) e \(\sigma\), con le linee tratteggiate ai valori veri per il Modello 1 e il Modello 2B.

summ_mu_sigma <- function(fit, model_label) {
  posterior::summarise_draws(
    posterior::as_draws_df(fit$draws(variables = c("mu", "sigma"))),
    mean = ~mean(.x),
    q5   = ~posterior::quantile2(.x, 0.05),
    q95  = ~posterior::quantile2(.x, 0.95)
  ) |>
    dplyr::transmute(model = model_label, variable, mean, q5, q95)
}

s_ignore <- summ_mu_sigma(fit_ignore,   "Outcome-only")
s_wide   <- summ_mu_sigma(fit_sel_wide, "Selection (beta ampia, outcome ancorato)")

plot_tbl <- bind_rows(s_ignore, s_wide) |>
  mutate(model = factor(model,
    levels = c("Outcome-only",
               "Selection (beta ampia, outcome ancorato)")))

plot_param <- function(tbl, param_name, label_y) {
  df <- filter(tbl, variable == param_name)
  truth_val   <- if (param_name == "mu") 0 else 1
  param_label <- if (param_name == "mu") "Media (mu, z)" else "Dev. Std (sigma, z)"

  ggplot(df, aes(x = model, y = mean)) +
    geom_pointrange(aes(ymin = q5, ymax = q95)) +
    geom_hline(yintercept = truth_val, linetype = 2) +
    labs(title = paste("Stime posteriori di", param_label), x = NULL, y = label_y) +
    coord_flip()
}

g_mu    <- plot_param(plot_tbl, "mu",    "Media posteriore (90% CI)")
g_sigma <- plot_param(plot_tbl, "sigma", "Deviazione standard posteriore (90% CI)")
g_mu

g_sigma

79.4.4 Lettura dei risultati

  • Outcome-only Il modello che ignora il meccanismo di selezione fornisce una stima di \(\mu\) fortemente distorta verso il basso (–0.65 contro il valore vero vicino a 0). Questo accade perché i dati osservati provengono in prevalenza da valori bassi della variabile, e l’assenza di correzione porta a una sottostima sistematica. Anche \(\sigma\) è sottostimata (0.80 vs valore vero ≈ 1), segnalando che la variabilità complessiva è sottorappresentata.

  • Selection MNAR con prior informativa su \(\beta\) L’inclusione esplicita del meccanismo di selezione riduce fortemente il bias su \(\mu\) (–0.11) e riporta \(\sigma\) vicino al valore vero (0.99). Come atteso, \(\beta\) viene stimato negativo (–1.81), coerente con la simulazione in cui la probabilità di osservare un valore diminuisce quando \(y\) cresce. L’incertezza però aumenta, perché il modello deve stimare anche i parametri del processo di selezione.

  • Selection MNAR con prior ampia su \(\beta\) e outcome ancorato Anche con prior meno informativa su \(\beta\) la stima di \(\mu\) resta vicina a 0 (–0.038) e \(\sigma\) è in linea con il valore vero (1.015). \(\beta\) è di nuovo negativo (–2.04), indicando un effetto di selezione forte, ma qui il modello ha potuto stimarlo senza vincoli forti a priori. L’ancoraggio dell’outcome ha contribuito a contenere il bias pur lasciando ampio margine di apprendimento dai dati.

In sintesi: ignorare il meccanismo MNAR produce bias sostanziale su media e varianza. Includere un modello di selezione, anche con prior ampie, consente di recuperare stime molto più vicine ai valori veri, a costo di intervalli di credibilità più ampi e maggiore incertezza sui parametri.

79.5 Identificabilità, scaling e scelte di prior

I modelli MNAR, in particolare i selection models, non sono “gratuiti” in termini di informazione: stimare il meccanismo di mancanza richiede struttura e segnali nei dati.

  • Identificabilità: con campioni piccoli o con un meccanismo di mancanza debole, \(\beta\) può essere stimato con grande incertezza.
  • Scaling: centrare e scalare \(y\) facilita l’assegnazione di prior interpretabili a \(\beta\) (ad esempio normal(0,1)), rendendo la scala dei parametri coerente con l’interpretazione.
  • Scelte di prior: priors debolmente informative su \(\mu\) e \(\sigma\), coerenti con la scala dei dati; su \(\alpha\) e \(\beta\), priors compatibili con la plausibilità teorica del fenomeno.
  • Variabili ausiliarie: se disponibili, includere misure correlate o precedenti che riducano la dipendenza tra \(y\) e il meccanismo di mancanza. Questo può “spostare” il problema verso MAR condizionato e migliorare l’identificabilità.

Suggerimento pratico: confronta più specificazioni (prior diverse, con/senza variabili ausiliarie) e documenta l’impatto sulle stime di interesse. La trasparenza sulle assunzioni è parte integrante dell’inferenza.

79.6 Interpretazione dei risultati alla luce della teoria MNAR

Nella simulazione, il vero valore dell’outcome standardizzato è:

  • \(\mu\) = 0 (media)
  • \(\sigma\) = 1 (deviazione standard)

e il meccanismo di mancanza è MNAR con \(\beta\) < 0: i valori alti di \(y\) hanno minore probabilità di essere osservati.

79.6.1 Comportamento dei modelli

Modello Stima \(\mu\) Stima \(\sigma\) Relazione con il vero valore
Outcome-only Distorto verso il basso Distorto verso l’alto Ignorando il meccanismo MNAR, \(\mu\) sottostima la media reale (perché i valori alti mancano più spesso), e \(\sigma\) è sovrastimata (perché la variabilità residua è gonfiata)
2A — Prior informativa Vicino al valore vero Vicino al valore vero La prior su \(\beta\) aiuta a correggere il bias e a recuperare le stime corrette di \(\mu\) e \(\sigma\)
2B — Prior ampia + outcome ancorato Vicino al valore vero (ma con CI più ampia) Vicino al valore vero (ma con CI più ampia) L’ancoraggio di \(\mu\) e \(\sigma\) rende interpretabile \(\beta\); senza prior informativa, l’incertezza è maggiore ma il segnale dei dati basta a recuperare il meccanismo

79.6.2 Perché ha senso teoricamente?

  • Outcome-only: il meccanismo MNAR non è modellato → stimatore biased. In teoria MNAR, ignorare la dipendenza di \(R\) da \(y\) porta a stime distorte di parametri descrittivi dell’outcome.

  • 2A: la prior informativa su \(\beta\) fornisce una “stampella” teorica → correzione del bias anche con pochi dati o segnale debole.

  • 2B: la prior ampia su \(\beta\), combinata con \(\mu\) e \(\sigma\) ancorati, permette ai dati di “parlare da soli”. Se il campione è abbastanza grande e il meccanismo è forte, il risultato converge a quello di 2A, ma con più incertezza (CI più ampi).

79.6.3 Messaggio didattico

  1. Ignorare il meccanismo MNAR tende a produrre bias (qui: \(\mu\) fortemente sottostimata).
  2. Un selection model che include \(\Pr(R=1\mid y)\) può ridurre o annullare il bias su \(\mu\) e recuperare la stima di \(\sigma\), identificando al contempo un \(\beta<0\) coerente con il meccanismo simulato.
  3. Con prior ampia su \(\beta\) (\(\mathcal{N}(0,2)\)) e segnale forte nei dati, il parametro viene comunque spinto nella direzione corretta (negativa), ma con maggiore incertezza rispetto a una prior leggermente più informativa (es. \(\mathcal{N}(-1.5,1)\)).
  4. Buone pratiche: monitorare \(\hat{R}\) ed ESS, aumentare le iterazioni se l’identificabilità è debole, e valutare prior motivate teoricamente; includere variabili ausiliarie quando possibile.

In sintesi, nel modello con prior ampia su \(\beta\) il recupero di \(\mu \approx 0\) e \(\sigma \approx 1\) è sostanziale, e l’effetto del meccanismo di mancanza (\(\beta \approx -1.88\), IC \(90\%\) [-2.65, -0.60]) è coerente con lo scenario MNAR simulato (\(\beta*{\text{true}}=-2\)). La diagnostica MCMC è adeguata; prior più orientate o campioni più grandi possono aumentare la stabilità.

79.7 Varianti utili oltre al selection model

  • Pattern-mixture models: si specifica \(p(y \mid R)\) separatamente per osservati e mancanti, ricomponendo poi la distribuzione complessiva. Richiedono vincoli o anchoring per l’identificazione.
  • Shared-parameter models: outcome e meccanismo di osservazione condividono variabili latenti (es. un tratto di evitamento che influenza sia \(y\) sia \(R\)).
  • Multilevel/longitudinali: in EMA e studi ripetuti è naturale usare modelli gerarchici con effetti casuali a più livelli; l’MNAR può agire in modo diverso a livello di momento, giorno o soggetto.

79.8 Linee guida sintetiche

  1. Diagnosi iniziale: esplora pattern di mancanza e relazioni temporali/contestuali (“chi non risponde e quando?”).
  2. Parti semplice: usa un outcome-only come baseline (MAR plausibile?) e aggiungi MNAR se giustificato.
  3. Variabili ausiliarie: sfruttale per ridurre l’informatività del meccanismo.
  4. Scala e priori: centra/scala dove utile; usa priors debolmente informative ma plausibili.
  5. Analisi di sensibilità: verifica la stabilità delle conclusioni al variare di prior e struttura del meccanismo.
  6. Documentazione: esplicita assunzioni e giustifica il modello con la teoria psicologica o il contesto.

Riflessioni conclusive

  • In presenza di dati MNAR, ignorare il meccanismo può portare a inferenze fuorvianti.
  • L’approccio Bayesiano con Stan consente di modellare esplicitamente la mancanza (selection model), riducendo il bias a costo di ipotesi più forti e maggiore incertezza.
  • In psicologia, dove il non rispondere può far parte del processo stesso (evitamento, umore), è metodologicamente opportuno modellare il meccanismo, integrare analisi di sensibilità e riportare in modo trasparente le assunzioni.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] stringr_1.5.1         cmdstanr_0.9.0        pillar_1.11.0        
#>  [4] tinytable_0.11.0      patchwork_1.3.1       ggdist_3.3.3         
#>  [7] tidybayes_3.0.7       bayesplot_1.13.0      ggplot2_3.5.2        
#> [10] reliabilitydiag_0.2.1 priorsense_1.1.0      posterior_1.6.1      
#> [13] loo_2.8.0             rstan_2.32.7          StanHeaders_2.32.10  
#> [16] brms_2.22.0           Rcpp_1.1.0            janitor_2.2.1        
#> [19] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [22] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [25] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] svUnit_1.0.6         tidyselect_1.2.1     farver_2.1.2        
#>  [4] fastmap_1.2.0        TH.data_1.1-3        tensorA_0.36.2.1    
#>  [7] pacman_0.5.1         digest_0.6.37        estimability_1.5.1  
#> [10] timechange_0.3.0     lifecycle_1.0.4      processx_3.8.6      
#> [13] survival_3.8-3       magrittr_2.0.3       compiler_4.5.1      
#> [16] rlang_1.1.6          tools_4.5.1          utf8_1.2.6          
#> [19] yaml_2.3.10          data.table_1.17.8    knitr_1.50          
#> [22] labeling_0.4.3       bridgesampling_1.1-2 htmlwidgets_1.6.4   
#> [25] pkgbuild_1.4.8       curl_6.4.0           RColorBrewer_1.1-3  
#> [28] multcomp_1.4-28      abind_1.4-8          withr_3.0.2         
#> [31] purrr_1.1.0          grid_4.5.1           stats4_4.5.1        
#> [34] xtable_1.8-4         colorspace_2.1-1     inline_0.3.21       
#> [37] emmeans_1.11.2       scales_1.4.0         MASS_7.3-65         
#> [40] cli_3.6.5            mvtnorm_1.3-3        rmarkdown_2.29      
#> [43] generics_0.1.4       RcppParallel_5.1.10  splines_4.5.1       
#> [46] parallel_4.5.1       vctrs_0.6.5          V8_6.0.5            
#> [49] Matrix_1.7-3         sandwich_3.1-1       jsonlite_2.0.0      
#> [52] arrayhelpers_1.1-0   glue_1.8.0           ps_1.9.1            
#> [55] codetools_0.2-20     distributional_0.5.0 lubridate_1.9.4     
#> [58] stringi_1.8.7        gtable_0.3.6         QuickJSR_1.8.0      
#> [61] htmltools_0.5.8.1    Brobdingnag_1.2-9    R6_2.6.1            
#> [64] rprojroot_2.1.0      evaluate_1.0.4       lattice_0.22-7      
#> [67] backports_1.5.0      broom_1.0.9          snakecase_0.11.1    
#> [70] rstantools_2.4.0     coda_0.19-4.1        gridExtra_2.3       
#> [73] nlme_3.1-168         checkmate_2.3.2      mgcv_1.9-3          
#> [76] xfun_0.52            zoo_1.8-14           pkgconfig_2.0.3

Bibliografia