42  La verosimiglianza

In questo capitolo, imparerai a:

• Comprendere il concetto di verosimiglianza: Scoprirai il ruolo fondamentale che la verosimiglianza svolge nella stima dei parametri statistici.
• Generare grafici della funzione di verosimiglianza:
  • Implementare grafici per la funzione di verosimiglianza nel caso binomiale.
• Interpretare i grafici della funzione di verosimiglianza: Sviluppare le competenze necessarie per analizzare e trarre conclusioni dai grafici generati.
• Capire il principio di stima di massima verosimiglianza (MLE): Approfondiremo il metodo di stima di massima verosimiglianza.

Prerequisiti

• Leggere il capitolo Estimation (Schervish & DeGroot, 2014).
• Leggere il capitolo Bayes’ rule (Johnson et al., 2022).

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

42.1 Introduzione

I ricercatori impiegano una varietà di modelli matematici per descrivere e prevedere il comportamento dei dati osservati. Questi modelli si differenziano principalmente per la loro struttura funzionale, ossia per il modo in cui stabiliscono relazioni tra le variabili osservate e i parametri teorici. La selezione del modello ottimale avviene mediante un confronto sistematico tra le previsioni teoriche generate dai diversi modelli e i dati empirici. Il modello le cui previsioni mostrano il miglior accordo con le osservazioni sperimentali viene considerato la rappresentazione più adeguata del fenomeno in esame.

In questo processo di valutazione, la funzione di verosimiglianza svolge un ruolo fondamentale: per ciascun possibile valore dei parametri, essa quantifica la plausibilità dei dati osservati qualora questi fossero effettivamente generati dal modello in esame. In altri termini, la verosimiglianza costruisce una vera e propria mappa di plausibilità parametrica, consentendo di identificare le combinazioni di parametri che massimizzano la coerenza tra modello e realtà osservata.

42.1.1 Il Principio della Verosimiglianza

La verosimiglianza quantifica la plausibilità di ciascun valore parametrico condizionatamente ai dati osservati. In termini intuitivi, essa rappresenta una misura di coerenza tra i parametri del modello e l’evidenza empirica disponibile.

Definizione 42.1 Sia \(Y\) un vettore aleatorio la cui distribuzione è caratterizzata da una funzione di densità (per variabili continue) o di massa di probabilità (per variabili discrete), denotata da \(f(y \mid \theta),\) dove \(\theta \in \Theta\) è un vettore di parametri definito nello spazio parametrico \(\Theta\).

Dopo aver osservato una realizzazione concreta \(y\) di \(Y\), la funzione di verosimiglianza è definita come:

\[ L(\theta; y) = f(y \mid \theta), \]

dove:

• \(y\) è fissato (corrisponde ai dati osservati),
  
• \(\theta\) è variabile (rappresenta l’oggetto di inferenza).

Questa funzione assegna a ogni possibile configurazione parametrica un grado di supporto empirico, rivelando quali valori di \(\theta\) siano più consoni con l’evidenza sperimentale.

42.1.2 Relazione tra Verosimiglianza e Funzione di Probabilità

Sebbene la funzione di probabilità (o densità) e la funzione di verosimiglianza condividano la stessa forma matematica – \(f(y \mid \theta)\) – il loro significato concettuale differisce sostanzialmente in base al contesto inferenziale.

42.1.2.1 Due prospettive a confronto

1. Funzione di probabilità (densità/massa)
   • Parametri (\(\theta\)) fissi: assumiamo che siano noti o ipotizzati.
     
   • Dati (\(y\)) aleatori: descrive la distribuzione dei possibili risultati.
     
   • Interpretazione: \(f(y \mid \theta)\) quantifica la probabilità (o densità) di osservare \(y\) sotto un modello con parametri \(\theta\).
     
   • Domanda chiave:
     “Se il modello fosse \(\theta\), quanto sarebbero probabili questi dati?”
2. Funzione di verosimiglianza
   • Dati (\(y\)) fissi: corrispondono alle osservazioni effettive.
     
   • Parametri (\(\theta\)) variabili: rappresentano l’incertezza da risolvere.
     
   • Interpretazione: \(L(\theta; y) = f(y \mid \theta)\) misura la plausibilità relativa di \(\theta\) alla luce di \(y\).
     
   • Domanda chiave:
     “Alla luce di questi dati, quanto sono credibili i diversi \(\theta\)?”

42.1.2.2 Implicazioni per l’inferenza statistica

• Approccio frequentista:
  La verosimiglianza è uno strumento per stimare i parametri (es. stima di massima verosimiglianza), senza assegnare loro una distribuzione di probabilità.

• Approccio bayesiano:
  La verosimiglianza agisce come ponte tra dati e parametri, combinando l’informazione empirica con le credenze iniziali (prior) per derivare la distribuzione a posteriori:

  \[ P(\theta \mid y) \propto L(\theta; y) \cdot P(\theta). \]

  In questa visione, i dati aggiornano la nostra conoscenza su \(\theta\) attraverso la verosimiglianza.

42.1.2.3 Sintesi delle differenze

Caratteristica	Funzione di probabilità	Funzione di verosimiglianza
Variabile di interesse	\(y\) (aleatoria)	\(\theta\) (incognita)
Ruolo epistemologico	Genera dati ipotetici	Valuta parametri plausibili
Contesto d’uso	Modellistica predittiva	Inferenza parametrica

Questa dualità riflette un principio fondamentale: la stessa formula matematica assume significati distinti a seconda che l’obiettivo sia la descrizione del processo generativo o l’inferenza sui suoi parametri. La verosimiglianza, in particolare, è il motore dell’apprendimento statistico, trasformando dati in conoscenza.

42.1.3 La Log-Verosimiglianza

In molti contesti statistici e computazionali, risulta conveniente lavorare con la log-verosimiglianza, definita come il logaritmo (naturale) della funzione di verosimiglianza:

\[ \ell(\theta; y) = \log L(\theta; y) = \log f(y \mid \theta). \]

Questa trasformazione offre notevoli vantaggi sotto diversi aspetti:

42.1.3.1 Vantaggi Computazionali

• Stabilità numerica:
  Il prodotto di probabilità molto piccole può portare a valori numericamente instabili (underflow). Il logaritmo converte questi prodotti in somme, più gestibili dal punto di vista computazionale.

• Efficienza nei modelli con dati indipendenti:
  Nel caso di osservazioni indipendenti e identicamente distribuite (i.i.d.), la log-verosimiglianza complessiva diventa la somma dei contributi individuali:

  \[ \ell(\theta; y_1, \dots, y_n) = \sum_{i=1}^n \log f(y_i \mid \theta), \]

  semplificando notevolmente i calcoli.

42.1.3.2 Vantaggi Analitici

• Ottimizzazione più semplice:
  Le derivate della log-verosimiglianza presentano un’espressione matematica più semplice rispetto a quelle della verosimiglianza originale, grazie alle proprietà del logaritmo che trasformano prodotti in somme. Questa semplificazione è particolarmente vantaggiosa nei metodi di ottimizzazione numerica come la massimizzazione della verosimiglianza (MLE), dove la stima dei parametri avviene risolvendo il sistema di equazioni ottenuto uguagliando a zero il gradiente (derivate prime).

• Proprietà additive:
  La forma additiva della log-verosimiglianza è particolarmente utile nei modelli gerarchici o nei casi in cui i dati provengono da più fonti indipendenti.

42.1.3.3 Equivalenza con la Massimizzazione della Verosimiglianza

Poiché il logaritmo è una funzione monotona crescente, massimizzare \(\ell(\theta; y)\) equivale a massimizzare \(L(\theta; y)\). Pertanto, le stime di massima verosimiglianza (MLE) possono essere ottenute indifferentemente dall’una o dall’altra.

In sintesi, la log-verosimiglianza combina efficienza computazionale e semplicità analitica, rendendola uno strumento fondamentale per l’inferenza statistica e l’analisi dati moderna.

42.2 Modellazione Statistica del Lancio di una Moneta

Per illustrare concretamente il concetto di verosimiglianza, consideriamo il classico problema della stima della probabilità di ottenere “testa” in una moneta. Sia \(\theta\) questa probabilità incognita.

42.2.1 Modello Probabilistico

Assumiamo:

1. Indipendenza: ogni lancio è statisticamente indipendente
2. Stazionarietà: la probabilità \(\theta\) rimane costante per tutti i lanci

Per una sequenza di n lanci con y teste, la probabilità congiunta è:

\[ P(\text{dati}|\theta) = \prod_{i=1}^n P(\text{esito}_i|\theta) = \theta^y(1-\theta)^{n-y} \]

42.2.2 Verosimiglianza e Sua Interpretazione

La funzione di verosimiglianza:

\[ L(\theta|\text{dati}) \propto \theta^y(1-\theta)^{n-y} \]

rappresenta la plausibilità relativa dei diversi valori di \(\theta\) alla luce dei dati osservati. Notiamo che:

1. Forma funzionale: corrisponde al nucleo della distribuzione binomiale
2. Costante di proporzionalità: il coefficiente binomiale è omesso poiché non influenza la stima di massima verosimiglianza
3. Interpretazione: valori di \(\theta\) che massimizzano \(L(\theta \mid \text{dati})\) sono quelli che meglio “spiegano” i dati osservati

42.2.3 Esempio 1: Due lanci

Immaginiamo di lanciare una moneta due volte e di osservare una testa e una croce. Il nostro obiettivo è stimare \(p_H\), cioè la probabilità che la moneta cada su testa. Per iniziare, valutiamo quanto sono plausibili due diversi valori di \(p_H\) alla luce dei dati osservati, calcolando la funzione di verosimiglianza.

• Se \(p_H = 0.5\) (una moneta equa), allora:

  \[ L(0.5) = 0.5^1 \cdot (1 - 0.5)^1 = 0.25 . \]

• Se \(p_H = 0.4\), allora:

  \[ L(0.4) = 0.4^1 \cdot 0.6^1 = 0.24 . \]

In entrambi i casi, la funzione di verosimiglianza ci dice quanto sia plausibile quel valore di \(p_H\), dati i risultati che abbiamo osservato (una testa e una croce). Come possiamo notare, il valore \(p_H = 0.5\) è più compatibile con i dati osservati rispetto a \(p_H = 0.4\).

42.2.4 Calcolo della verosimiglianza su una griglia di valori

Ora ripetiamo questo calcolo per molti valori diversi di \(p_H\), compresi tra 0 e 1. Questo ci permette di visualizzare la funzione di verosimiglianza e di vedere per quali valori di \(p_H\) essa è più alta.

# Parametri osservati
n <- 2             # Numero totale di lanci
y <- 1             # Numero di teste osservate

# Griglia di valori per p_H da 0 a 1
p_H <- seq(0, 1, length.out = 100)

# Calcolo della funzione di verosimiglianza
likelihood <- p_H^y * (1 - p_H)^(n - y)

42.2.5 Rappresentazione grafica

Il grafico seguente mostra la funzione di verosimiglianza per i 100 valori di \(p_H\). Ogni punto della curva indica quanto è compatibile quel valore di \(p_H\) con i dati che abbiamo osservato.

ggplot(data.frame(p_H, likelihood), aes(x = p_H, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  labs(
    title = "Funzione di Verosimiglianza per 2 Lanci\n(1 Testa, 1 Croce)",
    x = expression(p[H]),
    y = "Verosimiglianza"
  )

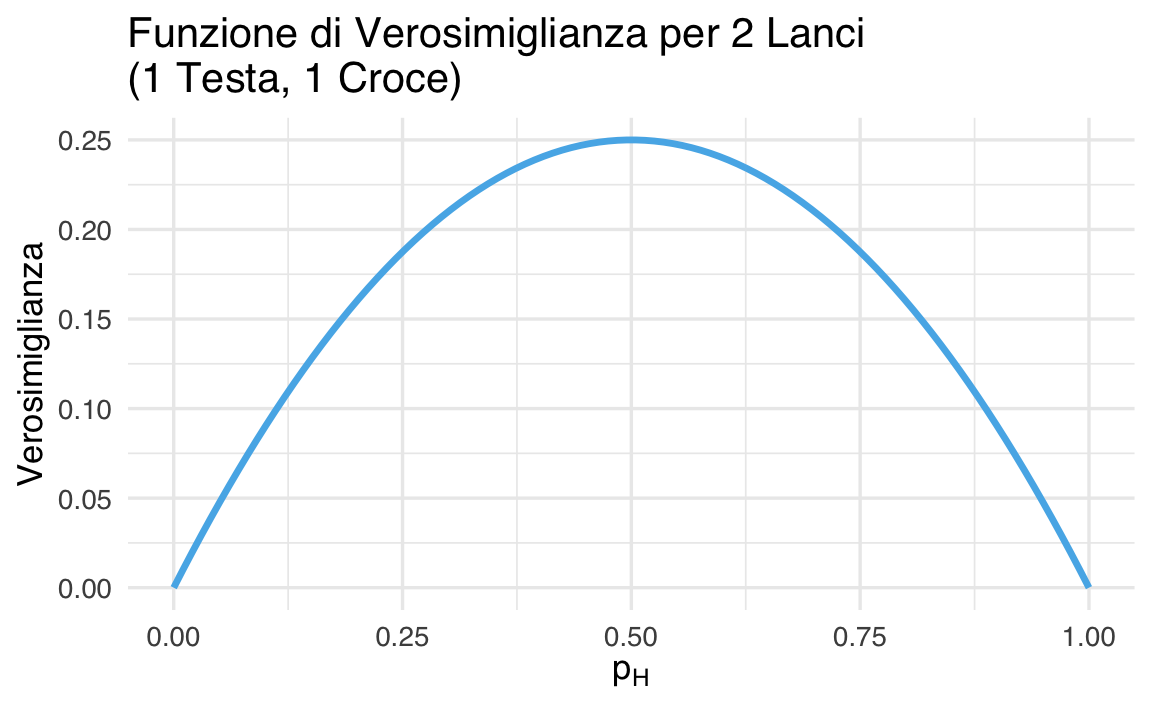
42.2.6 Cosa ci dice il grafico?

• La funzione di verosimiglianza raggiunge il suo massimo per \(p_H = 0.5\), che corrisponde alla proporzione osservata (1 testa su 2 lanci).
• Questo valore di \(p_H\) è quindi il più plausibile secondo i dati: rappresenta la stima di massima verosimiglianza.
• I valori estremi (vicini a 0 o a 1) hanno verosimiglianza molto bassa: non spiegano bene il fatto che abbiamo ottenuto una testa e una croce.

Ecco una versione migliorata e più didattica del tuo Esempio 2: Tre lanci, pensata per studenti che stanno imparando il concetto di verosimiglianza passo dopo passo. Mantiene l’approccio del primo esempio e rafforza la continuità logica, l’intuizione e l’interpretazione dei risultati, con un linguaggio semplice ma preciso.

42.2.7 Esempio 2: Tre lanci

Proseguiamo con un secondo esperimento: lanciamo una moneta tre volte, e otteniamo una testa e due croci. Anche in questo caso, vogliamo stimare \(p_H\), la probabilità che la moneta cada su testa, e valutare quali valori di \(p_H\) sono più compatibili con i dati osservati.

Iniziamo calcolando la verosimiglianza per due valori specifici:

• Se \(p_H = 0.5\) (moneta equa): \[ L(0.5) = 0.5^1 \cdot (1 - 0.5)^2 = 0.5 \cdot 0.25 = 0.125 \]

• Se \(p_H = 0.4\): \[ L(0.4) = 0.4^1 \cdot 0.6^2 = 0.4 \cdot 0.36 = 0.144 \]

Come vediamo, in questo caso \(p_H = 0.4\) ha una verosimiglianza maggiore rispetto a \(p_H = 0.5\): questo suggerisce che il valore 0.4 spiega meglio i dati (1 testa su 3 lanci) rispetto alla moneta equa.

42.2.8 Calcolo su una griglia di valori

Calcoliamo ora la verosimiglianza per 100 valori compresi tra 0 e 1 per visualizzare la funzione su tutto l’intervallo di probabilità.

# Parametri osservati
n <- 3             # Numero totale di lanci
y <- 1             # Numero di teste osservate

# Sequenza di valori possibili per p_H
p_H <- seq(0, 1, length.out = 100)

# Calcolo della funzione di verosimiglianza
likelihood <- p_H^y * (1 - p_H)^(n - y)

42.2.9 Rappresentazione grafica

Il grafico seguente mostra la funzione di verosimiglianza: ci dice quanto ogni valore di \(p_H\) è compatibile con l’osservazione di 1 testa e 2 croci.

# Mostra la curva della verosimiglianza
ggplot(data.frame(p_H, likelihood), aes(x = p_H, y = likelihood)) +
  geom_line(linewidth = 1.2) +
  labs(
    title = "Funzione di Verosimiglianza per 3 Lanci\n(1 Testa, 2 Croci)",
    x = expression(p[H]),
    y = "Verosimiglianza"
  )

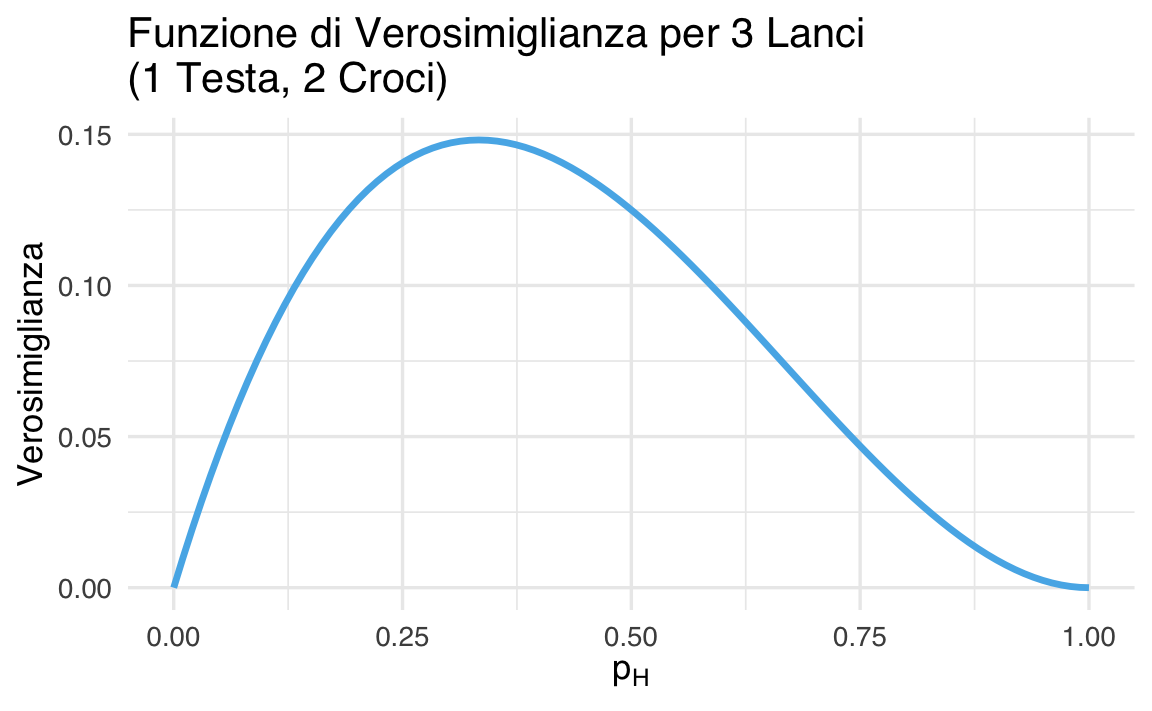
42.2.10 Cosa osserviamo?

• Il massimo della funzione di verosimiglianza non è più in \(p_H = 0.5\), ma più vicino a 0.33, cioè alla proporzione osservata (1 testa su 3 lanci).
• Questo riflette il fatto che il valore di \(p_H\) che meglio spiega i dati è quello che riproduce la frequenza osservata.
• La curva è più stretta rispetto al caso con 2 lanci: abbiamo più informazioni, quindi possiamo stimare \(p_H\) con maggiore precisione.
• Anche qui, i valori estremi di \(p_H\) (vicino a 0 o 1) hanno verosimiglianze basse, perché non giustificano bene l’osservazione di una testa e due croci.

42.2.11 Interpretazione dei Risultati

• La funzione di verosimiglianza raggiunge il massimo per valori di \(p_H\) vicini alla proporzione di teste osservata.
• Quando il numero di lanci aumenta, la curva diventa più “stretta”: i dati ci permettono di stimare \(p_H\) in modo più preciso.
• Valori estremi di \(p_H\) (vicini a 0 o 1) hanno verosimiglianze basse: non spiegano bene i dati osservati.

In sintesi, abbiamo visto come costruire la funzione di verosimiglianza a partire dai dati osservati, senza usare direttamente la distribuzione binomiale completa.
La tua sezione è già molto chiara, ma possiamo migliorarla ulteriormente per renderla ancora più didattica e accessibile a studenti principianti, mantenendo un linguaggio preciso e coerente con le sezioni precedenti.
L’obiettivo è aiutare gli studenti a vedere come la distribuzione binomiale si collega alla verosimiglianza e alla stima del parametro.

42.3 Verosimiglianza binomiale

Torniamo al nostro esperimento con la moneta, ma questa volta lo rendiamo un po’ più realistico: lanciamo la moneta \(n = 30\) volte e otteniamo \(y = 23\) teste.

Per modellare il numero totale di teste osservate, utilizziamo la distribuzione binomiale, che ci dice qual è la probabilità di ottenere esattamente \(y\) successi su \(n\) prove, quando la probabilità di successo in ogni singolo lancio è \(\theta\):

\[ P(Y = y \mid \theta) = \binom{n}{y} \theta^y (1 - \theta)^{n - y}. \]

In questo contesto:

• \(Y\) è una variabile casuale che rappresenta il numero di teste ottenute,
• \(y = 23\) è il valore osservato,
• \(\theta\) (o \(p_H\)) è la probabilità incognita di ottenere testa in un singolo lancio.

42.3.1 Dalla distribuzione alla verosimiglianza

Una volta osservati i dati (\(y = 23\)), possiamo considerarli fissati e analizzare quanto ciascun valore possibile del parametro \(\theta\) (la probabilità di ottenere testa) sia compatibile con questi dati. Per farlo, possiamo riutilizzare direttamente la formula della distribuzione binomiale, trattandola come funzione di \(\theta\) anziché come funzione di \(y\):

\[ L(\theta \mid y = 23) = \binom{30}{23} \theta^{23} (1 - \theta)^7. \]

Questa è la funzione di verosimiglianza, che ci dice quanto ogni valore di \(\theta\) sia plausibile alla luce dei dati osservati. A differenza degli esempi precedenti (in cui abbiamo ignorato le costanti moltiplicative), qui non abbiamo bisogno di semplificare la formula: la funzione dbinom() in R calcola automaticamente l’intera espressione, costante inclusa.

42.3.2 Visualizzazione della funzione di verosimiglianza

Il codice seguente costruisce il grafico della funzione di verosimiglianza, calcolando per ogni valore di \(\theta\) la probabilità di osservare 23 successi su 30 prove:

# Parametri osservati
n <- 30       # Numero totale di lanci
y <- 23       # Numero di teste osservate

# Griglia di valori possibili per p_H
p_H <- seq(0, 1, length.out = 1000)

# Calcolo della funzione di verosimiglianza (usando la binomiale completa)
likelihood <- dbinom(y, size = n, prob = p_H)

# Creazione del data frame
data <- data.frame(p_H, likelihood)

# Grafico della funzione di verosimiglianza
ggplot(data, aes(x = p_H, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  labs(
    title = "Funzione di Verosimiglianza per 30 Lanci di Moneta (23 Teste)",
    x = expression(p[H]),
    y = "Verosimiglianza"
  )

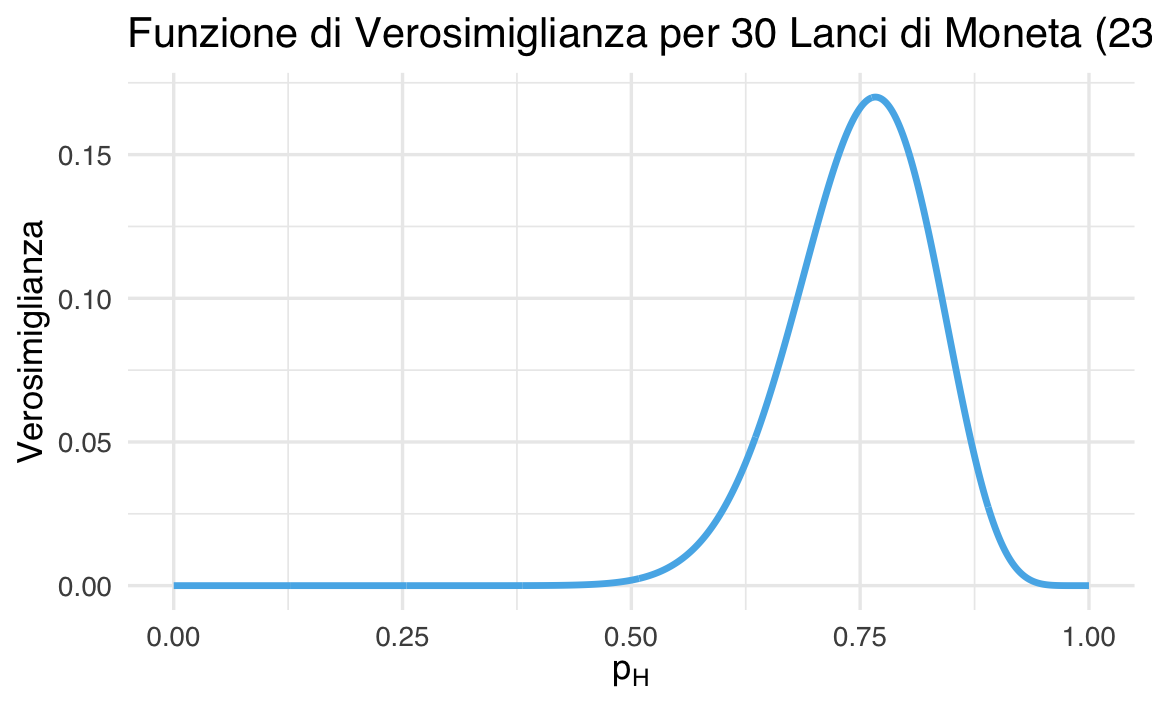
42.3.3 Interpretazione del risultato

Osservando il grafico, vediamo che:

• la funzione di verosimiglianza raggiunge il suo massimo in corrispondenza di \(p_H \approx 0.77\);
• questo significa che il valore di \(\theta\) (cioè \(p_H\)) che rende più plausibile l’osservazione di 23 teste su 30 è circa 0.77;
• in altre parole, la stima di massima verosimiglianza (MLE) per la probabilità di ottenere testa è: \[ \hat{p}_H = \frac{23}{30} \approx 0.767. \]

Questo risultato è del tutto intuitivo: la stima migliore è la proporzione osservata di teste.
La verosimiglianza ci mostra quali altri valori di \(\theta\) sono meno compatibili con i dati.

In sintesi, abbiamo visto come utilizzare direttamente la distribuzione binomiale per costruire la funzione di verosimiglianza. Questa funzione è uno strumento fondamentale per confrontare diversi valori possibili del parametro \(\theta\) (cioè la probabilità di successo) alla luce dei dati osservati.

Nel caso della moneta lanciata 30 volte con 23 teste, abbiamo trattato il numero di successi osservati (\(y = 23\)) come un dato fisso, e abbiamo valutato per quali valori di \(\theta\) questa osservazione sarebbe più plausibile.

In R, per calcolare la funzione di verosimiglianza non serve riscrivere manualmente la formula della binomiale. Possiamo usare la funzione dbinom(), che calcola le probabilità (o masse) della distribuzione binomiale per un dato numero di successi \(y\), un numero totale di prove \(n\), e una certa probabilità di successo \(\theta\).

Ad esempio, nel codice:

likelihood <- dbinom(y, size = n, prob = p_H)

• y è il numero di successi osservati (23),
• n è il numero totale di prove (30),
• p_H è un vettore di valori di \(\theta\) tra 0 e 1.

Il risultato likelihood è un vettore che contiene, per ciascun valore di \(\theta\), la verosimiglianza associata a quel valore: cioè, quanto quel valore di \(\theta\) è compatibile con i dati che abbiamo osservato.

Riassumendo:

• dbinom() fornisce la funzione di probabilità della binomiale,
• fissando \(y\) e variando \(\theta\), usiamo dbinom() per costruire la funzione di verosimiglianza,
• possiamo poi tracciare un grafico di questa funzione per visualizzare quali valori di \(\theta\) sono più plausibili.

Questa strategia mostra come la verosimiglianza possa essere costruita direttamente a partire da una distribuzione conosciuta (in questo caso, la binomiale) e implementata facilmente in R con strumenti standard.

42.4 La Stima di Massima Verosimiglianza

Nel momento in cui osserviamo dei dati e vogliamo stimare un parametro incognito (ad esempio, la probabilità \(\theta\) che una moneta dia “testa”), un metodo classico è la stima di massima verosimiglianza (Maximum Likelihood Estimation, o MLE).

Anche se nella prospettiva bayesiana ci interessa la distribuzione completa dei valori plausibili del parametro (e non un singolo valore stimato), è utile conoscere il concetto di MLE, che rappresenta il valore di \(\theta\) che rende i dati osservati più compatibili con il modello. Più avanti vedremo come la MLE corrisponde, nel caso di una prior uniforme, al valore massimo della distribuzione a posteriori.

42.4.1 L’idea di Fondo

La logica è semplice. Una volta osservati i dati, ci chiediamo: quali valori del parametro sono più compatibili con ciò che abbiamo visto? Il valore che risulta più plausibile è la stima di massima verosimiglianza.

Immagina di “provare” tanti valori di \(\theta\), e per ciascuno chiederti: “se fosse questo il vero valore di \(\theta\), quanto sarebbe plausibile osservare questi dati?” Il valore che meglio spiega i dati è quello scelto come stima.

42.4.2 Un Esempio Concreto

Hai lanciato una moneta 30 volte e hai osservato 23 teste. La tua domanda è: quanto è sbilanciata la moneta?

Utilizziamo la funzione di verosimiglianza, che ci dice quanto ogni valore possibile di \(\theta\) è compatibile con i dati osservati. Più alta è la verosimiglianza, più plausibile è il valore di \(\theta\).

42.4.3 Una metafora visiva

Immagina di osservare una curva che rappresenta la verosimiglianza al variare del parametro \(\theta\).
La curva si alza, raggiunge un punto massimo, e poi scende: proprio come una collina.

Quel punto più alto della curva rappresenta il valore di \(\theta\) che è più compatibile con i dati osservati: è il valore per cui i dati risultano più verosimili, secondo il modello.

Quel valore è chiamato stima di massima verosimiglianza (maximum likelihood estimate): è il punto in cima alla collina della verosimiglianza.

42.4.4 Come si Trova il Massimo?

Dal punto di vista matematico, il massimo di una funzione si trova dove la sua pendenza (la derivata) è zero: cioè, dove smette di salire e inizia a scendere.

Per la verosimiglianza binomiale (trasformata in log-verosimiglianza), questo calcolo si può fare in modo esatto. Se hai osservato \(y\) successi su \(n\) prove, la log-verosimiglianza è:

\[ \ell(\theta) = y \log \theta + (n - y) \log(1 - \theta), \]

e la derivata si annulla quando:

\[ \hat{\theta} = \frac{y}{n}. \]

In altre parole, la MLE è semplicemente la proporzione osservata di successi.

42.4.5 Un punto Importante per l’Approccio Bayesiano

Nel contesto bayesiano, non ci limitiamo a cercare il valore più plausibile del parametro, ma costruiamo una distribuzione completa che rappresenta l’incertezza su \(\theta\). Tuttavia, il punto in cui la distribuzione a posteriori raggiunge il suo massimo viene chiamato MAP (Maximum A Posteriori), e se assumiamo una distribuzione a priori uniforme, MLE e MAP coincidono. Quindi, la MLE può essere vista come un caso speciale del ragionamento bayesiano, utile per introdurre il concetto di compatibilità tra parametri e dati.

42.5 Calcolare la MLE in R

42.5.1 Metodo 1: Valutazione su Griglia

# Parametri
n <- 30
y <- 23
theta <- seq(0, 1, length.out = 10000)

# Calcolo della verosimiglianza binomiale
likelihood <- dbinom(y, size = n, prob = theta)

# Trova il massimo
max_index <- which.max(likelihood)
optimal_theta <- theta[max_index]

# Risultato
optimal_theta
#> [1] 0.7667

Spiegazione:

• dbinom() calcola la verosimiglianza per ogni valore di \(\theta\);
• which.max() individua il massimo;
• theta[max_index] restituisce la stima MLE.

42.5.2 Metodo 2: Ottimizzazione Numerica

In alternativa, possiamo trovare la MLE senza usare griglie, con un approccio più efficiente.

# Funzione log-verosimiglianza negativa
neg_log_likelihood <- function(theta) {
  - (y * log(theta) + (n - y) * log(1 - theta))
}

# Ottimizzazione numerica
result <- optim(
  par = 0.5,
  fn = neg_log_likelihood,
  method = "Brent",
  lower = 1e-6,
  upper = 1 - 1e-6
)

optimal_theta_numerical <- result$par
optimal_theta_numerical
#> [1] 0.7667

Nota: abbiamo calcolato la log-verosimiglianza negativa, perché optim() cerca minimi per default.

42.5.3 Confronto tra le Soluzioni

c(
  "Griglia" = optimal_theta, 
  "Ottimizzazione" = optimal_theta_numerical, 
  "Analitica" = y / n
)
#>        Griglia Ottimizzazione      Analitica 
#>         0.7667         0.7667         0.7667

Tutti i metodi restituiscono lo stesso risultato:
\[ \hat{\theta} = \frac{23}{30} \approx 0.767. \]

42.6 Verosimiglianza Congiunta

Abbiamo visto che, nel caso di una sequenza di \(n\) lanci di una moneta, la funzione di verosimiglianza si basa sulla distribuzione binomiale. In questo caso, trattiamo un esperimento Bernoulliano ripetuto \(n\) volte, e la nostra osservazione è il numero totale di successi (teste). Il numero complessivo di successi segue una distribuzione binomiale, e la funzione di verosimiglianza assume la forma:

\[ \mathcal{L}(\theta) = P(Y = y \mid \theta) = \binom{n}{y} \theta^y (1 - \theta)^{n - y}. \]

Qui la verosimiglianza è espressa direttamente in termini del numero totale di successi e insuccessi, senza dover scrivere il contributo di ogni singolo lancio.

Tuttavia, possiamo affrontare la questione da una prospettiva diversa: invece di considerare il numero totale di successi, possiamo pensare alla verosimiglianza come il prodotto delle probabilità di ogni singolo lancio. Questo ci porta a una generalizzazione importante: la verosimiglianza congiunta di più osservazioni indipendenti.

42.6.1 Dal Caso Binomiale alla Verosimiglianza Congiunta

Nel caso dei lanci della moneta, le singole osservazioni sono prove Bernoulliane indipendenti, ovvero ogni singolo lancio è un’osservazione indipendente che segue una distribuzione Bernoulli con parametro \(\theta\):

\[ P(Y_i = 1 \mid \theta) = \theta, \quad P(Y_i = 0 \mid \theta) = 1 - \theta. \]

Se trattiamo ogni prova individualmente, la funzione di verosimiglianza per una singola osservazione è:

\[ \mathcal{L}(\theta \mid y_i) = \theta^{y_i} (1 - \theta)^{1 - y_i}. \]

Ora, per un campione di \(n\) osservazioni indipendenti, la verosimiglianza congiunta è il prodotto delle verosimiglianze delle singole osservazioni:

\[ \mathcal{L}(\theta \mid y_1, y_2, \dots, y_n) = \prod_{i=1}^{n} \theta^{y_i} (1 - \theta)^{1 - y_i}. \]

Riconosciamo che questa espressione è identica alla funzione di verosimiglianza della distribuzione binomiale, perché il numero totale di successi è:

\[ y = \sum_{i=1}^{n} y_i. \]

Quindi, riscrivendo la verosimiglianza congiunta, otteniamo:

\[ \mathcal{L}(\theta) = \theta^{\sum y_i} (1 - \theta)^{n - \sum y_i} = \theta^y (1 - \theta)^{n - y}. \]

Questa è proprio la verosimiglianza della distribuzione binomiale! Questo mostra che il caso binomiale può essere visto come una forma compatta di verosimiglianza congiunta per prove Bernoulliane indipendenti.

42.6.2 Perché è Importante la Verosimiglianza Congiunta?

L’idea della verosimiglianza congiunta è fondamentale perché ci permette di estendere i concetti di verosimiglianza dal caso di una singola osservazione al caso di molte osservazioni indipendenti. Questo è utile in molti contesti statistici:

1. stimare parametri basandosi su un intero campione invece che su una singola osservazione;
2. definire modelli statistici più complessi, in cui le osservazioni sono indipendenti ma possono avere diverse distribuzioni.

In sintesi, l’esempio binomiale mostra che la verosimiglianza congiunta di prove Bernoulliane indipendenti si riconduce alla verosimiglianza binomiale. Tuttavia, la vera potenza della verosimiglianza congiunta si manifesta in distribuzioni continue come la normale, dove la produttoria delle densità di probabilità per singole osservazioni è chiaramente distinta dalla funzione di verosimiglianza per il campione intero.

La chiave per comprendere il concetto è rendersi conto che la verosimiglianza di un’intera sequenza di prove indipendenti è il prodotto delle singole verosimiglianze.

42.6.3 Esempio: Osservazioni Raggruppate

Per illustrare il concetto di verosimiglianza congiunta nel caso della distribuzione binomiale, consideriamo quattro gruppi distinti di osservazioni binomiali indipendenti:

• gruppo 1: 23 successi su 30 prove,
• gruppo 2: 20 successi su 28 prove,
• gruppo 3: 29 successi su 40 prove,
• gruppo 4: 29 successi su 36 prove.

Poiché ogni gruppo segue una distribuzione binomiale indipendente con lo stesso parametro \(\theta\), la log-verosimiglianza congiunta si ottiene sommando le log-verosimiglianze di ciascun gruppo:

\[ \log \mathcal{L}(\theta) = \sum_{i=1}^{4} \left[ y_i \log(\theta) + (n_i - y_i) \log(1 - \theta) \right], \]

dove:

• \(n_i\) è il numero totale di prove nel gruppo \(i\),
• \(y_i\) è il numero di successi nel gruppo \(i\).

Sostituendo i valori specifici:

\[ \begin{aligned} \log \mathcal{L}(\theta) &= [23\log(\theta) + (30-23)\log(1 - \theta)] \\ &\quad + [20\log(\theta) + (28-20)\log(1 - \theta)] \\ &\quad + [29\log(\theta) + (40-29)\log(1 - \theta)] \\ &\quad + [29\log(\theta) + (36-29)\log(1 - \theta)]. \end{aligned} \]

Questa formula ci permette di calcolare quanto è plausibile il valore del parametro \(\theta\), tenendo conto simultaneamente di tutte le osservazioni nei quattro gruppi.

42.6.4 Implementazione in R

Supponiamo di avere i dati di quattro gruppi indipendenti, e vogliamo trovare la stima del parametro \(\theta\) che massimizza la log-verosimiglianza congiunta. Procederemo passo dopo passo.

1. Definire una funzione per la log-verosimiglianza congiunta.

Questa funzione riceve un valore di \(\theta\) e una lista di gruppi. Ogni gruppo contiene il numero totale di prove e il numero di successi. La funzione calcola la somma delle log-verosimiglianze per ciascun gruppo.

# Funzione che calcola la log-verosimiglianza congiunta
log_verosimiglianza_congiunta <- function(theta, dati) {
  # Limitiamo theta per evitare log(0)
  if (theta <= 0) theta <- 1e-10
  if (theta >= 1) theta <- 1 - 1e-10

  # Inizializziamo il totale
  somma_loglik <- 0

  # Per ogni gruppo, calcoliamo il contributo alla log-verosimiglianza
  for (i in 1:length(dati)) {
    gruppo <- dati[[i]]   # Estrae il gruppo i-esimo
    n <- gruppo[1]        # Numero totale di prove
    y <- gruppo[2]        # Numero di successi

    # Aggiunge il contributo del gruppo alla somma totale
    somma_loglik <- somma_loglik + y * log(theta) + (n - y) * log(1 - theta)
  }

  # Restituiamo il valore negativo (perché optim() cerca minimi)
  return(-somma_loglik)
}

2. Inserire i dati.

Qui definiamo i dati per ciascun gruppo come coppie (numero di prove, numero di successi):

# Dati osservati per ciascun gruppo
dati_gruppi <- list(
  c(30, 23),
  c(28, 20),
  c(40, 29),
  c(36, 29)
)

3. Trovare la stima di θ che massimizza la verosimiglianza.

Usiamo optim() per trovare numericamente il valore di \(\theta\) che minimizza il valore negativo della log-verosimiglianza, ovvero che massimizza la log-verosimiglianza.

# Ricerca del valore ottimale di theta
result <- optim(
  par = 0.5,                            # Valore iniziale
  fn = log_verosimiglianza_congiunta,  # Funzione da minimizzare
  dati = dati_gruppi,                  # Passiamo i dati
  method = "L-BFGS-B",                 # Metodo con vincoli
  lower = 0, upper = 1                 # Vincoli: theta tra 0 e 1
)

# Stima ottimale trovata
result$par
#> [1] 0.7537

4. Visualizzare la log-verosimiglianza.

Costruiamo ora un grafico che mostri come varia la log-verosimiglianza al variare di \(\theta\).

# Valori di theta da esplorare
theta_values <- seq(0.01, 0.99, length.out = 100)

# Vettore per salvare i valori di log-verosimiglianza
log_likelihood_values <- numeric(length(theta_values))

# Calcoliamo il valore della funzione per ogni valore di theta
for (i in 1:length(theta_values)) {
  t <- theta_values[i]
  log_likelihood_values[i] <- log_verosimiglianza_congiunta(t, dati_gruppi)
}

Ora costruiamo il grafico:

ggplot(
  data.frame(theta = theta_values, log_likelihood = log_likelihood_values),
  aes(x = theta, y = log_likelihood)
) +
  geom_line(color = "blue", linewidth = 1.2) +
  labs(
    title = "Funzione di Log-Verosimiglianza Congiunta",
    x = expression(theta),
    y = "Log-verosimiglianza negativa"
  )

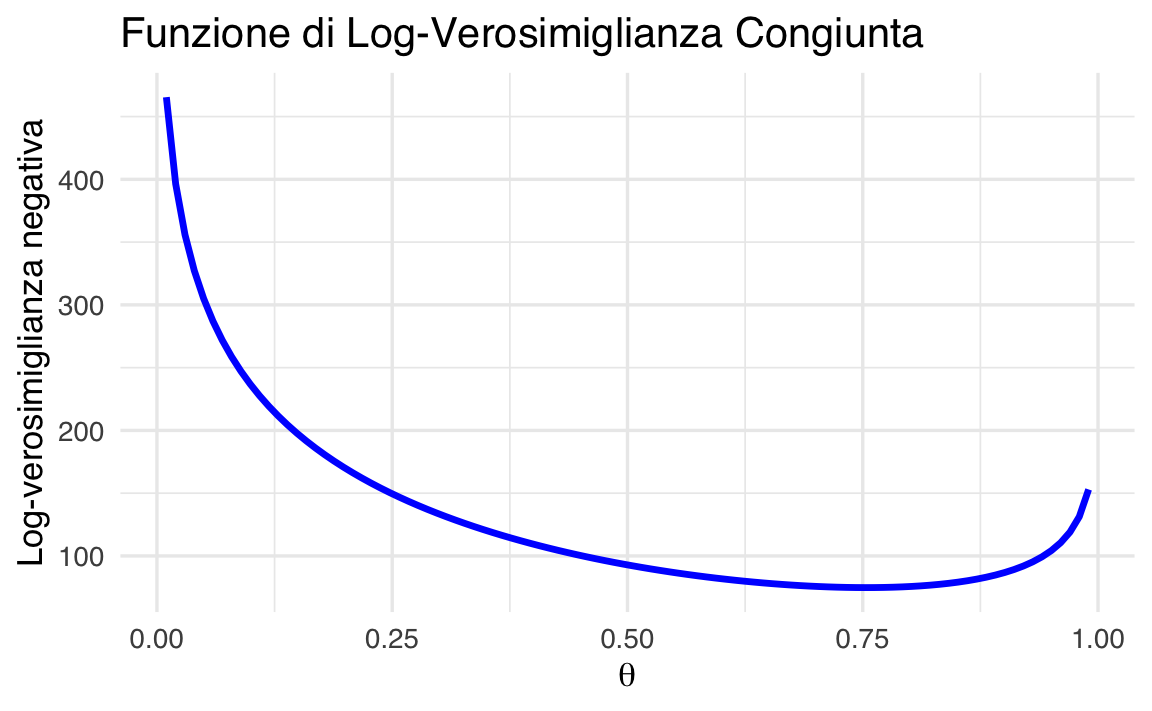
Con questo esempio abbiamo visto che:

• la log-verosimiglianza congiunta si ottiene sommando le log-verosimiglianze dei singoli gruppi;
• è possibile trovare la stima ottimale di \(\theta\) numericamente, senza formule complicate;
• il grafico della log-verosimiglianza ci aiuta a visualizzare il punto in cui il modello è più compatibile con i dati.

Questo approccio — basato sull’uso della verosimiglianza e della sua somma tra gruppi indipendenti — sarà anche la base per il passaggio all’inferenza bayesiana, dove aggiungeremo una distribuzione a priori per ottenere una distribuzione a posteriori di \(\theta\).

42.7 La Verosimiglianza Marginale

La verosimiglianza marginale è un concetto fondamentale nell’inferenza bayesiana, utilizzato per valutare quanto un modello sia compatibile con i dati osservati, tenendo conto dell’incertezza sui parametri.

A differenza della verosimiglianza standard, che misura la plausibilità dei dati per un valore fisso del parametro, la verosimiglianza marginale considera tutti i possibili valori del parametro, pesandoli in base alla loro probabilità a priori. Questo approccio permette di integrare l’incertezza nella valutazione del modello.

42.7.1 Caso con Parametri Discreti

Per comprendere meglio il concetto, consideriamo un esperimento in cui eseguiamo 10 tentativi e otteniamo 7 successi. Supponiamo che la probabilità di successo \(\theta\) possa assumere solo tre valori discreti:

\[ \theta \in \{0.1, 0.5, 0.9\}. \]

Per calcolare la verosimiglianza marginale, dobbiamo:

1. Assegnare una probabilità a priori a ciascun valore di \(\theta\), ad esempio:

   • Distribuzione uniforme: \[ p(\theta = 0.1) = p(\theta = 0.5) = p(\theta = 0.9) = \frac{1}{3}. \]
   • Distribuzione non uniforme (ad esempio, dando più peso a \(\theta = 0.5\)): \[ p(\theta = 0.1) = \frac{1}{4}, \quad p(\theta = 0.5) = \frac{1}{2}, \quad p(\theta = 0.9) = \frac{1}{4}. \]

2. Calcolare la probabilità di osservare 7 successi su 10 prove per ogni valore di \(\theta\):

   \[ p(k=7 \mid \theta) = \binom{10}{7} \theta^7 (1 - \theta)^3. \]

3. Moltiplicare ciascuna di queste probabilità per la corrispondente probabilità a priori e sommare i risultati:

   \[ p(k=7 \mid n=10) = \sum_{i} p(k=7 \mid \theta_i) p(\theta_i). \]

Sostituendo i valori per la distribuzione uniforme:

\[ p(k=7 \mid n=10) = \binom{10}{7} 0.1^7 (0.9)^3 \cdot \frac{1}{3} + \binom{10}{7} 0.5^7 (0.5)^3 \cdot \frac{1}{3} + \binom{10}{7} 0.9^7 (0.1)^3 \cdot \frac{1}{3}. \]

Questa somma rappresenta la verosimiglianza marginale, ossia la probabilità di ottenere 7 successi su 10, considerando tutte le possibili incertezze su \(\theta\).

42.7.2 Caso con Parametri Continui

Nella maggior parte delle situazioni, il parametro \(\theta\) non assume solo pochi valori discreti, ma può variare continuamente in un intervallo (ad esempio, tra 0 e 1). In questo caso, invece di sommare, dobbiamo integrare:

\[ p(k=7 \mid n=10) = \int_{0}^{1} \binom{10}{7} \theta^7 (1 - \theta)^3 p(\theta) \, d\theta. \]

Qui:

• \(p(\theta)\) è la distribuzione a priori di \(\theta\).
• L’integrale rappresenta una media ponderata della probabilità di ottenere i dati, considerando tutti i valori di \(\theta\).

Ad esempio, se \(\theta \sim \text{Beta}(2,2)\), la verosimiglianza marginale diventa:

\[ p(k=7 \mid n=10) = \int_{0}^{1} \binom{10}{7} \theta^7 (1 - \theta)^3 \frac{\theta (1-\theta)}{B(2,2)} \, d\theta. \]

Questo tipo di calcolo viene spesso risolto numericamente.

42.7.3 Calcolo Numerico della Verosimiglianza Marginale in R

Se vogliamo calcolare la verosimiglianza marginale numericamente, possiamo usare l’integrazione numerica in R.

Caso con Parametri Discreti.

# Definiamo i valori possibili di theta e le probabilità a priori
theta_vals <- c(0.1, 0.5, 0.9)
prior_probs <- c(1/3, 1/3, 1/3)  # Distribuzione uniforme

# Calcoliamo la verosimiglianza per ciascun valore di theta
likelihoods <- dbinom(7, size = 10, prob = theta_vals)

# Calcoliamo la verosimiglianza marginale sommando i contributi ponderati
marginal_likelihood <- sum(likelihoods * prior_probs)
print(marginal_likelihood)
#> [1] 0.0582

Caso con Parametri Continui.

# Definiamo la funzione di verosimiglianza pesata dalla prior
integrand <- function(theta) {
  dbinom(7, size = 10, prob = theta) * dbeta(theta, shape1 = 2, shape2 = 2)
}

# Eseguiamo l'integrazione numerica
marginal_likelihood <- integrate(integrand, lower = 0, upper = 1)$value
print(marginal_likelihood)
#> [1] 0.1119

42.7.4 Interpretazione della Verosimiglianza Marginale

La verosimiglianza marginale rappresenta la probabilità complessiva dei dati, tenendo conto di tutte le possibili incertezze sul parametro \(\theta\).

• Se la verosimiglianza marginale è alta, significa che il modello nel suo insieme è compatibile con i dati osservati.
• Se la verosimiglianza marginale è bassa, significa che, indipendentemente dal valore di \(\theta\), il modello non spiega bene i dati.

A differenza della verosimiglianza classica, che valuta quanto siano probabili i dati per un singolo valore di \(\theta\), la verosimiglianza marginale considera tutte le possibili ipotesi sul parametro.

42.7.5 Ruolo nella Statistica Bayesiana

La verosimiglianza marginale svolge un ruolo cruciale nell’inferenza bayesiana perché appare nella formula di Bayes:

\[ p(\theta \mid D) = \frac{p(D \mid \theta) p(\theta)}{p(D)}, \]

dove \(p(D)\) è la verosimiglianza marginale. Questa quantità:

1. serve da fattore di normalizzazione per la distribuzione a posteriori \(p(\theta \mid D)\);

2. permette di confrontare modelli diversi, attraverso il fattore di Bayes:

   \[ BF = \frac{p(D \mid M_1)}{p(D \mid M_2)}, \]

   dove \(M_1\) e \(M_2\) sono due modelli diversi.

In conclusione, la verosimiglianza marginale è un concetto chiave nell’inferenza bayesiana, che ci permette di valutare quanto un modello sia coerente con i dati, tenendo conto di tutte le possibili incertezze sui parametri:

• per parametri discreti, si calcola come una somma ponderata;
• per parametri continui, si calcola con un integrale;
• è essenziale per il calcolo della distribuzione a posteriori e per il confronto tra modelli.

42.8 Verosimiglianza Gaussiana

La distribuzione gaussiana (o distribuzione normale) è una delle distribuzioni più utilizzate in statistica perché descrive molti fenomeni naturali e psicologici. In questo capitolo esploreremo come si calcola la verosimiglianza, ovvero la plausibilità dei parametri, nel caso della distribuzione normale.

42.8.1 Caso di una Singola Osservazione

Immaginiamo di misurare il Quoziente Intellettivo (QI) di una persona e ottenere un valore specifico, ad esempio 114. Assumiamo che il QI segua una distribuzione normale con media \(\mu\) sconosciuta e deviazione standard \(\sigma\) nota (ad esempio \(\sigma = 15\)).

La funzione di densità di probabilità per una distribuzione normale è:

\[ f(y \mid \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(y-\mu)^2}{2\sigma^2}\right) , \]

dove:

• \(y\) è il valore osservato,
• \(\mu\) è la media (il parametro che vogliamo stimare),
• \(\sigma\) è la deviazione standard (conosciuta).

La verosimiglianza misura quanto diversi valori di \(\mu\) sono plausibili, dato il valore osservato (114).

Esempio pratico in R:

# Dati iniziali
y_obs <- 114
sigma <- 15
mu_values <- seq(70, 160, length.out = 1000)

# Calcolo della verosimiglianza
likelihood <- dnorm(y_obs, mean = mu_values, sd = sigma)

# Grafico della verosimiglianza
ggplot(data.frame(mu = mu_values, likelihood = likelihood), aes(x = mu, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  labs(
    title = "Verosimiglianza per un singolo valore di QI (114)",
    x = "Media (μ)",
    y = "Verosimiglianza"
  )

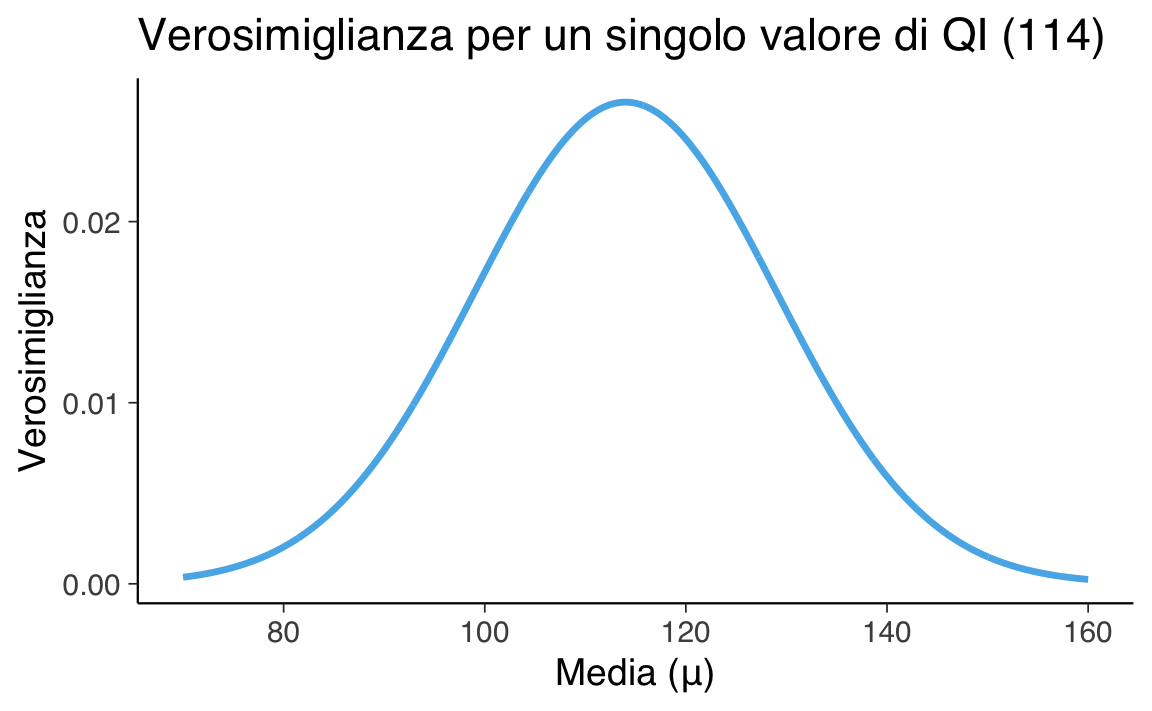
Qual è il valore migliore per \(\mu\)?

Il valore migliore di \(\mu\) sarà quello che rende massima la verosimiglianza. In questo semplice caso, è esattamente il valore osservato (114):

mu_ottimale <- mu_values[which.max(likelihood)]
cat("Il valore ottimale di μ è:", mu_ottimale)
#> Il valore ottimale di μ è: 114

42.8.2 Log-Verosimiglianza

Spesso, per semplicità di calcolo, si usa la log-verosimiglianza, che trasforma i prodotti in somme, rendendo i calcoli più semplici e stabili:

\[ \log L(\mu \mid y, \sigma) = -\frac{1}{2}\log(2\pi) - \log(\sigma) - \frac{(y-\mu)^2}{2\sigma^2}. \]

Calcolo pratico con R:

# Funzione di log-verosimiglianza negativa usando dnorm()
negative_log_likelihood <- function(mu, y, sigma) {
  # Ritorniamo il valore negativo della log-verosimiglianza
  -dnorm(y, mean = mu, sd = sigma, log = TRUE)
}

result <- optim(
  par = 100, # Valore iniziale
  fn = negative_log_likelihood,
  y = y_obs,
  sigma = sigma,
  method = "L-BFGS-B",
  lower = 70,
  upper = 160
)

mu_max_loglik <- result$par
cat("Il valore ottimale di μ dalla log-verosimiglianza è:", mu_max_loglik)
#> Il valore ottimale di μ dalla log-verosimiglianza è: 114

In questo caso, otteniamo nuovamente \(\mu = 114\).

42.8.3 Campione di Osservazioni Indipendenti

Supponiamo di aver raccolto i punteggi alla scala BDI-II per 30 persone. Ciascun punteggio è un’osservazione indipendente da una distribuzione normale con media incognita \(\mu\) e deviazione standard nota \(\sigma = 6.5\).

# Dati osservati (punteggi BDI-II)
y <- c(
  26, 35, 30, 25, 44, 30, 33, 43, 22, 43, 24, 19, 39, 31, 25, 
  28, 35, 30, 26, 31, 41, 36, 26, 35, 33, 28, 27, 34, 27, 22
)

sigma <- 6.5

42.8.4 Calcolo della Log-Verosimiglianza

Definiamo una funzione che calcola la log-verosimiglianza totale:

log_likelihood <- function(mu, y, sigma) {
  sum(dnorm(y, mean = mu, sd = sigma, log = TRUE))
}

Esploriamo ora un intervallo di valori plausibili per \(\mu\) e calcoliamo la log-verosimiglianza per ciascun valore:

# Intervallo di valori possibili per μ
mu_range <- seq(mean(y) - 2 * sigma, mean(y) + 2 * sigma, length.out = 1000)

# Inizializza vettore dei risultati
log_lik_values <- numeric(length(mu_range))

# Ciclo esplicito per chiarezza didattica
for (i in seq_along(mu_range)) {
  mu_val <- mu_range[i]
  log_lik_values[i] <- log_likelihood(mu_val, y, sigma)
}

42.8.5 Visualizzazione della Log-Verosimiglianza

ggplot(
  data.frame(mu = mu_range, log_likelihood = log_lik_values),
  aes(x = mu, y = log_likelihood)
) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  geom_vline(xintercept = mean(y), linetype = "dashed", color = "red") +
  labs(
    title = "Log-verosimiglianza per punteggi BDI-II",
    x = expression(mu),
    y = "Log-verosimiglianza"
  )

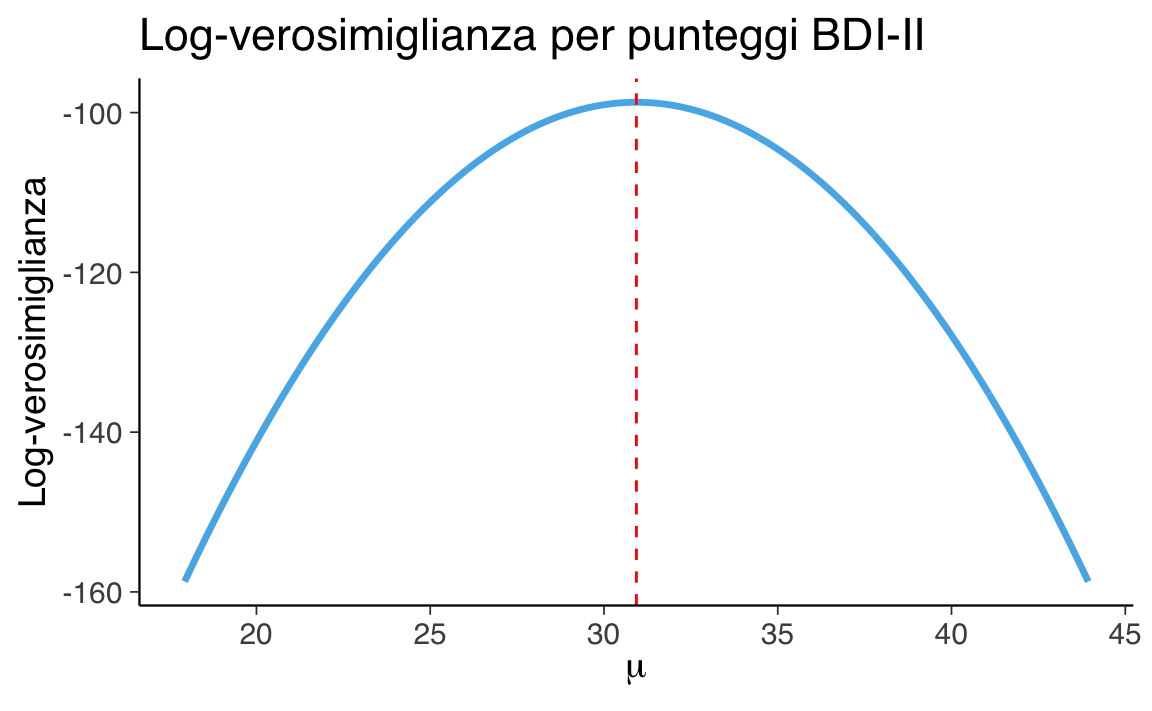
La linea tratteggiata rossa indica la media campionaria, che — come ci aspettiamo — è anche il valore che massimizza la log-verosimiglianza.

42.8.6 Ottimizzazione Numerica

Se volessimo calcolare il valore ottimale di \(\mu\) in modo automatico:

# Funzione negativa da minimizzare
negative_log_likelihood <- function(mu, y, sigma) {
  -sum(dnorm(y, mean = mu, sd = sigma, log = TRUE))
}

# Ottimizzazione con limiti
result <- optim(
  par = mean(y),                   # Valore iniziale
  fn = negative_log_likelihood,   # Funzione da minimizzare
  y = y,
  sigma = sigma,
  method = "L-BFGS-B",
  lower = min(mu_range),
  upper = max(mu_range)
)

mu_optimal <- result$par
cat("Il valore ottimale di μ è:", mu_optimal)
#> Il valore ottimale di μ è: 30.93

• Abbiamo utilizzato dnorm(..., log = TRUE) per calcolare in modo semplice e numericamente stabile la log-verosimiglianza.
• Il valore di \(\mu\) che massimizza la log-verosimiglianza corrisponde alla media campionaria.
• Questo è un caso in cui la stima di massima verosimiglianza ha una forma chiusa, ma l’approccio numerico resta utile e generalizzabile.

42.9 Il rapporto di verosimiglianze

Quando conduciamo un’analisi statistica, spesso ci troviamo di fronte alla necessità di confrontare due modelli che cercano di spiegare gli stessi dati. Immaginiamo, ad esempio, di voler capire qual è la media di una certa variabile (come il punteggio a un test, il tempo di reazione, ecc.). Potremmo avere due ipotesi alternative sull’effettivo valore della media:

• secondo un primo modello, la media è \(\mu_1\) (ad esempio, l’ipotesi “nulla”, che rappresenta uno stato di riferimento o di assenza di effetto),
• secondo un secondo modello, la media è \(\mu_2\) (ad esempio, l’ipotesi “alternativa”, che rappresenta un cambiamento o un effetto).

Per decidere quale modello è più compatibile con i dati osservati, possiamo usare la verosimiglianza (likelihood). La verosimiglianza misura quanto bene un certo valore del parametro spiega i dati osservati. Più la verosimiglianza è alta, più i dati sono “coerenti” con quel valore.

42.9.1 Il confronto

Per confrontare i due modelli, calcoliamo la verosimiglianza dei dati in ciascun caso, e ne facciamo il rapporto:

\[ \lambda = \frac{L(\mu_2 \mid \text{dati})}{L(\mu_1 \mid \text{dati})} \tag{42.1}\]

dove:

• \(L(\mu_2 \mid \text{dati})\) è la verosimiglianza del modello alternativo (cioè, quanto sono compatibili i dati con \(\mu_2\)),
• \(L(\mu_1 \mid \text{dati})\) è la verosimiglianza del modello nullo (cioè, quanto sono compatibili i dati con \(\mu_1\)).

Questa quantità si chiama rapporto di verosimiglianze (likelihood ratio, LR), e rappresenta uno strumento per quantificare quanto i dati favoriscono un modello rispetto all’altro.

42.9.2 Come si interpreta \(\lambda\)?

• Se \(\lambda > 1\), significa che i dati supportano più il modello alternativo: i dati sono più probabili sotto \(\mu_2\) che sotto \(\mu_1\).
• Se \(\lambda < 1\), significa che i dati supportano più il modello nullo: i dati sono più probabili sotto \(\mu_1\) che sotto \(\mu_2\).
• Se \(\lambda \approx 1\), allora i dati non permettono di distinguere chiaramente tra i due modelli.

Il rapporto di verosimiglianze ci dice quale modello rende i dati osservati più “plausibili”.

42.9.3 Un Esempio

Immagina di aver lanciato una moneta 10 volte e di aver ottenuto 7 teste. Ti chiedi ora quale tra questi due modelli spiega meglio i dati:

• Modello 1 (nullo): la moneta è equa, quindi la probabilità di testa è \(\mu_1 = 0.5\);
• Modello 2 (alternativo): la moneta è truccata a favore delle teste, e la probabilità di testa è \(\mu_2 = 0.7\).

42.9.4 Calcolo delle verosimiglianze

Useremo la distribuzione binomiale, che descrive il numero di successi (in questo caso, teste) in un numero fisso di prove (10 lanci), dato un certo valore di probabilità.

La verosimiglianza è semplicemente la probabilità di ottenere 7 teste su 10 lanci, sotto ciascun modello:

• sotto il modello nullo (\(\mu_1 = 0.5\)):

  \[ L(0.5 \mid \text{7 teste}) = \binom{10}{7} (0.5)^7 (1 - 0.5)^3 = 120 \cdot (0.5)^{10} \approx 0.117 \]

• sotto il modello alternativo (\(\mu_2 = 0.7\)):

  \[ L(0.7 \mid \text{7 teste}) = \binom{10}{7} (0.7)^7 (0.3)^3 \approx 120 \cdot 0.0824 \cdot 0.027 = 0.267 \]

42.9.5 Calcolo del rapporto di verosimiglianze

Ora possiamo calcolare il rapporto:

\[ \lambda = \frac{L(0.7 \mid \text{7 teste})}{L(0.5 \mid \text{7 teste})} \approx \frac{0.267}{0.117} \approx 2.28 \]

Questo significa che i dati sono circa 2.3 volte più compatibili con l’ipotesi che la moneta sia truccata (con \(\mu = 0.7\)) rispetto a quella che sia equa (\(\mu = 0.5\)).

42.9.6 Visualizzare le funzioni di verosimiglianza

Possiamo visualizzare graficamente come cambia la verosimiglianza al variare della probabilità di testa (\(\theta\)), mantenendo fisso il numero di lanci e il numero di teste osservate.

42.9.6.1 Codice R

# Parametri osservati
n <- 10        # numero totale di lanci
x <- 7         # numero di teste osservate

# Sequenza di probabilità (theta)
theta <- seq(0, 1, length.out = 100)

# Verosimiglianza per ogni theta
likelihood <- dbinom(x, size = n, prob = theta)

# Crea dataframe per ggplot
df <- data.frame(theta = theta, likelihood = likelihood)

# Verosimiglianza nei due modelli
L_0.5 <- dbinom(x, size = n, prob = 0.5)
L_0.7 <- dbinom(x, size = n, prob = 0.7)
LR <- L_0.7 / L_0.5

# Crea grafico
ggplot(df, aes(x = theta, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  geom_vline(xintercept = 0.5, linetype = "dashed", color = "red") +
  geom_vline(xintercept = 0.7, linetype = "dashed", color = "darkgreen") +
  geom_point(aes(x = 0.5, y = L_0.5), color = "red", size = 3) +
  geom_point(aes(x = 0.7, y = L_0.7), color = "darkgreen", size = 3) +
  labs(
    title = "Funzione di verosimiglianza per 7 teste su 10 lanci",
    x = expression(theta),
    y = "Verosimiglianza"
  ) +
  annotate(
    "text", x = 0.5, y = L_0.5 + 0.01, 
    label = "mu == 0.5", 
    parse = TRUE, hjust = -0.2, color = "red"
  ) +
  annotate(
    "text", x = 0.7, y = L_0.7 + 0.01, 
    label = "mu == 0.7", parse = TRUE, hjust = -0.2, color = "darkgreen")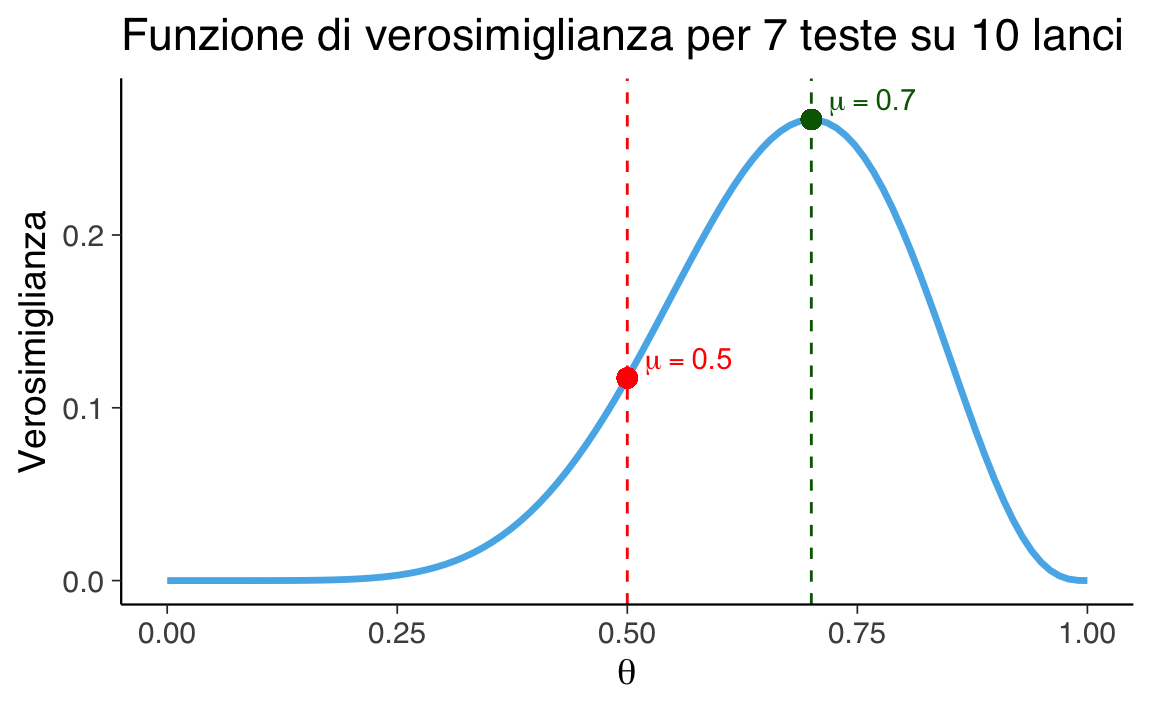

# Stampa dei risultati numerici
cat("L(mu = 0.5) =", round(L_0.5, 3), "\n")
#> L(mu = 0.5) = 0.117
cat("L(mu = 0.7) =", round(L_0.7, 3), "\n")
#> L(mu = 0.7) = 0.267
cat("Likelihood Ratio =", round(LR, 2), "\n")
#> Likelihood Ratio = 2.28

Il grafico mostra come cambia la verosimiglianza al variare di \(\theta\), e indica visivamente i valori assunti nei due modelli specifici. Si vede chiaramente che \(\theta = 0.7\) è più compatibile con l’osservazione di 7 teste.

In sintesi, il rapporto di verosimiglianze è uno strumento per confrontare due ipotesi. Non richiede che una delle due sia vera, ma solo di confrontare quanto bene ciascuna spiega i dati osservati. In questo esempio, i dati favoriscono l’ipotesi che la moneta sia truccata, ma non in modo schiacciante. Il valore di \(\lambda = 2.28\) indica un’evidenza moderata a favore del modello alternativo.

42.9.7 Rapporti di Verosimiglianza Aggiustati e Criterio di Akaike

Spesso il rapporto di verosimiglianza “grezzo” (\(\lambda\)) deve essere aggiustato per tenere conto della differenza nel numero di parametri tra i modelli confrontati. Infatti, quando confrontiamo due modelli, quello con più parametri tende quasi sempre a descrivere meglio i dati osservati, ma ciò può essere dovuto semplicemente alla sua maggiore complessità. Questo fenomeno è noto come sovradattamento (overfitting).

Per correggere questa tendenza, si usa un rapporto di verosimiglianza aggiustato (Adjusted Likelihood Ratio, indicato con \(\lambda_{\text{adj}}\). Questo tipo di aggiustamento penalizza i modelli più complessi, rendendo il confronto tra modelli più equo e affidabile.

42.9.8 Relazione con il Criterio di Akaike (AIC)

Una modalità comune per effettuare questa correzione è tramite il Criterio di Akaike (AIC). L’AIC è definito come:

\[ \text{AIC} = 2k - 2\log(\lambda), \tag{42.2}\]

in cui:

• \(k\) è il numero dei parametri del modello.
• \(\lambda\) è il rapporto di verosimiglianza grezzo.

Da questa equazione possiamo ricavare una formula per calcolare il rapporto di verosimiglianza aggiustato utilizzando l’AIC:

\[ \lambda_{\text{adj}} = \lambda \times e^{(k_1 - k_2)}, \]

dove:

• \(k_1\) è il numero di parametri del modello più semplice,
• \(k_2\) è il numero di parametri del modello più complesso,
• \(e^{(k_1 - k_2)}\) è il fattore correttivo che penalizza il modello più complesso.

In breve, più parametri ha un modello, maggiore sarà la penalizzazione applicata.

42.9.9 Rapporto tra Likelihood Ratio e AIC

Il rapporto di verosimiglianza aggiustato tramite l’AIC consente di confrontare in modo equo modelli con un numero differente di parametri. Senza questa correzione, rischieremmo di scegliere sempre modelli più complessi, indipendentemente dalla loro reale capacità esplicativa, con il rischio di sovrastimare la qualità della loro spiegazione.

Utilizzare il rapporto di verosimiglianza aggiustato, quindi, permette di scegliere il modello migliore considerando sia la capacità di adattarsi ai dati, sia la semplicità del modello stesso.

42.9.10 Illustrazione

Immaginiamo un semplice esperimento psicologico sulla memoria visiva. Vogliamo capire se mostrare immagini emotivamente intense aiuta le persone a ricordare meglio, rispetto a immagini neutre.

Abbiamo due gruppi di partecipanti:

• il gruppo neutro vede 30 immagini neutre e ne ricorda correttamente 14;
• il gruppo emozionale vede 30 immagini emotivamente intense e ne ricorda 22.

42.9.11 Obiettivo

Vogliamo confrontare due modelli alternativi:

• modello nullo (H₀): la probabilità di ricordare un’immagine è uguale nei due gruppi;
• modello alternativo (H₁): la probabilità di ricordare è diversa nei due gruppi.

42.9.12 Dati osservati

successi_neutro <- 14
successi_emozione <- 22
prove <- 30

42.9.13 1. Calcolo della Verosimiglianza

Ipotesi nulla: probabilità comune.

Se la probabilità è la stessa in entrambi i gruppi, possiamo stimarla combinando i successi totali:

p_null <- (successi_neutro + successi_emozione) / (2 * prove)

Log-verosimiglianza sotto H₀.

Sotto l’ipotesi nulla, i dati di entrambi i gruppi devono essere spiegati da una sola probabilità:

ll_null <- dbinom(successi_neutro, prove, p_null, log = TRUE) + 
           dbinom(successi_emozione, prove, p_null, log = TRUE)

Ipotesi alternativa: probabilità diversa per ogni gruppo.

Stimiamo separatamente la probabilità di ricordare in ciascun gruppo:

p_neutro <- successi_neutro / prove
p_emozione <- successi_emozione / prove

Log-verosimiglianza sotto H₁.

Ogni gruppo ha la propria verosimiglianza:

ll_alt <- dbinom(successi_neutro, prove, p_neutro, log = TRUE) + 
          dbinom(successi_emozione, prove, p_emozione, log = TRUE)

42.9.14 2. Confronto tra Modelli

Rapporto di verosimiglianza (non penalizzato).

Calcoliamo il rapporto tra le due verosimiglianze:

lr <- exp(ll_alt - ll_null)

Questo ci dice quanto meglio il modello alternativo spiega i dati rispetto al modello nullo.

42.9.15 3. Penalizzazione per la Complessità

I modelli più complessi tendono a spiegare meglio i dati, ma rischiano di adattarsi troppo. Per questo, usiamo un criterio che penalizza la complessità: l’AIC (Akaike Information Criterion).

Numero di parametri:

k_null <- 1  # un'unica probabilità per entrambi i gruppi
k_alt <- 2   # probabilità distinte per ciascun gruppo

Calcolo dell’AIC per ciascun modello:

AIC_null <- 2 * k_null - 2 * ll_null
AIC_alt <- 2 * k_alt - 2 * ll_alt

Rapporto di verosimiglianza aggiustato.

Usiamo l’AIC per calcolare una versione penalizzata del rapporto di verosimiglianze:

lr_adj <- exp((AIC_null - AIC_alt) / 2)

Risultati:

cat("Rapporto di verosimiglianza grezzo:", round(lr, 2), "\n")
#> Rapporto di verosimiglianza grezzo: 9.54
cat("Rapporto di verosimiglianza aggiustato (λ_adj):", round(lr_adj, 2), "\n")
#> Rapporto di verosimiglianza aggiustato (λ_adj): 3.51

Interpretazione:

• se λ_adj > 1, i dati sono più compatibili con il modello alternativo (due probabilità distinte);
• se λ_adj ≈ 1, non c’è abbastanza evidenza per preferire un modello all’altro.

42.9.16 4. Test del Rapporto di Verosimiglianza

Possiamo testare formalmente se la differenza tra i modelli è rilevante o potrebbe essere dovuta al caso.

La statistica test è:

\[ -2 \cdot (\log L_{H_0} - \log L_{H_1}) \]

Questa statistica segue (approssimativamente) una distribuzione chi-quadrato con un numero di gradi di libertà pari alla differenza nel numero di parametri tra i modelli:

LR_test <- -2 * (ll_null - ll_alt)
df <- k_alt - k_null
p_value <- 1 - pchisq(LR_test, df)

cat("Statistica test (-2 log LR):", round(LR_test, 2), "\n")
#> Statistica test (-2 log LR): 4.51
cat("Gradi di libertà:", df, "\n")
#> Gradi di libertà: 1
cat("Valore p del test:", round(p_value, 4), "\n")
#> Valore p del test: 0.0337

In sintesi,

• se p < 0.05, possiamo concludere che il modello alternativo è da preferire: i dati sono difficilmente compatibili con l’ipotesi di probabilità uguali nei due gruppi;
• se p > 0.05, non abbiamo evidenza sufficiente per preferire il modello alternativo.

Nel nostro esempio:

• la statistica test è ≈ 4.48;
• il valore-p è ≈ 0.0337.

👉 Poiché il valore-p è inferiore a 0.05, possiamo concludere che il gruppo emozionale ha una probabilità di ricordare credibilmente diversa da quella del gruppo neutro.

42.10 Riflessioni Conclusive

La funzione di verosimiglianza costituisce il fulcro dell’inferenza statistica, permettendo di quantificare la plausibilità dei parametri di un modello alla luce dei dati osservati. La sua costruzione poggia su tre elementi fondamentali: la scelta del modello generatore dei dati, lo spazio dei parametri e le evidenze empiriche.

Nel caso di modelli binomiali e gaussiani, la verosimiglianza assume forme analiticamente maneggevoli, facilitando sia la stima puntuale che la valutazione di ipotesi. In particolare:
- Per la distribuzione normale, la stima di massima verosimiglianza di () coincide con la media campionaria, mentre la sua rappresentazione grafica offre una chiara indicazione della precisione della stima.
- L’uso della log-verosimiglianza non solo semplifica i calcoli, ma migliora anche la stabilità numerica, specialmente in contesti con campioni di grandi dimensioni.
- Il rapporto di verosimiglianza emerge come strumento versatile, capace di coniugare bontà di adattamento e parsimonia, come dimostrato da criteri quali l’AIC.

Questi strumenti non sono meri artifici tecnici, ma rappresentano un linguaggio comune per confrontare modelli e interpretare risultati in modo rigoroso. La loro corretta applicazione richiede tuttavia una comprensione approfondita delle assunzioni sottostanti, affinché le conclusioni tratte riflettano fedelmente la realtà dei dati.

In definitiva, la verosimiglianza – nelle sue diverse forme – rimane una guida indispensabile per navigare il complesso rapporto tra teoria e osservazione, offrendo un equilibrio tra flessibilità metodologica e robustezza inferenziale.

Esercizi

Problemi

Spiega ciascuno dei concetti seguenti con una frase:

• probabilità.
• funzione di massa di probabilità.
• funzione di densità di probabilità.
• distribuzione di probabilità.
• distribuzione di probabilità discreta.
• distribuzione di probabilità continua.
• funzione di distribuzione cumulativa (cdf).
• verosimiglianza

Problemi

Supponi di aver misurato il livello di ansia (ad esempio usando una scala standardizzata) in un campione di 15 persone con i seguenti punteggi:

ansia <- c(23, 27, 30, 29, 25, 28, 26, 24, 31, 29, 27, 26, 28, 30, 25)

Assumendo che la deviazione standard sia nota e pari a 3.5, svolgi le seguenti attività in R:

1. Calcola la funzione di verosimiglianza gaussiana per diversi valori di \(\mu\) nell’intervallo da 20 a 35.
2. Trova numericamente il valore di \(\mu\) che rende massima la verosimiglianza (stima di massima verosimiglianza, MLE).
3. Disegna un grafico della funzione di verosimiglianza per visualizzare il risultato.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] thematic_0.1.7   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [5] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.13.0 psych_2.5.3     
#>  [9] scales_1.4.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [13] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [17] readr_2.1.5      tidyr_1.3.1      tibble_3.3.0     ggplot2_3.5.2   
#> [21] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] generics_0.1.4     stringi_1.8.7      lattice_0.22-7    
#>  [4] hms_1.1.3          digest_0.6.37      magrittr_2.0.3    
#>  [7] evaluate_1.0.4     grid_4.5.0         timechange_0.3.0  
#> [10] RColorBrewer_1.1-3 fastmap_1.2.0      rprojroot_2.0.4   
#> [13] jsonlite_2.0.0     mnormt_2.1.1       cli_3.6.5         
#> [16] rlang_1.1.6        withr_3.0.2        tools_4.5.0       
#> [19] parallel_4.5.0     tzdb_0.5.0         pacman_0.5.1      
#> [22] vctrs_0.6.5        R6_2.6.1           lifecycle_1.0.4   
#> [25] htmlwidgets_1.6.4  pkgconfig_2.0.3    pillar_1.10.2     
#> [28] gtable_0.3.6       glue_1.8.0         xfun_0.52         
#> [31] tidyselect_1.2.1   rstudioapi_0.17.1  farver_2.1.2      
#> [34] htmltools_0.5.8.1  nlme_3.1-168       labeling_0.4.3    
#> [37] rmarkdown_2.29     compiler_4.5.0

Bibliografia

Johnson, A. A., Ott, M., & Dogucu, M. (2022). Bayes Rules! An Introduction to Bayesian Modeling with R. CRC Press.

Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK: