51 Controllo predittivo a priori
Introduzione
Nell’analisi bayesiana, la specificazione della distribuzione a priori (prior) rappresenta un passaggio cruciale e delicato. Attraverso la prior, formalizziamo matematicamente le nostre convinzioni o aspettative riguardo ai parametri del modello prima di osservare i dati. Ma come possiamo valutare se la nostra scelta è appropriata?
Uno strumento essenziale per questa verifica è il controllo predittivo a priori (prior predictive check, PPC; Gelman et al. (2020)).
51.0.1 L’idea fondamentale
Il prior predictive check si basa su una domanda chiave:
Se questa distribuzione a priori riflette davvero le nostre aspettative, quali dati dovremmo osservare in pratica?
In altre parole, simuliamo dati plausibili generati dal modello prima di analizzare i dati reali, per verificare se le nostre assunzioni iniziali producono risultati coerenti con la realtà teorica o empirica del fenomeno studiato.
51.0.2 Perché è importante?
Nei modelli bayesiani, le distribuzioni a priori codificano la nostra conoscenza (o ignoranza) preliminare. Tuttavia:
-
prior apparentemente innocue possono, combinate con il modello di verosimiglianza, generare previsioni implausibili (es., valori al di fuori del range possibile, comportamenti estremi non realistici);
- prior troppo informative possono dominare ingiustificatamente l’evidenza dei dati, mentre prior troppo vaghe possono portare a stime instabili.
Il prior predictive check ci permette di esplorare la distribuzione predittiva a priori, \(p(\tilde{y})\), dove \(\tilde{y}\) sono dati simulati, per identificare incongruenze prima della fase inferenziale.
51.1 La definizione formale
Non conoscendo i parametri \(\theta\), non possiamo formulare un’unica predizione \(p(\tilde y \mid \theta)\). Invece, la distribuzione predittiva a priori \(p(\tilde y)\) combina le predizioni di tutti i possibili valori di \(\theta\), pesandoli in base alla loro plausibilità a priori.
È come consultare un gruppo di esperti (i possibili \(\theta\)) e aggregare i loro giudizi, ponderandoli in base a quanto li riteniamo affidabili prima di osservare qualsiasi dato. La formula che descrive questo processo è:
\[ p(\tilde y \mid \text{prior}) = \int p(\tilde y \mid \theta)\, p(\theta)\, d\theta . \tag{51.1}\]
Questo integrale rappresenta una combinazione (mixture) di distribuzioni.1 Non stiamo calcolando una media aritmetica di singoli valori di \(\tilde y\), ma piuttosto mescolando intere distribuzioni condizionate \(p(\tilde y \mid \theta)\), ciascuna ponderata dalla sua probabilità a priori \(p(\theta)\).
51.2 Implementazione e valutazione del PPC
Per verificare l’adeguatezza della distribuzione a priori, seguiamo un approccio sistematico:
Definizione del modello generativo
Si stabilisce la relazione tra parametri e dati attraverso la verosimiglianza \(p(y \mid \theta)\), includendo eventuali funzioni di collegamento (logit, log) necessarie per garantire coerenza con il dominio delle variabili.Specificazione della distribuzione a priori
Le prior dovrebbero riflettere conoscenze preliminari debolmente informative, adattate alla scala naturale del problema. Per parametri con vincoli naturali (es., deviazioni standard positive), si utilizzano distribuzioni a supporto ristretto (half-normal, esponenziale).-
Simulazione della distribuzione predittiva
Per ciascuna iterazione:- si campiona un insieme di parametri \(\theta^{(s)}\) dalla prior \(p(\theta)\),
- si generano dati sintetici \(\tilde{y}^{(s)}\) dalla verosimiglianza \(p(y \mid \theta^{(s)})\).
L’insieme delle simulazioni \(\{\tilde{y}^{(s)}\}_{s=1}^S\) approssima la distribuzione predittiva a priori.
- si campiona un insieme di parametri \(\theta^{(s)}\) dalla prior \(p(\theta)\),
-
Validazione empirica
Le simulazioni vengono confrontate con i vinciti teorici del problema:-
Aderenza al dominio: I valori simulati devono rispettare i limiti naturali della variabile (es., probabilità in [0,1], tempi positivi).
-
Realismo quantitativo: Gli ordini di grandezza devono essere plausibili per il fenomeno studiato.
- Comportamento distributivo: La dispersione e la forma della distribuzione devono essere coerenti con l’aspettativa teorica.
-
Aderenza al dominio: I valori simulati devono rispettare i limiti naturali della variabile (es., probabilità in [0,1], tempi positivi).
51.3 Esempio: un test a 10 domande
Questo esempio mostra bene l’idea di fondo: una prior sui parametri (competenza media e variabilità tra studenti) implica predizioni sui punteggi osservabili. Se la prior assegna troppa probabilità a esiti come 0/10 o 10/10 senza basi empiriche, significa che sta “spingendo” verso scenari estremi.
Immaginiamo uno studente che affronta un test di 10 domande. Il numero di risposte corrette segue una binomiale:
\[ y \sim \text{Binomiale}(n=10, p), \]
dove \(p\) è la probabilità di risposta corretta a una singola domanda. La prior agisce su \(p\), ma ciò che osserviamo sono i punteggi \(y\): il prior predictive check trasferisce l’incertezza su \(p\) alla distribuzione dei punteggi.
51.3.1 Scenario 1: prior debole (alta incertezza)
Se scegliamo una prior molto larga, lasciamo spazio anche a valori estremi di \(p\). Un esempio comune è la prior Beta(2,2):
- media: \(E[p] = 0.5\),
- varianza relativamente ampia,
- equivalente a 4 risposte “immaginarie” (2 corrette e 2 errate).
Questa prior favorisce valori centrali, ma consente anche valori vicini a 0 e 1. La predittiva a priori \(y \mid p \sim \text{Binom}(10,p)\) diventa una Beta–Binomiale, che simula punteggi variabili da 0 a 10.
n <- 10; S <- 10000
p_sim <- rbeta(S, 2, 2)
y_sim <- rbinom(S, size = n, prob = p_sim)
tibble(y_sim) |>
ggplot(aes(x = y_sim)) +
geom_histogram(aes(y = after_stat(density)), bins = 11) +
labs(title = "Predittiva a priori con Beta(2,2)",
x = "Numero di risposte corrette su 10", y = "Densità")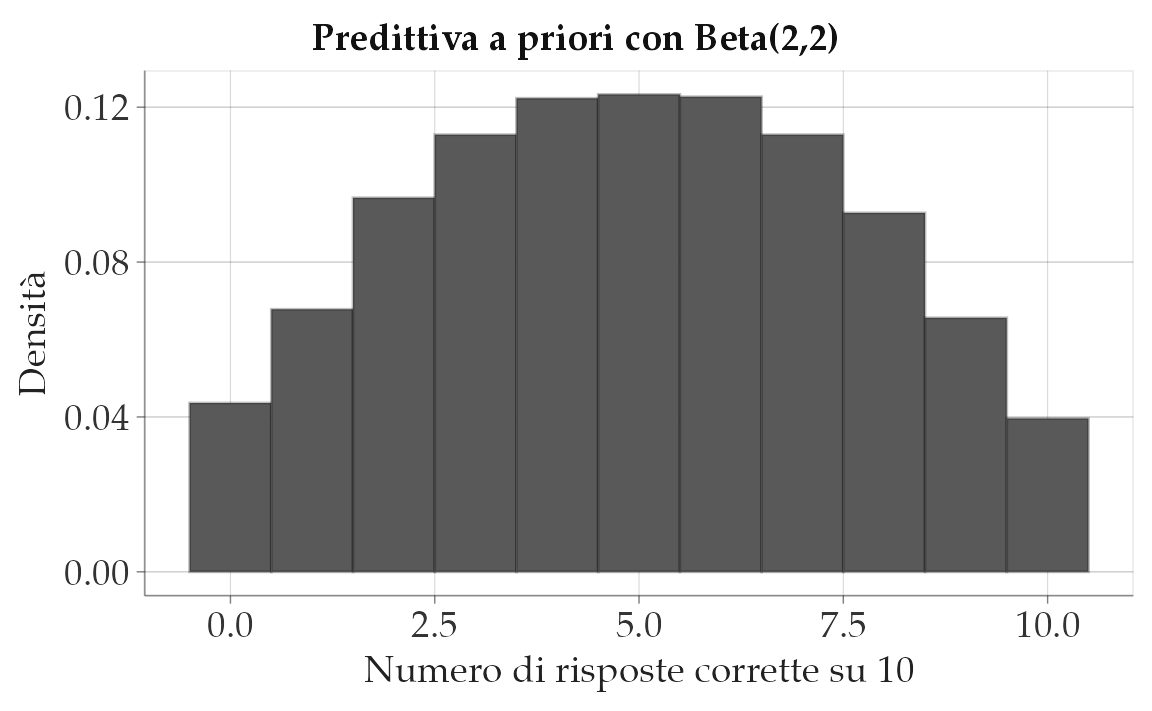
Lettura. Stiamo immaginando studenti molto eterogenei: alcuni quasi sempre corretti, altri quasi sempre sbagliati, altri a metà. Il modello produce punteggi estremi (0 o 10) più spesso di quanto ci aspetteremmo nella realtà: segnale che la prior è troppo permissiva.
51.3.2 Scenario 2: prior informativa (studente preparato)
Supponiamo invece di credere che gli studenti siano mediamente preparati. Una prior plausibile è Beta(10,3):
- media circa 0.77,
- varianza più contenuta,
- equivalente a 13 risposte “immaginarie” (10 corrette e 3 errate).
Questa prior concentra le probabilità su valori alti di \(p\), traducendosi in punteggi tipici tra 6 e 9 risposte corrette.
p_buono <- rbeta(S, 10, 3)
y_buono <- rbinom(S, size = n, prob = p_buono)
tibble(y_buono) |>
ggplot(aes(x = y_buono)) +
geom_histogram(aes(y = after_stat(density)), bins = 11) +
labs(title = "Predittiva a priori con Beta(10,3)",
x = "Numero di risposte corrette su 10", y = "Densità")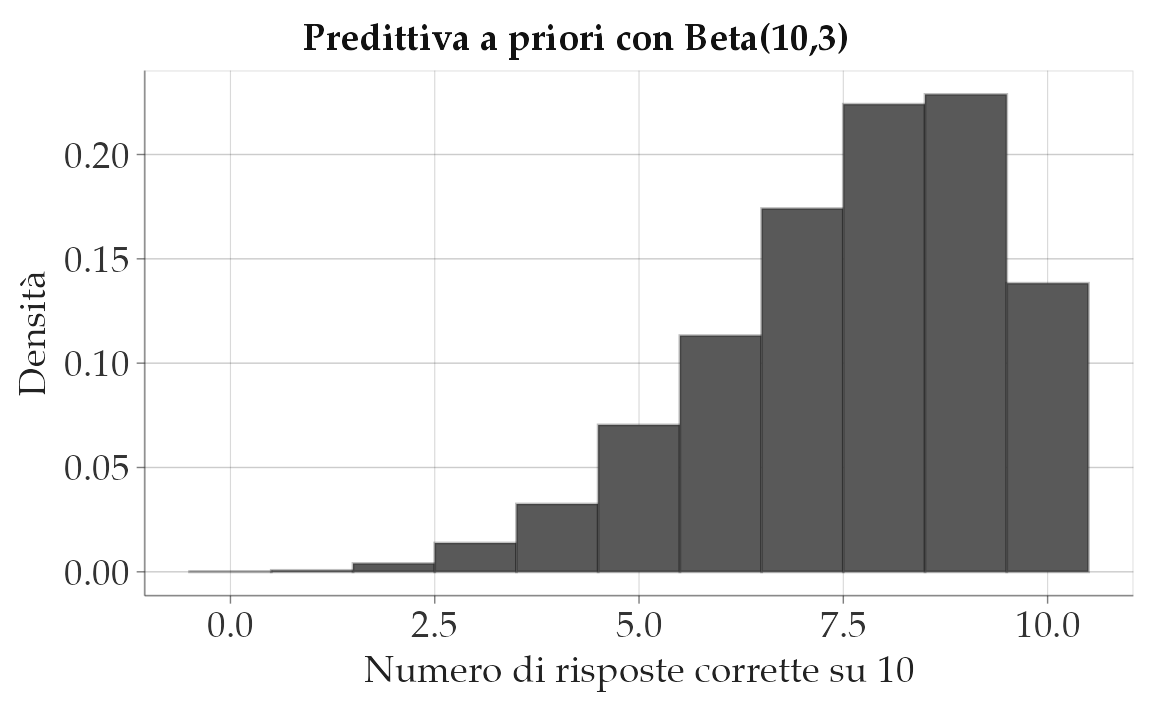
Lettura. I punteggi estremamente bassi (0–3) diventano improbabili, mentre le distribuzioni si concentrano su esiti più realistici per studenti preparati.
51.3.3 Perché è utile?
Il confronto tra scenari evidenzia che la prior non è solo un dettaglio tecnico: traduce in probabilità ciò che riteniamo plausibile sul comportamento degli studenti.
- Se i dati simulati sembrano irrealistici (molti 0/10 inattesi), la prior va corretta.
- Se i dati simulati sono coerenti con le aspettative, la prior è adeguata.
Il PPC diventa così un ponte tra formule e fenomeni concreti: rende trasparente la scelta dei modelli e permette di diagnosticare eventuali incoerenze prima di analizzare i dati reali.
51.4 PPC con brms
Finora abbiamo simulato con le funzioni di base in R. Con brms possiamo ottenere lo stesso effetto in modo più diretto, semplicemente specificando l’opzione sample_prior = "only". Così non usiamo alcun dato reale: generiamo punteggi solo dalla prior.
n_students <- 50
n_items <- 10
dummy_data <- tibble(
correct = 0L, # segnaposto: serve per la sintassi
n_trials = n_items
) |> slice(rep(1, n_students))
priors <- c(
prior(normal(0, 1.5), class = "Intercept") # prior su logit(p)
)
fit_prior_only <- brm(
bf(correct | trials(n_trials) ~ 1),
data = dummy_data,
family = binomial(),
prior = priors,
sample_prior = "only", # <-- prior predictive
chains = 4, iter = 1000, cores = 4,
backend = "cmdstanr", seed = 123
)yrep <- posterior_predict(fit_prior_only)
ppc_bars(y = rep(0, n_students), yrep = yrep[1:200, ]) +
ggtitle("Prior predictive check (binomiale, intercetta-logit)")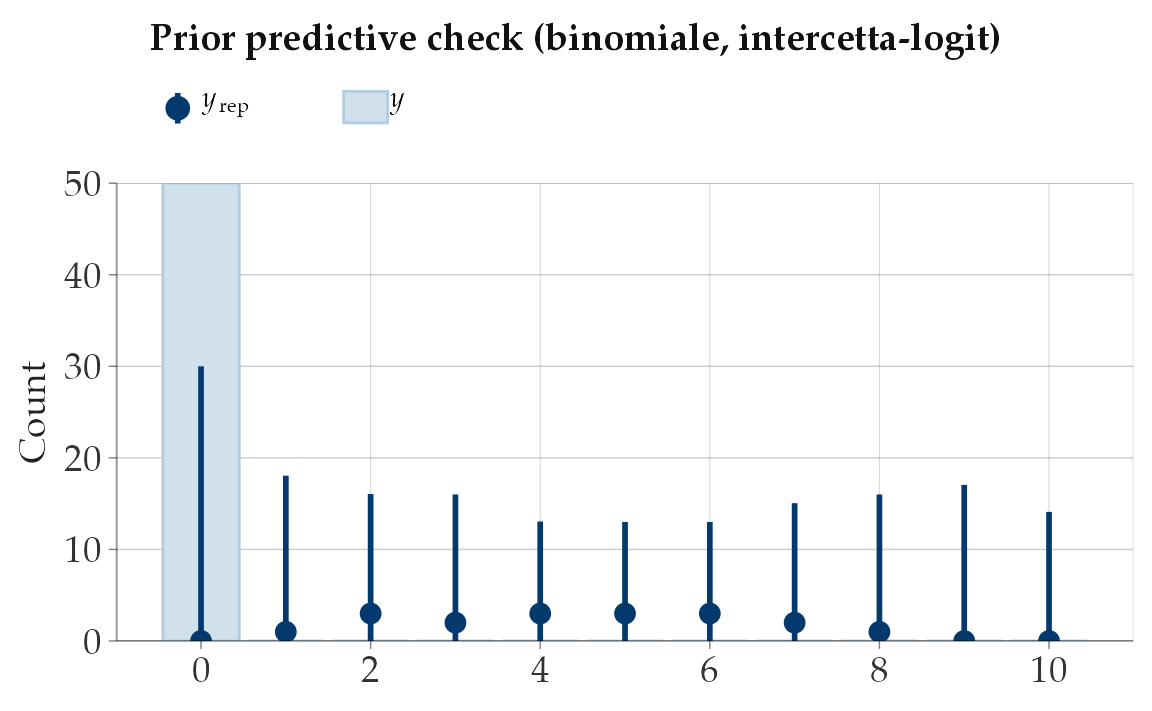
Interpretazione.
- La prior Normal(0,1.5) è posta sull’intercetta in scala logit.
- In pratica significa che la probabilità di risposta corretta \(p\) cade di solito tra ~0.05 e ~0.95: quindi escludiamo valori estremi (0 o 1) sistematici, ma restiamo aperti a una gamma ampia.
- Il grafico mostra quali distribuzioni di punteggi (0–10 su 10) consideriamo plausibili prima di vedere i dati.
51.5 PPC con Stan
Con Stan possiamo fare lo stesso, ma in modo ancora più esplicito: specifichiamo solo la prior, senza likelihood, e simuliamo i dati fittizi nel blocco generated quantities. Questo serve a capire cosa accade sotto il cofano.
binom_prior_ppc_stan <- '
data {
int<lower=1> N; // numero di studenti fittizi
int<lower=1> n_items; // numero di item per studente
}
parameters {
real alpha; // intercetta in logit
}
model {
alpha ~ normal(0, 1.5); // prior weakly-informative
// Nessuna likelihood: solo prior
}
generated quantities {
vector[N] p; // probabilità individuali
array[N] int y_rep; // punteggi simulati
for (i in 1:N) {
p[i] = inv_logit(alpha); // da logit a probabilità
y_rep[i] = binomial_rng(n_items, p[i]);
}
}
'
writeLines(binom_prior_ppc_stan, "binom_prior_ppc.stan")Compiliamo e lanciamo:
mod_binom <- cmdstan_model("binom_prior_ppc.stan")
fit_binom <- mod_binom$sample(
data = list(N = 100, n_items = 10),
chains = 4, iter_warmup = 500, iter_sampling = 1000,
seed = 123, refresh = 0
)Estraiamo i punteggi simulati e guardiamo la distribuzione della media:
draws <- fit_binom$draws(variables = "y_rep", format = "draws_matrix")
y_rep <- as_draws_matrix(draws)
tibble(mu = rowMeans(y_rep)) |>
ggplot(aes(x = mu)) +
geom_histogram(bins = 30) +
labs(title = "Predittiva a priori (Stan, binomiale, intercetta-logit)",
x = "Media risposte corrette su 10", y = "Frequenza")
51.5.1 Lettura
- Ogni iterazione estrae un valore di \(\alpha\) dalla prior Normal(0,1.5).
- Lo trasformiamo in probabilità di successo con \(p = \text{inv\_logit}(\alpha)\).
- Con quel \(p\) simuliamo 10 risposte per 100 studenti fittizi.
- Il grafico mostra la distribuzione della media dei punteggi simulati.
Così vediamo chiaramente quali punteggi il modello considera plausibili solo sulla base della prior. Se avessimo scelto una prior più stretta (es. Normal(2,0.5) sul logit), i punteggi si sarebbero concentrati verso l’alto (più risposte corrette attese).
51.6 Esempi di modelli più complessi
In precedenza ci siamo occupati di modelli semplici, una singola proporzione. Vediamo ora esempi di modelli più complessi. L’obiettivo è mostrare come diverse prior sui parametri si traducano in implicazioni sui dati. Usiamo tre casi:
- Modello gaussiano (intercetta e varianza);
- Regressione lineare (scala dei coefficienti e della varianza);
- Regressione logistica (scala dei coefficienti su logit e probabilità implicite).
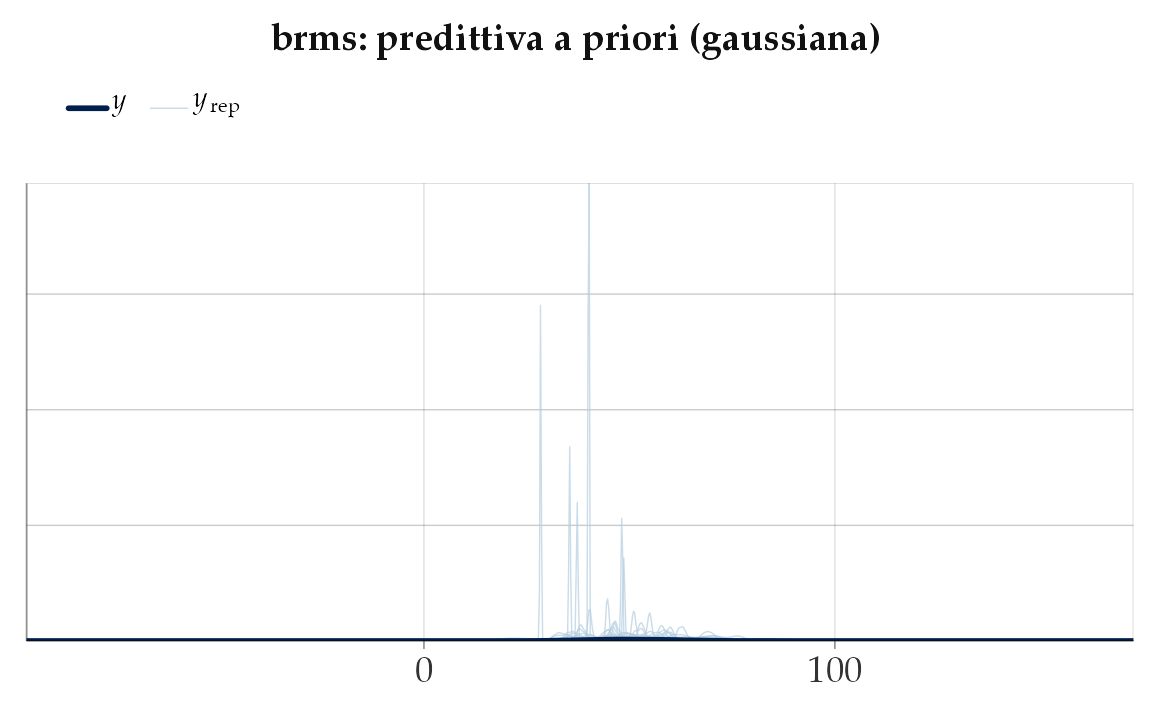
51.6.1 Modello gaussiano semplice
Ipotizziamo che il meccanismo generatore dei dati sia: \(y \sim \mathcal{N}(\mu, \sigma)\).
Domanda: scelte di prior su \(\mu\) e \(\sigma\) producono esiti \(y\) plausibili per la tua variabile psicologica (es. punteggi 0–100)?
S <- 10000
# Scenario A: prior molto larga
mu_A <- rnorm(S, 50, 50) # media plausibile ma molto incerta
sigma_A <- rexp(S, rate = 1/20) # sigma ~ Exp(mean=20), molto larga
yA <- rnorm(S, mu_A, sigma_A)
# Scenario B: prior più informativa
mu_B <- rnorm(S, 50, 10)
sigma_B <- rexp(S, rate = 1/10) # mean=10
yB <- rnorm(S, mu_B, sigma_B)
bind_rows(
tibble(y = yA, scenario = "A: prior larghissima"),
tibble(y = yB, scenario = "B: prior informativa")
) |>
ggplot(aes(x = y, fill = scenario)) +
geom_density(alpha = 0.35) +
labs(title = "Predittiva a priori (gaussiana)",
x = "y (es. punteggio 0–100)", y = "Densità")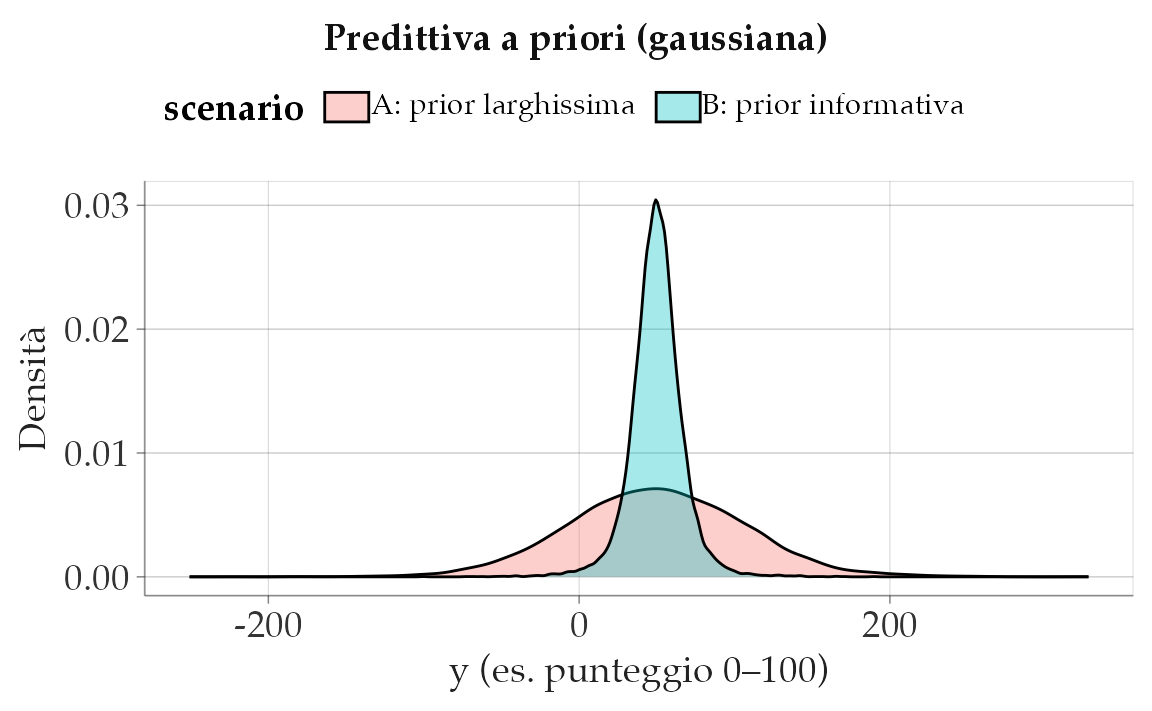
Lettura. Se i punteggi sono noti per essere tra 0 e 100, lo Scenario A potrebbe generare troppi valori negativi o >100: prior da ritarare (più informativa su \(\mu\) e/o \(\sigma\)).
51.6.1.1 Versione Stan: prior-only, generazione in generated quantities
gauss_prior_ppc_stan <- '
data {
int<lower=1> N;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(50, 10);
sigma ~ exponential(1.0/10); // mean 10
}
generated quantities {
vector[N] y_rep;
for (i in 1:N) {
y_rep[i] = normal_rng(mu, sigma);
}
}
'
writeLines(gauss_prior_ppc_stan, "gauss_prior_ppc.stan")mod_gauss <- cmdstan_model("gauss_prior_ppc.stan")fit_gauss <- mod_gauss$sample(
data = list(N = 200),
chains = 4, iter_warmup = 500, iter_sampling = 1000, seed = 123,
refresh = 0
)yrep_g <- fit_gauss$draws("y_rep", format = "draws_matrix")
as_tibble(yrep_g) |>
pivot_longer(everything(), values_to = "y") |>
ggplot(aes(x = y)) +
geom_density() +
labs(title = "Stan: predittiva a priori (gaussiana)", x = "y", y = "Densità")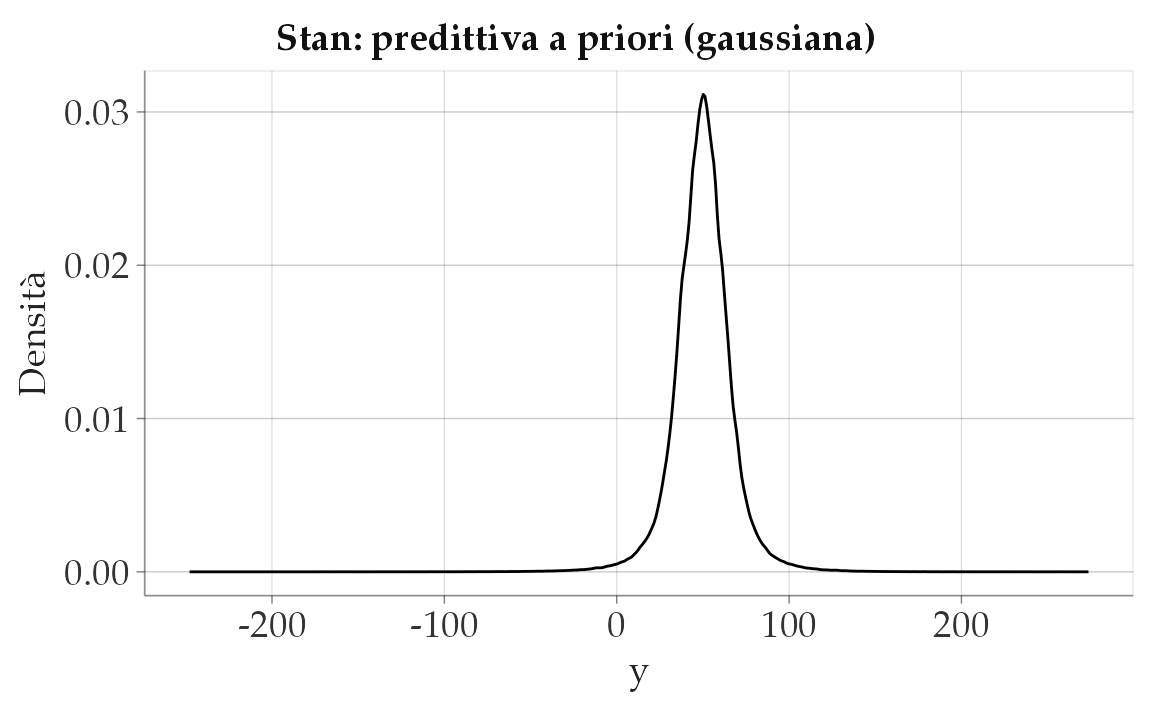
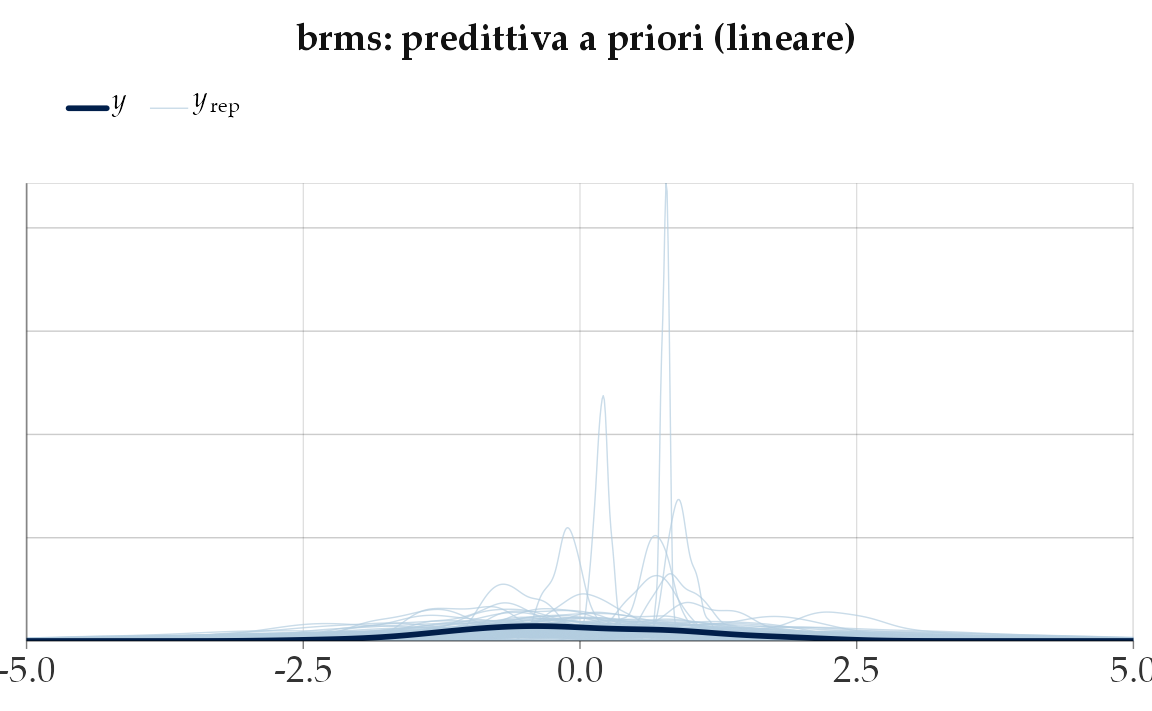
51.6.2 Regressione lineare
Consideriamo il modello generatore:
\[ y = \alpha + \beta x + \varepsilon, \qquad \varepsilon \sim \mathcal{N}(0,\sigma). \]
51.6.2.1 Perché è interessante
In regressione, il significato di \(\beta\) dipende dalla scala di \(x\):
- se \(x\) è standardizzato (media 0, deviazione standard 1), allora \(\beta\) indica la variazione media di \(y\) per 1 deviazione standard di \(x\).
- ad esempio, una prior \(\beta \sim \mathcal{N}(0,1)\) equivale a dire: “effetti moderati sono plausibili; effetti oltre 3 deviazioni standard sono rari”.
I prior predictive checks ci aiutano a rispondere a due domande:
- Le rette simulate generano valori di \(y\) compatibili con la scala del fenomeno?
- La dispersione intorno alla retta (determinata da \(\sigma\)) è realistica?
Se la risposta è “no”, occorre rivedere la prior su \(\alpha,\beta,\sigma\) o trasformare \(y\).
51.6.2.2 Scenario C: prior troppo larga
Qui imponiamo varianze enormi su \(\alpha\) e \(\beta\). Risultato: i valori simulati di \(y\) diventano irrealistici (troppo negativi o troppo alti rispetto alla scala dei dati).
Lettura. Una prior enorme su \(\sigma\) e su \(\beta\) rende molto probabili valori assurdi per \(y\). Non è “essere umili”: è incoerente con il dominio empirico.
51.6.2.3 Scenario D: prior weakly-informative
Qui scegliamo prior centrate e con varianze moderate.
- \(\alpha \sim \mathcal{N}(0,1)\) e \(\beta \sim \mathcal{N}(0,1)\): effetti possibili, ma non sproporzionati.
- \(\sigma \sim \text{Exp}(1/2)\): media 2, compatibile con la variabilità tipica di punteggi psicologici standardizzati.
alpha_D <- rnorm(S, 0, 1)
beta_D <- rnorm(S, 0, 1)
sigma_D <- rexp(S, rate = 1/2) # media ~2
yD <- rnorm(S, alpha_D + beta_D * x, sigma_D)
bind_rows(
tibble(y = yC, scenario = "C: prior molto larga"),
tibble(y = yD, scenario = "D: prior W.I.")
) |>
ggplot(aes(x = y, fill = scenario)) +
geom_density(alpha = 0.35) +
labs(title = "Predittiva a priori (regressione lineare)",
x = "Valori simulati di y", y = "Densità")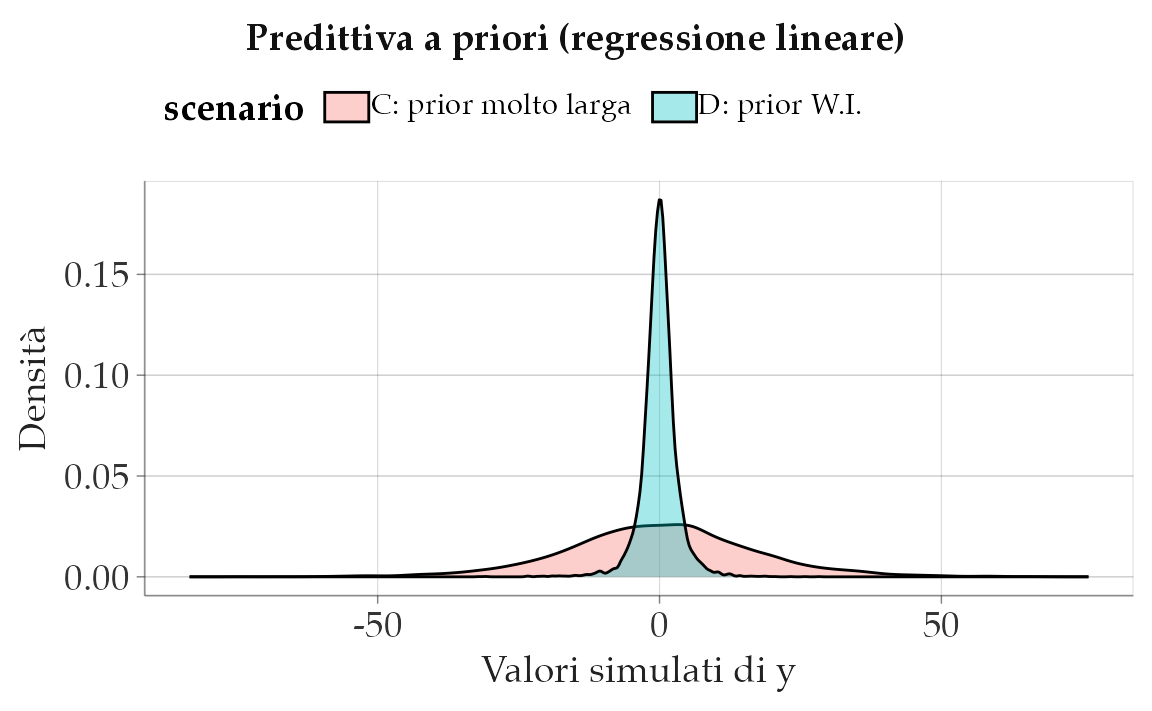
Lettura. Con prior weakly-informative, la distribuzione di \(y\) resta ampia ma plausibile. Con prior larghe, invece, \(y\) è disperso in modo irrealistico.
51.6.2.4 Versione in Stan: prior-only
Per rendere più esplicito il concetto, scriviamo un modello Stan in cui non inseriamo dati osservati: simuliamo soltanto dalla prior.
linear_prior_ppc_stan <- '
data {
int<lower=1> N;
vector[N] x;
}
parameters {
real alpha;
real beta;
real<lower=0> sigma;
}
model {
alpha ~ normal(0, 1);
beta ~ normal(0, 1);
sigma ~ exponential(1.0/2); // media 2
}
generated quantities {
vector[N] y_rep;
for (i in 1:N) {
y_rep[i] = normal_rng(alpha + beta * x[i], sigma);
}
}
'
writeLines(linear_prior_ppc_stan, "linear_prior_ppc.stan")Eseguiamo la simulazione:
mod_lin <- cmdstan_model("linear_prior_ppc.stan")
x_new <- runif(200, -2, 2)
fit_lin <- mod_lin$sample(
data = list(N = length(x_new), x = x_new),
chains = 4, iter_warmup = 500, iter_sampling = 1000, seed = 123,
refresh = 0
)Visualizziamo la distribuzione di \(y\):
yrep_l <- fit_lin$draws("y_rep", format = "draws_matrix")
as_tibble(yrep_l) |>
pivot_longer(everything(), values_to = "y") |>
ggplot(aes(x = y)) +
geom_density() +
labs(title = "Stan: predittiva a priori (regressione lineare)",
x = "Valori simulati di y", y = "Densità")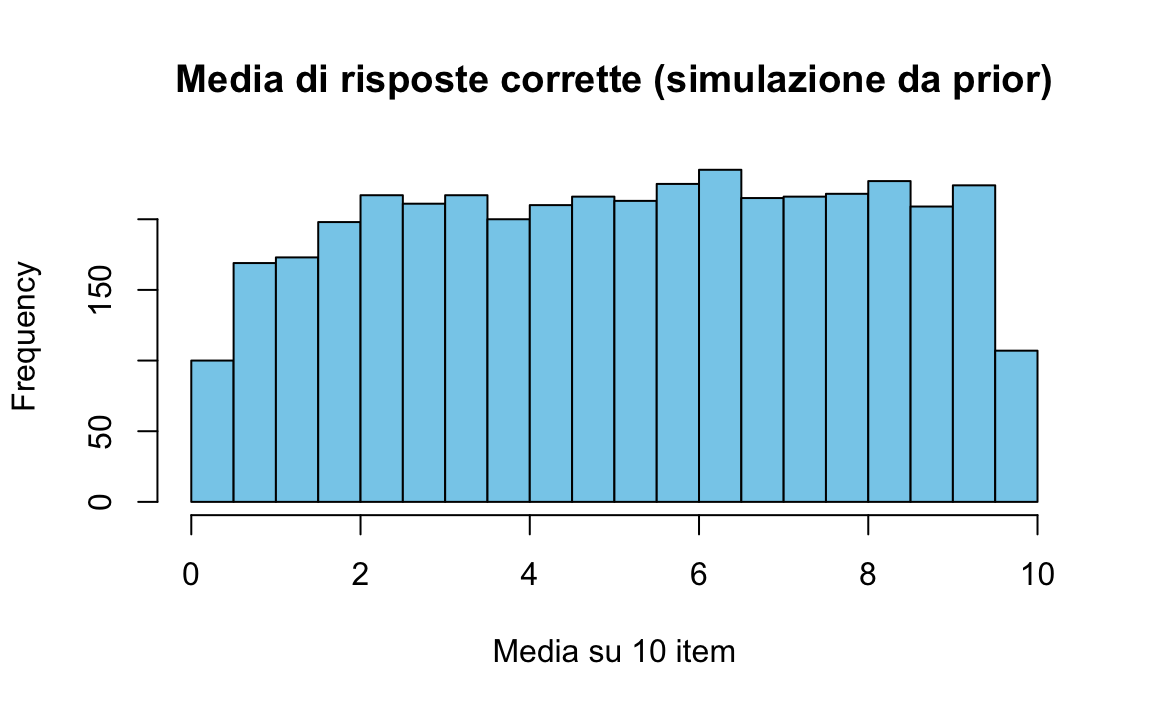
51.6.2.5 Cosa impariamo
- La scala delle prior su \(\alpha,\beta,\sigma\) determina la scala dei dati simulati.
- Se i valori di \(y\) simulati sono fuori dal dominio realistico (es. punteggi < 0 o > 100), i prior vanno rivisti.
- Con prior weakly-informative (centrati, varianza moderata), le simulazioni diventano coerenti col contesto psicologico.
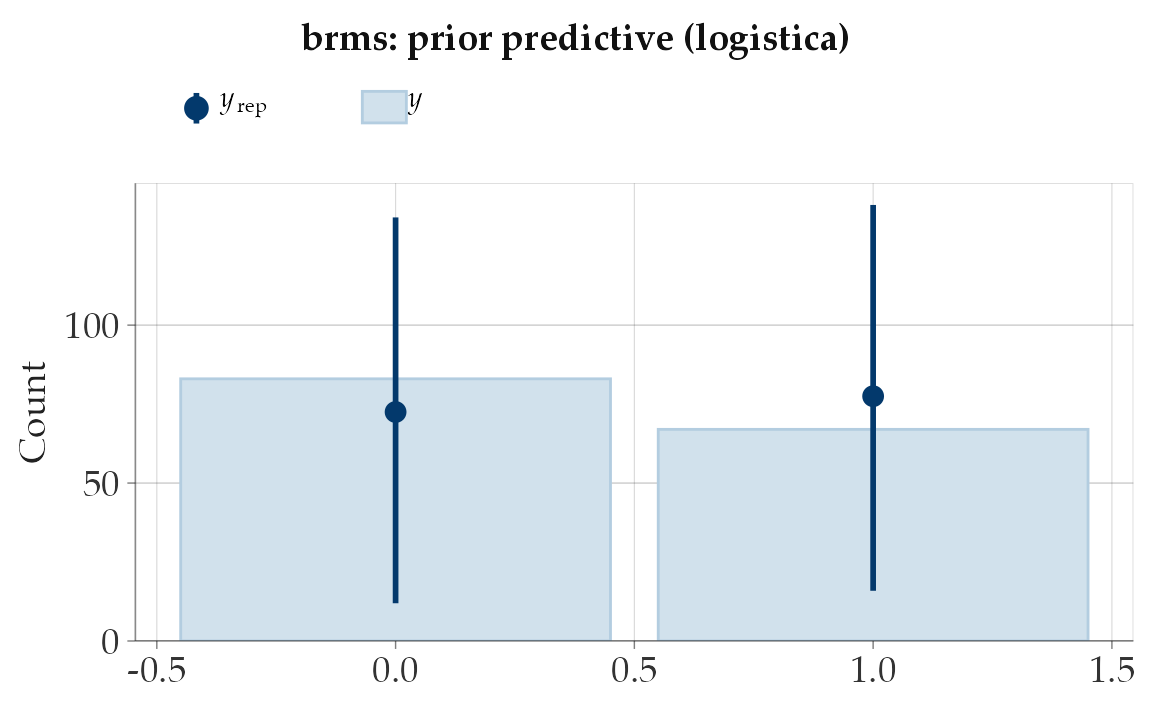
51.6.3 Regressione logistica
Nella regressione logistica, il modello per un esito binario è:
\[ \text{logit}\, P(y=1 \mid x) = \alpha + \beta x . \]
Qui \(\alpha\) e \(\beta\) vivono sulla scala logit, non direttamente sulle probabilità. Ricorda che il logit è molto “ripido”: differenze di 2–3 unità sul logit si traducono in variazioni enormi di probabilità (da ~0.1 a ~0.9).
51.6.3.1 Perché è importante
- Con predittori standardizzati (media 0, varianza 1), una prior \(\beta \sim \mathcal{N}(0,1)\) implica che effetti moderati sono plausibili, mentre probabilità quasi certe (0 o 1) rimangono rare.
- Una prior \(\beta \sim \mathcal{N}(0,2.5)\), invece, consente valori di logit fino a ±5, che corrispondono a probabilità estremamente vicine a 0 o 1: rischiamo quindi di “dare per certe” decisioni prima ancora di vedere i dati.
Il PPC serve proprio a verificare se le probabilità implicite dalle prior sono coerenti con ciò che ci aspettiamo nel nostro dominio applicativo.
51.6.3.2 Simulazioni in R
S <- 10000
x <- rnorm(S, 0, 1) # standardizzare è buona pratica
# Scenario E: prior larga
alpha_E <- rnorm(S, 0, 2.5)
beta_E <- rnorm(S, 0, 2.5)
pE <- plogis(alpha_E + beta_E * x)
yE <- rbinom(S, 1, pE)
# Scenario F: prior weakly-informative
alpha_F <- rnorm(S, 0, 1)
beta_F <- rnorm(S, 0, 1)
pF <- plogis(alpha_F + beta_F * x)
yF <- rbinom(S, 1, pF)
tibble(p = pE, scenario = "E: prior larga") |>
bind_rows(tibble(p = pF, scenario = "F: prior W.I.")) |>
ggplot(aes(x = p, fill = scenario)) +
geom_density(alpha = 0.35) +
labs(title = "Probabilità implicite dalla prior (logistica)",
x = "p(x) = P(y=1|x)", y = "Densità")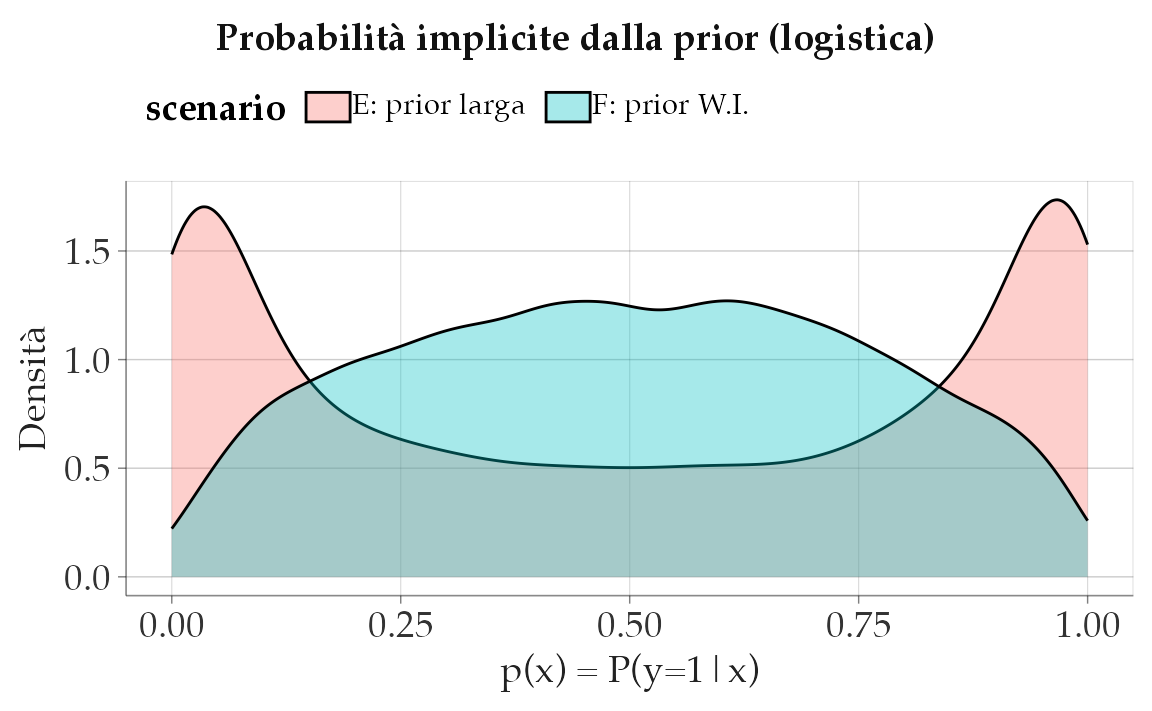
Lettura.
- Con la prior larga (Scenario E), le probabilità implicite sono spesso vicine a 0 o 1: significa che il modello, prima dei dati, crede frequenti le situazioni di “certezza assoluta”.
- Con la prior più stretta (Scenario F), le probabilità restano distribuite in una gamma più plausibile (0.05–0.95), che riflette meglio l’incertezza tipica in psicologia.
51.6.3.3 Regola pratica
- Con predittori standardizzati, usare \(\mathcal{N}(0,1)\) o \(\mathcal{N}(0,1.5)\) per i coefficienti logit è spesso una scelta sicura: consente abbastanza variabilità senza produrre predizioni estreme.
- Prior troppo larghe possono generare modelli “rigidi” che, prima dei dati, assumono già risposte quasi deterministiche.
51.6.3.4 Versione Stan: prior-only
Possiamo rendere tutto più esplicito con un modello Stan che non usa dati osservati e genera solo predizioni dalla prior.
logistic_prior_ppc_stan <- '
data {
int<lower=1> N;
vector[N] x;
}
parameters {
real alpha;
real beta;
}
model {
alpha ~ normal(0, 1);
beta ~ normal(0, 1);
}
generated quantities {
vector[N] p;
array[N] int y_rep;
for (i in 1:N) {
p[i] = inv_logit(alpha + beta * x[i]);
y_rep[i] = bernoulli_rng(p[i]);
}
}
'
writeLines(logistic_prior_ppc_stan, "logistic_prior_ppc.stan")Eseguiamo il modello:
mod_log <- cmdstan_model("logistic_prior_ppc.stan")
x_new <- rnorm(300)
fit_log <- mod_log$sample(
data = list(N = length(x_new), x = x_new),
chains = 4, iter_warmup = 500, iter_sampling = 1000,
seed = 123, refresh = 0
)Visualizziamo le probabilità implicite:
post_p <- fit_log$draws("p", format = "draws_matrix")
as_tibble(post_p) |>
pivot_longer(everything(), values_to = "p") |>
ggplot(aes(x = p)) +
geom_density() +
labs(title = "Stan: probabilità implicite dalla prior (logistica)",
x = "p(x)", y = "Densità")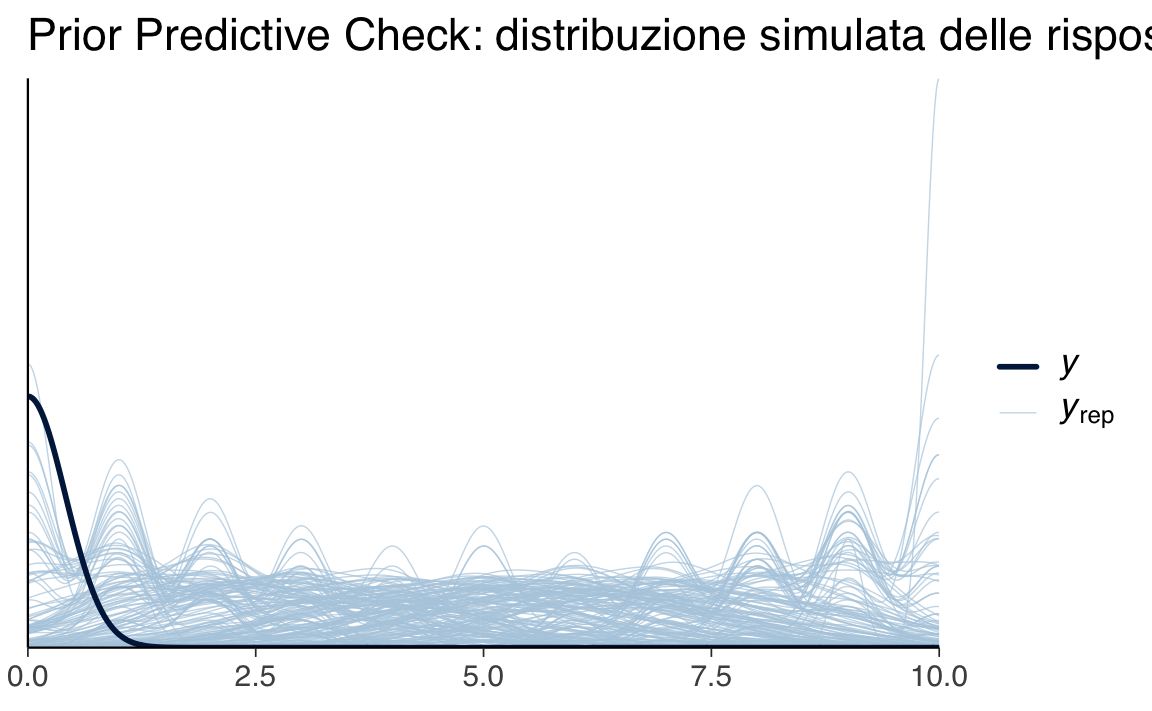
51.6.3.5 Cosa impariamo
- Le prior in regressione logistica hanno un impatto diretto sulle probabilità implicite.
- Una prior troppo larga equivale a dire che, prima dei dati, consideriamo probabile avere quasi sempre risposte certe (0 o 1).
- Una prior moderata mantiene invece l’incertezza, riflettendo meglio la realtà psicologica.
51.7 Consigli pratici per specificare le prior
-
Lavora sempre sulla scala giusta
- Se possibile, standardizza i predittori (media 0, deviazione standard 1).
- Così i coefficienti hanno un significato uniforme: una Normal(0,1) indica effetti “moderati” (spostamenti di circa 1 dev. std nell’esito per 1 dev. std nel predittore).
-
Coefficienti di regressione (\(\beta\))
- Un buon punto di partenza sono prior Normal(0, 0.5–2).
- Con \(\beta \sim \mathcal{N}(0,1)\): effetti piccoli/moderati sono plausibili, effetti enormi restano possibili ma meno probabili.
- Attenzione: se non standardizzi \(x\), la scala di \(\beta\) cambia e queste regole non valgono più.
-
Intercetta (\(\alpha\))
- Con outcome gaussiano, centra \(y\) per rendere \(\alpha\) interpretabile.
- Con outcome binario (link logit), una Normal(0,1–1.5) implica probabilità tipiche tra 0.05 e 0.95; una Normal(0,2.5) è molto più permissiva (quasi-certezze frequenti).
-
Varianze o scale (\(\sigma\))
- Usa prior sempre positive (HalfNormal, Exponential).
- Scegli la media dell’Exponential nell’ordine di grandezza plausibile per il dominio: ad esempio, per punteggi 0–100 una prior Exponential(mean ≈ 5–10) è ragionevole.
- Verifica sempre con simulazioni che la dispersione generata sia coerente.
-
Link non lineari (logit, log)
- Non pensare solo in termini di coefficienti logit o log: traduci sempre in probabilità implicite (per logit) o in rate attese (per log).
- Chiediti: “Queste prior implicano che i soggetti abbiano davvero probabilità quasi 0 o 1 di successo?”
-
Diagnosi e trasparenza
- Fai sempre prior predictive checks: se i dati simulati sono “assurdi” (es. punteggi negativi o fuori scala), la prior è mal calibrata.
- Documenta cosa hai provato, cosa hai cambiato e perché: fa parte del rigore dell’analisi bayesiana.
brms per i tre casi
Modello gaussiano.
N <- 100
df_g <- tibble(y = rnorm(N, 50, 10)) # placeholder, non usato con "only"
fit_g_prior <- brm(
bf(y ~ 1),
data = df_g,
family = gaussian(),
prior = c(
prior(normal(50, 10), class = "Intercept"),
prior(exponential(0.1), class = "sigma")
# prior(exponential(1.0/10), class = "sigma")
),
sample_prior = "only",
chains = 4, iter = 1000, cores = 4,
backend = "cmdstanr", seed = 123
)yrep_g <- posterior_predict(fit_g_prior)
ppc_dens_overlay(y = df_g$y, yrep = yrep_g[1:200, ]) +
ggtitle("brms: predittiva a priori (gaussiana)")
Regressione lineare.
fit_l_prior <- brm(
bf(y ~ 1 + x),
data = df_l,
family = gaussian(),
prior = c(
prior(normal(0, 1), class = "Intercept"),
prior(normal(0, 1), class = "b", coef = "x"),
prior(exponential(0.5), class = "sigma") # <-- 0.5 (oppure 1.0/2)
# prior(exponential(1.0/2), class = "sigma") # <-- equivalente
),
sample_prior = "only",
chains = 4, iter = 1000, cores = 4,
backend = "cmdstanr", seed = 123
)yrep_l <- posterior_predict(fit_l_prior)
ppc_dens_overlay(y = df_l$y, yrep = yrep_l[1:200, ]) +
ggtitle("brms: predittiva a priori (lineare)") +
xlim(-5, 5)
Regressione logistica.
yrep_log <- posterior_predict(fit_log_prior)
ppc_bars(y = df_log$y, yrep = yrep_log[1:200, ]) +
ggtitle("brms: prior predictive (logistica)")
Riflessioni conclusive
Il controllo predittivo a priori rappresenta un momento fondamentale nell’analisi bayesiana, dove la struttura matematica del modello incontra la conoscenza sostantiva del fenomeno studiato. Questo processo va ben oltre una mera verifica tecnica, configurandosi come un vero e proprio esercizio epistemologico che valuta la coerenza tra le nostre aspettative teoriche e le implicazioni quantitative del modello.
Nella pratica di ricerca, è opportuno documentare con chiarezza:
- la procedura di simulazione dei dati a partire dalle distribuzioni a priori,
- le eventuali incongruenze riscontrate tra i dati simulati e le aspettative teoriche,
- le modifiche apportate alle distribuzioni a priori in risposta a tali incongruenze,
- i risultati finali ottenuti dopo la ricalibrazione del modello.
Questa documentazione non costituisce un appesantimento metodologico, ma piuttosto un elemento chiave per garantire trasparenza e riproducibilità. Prendiamo ad esempio il caso di un test psicometrico con 10 domande: l’adozione di una distribuzione Beta(2,2) riflette una sostanziale incertezza a priori, producendo simulazioni con ampia variabilità di punteggi, mentre una Beta(10,2) esprime la convinzione che i rispondenti siano generalmente preparati, concentrando le previsioni su punteggi elevati.
In ambito psicologico, dove i costrutti teorici spesso presentano confini sfumati, questo approccio assume particolare rilevanza. A differenza delle metodologie che iniziano l’analisi solo dopo la raccolta dei dati, il framework bayesiano promuove una riflessione anticipata sulle ipotesi modellistiche e sulle loro conseguenze predittive.
Il controllo predittivo a priori si configura dunque come un potente strumento diagnostico:
- segnala discrepanze tra le assunzioni del modello e la realtà empirica,
- guida la riparametrizzazione delle distribuzioni a priori,
- rafforza la validità ecologica delle analisi successive.
Rendendo esplicite le implicazioni delle nostre scelte modellistiche, questa pratica favorisce lo sviluppo di analisi più consapevoli e robuste. In ultima analisi, il controllo predittivo a priori non costituisce un semplice passaggio tecnico, ma un momento essenziale per costruire modelli che riflettano autenticamente la complessità dei fenomeni psicologici che intendiamo studiare.
Informazioni sull’ambiente di sviluppo
sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Zagreb
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] cmdstanr_0.9.0 pillar_1.11.0 tinytable_0.11.0
#> [4] patchwork_1.3.1 ggdist_3.3.3 tidybayes_3.0.7
#> [7] bayesplot_1.13.0 ggplot2_3.5.2 reliabilitydiag_0.2.1
#> [10] priorsense_1.1.0 posterior_1.6.1 loo_2.8.0
#> [13] rstan_2.32.7 StanHeaders_2.32.10 brms_2.22.0
#> [16] Rcpp_1.1.0 sessioninfo_1.2.3 conflicted_1.2.0
#> [19] janitor_2.2.1 matrixStats_1.5.0 modelr_0.1.11
#> [22] tibble_3.3.0 dplyr_1.1.4 tidyr_1.3.1
#> [25] rio_1.2.3 here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] gridExtra_2.3 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.3 multcomp_1.4-28
#> [7] snakecase_0.11.1 compiler_4.5.1 reshape2_1.4.4
#> [10] systemfonts_1.2.3 vctrs_0.6.5 stringr_1.5.1
#> [13] pkgconfig_2.0.3 arrayhelpers_1.1-0 fastmap_1.2.0
#> [16] backports_1.5.0 labeling_0.4.3 rmarkdown_2.29
#> [19] ps_1.9.1 ragg_1.4.0 purrr_1.1.0
#> [22] xfun_0.52 cachem_1.1.0 jsonlite_2.0.0
#> [25] broom_1.0.9 parallel_4.5.1 R6_2.6.1
#> [28] stringi_1.8.7 RColorBrewer_1.1-3 lubridate_1.9.4
#> [31] estimability_1.5.1 knitr_1.50 zoo_1.8-14
#> [34] Matrix_1.7-3 splines_4.5.1 timechange_0.3.0
#> [37] tidyselect_1.2.1 abind_1.4-8 yaml_2.3.10
#> [40] codetools_0.2-20 curl_6.4.0 processx_3.8.6
#> [43] pkgbuild_1.4.8 plyr_1.8.9 lattice_0.22-7
#> [46] withr_3.0.2 bridgesampling_1.1-2 coda_0.19-4.1
#> [49] evaluate_1.0.4 survival_3.8-3 RcppParallel_5.1.10
#> [52] tensorA_0.36.2.1 checkmate_2.3.2 stats4_4.5.1
#> [55] distributional_0.5.0 generics_0.1.4 rprojroot_2.1.0
#> [58] rstantools_2.4.0 scales_1.4.0 xtable_1.8-4
#> [61] glue_1.8.0 emmeans_1.11.2 tools_4.5.1
#> [64] data.table_1.17.8 mvtnorm_1.3-3 grid_4.5.1
#> [67] QuickJSR_1.8.0 colorspace_2.1-1 nlme_3.1-168
#> [70] cli_3.6.5 textshaping_1.0.1 svUnit_1.0.6
#> [73] Brobdingnag_1.2-9 V8_6.0.5 gtable_0.3.6
#> [76] digest_0.6.37 TH.data_1.1-3 htmlwidgets_1.6.4
#> [79] farver_2.1.2 memoise_2.0.1 htmltools_0.5.8.1
#> [82] lifecycle_1.0.4 MASS_7.3-65Bibliografia
Immagina di voler sapere che gusto avrà un succo se mescoli vari ingredienti. Non fai la media del gusto di singoli bicchieri, ma prendi un po’ di ogni succo (distribuzione) e li mescoli: il risultato è una nuova bevanda (la distribuzione predittiva a priori).↩︎